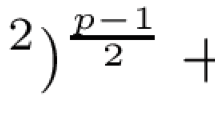Regularity results for solutions to elliptic obstacle problems in limit cases

Abstract

We prove the Lewy–Stampacchia’s inequality for elliptic variational inequalities with obstacle involving Leray–Lions type operator whose simpler model case is given by the following

$$\begin{aligned} u \in W^{1,N}_0(\Omega )\mapsto -\Delta _N u-\text {div}\left( B (x) |u|^{N-2}u \right) \end{aligned}$$

where $\Omega$ is a smooth bounded domain of $\mathbb {R}^N$ with $N\geqslant 2$, $\Delta _N u$ denotes the classical N–Laplacian operator and the coefficient $B:\Omega \rightarrow \mathbb {R}^N$ belongs to a suitable Lorentz–Zygmund space. For this kind of obstacle problems, we also provide regularity results and amongst them we give sufficient conditions to get boundedness of solutions.

1 Introduction

We let $\Omega$ be a Lipschitz bounded domain of ${{\,\mathrm{\mathbb {R}}\,}}^N$ with $N\geqslant 2$. In the present paper, we consider some obstacle problem involving a Leray–Lions operator of the type

$$\begin{aligned} {{\,\mathrm{\mathcal {A}}\,}}u:=-\text {div}A(x,u,\nabla u), \end{aligned}$$

(1)

where $A:\Omega \times {{\,\mathrm{\mathbb {R}}\,}}\times {{\,\mathrm{\mathbb {R}}\,}}^N\rightarrow {{\,\mathrm{\mathbb {R}}\,}}^N$ is a Carathéodory vector field satisfying the following assumptions

$$\begin{aligned} \begin{aligned}&\text {for some }\alpha >0\text { and some nonnegative functions }a\in L^{N,\infty }\log ^{}L (\Omega ), \phi \in L^N(\Omega )\text { we have} \\&A(x,u,\xi )\cdot \xi \geqslant \alpha |\xi |^N-\left( a(x)|u|\right) ^N-\phi ^N(x)\quad \text {for a.e. } x\in \Omega \; \text {and for all} \, (u,\xi )\in {{\,\mathrm{\mathbb {R}}\,}}\times {{\,\mathrm{\mathbb {R}}\,}}^N; \end{aligned}\nonumber \\ \end{aligned}$$

(2)

$$\begin{aligned} \begin{aligned}&\text {for some }\beta >\alpha \text { and some nonnegative function }b\in L^{N,\infty }\log ^{}L (\Omega )\,\, \text {we have}\\&|A(x,u,\xi )|\leqslant \beta |\xi |^{N-1}+\left( b(x)|u|\right) ^{N-1}+\phi ^{N-1}(x)\quad \text {for a.e. }x\in \Omega , ~ \text {and for all } \, (u,\xi )\in {{\,\mathrm{\mathbb {R}}\,}}\times {{\,\mathrm{\mathbb {R}}\,}}^N; \end{aligned}\nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned} \begin{aligned} \left( A(x,u,\xi )-A(x,u,\eta )\right) \cdot (\xi -\eta )>0\quad \text {for a.e. }x\in \Omega , \text {for all }u \in \mathbb {R}\text { and }\xi ,\eta \in \mathbb {R}^N \ with\ \xi \not = \eta . \end{aligned}\nonumber \\ \end{aligned}$$

(4)

The function space $L^{N,\infty }\log ^{}L (\Omega )$ is the Lorentz–Zygmund space (see Sect. 2.2 for more precise definitions) which consists of real measurable functions u in $\Omega$ such that

$$\begin{aligned} \mathop {\mathrm {ess\,sup}}\limits _{0<t<|\Omega |}t^{\frac{1}{N}}\left( 1+\log \frac{|\Omega |}{t}\right) u^*(t)<\infty \end{aligned}$$

(5)

where $u^*$ is the decreasing rearrangement of u. The structure assumptions (2), (3), (4) and the presence of coefficients in the lower order term fulfilling (5) are modeled on an operator of the form

$$\begin{aligned} {{\,\mathrm{\mathcal {A}}\,}}_{N,\gamma } u:=-\Delta _N u-\text {div}\left( \displaystyle \frac{\gamma |u|^{N-2}u }{|x|^{N-1} \left( 1+\log \frac{R}{|x|}\right) ^{N-1}}\frac{x}{|x|}\right) \end{aligned}$$

(6)

where $\gamma >0$, $R:=\sup _{x\in \Omega } |x|$ and $0\in \Omega$. In the right–hand side of (6) we adopt the usual notation $\Delta _N u:=\text {div}\left( |\nabla u|^{N-2}\nabla u\right)$ for the N–Laplacian operator.

Let us now give a more precise statement of the obstacle problem we consider in the present paper. For a classical overview on topic we refer for instance to [25, 33]. We let $\psi :\Omega \rightarrow [-\infty ,+\infty ]$ be a measurable function and consider the set

$$\begin{aligned} {{\,\mathrm{\mathcal {K}}\,}}_\psi (\Omega ):=\left\{ v\in W^{1,N}_0(\Omega ):v\geqslant \psi \text { a.e. in }\Omega \right\} . \end{aligned}$$

Assume

$$\begin{aligned} \Phi \in W^{-1,N^\prime }(\Omega ). \end{aligned}$$

(7)

A function $u \in {{\,\mathrm{\mathcal {K}}\,}}_\psi (\Omega )$ satisfying a variational inequality of the type

$$\begin{aligned} \int _\Omega A(x,u,\nabla u)\cdot \nabla (v-u) dx \geqslant \left\langle \Phi ,v-u\right\rangle \qquad \forall v \in {{\,\mathrm{\mathcal {K}}\,}}_\psi (\Omega ) \end{aligned}$$

(8)

is called a solution to the obstacle problem involving the operator ${{\,\mathrm{\mathcal {A}}\,}}$. Hereafter $\left\langle \cdot ,\cdot \right\rangle$ denotes the duality product between $W^{-1,N^\prime }(\Omega )$ and $W^{1,N}_0(\Omega )$ so assumption (7) means that

$$\begin{aligned} \Phi =|f|^{N-2}f-\text {div}\left( |F|^{N-2}F\right) \end{aligned}$$

for some

$$\begin{aligned} f\in L^N(\Omega ), \quad F\in L^N(\Omega ,\mathbb {R}^N). \end{aligned}$$

In turn, we have

$$\begin{aligned} \left\langle \Phi ,\varphi \right\rangle =\int _\Omega \left( |f|^{N-2}f\varphi +|F|^{N-2}F\cdot \nabla \varphi \right) \,\mathrm d x \qquad \text {for every }\varphi \in C^{\infty }_0(\Omega ). \end{aligned}$$

We point out that obstacle problems for monotone or pseudomonotone operators have been previously considered in [5,6,7, 17, 27, 29]. In the peculiar case $\psi \equiv -\infty$, the solution of the obstacle problem is actually a solution of the Dirichlet problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\text {div}A(x,u,\nabla u)=\Phi &{}\quad \text {in }\Omega \\ u=0&{}\quad \text {on }\partial \Omega \end{array}\right. } \end{aligned}$$

(9)

in the sense that $u \in W^{1,N}_0(\Omega )$ is such that

$$\begin{aligned} \int _\Omega A(x,u,\nabla u) \cdot \nabla \varphi \,\mathrm d x = \left\langle \Phi ,\varphi \right\rangle \qquad \text {for every }\varphi \in C^{\infty }_0(\Omega ). \end{aligned}$$

(10)

The summability of the coefficients in the lower order term comes into play for the pairing in (8) to be well defined. Thanks to the embedding Sobolev type theorem of Brezis-Wainger [8] and Hansson [24], the membership of the coefficients a and b to $L^{N,\infty }\log ^{}L(\Omega )$ provides a necessary and sufficient condition to get

$$\begin{aligned} A(x,u,\nabla u)\in L^{\frac{N}{N-1}}\left( \Omega ,\mathbb {R}^N\right) \quad \text {whenever }u \in W^{1,N}_0(\Omega ). \end{aligned}$$

(11)

See Corollary 2.3 below for more details.

Linear and nonlinear operators similar to (1) with growth exponent $p\in (1,N)$ have been already considered in literature. We point out that the treatment of problems involving variational inequalities as in (8) in the limit case considered here differs from the case where the principal part behaves like the p–Laplacian with $1<p<N$ and the analogous of the coefficients a and b in inequalities (2) and (3) are in $L^N(\Omega )$ [4, 34] or in the weak-Lebesgue space $L^{N,\infty }(\Omega )$ with distance to bounded functions not large enough [14, 18, 22, 30, 37]. We refer to Section 7 for a discussion on the optimality of our assumptions. We also remark that, when $\Omega$ is bounded, $L^{N,\infty }$ $(\Omega )$ is strictly larger than $L^N (\Omega )$, while $L^{N,\infty }\log L (\Omega )$ is strictly smaller than $L^N (\Omega )$, and this aspect will be crucial in our context.

This paper concerns the existence and regularity issues of a solution to problem (8). Before we enter into details, we recall that $L^\infty (\Omega )$ is not dense in $L^{N,\infty }\log L(\Omega )$, so one can define the distance to $L^\infty (\Omega )$ in $L^{N,\infty }\log L (\Omega )$ by setting

$$\begin{aligned} {{\,\mathrm{\textrm{dist}}\,}}_{L^{N,\infty }\log ^{}L(\Omega )}(u,L^\infty (\Omega )):=\inf _{h\in L^\infty (\Omega )}\llbracket u-h\rrbracket _{L^{N,\infty }\log ^{}L(\Omega )} \end{aligned}$$

(12)

where

$$\begin{aligned} \llbracket u \rrbracket _{L^{N,\infty }\log ^{}L (\Omega )}&:=\mathop {\mathrm {ess\,sup}}\limits _{0<t<|\Omega |}t^{\frac{1}{N}}\left( N+\log \frac{R^N_\Omega \omega _N }{t}\right) u^*(t) \end{aligned}$$

with $R_\Omega := \sup _{x\in \Omega }|x|$ and $\omega _N$ denotes the measure of the unit ball in $\mathbb {R}^N$.

We assume that

$$\begin{aligned} \psi \in W^{1, N }(\Omega ), \end{aligned}$$

(13)

such that

$$\begin{aligned} \psi \le 0\quad \text {on } \partial \Omega . \end{aligned}$$

(14)

We point out that this inequality has to be understood in the sense of traces, i.e. $(\psi -w ) ^+\in W_0^{1,N}(\Omega )$ for all $w \in W_0^{1,N}(\Omega )$. This in turn implies that $\mathcal {K} _{\psi }(\Omega )$ is nonempty, as the positive part $\psi ^+$ of $\psi$ is an element of $\mathcal {K} _{\psi }(\Omega )$.

We define

$$\begin{aligned} g:=\Phi +\text {div}A(x,\psi ,\nabla \psi ) \end{aligned}$$

(15)

and we assume that g is an element of the order dual of $W^{1,N}_0(\Omega )$, that is

$$\begin{aligned} g=g^+-g^-\quad \text {where }g^\pm \in \left( W^{-1,N^\prime }(\Omega )\right) ^+. \end{aligned}$$

(16)

An element $h\in W^{-1,N^\prime }(\Omega )$ belongs to $\left( W^{-1,N^\prime }(\Omega )\right) ^+$ if $\langle h, w\rangle \geqslant 0$ for all $w \in W_0^{1,p}(\Omega )$ such that $w \geqslant 0$ a.e. in $\Omega$.

We are in a position to state some existence result for a solution to the obstacle problem satisfying a Lewy–Stampacchia type inequality.

Theorem 1.1

Let assumptions (2)–(4), (7) and (13)–(16) be in charge. If we suppose that

$$\begin{aligned} \text { dist}_{L^{N,\infty }\log L(\Omega )}(a,L^\infty (\Omega ))<(N-1)(\omega _N\alpha )^{1/N}, \end{aligned}$$

(17)

then there exists a solution $u \in \mathcal {K}_\psi (\Omega )$ to the obstacle problem involving ${{\,\mathrm{\mathcal {A}}\,}}$ satisfying the following Lewy–Stampacchia inequality

$$\begin{aligned} 0 \leqslant -\text {div}A(x,u,\nabla u)-\Phi \leqslant g^-. \end{aligned}$$

(18)

The Lewy-Stampacchia’s inequality was established for the first time in [28] and it plays a crucial role in existence and regularity theory for variational inequalities driven by various kind of operators, see for instance [5, 11, 23, 29] and the reference therein. The existence of a solution to the problem (9) under the only assumptions (13) and (14) is not addressed in details in this paper, since it is a byproduct of the proof of Theorem 1.1 and it can be shown in a similar fashion as [14, 15]. We explicitly remark that condition (16) is satisfied when $g \in L^{N^\prime }(\Omega )$ and it occurs just to show existence of a solution to the obstacle problem.

As a consequence of the interplay between a proper bound on the distance to $L^\infty (\Omega )$ and the regularity of the obstacle function on one hand and the source term on the other, we are able to prove some improvement of the summability of solutions (in the scale of Lorentz–Zygmund spaces).

Theorem 1.2

Assume that (2)–(4) and (14) are in charge and let $u \in {{\,\mathrm{\mathcal {K}}\,}}_\psi (\Omega )$ be a solution to the obstacle problem involving ${{\,\mathrm{\mathcal {A}}\,}}$. For $\lambda >1$, let $\phi , f \in L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L(\Omega )$ and $F \in L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L(\Omega ,\mathbb {R}^N)$. Let also $\psi \in W^1\,L^{N,\lambda N}\log ^{ \frac{\lambda -1}{\lambda }}L(\Omega )$. If

$$\begin{aligned} \text { dist}_{L^{N,\infty }\log L(\Omega )}(a,L^\infty (\Omega ))<\lambda ^{-1}(N-1)(\omega _N\alpha )^{1/N}, \end{aligned}$$

(19)

then

$$\begin{aligned} u\in L^{\infty ,\lambda N}\log ^{-\frac{1}{\lambda }}L(\Omega ). \end{aligned}$$

(20)

In particular,

$$\begin{aligned} u\in \textrm{EXP}_{\lambda N /(N-1)} (\Omega ). \end{aligned}$$

(21)

Concerning the existence of bounded solutions, we are able to prove the following result.

Theorem 1.3

Assume that (2)–(4) and (14) are in charge and let $u \in {{\,\mathrm{\mathcal {K}}\,}}_\psi (\Omega )$ be a solution to the obstacle problem involving ${{\,\mathrm{\mathcal {A}}\,}}$. For $\gamma >1$, let $\phi ,f\in L^{N,\infty }\log ^{\gamma }L(\Omega )$, $F\in L^{N,\infty }\log ^{\gamma }L(\Omega ,\mathbb {R}^N)$. Let also $\psi \in W^1 L^{N,\infty }\log ^{\gamma }L(\Omega )$. Then $u\in L^{\infty }(\Omega )$.

The proof of Theorem 1.1 is based upon a penalization argument, which is a tool so effective to provide both existence and validity of the Lewy–Stampacchia inequality (18). In few words, a solution to the obstacle problem is obtained as the limit of a sequence of solutions to suitable Dirichlet problems which are a generalization of (9). It is worth to mention here that condition (17) turns to be essential to get existence results for the Dirichlet problem (9). We are going to discuss this issue in details in Sect. 4. The proofs of Theorems 1.2 and 1.3 apply verbatim to the Dirichlet problem (9) (see Theorem 7.1 below for a precise statement).

In case the coefficients in the lower order term vanishes, an elliptic equation with right-hand side in a Zygmund space has been considered in [13]. N-Laplacian type equations have been also considered in [12, 20].

2 Preliminaries

2.1 Notation

If A and B are two quantities, we use $A\lesssim B$ to denote that there exists a constant $C>0$, depending on the appropriate parameters, such that $A\leqslant CB$. We also say that a Banach space X is embedded in another Banach space Y if there exists a bounded linear immersion map $\iota :X\rightarrow Y$. Equivalently, X can be identified with a subset of Y in a linear way - usually in a natural way - and $\Vert \cdot \Vert _Y\lesssim \Vert \cdot \Vert _X$.

The truncation at a level $\sigma >0$ will be denoted by $T_\sigma (\cdot )$ and is defined by

$$\begin{aligned} T_\sigma (z):= {\left\{ \begin{array}{ll} \sigma &{}\quad \text {if }z>\sigma \\ z&{}\quad \text {if }|z|\leqslant \sigma \\ -\sigma &{}\quad \text {if }z<-\sigma \end{array}\right. } \qquad \text {for all }z\in \mathbb {R}. \end{aligned}$$

2.2 Lorentz–Zygmund spaces

Throughout this section we let $\Omega$ be a bounded domain in ${{\,\mathrm{\mathbb {R}}\,}}^N$. For a real measurable function u defined in $\Omega$, we let $\mu _u:[0,\infty )\rightarrow [0,|\Omega |]$ be the distribution function of u, namely

$$\begin{aligned} \mu _u(k):=\left| \{x\in \Omega :\,|u(x)|>k\}\right| \quad \text {for }k\geqslant 0. \end{aligned}$$

The decreasing rearrangement of u is denoted by $u^*$ and defined through the formula

$$\begin{aligned} u^*(t):=\inf \{ k>0:\, \mu _u(k)\leqslant t \} \quad \text {for }t\in [0,|\Omega |]. \end{aligned}$$

As an immediate consequence of the latter definition, one gets that u and $u^*$ have the same distribution function. Also, it is well known that the following Hardy–Littlewood inequality holds

$$\begin{aligned} \int _\Omega |u(x)v(x)|\,\mathrm d x\leqslant \int _0^{|\Omega |} u^*(t) v^*(t) \,\mathrm d t \end{aligned}$$

for all real measurable functions u and v defined in $\Omega$.

For $p,q\in (0,\infty ]$ and $\alpha \in \mathbb {R}$ the Lorentz–Zygmund space $L^{p,q}\log ^{\alpha }L(\Omega )$ consists of all real measurable functions u in $\Omega$ such that the quantity

$$\begin{aligned} \Vert u\Vert _{L^{p,q}\log ^{\alpha }L(\Omega )}:=\left\| t^{\frac{1}{p}-\frac{1}{q}}\left( 1+\log \frac{|\Omega |}{t}\right) ^{\alpha }u^*(t)\right\| _{L^q(0,|\Omega |)} \end{aligned}$$

(22)

is finite, where we use the convention $1/\infty =0$. In particular, if $q<\infty$ we have

$$\begin{aligned} \Vert u\Vert _{L^{p,q}\log ^{\alpha }L(\Omega )}=\left( \int _0^{|\Omega |}\left( t^{1/p}\left( 1+\log \frac{|\Omega |}{t}\right) ^\alpha u^*(t)\right) ^{ q }\frac{\,\mathrm d t}{t}\right) ^{1/q} \end{aligned}$$

while

$$\begin{aligned} \Vert u\Vert _{L^{p,\infty }\log ^{\alpha }L(\Omega )}=\mathop {\mathrm {ess\,sup}}\limits _{0<t<|\Omega |}t^{\frac{1}{p}}\left( 1+\log \frac{|\Omega |}{t}\right) ^{\alpha }u^*(t). \end{aligned}$$

The quantity $\Vert \cdot \Vert _{L^{p,q}\log ^{\alpha }L(\Omega ) }$ defines a quasinorm which is equivalent to a norm with respect to which $L^{p,q}\log ^{\alpha }L(\Omega )$ is complete. Moreover, the space ${L^{p,q}\log ^{\alpha }L(\Omega )}$ includes the Lorentz spaces $L^{p,q}(\Omega )$ (which corresponds to the case $\alpha =0$) and the Zygmund space $L^p\log ^\beta (\Omega )$ (which corresponds to the case $p=q$ and $\alpha =p\beta$).

It is worth to mention here that, for $\gamma >0$ the class $L^{\infty ,\infty }\log ^{1 / \gamma }L (\Omega )$ coincides with the space $\textrm{EXP}^{\gamma }(\Omega )$ of exponentially integrable functions, which is defined as the class of real measurable functions u in $\Omega$ for which there exists $\lambda =\lambda (u)>0$ such that

$$\begin{aligned} \int _\Omega \exp \left( \frac{|u(x)|^\gamma }{\lambda }\right) \,\mathrm d x<\infty . \end{aligned}$$

Inclusion relations among these spaces can be described taking into account several different cases. We start by recalling that Lorentz–Zygmund spaces decrease with the primary index regardless of what the other exponents does, in the sense that

$$\begin{aligned} L^{p_1,q_1}\log ^{\alpha _1}L (\Omega ) \subset L^{p_2,q_2}\log ^{\alpha _2}L (\Omega ) \quad \text {if}\quad p_1>p_2 \quad \text {and for any} \quad 0<q_1,q_2<\infty , \alpha ,\beta \in \mathbb {R}. \end{aligned}$$

On the other hand, if the primary exponent does not change and is finite, then

$$\begin{aligned} L^{p,q_1}\log ^{\alpha _1}L (\Omega ) \subset L^{p,q_2}\log ^{\alpha _2}L (\Omega ) \quad \text {if} \quad \left. \begin{array}{rl} &{} \text {either} \quad q_1\leqslant q_2 \quad \text {and}\quad \alpha _1\geqslant \alpha _2 \\ \, \\ &{} \text {or}\quad q_1>q_2 \quad \text {and} \quad \alpha _1+1/q_1 > \alpha _2+1/q_2 \end{array} \right. \end{aligned}$$

while

$$\begin{aligned} L^{\infty ,q_1}\log ^{\alpha _1}L (\Omega ) \subset L^{\infty ,q_2}\log ^{\alpha _2}L (\Omega ) \quad \text {if} \quad \left. \begin{array}{rl} &{} \text {either} \quad \alpha _1+1/q_1 > \alpha _2+1/q_2 \\ \, \\ &{} \text {or}\quad q_1 \leqslant q_2 \quad \text {and} \quad \alpha _1+1/q_1 = \alpha _2+1/q_2 \leqslant 0. \end{array} \right. \end{aligned}$$

It is also interesting to see the dual of $L^{p,q}\log ^{\alpha }L(\Omega )$. It can be shown [3] that if $1<p<\infty$ and $1\leqslant q<\infty$ the duality relation

$$\begin{aligned} \left( L^{p,q}\log ^{\alpha }L(\Omega ) \right) ^*=L^{p',q'}\log ^{-\alpha }L (\Omega ) \end{aligned}$$

holds, where as usual, for an exponent $p\in [1,\infty ]$ we denote by $p'\in [1,\infty ]$ its conjugate exponent defined by the relation

$$\begin{aligned} \frac{1}{p}+\frac{1}{p'}=1, \end{aligned}$$

with the convention $1/\infty =0$.

We will later need to use the following generalized Hölder-type inequality for Lorentz–Zygmund spaces.

Lemma 2.1

Let $\Omega \subset {{\,\mathrm{\mathbb {R}}\,}}^N$ be a bounded open set. Let $1\leqslant p,p_1,p_2,q_1,q_2\leqslant \infty$ and $\alpha \in {{\,\mathrm{\mathbb {R}}\,}}$ be such that

$$\begin{aligned} \frac{1}{p_1}+\frac{1}{p_2}=\frac{1}{q_1}+\frac{1}{q_2}=\frac{1}{p}. \end{aligned}$$

Then

$$\begin{aligned} \Vert fg\Vert _{L^p(\Omega )}\leqslant \Vert f\Vert _{L^{p_1,q_1}\log ^{\alpha }L(\Omega )}\Vert g\Vert _{L^{p_2,q_2}\log ^{-\alpha }L(\Omega )} \end{aligned}$$

for all $f\in L^{p_1,q_1}\log ^{\alpha }L(\Omega )$ and all $g\in L^{p_2,q_2}\log ^{-\alpha }L(\Omega )$.

Proof

From the Hardy–Littlewood inequality we know that $\Vert fg\Vert _{L^p(\Omega )}\leqslant \Vert f^*(t)g^*(t)\Vert _{L^p(0,|\Omega |)}$. We therefore have

$$\begin{aligned}&\Vert fg\Vert _{L^p(\Omega )}\leqslant \Vert f^*(t)g^*(t)\Vert _{L^p(0,|\Omega |)}\\&\quad =\left\| \left( t^{\frac{1}{p_1}-\frac{1}{q_1}}\left( 1+\log \frac{|\Omega |}{t}\right) ^{\alpha } f^*(t)\right) \left( t^{\frac{1}{p_2}-\frac{1}{q_2}}\left( 1+\log \frac{|\Omega |}{t}\right) ^{-\alpha } g^*(t)\right) \right\| _{L^p(0,|\Omega |)}\\&\quad \leqslant \left\| t^{\frac{1}{p_1}-\frac{1}{q_1}}\left( 1+\log \frac{|\Omega |}{t}\right) ^{\alpha } f^*(t)\right\| _{L^{q_1}(0,|\Omega |)}\left\| t^{\frac{1}{p_2}-\frac{1}{q_2}}\left( 1+\log \frac{|\Omega |}{t}\right) ^{-\alpha } g^*(t)\right\| _{L^{q_2}(0,|\Omega |)}\\&\quad =\Vert f\Vert _{L^{p_1,q_1}\log ^{\alpha }L(\Omega )}\Vert g\Vert _{L^{p_2,q_2}\log ^{-\alpha }L(\Omega )}. \end{aligned}$$

The proof is complete. $\square$

2.3 Lorentz–Zygmund–Sobolev spaces

Let $0<p,q\leqslant \infty$ and $\alpha \in {{\,\mathrm{\mathbb {R}}\,}}$. We define the Lorentz–Zygmund–Sobolev space $W^1L^{p,q}\log ^{\alpha }L(\Omega )$ as the space of all $f\in L^{p,q}\log ^{\alpha }L(\Omega )\cap W^{1,1}(\Omega )$ such that

$$\begin{aligned}{}[f]_{W^1L^{p,q}\log ^{\alpha }L(\Omega )}:=\left\| \left| \nabla f\right| \right\| _{L^{p,q}\log ^{\alpha }L(\Omega )}<\infty \end{aligned}$$

endowed with the norm $\Vert f\Vert _{W^1L^{p,q}\log ^{\alpha }L(\Omega )}:=\Vert f\Vert _{L^{p,q}\log ^{\alpha }L(\Omega )}+[f]_{W^1L^{p,q}\log ^{\alpha }L(\Omega )}$, and its subspace $W^1_0L^{p,q}\log ^{\alpha }L(\Omega )$ as the closure of the space $C^\infty _c(\Omega )$ in $W^1L^{p,q}\log ^{\alpha }L(\Omega )$, endowed with the norm $\left\| \left| \nabla \left( \cdot \right) \right| \right\| _{L^{p,q}\log ^{\alpha }L(\Omega )}$.

Now, we discuss some embedding results in the scale of the Lorentz–Zygmung spaces. First, we want to recall that Yudovich [36], Pohozaev [32] and Trudinger [35] independently proved that $W^{1,N}_0(\Omega ) \hookrightarrow \textrm{EXP}^{N/(N-1)}(\Omega )$. This embedding result have been later generalized in the independent papers Brezis–Wainger [8] and Hansson [24], where it is shown that $W^{1,N}_0(\Omega ) \hookrightarrow L^{\infty ,N}\log ^{-1}L (\Omega )$. Such embedding is optimal in the context of rearrangement–invariant space and there is a relevant Sobolev type inequality naturally connected with this embedding. To provide a sharp form of such inequality, we follow [10]. Let $\omega _N$ be the measure of the unit ball in $\mathbb {R}^N$. If

$$\begin{aligned} R_\Omega :=\sup _{x\in \Omega }|x|, \end{aligned}$$

for $p,q\in (0,\infty ]$ and $\alpha \in \mathbb {R}$ we define

$$\begin{aligned}{} & {} \llbracket u \rrbracket _{L^{p,q}\log ^{\alpha }L(\Omega )}:=\left( \int _0^{|\Omega |}\left( t^{1/p}\left( N+\log \frac{ R^N_\Omega \omega _N }{t}\right) ^\alpha u^*(t)\right) ^{ q }\frac{\,\mathrm d t}{t}\right) ^{1/q} \quad \text {if }q<\infty ,\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned}{} & {} \llbracket u \rrbracket _{L^{p,\infty }\log ^{\alpha }L(\Omega )}:=\mathop {\mathrm {ess\,sup}}\limits _{0<t<|\Omega |}t^{\frac{1}{p}}\left( N+\log \frac{R^N_\Omega \omega _N }{t}\right) ^{\alpha }u^*(t).\nonumber \\ \end{aligned}$$

(24)

For the cases we are interested in, (23) and (24) define quasinorms equivalent to $\Vert \cdot \Vert _{L^{p,q}\log ^{\alpha }L(\Omega )}$.

With this notation at hand, we have the following Sobolev type inequality.

Theorem 2.2

Let $\Omega \subset {{\,\mathrm{\mathbb {R}}\,}}^N$ be a bounded open set with Lipschitz boundary. If $u \in W^{1,N}_0(\Omega )$ then $u\in L^{\infty ,N}\log ^{-1}L (\Omega )$ and

$$\begin{aligned} (N-1)\omega _N^{1/N} \llbracket u \rrbracket _{L^{\infty ,N}\log ^{-1}L (\Omega )} \leqslant \Vert \nabla u\Vert _{L^N(\Omega )}. \end{aligned}$$

(25)

Inequality (25) appears in [10] (see formula (1.13) there) and it is known to be equivalent to the Hardy inequality

$$\begin{aligned} \left( \frac{N-1}{N}\right) ^N \int _ \Omega \frac{|v(x)|^N}{|x|^N\left( 1+\log \frac{D}{|x|}\right) ^N} \,\mathrm d x \leqslant \int _\Omega |\nabla v|^N\,\mathrm d x \end{aligned}$$

(26)

which holds true for every $v \in W^{1,N}_0(\Omega )$, provided $\Omega$ is a smooth bounded open subset of $\mathbb {R}^N$ with $0\in \Omega$ and $D\geqslant R_\Omega$.

Since Lemma 2.1 holds also for the $\llbracket \cdot \rrbracket _{L^{p,q}\log ^{\alpha }L}$ norms, a consequence of Theorem 2.2 is the following corollary.

Corollary 2.3

Let $\Omega \subset {{\,\mathrm{\mathbb {R}}\,}}^N$ be a bounded open set with Lipschitz boundary. Then

$$\begin{aligned} \Vert fg\Vert _{L^N(\Omega )}\leqslant S_N\llbracket f\rrbracket _{L^{N,\infty }\log ^{}L (\Omega ) }\Vert \nabla g\Vert _{L^N(\Omega )} \end{aligned}$$

for all $f\in L^{N,\infty }\log ^{}L(\Omega )$ and $g\in W^{1,N}_0(\Omega )$, where $S_N=(N-1)\omega _N^{1/N}$.

We remark that $L^\infty (\Omega )$ is not dense in $L^{p,\infty }\log ^{\alpha }L(\Omega )$ for $1<p<\infty$. For such spaces, distance to $L^\infty$ has been widely studied along with its applications - see for instance [1, 2, 9].

2.4 Fixed point theorems and approximation results

To prove existence results, we shall use the Leray–Schauder fixed point theorem in a version proposed in [19, Theorem 11.3 pg. 280].

Theorem 2.4

Let $\mathcal {F}$ be a compact mapping of a Banach space X into itself, and suppose there exists a constant M such that $\Vert x\Vert _{X}<M$ for all $x\in X$ and $\lambda \in [0,1]$ satisfying $x=\lambda \mathcal {F}(x).$ Then, $\mathcal {F}$ has a fixed point.

We recall that a continuous mapping between two Banach spaces is called compact if the images of bounded sets are precompact.

In the sequel, we will need the following approximation result (see [29]).

Theorem 2.5

Assume that $q>1$ and $\Omega$ is a Lipschitz bounded domain of $\mathbb {R}^N$. Let $h \in \left( W^{-1,q^\prime }(\Omega )\right) ^+$. Then, there exists a sequence $(h_n)_{n\in \mathbb {N}}$ of nonnegative functions in $W_0^{1,q}(\Omega )$ such that $h_n \rightarrow h$ strongly in $W^{-1,q^\prime }(\Omega )$.

We mention here a weak compactness result proved in [14, Lemma 2].

Lemma 2.6

Let $\mathcal {B}$ be a nonempty subset of $W^{1,p}_0(\Omega )$ with $p>1$. Assume that there exists a constant $C>0$ such that

$$\begin{aligned} \Vert \nabla u \Vert _{L^p(\Omega \setminus \Omega _\sigma )}^p\leqslant C\left( 1+\Vert u \Vert _{L^p(\Omega \setminus \Omega _\sigma )}^p \right) \end{aligned}$$

(27)

for any $\sigma >0$ and $u \in \mathcal {B}$, where $\Omega _\sigma :=\{x\in \Omega :\,|u(x)| \geqslant \sigma \}$. Then, there exists a constant $M>0$ such that

$$\begin{aligned} \Vert u \Vert _{W^{1,p}(\Omega )}\leqslant M\, \end{aligned}$$

(28)

for any $u \in \mathcal {B}$.

3 A technical tool

Throughout this section we let all the assumptions (2)–(4), (13)–(16) be in charge and for subsequent purposes, we want to describe the properties of Carathéodory vector field

$$\begin{aligned} \hat{A}(x, u,\eta ):=A(x, u+ \psi ^+,\eta +\nabla \psi ^+). \end{aligned}$$

(29)

The vector field $\hat{A}$ satisfies some conditions similar to (2), (3) and (4). We want to discuss the properties of $\hat{A}$ providing some details, as for instance (19) is made in terms of the constant $\alpha$ and the coefficient a. As in [16], we prove the following.

Lemma 3.1

Let the assumptions (2)–(4), and (13)–(16) be in charge. For all $\varepsilon >0$ and $\vartheta \in (0,1)$, we obtain

$$\begin{aligned} \hat{A}(x,u,\xi )\cdot \xi \geqslant \hat{\alpha }\,|\xi |^N-(\hat{a}\,|u|)^N-\hat{\phi }, \end{aligned}$$

(30)

where

$$\begin{aligned} \hat{\alpha }:=(\alpha -\beta \,\varepsilon ^N)\,\vartheta ^N,\qquad \hat{a}:=\frac{b+\varepsilon \,a}{\vartheta }\end{aligned}$$

and $\hat{\phi }$ is a suitable nonnegative function in $L^1(\Omega )$. Moreover, the following estimate holds

$$\begin{aligned}{} & {} {{\,\mathrm{\textrm{dist}}\,}}_{L^{N,\infty }\log ^{}L(\Omega )}(\hat{a},L^\infty (\Omega )) \nonumber \\{} & {} \qquad \leqslant \frac{1+\sqrt{\varepsilon }}{\vartheta }\, {{\,\mathrm{\textrm{dist}}\,}}_{L^{N,\infty }\log ^{}L(\Omega )}(a,L^\infty (\Omega ))+\frac{\sqrt{\varepsilon }(1+\sqrt{\varepsilon })}{\vartheta }\,\Vert a\Vert _{L^{N,\infty }\log ^{}L(\Omega )}. \end{aligned}$$

(31)

Proof

By Young’s inequality one gets

$$\begin{aligned} \hat{A}(x,u, \xi )\cdot \xi \geqslant (\alpha -\beta \,\varepsilon ^N)\,|\xi +\nabla \psi ^+|^N - \left( a^N+\varepsilon ^N\,b^N\right) |u+\psi ^+|^N - \phi _1 \end{aligned}$$

with a suitable $\phi _1\in L^1(\Omega )$. As $\mathbb {R}\ni t\mapsto |t|^N$ is convex, there exists $C=C(\vartheta ,N)>0$ such that

$$\begin{aligned}|\xi +\nabla \psi ^+|^N \geqslant \vartheta ^p\,|\xi |^N-C\,|\nabla \psi ^+|^N,\qquad |u+\psi ^+|^p \leqslant \vartheta ^{-p}\,|u|^N+C\,|\psi ^+|^N.\end{aligned}$$

Hence, (30) is proved. Estimate (31) follows by the definition of $\hat{a}$. $\square$

4 Auxiliary Dirichlet problems

We consider the following

$$\begin{aligned} {\left\{ \begin{array}{ll} -\text {div}A(x,u,\nabla u)+B(x,u)=\Phi &{}\quad \text {in }\Omega \\ u=0&{}\quad \text {on }\partial \Omega \end{array}\right. } \end{aligned}$$

(32)

where $B:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function satisfying

$$\begin{aligned} |B(x,u)|\leqslant \gamma |u|+ M(x) \qquad \text {for a.e. }x \in \Omega \text { and for all }u\in \mathbb {R} \end{aligned}$$

(33)

with $\gamma >0$ and $M\in L^N(\Omega )$, and a sign condition of the type

$$\begin{aligned} B(x,u)u \geqslant 0 \qquad \text {for a.e. }x \in \Omega \text { and for all }u\in \mathbb {R}. \end{aligned}$$

(34)

Proposition 4.1

Let $\Phi \in W^{-1,N'}(\Omega )$ and $A:\Omega \times \mathbb {R}^N\rightarrow \mathbb {R}^N$ a Carathéodory vector field satisfying (2), (3) and (4). If

$$\begin{aligned} \text { dist}_{L^{N,\infty }\log L(\Omega )}(a,L^\infty (\Omega ))<(N-1)(\omega _N\alpha )^{1/N}, \end{aligned}$$

(35)

then there exists $u\in W^{1,N}_0(\Omega )$ solving problem (32).

Proof

We divide this proof into several steps.

Step 1: the case of bounded coefficients.

Here we consider the case in which A satisfies (2) and (3) with $a,b\in L^\infty (\Omega )$. As in [14] we consider, for a fixed $v\in W^{1,N}_0(\Omega )$,

$$\begin{aligned} A_v(x,\xi ):=A(x,v,\xi ), \qquad B_v(x):=B(x,v). \end{aligned}$$

Thanks to a classical result by Leray and Lions [26] we obtain existence of a solution to

$$\begin{aligned} -\text {div}A_v(x,\nabla u)+B_v(x)=\Phi , \end{aligned}$$

(36)

which is unique because of the monotonicity assumption (4). It is not difficult to prove that, for a fixed $\Phi \in W^{-1,N'}(\Omega )$, the map

$$\begin{aligned} {{\,\mathrm{\mathcal {F}}\,}}:v\in W^{1,N}_0(\Omega )\mapsto u\in W^{1,N}_0(\Omega ) \end{aligned}$$

sending v to the solution u of (36) is compact.

We want to use Leray-Schauder fixed point theorem to the map ${{\,\mathrm{\mathcal {F}}\,}}$ to construct a solution $u\in W^{1,N}_0(\Omega )$ to problem (9). Let $0<t\leqslant 1$ and let u be a solution to $u=t{{\,\mathrm{\mathcal {F}}\,}}(u)$, i.e.

$$\begin{aligned} -\text {div}A\left( x,u,\frac{1}{t}\nabla u\right) +B(x,u)=\Phi . \end{aligned}$$

(37)

By using condition (34) we have

$$\begin{aligned} B(x,u)T_\sigma (u) \geqslant 0 \qquad \text {a.e. in } \Omega \end{aligned}$$

(38)

We use $T_\sigma u$ as test for some $\sigma >0$ and use conditions (2) and (38) to obtain

$$\begin{aligned} \alpha t^{1-N}\int _\Omega \left| \nabla T_\sigma u\right| ^N\,\mathrm d x\leqslant \Vert \Phi \Vert _{W^{-1,N'(\Omega )} }\Vert \nabla T_\sigma u\Vert _{L^N (\Omega ) }+\int _\Omega \left( a|u|\right) ^N\chi _{\left\{ |u|<\sigma \right\} }+\varphi ^N {\chi _{\left\{ |u|<\sigma \right\} }}\,\mathrm d x. \end{aligned}$$

Applying Young inequality and using the fact that $t^{1-N}\geqslant 1$ we get

$$\begin{aligned} \alpha \int _\Omega \left| \nabla T_\sigma u(x)\right| ^N\,\mathrm d x&\leqslant \alpha t^{1-N}\int _\Omega \left| \nabla T_\sigma u(x)\right| ^N\,\mathrm d x\\&\leqslant \Vert \Phi \Vert _{W^{-1,N'} (\Omega )} \left\| \nabla T_\sigma u\right\| _{L^N (\Omega ) }+\int _{{\left\{ |u|<\sigma \right\} }} \left( a(x)\left| u(x)\right| \right) ^N+\varphi ^N(x)\,\mathrm d x\\&\leqslant \frac{1}{\alpha ^{\frac{1}{N-1}} N'}\Vert \Phi \Vert _{W^{-1,N'}{(\Omega )}}^{N'}+\frac{\alpha }{N}\left\| \nabla T_\sigma u\right\| _{L^N {(\Omega )}}^N\\&\quad +\int _{ {\left\{ |u|<\sigma \right\} }} \left( a(x)\left| u(x)\right| \right) ^N+\varphi ^N(x)\,\mathrm d x\\ \end{aligned}$$

and therefore

$$\begin{aligned} \frac{\alpha }{N'}\left\| \nabla u\right\| _{L^N(\left\{ |u|<\sigma \right\} )}^N\leqslant \frac{1}{\alpha ^{\frac{1}{N-1}} N'}\Vert \Phi \Vert _{W^{-1,N'} {(\Omega )}}^{N'}+\Vert a\Vert _{L^\infty {(\Omega )}}\Vert u\Vert _{L^N(\left\{ |u|<\sigma \right\} )}^N+\Vert \varphi \Vert _{L^N {(\Omega )}}^N \end{aligned}$$

and we apply Lemma 2.6 to obtain that $\Vert u\Vert _{W^{1,N}(\Omega )}\leqslant K$ for some constant K independent of u.

Step 2: we prove the result in the general case by using an approximation argument.

For $n\in {{\,\mathrm{\mathbb {N}}\,}}$ we define

$$\begin{aligned} \theta _n(x)=\frac{T_n\left( \max \left\{ a(x),b(x)\right\} \right) }{\max \left\{ a(x),b(x)\right\} } \end{aligned}$$

and we see that the field $A_n(x,u,\xi ):=A(x,\theta _nu,\xi )$ satisfies

$$\begin{aligned}{} & {} \langle A_n(x,u,\xi ),\xi \rangle \geqslant \alpha |\xi |^N-\left( T_na(x)|u|\right) ^N-\varphi ^N(x)\quad \forall (x,u,\xi )\in \Omega \times {{\,\mathrm{\mathbb {R}}\,}}\times {{\,\mathrm{\mathbb {R}}\,}}^N;\nonumber \\ \end{aligned}$$

(39)

$$\begin{aligned}{} & {} |A_n(x,u,\xi )|\leqslant \beta |\xi |^{N-1}+\left( T_nb(x)|u|\right) ^{N-1}+\varphi ^{N-1}(x)\quad \forall (x,u,\xi )\in \Omega \times {{\,\mathrm{\mathbb {R}}\,}}\times {{\,\mathrm{\mathbb {R}}\,}}^N;\nonumber \\ \end{aligned}$$

(40)

$$\begin{aligned}{} & {} \langle A_n(x,u,\xi )-A_n(x,u,\eta ),\xi -\eta \rangle >0\quad \forall (x,u)\in \Omega \times {{\,\mathrm{\mathbb {R}}\,}}\end{aligned}$$

(41)

for all $\xi \ne \eta$ in ${{\,\mathrm{\mathbb {R}}\,}}^N$.

For a fixed $\Phi \in W^{-1,N'}(\Omega )$, what we proved in Step 1 provides the existence of a solution $u_n\in W^{1,N}_0(\Omega )$ to the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\text {div}A_n(x,u_n,\nabla u_n)+B(x,u_{ n })=\Phi &{}\text {in }\Omega \\ u_n=0&{}\text {on }\partial \Omega . \end{array}\right. } \end{aligned}$$

(42)

We want to apply again Lemma 2.6. We test problem (42) by $T_\sigma u$ and we use (39) and (38) to obtain

$$\begin{aligned} \alpha \int _\Omega \left| \nabla T_\sigma u_n\right| ^N\,\mathrm d x\leqslant \Vert \Phi \Vert _{W^{-1,N'}{(\Omega )}}\Vert \nabla T_\sigma u_n\Vert _{L^N {(\Omega )}}+\int _\Omega \left( \left( a|u_n|\right) ^N\chi _{\left\{ |u_n|<\sigma \right\} }+\varphi ^N\right) \,\mathrm d x. \end{aligned}$$

The latter relation clearly implies

$$\begin{aligned} \alpha ^{\frac{1}{N}}\left\| \nabla T_\sigma u_n\right\| _{L^N {(\Omega )}}\leqslant \left( \Vert \Phi \Vert _{W^{-1,N'}{(\Omega )}}\left\| \nabla T_\sigma u_n\right\| _{L^N {(\Omega )}}\right) ^{\frac{1}{N}}+\left\| au_n\chi _{\left\{ |u_n|<\sigma \right\} }\right\| _{L^N {(\Omega )}}+\Vert \varphi \Vert _{L^N{(\Omega )}}. \end{aligned}$$

We now take $M>0$ and write a as $\left( a-T_Ma\right) +T_Ma$, so if we apply the triangle inequality we obtain

$$\begin{aligned} \left\| au_n\chi _{\left\{ |u_n|<\sigma \right\} }\right\| _{L^N{(\Omega )}}&\leqslant \left\| \left( a-T_Ma\right) u_n\chi _{\left\{ |u_n|<\sigma \right\} }\right\| _{L^N {(\Omega )}}+\left\| \left( T_Ma\right) u_n\chi _{\left\{ |u_n|<\sigma \right\} }\right\| _{L^N {(\Omega )}}\\&\leqslant \left\| \left( a-T_Ma\right) u_n\chi _{\left\{ |u_n|<\sigma \right\} }\right\| _{L^N{(\Omega )}}+M\left\| u_n\chi _{\left\{ |u_n|<\sigma \right\} }\right\| _{L^N {(\Omega )}}. \end{aligned}$$

We can now use Corollary 2.3 to manage the first term in the right hand side

$$\begin{aligned} \left\| \left( a-T_Ma\right) u_n\chi _{\left\{ |u_n|<\sigma \right\} }\right\| _{L^N {(\Omega )}}\leqslant S_N\llbracket a-T_Ma \rrbracket _{L^{N,\infty }\log ^{}L{(\Omega )}}\Vert \nabla T_\sigma u_n \Vert _{L^N {(\Omega )}}. \end{aligned}$$

Using assumption (17) and the fact that

$$\begin{aligned} \textrm{dist} _{L^{N,\infty }\log L {(\Omega )}} (a,L^\infty {(\Omega )})=\lim _{M\rightarrow \infty } \llbracket a-T_Ma\rrbracket _{L^{N,\infty }\log ^{}L{(\Omega )}} \end{aligned}$$

that can be proved as in [14], we can choose M large enough to have

$$\begin{aligned} S_N\llbracket a-T_Ma\rrbracket _{L^{N,\infty }\log ^{}L{(\Omega )}}<\alpha ^{\frac{1}{N}} \end{aligned}$$

so that we have

$$\begin{aligned} C\Vert \nabla T_\sigma u_n\Vert _{L^N {(\Omega )}}\leqslant \left( \Vert \Phi \Vert _{W^{-1,N'}{(\Omega )}}\Vert \nabla T_\sigma u_n\Vert _{L^N {(\Omega )}}\right) ^{\frac{1}{N}}+M\Vert u_n\chi _{\left\{ |u_n|<\sigma \right\} }\Vert _{L^N {(\Omega )}}+\Vert \varphi \Vert _{L^N {(\Omega )}}. \end{aligned}$$

Applying Young inequality we show that the assumptions of Lemma 2.6 and obtain

$$\begin{aligned} \Vert u_n\Vert _{W^{1,N}(\Omega )}\leqslant K\qquad \forall n\in {{\,\mathrm{\mathbb {N}}\,}}\end{aligned}$$

(43)

for some $K>0$ independent of n.

Due to (43) we can assume that there exists $u\in W^{1,N}_0(\Omega )$ such that

$$\begin{aligned} u_n\rightharpoonup u&\quad \text {in }W^{1,N}_0(\Omega )\\ u_n\rightarrow u&\quad \text {in }L^q {(\Omega )}\text { for all }1<q<\infty \text { and a.e. in }\Omega . \end{aligned}$$

We test equation (9) with $T_1(u_n-u)$ and obtain

$$\begin{aligned} \int _\Omega A_n(x,u_n,\nabla u_n)\nabla (u_n-u)\chi _{\left\{ |u_n-u|\leqslant 1\right\} }=\langle \Phi ,\nabla T_1(u_n-u)\rangle . \end{aligned}$$

Since $T_1(u_n-u)\rightharpoonup 0$ in $W^{1,N}_0(\Omega )$, we have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\int _\Omega A_n(x,u_n,\nabla u_n)\nabla T_1(u_n-u)=0. \end{aligned}$$

Let us show that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\int _\Omega A_n(x,u_n,\nabla u)\nabla T_1(u_n-u)=0. \end{aligned}$$

Since $\nabla u_n\overset{W^{1,N}_0(\Omega )}{\rightharpoonup }\nabla u$, it suffices to prove that $A_n(x,u_n,\nabla u_n)\chi _{\left\{ |u_n-u|\leqslant 1\right\} }$ is compact. Using growth condition (3) we have

$$\begin{aligned} \left( A_n(x,u_n,\nabla u)\right) ^{N'}\chi _{\left\{ |u_n-u|\leqslant 1\right\} }\leqslant C\left( \left| \nabla u\right| ^N+\varphi ^N+\left( b|u|\right) ^N+\left( b\left| u_n-u\right| \right) ^N\chi _{\left\{ |u_n-u|\leqslant 1\right\} }\right) \end{aligned}$$

and since $b\in L^{N,\infty }\log ^{}L(\Omega )\hookrightarrow L^N(\Omega )$ we can pass to the limit. We therefore have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\int _\Omega \left( A_n\left( x,u_n,\nabla u_n\right) -A_n\left( x,u_n,\nabla u\right) \right) \nabla \left( u_n-u\right) \chi _{\left\{ |u_n-u|\leqslant 1\right\} }=0 \end{aligned}$$

and, up to a subsequence,

$$\begin{aligned} \left( A_n\left( x,u_n,\nabla u_n\right) -A_n\left( x,u_n,\nabla u\right) \right) \nabla (u_n-u)\rightarrow 0. \end{aligned}$$

Reasoning as in [26, Lemma 3.3] we obtain $\nabla u_n\rightarrow \nabla u$ a.e. in $\Omega$ and

$$\begin{aligned} A_n(x,u_n,\nabla u_n)\rightharpoonup A(x,u,\nabla u)\quad \text { in }L^{N'}(\Omega ) \end{aligned}$$

which concludes the proof. $\square$

To conclude this section, we provide an example which shows that a condition on the distance as in (35) is crucial to get existence of a solution to our problem.

Example 4.1

Let $\gamma >0$ and consider the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u-\text {div}\left( \displaystyle \frac{\gamma x}{|x|^2(1-\log |x|)}u\right) =-\text {div}\left( \displaystyle \frac{x}{|x|^2(1-\log |x|)^\gamma }\right) &{}\quad \text {in }B\\ u=0&{}\quad \text {on }\partial B \end{array}\right. } \end{aligned}$$

(44)

for $u\in W^{1,2}_0(B)$, where B is the unit ball in ${{\,\mathrm{\mathbb {R}}\,}}^2$. The underlying operator for problem (44) is given by

$$\begin{aligned} A(x,u,\xi )=\xi + \gamma \frac{u}{|x|(1-\log |x|)}\frac{x}{|x|}{.} \end{aligned}$$

By using Young’s inequality we get

$$\begin{aligned} A(x,u,\xi )\cdot \xi \geqslant \frac{1}{2} |\xi |-\frac{1}{2} \left( \gamma a(x) u\right) ^2 \end{aligned}$$

(45)

where

$$\begin{aligned} a(x)= \frac{1}{|x| (1-\log |x|)}. \end{aligned}$$

If we consider the adjoint problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta v+\displaystyle \frac{\gamma x\cdot \nabla v}{|x|^2(1-\log |x|)}=0&{}\quad \text {in }B\\ v=0&{}\quad \text {on }\partial B \end{array}\right. } \end{aligned}$$

(46)

we have that a solution is given by

$$\begin{aligned} v(x)= {\left\{ \begin{array}{ll} \frac{1}{\gamma -1}\left( 1-(1-\log |x|)^{1-\gamma }\right) &{}\quad \text {if }\gamma \ne 1\\ -\log (1-\log |x|)&{}\quad \text {if }\gamma =1, \end{array}\right. } \end{aligned}$$

and in particular it satisfies

$$\begin{aligned} \nabla v=\frac{x}{|x|^2(1-\log |x|)^\gamma }. \end{aligned}$$

Let us now assume that there exists a solution u to problem (44). If $\gamma >\frac{1}{2}$ we have that $v\in W^{1,2}_0(B)$, so we can test it in (44) and we obtain

$$\begin{aligned} 0=\int _B|\nabla v|^2\,\mathrm d x, \end{aligned}$$

which is impossible and therefore problem (44) does not admit a solution if $\gamma >\frac{1}{2}$. This result is also sharp in terms of the parameter $\gamma$. For the function a it results that

$$\begin{aligned} a^*(t)=\pi ^{\frac{1}{2}}t^{-\frac{1}{2}}\left( 1+\frac{1}{2}\log \frac{\pi }{t}\right) ^{-1} \end{aligned}$$

and a direct computation (see for instance [31]) gives us

$$\begin{aligned} {{\,\mathrm{\textrm{dist}}\,}}_{L^{2,\infty }\log ^{}L(B)}(a,L^\infty (B))=2\sqrt{\pi }. \end{aligned}$$

Taking into account (45), if we impose condition (35) we are forced to require $\gamma <\frac{1}{2}$. $\square$

5 Regularity

In this section we prove Theorems 1.2 and 1.3.

5.1 Improving the summability in the scale of Lorentz–Zygmund spaces

Proof of Theorem 1.2

We divide the proof in several steps.

Step 1: we prove that

$$\begin{aligned} |u|^\lambda \in W^{1,N}_0(\Omega )\end{aligned}$$

(47)

under the assumption

$$\begin{aligned} \psi \leqslant 0 \qquad \text {a.e. in }\Omega . \end{aligned}$$

(48)

Clearly, (47) implies (20).

We notice that $v=T_ku$ is a valid test function since if $u>0$ then $v>0\geqslant \psi$, while if $u\leqslant 0$ then $v\geqslant u\geqslant \psi$. Using the structural assumption (2) we obtain

$$\begin{aligned} \alpha \int _{ E_k }|\nabla u|^N\,\mathrm d x&\leqslant \int _{E_k}|f|^{N-1}|u-T_ku|\,\mathrm d x +\int _{E_k}|F|^{N-1}|\nabla u|\,\mathrm d x\\&\quad +\int _{E_k}\left( a|u|\right) ^N\,\mathrm d x +\int _{E_k}\phi ^N\,\mathrm d x \end{aligned}$$

where $E_k:=\left\{ x\in \Omega :|u(x)|>k\right\}$. Applying a Young inequality we obtain

$$\begin{aligned} (\alpha -\varepsilon )\int _{E_k}|\nabla u|^N\,\mathrm d x\leqslant \int _{E_k} \left[ C|f|^N+C|F|^N+|u|^N+\left( a|u|\right) ^N+\phi ^N \right] \,\mathrm d x, \end{aligned}$$

where $\varepsilon >0$ is a parameter we will choose later and C is a constant depending on $\varepsilon$. Multiplying by $k^{(\lambda -1)N-1}$ and integrating on [0, K] gives, thanks to Fubini theorem,

$$\begin{aligned} (\alpha -\varepsilon )\int _\Omega \left| \nabla u\right| ^N\left| T_Ku\right| ^{(\lambda -1)N}\,\mathrm d x{} & {} \leqslant \int _\Omega \left( C|f|^N+C|F|^N+|u|^N+\left( a|u|\right) ^N+ \phi ^N\right) \\{} & {} \qquad \times \left| T_Ku\right| ^{(\lambda -1)N}\,\mathrm d x \end{aligned}$$

which implies

$$\begin{aligned} (\alpha -\varepsilon )^{\frac{1}{N}}\left\| \nabla u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}&\leqslant C\left( \left\| f\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}+ \left\| F\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}\right) \\ {}&\quad + \left\| u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}+ \left\| au\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}\\ {}&\quad + \left\| \phi \left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}. \end{aligned}$$

Let $M>0$. If we write $a=T_Ma+(a-T_Ma)$, we can give an estimate of $\left\| au\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}$:

$$\begin{aligned} \left\| au\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}&\leqslant \left\| \left( a-T_Ma\right) u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}+\left\| \left( T_Ma\right) u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}\\&\leqslant \left\| \left( a-T_Ma\right) u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}+M\left\| u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}. \end{aligned}$$

To simplify this inequality, we use Corollary 2.3 on the first term on the right hand side to obtain

$$\begin{aligned} \left\| \left( a-T_Ma\right) u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}\leqslant S_N \llbracket a-T_Ma\rrbracket _{L^{N,\infty }\log ^{}L {(\Omega )}}\left\| \nabla \left( u\left| T_Ku\right| ^{\lambda -1}\right) \right\| _{L^N {(\Omega )}}. \end{aligned}$$

We now notice that $\nabla \left( u\left| T_Ku\right| ^{\lambda -1}\right) \leqslant \lambda \left| \nabla u\right| \left| T_Ku\right| ^{\lambda -1}$, so that

$$\begin{aligned} \left\| \left( a-T_Ma\right) u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}\leqslant \lambda S_N\llbracket a-T_Ma \rrbracket _{L^{N,\infty }\log ^{}L {(\Omega )}}\left\| \nabla u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}} \end{aligned}$$

and recalling the assumption (19) we have that by choosing M large enough and $\varepsilon$ small enough we get

$$\begin{aligned} \left\| \nabla u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}\lesssim & {} \left\| f\left| T_ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}+ \left\| F\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}+ \left\| u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}\\{} & {} + \left\| \phi \left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}. \end{aligned}$$

If we use Lemma 2.1 we can write

$$\begin{aligned} \left\| f\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}&\leqslant \left\| f\right\| _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L {(\Omega )}}\left\| \left( T_Ku\right) ^{\lambda -1}\right\| _{L^{\infty ,\frac{\lambda N}{\lambda -1}}\log ^{\frac{1-\lambda }{\lambda }}L {(\Omega )}}\\&=\left\| f\right\| _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L {(\Omega )}}\left\| T_Ku\right\| _{L^{\infty ,\lambda N}\log ^{-\frac{1}{\lambda }}L {(\Omega )}}^{\lambda -1} \end{aligned}$$

and similarly for F and u. We can then apply Corollary 2.3

$$\begin{aligned} \left\| T_Ku\right\| _{L^{\infty ,\lambda N}\log ^{-\frac{1}{\lambda }}L {(\Omega )}}^{\lambda -1}=\left\| \left| T_Ku\right| ^\lambda \right\| _{L^{\infty ,N}\log ^{-1}L{(\Omega )}}^{\frac{\lambda -1}{\lambda }}\lesssim \left\| \nabla \left| T_Ku\right| ^\lambda \right\| _{L^N {(\Omega )}}^{\frac{\lambda -1}{\lambda }}\lesssim \left\| \nabla u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N{(\Omega )}}^{\frac{\lambda -1}{\lambda }} \end{aligned}$$

to obtain

$$\begin{aligned} \left\| \nabla u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N {(\Omega )}}&\lesssim \left( \Vert f\Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}+\Vert F\Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}\right. \\ {}&\quad + \left. \Vert u\Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}+\Vert \phi \Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}\right) \left\| \nabla u\left| T_Ku\right| ^{\lambda -1}\right\| _{L^N{(\Omega )}}^{\frac{^\lambda -1}{\lambda }}\\&\lesssim \left( \Vert f\Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}+\Vert F\Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}\right. \\ {}&\quad + \left. \Vert u\Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}+\Vert \phi \Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}\right) ^\lambda . \end{aligned}$$

Taking the limit $K\rightarrow +\infty$ we finally get

$$\begin{aligned} \left\| \nabla |u|^\lambda \right\| _{L^N {(\Omega )}}\lesssim & {} \left( \Vert f\Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}+\Vert F\Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}+\Vert u\Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}\right. \\{} & {} \quad \left. +\Vert \phi \Vert _{L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L{(\Omega )}}\right) ^\lambda , \end{aligned}$$

which concludes the proof, since $u\in L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L(\Omega )\hookrightarrow W^{1,N}_0(\Omega )$.

Step 2: we get rid of assumption (48).

We consider the vector field $\hat{A}$ as in (29) and we define $\hat{\psi }:= \psi - \psi ^+$. As $\hat{\psi } \leqslant 0$ a.e. in $\Omega$, we obtain the existence of a function $\hat{u} \in \mathcal {K}_{\hat{\psi }}(\Omega )$ such that the following variational inequality

$$\begin{aligned} \begin{aligned} \int _{\Omega } \hat{A}(x, \hat{u},\nabla \hat{u}) \cdot \nabla (\hat{v} -\hat{u}) \,\mathrm d x \geqslant \langle \Phi ,\hat{v} -\hat{u} \rangle \end{aligned} \end{aligned}$$

(49)

holds true for every admissible function $\hat{v} \in \mathcal {K}_{\hat{\psi }} (\Omega )$. Since any $v \in \mathcal {K}_{ \psi } (\Omega )$ can be rewritten as $v= \hat{v} + \psi ^+$ for some $\hat{v} \in \mathcal {K}_{\hat{\psi }} (\Omega )$. Hence, the variational inequality (8) holds true with $u:=\hat{u} + \psi ^+$ and any admissible function $v \in \mathcal {K}^\prime _{\psi }(\Omega _T)$. It remains to show that u satisfies the required summability. By Step 1, we observe that $|\hat{u}|^\lambda \in W^{1,N}_0(\Omega )$ and so $\hat{u} \in L^{\infty ,\lambda N}\log ^{-\frac{1}{\lambda }}L(\Omega )$. On the other hand $\psi ^+ \in L^{\infty ,\lambda N}\log ^{-\frac{1}{\lambda }}L(\Omega )$ by Theorem 4.2 in [21] and this proves the result. $\square$

5.2 Boundedness

Let us now prove the boundedness result.

Proof of Theorem 1.3

We divide the proof in several steps.

Step 1: we prove the result under the assumption (48).

Let $k>0$ and let us define the function

$$\begin{aligned} z\in \mathbb {R} \mapsto \sigma _k(z)=\frac{\textrm{sign}(z)}{N-1}\left( (1+T_k|z|)^{1-N}-(1+|z|)^{1-N})\right) . \end{aligned}$$

We have $\sigma _k(u) \in W^{1,N}_0(\Omega )$ and

$$\begin{aligned} \nabla \sigma _k(u)=\frac{\nabla u}{(1+|u|)^N}\chi _{E_k}, \end{aligned}$$

where $E_k:=\{|u|>k\}$. It is not difficult to prove that $v_k:=u-\sigma _k(u) \in \mathcal {K} _\psi (\Omega )$. Indeed, $\sigma _k(u)=0$ on the set where $|u(x)|\leqslant k$. On the other hand, if $u(x)<-k$ then $\sigma _k(u)<0$. Finally, if $u >k$ we notice that $v_k=V(u)$ with

$$\begin{aligned} V(z):=z-\frac{(1+k)^{1-N}-(1+z)^{1 - N}}{N-1}, \end{aligned}$$

and $V'(z)>0$ for $z>k$, which gives $v_k>0\geqslant \psi$. We can therefore test our problem with $v_k$ and applying assumption (2) and Poincaré inequality we get

$$\begin{aligned} \alpha \int _{E_k}\frac{|\nabla u|^N}{(1+|u|)^N}\,\mathrm d x{} & {} \leqslant \int _{E_k}\frac{a^N|u|^N}{(1+|u|)^N}\,\mathrm d x + \int _{E_k}\frac{\phi ^N}{(1+|u|)^N}\,\mathrm d x \nonumber \\{} & {} \qquad + \int _{E_k}|f|^{N-1} |\sigma _k(u)|\,\mathrm d x+ \int _{E_k}|F|^{N-1} |\nabla \sigma _k(u)|\,\mathrm d x \nonumber \\{} & {} \leqslant \Vert a\Vert ^N_{L^N(\Omega )} + \Vert \phi \Vert ^N_{L^N(\Omega )} + C \left( \Vert f\Vert ^{N-1}_{L^N(\Omega )} + \Vert F\Vert ^{N-1}_{L^N(\Omega )} \right) \Vert \nabla \sigma _k(u)\Vert _{L^N(\Omega )}{.}\nonumber \\ \end{aligned}$$

(50)

We observe that $|\nabla \sigma _k(u)|^N \leqslant \frac{|\nabla u|^N}{(1+|u|)^N}\chi _{E_k}$. Hence, by using Young inequality and reabsorbing in the left–hand side, we obtain

$$\begin{aligned} \Vert \nabla \log (1+|u|)\Vert _{L^N(E_k)}\lesssim \Vert f\Vert _{L^N(E_k)}+\Vert F\Vert _{L^{N}(E_k)}+\Vert a\Vert _{L^N(E_k)}+\Vert \phi \Vert _{L^N(E_k)}. \end{aligned}$$

For subsequent estimates, it is convenient to compute the norm $\Vert \chi _{G}\Vert _{L^{\infty ,N}\log ^{-\gamma }L(\Omega )}$ of the characteristich function of a measurable set G contained in $\Omega$. As $\left( \chi _{G}\right) ^* = \chi _{(0,|G|)}$, the definition of $\Vert \cdot \Vert _{L^{\infty ,N}\log ^{-\gamma }L(\Omega )}$–norm leads to the following

$$\begin{aligned} \Vert \chi _{G}\Vert _{L^{\infty ,N}\log ^{-\gamma }L(\Omega )}&=\left( \int _0^{|G|}\frac{1}{t\left( 1+\log \frac{|\Omega |}{t}\right) ^{\gamma N}}\,\mathrm d t\right) ^{1/N} \\&=(\gamma N-1)^{-\frac{1}{N}}\left( 1+\log \frac{|\Omega |}{|G|}\right) ^{\frac{1}{N}-\gamma }. \end{aligned}$$

In the last line we compute the exact value of the integral since $\gamma > 1/N$. We proceed further and because of Lemma 2.1 we deduce

$$\begin{aligned} \Vert f\Vert _{L^N(E_k)}&=\Vert f\chi _{E_k}\Vert _{L^N(\Omega )}\\&\leqslant \Vert \chi _{E_k}\Vert _{L^{\infty ,N}\log ^{-\gamma }L (\Omega ) }\Vert f\Vert _{L^{N,\infty }\log ^{\gamma }L(\Omega ) }\\&=(\gamma N-1)^{-\frac{1}{N}}\left( 1+\log \frac{|\Omega |}{|E_k|}\right) ^{\frac{1}{N}-\gamma }\Vert f\Vert _{L^{N,\infty }\log ^{\gamma }L(\Omega )}, \end{aligned}$$

and similarly

$$\begin{aligned} \Vert F\Vert _{L^N(E_k)}\leqslant (\gamma N-1)^{-\frac{1}{N}}\left( 1+\log \frac{|\Omega |}{|E_k|}\right) ^{\frac{1}{N}-\gamma }\Vert F\Vert _{L^{N,\infty }\log ^{\gamma }L(\Omega )}, \end{aligned}$$

$$\begin{aligned} \Vert a\Vert _{L^N(E_k)}\leqslant (\gamma N-1)^{-\frac{1}{N}}\left( 1+\log \frac{|\Omega |}{|E_k|}\right) ^{\frac{1}{N}-\gamma }\Vert a\Vert _{L^{N,\infty }\log ^{\gamma }L(\Omega )}, \end{aligned}$$

$$\begin{aligned} \Vert \phi \Vert _{L^{N}(E_k)}\leqslant (\gamma N-1)^{-\frac{1}{N}}\left( 1+\log \frac{|\Omega |}{|E_k|}\right) ^{\frac{1}{N}-\gamma }\Vert \phi \Vert _{L^{N,\infty }\log ^{\gamma }L(\Omega )}. \end{aligned}$$

We take into account previous estimates and we get

$$\begin{aligned} \Vert \nabla \log (1+|u|)\Vert _{L^N(E_k)}\leqslant C \left( 1+\log \frac{|\Omega |}{|E_k|}\right) ^{\frac{1}{N}-\gamma } \end{aligned}$$

where

$$\begin{aligned} C=C\left( N,\gamma ,\Vert f\Vert _{L^{N,\infty }\log ^{\gamma }L(\Omega )},\Vert F\Vert _{L^{N,\infty }\log ^{\gamma }L(\Omega )},\Vert a\Vert _{L^{N,\infty }\log ^{\gamma }L(\Omega )},\Vert \phi \Vert _{L^{N,\infty }\log ^{\gamma }L(\Omega )}\right) . \end{aligned}$$

Let us define $w(z):=\log (1+|z|) \textrm{sign} \,z$ and $L:=\log (1+k)$. We set $G_L(m):=m-T_L m$ for $m\in \mathbb {R}$. Then $G_L (w(u)) \in W^{1,N}_0(\Omega )$ and in particular $G_L (w(u))=\textrm{sign}(u)\log \left( \frac{1+|u|}{1+k}\right) \chi _{E_k}$. Hence, Sobolev embedding theorem applied to $G_L (w(u))$ provides the estimate

$$\begin{aligned} \Vert \nabla \log (1+|u|)\Vert _{L^N(E_k)}&\geqslant \frac{1}{S_N}\left\| \log \left( \frac{1+|u|}{1+k}\right) \chi _{E_k}\right\| _{L^{\infty ,N}\log ^{-1}L(\Omega )}\\&\geqslant \frac{1}{S_N}\left\| \log \left( \frac{1+|u|}{1+k}\right) \chi _{E_h}\right\| _{L^{\infty ,N}\log ^{-1}L(\Omega )}\\&\geqslant \frac{1}{S_N}\log \left( \frac{1+h}{1+k}\right) \Vert \chi _{E_h}\Vert _{L^{\infty ,N}\log ^{-1}L(\Omega )}\\&\geqslant \frac{(N-1)^{-\frac{1}{N}}}{S_N}\log \left( \frac{1+h}{1+k}\right) \left( 1+\log \frac{|\Omega |}{|E_h|}\right) ^{-\frac{1}{N'}} \end{aligned}$$

as long as $h>k$. This implies

$$\begin{aligned} \left( 1+\log \frac{|\Omega |}{|E_h|}\right) ^{-\frac{1}{N'}}\lesssim \frac{\displaystyle \left( 1+\log \frac{|\Omega |}{|E_k|}\right) ^{\frac{1}{N}-\gamma }}{\displaystyle \log \frac{1+h}{1+k}} \end{aligned}$$

if $h>k>0$. If we set $h=\exp \eta -1$, $k=\exp \kappa -1$ and define, for $t>0$,

$$\begin{aligned} \phi (t)={\left\{ \begin{array}{ll} \displaystyle \left( 1+\log \frac{|\Omega |}{\left| E_{\exp t-1}\right| }\right) ^{-\frac{1}{N'}}&{}\quad \text {if }|E_{\exp t-1 }|>0\\ 0&{}\quad \text {otherwise} \end{array}\right. }, \end{aligned}$$

we obtain

$$\begin{aligned} \phi (\eta )\lesssim \frac{1}{\eta -\kappa }\phi ^\beta (\kappa ) \end{aligned}$$

with $\beta =\frac{\gamma -\frac{1}{N}}{1-\frac{1}{N}}>1$, so $\phi$ satisfies the assumptions [34, Lemme 4.1] and there is $\theta >\tau$ such that $\phi (\theta )=0$, or equivalently that $|u(x)|\leqslant \log \theta$ almost everywhere.

Step 2: we get rid of assumption (48).

We adopt the same argument as in previous Step 2. By adopting the same notation, the only fact that we need to prove is that $u=\hat{u}+\psi ^+$ is bounded in $\Omega$. As $\hat{u}$ is bounded in $\Omega$ by previous step, we show that $\psi ^+$ is bounded in $\Omega$ as well. As $\gamma >1$, we have $\nabla \psi ^+ \in L^{N,1}(\Omega )$ and so $\psi ^+$ is bounded in $\Omega$ by Theorem 4.5 in [21]. $\square$

6 The Lewy–Stampacchia inequality

6.1 A penalized problem

In order to prove Theorem 1.1, we need to consider a penalized problem of the type

$$\begin{aligned} {\left\{ \begin{array}{ll} -\text {div}A\left( x,u_\delta \vee \psi ,\nabla u_\delta \right) =\Phi +\displaystyle \frac{1}{\delta }(\psi -u_\delta )^+&{}\quad \text {in }\Omega \\ u_\delta =0&{}\quad \text {on }\partial \Omega \end{array}\right. } \end{aligned}$$

(51)

where $\delta >0$ and $s \vee t:=\max \left\{ s,t\right\}$ for all $s,t\in \mathbb {R}$. We add the following assumption on the obstacle function

$$\begin{aligned} \psi \leqslant 0 \quad \text {a.e. }in \quad \Omega . \end{aligned}$$

(52)

As a consequence of Theorem 4.1 we easily prove the following a priori estimates related to the penalized problem (51).

Corollary 6.1

Let assumptions (2)–(4), (19) (16) and (52) be in charge. For every $\delta >0$, there exists a solution $u_\delta$ to problem (51) satisfying the estimate

$$\begin{aligned} \Vert \nabla u_\delta \Vert _{L^N(\Omega )}^N\leqslant C \end{aligned}$$

(53)

for some positive constant C independent of $\delta$. In particular, there exists $u\in \mathcal {K}_\psi (\Omega )$ which is a solution to the variational inequality (8) and

$$\begin{aligned} u_\delta \rightarrow u&\quad \text {in }L^N(\Omega ),\end{aligned}$$

(54)

$$\begin{aligned} \nabla u_\delta \rightharpoonup \nabla u&\quad \text {in }L^N(\Omega ;{{\,\mathrm{\mathbb {R}}\,}}^N) \text { and a.e. in }\Omega . \end{aligned}$$

(55)

Proof

Estimate (53) can be proved by using the same argument which gives (43). It is clear that (53) implies the existence of $u \in W^{1,N}_0(\Omega )$ such that (54) holds and $\nabla u_\delta \rightharpoonup \nabla u$ weakly in $L^N(\Omega ;{{\,\mathrm{\mathbb {R}}\,}}^N)$. Next stage of our proof consists in proving that u is greater than or equal to the obstacle function $\psi$ a.e. in $\Omega$. To this aim, we test equation (51) by $(\psi -u_\delta )^+$, and we get in turn

$$\begin{aligned} \frac{1}{\delta }&\int _\Omega \left| \left( \psi -u_\delta \right) ^+\right| ^2\,\mathrm d x=-\langle \Phi ,\left( \psi -u_\delta \right) ^+\rangle +\int _\Omega A\left( x,u_\delta \vee \psi ,\nabla u_\delta \right) \cdot \nabla \left( \psi -u_\delta \right) ^+\,\mathrm d x\\&=-\langle \Phi ,\left( \psi -u_\delta \right) ^+\rangle +\int _\Omega A\left( x,\psi ,\nabla u_\delta \right) \cdot \nabla \left( \psi -u_\delta \right) ^+\,\mathrm d x\\&\leqslant \left| \langle \Phi ,\left( \psi -u_\delta \right) ^+\rangle \right| +\int _\Omega \left( \beta |\nabla u_\delta |^{N-1}+\left( b|u_\delta |\right) ^{N-1}+\phi ^{N-1}\right) \left| \nabla \left( \psi -u_\delta \right) ^+\right| \,\mathrm d x\\&\leqslant C\left( \Vert \Phi \Vert _{W^{-1,N'}(\Omega )}+ \Vert b \Vert _{L^{N,\infty }\log L(\Omega )} \Vert \nabla u_\delta \Vert _{L^N {(\Omega )}}^{N-1}+\Vert \nabla \psi \Vert _{L^N {(\Omega )}}^{N-1}+\Vert \phi \Vert _{L^N {(\Omega )}}^{N-1}\right) \\&\quad \ \times \Vert \nabla \left( \psi -u_\delta \right) ^+\Vert _{L^N(\Omega )}. \end{aligned}$$

We have that

$$\begin{aligned}{} & {} \Vert \nabla \left( \psi -u_\delta \right) ^+\Vert _{L^N(\Omega )}\leqslant \Vert \nabla \left( \psi -u_\delta \right) \Vert _{L^N(\Omega )}\leqslant \Vert \nabla u_\delta \Vert _{L^N(\Omega )}+\Vert \nabla \psi \Vert _{L^N(\Omega )} \end{aligned}$$

and using estimate (53) we obtain that

$$\begin{aligned} \frac{1}{\delta }\int _\Omega \left| \left( \psi -u_\delta \right) ^+\right| ^2\,\mathrm d x\leqslant C(N,\Omega ,\alpha ,a,\Phi ,\phi ,\psi ){,} \end{aligned}$$

where in particular the right hand side does not depend on $\delta$. Letting $\delta \rightarrow 0$ we obtain that $(\psi -u)^+=0$ almost everywhere, i.e. $u\in \mathcal {K}_\psi (\Omega )$.

We claim that $\nabla u_\delta \rightarrow \nabla u$ a.e. in $\Omega$. We test problem (51) with $T_1(u_\delta -u)$ to obtain

$$\begin{aligned}&\int _\Omega A(x,u_\delta \vee \psi ,\nabla u_\delta )\cdot \nabla (u_\delta -u)\chi _{\left\{ |u_\delta -u|\leqslant 1\right\} }\,\mathrm d x \\&\quad =\langle \Phi ,T_1(u_\delta -u)\rangle \\&\qquad +\frac{1}{\delta }\int _\Omega (\psi -u_\delta )^+T_1(u_\delta -u)\,\mathrm d x\\&\quad \leqslant \langle \Phi ,T_1(u_\delta -u)\rangle . \end{aligned}$$

Since $u_\delta -u\leqslant u_\delta -\psi <0$ when $\psi -u_\delta >0$ (up to a negligible set). Moreover, since $u\geqslant \psi$, the remaining term on the right hand side goes to zero as well, so that

$$\begin{aligned} \limsup _{\delta \rightarrow 0}\int _\Omega A(x,u_\delta \vee \psi ,\nabla u_\delta )\cdot \nabla (u_\delta -u)\chi _{\left\{ |u_\delta -u|\leqslant 1\right\} }\,\mathrm d x\leqslant 0. \end{aligned}$$

Using the fact that $u_\delta \rightarrow u$ in $L^N(\Omega )$ and assumption (2) we can apply the dominated convergence theorem to show that

$$\begin{aligned} \lim _{\delta \rightarrow 0}\int _\Omega A(x,u_\delta \vee \psi ,\nabla u)\cdot \nabla (u_\delta -u)\chi _{\left\{ |u_\delta -u|\leqslant 1\right\} }\,\mathrm d x=0 \end{aligned}$$

and therefore

$$\begin{aligned} \limsup _{\delta \rightarrow 0}\int _\Omega \left( A(x,u_\delta \vee \psi ,\nabla u_\delta )-A(x,u_\delta \vee \psi ,\nabla u)\right) \cdot \nabla (u_\delta -u)\chi _{\left\{ |u_\delta -u|\leqslant 1\right\} }\,\mathrm d x\leqslant 0. \end{aligned}$$

Assumption (4) implies that we must also have

$$\begin{aligned} \left( A(x,u_\delta \vee \psi ,\nabla u_\delta )-A(x,u_\delta \vee \psi ,\nabla u)\right) \cdot \nabla (u_\delta -u)\chi _{\left\{ |u_\delta -u|\leqslant 1\right\} }\rightarrow 0\quad \text {a.e. in }\Omega \end{aligned}$$

and since $u_\delta \rightarrow u$ in $L^N(\Omega )$

$$\begin{aligned} \left( A(x,u_\delta \vee \psi ,\nabla u_\delta )-A(x,u_\delta \vee \psi ,\nabla u)\right) \cdot \nabla (u_\delta -u)\rightarrow 0\quad \text {a.e. in }\Omega . \end{aligned}$$

We conclude the proof of our claim by using [26, Lemma 3.1]. $\square$

Proposition 6.2

Let assumptions (2)–(4), (16), (19) and (52) be in charge. Assume further that

$$\begin{aligned} g^-\in W_0^{1,N}(\Omega ).\end{aligned}$$

Then, the solution $u \in \mathcal {K}_\psi (\Omega )$ provided by Corollary 6.1 satisfies the Lewy–Stampacchia inequality (18).

Proof

To simplify the proof, we set

$$\begin{aligned} \mu _\delta =\frac{1}{\delta }\left( \psi -u_\delta \right) ^+{,} \end{aligned}$$

(56)

and also we define

$$\begin{aligned} z_\delta :=g^--\frac{1}{\delta }\left( \psi -u_\delta \right) ^+. \end{aligned}$$

Therefore, the equation in problem (51) gives us

$$\begin{aligned} z_\delta =g^++\text {div}\left[ A(x,u_\delta \vee \psi ,\nabla u_\delta ) - A(x,\psi ,\nabla \psi ) \right] {.} \end{aligned}$$

As $g^-\in W^{1,N}_0(\Omega )$, also $z_\delta \in W^{1,N}_0(\Omega )$, so we may test problem (51) by $-z_\delta ^-$ and by using the obvious relation $-z_\delta ^-z_\delta =|z_\delta ^-|^2$ we obtain

$$\begin{aligned} \int _\Omega |z^-_\delta |^2 \,\mathrm d x =\int _\Omega \left[ A(x,u_\delta \vee \psi ,\nabla u_\delta ) - A(x,\psi ,\nabla \psi ) \right] \cdot \nabla z_\delta ^- \,\mathrm d x-\langle g^+,z_\delta ^- \rangle . \end{aligned}$$

(57)

We observe that $z_\delta ^-$ vanishes on the set where $u_\delta \geqslant \psi$ and we recall that $g^+$ is a nonnegative element of $W^{-1,N^\prime }(\Omega )$. We deduce from (57) that

$$\begin{aligned} \int _\Omega |z^-_\delta |^2 \,\mathrm d x \leqslant \int _{\{z_\delta ^-\ne 0\}} \left[ A(x,\psi ,\nabla u_\delta ) - A(x,\psi ,\nabla \psi ) \right] \cdot \nabla z_\delta ^- \,\mathrm d x. \end{aligned}$$

(58)

As already mentioned, to obtain the latter relation we used the fact that $\psi >u_\delta$ a.e. in $\{z_\delta ^-\ne 0\}$. Moreover, it is clear that $g^- - \mu _\delta <0$ a.e. in $\{z_\delta ^-\ne 0\}$, and so (58) gives us

$$\begin{aligned} \begin{aligned} \int _\Omega |z^-_\delta |^2 \,\mathrm d x \leqslant&\frac{1}{\delta }\int _{\{z_\delta ^-\ne 0\}} \left[ A(x,\psi ,\nabla u_\delta ) - A(x,\psi ,\nabla \psi ) \right] \cdot ( \nabla \psi - \nabla u_\delta ) \,\mathrm d x \\&- \int _{\{z_\delta ^-\ne 0\}} \left[ A(x,\psi ,\nabla u_\delta ) - A(x,\psi ,\nabla \psi ) \right] \cdot \nabla g^- \,\mathrm d x{.} \end{aligned} \end{aligned}$$

(59)

By monotonicity, the first term in the right hand side of (59) is less than or equal to zero, so we have

$$\begin{aligned} \int _\Omega |z^-_\delta |^2 \,\mathrm d x \leqslant \int _{\Omega } \chi _{\{\psi >u_\delta \}} \left| A(x,\psi ,\nabla u_\delta ) - A(x,\psi ,\nabla \psi ) \right| |\nabla g^-| \,\mathrm d x. \end{aligned}$$

(60)

By using (54) and (55) we deduce that $\chi _{\{\psi >u_\delta \}} \left| A(x,\psi ,\nabla u_\delta ) - A(x,\psi ,\nabla \psi ) \right| \rightharpoonup 0$ weakly in $L^{N^\prime }(\Omega )$ and so $z^-_\delta \rightarrow 0$ strongly in $L^2(\Omega )$. Finally, we obtain the Lewy–Stampacchia inequality (18) passing to the limit as $\delta \rightarrow 0$ in $\mu _\delta - g^- \leqslant z_\delta ^-$. $\square$

We now consider the general case.

Proof of Theorem 1.1

We assume at first that (52) holds, namely $\psi \leqslant 0$ a.e. in $\Omega$. Let us consider a sequence $\hat{g}_n \in W^{1,N}_0(\Omega )$ with $\hat{g}_n \geqslant 0$ a.e. in $\Omega$ such that $\hat{g}_n \rightarrow g^-$ in $W^{-1,N^\prime }_0(\Omega )$. Accordingly, we define

$$\begin{aligned} \Phi _n: = g^+-\hat{g}_n-\text {div}A(x,\psi ,\nabla \psi ).\end{aligned}$$

By Proposition 6.2 we easily see that there exists $u_n\in W^{1,N}_0(\Omega )$ solving the obstacle problem

$$\begin{aligned} \int _\Omega A(x,u_n,\nabla u_n)\cdot \nabla (v-u_n)\,dx\geqslant \langle \Phi _n,v-u_n\rangle \quad \forall v\in K_\psi (\Omega ){.} \end{aligned}$$

Moreover, the Lewy–Stampacchia inequality

$$\begin{aligned} 0 \leqslant -{{\,\textrm{div}\,}}A(x,u_n,\nabla u_n) -\Phi _n \leqslant \hat{g}_n \end{aligned}$$

(61)

holds. We remark that $u_n-T_\sigma (u_n) \in \mathcal {K}_\psi (\Omega )$ and reasoning as in Proposition 4.1, the estimate

$$\begin{aligned} \Vert \nabla u_n\Vert _{L^N(\Omega )}\leqslant M \end{aligned}$$

holds with a constant $M>0$ independent from n, and satisfying a Lewy-Stampacchia inequality. As before, there exists $u\in W^{1,N}_0(\Omega )$ such that $u_n\rightarrow u$ in $L^N(\Omega )$ and $\nabla u_n\rightharpoonup \nabla u$ in $L^N(\Omega ;{{\,\mathrm{\mathbb {R}}\,}}^N)$. Testing with $w_n:=u_n-T_1(u_n-u)$ and reasoning as we did previously, we get $\nabla u_n\rightarrow \nabla u$ a.e. in $\Omega$.

We fix $\lambda >0$ and observe that $u_n-T_\lambda (u_n-v) \in \mathcal {K}_\psi (\Omega )$ for a fixed $v \in \mathcal {K}_\psi (\Omega )$. Therefore we have

$$\begin{aligned} \int _\Omega A(x,u_n,\nabla u_n)\cdot \nabla T_\lambda ( u_n-v)\,dx\leqslant \langle \Phi _n,T_\lambda (u_n-v)\rangle . \end{aligned}$$

Using again the dominated convergence theorem, we are able to pass to the limit as $n\rightarrow \infty$, to get

$$\begin{aligned} \int _\Omega A(x,u,\nabla u )\cdot \nabla T_\lambda ( u -v)\,dx\leqslant \langle \Phi ,T_\lambda (u -v)\rangle . \end{aligned}$$

It follows that

$$\begin{aligned} \int _\Omega A(x,u,\nabla u )\cdot \nabla ( u -v)\,dx\leqslant \langle \Phi , (u -v)\rangle \end{aligned}$$

by passing to the limit as $\lambda \rightarrow \infty$. On the other hand, the Lewy–Stampacchia inequality claimed in the statement of Theorem 1.1 follows by passing to the limit in (61). To get rid of assumption (52) we construct an operator $\tilde{A}$ as in Lemma 3.1 and use it to deduce a result for our case as done in the last parts of the proofs of Theorems 1.2 and 1.3. $\square$

7 Concluding remarks

A careful inspection of the proofs of both Theorems 1.2 and 1.3 allows us to conclude that those regularity results hold for all solutions to problem (9) under the same assumptions on $f,F,\phi$. Precisely, we have the following result.

Proposition 7.1

Let $u \in W^{1,N}_0(\Omega )$ solve the Dirichlet problem (11), under the assumptions (2)–(4). If $\phi \in L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L(\Omega ), f \in L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L(\Omega ), F \in L^{N,\lambda N}\log ^{\frac{\lambda -1}{\lambda }}L(\Omega ,\mathbb {R}^N)$ for some $\lambda >1$, then (20) holds true. Moreover, if $\phi ,f\in L^{N,\infty }\log ^{\gamma }L(\Omega )$, $F\in L^{N,\infty }\log ^{\gamma }L(\Omega ,\mathbb {R}^N)$ for some $\gamma >1$, then $u \in L^\infty (\Omega )$.

The first part of previous theorem would dare to say that boundedness of solutions to problem (9) can be obtained only by assuming that

$$\begin{aligned} a \in \textrm{clos} \left( L^{N,\infty }\log L(\Omega ),L^\infty (\Omega )\right) \quad \text {and} \quad f,F \in L^{N,\infty }\log L(\Omega ). \end{aligned}$$

Here $\textrm{clos} \left( L^{N,\infty }\log L(\Omega ),L^\infty (\Omega )\right)$ denotes the closure of $L^\infty (\Omega )$ in $L^{N,\infty }\log ^{}L (\Omega )$, or equivalently the class of all $g\in L^{N,\infty }\log ^{}L (\Omega )$ such that

$$\begin{aligned} {{\,\mathrm{\textrm{dist}}\,}}_{L^{N,\infty }\log ^{}L(\Omega )}(g,L^\infty (\Omega ))=0 \end{aligned}$$

so in particular, recalling that

$$\begin{aligned} {{\,\mathrm{\textrm{dist}}\,}}_{L^{N,\infty }\log ^{}L(\Omega )}(f,L^\infty (\Omega )) =\limsup _{\lambda \rightarrow \infty }\lambda \left( \mu _a(\lambda )\right) ^{1/N}\log \frac{|\Omega |}{\mu _a(\lambda )}. \end{aligned}$$

then $\textrm{clos} \left( L^{N,\infty }\log L(\Omega ),L^\infty (\Omega )\right)$ contains any function such that

$$\begin{aligned} \mathop {\mathrm {ess\,sup}}\limits _{\lambda >0}\lambda \left( \mu _a(\lambda )\right) ^{1/N}\left( 1+\log \frac{|\Omega |}{\mu _a(\lambda )}\right) \rho (\lambda )<\infty \end{aligned}$$

with $\rho$ being a positive function such that $\lim \nolimits _{\lambda \rightarrow \infty }\rho (\lambda )=\infty$. The following counterexample shows that the set of assumptions we introduced before does not lead to boundedness of solutions, even if the stronger assumption

$$\begin{aligned} f, F\in \textrm{clos} \left( L^{N,\infty }\log L(\Omega ),L^\infty (\Omega )\right) \end{aligned}$$

is in charge.

Example 7.1

Let $\theta \in (0,1)$ and B the unit ball in ${{\,\mathrm{\mathbb {R}}\,}}^2$. Consider, for $u\in W^{1,2}_0(B)$ the equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle -\Delta u-\text {div}\left( a(|x|)u(x)\frac{x}{|x|}\right) =-\text {div}\left( F(|x|)\frac{x}{|x|}\right) &{}\quad \text {in }B\\ u=0&{}\quad \text {on }\partial B \end{array}\right. } \end{aligned}$$

(62)

with

$$\begin{aligned} a(r)=\frac{1}{r\left( 1-\log r\right) \left( 1-\log \left( 1-\log r\right) \right) },\quad F(r)=-\frac{1}{r\left( 1-\log r\right) \left( 1-\log \left( 1-\log r\right) \right) ^{\theta }}{,} \end{aligned}$$

for $r\in (0,1)$. In particular, $a\in L^{2,\infty }(\log L)^{}(\log \log L)^{}(B)$ and $F\in L^{2,\infty }(\log L)(\log \log L)^{\theta }(B)$, which can be defined in an obvious way and are both contained in $\textrm{clos} \left( L^{2,\infty }\log L(B),L^\infty (B)\right)$. It can be shown that the function

$$\begin{aligned} u(x)=\frac{1}{\theta }\left( 1-\log \left( 1-\log \left| x\right| \right) \right) \left( 1-\left( 1-\log \left( 1-\log \left| x\right| \right) \right) ^{-\theta }\right) \end{aligned}$$

is the unique solution of problem (62). $\square$