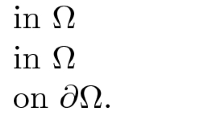$L^\infty$ a-priori estimates for subcritical p-laplacian equations with a Carathéodory non-linearity

Abstract

Let us consider a quasi-linear boundary value problem $-\Delta _p u= f(x,u),$ in $\Omega ,$ with Dirichlet boundary conditions, where $\Omega \subset \mathbb {R}^N$, with $p<N,$ is a bounded smooth domain strictly convex, and the non-linearity f is a Carathéodory function p-super-linear and subcritical. We provide $L^\infty$ a priori estimates for weak solutions, in terms of their $L^{p^*}$-norm, where $p^*= \frac{Np}{N-p}\$ is the critical Sobolev exponent. No hypotheses on the sign of the solutions, neither of the non-linearities are required. This method is based in elliptic regularity for the p-Laplacian combined either with Gagliardo–Nirenberg or with Caffarelli–Kohn–Nirenberg interpolation inequalities. By a subcritical non-linearity we mean, for instance, $|f(x,s)|\le |x|^{-\mu }\, \tilde{f}(s),$ where $\mu \in (0,p),$ and $\tilde{f}(s)/|s|^{p_{\mu }^*-1}\rightarrow 0$ as $|s|\rightarrow \infty$, here $p^*_{\mu }:=\frac{p(N-\mu )}{N-p}$ is the critical Hardy–Sobolev exponent. Our non-linearities includes non-power non-linearities. In particular we prove that when $f(x,s)=|x|^{-\mu }\,\frac{|s|^{p^*_{\mu }-2}s}{\big [\log (e+|s|)\big ]^\alpha },$ with $\mu \in [1,p),$ then, for any $\varepsilon >0$ there exists a constant $C_\varepsilon >0$ such that for any solution $u\in H^1_0(\Omega )$, the following holds

$$\begin{aligned} \Big [\log \big (e+\Vert u\Vert _{\infty }\big )\Big ]^\alpha \le C_\varepsilon \, \Big (1+\Vert u\Vert _{p^*}\Big )^{\, (p^*_{\mu }-p)(1+\varepsilon )}\,, \end{aligned}$$

where $C_\varepsilon$ is independent of the solution u.

1 Introduction

Let us consider the following quasi-linear boundary value problem involving the p-Laplacian

$$\begin{aligned} -\Delta _p u= f(x,u), \quad \text{ in } \Omega , \qquad u= 0,\quad \text{ on } \partial \Omega , \end{aligned}$$

(1.1)

where $\Delta _p (u)=$ div$(|Du|^{p-2}Du)$ is the p-Laplacian operator, $1<p<\infty$, $\Omega \subset \mathbb {R}^N$, $N>p,$ is a bounded, strictly convex, open subset with $C^{2}$ boundary $\partial \Omega$, and the non-linearity $f:\bar{\Omega }\times \mathbb {R}\rightarrow \mathbb {R}$ is Carathéodory function (that is, the mapping $f(\cdot ,s)$ is measurable for all $s\in \mathbb {R}$, and the mapping $f(x,\cdot )$ is continuous for almost all $x\in \Omega$), and subcritical (see definition 1.1).

We analyze the effect of the smoothness of the subcritical non-linearity $f=f(x,u)$ on the $L^\infty (\Omega )$ a priori estimates of weak solutions to (1.1). This study is usually focused on positive classical solutions, see the classical references of de Figueiredo-Lions-Nussbaum, and of Gidas-Spruck [15, 20], see also [7, 8].

A natural question concerning the class of uniformly bounded solutions is the following one,

• (Q1) those $L^\infty (\Omega )$ estimates apply also to a bigger class of solutions, in particular to weak solutions (and to changing sign solutions)?.

Another natural question with respect to the class of subcritical non-linearities, can be stated as follows,

• (Q2) those $L^\infty (\Omega )$ estimates are valid into a bigger class of non-linearities (not asymptotically powers), and in particular to non-smooth non-linearities (with possibly changing sign weights)?.

In this paper we extend the previous work in [28] for $p=2$, and provide sufficient conditions guarantying uniform $L^\infty (\Omega )$ a priori estimates for any $u\in W_0^{1,p}(\Omega )$ weak solution to (1.1), in terms of their $L^{p^*}(\Omega )$ bounds, in the class of Carathéodory subcritical generalized problems. In this class, we state that any set of weak solutions uniformly $L^{p^*} (\Omega )$ a priori bounded is universally $L^\infty (\Omega )$ a priori bounded. Our theorems allow changing sign weights, and singular weights, and also apply to changing sign solutions.

Problem (1.1) with $f(x,s)=|x|^{-\mu } |s|^{q-1}s,$ $\mu >0$, is known as Hardy’s problem, due to its relation with the Hardy–Sobolev inequality. The Caffarelli–Kohn–Nirenberg interpolation inequality for radial singular weights [6], states that whenever $0\le \mu \le p$,

$$\begin{aligned} p_{\mu }^*:=\frac{p(N-\mu )}{N-p}, \end{aligned}$$

is the critical exponent of the Hardy–Sobolev embedding $\quad W_0^{1,p}(\Omega )\hookrightarrow \$ $L^{p_{\mu }^*}(\Omega , |x|^{-\mu })\,$ (this embedding is continuous but not compact). For the case $0\le \mu \le p$, using a Pohozaev type identity, Pucci and Servadei prove some non-existence results in $\mathbb {R}^N$, [31]. Some existence and non-existence results for power like non-linearities can be found in [1, 18, 19, 22], see also [32] for the case $p=N$.

Usually the term subcritical non-linearity is reserved for power like non-linearities. Next, we expand this concept to non-linearities including the class $o\big (|s|^{p_{\mu }^*-1}\big )$.

Let

$$\begin{aligned} p_{N/r}^*:=\frac{p^*}{r'}=p^*\left( 1-\frac{1}{r}\right) , \end{aligned}$$

(1.2)

where $r'$ is the conjugate exponent of r, $1/r+1/r'=1$.

Definition 1.1

By a subcritical non-linearity we mean that f satisfies one of the two following growth conditions:

(H0) :

$$\begin{aligned} |f(x,s)|\le |a(x)|\, \tilde{f}(s) \end{aligned}$$

(1.3)

where $a\in L^r(\Omega )$ with $N/p<r\le \infty$, and $\tilde{f}:\mathbb {R}\rightarrow [0,+\infty )$ is continuous and satisfies

$$\begin{aligned} \tilde{f}(s)>0 \ \text {for}\ |s|>s_0,\ \text { and }\ \lim _{s \rightarrow \pm \infty } \frac{\tilde{f}(s)}{|s|^{p_{N/r}^*-1}}=0; \end{aligned}$$

(1.4)

or

(H0)’:

$$\begin{aligned} |f(x,s)|\le |x|^{-\mu }\, \tilde{f}(s), \end{aligned}$$

(1.5)

where $\mu \in (0,p),$ $0\in \overline{\Omega }$, and $\tilde{f}:\mathbb {R}\rightarrow [0,+\infty )$ is continuous and satisfies

$$\begin{aligned} \tilde{f}(s)>0 \ \text {for}\ |s|>s_0,\ \text { and }\ \lim _{|s| \rightarrow \infty } \ \frac{\tilde{f}(s)}{|s|^{p_{\mu }^*-1}}=0 \ . \end{aligned}$$

(1.6)

Remark 1.2

Obviously $|a(x)|\, \tilde{f}(s)\le |a(x)|\,(1+\tilde{f}(s))$, and we can always redefine $\tilde{f}$ in order to satisfy $\tilde{f}(s)>0 \ \text {for}\ |s|>0$.

Moreover, $\tilde{f}:\mathbb {R}\rightarrow [0,+\infty )$ from (H0) or (H0)’ satisfies the following hypothesis:

(H1) :

there exists a constant $c_0>0$ such that

$$\begin{aligned} \limsup _{s\rightarrow +\infty }\ \dfrac{\max _{[-s,s]}\, \tilde{f}}{\max \big \{\tilde{f}(-s),\tilde{f}(s)\big \}}\, \le \, c_0. \end{aligned}$$

(1.7)

Throughout the paper, we will assume either (H0) and (H1) or (H0)’ and (H1).

Remark 1.3

1. Observe that in particular, if $\tilde{f}(s)$ is monotone, then (H1) is obviously satisfied with $c_0=1$.

2. Assume that (H0) holds. Thanks to Sobolev embeddings, for any $u\in W_0^{1,p}(\Omega )$,

$$\begin{aligned} \tilde{f}(u)\in L^{\frac{p^*}{p_{N/r}^*-1}}(\Omega )&\qquad \text{ with }\quad \frac{p_{N/r}^*-1}{p^*}=1-\frac{1}{r}+\frac{1}{N}-\frac{1}{p}, \\ \text {and}\ f(\cdot ,u)\in L^{(p^*)'}(\Omega )&\qquad \forall a\in L^r(\Omega ), \text { where } \frac{1}{(p^*)'}=1-\frac{1}{p}+\frac{1}{N}. \end{aligned}$$

Moreover, since $r>N/p,$ then $p_{N/r}^*>p.$

3. Assume that (H0)’ holds. Again, by Sobolev embeddings, for any $u\in W_0^{1,p}(\Omega )$,

$$\begin{aligned} \tilde{f}(u)\in L^{\frac{p^*}{p_{\mu }^*-1}}(\Omega )&\qquad \text{ with }\quad \frac{p_{\mu }^*-1}{p^*}=1-\frac{\mu }{N}-\frac{1}{p}+\frac{1}{N}. \end{aligned}$$

Let $a(x)=|x|^{-\mu }$, $a\in L^q(\Omega )$ for any $q<N/\mu$, so $f(\cdot ,u)\in L^{q}(\Omega )$ for any $q<(p^*)'$.

From the sharp Caffarelli–Kohn–Nirenberg interpolation inequality for singular weights, (see [6], see also Theorem A.1 and Corollary A.2), it can be checked that if $u\in W_0^{1,p}(\Omega )$, then

$$\begin{aligned} f(\cdot ,u)\in L^{(p^*)'}(\Omega ) \qquad \text{ for } \text{ any }\quad \mu \le p-1+p/N \end{aligned}$$

(see Corollary A.2.(ii), (A.14)).

Also, if $u\in W^{1,q}(\Omega )$, with $q>p$, then

$$\begin{aligned} f(\cdot ,u)\in L^{(p^*)'}(\Omega ) \qquad \text{ for } \text{ any }\quad \mu \in (0,p) \end{aligned}$$

(see Corollary A.2.(iii.a), (A.16)).

Observe that $p_{\mu }^*>p$ for $\mu \in (0,p)$, and that $p-1+p/N<p$.

Definition 1.4

By a weak solution we mean a function $u \in W_0^{1,p}(\Omega )$ such that $f(\cdot ,u)\in L^{(p^*)'}(\Omega ),$ and

$$\begin{aligned} \int _{\Omega }|\nabla u|^{p-2}\nabla u\cdot \nabla \varphi =\int _{\Omega } f(x,u)\varphi , \quad \quad \forall \varphi \in W_0^{1,p}(\Omega ). \end{aligned}$$

Remark 1.5

The exponent $(p^*)'$ is called the duality exponent, and the condition $f(\cdot ,u)\in L^{(p^*)'}(\Omega )$ guarantees by Sobolev’s embeddings that $f(\cdot ,u)$ belongs to the dual space $W^{-1,p'}(\Omega )$. If other cases, we enter into the field of problems with measure data, and other definitions of solutions have to be considered (see [2, 25]).

Throughout the paper, by a solution we will refer to this weak solution. This definition of solution is tied to question (Q1). By an estimate of Brezis–Kato [4], based on Moser’s iteration technique [26], and elliptic regularity, we will state sufficient conditions guarantying that any weak solution to (1.1) with a Carathéodory subcritical non-linearity is a continuous function, and in fact it is a strong solution, see Lemma 2.2.

Our definition of a subcritical non-linearity includes non-linearities such as

$$\begin{aligned} f^{(1)}(x,s):= \frac{a(x)|s|^{p_{N/r}^*-2}s}{\big [\log (e+|s|)\big ]^\alpha }, \ \ \text {or}\ \ f^{(2)}(x,s):= \frac{|x|^{-\mu }|s|^{p_{\mu }^*-2}s}{\Big [\log \big [e+\log (1+|s|)\big ]\Big ]^\alpha }, \end{aligned}$$

for any $\alpha >0$, and either any $a\in L^r(\Omega ),$ with $N/p<r\le +\infty$, or $\mu \in (0,p)$. These non-linearities exemplify question (Q2).

One of our main results, Theorem 1.6, applied in particular to $f(x,s)=f^{(1)}(x,s)$ with $a\in L^r(\Omega )$ for $r\in (N/p,N]$, implies that for any $\varepsilon >0$ there exists a constant $C>0$ depending only on $\varepsilon ,\ \Omega ,$ r and N such that for any $u\in W_0^{1,p}(\Omega )$ solution to (1.1), the following holds:

$$\begin{aligned} \Big [\log \big (e+\Vert u\Vert _{\infty }\big )\Big ]^\alpha \le C \Vert a\Vert _r^{\ 1+\varepsilon } \ \Big (1+\Vert u\Vert _{p^*}\Big )^{\, (p_{N/r}^*-p)(1+\varepsilon )}, \end{aligned}$$

where C is independent of the solution u.

Related results concerning those non-power non-linearities $f(x,s)=f^{(1)}(x,s)$ with $r = \infty$ can be found in [14], and for $p=2$ in [12] analyzing what happen when $\alpha \rightarrow 0$, in [13] with changing sign weights, in [23] for systems, and in [29] for the radial case.

Moreover, our second main result, Theorem 1.7, applied to $f(x,s)=f^{(2)}(x,s)$ with $\mu \in [1,p^2/N],$ implies that for any $\varepsilon >0$ there exists a constant $C>0$ depending on $\varepsilon$, $\mu$, N, and $\Omega ,$ such that for any $u\in W_0^{1,p}(\Omega )$ solution to (1.1), the following holds:

$$\begin{aligned} \Big [\log \big [e+\log \big (1+\Vert u\Vert _{\infty }\big )\big ]\Big ]^\alpha \le C \ \Big (1+\Vert u\Vert _{p^*}\Big )^{\, (p_{\mu }^*-p)(1+\varepsilon )}, \end{aligned}$$

and where C is independent of the solution u.

To state our main results, for a non-linearity f satisfying (H0), let us define

$$\begin{aligned} h(s)=h_{N/r}(s):=\frac{|s|^{p_{N/r}^*-1}}{\displaystyle \max \big \{\tilde{f}(-s),\tilde{f}(s)\big \}}\qquad \text{ for }\quad |s|> 0, \end{aligned}$$

(1.8)

(see Remark 1.2). And for a non-linearity f satisfying (H0)’, define

$$\begin{aligned} h(s)=h_{\mu }(s):=\frac{|s|^{p_{\mu }^*-1}}{\displaystyle \max \big \{\tilde{f}(-s),\tilde{f}(s)\big \}}, \qquad \text{ for }\quad |s|> 0. \end{aligned}$$

(1.9)

By sub-criticality, (see (1.4) or (1.6) respectively),

$$\begin{aligned} h(s)\rightarrow \infty \qquad \text{ as }\quad s\rightarrow \infty . \end{aligned}$$

(1.10)

Let u be a solution to (1.1). We estimate $h\big (\Vert u\Vert _{\infty }\big )$, in terms of the $L^{p^*}$-norm of u. This result is robust, and holds for solutions and non-linearities without any sign restriction.

Our first main results is the following theorem.

Theorem 1.6

Assume that $f:\overline{\Omega }\times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function satisfying (H0)-(H1).

Then, for any $u\in W_0^{1,p}(\Omega )$ weak solution to (1.1), the following holds:

• (i) either there exists a constant $C>0$ such that $\Vert u\Vert _{\infty }\le C$, where C is independent of the solution u,

• (ii) either for any $\varepsilon >0$ there exists a constant $C>0$ such that

  $$\begin{aligned} h\big (\Vert u\Vert _{\infty }\big ) \le C \Vert a\Vert _r^{\ A+\varepsilon } \ \Big (1+\Vert u\Vert _{p^*}\Big )^{\, (p_{N/r}^*-p)(A+\varepsilon )}, \end{aligned}$$

  where h is defined by (1.8),

  $$\begin{aligned} A:= {\left\{ \begin{array}{ll} 1, &{}\qquad \text{ if }\quad r\le N,\\[.1cm] \displaystyle \frac{p_{N/r}^*-1}{p_{N/p}^*},&{}\qquad \text{ if }\quad r> N, \end{array}\right. } \end{aligned}$$

  and C depends only on $\varepsilon$, $c_0$ (defined in (1.7)), r, N, and $\Omega ,$ and it is independent of the solution u.

Our second main result is the following theorem.

Theorem 1.7

Assume that $f:\overline{\Omega }\times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function satisfying (H0)’ with $\mu \le p^2/N$, and (H1).

Then, for any $u\in W_0^{1,p}(\Omega )$ solution to (1.1), the following holds:

• (i) either there exists a constant $C>0$ such that $\Vert u\Vert _{\infty }\le C$, where C is independent of the solution u,

• (ii) either for any $\varepsilon >0$ there exists a constant $C>0$ such that

  $$\begin{aligned} h\big (\Vert u\Vert _{\infty }\big )\le C_\varepsilon \ \Big (1+\Vert u\Vert _{p^*}\Big )^{\, (p_{\mu }^*-p)(B+\varepsilon )}\ , \end{aligned}$$

  where h is defined by (1.9),

  $$\begin{aligned} B:= {\left\{ \begin{array}{ll} \displaystyle \frac{p_\mu ^*-1}{p_{N/p}^*}=1+\frac{p(1-\mu )}{(p-1)N},&{}\text {if}\ \mu \in (0,1) \cap (0,p^2/N],\\[.1cm] 1,&{}\text {if}\ \mu \in [1,p^2/N], \end{array}\right. } \end{aligned}$$

  (1.11)

  and C depends only on $\varepsilon$, $c_0$ (defined in (1.7)), $\mu$, N, and $\Omega ,$ and it is independent of the solution u.

As an immediate consequence of Theorem 1.6, and Theorem 1.7, as soon as we have a universal a priori $L^{p^*}$- norm for weak solutions to (1.1) in $W_0^{1,p}(\Omega ),$ then solutions are a priori universally bounded in the $L^{\infty }$- norm.

This results hold for positive, negative and changing sign non-linearities, and also for positive, negative and changing sign solutions. The techniques and ideas introduced in [28] are robust enough to be used for proving analogues results in other non-linear problems. Here we present the work for the p-Laplacian. The work for nonlinear boundary conditions is actually in preparation by Chhetri, Mavinga, and the author.

This paper is organized in the following way. Section 2 collects some well known results. In Sect. 3, we prove Theorem 1.6, using Gagliardo–Nirenberg interpolation inequality. In Sect. 4, we prove Theorem 1.7. It yields on the Caffarelli–Kohn–Nirenberg interpolation inequality, which is written in Appendix A, by the sake of completeness.

2 Preliminaries and known results

2.1 Gradient Regularity

We are going to use the following result about the summability of the gradient for solutions to equations involving the p-Laplacian operator.

Theorem 2.1

(Gradient Regularity) Let $\Omega$ be a smooth bounded domain in $\mathbb {R}^N$, $N \ge 2$, and let $u \in W_0^{1,p}(\Omega )$, $1< p < \infty$, be a solution to the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta _p (u) = g &{}\qquad \text {in }\, \Omega \\ \qquad \ \ u = \, 0 &{}\qquad \text {on }\, \partial \Omega , \end{array}\right. } \end{aligned}$$

with $g \in L^q(\Omega )$. We assume that

$$\begin{aligned} {\left\{ \begin{array}{ll} 1<q< \infty &{} \text { if } \quad p \ge N, \\ (p^{*})' \le q< \infty &{} \text { if } \quad 1< p < N. \end{array}\right. } \end{aligned}$$

Here $p^*= \frac{Np}{N-p}$ is the critical exponent for Sobolev embedding, and $(p^{*})' = \frac{p^*}{p^* -1}= \frac{Np}{Np-N+p}$, is its conjugate exponent.

• (i) If $q<N$, then $\ \Vert \nabla u \Vert _{L^{q^*(p-1)} (\Omega )} \le C \Vert g \Vert _ {L^q (\Omega ) }^{\,\frac{1}{(p-1)}}$

• (ii) If $q\ge N$, then $\ \Vert \nabla u \Vert _{L^{\sigma } (\Omega )} \le C \Vert g \Vert _ {L^q (\Omega ) }^{\,\frac{1}{(p-1)}}$ for any $\sigma < \infty$.

Here C is a constant that depends on p, N, q.

The previous theorem follows from different results proved in several papers (see [2, 5, 10, 16, 17, 21, 25], the survey [11], and the references therein), where more general situations are also considered.

2.2 Improved regularity of the weak solutions

We first collect a regularity Lemma for any weak solution to (1.1) with a non-linearity of sub-critical growth, in fact weak solutions in $W_0^{1,p}(\Omega )$ are in $L^q$ for any finite $q \ge 1$, see [30, Theorem 2.1, Theorem 2.2].

Lemma 2.2

(Improved regularity) Assume that $u\in W_0^{1,p}(\Omega )$ weakly solves (1.1) for a Carathéodory non-linearity $f:\bar{\Omega }\times \mathbb {R}\rightarrow \mathbb {R}$ with sub-critical growth, satisfying either (H0), either (H0)’ with $\mu \le p^2/N$, (see (1.3)–(1.4) or (1.5)–(1.6) respectively).

Then, $u\in L^q(\Omega )$ for any $1\le q<\infty$. Moreover, $u\in L^\infty (\Omega )$.

Proof

We first adapt to the p-Laplacian the technique used in [15] (based in Brezis–Kato, see [4]) to get the $L^q$ estimates for any finite $q \ge 1$. Let u be a weak solution to (1.1). For $t> 0,\ \lambda >0$, define

$$\begin{aligned} \varphi =\varphi _{t,\lambda }:= u \min \big \{|u|^{2t},\lambda ^2 \big \}, \end{aligned}$$

and

$$\begin{aligned} \psi =\psi _{t,\lambda }:= u \Big (\min \big \{|u|^{2t},\lambda ^2 \big \}\Big )^\frac{1}{p} . \end{aligned}$$

We observe that

$$\begin{aligned} |u|^{p-1}|\varphi |=|\psi |^p, \end{aligned}$$

(2.1)

and that $\varphi ,\psi \in W_0^{1,p}(\Omega )$ since $u \in W_0^{1,p}(\Omega )$, and $\varphi ,\ \psi ,$ $\nabla \varphi ,\ \nabla \psi \in L^p(\Omega )$. Indeed,

$$\begin{aligned} \nabla \big (\min \{|u|^{2t}, \lambda ^2\}\big ) =\left\{ \begin{array}{ll} 2t\, u |u|^{2t-2}\nabla u; \quad &{}|u|^t < \lambda \\ \\ 0; \quad &{} |u|^t > \lambda , \end{array} \right. \end{aligned}$$

(2.2)

and

$$\begin{aligned} \nabla \Big (\big (\min \big \{|u|^{2t},\lambda ^2 \big \}\big )^\frac{1}{p}\Big ) =\left\{ \begin{array}{ll} \frac{2t}{p}\, u |u|^{\frac{2t}{p}-2}\nabla u; \quad &{}|u|^t < \lambda \\ \\ 0; \quad &{} |u|^t > \lambda , \end{array} \right. \end{aligned}$$

(2.3)

so $\nabla \varphi$ is given by

$$\begin{aligned} \nabla \varphi = \left\{ \begin{array}{ll} (1+2t)|u|^{2t}\nabla u; \quad &{}|u|^{t} \le \lambda ,\\ \\ \lambda ^2 \nabla u; \quad &{}|u|^t >\lambda , \end{array} \right. \end{aligned}$$

(2.4)

and $\nabla \psi$ by

$$\begin{aligned} \nabla \psi = \left\{ \begin{array}{ll} (1+\frac{2t}{p})|u|^{\frac{2t}{p}}\nabla u; \quad &{}|u|^{t} \le \lambda ,\\ \\ \lambda ^\frac{2}{p} \nabla u; \quad &{}|u|^t >\lambda . \end{array} \right. \end{aligned}$$

(2.5)

In particular

$$\begin{aligned} \int _{\Omega }|\nabla \varphi |^{p}&= (1+2t)^p\,\int _{\Omega \cap \{|u|^t< \lambda \}} |u|^{2tp}|\nabla u|^{p}\, +\lambda ^{2p}\,\int _{\Omega \cap \{|u|^t > \lambda \}} |\nabla u|^{p}\\&\le (1+2t)^p\,\lambda ^{2p}\,\int _{\Omega } |\nabla u|^{p}<+\infty \,, \end{aligned}$$

so, for each $t> 0,\ \lambda >0$ fixed, $\varphi =\varphi _{t,\lambda } \in W_0^{1,p}(\Omega )$. Likewise

$$\begin{aligned} \int _{\Omega }|\nabla \psi |^{p}= \Big (1+\frac{2t}{p}\Big )^p\int _{\Omega \cap \{|u|^t< \lambda \}} |u|^{2t}|\nabla u|^{p} +\lambda ^2\,\int _{\Omega \cap \{|u|^t > \lambda \}} |\nabla u|^{p}<+\infty , \end{aligned}$$

and, for each $t> 0,\ \lambda >0$ fixed, $\psi =\psi _{t,\lambda } \in W_0^{1,p}(\Omega )$.

Now, using (2.4), we get

$$\begin{aligned} \int _{\Omega }|\nabla u|^{p-2}\nabla u\cdot \nabla \varphi = (1+2t)\,\int _{\Omega \cap \{|u|^t < \lambda \}} |u|^{2t}|\nabla u|^{p}\, +\lambda ^2\,\int _{\Omega \cap \{|u|^t > \lambda \}} |\nabla u|^{p}, \end{aligned}$$

hence

$$\begin{aligned} \int _{\Omega }|\nabla \psi _{t,\lambda }|^{p}\le C \int _{\Omega }|\nabla u|^{p-2}\nabla u\cdot \nabla \varphi _{t,\lambda }, \end{aligned}$$

(2.6)

for $C=C(t,p):=\max \Big \{1,\frac{\left( 1+\frac{2t}{p}\right) ^p}{1+2t}\Big \}.$ Now, using Sobolev embeddings on the previous inequality, and testing the equation $- \Delta _p u = f(x,u)$ with $\varphi$, we can write

$$\begin{aligned} \Vert \psi \Vert _{p^*}^{\, p}&\le C_{t}\int _{\Omega } f(x,u)\varphi , \end{aligned}$$

where $C_{t}$ is a uniform constant depending on t,  p,  N, and $\Omega$, but independent of $\lambda$.

(i) We start assuming (H0), see (1.3)–(1.4). By sub-criticality, (see (1.4)), for any $\varepsilon >0$, there exists $s_{\varepsilon }'$ such that

$$\begin{aligned} |f(x,s)| \le \varepsilon \, |a(x)|\, |s|^{p_{N/r}^*-1} \qquad \text{ if }\quad s \ge s_{\varepsilon }', \end{aligned}$$

so, for some constant $C_1>0$ depending on $\varepsilon$ but independent of $\lambda$, we get that

$$\begin{aligned} \Vert \psi \Vert _{p^*}^{\, p}&\le C_t \left( C_1+\varepsilon \int _{\Omega }|a(x)|\, |u|^{p_{N/r}^*-1}|\varphi | \right) \\&= C_t + \varepsilon C_{t} \int _{\Omega } |a(x)|\, |u|^{p_{N/r}^*-p} |\psi |^p , \end{aligned}$$

where we have used (2.1). By Hölder’s inequality with exponents r, $\frac{Nr}{pr-N}$, and $\frac{p^*}{p}$ (we observe that $\frac{1}{r}+\frac{pr-N}{Nr}+\frac{p}{p^*}=\frac{1}{r}+\frac{p}{N}-\frac{1}{r}+1-\frac{p}{N}=1$), and taking into account that $\left( p_{N/r}^*-p\right) \frac{Nr}{pr-N}=p^*$, we get that

$$\begin{aligned} \Vert \psi \Vert _{p^*}^{\, p}&\le C_t + \varepsilon C_{t} \Vert a\Vert _r \left( \int _{\Omega }\left( |u|^{p_{N/r}^*-p}\right) ^{\frac{Nr}{pr-N}} \right) ^{\frac{pr-N}{Nr}} \Vert \psi \Vert _{p^*}^{\, p} \\&=C_t +\varepsilon C_{t}\Vert a\Vert _r \left( \int _{\Omega }|u|^{p^*} \right) ^{\frac{pr-N}{Nr}}\Vert \psi \Vert _{p^*}^{\, p}\\&= C_t + \varepsilon C_{t}\Vert a\Vert _r \,\Vert u\Vert _{p^*}^{p_{N/r}^*-p} \Vert \psi \Vert _{p^*}^{\, p}\,. \end{aligned}$$

Since $u\in W_0^{1,p}(\Omega )$, we have that $\Vert u \Vert _{p^*}$ is bounded. Now, taking $\varepsilon$ small, for any fixed $0< t < \infty$, we get that, $\Vert \psi _{t,\lambda }\Vert _{p^*}$ is bounded with a bound depending on t, but independent of $\lambda$. Letting $\lambda \rightarrow \infty$, we deduce that $\int _\Omega |u|^{\frac{p+2t}{p}p^*}$ is bounded for any fixed $0< t < \infty$. Consequently, $\int _\Omega |u|^{ q}$ is bounded for any fixed $q > p^*$ (and since $\Omega$ is bounded in fact for any $q \in [ 1, \infty )$).

Finally, under (H0), $r>N/p$, and so $r^*(p-1)>N$. Hence, combining the above estimates, with the gradient regularity of Theorem 2.1, and using Sobolev embeddings, we deduce that $u\in L^\infty (\Omega )$.

(ii) We now assume (H0)’ with $\mu \le p^2/N$, see (1.5)–(1.6). By sub-criticality, (see (1.6)), for any $\varepsilon >0$, there exists $s_{\varepsilon }$ such that

$$\begin{aligned} |f(x,s)| \le \varepsilon \, |x|^{-\mu }|s|^{p_{\mu }^*-1} \qquad \text{ if }\quad s \ge s_{\varepsilon }, \end{aligned}$$

so that denoting by $C_1$ a constant depending on $\varepsilon$ but independent of $\lambda$, using (2.1), and by Hölder’s inequality with exponents $\frac{p^*}{p^*-p}$, $\frac{p^*}{p}$, we get that

$$\begin{aligned} \Vert \psi \Vert _{p^*}^{\, p}&\le C_t \left( C_1+\varepsilon \int _{\Omega }|x|^{-\mu } |u|^{p_{\mu }^*-1}|\varphi |\, dx \right) \nonumber \\&= C_t + \varepsilon C_{t} \int _{\Omega } |x|^{-\mu }|u|^{p_{\mu }^*-p} |\psi |^{p} \, dx \nonumber \\&\le C_t + \varepsilon C_{t} \left( \int _{\Omega } \left( |x|^{-\mu }|u|^{p_{\mu }^*-p}\right) ^{\frac{p^*}{p^*-p}}\right) ^{\frac{p^*-p}{p^*}} \left( \int _{\Omega }|\psi |^{p^*} \right) ^{\frac{p}{p^*}}\nonumber \\&= C_t + \varepsilon C_{t} \big \Vert |x|^{-\gamma }u\big \Vert _\rho ^{p_\mu ^*-p}\, \Vert \psi \Vert _{p^*}^{p}\,, \end{aligned}$$

where $\gamma :=\frac{\mu }{p_\mu ^*-p}$, and $\rho :=\frac{(p_\mu ^*-p)p^*}{p^*-p}\,$.

Now, since Caffarelli–Kohn–Nirenberg interpolation inequality, (see (A.12)–(A.13))

$$\begin{aligned} \big \Vert |x|^{-\gamma }u\big \Vert _\rho \le C\, \Vert \nabla u\Vert _{p}, \end{aligned}$$

(2.7)

where

$$\begin{aligned} \frac{1}{\rho }-\frac{\gamma }{N}=\frac{1}{p^*}, \qquad \text{ and }\quad 0< \gamma \le 1, \end{aligned}$$

(2.8)

which trivially holds for any $\mu \le p^2/N$. Then, the above can be written as

$$\begin{aligned} \Vert \psi \Vert _{p^*}^{p} \le C_t + \varepsilon C_{t}\, \Vert \nabla u\Vert _{p}^{\ p_\mu ^*-p}\, \Vert \psi \Vert _{p^*}^{p} \end{aligned}$$

Since $u\in W_0^{1,p}(\Omega )$, we have that $\Vert \nabla u\Vert _{p}$ is bounded. Now, taking $\varepsilon$ small, for any fixed $0< t < \infty$ we get that $\Vert \psi _{t,\lambda }\Vert _{p^*}$ is bounded with a bound independent of $\lambda$. Letting $\lambda \rightarrow \infty$, we deduce that $\int _\Omega |u|^{ \frac{p+2t}{p}p^*}$ is bounded, for any fixed $0< t < \infty$. Consequently, $\int _\Omega |u|^{ q}$ is bounded for any fixed $q > p^*$ (and since $\Omega$ is bounded in fact for any $q \in [ 1, \infty )$).

Finally, under hypothesis (H0)’, $\mu <p$, and so $\left( \frac{N}{\mu }\right) ^*(p-1)>N$. Hence, combining the above estimates, with the gradient regularity of Theorem 2.1, and using Sobolev embeddings, we deduce that $u\in L^\infty (\Omega )$.

3 Estimates of the $L^\infty$-norm of the solutions to (1.1) in presence of a Carathéodory non-linearity

Under hypothesis (H0)-(H1), we establish an estimate for the function h applied to the $L^\infty (\Omega )$-norm of any $u\in W_0^{1,p}(\Omega )$ solution to (1.1), in terms of their $L^{p^*} (\Omega )$-norm. From now on, C denotes several constants that may change from line to line, and are independent of u.

3.1 Proof of Theorem 1.6

The arguments of the proof use Gagliardo–Nirenberg interpolation inequality (see [27]), and are inspired in the equivalence between uniform $L^{p^*}(\Omega )$ a priori bounds and uniform $L^\infty (\Omega )$ a priori bounds for solutions to subcritical elliptic equations, see [9, Theorem 1.2] for the quasi-linear case and $f=f(u)$, and [24, Theorem 1.3] for the p-Laplacian and $f=f(x,u)$.

We first use elliptic regularity and Sobolev embeddings, and next, we invoke the Gagliardo–Nirenberg interpolation inequality (see [27]).

Proof

Let $\{u_k\}\subset W_0^{1,p}(\Omega )$ be any sequence of weak solutions to (1.1). Since Lemma 2.2, in fact $\{u_k\}\subset W_0^{1,p}(\Omega )\cap L^\infty (\Omega )$. If $\Vert u_k \Vert _{\infty }\le C,$ then (i) holds. Now, we argue on the contrary, assuming that there exists a sequence $\Vert u_k \Vert _{\infty } \rightarrow + \infty$ as $k \rightarrow \infty .$

We split the proof in two steps. Firstly, we write an $W^{1,q^*(p-1)}$ estimate for $q\in \big (N/p,\min \{r,N\}\big )$, and observe that $q^*(p-1)>N.$ Secondly, we invoke the Gagliardo–Nirenberg interpolation inequality for the $L^\infty$-norm in terms of its $W^{1,q^*(p-1)}$-norm and its $L^{p^*}$-norm.

Step 1. $W^{1,q^*(p-1)}$ estimates for $q\in \big (N/p,\min \{r,N\}\big )$.

Let us denote by

$$\begin{aligned} M_k:=\max \Big \{\tilde{f}\big (-\Vert u_k\Vert _{\infty }\big ),\tilde{f}\big (\Vert u_k\Vert _{\infty }\big )\Big \} \ge \frac{1}{2c_0} \,\max _{[-\Vert u_k\Vert _{\infty },\Vert u_k\Vert _{\infty }]}\tilde{f}, \end{aligned}$$

(3.1)

where the inequality holds by hypothesis (H1), see (1.7).

Let us take q in the interval $(N/p,N)\cap (N/p,r).$ Growth hypothesis (H0)(see (1.3)–(1.4)), hypothesis (H1) (see (1.7)), and Hölder inequality, yield the following

$$\begin{aligned} \displaystyle \int _{\Omega }\left| f\big (x,u_k(x)\big )\right| ^q\, dx&\le \int _{\Omega } |a(x)|^q \left( \tilde{f}\big (u_k(x)\big )\right) ^{q}\, dx\nonumber \\&=\int _{\Omega } |a(x)|^q \left( \tilde{f}\big (u_k(x)\big )\right) ^{t} \, \left( \tilde{f}\big (u_k(x)\big )\right) ^{q-t}\, dx\nonumber \\&\le C \left[ \int _{\Omega } |a(x)|^q\ \left( \tilde{f}\big (u_k(x)\big )\right) ^{t} \,dx\right] \ M_k^{\ q-t} \nonumber \\&\le C \left( \int _{\Omega } |a(x)|^{qs} \,dx\right) ^\frac{1}{s} \left( \int _{\Omega } \left( \tilde{f}\big (u_k(x)\big )\right) ^{ts'} \,dx\right) ^\frac{1}{s'} \ M_k^{\ q-t} \nonumber \\&\le C\Vert a\Vert _r^q\ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{p^*}{p_{N/r}^*-1}}\Big )^{t}\ M_k^{\ q-t}, \end{aligned}$$

(3.2)

where $\frac{1}{s}+\frac{1}{s'}=1$, $qs=r$, $C=c_0^{q-t}$ (for $c_0$ defined in (1.7)), and $ts'=\frac{p^*}{p_{N/r}^*-1}$, so

$$\begin{aligned} t&:=\frac{p^*}{p_{N/r}^*-1}\left( 1-\frac{q}{r}\right)<q \\&\iff \frac{1}{q}-\frac{1}{r}<\frac{p_{N/r}^*-1}{p^*} =1-\frac{1}{r}-\frac{1}{p}+\frac{1}{N} \nonumber \\&\iff \frac{1}{q}<1-\frac{1}{p}+\frac{1}{N}\iff \frac{1}{q}<1-\frac{1}{p^*}=\frac{1}{(p^*)'}\ \checkmark \nonumber \end{aligned}$$

(3.3)

since $p/N<1-\frac{1}{p^*}\iff p<N \checkmark$, and $q>N/p>(p^*)'.$

Since the gradient regularity for the p-Laplacian (see Theorem 2.1) we have that

$$\begin{aligned} \Vert \nabla u_k\Vert _{L^{q^*(p-1)} (\Omega )}\le C\ \left\| f\big (\cdot ,u_k(\cdot )\big )\right\| _q^{\ \frac{1}{p-1}}, \end{aligned}$$

(3.4)

where $1/q^*=1/q-1/N$, and $C=C(c_0,N,p,q,|\Omega |)$ and it is independent of u.

Now, substituting (3.2) into (3.4)

$$\begin{aligned} \Vert \nabla u_k\Vert _{L^{q^*(p-1)} (\Omega )} \le C\ \left( \Vert a\Vert _r\ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{p^*}{p_{N/r}^*-1}}\Big )^\frac{t}{q}\ M_k^{\ 1-\frac{t}{q}}\right) ^{\ \frac{1}{p-1}}, \end{aligned}$$

Step 2. Gagliardo–Nirenberg interpolation inequality.

Observe that since $q>N/p$, then $q^*(p-1)>N.$ Thanks to the Gagliardo–Nirenberg interpolation inequality, there exists a constant $C=C(N,q,|\Omega |)$ such that

$$\begin{aligned} \Vert u_k\Vert _{\infty }\le C \Vert \nabla u_k\Vert _{q^*(p-1)}^\sigma \ \Vert u_k\Vert _{p^*}^{1-\sigma } \end{aligned}$$

where

$$\begin{aligned} \nonumber \frac{1-\sigma }{p^*}&=\sigma \left( \frac{1}{N}-\frac{1}{q^*(p-1)}\right) \\&=\frac{\sigma }{p-1}\left( \frac{p-1}{N}-\frac{1}{q}+\frac{1}{N}\right) =\frac{\sigma }{p-1}\left( \frac{p}{N}-\frac{1}{q}\right) \nonumber \\&=\frac{\sigma }{p-1}\left[ 1-\frac{1}{q}-p\left( \frac{1}{p}-\frac{1}{N}\right) \right] =\frac{\sigma }{(p-1)p^*}\left( p_{N/q}^*-p\right) . \end{aligned}$$

(3.5)

Hence

$$\begin{aligned} \Vert u_k\Vert _{\infty }\le C \left[ \Vert a\Vert _r\ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{p^*}{p_{N/r}^*-1}}\Big )^{\frac{t}{q}}\ M_k^{\ 1-\frac{t}{q}} \right] ^\frac{\sigma }{p-1} \ \Vert u_k\Vert _{p^*}^{1-\sigma }, \end{aligned}$$

(3.6)

where $C=C(c_0,r,N,q,|\Omega |)$.

From definition of $M_k$ (see (3.1)), and definition of h (see (1.8)), we deduce that

$$\begin{aligned} M_k =\frac{\Vert u_k\Vert _{\infty }^{\ p_{N/r}^*-1}}{h\big (\Vert u_k\Vert _{\infty }\big )}. \end{aligned}$$

From (3.5)

$$\begin{aligned} \frac{1}{\sigma }&=1+\frac{1}{p-1}\left[ p_{N/q}^*-p\right] =\frac{1}{p-1}\left( p_{N/q}^*-1\right) . \end{aligned}$$

(3.7)

Moreover, since definition of t (see (3.3)), and definition of $p_{N/r}^*$ (see (1.2)

$$\begin{aligned} 1-\frac{t}{q}&=\frac{p^*\left( 1-\frac{1}{r}\right) -1-p^*\left( \frac{1}{q}-\frac{1}{r}\right) }{p_{N/r}^*-1} =\frac{p_{N/q}^*-1}{p_{N/r}^*-1}, \end{aligned}$$

(3.8)

which, joint with (3.7), yield

$$\begin{aligned} \left[ 1-\frac{t}{q}\right] \,\frac{\sigma }{p-1}\,{(p_{N/r}^*-1)}=1. \end{aligned}$$

Now (3.6) can be rewritten as

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )^{\ (1-\frac{t}{q})\frac{\sigma }{p-1}}\le C \left[ \Vert a\Vert _r\ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{p^*}{p_{N/r}^*-1}}\Big )^{\frac{t}{q}}\ \right] ^\frac{\sigma }{p-1} \ \Vert u_k\Vert _{p^*}^{1-\sigma }, \end{aligned}$$

or equivalently

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )\le C \Vert a\Vert _r^{\ \theta } \ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{p^*}{p_{N/r}^*-1}}\Big )^{\theta -1}\ \ \Vert u_k\Vert _{p^*}^{\ \vartheta }, \end{aligned}$$

where

$$\begin{aligned} \theta&:=(1-t/q)^{-1}=\frac{p_{N/r}^*-1}{p_{N/q}^*-1}, \end{aligned}$$

(3.9)

$$\begin{aligned} \vartheta&:=\frac{1-\sigma }{\sigma }(1-t/q)^{-1}(p-1) = \theta \ (p_{N/q}^*-p), \end{aligned}$$

(3.10)

see (3.8) and (3.5). Observe that since $q< r$, then $\theta > 1$. Moreover, since (3.9)

$$\begin{aligned} \theta -1 =\frac{p_{N/r}^*-p_{N/q}^*}{p_{N/q}^*-1}. \end{aligned}$$

(3.11)

Furthermore, from sub-criticality, see (1.4)

$$\begin{aligned} \int _\Omega |\tilde{f}(u_k) |^{\frac{p^*}{p_{N/r}^*-1}} \le C \left( 1+\int _\Omega |u_k|^{{p^*}}\, dx\right) , \end{aligned}$$

so

$$\begin{aligned} \Vert \tilde{f}(u_k) \Vert _{\frac{p^*}{p_{N/r}^*-1}} \le C \left( 1+\Vert u_k\Vert _{{p^*}}^{p_{N/r}^*-1}\right) . \end{aligned}$$

Consequently

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )\le C \Vert a\Vert _r^{\ \theta } \ \Big (1+\Vert u_k\Vert _{{p^*}}^{\Theta }\Big ), \end{aligned}$$

with

$$\begin{aligned} \Theta :=(p_{N/r}^*-1)(\theta -1)+\vartheta =(p_{N/r}^*-p)\theta , \end{aligned}$$

where we have used (3.11), (3.10), and (3.9).

Fixed $N>p$ and $r>N/p$, the function $q\rightarrow \theta =\theta (q)$ for $q\in \big (N/p,\min \{r,N\}\big )$, is decreasing, so

$$\begin{aligned} \inf _{q\in (N/p,\min \{r,N\})} \theta (q)=\theta \big (\min \{r,N\}\big )=A:={\left\{ \begin{array}{ll} 1,&{}\text {if}\ r\le N,\\ \frac{p_{N/r}^*-1}{p_{N/p}^*},&{}\text {if}\ r> N. \end{array}\right. } \end{aligned}$$

Finally, and since the infimum is not attained in $\big (N/p,\min \{r,N\}\big )$, for any $\varepsilon >0$, there exists a constant $C>0$ such that

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )\le C\ \Vert a\Vert _r^{\ A+\varepsilon } \ \Big (1+\Vert u_k\Vert _{p^*}^{\, (p_{N/r}^*-p)(A+\varepsilon )}\Big ), \end{aligned}$$

where $C=C(\varepsilon ,c_0,r,N,|\Omega |),$ ending the proof.

We end this section with an immediate corollary of Theorem 1.6: any sequence of solutions in $W_0^{1,p}(\Omega )$, uniformly bounded in the $L^{p^*} (\Omega )$-norm, is also uniformly bounded in the $L^{\infty } (\Omega )$-norm.

Corollary 3.1

Let $f:\overline{\Omega }\times \mathbb {R}\rightarrow \mathbb {R}$ be a Carathéodory function satisfying (H0)–(H1).

Let $\{u_k\}\subset W_0^{1,p}(\Omega )$ be any sequence of solutions to (1.1) such that there exists a constant $C_0>0$ satisfying

$$\begin{aligned} \Vert u_k\Vert _{{p^*}} \le C_0. \end{aligned}$$

Then, there exists a constant $C>0$ such that

$$\begin{aligned} \Vert u_k\Vert _{\infty } \le C. \end{aligned}$$

(3.12)

Proof

We reason by contradiction, assuming that (3.12) does not hold. So, at least for a sub-sequence again denoted as $u_k$, $\Vert u_k\Vert _{\infty } \rightarrow \infty$ as $k \rightarrow \infty .$ Now part (ii) of the Theorem 1.6 implies that

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big ) \le C. \end{aligned}$$

(3.13)

From hypothesis (H0)(see in particular (1.10)), for any $\varepsilon >0$ there exists $s_1>0$ such that $h(s)\ge 1/\varepsilon$ for any $s\ge s_1,$ and so $h\big (\Vert u_k\Vert _{\infty }\big )\ge 1/\varepsilon$ for any k big enough. This contradicts (3.13), ending the proof.

4 Estimates of the $L^\infty$-norm of the solutions to (1.1) in presence of radial singular weights

We start this section with their corresponding immediate corollary of Theorem 1.7: any sequence of solutions in $W_0^{1,p}(\Omega )$, uniformly bounded in the $L^{p^*} (\Omega )$-norm, is also uniformly bounded in the $L^{\infty } (\Omega )$-norm. Their proof is identical to that of Corollary 3.1, we omit it.

Corollary 4.1

Let $f:\overline{\Omega }\times \mathbb {R}\rightarrow \mathbb {R}$ be a Carathéodory function satisfying (H0)’–(H1).

Let $\{u_k\}\subset W_0^{1,p}(\Omega )$ be any sequence of solutions to (1.1) such that there exists a constant $C_0>0$ satisfying

$$\begin{aligned} \Vert u_k\Vert _{{p^*}} \le C_0. \end{aligned}$$

Then, there exists a constant $C>0$ such that

$$\begin{aligned} \Vert u_k\Vert _{\infty } \le C. \end{aligned}$$

4.1 Proof of Theorem 1.7

Proof

Let $\{u_k\}\subset W_0^{1,p}(\Omega )$ be any sequence of solutions to (1.1). Since Lemma 2.2, $\{u_k\}\subset W_0^{1,p}(\Omega )\cap L^\infty (\Omega )$. If $\Vert u_k \Vert _{\infty }\le C,$ then (i) holds.

Now, we argue on the contrary, assuming that there exists a sequence $\{u_k\}\subset W_0^{1,p}(\Omega )$ of solutions to (1.1), such that $\Vert u_k \Vert _{\infty } \rightarrow + \infty$ as $k \rightarrow \infty .$

By Morrey’s Theorem (see [3, Theorem 9.12]), observe that also

$$\begin{aligned} \Vert \nabla u_k \Vert _{s} \rightarrow + \infty \qquad \text{ as }\quad k \rightarrow \infty , \end{aligned}$$

(4.1)

for any $s>N$.

Step 1. $W^{1,q^*(p-1)}$ estimates for $q\in \big (N/p,\min \{N,N/\mu \}\big )$.

As in the proof of Theorem (), let us denote by

$$\begin{aligned} M_k:=\max \Big \{\tilde{f}\big (-\Vert u_k\Vert _{\infty }\big ),\tilde{f}\big (\Vert u_k\Vert _{\infty }\big )\Big \}\ge \frac{1}{2c_0} \,\max _{[-\Vert u_k\Vert _{\infty },\Vert u_k\Vert _{\infty }]}\tilde{f}, \end{aligned}$$

(4.2)

where the inequality is due to hypothesis (H1), see (1.7).

Let us take q in the interval $(N/p,N)\cap (N/p,N/\mu ).$ Using growth hypothesis (H0)’ (see (1.5)), hypothesis (H1) (see (1.7)), and Hölder inequality, we deduce

$$\begin{aligned} \displaystyle \int _{\Omega }\left| f\big (x,u_k(x)\big )\right| ^q\, dx&\le \int _{\Omega } |x|^{-\mu q} \left( \tilde{f}\big (u_k(x)\big )\right) ^{q}\, dx\nonumber \\&=\int _{\Omega } |x|^{-\mu q} \left( \tilde{f}\big (u_k(x)\big )\right) ^\frac{t}{p_{\mu }^*-1} \, \left( \tilde{f}\big (u_k(x)\big )\right) ^{q-\frac{t}{p_{\mu }^*-1}}\, dx\nonumber \\&\le C\ \left[ \int _{\Omega } |x|^{-\mu q}\ \big (1+u_k(x)^{t}\big ) \,dx\right] \ M_k^{\ q-\frac{t}{p_{\mu }^*-1}} \nonumber \\&\le C\,\Big (1+\big | |x|^{-\gamma } u_k\big |_{t}^{\ t}\Big )\ \ M_k^{\ q-\frac{t}{p_{\mu }^*-1}}, \end{aligned}$$

where $\gamma =\frac{\mu q}{t}$, $t\in \big (0, q\big (p_{\mu }^*-1\big )\big )$, $C=c_0^{q-\frac{t}{p_{\mu }^*-1}}$ (for $c_0$ defined in (1.7)), and where $M_k$ is defined by (4.2).

Since elliptic regularity see Theorem 2.1, we have that

$$\begin{aligned} \Vert \nabla u_k\Vert _{q^*(p-1)} \le C\ \left[ \Big (1+\big | |x|^{-\gamma } u_k\big |_{t}^{\ t}\Big )^{\,\frac{1}{q}}\ M_k^{\ 1-\frac{t}{q(p_{\mu }^*-1)}}\right] ^\frac{1}{p-1}, \end{aligned}$$

(4.3)

where $1/q^*=1/q-1/N$ (since $q>N/p$, then $q^*(p-1)>N$), and $C=C(N,q,|\Omega |).$

Step 2. Caffarelli–Kohn–Nirenberg interpolation inequality.

Since the Caffarelli–Kohn–Nirenberg interpolation inequality for singular weights (see [6], see also Theorem A.1, and Corollary A.2(ii)), there exists a constant $C>0$ depending on the parameters $N,\ q,\ \mu ,\theta \in [0,1]$ and t, such that

$$\begin{aligned} \big | |x|^{-\gamma } u_k\big |_{t} \le C \Vert \nabla u_k\Vert _{q^*(p-1)}^\theta \ \Vert u_k\Vert _{p^*}^{1-\theta }, \end{aligned}$$

(4.4)

where

$$\begin{aligned} \nonumber 0<\frac{1}{t}- \frac{\mu q}{N t}&= \theta \left( \frac{1}{q^*(p-1)}-\frac{1}{N}\right) +(1-\theta )\frac{1}{p^*}\\&=\frac{1}{p^*}-\theta \left( \frac{1}{p}-\frac{1}{q^*(p-1)}\right) \nonumber \\&=\frac{1}{p^*}- \frac{\theta }{p-1}\left( 1-\frac{1}{p} -\frac{1}{q}+\frac{1}{N}\right) =\frac{1}{p^*}- \frac{\theta (p_{N/q}^*-1)}{(p-1)p^*}. \end{aligned}$$

(4.5)

Observe that since $t<q(p_{\mu }^*-1)$, then the r.h.s. of (4.5) is bounded from below,

$$\begin{aligned} \frac{1}{p^*}- \frac{\theta }{(p-1)p^*}(p_{N/q}^*-1)=\frac{1}{t}\left( 1-\frac{\mu q}{N}\right) >\frac{1}{p_{\mu }^*-1}\left( \frac{1}{q}-\frac{\mu }{N}\right) , \end{aligned}$$

so,

$$\begin{aligned} \frac{\theta (p_{N/q}^*-1)}{(p-1)p^*} <\frac{p_{\mu }^*-1-p^*(\frac{1}{q}-\frac{\mu }{N})}{p^*(p_{\mu }^*-1)} =\frac{p_{N/q}^*-1}{p^*(p_{\mu }^*-1)}, \end{aligned}$$

and we get an upper bound for $\theta$, hence $0<\theta<\frac{p-1}{p_{\mu }^*-1}<1$.

Substituting now (4.4) into (4.3) we can write

$$\begin{aligned} \Vert \nabla u_k\Vert _{q^*(p-1)}\le C \left[ \Big (1+\Vert \nabla u_k\Vert _{q^*(p-1)}^{\theta t}\ \Vert u_k\Vert _{p^*}^{(1-\theta )t}\Big )^\frac{1}{q}\ M_k^{\ 1-\frac{t}{q(p_{\mu }^*-1)}}\right] ^\frac{1}{p-1}. \end{aligned}$$

Now, dividing by $\Vert \nabla u_k\Vert _{q^*(p-1)}^{\ \theta t/q(p-1)}$ and using (4.1) we obtain

$$\begin{aligned} \Big (\Vert \nabla u_k\Vert _{q^*(p-1)}\Big )^{1-\frac{\theta t}{q(p-1)}}\le C\left[ \Big (1+\Vert u_k\Vert _{p^*}^{\, \frac{(1-\theta )t}{q}}\Big )\ M_k^{\, 1-\frac{t}{q(p_{\mu }^*-1)}}\right] ^\frac{1}{p-1}. \end{aligned}$$

Let us check that

$$\begin{aligned} 1-\frac{\theta \, t}{q(p-1)}>0 \qquad \text{ for } \text{ any }\quad t<q\big (p_{\mu }^*-1\big ). \end{aligned}$$

(4.6)

Indeed, observe first that (4.5) is equivalent to

$$\begin{aligned} \theta =\frac{\frac{1}{p^*} -\frac{1}{t}+\frac{\mu q}{N t}}{\frac{1}{p}-\frac{1}{q^*(p-1)}}\, \end{aligned}$$

(4.7)

hence

$$\begin{aligned} \frac{\theta \, t}{q(p-1)}=\frac{\frac{1}{q}\left( \frac{t}{p^*} -1\right) + \frac{\mu }{N}}{\frac{p-1}{p}-\frac{1}{q^*}}=\frac{\frac{1}{q}\left( \frac{t}{p^*} -1\right) + \frac{\mu }{N}}{1-\frac{1}{q}-\frac{1}{p^*}}\, \end{aligned}$$

(4.8)

consequently

$$\begin{aligned} \frac{\theta \, t}{q(p-1)}<1&\iff \frac{1}{q}\left( \frac{t}{p^*} -1\right) + \frac{\mu }{N}< 1-\frac{1}{q}-\frac{1}{p^*}\\&\iff \frac{1}{q}\frac{t}{p^*}< 1-\frac{1}{p^*}-\frac{\mu }{N}\\&\iff \frac{t}{q}<p^*\left( 1- \frac{\mu }{N }\right) -1=p_{\mu }^*-1 \\&\iff t<q\big (p_{\mu }^*-1\big ), \end{aligned}$$

so, (4.6) holds.

Consequently,

$$\begin{aligned} \Vert \nabla u_k\Vert _{q^*(p-1)}\le C \Big (1+ \Vert u_k\Vert _{p^*}^{A_0}\Big )\ M_k^{B_0}, \end{aligned}$$

(4.9)

where

$$\begin{aligned} A_0:=\frac{\frac{(1-\theta )t}{q(p-1)}}{1-\frac{\theta \, t}{q(p-1)}},\qquad B_0:=\frac{\left( 1-\frac{t}{q(p_{\mu }^*-1)}\right) \frac{1}{p-1}}{1-\frac{\theta \, t}{q(p-1)}}. \end{aligned}$$

Step 3. Gagliardo–Nirenberg interpolation inequality.

Thanks to the Gagliardo–Nirenberg interpolation inequality (see [27]), there exists a constant $C=C(N,q,|\Omega |)$ such that

$$\begin{aligned} \Vert u_k\Vert _{\infty } \le C \Vert \nabla u_k\Vert _{q^*(p-1)}^\sigma \ \Vert u_k\Vert _{p^*}^{1-\sigma }, \end{aligned}$$

(4.10)

where

$$\begin{aligned} \frac{1-\sigma }{p^*}&=\sigma \left[ \frac{1}{N}-\frac{1}{q^*(p-1)}\right] . \end{aligned}$$

(4.11)

Hence, substituting (4.9) into (4.10) we deduce

$$\begin{aligned} \Vert u_k\Vert _{\infty }\le C \ \Big (1+ \Vert u_k\Vert _{p^*}^{\ \sigma \,A_0}\Big ) \ M_k^{\ \sigma B_0}\ \Vert u_k\Vert _{p^*}^{\ 1-\sigma }. \end{aligned}$$

(4.12)

From definition of $M_k$ (see (3.1)), and of h (see (1.9)), we obtain

$$\begin{aligned} M_k =\frac{\Vert u_k\Vert _{\infty }^{\ p_{\mu }^*-1}}{h\big (\Vert u_k\Vert _{\infty }\big )}. \end{aligned}$$

Now we check that

$$\begin{aligned} \sigma B_0\, (p_{\mu }^*-1)=1. \end{aligned}$$

(4.13)

Indeed, from (4.11)

$$\begin{aligned} \frac{1}{\sigma }&=1+p^*\left( \frac{1}{N}-\frac{1}{q^*(p-1)}\right) =\frac{p^*}{p}-\frac{p^*}{q^*(p-1)}\nonumber \\&= \frac{p^*}{p-1}\left[ 1-\frac{1}{p}-\frac{1}{q}+\frac{1}{N}\right] =\frac{1}{p-1}\big (p_{N/q}^*-1\big ). \end{aligned}$$

(4.14)

From (4.8), we deduce

$$\begin{aligned} \nonumber 1-\frac{\theta \, t}{q(p-1)}&=\frac{1-\frac{1}{q}-\frac{1}{p^*}-\frac{1}{q}\left( \frac{t}{p^*} -1\right) - \frac{\mu }{N}}{1-\frac{1}{q}-\frac{1}{p^*}}\\&=\frac{\left( 1-\frac{\mu }{N}\right) -\frac{1}{p^*}-\frac{t}{qp^*} }{1-\frac{1}{q}-\frac{1}{p^*}}=\frac{p_{\mu }^*-1-\frac{t}{q}}{p^*\left( 1-\frac{1}{q}\right) -1} =\frac{p_{\mu }^*-1-\frac{t}{q}}{p_{N/q}^*-1}\, . \end{aligned}$$

(4.15)

Moreover, since (4.15),

$$\begin{aligned}&\left( 1-\frac{t}{q(p_{\mu }^*-1)}\right) {\big (p_{\mu }^*-1\big )} \frac{1}{\Big (1-\frac{\theta \, t}{q(p-1)}\Big )}\\&\qquad =\left( p_{\mu }^*-1-\frac{t}{q}\right) \frac{1}{\Big (1-\frac{\theta \, t}{q(p-1)}\Big )}=p_{N/q}^*-1. \end{aligned}$$

Hence

$$\begin{aligned} B_0\, (p_{\mu }^*-1)=\frac{p_{N/q}^*-1}{p-1}. \end{aligned}$$

(4.16)

Taking into account (4.14) and (4.16), we deduce that (4.13) holds.

Consequently, we can rewrite (4.12) in the following way

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )^{\ \frac{1}{p_{\mu }^*-1}}\le C \ \Big (1+ \Vert u_k\Vert _{p^*}^{\ \sigma \,A_0}\Big )\, \Vert u_k\Vert _{p^*}^{\ 1-\sigma }, \end{aligned}$$

then

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )\le C\ \Big (1+ \Vert u_k\Vert _{p^*}^{\ \Theta }\Big ), \end{aligned}$$

with

$$\begin{aligned} \Theta&:= \big (p_{\mu }^*-1\big )\left[ 1+\sigma \,\frac{\frac{t}{q(p-1)}-1}{1-\frac{\theta \, t}{q(p-1)}}\right] . \end{aligned}$$

Since (4.14)–(4.15), $\sigma \left( 1-\frac{\theta \, t}{q(p-1)}\right) ^{-1}=(p-1)\, (p_{\mu }^*-1 -\frac{t}{q})^{-1}$, and substituting it into the above equation we obtain

$$\begin{aligned} \Theta&=\big (p_{\mu }^*-1\big )\left( \frac{p_{\mu }^*-p}{p_{\mu }^*-1 -\frac{t}{q}}\right) . \end{aligned}$$

Fixed $p<N$ and $\mu \in (0,p)$, the function $(t,q)\rightarrow \Theta =\Theta (t,q)$ for $(t,q)\in \big (0, q(p_{\mu }^*-1)\big )\times \big (N/p,\min \{N,N/\mu \}\big )$, is increasing in t and decreasing in q.

If $\mu \in [1,p)$, then $\min \{N,N/\mu \}=N/\mu$. Equation (4.5) with $q=q_k=(1-1/k)N/\mu \rightarrow N/\mu$, $t=t_k=\frac{2p^*}{k}\rightarrow 0$ and $\theta =\theta _k=\frac{p-1}{2(p_{N/q_k}^*-1)}\rightarrow \frac{p-1}{2(p_{\mu }^*-1)}$ is satisfied. Hence, when $\mu \in [1,p)$,

$$\begin{aligned} p_{\mu }^*-p\le \underset{t\in \big (0, (p_{\mu }^*-1)q\big ),\, q\in \big (\frac{N}{p},\frac{N}{\mu }\big )}{\inf }\ \Theta (t,q) \le \Theta \big (t_k,q_k\big )\rightarrow p_{\mu }^*-p. \end{aligned}$$

On the other hand, for $\mu \in (0,1)$, the $\min \{N,N/\mu \}=N$. For any $\varepsilon _k\rightarrow 0$, equation (4.5) with $q=q_k=N(1-\varepsilon _k)\rightarrow N$, and $t=t_k\rightarrow t_0\in [0,(p_\mu ^*-1)N]$, yields $\theta =\theta _k=\frac{(p-1)p^*}{p_{N/q_k}^*-1}\left[ \frac{1}{p^*}-\frac{1}{t_k}\big (1-\mu (1-1/k)\big )\right] \rightarrow p\left[ \frac{1}{p^*}-\frac{1}{t_0}(1-\mu )\right] \ge 0$, so $t_0\ge p^*(1-\mu )$. Hence, when $\mu \in (0,1)$,

$$\begin{aligned} \underset{t\in (p^*(1-\mu ), (p_{\mu }^*-1)N),\, q\in \big (\frac{N}{p},N\big )}{\inf }\, \Theta (t,q) =\Theta (p^*(1-\mu ),N)=(p_{\mu }^*-p)B, \end{aligned}$$

where B is defined by (1.11).

Since the infimum is not attained, for any $\varepsilon >0$, there exists a constant $C=C(\varepsilon ,c_0,\mu ,N,\Omega )$ such that

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )\le C \ \Big (1+\Vert u_k\Vert _{p^*}^{\, (p_{\mu }^*-p)(B+\varepsilon )}\Big ), \end{aligned}$$

which ends the proof.

Appendix A. The Caffarelli–Kohn–Nirenberg interpolation inequality

Theorem A.1

Let $s, q, t, \alpha , \beta , \sigma$ and $\theta$ be fixed real numbers (parameters) satisfying

$$\begin{aligned}{} & {} s, q \ge 1,\ \ t > 0,\ \ 0 \le \theta \le 1, \end{aligned}$$

(A.1)

$$\begin{aligned}{} & {} \frac{1}{s} + \frac{\alpha }{N},\ \frac{1}{q} + \frac{\beta }{N},\ \frac{1}{t}- \frac{\gamma }{N} > 0, \end{aligned}$$

(A.2)

where

$$\begin{aligned} \gamma = -\big [\theta \sigma + (1-\theta )\beta \big ]. \end{aligned}$$

(A.3)

Then, there exists a positive constant $C>0$ such that for all $u \in C^\infty _c(\mathbb {R}^N)$:

$$\begin{aligned} \big | |x|^{-\gamma } u\big |_{L^t(\mathbb {R}^N)} \le C\, \big \Vert |x|^\alpha \, |\nabla u|\big \Vert ^{\,\theta }_{L^s(\mathbb {R}^N)}\, \big \Vert |x|^\beta u\big \Vert ^{\, 1-\theta }_{L^q(\mathbb {R}^N)}, \end{aligned}$$

(A.4)

where

$$\begin{aligned}{} & {} \frac{1}{t}- \frac{\gamma }{N}= \theta \left( \frac{1}{s} + \frac{\alpha - 1}{N}\right) + (1 - \theta ) \left( \frac{1}{q} + \frac{\beta }{N}\right) , \end{aligned}$$

(A.5)

$$\begin{aligned}{} & {} 0 \le \alpha - \sigma \qquad \text{ if }\quad \theta > 0, \end{aligned}$$

(A.6)

and

$$\begin{aligned} \alpha - \sigma \le 1 \qquad \text{ if }\quad \ \theta > 0 \ \text { and }\ \frac{1}{s} + \frac{\alpha - 1}{N} = \frac{1}{t}- \frac{\gamma }{N}. \end{aligned}$$

(A.7)

Moreover, on any compact set in parameter space in which (A.1), (A.2), (A.5) and $0\le \alpha - \sigma \le 1$ hold, the constant C is bounded.

See [6] for a proof.

Corollary A.2

Suppose that $\Omega \subset \mathbb {R}^N$ is of class $C^1$ with $\partial \Omega$ bounded. Let $s, q, t, \sigma ,\theta$ be fixed real parameters satisfying (A.1)–(A.3) particularized for $\alpha =\beta =0$ (specifically $1 \le s,q < \infty$, $\frac{1}{t}> \frac{\gamma }{N}$ where $\gamma =(-\sigma )\theta$, $\theta \in [0,1]$).

Then,

(i) there exists a positive constant $C = C (\Omega , N, s, q, t, \sigma , \theta )$ such that for all $u\in W^{1,p}(\Omega )\cap L^{q}(\Omega )$:

$$\begin{aligned} \big | |x|^{-\gamma } u\big |_{L^t(\Omega )} \le C\, \big \Vert \nabla u\big \Vert ^{\,\theta }_{L^s(\Omega )}\, \big \Vert u\big \Vert ^{\, 1-\theta }_{L^q(\Omega )}, \end{aligned}$$

(A.8)

where

$$\begin{aligned}{} & {} \frac{1}{t}- \frac{\gamma }{N}= \theta \left( \frac{1}{s} - \frac{1}{N}\right) + (1 - \theta )\, \frac{1}{q}, \end{aligned}$$

(A.9)

$$\begin{aligned}{} & {} \sigma \le 0 \qquad \text{ if }\quad \theta > 0, \end{aligned}$$

(A.10)

and

$$\begin{aligned} 0\le -\sigma \le 1 \qquad \text{ if }\quad \theta > 0, \qquad \text{ and }\quad \frac{1}{s} - \frac{1}{N} = \frac{1}{t}- \frac{\gamma }{N}. \end{aligned}$$

(A.11)

In particular, for all $u\in W^{1,p}(\Omega )$ with $p\ne 2$, $p<N$,

$$\begin{aligned} |x|^{-\mu }|u|^{p^*_\mu -2}\in L^{\frac{N}{p}}(\Omega ). \end{aligned}$$

(ii) Moreover, if $s=p$, $q=p^*$, and $\sigma <0$ (so $\gamma >0$), there exists a positive constant $C = C (\Omega , N,p, t, \sigma )$ such that for all $u\in W^{1,p}(\Omega )$:

$$\begin{aligned} \big | |x|^{-\gamma } u\big |_{L^t(\Omega )} \le C\, \big \Vert \nabla u\big \Vert _{L^p(\Omega )}\, \end{aligned}$$

(A.12)

where

$$\begin{aligned} \frac{1}{t}- \frac{\gamma }{N}= \frac{1}{p} - \frac{1}{N}, \qquad \text{ and }\quad 0< \gamma \le 1. \end{aligned}$$

(A.13)

In particular, for all $u\in W^{1,p}(\Omega )$

$$\begin{aligned} |f(x,u)|\le C \big (1+|x|^{-\mu }|u|^{p^*_\mu -1}\big )\in L^{(p^*)'}(\Omega ),\text { if } \mu \le p-1+\frac{p}{N}. \end{aligned}$$

(A.14)

(iii) Besides, for all $u\in W^{1,q}(\Omega )$ with $q>p$:

$$\begin{aligned} \big | |x|^{-\gamma } u\big |_{L^t(\Omega )} \le C\, \big \Vert \nabla u\big \Vert _{L^p(\Omega )}\,, \end{aligned}$$

where

$$\begin{aligned} \frac{1}{t}- \frac{\gamma }{N}= \frac{1}{q} - \frac{1}{N}. \end{aligned}$$

(A.15)

In particular, for all $u\in W^{1,q}(\Omega )$ with $q>p$,

$$\begin{aligned}&\mathrm{(iii.a)} \ f(x,u)\le C \big (1+|x|^{-\mu }|u|^{p^*_\mu -1}\big )\in L^{(p^*)'}(\Omega ), \end{aligned}$$

(A.16)

$$\begin{aligned}&\text {and} \nonumber \\&\mathrm{(iii.b)}\ |x|^{-\mu }|u|^{p^*_\mu -2}\in L^{\frac{N}{p}}(\Omega ). \end{aligned}$$

(A.17)

Proof

(i) The proof can be obtained using that $C^\infty _c(\mathbb {R}^N)$ is dense in $L^p(\mathbb {R}^N)$ for any $1 \le p < \infty$, and the extension operator, $P:W^{1,p}(\Omega )\rightarrow W^{1,p}(\mathbb {R}^N)$, see [3, Theorem 9.7]. Moreover, (A.8)–(A.11) is a direct consequence of (A.4)–(A.7).

In particular, for all $u\in W^{1,p}(\Omega )$ with $p\ne 2$, $p<N$, choosing now $t=(p^*_\mu -2)\frac{N}{p}$, $\theta =1$, and $\sigma =-\frac{\mu }{p^*_\mu -2}$, we deduce from (A.3) that $\gamma =\frac{\mu }{p^*_\mu -2}$, hence

$$\begin{aligned} \frac{1}{t}- \frac{\gamma }{N}=\frac{p-\mu }{N(p^*_\mu -2)}\ne \frac{1}{p} - \frac{1}{N}\qquad \text{ when }\quad p\ne 2,\text { and } p<N, \end{aligned}$$

so (A.14) is accomplished.

(ii) Assume now $s=p$, $q=p^*$, and $\gamma >0$. Obviously, if $\gamma =(-\sigma )\theta >0$, then $0\ne \theta \in (0,1]$, and (A.6)–(A.7) imply

$$\begin{aligned} 0< (-\sigma )\le 1,\qquad \text{ so }\quad 0<\gamma \le 1. \end{aligned}$$

In particular, choosing $t=(p^*_\mu -1)(p^*)'$, $\theta =1$, and $\sigma =-\frac{\mu }{p^*_\mu -1}$, we deduce from (A.3) that $\gamma =\frac{\mu }{p^*_\mu -1}$, hence $\frac{1}{t}- \frac{\gamma }{N}=\frac{1}{p} - \frac{1}{N},$ and

$$\begin{aligned} \gamma \le 1\iff \mu \le p-1+\frac{p}{N}. \end{aligned}$$

Consequently, (A.14) holds.

(iii) Assume finally $p>2$.

(iii.a) Indeed, choosing $t=(p^*_\mu -1)(p^*)'$, and $\gamma =\frac{\mu }{p^*_\mu -1}$, we deduce from (A.15) that

$$\begin{aligned} \frac{1}{t}- \frac{\gamma }{N}=\frac{1}{p} - \frac{1}{N}<\frac{1}{p} - \frac{1}{N}, \end{aligned}$$

so (A.7) do not apply.

(iii.b) Choosing now $t=(p^*_\mu -2)\frac{N}{p}$, and $\theta =1$, we deduce from (A.13) that $\gamma =\frac{\mu }{p^*_\mu -2}$, so

$$\begin{aligned} \gamma \le 1\iff \mu \le 4/N. \end{aligned}$$