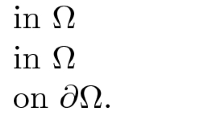$L^\infty (\Omega )$ a priori estimates for subcritical semilinear elliptic equations with a Carathéodory non-linearity

Abstract

We consider a semilinear boundary value problem $-\Delta u= f(x,u),$ in $\Omega ,$ with Dirichlet boundary conditions, where $\Omega \subset {\mathbb {R}}^N$ with $N> 2,$ is a bounded smooth domain, and f is a Carathéodory function, superlinear and subcritical at infinity. We provide $L^\infty (\Omega )$ a priori estimates for weak solutions in terms of their $L^{2^*}(\Omega )$-norm, where $2^*=\frac{2N}{N-2}\$ is the critical Sobolev exponent. In particular, our results also apply to $f(x,s)=a(x)\,\frac{|s|^{2^*_{N/r}-2}s}{\big [\log (e+|s|)\big ]^\beta }\,$, where $a\in L^r(\Omega )$ with $N/2<r\le \infty$, and $2_{N/r}^*:=2^*\left( 1-\frac{1}{r}\right)$. Assume $N/2<r\le N$. We show that for any $\varepsilon >0$ there exists a constant $C_\varepsilon >0$ such that for any solution $u\in H^1_0(\Omega )$, the following holds:

$$\begin{aligned} \Big [\log \big (e+\Vert u\Vert _{\infty }\big )\Big ]^\beta \le C _\varepsilon \, \Big (1+\Vert u\Vert _{2^*}\Big )^{\, (2^*_{N/r}-2)(1+\varepsilon )}. \end{aligned}$$

To establish our results, we do not assume any restrictions on the sign of the solutions, or on the non-linearity. Our approach is based on Gagliardo–Nirenberg and Caffarelli–Kohn–Nirenberg interpolation inequalities. Finally, we state sufficient conditions for having $H_0^1(\Omega )$ uniform a priori bounds for non-negative solutions, so finally we provide suficient conditions for having $L^\infty (\Omega )$ uniform a priori bounds, which holds roughly speaking for superlinear and subcritical non-linearities.

1 Introduction

Let us consider the following semilinear boundary value problem:

$$\begin{aligned} -\Delta u= f(x,u), \quad \text{ in } \Omega , \qquad u= 0,\quad \text{ on } \partial \Omega , \end{aligned}$$

(1.1)

where $\Omega \subset {\mathbb {R}}^N$, $N> 2,$ is a bounded, connected, open subset with $C^{2}$ boundary $\partial \Omega$, and the non-linearity $f:\overline{\Omega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function (that is, the mapping $f(\cdot ,s)$ is measurable for all $s\in {\mathbb {R}}$, and the mapping $f(x,\cdot )$ is continuous for almost all $x\in \Omega$), that is subcritical (see Definition 1.1).

We analyze the effect of the smoothness of the non-linearity $f=f(x,\cdot )$ on the $L^\infty (\Omega )$ a priori estimates of weak solutions to (1.1). Degree theory combined with a priori bounds in the sup-norm of solutions of parametrized versions of (1.1), is a very classical topic in elliptic equations, posed by Leray and Schauder in [18]. It provides a great deal of information about existence of solutions and the structure of the solution set. This study is usually focused on positive classical solutions, see the classical references of de Figueiredo–Lions–Nussbaum, and of Gidas–Spruck [11, 14], see also [7, 8].

A natural question concerning the class of solutions is the following one:

• (Q1) can those $L^\infty (\Omega )$ estimates be extended to a bigger class of solutions, in particular to weak solutions (with possibly sign changing solutions)?.

  Another question concerning the class of non-linearities, can be stated as follows:

• (Q2) can those estimates be extended to a bigger class of non-linearities, in particular to non-smooth non-linearities (with possibly sign changing weights)?.

In this paper, we provide sufficient conditions guarantying uniform $L^\infty (\Omega )$ a priori estimates for any $u\in H_0^{1}(\Omega )$ weak solution to (1.1), in terms of their $L^{2^*}(\Omega )$ bounds, in the class of Carathéodory generalized subcritical problems. In this class, we state that any set of weak solutions uniformly $L^{2^*} (\Omega )$ a priori bounded is universally $L^\infty (\Omega )$ a priori bounded. Our theorems allow sign changing weights, and singular weights, and also apply to sign changing solutions.

Problem (1.1) with $f(x,s)=|x|^{-\mu } |s|^{p-1}s,$ $\mu >0$, $p>1$ is known as Hardy’s problem, due to its relation with the Hardy-Sobolev inequality. The Caffarelli–Kohn–Nirenberg interpolation inequality for radial singular weights [4], states that whenever $0\le \mu \le 2$,

$$\begin{aligned} 2_{\mu }^*:=\frac{2(N-\mu )}{N-2}, \end{aligned}$$

(1.2)

is the critical exponent of the Hardy–Sobolev embedding $H_0^1(\Omega )\hookrightarrow \$ $L^{2_\mu ^*}(\Omega , |x|^{-\mu })\,$. Using variational methods, one obtains the existence of a nontrivial solution to (1.1) in $H_0^1(\Omega )$ whenever $1< p <2_\mu ^*-1$. For the case $0<\mu < 2$, using a Pohozaev type identity, we have that for $p\ge 2_\mu ^*-1$ there is no solution to Hardy’s problem in star-shaped domains with respect to the origin. But, there exist positive solutions for the problem with $p=2_\mu ^*-1$ depending on the geometry of the domain $\Omega$, see [16] and [5].

If $\mu \ge 2,$ it is known that Hardy’s problem has no positive solution in any domain $\Omega$ containing the origin, see [13, 1, Lemma 6.2], [12].

Usually the term subcritical non-linearity is reserved for power like non-linearities. We expand this concept in this paper below. Let

$$\begin{aligned} 2_{N/r}^*:=\frac{2^*}{r'}=2^*\left( 1-\frac{1}{r}\right) , \end{aligned}$$

(1.3)

where $r'$ is the conjugate exponent of r, $1/r+1/r'=1.$

Definition 1.1

A non-linearity $f:\overline{\Omega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is subcritical if it satisfies one the two following hypothesis:

• (H0)
  $$\begin{aligned} |f(x,s)|\le |a(x)|\, \tilde{f}(s) \end{aligned}$$

  (1.4)

  where $a\in L^r(\Omega )$ with $N/2<r\le \infty$, and $\tilde{f}:{\mathbb {R}}\rightarrow [0,+\infty )$ is continuous and satisfies

  $$\begin{aligned} \lim _{|s| \rightarrow \infty } \frac{\tilde{f}(s)}{|s|^{2_{N/r}^*-1}}=0, \end{aligned}$$

  (1.5)

(H0)’:

$$\begin{aligned} |f(x,s)|\le |x|^{-\mu }\, \tilde{f}(s), \end{aligned}$$

(1.6)

where $\mu \in (0,2),$ and $\tilde{f}:{\mathbb {R}}\rightarrow [0,+\infty )$ is continuous and satisfies

$$\begin{aligned} \lim _{|s| \rightarrow \infty } \ \frac{\tilde{f}(s)}{|s|^{2_{\mu }^*-1}}=0. \end{aligned}$$

(1.7)

Remark 1.2

Obviously $|a(x)|\, \tilde{f}(s)\le |a(x)|\,(1+\tilde{f}(s))$, and we can always redefine $\tilde{f}$ in order to satisfy $\tilde{f}(s)>0 \ \text {for}\ |s|>0$.

Moreover, $\tilde{f}:{\mathbb {R}}\rightarrow [0,+\infty )$ from (H0) or (H0)’ satisfies the following hypothesis:

• (H1) there exists a constant $c_0>0$ such that

  $$\begin{aligned} \limsup _{s\rightarrow +\infty }\ \dfrac{\max _{[-s,s]}\, \tilde{f}}{\max \big \{\tilde{f}(-s),\tilde{f}(s)\big \}}\, \le \, c_0. \end{aligned}$$

  (1.8)

Throughout the paper, we will assume either (H0) and (H1) or (H0)’ and (H1).

Remark 1.3

• 1. Observe that in particular, if $\tilde{f}(s)$ is monotone, then (H1) is obviously satisfied with $c_0=1$.

• 2. Thanks to Sobolev embeddings, for any $u\in H_0^{1}(\Omega )$,

  $$\begin{aligned} \tilde{f}(u)\in L^{\frac{2^*}{2_{N/r}^*-1}}(\Omega )&\qquad \text{ with }\quad \frac{2_{N/r}^*-1}{2^*}=\frac{1}{2}+\frac{1}{N} -\frac{1}{r}, \\ \text {and}\ f(\cdot ,u)\in L^{\frac{2N}{N+2}}(\Omega ). \end{aligned}$$

• 3. Again, by Sobolev embeddings, for any $u\in H_0^{1}(\Omega )$,

  $$\begin{aligned} \tilde{f}(u)\in L^{\frac{2^*}{2_{\mu }^*-1}}(\Omega )&\qquad \text{ with }\quad \frac{2_{\mu }^*-1}{2^*}=\frac{1}{2}+\frac{1}{N}-\frac{\mu }{N}. \end{aligned}$$

  If $a(x)=|x|^{-\mu }$, then $a\in L^p(\Omega )$ for any $p<N/\mu$, hence $f(\cdot ,u)\in L^{p}(\Omega )$ for any $p<\frac{2N}{N+2}$. From the sharp Caffarelli–Kohn–Nirenberg interpolation inequality for singular weights, in the particular case where $\alpha =\beta =0,\ p=2,\ q=2^*$ (see [4], see also Theorem A.1 and Corollary A.2), there exists a constant $C>0$ such that

  $$\begin{aligned} \big \Vert \,|x|^{-\gamma }\ u\,\big \Vert _{t} \le C \Vert \nabla u \Vert _{2} ,\quad \text {where}\ \frac{1}{t}- \frac{\gamma }{N}=\frac{1}{2}-\frac{1}{N}, \ \text {and}\ 0\le \gamma \le 1. \end{aligned}$$

  It can be checked that if $u\in H_0^1(\Omega )$, then $f(\cdot ,u)\in L^{\frac{2N}{N+2}}(\Omega )$ for any $\mu \le 1+2/N$ (see Corollary A.2.(ii.a), (A.15)). Also, if $u\in W^{1,p}(\Omega )$, with $p>2$, then $f(\cdot ,u)\in L^{\frac{2N}{N+2}}(\Omega )$ for any $\mu \in (0,2)$ (see Corollary A.2.(iii.a), (A.19)).

Definition 1.4

By a weak solution of (1.1) we mean a function $u \in H_0^{1}(\Omega )$ such that $f(\cdot ,u)\in L^{\frac{2N}{N+2}}(\Omega ),$ and

$$\begin{aligned} \int _{\Omega }\nabla u\nabla \varphi =\int _{\Omega } f(x,u)\varphi , \quad \quad \forall \varphi \in H_0^{1}(\Omega ). \end{aligned}$$

Throughout the paper, by a solution we will refer to this weak solution. This definition of solution is tied to question (Q1). By an estimate of Brezis-Kato [3], based on Moser’s iteration technique [21], and elliptic regularity, we will state sufficient conditions guarantying that any weak solution to (1.1) with a Carathéodory subcritical non-linearity is a continuous function, and in fact it is a strong solution, see Lemma 2.1 and Lemma 3.1.

Our definition of a subcritical non-linearity includes functions such as

$$\begin{aligned} f^{(1)}(x,s):= \frac{a(x)|s|^{2_{N/r}^*-2}s}{\big [\log (e+|s|)\big ]^\alpha }, \ \ \text {or} \quad f^{(2)}(x,s):= \frac{|x|^{-\mu }|s|^{2_{\mu }^*-2}s}{\Big [\log \big [e+\log (1+|s|)\big ]\Big ]^\alpha }, \end{aligned}$$

for any $\alpha >0$, and either any $a\in L^r(\Omega ),$ with $N/2<r\le \infty$, or any $\mu \in (0,2)$. These non-linearities exemplify question (Q2).

One of the main results, Theorem 1.5, applied to $f(x,s)=f^{(1)}(x,s)$ with $a\in L^r(\Omega )$ for $r\in (N/2,N]$, implies that for any $\varepsilon >0$ there exists a constant $C>0$ depending only on $\varepsilon ,\ \Omega ,$ r and N such that for any $u\in H_0^{1}(\Omega )$ solution to (1.1), the following holds:

$$\begin{aligned} \Big [\log \big (e+\Vert u\Vert _{\infty }\big )\Big ]^\alpha \le C \Vert a\Vert _r^{\ 1+\varepsilon } \ \Big (1+\Vert u\Vert _{2^*}\Big )^{\, (2_{N/r}^*-2)(1+\varepsilon )}, \end{aligned}$$

where C is independent of the solution u.

Related results concerning $f^{(1)}(x,s)$ with $r=\infty$ can be found in [10] for the p-Laplacian case, in [9] analyzing what happen when $\alpha \rightarrow 0$, in [19] for systems, in [25] for the radial case, and in [23, 24] for a summary.

To state our main results, for a non-linearity f satisfying (H0), define

$$\begin{aligned} h(s)=h_{N/r}(s):=\frac{|s|^{2_{N/r}^*-1}}{\displaystyle \max \big \{\tilde{f}(-s),\tilde{f}(s)\big \}},\qquad \text{ for }\quad |s|> 0, \end{aligned}$$

(1.9)

(see Remark 1.2). And for a non-linearity f satisfying (H0)’, define

$$\begin{aligned} h(s)=h_{\mu }(s):=\frac{|s|^{2_{\mu }^*-1}}{\displaystyle \max \big \{\tilde{f}(-s),\tilde{f}(s)\big \}}, \qquad \text{ for }\quad |s|> 0. \end{aligned}$$

(1.10)

By sub-criticality, (see (1.5) or (1.7) respectively),

$$\begin{aligned} h(s)\rightarrow \infty \qquad \text{ as }\quad |s|\rightarrow \infty . \end{aligned}$$

(1.11)

Let u be a solution to (1.1). We estimate $h\big (\Vert u\Vert _{\infty }\big )$, in terms of its $L^{2^*}(\Omega )$-norm. This result is robust, and holds for solutions and non-linearities without any sign restriction.

Our first main result is the following theorem.

Theorem 1.5

Assume that $f:\overline{\Omega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function satisfying (H0)-(H1).

Then, for any $u\in H_0^{1}(\Omega )$ weak solution to (1.1), the following holds:

• (i) either there exists a constant $C>0$ such that $\Vert u\Vert _{\infty }\le C$, where C is independent of the solution u,

• (ii) either, for any $\varepsilon >0$ there exists a constant $C>0$ such that

  $$\begin{aligned} h\big (\Vert u\Vert _{\infty }\big ) \le C \Vert a\Vert _r^{\ A+\varepsilon } \ \Big (1+\Vert u\Vert _{2^*}\Big )^{\, (2_{N/r}^*-2)(A+\varepsilon )}, \end{aligned}$$

  where h is defined by (1.9),

  $$\begin{aligned} A:= {\left\{ \begin{array}{ll} 1 , &{}\qquad \text{ if }\quad r\le N,\\ \displaystyle 1+\frac{2}{N}-\frac{2}{r} ,&{}\qquad \text{ if }\quad r> N, \end{array}\right. } \end{aligned}$$

  (1.12)

  and C depends only on $\varepsilon$, $c_0$ (defined in (1.8)), r, N, and $\Omega ,$ and it is independent of the solution u.

Our second main result is the following theorem.

Theorem 1.6

Assume that $f:\overline{\Omega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function satisfying (H0)’ and (H1). Assume also that one of the following two conditions hold

• (a) Either $\mu \le 4/N$;

• (b) either $u\in W^{1,p_0}(\Omega )$ with $p_0>2$.

Then, for any $u\in H_0^{1}(\Omega )$ solution to (1.1), the following holds:

• (i) either there exists a constant $C>0$ such that $\Vert u\Vert _{\infty }\le C$, where C is independent of the solution u,

• (ii) either, for any $\varepsilon >0$ there exists a constant $C>0$ such that

  $$\begin{aligned} h\big (\Vert u\Vert _{\infty }\big )\le C_\varepsilon \ \Big (1+\Vert u\Vert _{2^*} \Big )^{\, (2_{\mu }^*-2)(B+\varepsilon )}\ , \end{aligned}$$

  where h is defined by (1.10),

  $$\begin{aligned} B:= {\left\{ \begin{array}{ll} \displaystyle 1+\frac{2}{N}-\frac{2\mu }{N} ,&{}\text {if} \ \mu \in (0,1),\\ 1 ,&{}\text {if}\ \mu \in [1,2), \end{array}\right. } \end{aligned}$$

  (1.13)

  and C depends only on $\varepsilon$, $c_0$ (defined in (1.8)), $\mu$, N, and $\Omega ,$ and it is independent of the solution u.

As an immediate consequence, as soon as we have a universal a priori $L^{2^*}(\Omega )$- norm for weak solutions in $H_0^{1}(\Omega ),$ then solutions are a priori universally bounded in the $L^{\infty }(\Omega )$- norm. Our third main result is the following theorem.

Theorem 1.7

($L^\infty$ uniform a priori bound) Assume that $f:\overline{\Omega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function satisfying either hypothesis of Theorem 1.5, either hypothesis of Theorem 1.6. Assume also that there exists constants $K_i>0$, $i=1,2$, and $q>2$ such that

$$\begin{aligned} \mathrm{(H2)} \qquad \ f(x,s)s\ge K_1\,|s|^{q}-K_2 \quad \text {for a.e } x\in \Omega ,\ \text {for all}\, s \in {\mathbb {R}}. \end{aligned}$$

Then, there exists a constant $C>0$ such that for every non-negative weak solution u of (1.1),

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(\Omega )} \le C \end{aligned}$$

where C depends only on N and $\Omega$, but it is independent of the solution u.

As far as we know, our definition of weak solution is the optimal one for the purpose of $L^\infty (\Omega )$ a priori bounds. There are more singular solutions which are unbounded in $L^\infty (\Omega )$, which we briefly discuss below. We will say that a function u is an $L^1(\Omega )$-weak solution to (1.1) if

$$\begin{aligned} u\in L^1(\Omega ),\qquad f(\cdot ,u)\, \delta _\Omega \in L^1(\Omega ) \end{aligned}$$

where $\delta _\Omega (x):=dist(x,\partial \Omega )$ is the distance function with respect to the boundary, and

$$\begin{aligned} \int _\Omega \Big (u \Delta \varphi + f(x,u)\varphi \Big ) \, dx=0, \qquad \text{ for } \text{ all }\quad \varphi \in C^2(\overline{\Omega }), \quad \varphi \big |_{\partial \Omega }=0. \end{aligned}$$

Joseph and Lundgren in [17] shows that those $L^\infty (\Omega )$ a priori estimates are not applicable for $L^1(\Omega )$- weak solutions, or for super-critical non-linearities.

They posed the study of singular solutions. Working on non-linearities such as $f(s):=e^s$ or $f(s):=(1+s)^p$, they consider the following BVP depending on a multiplicative parameter $\lambda \in {\mathbb {R}}$,

$$\begin{aligned} -\Delta u=\lambda f(u), \quad \text{ in } \Omega , \qquad u= 0,\quad \text{ on } \partial \Omega , \end{aligned}$$

(1.14)

and look for classical radial positive solutions in the unit ball $B_1$. They obtain singular solutions as limit of classical solutions.

In particular, they obtain the explicit weak solution

$$\begin{aligned} u^{*}_1(x):=\log \frac{1}{|x|^2}, \quad u^{*}_1\in H_0^1(B_1), \end{aligned}$$

to (1.14), when $N>2$, $\lambda =2(N-2)$, and $f(s):=e^s$, see [17, p. 262].

They also found the explicit $L^1(\Omega )$ -weak solution

$$\begin{aligned} u^{*}_2(x):= \left( \frac{1}{|x|}\right) ^\frac{2}{p-1}-1, \ \ \text {with}\ p>\frac{N}{N-2},\ N>2, \ \ u^{*}_2\in W_0^{1,\frac{N}{N-1}}(B_1), \end{aligned}$$

to (1.14), where $f(s):=(1+s)^p$, and $\lambda =\frac{2}{p-1} \big (N-\frac{2p}{p-1}\big )>0$, see [17, (III.a)]. It holds that $u^{*}_2\in H_0^1(B_1)$ only when $p>2^*-1$. So, in the subcritical range $u^{*}_2$ is a singular $L^1(\Omega )$-weak solution to (1.14), not in $H^1(\Omega )$.

Let us focus on BVP with radial singular weights,

$$\begin{aligned} -\Delta u=\lambda |x|^{-\mu } (1+u)^p, \quad \text{ in } \Omega , \qquad u= 0,\quad \text{ on } \partial \Omega , \end{aligned}$$

(1.15)

with $N>2$, $\mu <2$ and $p>1$. It can be checked that

$$\begin{aligned} u^{*}_3(x):= \left( \frac{1}{|x|}\right) ^\frac{2-\mu }{p-1}-1, \ \ \text {with}\ p>\frac{N-\mu }{N-2}, \qquad u^{*}_3\in W_0^{1,\frac{N}{N-1}}(B_1), \end{aligned}$$

and $u^{*}_3$ is an $L^1(\Omega )$ -weak solution to (1.15), for $\lambda =\frac{2-\mu }{p-1} \big (N-2-\frac{2-\mu }{p-1}\big )>0$. It also holds that $u^{*}_3\in H_0^1(B_1)$ only when $p>2_\mu ^*-1$. So, in the subcritical range $u^{*}_3$ is a singular $L^1(\Omega )$-weak solution to (1.15), not in $H^1(\Omega )$.

Above examples of radially symmetric singular solutions to BVP’s on spherical domains, solve either super-critical problems ($u_1^*$) or are $L^1(\Omega )$-weak solutions not in $H_0^1(\Omega )$ ($u_2^*$ and $u_3^*$). Consequently, we restrict our study for $u\in H_0^{1}(\Omega )$ weak solutions to (1.1), in the class of generalized subcritical problems. It is natural to ask for uniform $L^\infty (\Omega )$ a priori estimates over non power non-linearities in non-spherical domains.

This paper is organized in the following way. In Sect. 2, using Gagliardo –Nirenberg inequality, we prove Theorem 1.5. In Sect. 3, we prove Theorem 1.6. It needs the Caffarelli–Kohn–Nirenberg inequality, which is written in Appendix A, by the sake of completeness. In Sect. 4, we prove Theorem 1.7.

2 Estimates of the $L^\infty (\Omega )$-norm of the solutions with Carathéodory non-linearities

In this section, assuming that f satisfy the subcritical growth condition (H0), we prove Theorem 1.5.

We first collect a regularity Lemma for any weak solution to (1.1) with a non-linearity of polynomial critical growth.

Lemma 2.1

(Improved regularity) Assume that $u\in H_0^1(\Omega )$ weakly solves (1.1) for a Carathéodory non-linearity $f:\overline{\Omega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ with polynomial critical growth

$$\begin{aligned} |f(x,s)|\le |a(x)|(1+|s|^{2_{N/r}^*-1}), \quad \text {with}\ a\in L^r(\Omega ),\quad N/2<r\le \infty . \end{aligned}$$

(2.1)

Then, the following hold:

• (i) If $r<N,$ then $u\in C^{\nu }(\overline{\Omega })\cap W^{2,r}(\Omega )$ for $\nu =2-\frac{N}{r}\in (0,1)$.

• (ii) If $r=N,$ then $u\in C^{\nu }(\overline{\Omega })\cap W^{2,r}(\Omega )$ for any $\nu <1$.

• (iii) If $N<r<\infty ,$ then $u\in C^{1,\nu }(\overline{\Omega })\cap W^{2,r}(\Omega )$ for $\nu =1-\frac{N}{r}\in (0,1)$.

• (iv) If $r=+\infty ,$ then $u\in C^{1,\nu }(\overline{\Omega })\cap W^{2,p}(\Omega )$ for any $\nu <1$ and any $p<\infty$.

Proof

Let $u\in H_0^1(\Omega )$ be a solution to (1.1). Since an estimate of Brezis-Kato [3], if

$$\begin{aligned} |f(x,u)|\le b(x)(1+|u|),\qquad \text{ with }\quad 0\le b\in L^{N/2}(\Omega ), \end{aligned}$$

(2.2)

then, $u\in L^q(\Omega )$ for any $q<\infty$ (see [26, Lemma B.3]).

Assume that f satisfies (2.1), then assumption (2.2) is satisfied with

$$\begin{aligned} b(x)=\frac{|a(x)|(1+|u|^{2_{N/r}^*-1})}{1+|u|} \le C\, |a(x)|(1+|u|^{2_{N/r}^*-2})\in L^{N/2}(\Omega ), \end{aligned}$$

using first that $2_{N/r}^*>2$ for $r>N/2$, and next the Hölder inequality.

Consequently, $u\in L^q(\Omega )$ for any $q<\infty$. The growth condition for f (see (2.1)), implies that $-\Delta u=f(x,u)\in L^p(\Omega )$ for any $p<r.$ Thus, by the Calderon-Zygmund inequality (see [15, Theorem 9.14]), $u\in W^{2,p}(\Omega ),$ for any $p\in (1,r).$

• (i) Assume $r<N.$ Choosing any $p\in (N/2,r)$, by Sobolev embeddings, $u\in W^{1,p^*}(\Omega ),$ where $\frac{1}{p^*}:= \frac{1}{p}- \frac{1}{N}<\frac{1}{N}.$ Since $p^*>N,$ $u\in C^{\nu }(\overline{\Omega })$ for $\nu =2-\frac{N}{p}$. Now, from elliptic regularity $u\in C^{\nu _0}(\overline{\Omega })\cap W^{2,r}(\Omega )$ for $\nu _0=2-\frac{N}{r}$.

• (ii) Assume $r=N.$ Choosing any $p\in (N/2,N)$, and reasoning as in (i), $u\in W^{1,p^*}(\Omega ),$ where $\frac{1}{p^*}:= \frac{1}{p}- \frac{1}{N}<\frac{1}{N}.$ Also $u\in C^{\nu }(\overline{\Omega })$ for any $\nu <1$. Now, from elliptic regularity $u\in C^{\nu }(\overline{\Omega })\cap W^{2,r}(\Omega )$ for any $\nu <1$.

• (iii) Assume $r>N.$ Choosing any $p\in (N,r)$, and reasoning as above, $u\in C^{1,\nu _0}(\overline{\Omega })\cap W^{2,r}(\Omega )$ for $\nu _0=1-\frac{N}{r}$.

• (iv) Assume $r=+\infty .$ Since elliptic regularity and Sobolev embeddings, $u\in C^{1,\nu }(\overline{\Omega })\cap W^{2,p}(\Omega )$ for any $\nu <1$ and any $p<\infty$.

$\square$

2.1 Proof of Theorem 1.5

The arguments of the proof use Gagliardo–Nirenberg interpolation inequality (see [22]), and are inspired in the equivalence between uniform $L^{2^*}(\Omega )$ a priori bounds and uniform $L^\infty (\Omega )$ a priori bounds for solutions to subcritical elliptic equations, see [6, Theorem 1.2] for the semilinear case and $f=f(u)$, and [20, Theorem 1.3] for the p-Laplacian case and $f=f(x,u)$.

We first use elliptic regularity and Sobolev embeddings, and next, we invoke the Gagliardo–Nirenberg interpolation inequality (see [22]).

From now on, C denotes several constants that may change from line to line, and are independent of u.

Proof of Theorem 1.5

Let $\{u_k\}\subset H_0^1(\Omega )$ be any sequence of weak solutions to (1.1). Since Lemma 2.1, in fact $\{u_k\}\subset H_0^1(\Omega )\cap L^\infty (\Omega )$.

If $\Vert u_k \Vert _{\infty }\le C,$ then (i) holds.

Now, we argue on the contrary, assuming that there exists a sequence $\Vert u_k \Vert _{\infty } \rightarrow + \infty$ as $k \rightarrow \infty .$

We split the proof in two steps. First, we write an $W^{2,q}(\Omega )$ estimate for $q\in \big (N/2,\min \{r,N\}\big ),$ then through Sobolev embeddings we get a $W^{1,q^*}$ estimate with $1/q^*=1/q-1/N<1/N.$ Secondly, we invoke the Gagliardo–Nirenberg interpolation inequality for the $L^\infty (\Omega )$-norm in terms of its $W^{1,q^*}$-norm and its $L^{2^*}(\Omega )$-norm.

Step 1. $W^{2,q}(\Omega )$ estimates for $q\in \big (N/2,\min \{r,N\}\big )$.

Let us denote by

$$\begin{aligned} M_k:=\max \Big \{\tilde{f}\big (-\Vert u_k\Vert _{\infty }\big ), \tilde{f}\big (\Vert u_k\Vert _{\infty }\big )\Big \} \ge (2c_0)^{-1}\,\max _{[-\Vert u_k\Vert _{\infty }, \Vert u_k\Vert _{\infty }]}\tilde{f}, \end{aligned}$$

(2.3)

where the inequality holds by hypothesis (H1), see (1.8).

Let us take q in the interval $(N/2,N)\cap (N/2,r).$ Growth hypothesis (H0) (see (1.4)), hypothesis (H1) (see (1.8)), and Hölder inequality, yield the following:

$$\begin{aligned}&\displaystyle \int _{\Omega }\left| f\big (x,u_k(x)\big )\right| ^q\, dx \\&\quad \le \int _{\Omega } |a(x)|^q \left( \tilde{f}\big (u_k(x)\big ) \right) ^{q}\, dx\nonumber \\&\quad = \int _{\Omega } |a(x)|^q \left( \tilde{f}\big (u_k(x) \big )\right) ^{t} \, \left( \tilde{f}\big (u_k(x)\big ) \right) ^{q-t}\, dx\nonumber \\&\quad \le C \left[ \int _{\Omega } |a(x)|^q \ \left( \tilde{f}\big (u_k(x)\big )\right) ^{t} \,dx\right] \ M_k^{\ q-t} \nonumber \\&\quad \le C \left( \int _{\Omega } |a(x)|^{qs} \,dx\right) ^\frac{1}{s} \left( \int _{\Omega } \left( \tilde{f}\big (u_k(x)\big )\right) ^{ts'} \,dx\right) ^\frac{1}{s'} \ M_k^{\ q-t} \nonumber \\&\quad \le C \Vert a\Vert _r^q\ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{2^*}{2_{N/r}^*-1}}\Big )^{t}\ M_k^{\ q-t}, \end{aligned}$$

where $\frac{1}{s}+\frac{1}{s'}=1$, $qs=r$, $C=(2c_0)^{\,q-t}$ (for $c_0$ defined in (1.8)), and $ts'=\frac{2^*}{2_{N/r}^*-1}$, so

$$\begin{aligned} t&:=\frac{2^*}{2_{N/r}^*-1}\left( 1-\frac{q}{r}\right)<q \\&\iff \frac{1}{q}-\frac{1}{r}<\frac{2_{N/r}^*-1}{2^*} =1-\frac{1}{r}-\frac{1}{2}+\frac{1}{N} \nonumber \\&\iff \frac{1}{q}<\frac{1}{2}+\frac{1}{N}\iff q>\frac{2N}{N+2}\ \checkmark \nonumber \end{aligned}$$

(2.4)

since $q>N/2>\frac{2N}{N+2}.$

Now, elliptic regularity and Sobolev embedding imply that

$$\begin{aligned} \Vert u_k \Vert _{W^{1,q^*} (\Omega )} \le C\ \Vert a\Vert _r\ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{2^*}{2_{N/r}^*-1}} \Big )^\frac{t}{q}\ M_k^{\ 1-\frac{t}{q}}, \end{aligned}$$

where $1/q^*=1/q-1/N$, and $C=C(c_0,r,N,q,|\Omega |)$ and it is independent of u. Observe that since $q>N/2$, then $q^*>N.$

Step 2. Gagliardo–Nirenberg interpolation inequality.

Thanks to the Gagliardo–Nirenberg interpolation inequality, there exists a constant $C=C(N,q,|\Omega |)$ such that

$$\begin{aligned} \Vert u_k\Vert _{\infty }\le C \Vert \nabla u_k \Vert _{q^*}^\sigma \ \Vert u_k\Vert _{2^*}^{1-\sigma } \end{aligned}$$

where

$$\begin{aligned} \frac{1-\sigma }{2^*}=\sigma \left( \frac{2}{N}-\frac{1}{q}\right) . \end{aligned}$$

(2.5)

Hence,

$$\begin{aligned} \Vert u_k\Vert _{\infty }\le C \left[ \Vert a\Vert _r\ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{2^*}{2_{N/r}^*-1}}\Big )^{\frac{t}{q}}\ M_k^{\ 1-\frac{t}{q}} \right] ^\sigma \ \Vert u_k\Vert _{2^*}^{1-\sigma }, \end{aligned}$$

(2.6)

where $C=C(c_0,r,N,q,|\Omega |)$.

From definition of $M_k$ (see (2.3)), and definition of h (see (1.9)), we deduce that

$$\begin{aligned} M_k =\frac{\Vert u_k\Vert _{\infty }^{\ 2_{N/r}^*-1}}{h\big (\Vert u_k\Vert _{\infty }\big )}. \end{aligned}$$

From (2.5),

$$\begin{aligned} \frac{1}{\sigma }=1+2^*\left( \frac{2}{N}-\frac{1}{q}\right) =2^*-1-\frac{2^*}{q} =2_{N/q}^*-1. \end{aligned}$$

(2.7)

Moreover, since definition of t (see (2.4)), and definition of $2_{N/r}^*$ (see (1.3)

$$\begin{aligned} 1-\frac{t}{q}=\frac{2^*\left( 1-\frac{1}{r}\right) -1 -2^*\left( \frac{1}{q}-\frac{1}{r}\right) }{2_{N/r}^*-1} =\frac{2_{N/q}^*-1}{2_{N/r}^*-1}, \end{aligned}$$

(2.8)

which, joint with (2.7), yield

$$\begin{aligned} \sigma \left[ 1-\frac{t}{q}\right] {(2_{N/r}^*-1)}=1. \end{aligned}$$

Now, (2.6) can be rewritten as

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )^{\ (1-\frac{t}{q})\sigma }\le C \left[ \Vert a\Vert _r\ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{2^*}{2_{N/r}^*-1}} \Big )^{\frac{t}{q}}\ \right] ^\sigma \ \Vert u_k\Vert _{2^*}^{1-\sigma }, \end{aligned}$$

or equivalently

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )\le C \Vert a\Vert _r^{\ \theta } \ \Big (\Vert \tilde{f}(u_k) \Vert _{\frac{2^*}{2_{N/r}^*-1}}\Big )^{\theta -1}\ \ \Vert u_k\Vert _{2^*}^{\ \vartheta }, \end{aligned}$$

where

$$\begin{aligned} \theta&:=(1-t/q)^{-1}=\frac{2_{N/r}^*-1}{2_{N/q}^*-1}, \end{aligned}$$

(2.9)

$$\begin{aligned} \vartheta&:=\frac{1-\sigma }{\sigma }(1-t/q)^{-1} = \theta \ (2_{N/q}^*-2), \end{aligned}$$

(2.10)

see (2.8) and (2.5). Observe that since $q< r$, then $\theta > 1$. Moreover, since (2.10) and (2.9),

$$\begin{aligned} \theta +\vartheta =\theta (2_{N/q}^*-1) =2_{N/r}^*-1. \end{aligned}$$

(2.11)

Furthermore, from sub-criticality, see (1.5)

$$\begin{aligned} \int _\Omega |\tilde{f}(u_k) |^{\frac{2^*}{2_{N/r}^*-1}} \le C \left( 1+\int _\Omega |u_k|^{{2^*}}\, dx\right) , \end{aligned}$$

so

$$\begin{aligned} \Vert \tilde{f}(u_k) \Vert _{\frac{2^*}{2_{N/r}^*-1}} \le C \left( 1+\Vert u_k\Vert _{{2^*}}^{2_{N/r}^*-1}\right) . \end{aligned}$$

Consequently,

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )\le C \Vert a\Vert _r^{\ \theta } \ \Big (1+\Vert u_k\Vert _{{2^*}}^{\Theta }\Big ), \end{aligned}$$

with

$$\begin{aligned} \Theta :=(2_{N/r}^*-1)(\theta -1)+\vartheta =(2_{N/r}^*-2)\theta , \end{aligned}$$

where we have used (2.11).

Fixed $N>2$ and $r>N/2$, the function $q\rightarrow \theta =\theta (q)$ for $q\in \big (N/2,\min \{r,N\}\big )$, is decreasing, so

$$\begin{aligned}&\inf _{q\in (N/2,\min \{r,N\})} \theta (q)=\theta \big (\min \{r,N\}\big )=A\\&\quad :={\left\{ \begin{array}{ll} 1,&{}\text {if}\ r\le N,\\ 1+\frac{2}{N}-\frac{2}{r},&{}\text {if}\ r> N. \end{array}\right. } \end{aligned}$$

Finally, and since the infimum is not attained in $\big (N/2,\min \{r,N\}\big )$, for any $\varepsilon >0$, there exists a constant $C>0$ such that

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )\le C\ \Vert a\Vert _r^{\ A+\varepsilon } \ \Big (1+\Vert u_k\Vert _{2^*}^{\, (2_{N/r}^*-2)(A+\varepsilon )}\Big ), \end{aligned}$$

where A is defined by (1.12), and $C=C(\varepsilon ,c_0,r,N,|\Omega |),$ ending the proof.

$\square$

2.2 $L^\infty (\Omega )$ a priori bounds of the solutions

As as immediate corollary of Theorem 1.5, we prove that any sequence of solutions in $H_0^{1}(\Omega )$, uniformly bounded in the $L^{2^*} (\Omega )$-norm, is also uniformly bounded in the $L^{\infty } (\Omega )$-norm.

Corollary 2.2

Let $f:\overline{\Omega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be a Carathéodory function satisfying (H0)–(H1).

Let $\{u_k\}\subset H_0^{1}(\Omega )$ be any sequence of solutions to (1.1) such that there exists a constant $C_0>0$ satisfying

$$\begin{aligned} \Vert u_k\Vert _{{2^*}} \le C_0. \end{aligned}$$

Then, there exists a constant $C>0$ such that

$$\begin{aligned} \Vert u_k\Vert _{\infty } \le C. \end{aligned}$$

(2.12)

Proof

We reason by contradiction, assuming that (2.12) does not hold. So, at least for a subsequence again denoted as $u_k$, $\Vert u_k\Vert _{\infty } \rightarrow \infty$ as $k \rightarrow \infty .$ Now, part (ii) of the Theorem 1.5 implies that

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big ) \le C. \end{aligned}$$

(2.13)

From hypothesis (H0) (see in particular (1.11)), for any $\varepsilon >0$ there exists $s_1>0$ such that $h(s)\ge 1/\varepsilon$ for any $s\ge s_1,$ and so $h\big (\Vert u_k\Vert _{\infty }\big )\ge 1/\varepsilon$ for any k big enough. This contradicts (2.13), ending the proof. $\square$

We next state a straightforward corollary, assuming that the non-linearity $\tilde{f}:{\mathbb {R}}\rightarrow (0,+\infty )$ satisfies also the following hypothesis:

(H1)’:

there exists a constant $c_0>0$ such that¹

$$\begin{aligned} \sup _{s>0}\ \dfrac{\max _{[-s,s]}\, \tilde{f}}{\max \big \{\tilde{f}(-s),\tilde{f}(s)\big \}}\, \le \, c_0. \end{aligned}$$

Corollary 2.3

Assume that $f:\overline{\Omega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function satisfying (H0) and (H1)’.

Then, for any $u\in H_0^{1}(\Omega )$ weak solution to (1.1), the following holds: for any $\varepsilon >0$ there exists a constant $C>0$ such that

$$\begin{aligned} h\big (\Vert u\Vert _{\infty }\big ) \le C \Vert a\Vert _r^{\ A+\varepsilon } \ \Big (1+\Vert u\Vert _{2^*}\Big )^{\, (2_{N/r}^*-2)(A+\varepsilon )}, \end{aligned}$$

where h is defined by (1.9), A is defined by (1.12), $C=C(c_0,r,N,\varepsilon ,|\Omega |)$, and C is independent of the solution u.

Since hypothesis (H1)’, for any sequence $\{u_k\}\subset H_0^1(\Omega )$ of weak solutions to (1.1),

$$\begin{aligned} M_k:=\max \Big \{\tilde{f}\big (-\Vert u_k\Vert _{\infty }\big ),\tilde{f} \big (\Vert u_k\Vert _{\infty }\big )\Big \} \ge (2c_0)^{-1}\,\max _{[-\Vert u_k\Vert _{\infty }, \Vert u_k\Vert _{\infty }]}\tilde{f}. \end{aligned}$$

The proof can be achieved just reproducing Step 1 and Step 2 of the proof of Theorem 1.5, which now hold for any any sequence of weak solutions to (1.1).

3 Estimates of the $L^\infty (\Omega )$-norm of the solutions with radial singular weights

In this section, assuming that $0\in \Omega$ and that f satisfies (H0)’ and (H1), we prove Theorem 1.6.

First, we also collect a regularity Lemma for any weak solution to (1.1) with $\tilde{f}(s)$ of polynomial critical growth, according to Caffarelli–Kohn–Nirenberg inequality.

Lemma 3.1

(Improved regularity) Assume that $u\in H_0^1(\Omega )$ weakly solves (1.1) for a Carathéodory non-linearity $f:\overline{\Omega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ with polynomial critical growth

$$\begin{aligned} |f(x,s)|\le |x|^{-\mu }\,\big (1+|s|^{2_{\mu }^*-1}\big ), \qquad \text{ with }\quad \mu \in (0,2). \end{aligned}$$

(3.1)

Assume also that one of the following two conditions hold:

• (a) Either $\mu \le 4/N$;

• (b) either $u\in W^{1,p_0}(\Omega )$ with $p_0>2$.

Then, $u\in L^\infty (\Omega )$.

Moreover, the following hold:

• (i) If $\mu < 1,$ then $u\in C^{1,\nu }(\overline{\Omega })\cap W^{2,p}(\Omega )$ for any $p<N/\mu$, and any $\nu <1-\mu$.

• (ii) If $\mu =1,$ then $u\in C^{\nu }(\overline{\Omega })\cap W^{2,p}(\Omega )$ for any $p<N$, and $\nu <1$.

• (iii.a) Assume (a), and that $N=3$. If $1<\mu \le 4/N,$ then $u\in C^{\nu }(\overline{\Omega })\cap W^{2,p}(\Omega )$ for any $p<N/\mu$, and $\nu <2-\mu$.

• (iii.b) Assume (b). If $1<\mu <2,$ then $u\in C^{\nu }(\overline{\Omega })\cap W^{2,p}(\Omega )$ for any $p<N/\mu$, and $\nu < 2-\mu$.

Proof

Let $u\in H_0^1(\Omega )$ be a solution to (1.1). We reason as in Lemma 2.1. Assume either that (a) or (b) hold.

If f satisfies (3.1), then Caffarelli–Kohn–Nirenberg interpolation inequality (see [4], and Theorem A.1) implies that assumption (2.2) is satisfied with

$$\begin{aligned} b(x)=\frac{|x|^{-\mu }(1+|u|^{2_{\mu }^*-1})}{1+|u|} \le C |x|^{-\mu }(1+|u|^{2_{\mu }^*-2})\in L^{\frac{N}{2}}(\Omega ). \end{aligned}$$

(3.2)

Observe that $2_{\mu }^*>2$ for $\mu \in (0,2)$. Indeed, in case (a), condition (3.2) hold, see Corollary A.2(ii.b), (A.16); in case (b), condition (3.2) also hold, see Corollary A.2.(iii.b), (A.20)).

Consequently, $u\in L^q(\Omega )$ for any $q<\infty$. The growth condition for f (see (1.6)–(1.7)), implies that $-\Delta u=f(x,u)\in L^p(\Omega )$ for any $p<N/\mu .$ Thus, by the Calderon–Zygmund inequality (see [15, Theorem 9.14]), $u\in W^{2,p}(\Omega ),$ for any $p<N/\mu .$ Now, choosing $p\in (N/2,N/\mu )$, we get that $u\in L^\infty (\Omega )$.

• (i) Assume $\mu < 1.$ Choosing any $p\in (N,N/\mu )$, by elliptic regularity, $u\in W^{2,p}(\Omega ),$ with $p>N.$ Then $u\in C^{1,\nu }(\overline{\Omega })$ for $\nu =1-\frac{N}{p}$, and finally, $u\in C^{1,\nu }(\overline{\Omega })\cap W^{2,p}(\Omega )$ for any $p<N/\mu$, and any $\nu <1-\mu$.

• (ii) Assume $\mu = 1.$ Choosing any $p\in (N/2,N)$, by elliptic regularity and Sobolev embeddings, $u\in W^{1,p^*}(\Omega ),$ where $\frac{1}{p^*}:= \frac{1}{p}- \frac{1}{N}<\frac{1}{N}.$ Also $u\in C^{\nu }(\overline{\Omega })$ for any $\nu <1$. Finally $u\in C^{\nu }(\overline{\Omega })\cap W^{2,p}(\Omega )$ for any $p<N$, and $\nu <1$.

• (iii.a) Assume $N=3$, and $1<\mu \le 4/N$. Choosing any $p\in (N/2,N/\mu )$, and reasoning as above, $u\in W^{1,p^*}(\Omega ),$ where $\frac{1}{p^*}:= \frac{1}{p}- \frac{1}{N}<\frac{1}{N}.$ Also $u\in C^{\nu }(\overline{\Omega })$ for $\nu =2-N/p<2-\mu$. Finally $u\in C^{\nu }(\overline{\Omega })\cap W^{2,p}(\Omega )$ for any $p<N/\mu$, and $\nu <2-\mu$.

• (iii.b) Assume (b). Reasoning as in case (iii.a), we reach the conclusion.

$\square$

3.1 Estimates of the $L^\infty (\Omega )$-norm of the solutions

Remark 3.2

Under condition (a), the definition of B, (1.13), can be rewritten

$$\begin{aligned} B:= {\left\{ \begin{array}{ll} \displaystyle 1+\frac{2}{N}-\frac{2\mu }{N} ,&{} \text {if}\ \mu \in (0,1)\cap (0,4/N],\\ 1 ,&{}\text {if}\ N=3,\ 4 \qquad \text{ and }\quad \mu \in [1,4/N], \end{array}\right. } \end{aligned}$$

3.2 Proof of Theorem 1.6

Since Lemma 3.1, assuming either (a) or (b), a solution $u\in H_0^1(\Omega )$ to (1.1) is in $L^\infty (\Omega )$. In the proof of Theorem 1.6, we will not distinguish if we are assuming condition (a) or (b).

Proof of Theorem 1.6

Let $\{u_k\}\subset H_0^1(\Omega )$ be any sequence of solutions to (1.1). Since Lemma 3.1, $\{u_k\}\subset H_0^1(\Omega )\cap L^\infty (\Omega )$. If $\Vert u_k \Vert _{\infty }\le C,$ then (i) holds.

Now, we argue on the contrary, assuming that there exists a sequence $\{u_k\}\subset H_0^1(\Omega )$ of solutions to (1.1), such that $\Vert u_k \Vert _{\infty } \rightarrow + \infty$ as $k \rightarrow \infty .$ By Morrey’s Theorem (see [2, Theorem 9.12]), observe that also

$$\begin{aligned} \Vert \nabla u_k \Vert _{p} \rightarrow + \infty \qquad \text{ as }\quad k \rightarrow \infty , \end{aligned}$$

(3.3)

for any $p>N$.

Step 1. $W^{2,q}(\Omega )$ estimates for $q\in \big (N/2,\min \{N,N/\mu \}\big )$.

As in the proof of Theorem (1.5), let us denote by

$$\begin{aligned} M_k :=\max \Big \{\tilde{f}\big (-\Vert u_k\Vert _{\infty }\big ), \tilde{f}\big (\Vert u_k\Vert _{\infty }\big )\Big \} \ge (c_0/2)^{-1}\max _{[-\Vert u_k\Vert _{\infty },\Vert u_k \Vert _{\infty }]}\tilde{f}, \end{aligned}$$

(3.4)

where the inequality is due to hypothesis (H1), see (1.8).

Let us take q in the interval $(N/2,N)\cap (N/2,N/\mu ).$ Using growth hypothesis (H0)’(see (1.6)), hypothesis (H1) (see (1.8)), and Hölder inequality, we deduce

$$\begin{aligned}&\displaystyle \int _{\Omega }\left| f\big (x,u_k(x)\big )\right| ^q\, dx\\&\quad \le \int _{\Omega } |x|^{-\mu q} \left( \tilde{f}\big (u_k(x) \big )\right) ^{q}\, dx\nonumber \\&\quad = \int _{\Omega } |x|^{-\mu q} \left( \tilde{f} \big (u_k(x)\big )\right) ^\frac{t}{2_{\mu }^*-1} \, \left( \tilde{f}\big (u_k(x)\big ) \right) ^{q-\frac{t}{2_{\mu }^*-1}}\, dx\nonumber \\&\quad \le C\ \left[ \int _{\Omega } |x|^{-\mu q} \ \big (1+u_k(x)^{t}\big ) \,dx\right] \ M_k^{\ q-\frac{t}{2_{\mu }^*-1}} \nonumber \\&\quad \le C\ \Big (1+\big \Vert \,|x|^{-\gamma }\ u_k \,\big \Vert _{t}^{\ t}\Big )\ \ M_k^{\ q-\frac{t}{2_{\mu }^*-1}}, \end{aligned}$$

where $\gamma =\frac{\mu q}{t}$, $t\in \big (0, q\big (2_{\mu }^*-1\big )\big )$, $C=(2c_0)^{q-\frac{t}{2_{\mu }^*-1}}$ (for $c_0$ defined in (1.8)), and where $M_k$ is defined by (3.4).

Combining now elliptic regularity with Sobolev embedding, we have that

$$\begin{aligned} \Vert \nabla u_k \Vert _{q^*} \le C\ \Big (1+\big \Vert \,|x|^{-\gamma } \ u_k\,\big \Vert _{t}^{\ t}\Big )^{\,\frac{1}{q}}\ M_k^{\ 1-\frac{t}{q(2_{\mu }^*-1)}}, \end{aligned}$$

(3.5)

where $1/q^*=1/q-1/N$ (since $q>N/2$, then $q^*>N$), and $C=C(N,q,|\Omega |).$

Step 2. Caffarelli–Kohn–Nirenberg interpolation inequality.

Since the Caffarelli–Kohn–Nirenberg interpolation inequality for singular weights (see [4], and also Theorem A.1, and Corollary A.2), there exists a constant $C>0$ depending on the parameters $N,\ q,\ \mu ,$ and t, such that

$$\begin{aligned} \big \Vert \,|x|^{-\gamma }\ u_k\,\big \Vert _{t} \le C \Vert \nabla u_k \Vert _{q^*}^\theta \ \Vert u_k\Vert _{2^*}^{1-\theta }, \end{aligned}$$

(3.6)

where

$$\begin{aligned} \frac{1}{t}- \frac{\mu q}{N t}= -\theta \left( \frac{2}{N}-\frac{1}{q}\right) +(1-\theta ) \frac{1}{2^*},\qquad \text{ with }\quad \theta \in (0,1], \end{aligned}$$

(3.7)

see (A.9)–(A.10).

Substituting now (3.6) into (3.5), we can write

$$\begin{aligned} \Vert \nabla u_k \Vert _{q^*}\le C \Big (1+\Vert \nabla u_k \Vert _{q^*}^{\theta t}\ \Vert u_k\Vert _{2^*}^{(1-\theta )t} \Big )^\frac{1}{q}\ M_k^{\ 1-\frac{t}{q(2_{\mu }^*-1)}}, \end{aligned}$$

now, dividing by $\Vert \nabla u_k \Vert _{q^*}^{\theta t/q}$ and using (3.3) we obtain

$$\begin{aligned} \Vert \nabla u_k \Vert _{q^*}^{1-\theta t/q}\le C \Big (1+\Vert u_k\Vert _{2^*}^{\ \frac{(1-\theta )t}{q}}\Big )\ M_k^{\ 1-\frac{t}{q(2_{\mu }^*-1)}}. \end{aligned}$$

Let us check that

$$\begin{aligned} 1-\theta \, \frac{t}{q}>0 \qquad \text{ for } \text{ any }\quad t<q\big (2_{\mu }^*-1\big ). \end{aligned}$$

(3.8)

Indeed, observe first that (3.7) is equivalent to

$$\begin{aligned} \theta =\frac{\frac{1}{2^*} -\frac{1}{t} +\frac{\mu q}{N t}}{\frac{1}{2}+ \frac{1}{N}-\frac{1}{q}}\ , \end{aligned}$$

(3.9)

moreover, from (3.9)

$$\begin{aligned} \theta \, \frac{t}{q}=\frac{\frac{1}{q} \left( \frac{t}{2^*} -1\right) + \frac{\mu }{N}}{\frac{1}{2}+ \frac{1}{N} -\frac{1}{q}}\ , \end{aligned}$$

(3.10)

consequently,

$$\begin{aligned} \theta \, \frac{t}{q}<1&\iff \frac{1}{q}\left( \frac{t}{2^*} -1\right) + \frac{\mu }{N}< \frac{1}{2}+ \frac{1}{N}-\frac{1}{q}\\&\iff \frac{1}{q}\frac{t}{2^*}< \frac{1}{2}+ \frac{1}{N}-\frac{\mu }{N}\pm 1\\&\iff \frac{t}{q}<2^*\left( 1- \frac{\mu }{N}\right) -2^*\left( \frac{1}{2}- \frac{1}{N}\right) =2_{\mu }^*-1 \\&\iff t<q\big (2_{\mu }^*-1\big ), \end{aligned}$$

so (3.8) holds.

Consequently,

$$\begin{aligned} \Vert \nabla u_k \Vert _{q^*}\le C \Big (1+ \Vert u_k\Vert _{2^*}^{\ \frac{(1-\theta )t}{q-\theta t}}\Big )\ M_k^{\ \big (1-\frac{t}{q(2_{\mu }^*-1)}\big )(1-\theta t/q)^{-1}}. \end{aligned}$$

(3.11)

Step 3. Gagliardo–Nirenberg interpolation inequality.

Thanks to the Gagliardo–Nirenberg interpolation inequality (see [22]), there exists a constant $C=C(N,q,|\Omega |)$ such that

$$\begin{aligned} \Vert u_k\Vert _{\infty } \le C \Vert \nabla u_k \Vert _{q^*}^\sigma \ \Vert u_k\Vert _{2^*}^{1-\sigma }, \end{aligned}$$

(3.12)

where

$$\begin{aligned} \frac{1-\sigma }{2^*}=\sigma \left( \frac{2}{N}-\frac{1}{q}\right) . \end{aligned}$$

(3.13)

Hence, substituting (3.11) into (3.12), we deduce

$$\begin{aligned} \Vert u_k\Vert _{\infty }\le C \ \Big (1+ \Vert u_k\Vert _{2^*}^{\ \sigma \,\frac{(1-\theta )t}{q-\theta t} +1-\sigma }\Big ) \ M_k^{\ \sigma \big (1-\frac{t}{q(2_{\mu }^*-1)}\big ) (1-\theta t/q)^{-1}} . \end{aligned}$$

(3.14)

From definition of $M_k$ (see (2.3)) and of h (see (1.10)), we obtain

$$\begin{aligned} M_k =\frac{\Vert u_k\Vert _{\infty }^{2_{\mu }^*-1}}{h\big (\Vert u_k\Vert _{\infty }\big )}. \end{aligned}$$

(3.15)

From (3.13),

$$\begin{aligned} \frac{1}{\sigma }=1+2^*\left( \frac{2}{N}-\frac{1}{q}\right) =2_{N/q}^*-1. \end{aligned}$$

(3.16)

From (3.10), we deduce

$$\begin{aligned} 1-\theta \, \frac{t}{q}&=\frac{\frac{1}{2}+ \frac{1}{N}-\frac{t}{2^*q} -\frac{\mu }{N}\pm 1}{\frac{1}{2}+ \frac{1}{N}-\frac{1}{q}}\nonumber \\&=\frac{\left( 1- \frac{\mu }{N}\right) -\frac{1}{2^*} -\frac{t}{2^*q} }{\frac{1}{2}+ \frac{1}{N}-\frac{1}{q}} =\frac{2_{\mu }^*-1-\frac{t}{q}}{2_{N/q}^*-1} \ , \end{aligned}$$

(3.17)

where we have used that, by definition of $2_{\mu }^*$ (see (1.2)), $\frac{2_{\mu }^*}{2^*}=1- \frac{\mu }{N}$.

Moreover, since (3.17),

$$\begin{aligned}&\left( 1-\frac{t}{q(2_{\mu }^*-1)}\right) {\big (2_{\mu }^*-1\big )} \frac{1}{(1-\theta t/q)} \nonumber \\&\quad =\left( 2_{\mu }^*-1-\frac{t}{q}\right) \frac{1}{(1-\theta t/q)}=2_{N/q}^*-1. \end{aligned}$$

(3.18)

Taking into account (3.16) and (3.18), we obtain

$$\begin{aligned} \sigma \Big (1-\frac{t}{q(2_{\mu }^*-1)}\Big ){\big (2_{\mu }^*-1\big )} (1-\theta t/q)^{-1}=1. \end{aligned}$$

(3.19)

Consequently, since (3.15), and (3.19), we can rewrite (3.14) in the following way:

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )^{\ \frac{1}{2_{\mu }^*-1}}\le C \ \Big (1+ \Vert u_k\Vert _{2^*}^{\ \sigma \,\frac{(1-\theta )t/q}{1-\theta t/q}+1-\sigma }\Big ), \end{aligned}$$

or equivalently

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big ) \le C\ \Big (1+ \Vert u_k\Vert _{2^*}^{\ \Theta }\Big ), \end{aligned}$$

where

$$\begin{aligned} \Theta := \big (2_{\mu }^*-1\big ) \left[ 1+\sigma \,\frac{t/q-1}{1-\theta t/q}\right] . \end{aligned}$$

Since (3.19), $\sigma (1-\theta t/q)^{-1}=(2_{\mu }^*-1 -\frac{t}{q})^{-1}$, and substituting it into the above equation, we obtain

$$\begin{aligned} \Theta =\big (2_{\mu }^*-1\big )\left( \frac{2_{\mu }^*-2}{2_{\mu }^*-1 -\frac{t}{q}}\right) . \end{aligned}$$

Fixed $N>2$ and $\mu \in (0,2)$, the function $(t,q)\rightarrow \Theta =\Theta (t,q)$ for $(t,q)\in \big (0, q(2_{\mu }^*-1)\big )\times \big (N/2,\min \{N,N/\mu \}\big )$, is increasing in t and decreasing in q.

For $\mu \in [1,2)$, $\min \{N,N/\mu \}=N/\mu$. If $q_k\rightarrow N/\mu$, Eq. (3.7) with $q=q_k$, $\theta =\theta _k<1$ and an arbitrary $t\in \big (0, (2_{\mu }^*-1)N/\mu \big )$ fixed, yields $\theta _k\rightarrow \frac{1}{2_{\mu }^*-1}<1$ (since $\mu <2$). Hence, when $\mu \in [1,2)$,

$$\begin{aligned} \underset{t\in \big (0, (2_{\mu }^*-1)\frac{N}{\mu }\big ),\, q\in \big (\frac{N}{2},\frac{N}{\mu }\big )}{\inf }\ \Theta (t,q) =\Theta \bigg (0,\frac{N}{\mu }\bigg )=2_{\mu }^*-2. \end{aligned}$$

On the other hand, for $\mu \in (0,1)$, $\min \{N,N/\mu \}=N$. If $q_k\rightarrow N,$ equation (3.7) with $q=q_k$, $\theta =\theta _k>0$ and t fixed, yields $\theta _k\rightarrow \frac{2}{2^*}-\frac{2(1-\mu )}{t}\ge 0$, so $t\ge 2^*(1-\mu )$. Hence, when $\mu \in (0,1)$,

$$\begin{aligned} \underset{t\in [2^*(1-\mu ), (2_{\mu }^*-1)N),\, q\in \big (\frac{N}{2},N\big )}{\inf }\, \Theta (t,q) =\Theta (2^*(1-\mu ),N)=(2_{\mu }^*-2)B, \end{aligned}$$

where B is defined by (1.13).

Since the infimum is not attained, for any $\varepsilon >0$, there exists a constant $C=C(\varepsilon ,c_0,\mu ,N,\Omega )$ such that

$$\begin{aligned} h\big (\Vert u_k\Vert _{\infty }\big )\le C \ \Big (1+\Vert u_k\Vert _{2^*}^{\, (2_{\mu }^*-2)(B+\varepsilon )}\Big ) , \end{aligned}$$

which ends the proof. $\square$

4 Uniform $L^\infty$ a priori estimates

Proof of Theorem 1.7

We will show $\Vert u\Vert _{H_0^1(\Omega )}\le C$, where C is independent of u, once achieved, either Theorem 1.5, either Theorem 1.6 will finished the proof.

We prove it by contradiction. Suppose there exists a sequence $\{u_k\}$ of non-negative weak solutions of (1.1) such that $\Vert u_k\Vert _{H_0^1(\Omega )} \rightarrow \infty$ as $k \rightarrow \infty$. Let $\displaystyle U_k:=\frac{u_k}{\Vert u_k\Vert _{H_0^1(\Omega )}}$. Then, by the reflexivity of $H_0^1(\Omega )$, $U_k \rightharpoonup U$ in $H_0^1(\Omega )$ up to a subsequence. By the compactness of the trace operator, $U_k \rightarrow U$ in $L^{p+1}(\Omega )$.

Step 1: $U =0$ a.e. on $\Omega$.

Since $u_k$ is a weak solution of (1.1), we have

$$\begin{aligned} \int _{\Omega }\nabla u_k \nabla \psi = \int _{\Omega }f(x,u_k) \psi \quad \text{ for } \text{ all } \quad \psi \in H_0^1(\Omega )\,. \end{aligned}$$

(4.1)

Then dividing both sides of (4.1) by $\Vert u_k\Vert _{H_0^1(\Omega )}$, we have

$$\begin{aligned} \int _{\Omega }\nabla U_k \nabla \psi = \int _{\Omega }\frac{f(x,u_k)}{\Vert u_k\Vert _{H_0^1(\Omega )}} \psi \quad \text{ for } \text{ all } \quad \psi \in H_0^1(\Omega )\,. \end{aligned}$$

(4.2)

Taking $\psi =U_k$ as a test function, we have

$$\begin{aligned} 1=\int _{\Omega }|\nabla U_k|^2 =\int _{\Omega }\frac{f(x,u_k)}{\Vert u_k\Vert _{H_0^1(\Omega )}}U_k, \end{aligned}$$

(4.3)

which implies

$$\begin{aligned} \int _{\Omega }\frac{f\big (x,u_k\big )}{\Vert u_k\Vert ^{q}_{H_0^1(\Omega )}}u_k =\int _{\Omega }\frac{f\big (x,u_k\big )}{\Vert u_k\Vert ^{q-1}_{H_0^1(\Omega )}}U_k =\frac{1}{\Vert u_k\Vert ^{q-2}_{H_0^1(\Omega )}} \rightarrow 0 \text{ as } k \rightarrow \infty \,, \end{aligned}$$

since $q>2$. Therefore,

$$\begin{aligned} K_1\Vert U_k\Vert _{L^{q}(\partial \Omega )}^{q}-K_2 \frac{|\partial \Omega |}{\Vert u_k\Vert ^{q}_{H_0^1(\Omega )}}\le \int _{\Omega }\frac{f(x,u_k)}{\Vert u_k\Vert ^{q}_{H_0^1(\Omega )}}u_k \rightarrow 0 \text{ as } k \rightarrow \infty \,, \end{aligned}$$

so $\Vert U_k\Vert _{L^{q}(\partial \Omega )}\rightarrow 0$. Since $U_k \rightarrow U$ in $L^{s}(\Omega )$ for all $s<2^*$, we have that $U=0$ a.e. on $\Omega$.

Step 2: A contradiction.

Since

$$\begin{aligned} U_k \rightharpoonup 0 \text{ in } H_0^1(\Omega ), \end{aligned}$$

it follows from (4.2) that for all $\psi \in H_0^1(\Omega )$

$$\begin{aligned} \lim \limits _{k \rightarrow \infty }\int _{\Omega } \frac{f(x,u_k)}{\Vert u_k\Vert _{H_0^1(\Omega )}} \psi =\int _{\Omega }\nabla U \nabla \psi =0\,. \end{aligned}$$

(4.4)

Let $g_k:=\, \frac{f(x,u_k)}{\Vert u_k\Vert _{H_0^1(\Omega )}}$, by sub-criticality and Lemma 2.1, $\{g_k\}_k\subset L^\infty (\Omega )$. Fix $q< 2^*$. Since (4.4), $\int _{\Omega }g_k \psi \rightarrow 0,$ for any $\psi \in L^{q}(\Omega )$ (due to $H_0^1(\Omega )$ is dense in $L^{q}(\Omega )$). Let $x_k:=U_k \rightarrow 0$ in $L^{q}(\Omega )$. By Brezis [2, Prop. 3.13 (i) and (iv)], $\langle g_k, x_k\rangle \rightarrow 0$, that is,

$$\begin{aligned} \lim \limits _{k \rightarrow \infty }\int _{\Omega }\frac{f(x,u_k)}{\Vert u_k\Vert _{H_0^1(\Omega )}}U_k=0 \end{aligned}$$

a contradiction to (4.3). Hence, the conclusion of Theorem 1.7 holds, completing the proof. $\square$

Appendix A. The Caffarelli–Kohn–Nirenberg interpolation inequality

Theorem A.1

Let $p, q, t, \alpha , \beta , \sigma$ and $\theta$ be fixed real numbers (parameters) satisfying

$$\begin{aligned}&p, q \ge 1,\ \ t > 0,\ \ 0 \le \theta \le 1, \end{aligned}$$

(A.1)

$$\begin{aligned}&\frac{1}{p} + \frac{\alpha }{N},\ \frac{1}{q} + \frac{\beta }{N} ,\ \frac{1}{t}- \frac{\gamma }{N} > 0 , \end{aligned}$$

(A.2)

where

$$\begin{aligned} \gamma = -\big [\theta \sigma + (1-\theta )\beta \big ] . \end{aligned}$$

(A.3)

Then, there exists a positive constant $C>0$ such that for all $u \in C^\infty _c({\mathbb {R}}^N)$:

$$\begin{aligned} \big \Vert |x|^{-\gamma } u\big \Vert _{L^t({\mathbb {R}}^N)} \le C\, \big \Vert |x|^\alpha \, |\nabla u|\big \Vert ^{\,\theta }_{L^p({\mathbb {R}}^N)}\, \big \Vert |x|^\beta u\big \Vert ^{\, 1-\theta }_{L^q({\mathbb {R}}^N)}, \end{aligned}$$

(A.4)

where

$$\begin{aligned}&\frac{1}{t}- \frac{\gamma }{N}= \theta \left( \frac{1}{p} + \frac{\alpha - 1}{N}\right) + (1 - \theta ) \left( \frac{1}{q} + \frac{\beta }{N}\right) , \end{aligned}$$

(A.5)

$$\begin{aligned}&0 \le \alpha - \sigma \qquad \text{ if }\quad \theta > 0, \end{aligned}$$

(A.6)

and

$$\begin{aligned} \alpha - \sigma \le 1 \qquad \text{ if }\quad \ \theta > 0 \ \text { and }\ \frac{1}{p} + \frac{\alpha - 1}{N} = \frac{1}{t}- \frac{\gamma }{N}. \end{aligned}$$

(A.7)

Moreover, on any compact set in parameter space in which (A.1), (A.2), (A.5) and $0\le \alpha - \sigma \le 1$ hold, the constant C is bounded.

See [4] for a proof.

Corollary A.2

Suppose that $\Omega \subset {\mathbb {R}}^N$ is of class $C^1$ with $\partial \Omega$ bounded. Let $p, q, t, \sigma ,\theta$ be fixed real parameters satisfying (A.1)–(A.3) particularized for $\alpha =\beta =0$. Specifically,

$$\begin{aligned} 1 \le p,q < \infty , \qquad \text{ and }\quad \frac{1}{t}> \frac{\gamma }{N} \qquad \text{ where }\quad \gamma =(-\sigma )\theta . \end{aligned}$$

(A.8)

Then,

(i) there exists a positive constant $C = C (\Omega , N, p, q, t, \sigma , \theta )$ such that for all $u\in W^{1,p}(\Omega )\cap L^{q}(\Omega )$:

$$\begin{aligned} \big \Vert |x|^{-\gamma } u\big \Vert _{L^t(\Omega )} \le C\, \big \Vert \nabla u\big \Vert ^{\,\theta }_{L^p(\Omega )}\, \big \Vert u\big \Vert ^{\, 1-\theta }_{L^q(\Omega )}, \end{aligned}$$

(A.9)

where

$$\begin{aligned}&\frac{1}{t}- \frac{\gamma }{N}= \theta \left( \frac{1}{p} - \frac{1}{N}\right) + (1 - \theta )\, \frac{1}{q} , \end{aligned}$$

(A.10)

$$\begin{aligned}&\sigma \le 0 \qquad \text{ if }\quad \theta > 0, \end{aligned}$$

(A.11)

and

$$\begin{aligned} \sigma \ge -1 \qquad \text{ if }\quad \theta > 0 \qquad \text{ and }\quad \frac{1}{p} - \frac{1}{N} = \frac{1}{t}- \frac{\gamma }{N}. \end{aligned}$$

(A.12)

(ii) Moreover, if $p=2$, $q=2^*$, and $\sigma <0$ (so $\gamma >0$), there exists a positive constant $C = C (\Omega , N, t, \sigma ,\theta )$ such that for all $u\in H^{1}(\Omega )$:

$$\begin{aligned} \big \Vert |x|^{-\gamma } u\big \Vert _{L^t(\Omega )} \le C\, \big \Vert \nabla u\big \Vert _{L^2(\Omega )}\, \end{aligned}$$

(A.13)

where

$$\begin{aligned} \frac{1}{t}- \frac{\gamma }{N}= \frac{1}{2} - \frac{1}{N}, \qquad \text{ and }\quad 0< \gamma \le 1. \end{aligned}$$

(A.14)

In particular, for all $u\in H^{1}(\Omega )$

$$\begin{aligned} \mathrm{(ii.a)} \ f(x,u)\le C \big (1+|x|^{-\mu }|u|^{2^*_\mu -1}\big ) \in L^{\frac{2N}{N+2}}(\Omega ),\text { if } \mu \le 1+\frac{2}{N}, \end{aligned}$$

(A.15)

and

$$\begin{aligned} \mathrm{(ii.b)}\ |x|^{-\mu }|u|^{2^*_\mu -2} \in L^{\frac{N}{2}}(\Omega ),\text { if } \mu \le 4/N. \end{aligned}$$

(A.16)

(iii) Besides, for all $u\in W^{1,p}(\Omega )$ with $2<p<\infty$:

$$\begin{aligned} \big \Vert |x|^{-\gamma } u\big \Vert _{L^t(\Omega )} \le C\, \big \Vert \nabla u\big \Vert _{L^p(\Omega )}\,, \end{aligned}$$

(A.17)

where

$$\begin{aligned} \frac{1}{t}- \frac{\gamma }{N}= \frac{1}{p} - \frac{1}{N}. \end{aligned}$$

(A.18)

In particular, for all $u\in W^{1,p}(\Omega )$ with $2<p<\infty$,

$$\begin{aligned}&\mathrm{(iii.a)} \ f(x,u)\le C \big (1+|x|^{-\mu }|u|^{2^*_\mu -1}\big ) \in L^{\frac{2N}{N+2}}(\Omega ), \end{aligned}$$

(A.19)

and

$$\begin{aligned} \mathrm{(iii.b)}\ |x|^{-\mu }|u|^{2^*_\mu -2}\in L^{\frac{N}{2}}(\Omega ). \end{aligned}$$

(A.20)

Proof

• (i) The proof can be obtained using that $C^\infty _c({\mathbb {R}}^N)$ is dense in $L^p({\mathbb {R}}^N)$ for any $1 \le p < \infty$, and the extension operator, $P:W^{1,p}(\Omega )\rightarrow W^{1,p}({\mathbb {R}}^N)$, see [2, Theorem 9.7]. Moreover, (A.9)–(A.12) are a particular case of (A.4)–(A.7) for $\alpha =\beta =0$.

• (ii) Assume now $p=2$, $q=2^*$, and $\sigma <0$, then (A.13)–(A.14) are a particular case of (A.9)–(A.10) for $\theta =1$. Moreover, (A.8), and (A.6)–(A.7) imply

  $$\begin{aligned} 0< (-\sigma )\le 1,\qquad \text{ so }\quad 0<\gamma \le 1. \end{aligned}$$

• (ii.a) Indeed, choosing $t=(2^*_\mu -1)\frac{2N}{N+2}$, $\theta =1$, and $\sigma =-\frac{\mu }{2^*_\mu -1}$, we deduce from (A.8) that $\gamma =\frac{\mu }{2^*_\mu -1}$, hence

  $$\begin{aligned} \frac{1}{t}- \frac{\gamma }{N}=\frac{1}{2} - \frac{1}{N}, \end{aligned}$$

  and

  $$\begin{aligned} \gamma \le 1\iff \mu \le 1+\frac{2}{N}. \end{aligned}$$

  Consequently, (A.15) holds.

• (ii.b) Choosing now $t=(2^*_\mu -2)\frac{N}{2}$, $\theta =1$, and $\sigma =-\frac{\mu }{2^*_\mu -2}$, we deduce from (A.8) that $\gamma =\frac{\mu }{2^*_\mu -2}$, then

  $$\begin{aligned} \frac{1}{t}- \frac{\gamma }{N}=\frac{1}{2} - \frac{1}{N}, \end{aligned}$$

  and

  $$\begin{aligned} \gamma \le 1\iff \mu \le 4/N. \end{aligned}$$

  Hence, (A.16) holds.

• (iii) Assume finally $2<p<\infty$, then (A.17)–(A.18) are a particular case of (A.9)–(A.10).

• (iii.a) Indeed, choosing $t=(2^*_\mu -1)\frac{2N}{N+2}$, $\theta =1$, and $\sigma =-\frac{\mu }{2^*_\mu -1}$, we deduce from (A.8) that $\gamma =\frac{\mu }{2^*_\mu -1}$, hence

  $$\begin{aligned} \frac{1}{t}- \frac{\gamma }{N}=\frac{1}{2} - \frac{1}{N}<\frac{1}{p} -\frac{1}{N}, \end{aligned}$$

  so (A.12) do not apply.

• (iii.b) Choosing now $t=(2^*_\mu -2)\frac{N}{2}$, $\theta =1$, and $\sigma =-\frac{\mu }{2^*_\mu -2}$, we deduce from (A.8) that $\gamma =\frac{\mu }{2^*_\mu -2}$, so $\frac{1}{t}- \frac{\gamma }{N}=\frac{1}{2} - \frac{1}{N}<\frac{1}{p} - \frac{1}{N},$ and (A.12) do not apply.

$\square$