Introduction

Dewey (1933) describes reflection as an “active, persistent, and careful consideration of any belief or supposed form of knowledge in the light of the grounds that support it and further conclusions to which it tends” (p. 9). Schön (1983) further develops Dewey’s notion of reflection with the concepts of reflection-in-action and reflection-on-action. Reflection-in-action takes place during an action, and reflection-on-action takes place after an event has occurred. A related concept, which was developed from Schön’s work, is reflection-for-action (Killion and Todnem 1991; Grushka et al. 2005). Reflection-for-action is thinking about future actions with the intention of improving or changing a practice. This type of reflection requires teachers to anticipate what will occur during a lesson, as well as reflect on their past experiences, before a lesson occurs (Farrell 2013). The main problem teachers have in doing reflection-for-action is knowing what they should reflect on to be able to make improvements or changes in their own practice. Reflection-for-action has a strong connection to reflection-in-action, and mathematics teachers’ choice or design of examples could help them succeed in their teaching. This article is an attempt to describe how teachers’ reflection-for-action helps them to review what has been accomplished and identify constructive guidelines so they succeed in the teaching process. There are two main purposes in this article. The first is to address the possibility of encouraging teachers’ engagement in their choice or design of examples concerning arithmetic and algebra. The second is to address the possibility of supporting teachers’ choice or design of examples in arithmetic and algebra.

Olteanu (2016) points out that reflection-for-action is connected to the intended object of learning (a planning stage), which refers to the content that students should learn and that is to be covered in the classroom. In addition, reflection-for-action is connected to the enacted object of learning (what appears in a classroom) and to the lived object of learning (what is possible for students to experience within a learning environment). Although planning and execution are two different processes, the focus in this article is only on the relationship between the intended object of learning and the process of reflection-for-action. The choice or design of examples plays a crucial role in reflection-for-action; according to Leinhardt (2001), examples constitute a fundamental part of a good explanation and a ground for good teaching. For this reason, this article focuses on the improvement of the design of examples as a consequence of the teachers’ reflection-for-action. The questions which guide the issues in this article are as follows: (1) How can teachers’ engagement in their choice or design of examples be encouraged? and (2) How can the choice or design of examples be supported?

Background

Certain terms in mathematics education, such as “examples” and ‘tasks”, have taken on meanings that may not be clear to all parties involved in the educational process. The distinction between a task and an example is that the first is about what the learner is asked to do (Christiansen and Walther 1986), and the second is a fundamental part of a good explanation (Leinhardt 2001). Watson and Mason (2002) use the term “example” in accordance with Bills et al. (2006) to mean raw material used for generalising, including “intuiting relationships and inductive reasoning; illustrating concepts and principles; indicating a larger class; motivating; exposing possible variation and change; and practising technique” (p. 127). After reviewing the use of examples from historical, theoretical, teaching and learning perspectives, Bills et al. (2006) describe examples from the teaching perspective as fundamental tools for communication and instructional explanation. They distinguish two attributes of good examples: transparency and generalisability. Transparency allows a learner to recognize an example as being generic (e.g. f(x) = (x − 1)2 + 1 is transparent with respect to the coordinates of the vertex), and generalisability allows a learner to identify an example’s arbitrary and changeable features (e. g. f(x) = (x − a)2 + b). Teachers may use the explanatory nature of examples (e.g. by using a counter-example) to illustrate certain ideas through their lens (Peled and Zaslavsky 1997). Mason and Pimm (1984) point out that generic examples are transparent to the general case, allowing one to see the general through the particular (e.g. the order in which operations should be done to calculate an arithmetical expression). Examples may consist of a simple expression or comprise a complex multi-stage problem. Zaslavsky (2010) distinguishes among specific, semi-general and general examples, and identifies the following reasons for teachers’ use of examples: conveying generality and invariance, explaining and justifying notations and conventions, establishing the status of students’ conjectures and assertions, connecting mathematical concepts to real-life experiences and the challenge of constructing examples with given constraints. For instance, a general example could be used to show the distributive property of multiplication over addition for algebraic expressions, a semi-general example could be used to show the distributive property for real numbers and a specific example could be used to calculate 5 × 23 via the distributive property.

Bills et al. (2006) state that an important pedagogic distinction can be made between examples of a concept and examples of the application of a procedure. The latter include worked-out examples and exercises. Worked-out examples are characterised by the procedure being applied and performed by the teacher or textbook author, while exercises are tasks that students complete. Atkinson et al. (2000, p. 181) stress that worked examples “typically include a problem statement and a procedure for solving the problem; together, these are meant to show how other similar problems might be solved. In a sense, they provide an expert’s problem-solving model for the learner to study and emulate”. They note three principles for how such examples should be designed: (1) integration of example parts (text and diagrams), (2) use of multiple modalities (integrating aural and visual information) and (3) clarity of sub-goal structure (integrating steps and sub-goals). Although examples are important for helping students develop generalisations of structures, little research has been done on teachers’ choice of examples (Bills et al. 2006; Bills and Rowland 1999).

In mathematics education, a task is often defined as “a classroom activity, the purpose of which is to focus students’ attention on a particular mathematical idea” (Stein et al. 1996, p. 460). Doyle (1983, p.161) specifies that “tasks influence learners by directing their attention to particular aspects of content and by specifying ways of processing information”. Teachers’ work with tasks has been investigated in different ways (e.g. Gueudet and Trouche 2012; Pepin et al. 2013; Jones and Pepin 2016; Remillard 2005). Shimizu et al. (2010) point out that when teachers select a task for their teaching, they may think of task attributes such as context, complexity, representation, form and degree of openness. Jones and Pepin (2016) note that the design of mathematical tasks is perceived sometimes as something distinct from the teaching and learning process, and sometimes as integral to it.

The classroom use of mathematical tasks as well as the importance of selecting and setting appropriate tasks in teaching mathematics has been addressed by several researchers (Clarke et al. 2006; Doyle 1988; Keitel 2006; Hiebert and Wearne 1993; Stein and Lane 1996; Martin 2007; Mok and Kaur 2006). Sullivan (2011) discusses the importance of well-chosen mathematics tasks in supporting student learning, and presents some examples of types of tasks that invite students to reflect on the effect of their actions: tasks that focus on procedural fluency, tasks using models or representations that engage students, contextualised practical tasks, open-ended tasks and tasks that involve constraints. Swan (2005, 2011) proposed five types of tasks: classifying mathematical objects, interpreting multiple representations, evaluating mathematical statements, creating problems for others to solve and analysing reasoning and solutions. There are both similarities and differences between Sullivan’s (2011) and Swan’s (2005, 2011) approaches to mathematical tasks. Sullivan describes actions and tasks relevant for student learning, and explains that conceptual understanding includes the comprehension of mathematical concepts, operations and relations, while Swan argues in a broad sense for the constructive use of students’ prior knowledge. The tasks are the focus of classroom work, and the nature of these tasks influences the relationship between the teacher and the students (Ames 1992; Christiansen and Walther 1986). Kilpatrick et al. (2001) argue that it is not possible to foster adaptive reasoning and strategic competence in students without providing them with tasks that are designed to promote these actions. Various research and development teams have undertaken collaborative efforts aimed at developing and testing task designs for improving the teaching and learning of mathematics (e.g. Jung and Brady 2016; Wake et al. 2016). However, as Kamin (2010) affirms, in mathematics classes, tasks are typically associated with lists of exercises often involving repetitive groups of similar questions. The different meanings ascribed to mathematical examples and tasks arise from the different perspectives of mathematics teachers, researchers and educators of mathematics teachers.

Because “the selection of examples is the art of teaching mathematics” (Leinhardt et al. 1990, p. 52), the focus of this article is on the teacher’s choices or design of examples rather than on the use of tasks as a classroom activity. I have adopted Watson and Mason’s (2002) view of what constitutes an example, that is, any particular case of a larger class (idea, concept, technique, etc.) from which students can reason and generalise. Here, design of examples refers to mathematical examples that are designed by teachers for teaching. The distinction between examples and tasks is a problem not only for research and researchers but also for teachers in their everyday work. It is not possible for teachers to perform their professional role without being able to distinguish between what must be done and what might be done to achieve their professional aims and carry out their professional duty. Hence, there is confluence between the interests of the researcher and those of the teacher in being able to distinguish between mathematical examples and mathematical tasks. In exploring the use of mathematical examples from the perspective of teachers, this article adds new knowledge to the field.

Theoretical approach

In the study, the concepts from variation theory (e.g. Lo 2012; Marton 2015; Marton and Tsui 2004; Runesson 2006) guided the analyses of the benefits of reflection-for-action. Reflection can be encouraged by having teachers view themselves on video (Kersting et al. 2010; Kucan 2007; Santagata and Angelici 2010) or through group discussions (Pareja Roblin and Margalef 2013). This study used an iterative process in which a lesson is built on the previous lesson, which encourages reflection. During the iterative process, the teachers paid attention to concepts from variation theory (critical aspects and patterns of variation) in order to identify opportunities for students to learn the object of learning.

The object of learning concerns a specific way of understanding a particular content taught in school (Marton and Booth 1997). The focus is not only on the content that the teacher wishes the students to learn (the direct object of learning) but also on the abilities that the students can develop through learning the content (the indirect object of learning). To learn something, the students must discern what is to be learned (the content). This consists of several aspects, and to discern an aspect of the object of learning, a student must experience variation corresponding to that aspect. If an aspect of the object of learning is not discerned, then it becomes a critical aspect for the student. Olteanu (2014) separates the critical aspects into intended critical aspects (the aspects of the content that teachers intend to present in the classroom and are assumed to be critical for students); enacted critical aspects (the aspects of the content that teachers focus on during the lesson) and lived critical aspects (the critical aspects of the object of learning that the students distinguish).

To make it possible for students to experience variation, certain patterns of variation and invariance must be used (Marton and Pang 2008). The patterns of variation are described in the literature as contrast, separation, generalisation, fusion and similarity (Marton 2015; Marton and Tsui 2004; Olteanu and Olteanu 2012). When using contrast, a teacher lets learners simultaneously discern a quality, X, and a different quality, non-X. For instance, to help learners discern a rational number, the teacher lets them discern a non-example of a fraction, such as a natural number. In using separation, a teacher keeps the other dimensions of variation invariant or varies them at a different rate. For instance, to help learners discern the numerator in a fraction, a teacher lets them discern a variation in the numerator by keeping the denominator invariant. In this way, the numerator is different from the other dimensions of variation that affect the value of the fraction. In generalisation, a teacher keeps a value in one of the dimensions of variation invariant while varying the other dimensions. For instance, to generalise the concept of a fraction, the teacher may provide different examples that involve this fraction. In fusion, a teacher gives the learner the opportunity to experience two (or more) dimensions of variation simultaneously. For instance, to help learners discern the value of a fraction, a teacher lets them simultaneously discern both the denominator and the numerator in determining the value of the fraction. In using similarity, a teacher keeps the property of two or more expressions invariant so they have the same meaning, and varies the illustrations or the representation of expressions to indicate some kind of generality. For instance, to help learners discern a fraction, a teacher lets them simultaneously discern the fraction by illustrating it on a number line, by using a circle model, a bar model, a block model and so on, or by giving a different name to the numerator and the denominator such as number of shaded parts and number of equal parts.

Marton (2015) asserts that an object of learning has a structure and a meaning, where structure refers to the relationship between the parts and the whole. Olteanu (2014) identified six categories that can be used to analyse the structure of an object of learning: the whole (e.g. the expression 5 − 3 + 2), the parts that form the whole (e.g. 5, 3, 2), the relation between the parts (e.g. the operation), the transformation between the parts (e.g. rewriting as 2 + 2), the relation between the parts and the whole (e.g. 2, +, 2) and the relation between different wholes (e.g. the relation between 2 + 2 and 4). The meaning depends on the methods used to discern the structure of the object of learning.

In order to give students the opportunity to discern aspects of the object of learning, it is necessary for teachers to reflect before the lesson on what varies and what is invariant in the choice or design of the examples, and hence on the patterns of variation. The teachers, who worked with a researcher, planned the lesson(s) with a special focus on making it possible for the students to discern aspect(s) of the object of learning (Marton 2015). In this process, the instructional planning (the intended object of learning) identified the relationship between the teachers’ reflection-for-action in choosing or designing examples and the teachers’ own experiences, previous research and the exploration of students’ prior understanding. Several researchers have found that instructional planning plays a powerful role in teaching and allows teachers to use empirical evidence as their source of reference when they want to improve their teaching (e.g. Farrell 2013; Ruys et al. 2012). For example, when an example does not go well, a teacher may turn to their plan and check how the examples were done. Farrell (2013) suggests three approaches to use in instructional planning: forward planning (identifying the content of a lesson prior to deciding on the methodology to be used in a particular lesson), central planning (selecting the methods to be used in teaching before selecting the content to be delivered to the students) and backward planning (deciding on the lesson outcomes before deciding on the instructional activities). These approaches determine the direction of the lesson in terms of the examples, and determine how to open up dimensions of variation to help students discern aspects of the object of learning.

Jay and Johnson (2002) have developed a typology of reflection involving three intertwined dimensions: descriptive, comparative and critical reflection. In the descriptive dimension, the practitioner describes the matter for reflection; in the comparative dimension, the practitioner reframes the matter for reflection in the light of alternative views, perspectives and research and in the critical dimension, a new perspective is established. In this article, the typology of Jay and Johnson (2002) is related to the use of examples in reflection-for-action when a teacher intends to teach arithmetic and algebra.

Methods

Research design

The study reported in this article forms part of a longitudinal research project intended to make educational research in mathematics more useful to teachers by focusing on what teachers keep in mind about students’ learning. The project was conducted in Sweden, where most students begin their first year of school in the next autumn term after their seventh birthday. Compulsory school consists of nine school years divided into grades 1–3, 4–6 and 7–9. All students who have completed compulsory school are entitled to a 3-year upper secondary school education. The study included 3 years of iterative cycles involving 22 teachers from compulsory school to upper secondary school. The teachers’ participation was voluntary. Those teachers who agreed to participate in the project received written information about the project and were given the opportunity to ask questions in connection with the project leader’s school visits. In addition, three researchers participated in the study. For this article, four of the teachers were selected for the analysis because a common object of learning could be identified in their teaching. An educational design research approach was used in the project (Reeves 2011). This kind of research seeks to contribute to the knowledge base about improving learning and teaching in real-life contexts (Plomp 2013). The design of the study emerged from the research process, with the data emerging from each iteration serving to guide and improve the teaching and learning. The educational design research was conducted in four phases: (1) analysis of practical problems, (2) development of solutions informed by existing design, (3) iterative cycles of testing and refinement and (4) reflection to produce a new design and enhance future implementation. The process is illustrated in Fig. 1. For the study, the teachers had indicated that one of the practical problems they had was developing, designing or adapting their own examples to create progression in students’ learning. Designing or adapting examples is not the usual practice in Sweden; most teachers use the examples and methods presented in the textbooks. Several steps were used in each phase, all of which have been described in previous articles (e.g. Olteanu and Olteanu 2012; Olteanu 2014).

Fig. 1
figure 1

The four project phases and the steps performed in each

Full size image

In the first phase, the teachers examined the course module and curriculum to identify the intended object of learning (step 1), then identified the actual object of learning (step 2). Following this, the researchers explained the various concepts used in variation theory to the teachers, who put them into practice (steps 3–4). Phase two began with the teachers working to identify the intended critical aspects in their students’ learning (step 5). Following this, tests and interviews were conducted with the students to identify the lived critical aspects of their learning (steps 6–7). Based on the lived critical aspects identified, and the differences between the intended, enacted and lived critical aspects, the key concept of the theory of variation was explained again to the teachers (step 8). The teachers planned and implemented six new lessons (step 9). After each lesson, the teachers wrote a detailed report (journal) to open up patterns of variation in the identified lived critical aspects (step 10). After the implementation of the lessons, the students took different tests (step 11). The iterative cycles of testing and refinement in phase 3 involved steps 3–11. In phase 4, the teacher and researchers reflected so as to enhance future implementation, which involved steps 5–10. The teachers documented the planning of each lesson in a journal in all four phases. Journal writing gives teachers the opportunity to describe and explore their own teaching practices (e.g. Vanhulle 2005; Ekiz 2006), and can help them to develop their reflective skills (Calderhead 1989; Ferraro 2000). Most of the time, the teachers worked in groups (grades 1–3, 4–6, 7–9 and upper secondary school). Each group documented each of their discussions in a written report. At the end of each school year, the teachers had a joint meeting where they shared their experiences with each other.

Participants

To achieve a better understanding of the central phenomenon—reflection-for-action—four teachers and topics in mathematics were selected from the longitudinal study. Two of the teachers worked in a compulsory school in grades 4–6, and two worked in the first year in an upper secondary school. All four had completed a teacher-training program and worked as mathematics teachers for more than 12 years. They were not specialists in mathematics, but had a common interest in improving students’ learning. These four teachers were selected because they had worked with the same object of learning during the 3 years of the project, while the other teachers in the project had worked with other objects of learning such as the natural or rational numbers and their properties, functions, derivatives and so on. The compulsory school teachers had taught the same group of students in grades 4, 5 and 6, while the upper secondary teachers had taught new classes of students each year. The teachers from the compulsory school planned their lessons together, as did those from the upper secondary school. In addition, all four teachers met with each other during the project.

Two topics (arithmetic and algebra) have been selected for presentation in this article. These particular topics were selected because they are often interrelated in a teaching situation, and the strategies used to solve word problems in algebra are frequently grounded in arithmetic strategies.

Data collection

Each teacher conducted 18 lessons during the 3 years (six lessons per year). Since the aim of this article is to discuss how teachers’ engagement in their choice or construction of examples in arithmetic and algebra could be encouraged and how choice or construction of examples can be supported, their journals were analysed qualitatively for content, following the procedures advised by Jay and Johnson (2002) and Farrell (2013). The content in focus for this article was taught in the classroom in five lessons in compulsory school (one lesson in the first year of the project, and two lessons in years 2 and 3), and six lessons in upper secondary school (two lessons in each year of the project). One of the six lessons in the compulsory school treated another object of learning that is not discussed in this article.

Data analysis

Firstly, analyses were conducted to identify the lessons in which the content that was intended to be handled in the classroom was the same or approximately the same in the compulsory and upper secondary schools. Secondly, analyses were conducted to determine the typology of reflection done during the project. In the descriptive dimension, the analysis focused on two questions: (1) What examples were chosen? and (2) What was the potential in the examples to open up dimensions of variation? In the comparative dimension, the analysis focused on another two questions: (1) What does research contribute to an understanding of this matter? and (2) How can the teachers together with the researchers improve what is not working? In the critical dimension, the analysis focused on one question: What are the implications of the object of learning when viewed from these alternative perspectives? The subheadings used in the “Results” section of this article are based on the typology of reflection. Thirdly, the analyses focused on how the categories in the instructional planning were related to the typology of reflection. Fourthly and finally, for every approach used in the instructional planning, the analysis focused on identifying the examples in which different dimensions of variation had opened up. In reporting the findings, pseudonyms are used and teachers are identified as “T” followed by a number.

Results

The descriptive dimension

In the first year of the project, the teachers identified the content that was to be covered in the lessons by examining the content specified in the curriculum. For example, one learning objective specified by the National Agency for Education in Sweden for compulsory school is that students be able to use the main methods of calculating, using natural numbers and the methods in different situations (in years 1–9). In upper secondary school, one learning objective is to use first-degree equations in different situations. However, in the instructional planning, the teachers did not focus on aspects of the object of learning, but on the teaching arrangements, such as working in groups or individually.

Forward planning

In the first year of the project, the teachers examined the course module and curriculum to identify the intended object of learning, specifically, the curriculum corresponding to grades 4–6 and to the first course in mathematics in upper secondary school. One of the objectives in the curriculum for grades 4–6 is “Rational numbers and their properties. Main methods of calculating using natural numbers […]. Using the methods in different situations.” (Swedish National Agency for Education 2016, p. 57). Because the objective specifies only the end result, the teachers started to identify the content of the lessons to be taught (the direct object of learning). Based on their experience, they decided to develop the students’ ability to correctly choose the operations (addition, subtraction, multiplication and division) to be used in different situations (the object of learning).

Central planning

In the first year of the project, the teachers often chose examples connected with the object of learning from textbooks. In these examples, the focus was on the order in which operations should be done: parentheses, exponents, multiplication and division (from left to right) and addition and subtraction (from left to right). Often, the examples consisted of a simple expression on which the students were expected to perform the procedure.

Backward planning

Two types of examples were identified that allowed different patterns of variation to be used. One example used in grade 4 was

Calculate: 3 + 4 × 2

It seems that teachers interpreted the calculation differently, resulting in two different answers:

Method 1

Method 2

3 + 4 × 2 =

3 + 4 × 2 =

= 7 × 2

= 3 + 8

= 14

= 11

In method 1, addition is performed first, then multiplication, whereas in method 2, multiplication is performed first, then addition. This indicates that the teachers intended to open up a dimension of variation by using contrast as a pattern of variation. In this way, the teachers intended to draw the students’ attention to the facts that when performing arithmetic operations there can be only one correct answer, and that the convention is for multiplication to come before addition. In other words, the teachers drew the students’ attention to the relation between the parts (operations) and to the different ways to relate the parts to each other. Another example in which contrast was again used as a pattern of variation was from the first year of upper secondary school lessons:

Calculate: 30 ÷ 5 × 2 + 1

 

Method 1

Method 2

30 ÷ 5 = 6

5 × 2 = 10

6 × 2 = 12

30 ÷ 10 = 3

12 + 1 = 13

3 + 1 = 4

In this example, the focus was on pointing out that even though multiplication has the same priority as division, when both operations are present in the expression, then they are performed in order from left to right. Even in this example, the teacher intended to draw the students’ attention to the relation between the parts (operations) and the different ways to relate the parts to each other.

Unlike the teachers in compulsory school, the teachers in upper secondary school used word problems to develop their students’ ability to use first-degree equations in different situation. Some examples were as follows:

There are three numbers. The first number is twice the second number. The third is twice the first number. Their sum is 112. What are the numbers? (Example 1)

Maria wins the jackpot in a marble game and doubles her number of marbles. If later she wins 55 more, bringing her total to 127, how many marbles did she have at the beginning? (Example 2)

The examples were chosen to help students use equations to improve their procedural fluency. The teachers intended to open up a dimension of variation using fusion as the pattern of variation to let the students discern the structure in the example, namely the relationships between the parts and the whole (Table 1). This means that students had to simultaneously discern the literal meaning of the sentence, the mathematical meaning of the sentence and the connection between these meanings. In other words, the teachers intended to develop their students’ ability to connect reading skills and mathematical skills with a focus on the whole, the parts that form the whole, the relation between the parts, the transformation between the parts, the relation of the parts to the whole and the relation between different wholes (Table 1).

Table 1 Examples and their structure (first year of upper secondary school)—the intended object of learning
Full size table

The students did not have the opportunity to experience other models to relate the parts to the whole. At the end of the first year, the students took a test in which one of the tasks was similar to the example presented in this section. The results showed that about 40% of those in grade 4 (compulsory school) had not grasped the order in which operations should be done. Similarly, about 35% of those in upper secondary school could not perform the kind of tasks their teachers had planned that year. Some students tried to guess the answer using arithmetic thinking, and other students did not even try to complete the tasks. The lived critical aspects identified by the teachers here concerned correctly choosing operations in different situations (compulsory school), and setting up a first-degree equation that related to a word example (upper secondary school).

The comparative dimension

The comparative dimension of reflection-for-action could be identified in the second and third years of the project. During this period, the teachers reviewed concepts from variation theory and put them into practice in grades 5 and 6 with the same students that they had taught in grade 4. In the upper secondary school, the teachers taught new students at the same grade level as in the first year of the project. As a result, the conditions for teachers’ reflection-for-action were different in the compulsory and upper secondary schools (Table 2).

Table 2 The conditions for reflection-for-action
Full size table

The teachers and the students in the compulsory school were invariant during the 3 years of the study. The teachers in the upper secondary school were also invariant, but the students varied. The object of learning was invariant for both compulsory school and upper secondary schools, namely correctly choosing operations in different situations (compulsory school) and setting up a first-degree equation that related to a word problem (upper secondary school). In addition, the teachers and the researchers met and discussed the outcomes in connection with the object of learning. One set of results related to the choice of operation in which a word problem was presented, and the task was to decide which operation would be appropriate for finding the answer without having to carry out the calculation (as used, for example, in Fischbein et al. 1985; Bell et al. 1989 and many others). The other set of results related to the visual representation of relations among quantities (including known and unknown quantities) in the problem, using a rectangular bar (Cheong 2002; Fong 1999; Kho 1982).

Forward planning

The object of learning was the same as in the first year of the project. Based on the articles they had read, the students’ performance on the test, their experience of the object of learning at the end of the first year and their own observations during the lessons, the compulsory school teachers choose examples that used the four operations in new situations. The teachers in upper secondary school made their choices on the same basis as the compulsory school teachers, but chose examples to thoroughly focus on the relationship between the text and the visualisation of the text. For this reason, these teachers used the same examples as in the first year of the project. One reason the teachers gave for making this choice was that they wanted to use several patterns of variation and enhance the use of strategies to visualise the text. In addition, all the teachers reported using feedback from their observations during the lessons and from the students’ tests.

The students solved many exercises in order to understand the order of operation, but many of the students couldn’t understand what they were doing. I’ll use other examples that make it possible for the students to think about what they are doing and how to count. (T1, compulsory school).

I observed students during the lessons. Based on their reactions, I can change the method of teaching by thinking more about which patterns of variation I used. (T3, upper secondary school).

Central planning

To eliminate the students’ confusion about the order in which operations should be done, the compulsory school teachers designed two kinds of examples that referred to the order of operations. The first kind was as follows:

Fill in the missing operations. Use the operations +, −, x, ÷ to make each sentence true.

1☐ 2☐ 3☐ 4 = 1

1☐ 2☐ 3☐ 4 = 2

1☐ 2☐ 3☐ 4 = 3

1☐ 2☐ 3☐ 4 = 4

In these examples, the teachers focused on the choices of operations that students made and how the wrong choices could be explained. The choices gave the students the opportunity to experience separation and contrast as patterns of variation. In this way, the examples gave the students the opportunity to discern that performing the operations in a different order resulted in different answers, even though the numbers used to carry out these operations were the same. In other words, the students had the opportunity to discern the relation between parts (the numbers in the expression) and that the parts could be related to each other in different ways (the use of operations). Completion of these examples required a holistic view and attention to similarities and differences among the examples.

The second kind of example focused on deciding which mathematical operation (addition, subtraction, multiplication or division) or combination of operations would be useful in solving a word problem. For this purpose, the teacher used a set of examples involving addition, subtraction, multiplication and division. The examples were complex and required the students not only to solve each example but also to explain the relationship between quantities.

Maria and Per have 240kr between them. How much money does each child have if Maria has 20kr more than Per? (Example 3)

Sofia is 5 years older than Anneli and 3 years younger than Johan. The total of their ages is 43 years. Find Sofia’s age. (Example 4)

In these examples, the teachers focused on choosing mathematical operations as an important aspect of the larger process of translating sentences into mathematical expressions. The examples used fusion as a pattern of variation, and the students had to simultaneously discern the whole, the parts that formed the whole, the relation between the parts, the transformation between the parts, the relation between the parts and the whole and the relation between different wholes (Table 3).

Table 3 Structure of the examples used in compulsory school in years 2 and 3 of the study
Full size table

Although the upper secondary school teachers used the same examples as in the first year, in the second year they planned to start the lesson with the examples used in the compulsory school. The teachers did this because they realised that the students had to better discern the connection between the text and the way to visualise it. In this way, the teachers kept the meaning of the method used to solve the examples invariant, and varied the context of examples. This means that the teachers opened up a dimension of variation by similarity.

Backward planning

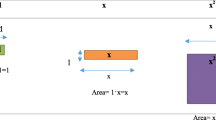
Based on their discussions of previous research results from mathematics education, the teachers had realised that visualisation is important in mathematics. They also realised that the ability to visualise is an important tool for problem solving, pattern spotting and reasoning in mathematics. To give the students good opportunities to discern the structure in word examples, the teachers intended to develop the students’ visualisation skills. All the teachers decided to associate each example with a figurative scheme that modelled the relationship between quantities (Fig. 2).

Fig. 2
figure 2

Figurative scheme

Full size image

The figurative scheme was a representation of the unknown elements with segments that showed the relation between the elements or between the given elements and the quantities provided by the problem. Unlike researchers who used a rectangular bar (Fong 1999; Kho 1982; Cheong 2002), these teachers used a linear model. They did this because a rectangular bar can be confused with the model used to illustrate multiplication. By using the figurative scheme, the teachers used similarity and separation as patterns of variation. The use of those patterns gave the students the opportunity to simultaneously discern the parts, the relation between the parts, the relation between the parts and the whole and the relation between different wholes in two representations (text and geometric).

The figurative scheme facilitated students’ understanding of the mathematical structure of the problem and the transformation from the real situation represented in words to a geometric representation of the relations between numbers that appeared in the text. (T1, compulsory school)

The figurative scheme promotes making distinctions in the relations between numbers before considering the choice of operations. (T1, compulsory school)

In the upper secondary school, the teachers used the algebraic representation of the word example in parallel with the figurative scheme. The same patterns of variation (separation and similarity) were used as in the first year, but this time the students had the opportunity to distinguish the relationships between the parts, the relation between the parts, the relation between the parts and the whole and the relation between different wholes in three representations (Table 3).

The use of the figurative scheme with no unknowns provided students with a complete representation of the structure in the word example so that mathematical relations in the example were clear to the students. (T3, upper secondary school)

After the students distinguished the structure in the word example, the rest of the solution process was about using information from the example of the diagram. (T2, upper secondary school)

The critical dimension

The critical dimension of teachers’ reflection-for-action was strongly connected to their analysis of the lived critical aspects. The analysis gave the compulsory school teachers the opportunity to choose new examples aimed at developing the students’ ability to know when to use which operation and how to develop a useful mathematical expression in order to solve it. One teacher from the upper secondary school thought that:

It is important to represent the text in the example using the figurative scheme and after that to transform the diagram into an algebraic equation. The last step is to solve the algebraic equation to provide a complete answer to the question. (T4, upper secondary school)

The teachers in upper secondary school focused on the basic structure of the figurative scheme, and used this scheme in additive and multiplicative word examples. In this way, the teachers kept the figurative scheme invariant, and varied the structure of the examples and the mathematical relations among the quantities.

Discussion and conclusion

The results of this study provide an understanding of how reflection-for-action could help mathematics teachers succeed in their teaching by encouraging their engagement in their choice or design of examples and supporting them in choosing or creating examples. In regard to encouraging teachers’ engagement, the results show that the use of different patterns of variation is a good basis on which to create a chain of examples that give the teachers the opportunity to succeed in their teaching. Following Jay and Johnson’s (2002) typology of reflection, the results in this study show that in their forward planning (Farrell 2013) the teachers described the use of examples such as worked-out examples and exercises (Bills et al. 2006) found in textbooks. The teachers in the compulsory school reframed the examples as specific examples (Zaslavsky 2010) by using contrast as a pattern of variation. These examples had the potential to give the students the opportunity to experience the explanatory nature of examples (Peled and Zaslavsky 1997)—here, to experience that multiplication comes before addition and that operations of the same priority are performed from left to right. The teachers in the upper secondary school contextualised practical tasks (Sullivan 2011) by using fusion as a pattern of variation to give the students the opportunity to interpret two representations (Table 1). The teachers had gained a new perspective on their choice or design of examples as a result of analysing the lived object of learning at the end of the first year.

In the second and third years, all the teachers kept the object of learning invariant. This time, the teachers in the compulsory school chose examples that integrated text and figurative scheme, aural and visual information and steps and sub-goals (Atkinson et al. 2000). In this way, the teachers opened up dimensions of variation that could give the students the opportunity to discern the whole, the parts that formed the whole, the relation between the parts, the transformation between the parts, the relation between the parts and the whole and the relation between different wholes (Table 3). The teachers’ reflection-for-action on the use of the figurative scheme alongside algebraic equations revealed that the teachers intended to enhance the students’ accuracy and to reduce the frequency of conceptual errors.

The teachers in the upper secondary school viewed the inconsistencies that happened in the solving of word examples as positive occurrences that strengthened their decision-making process in central and backward planning (Farrell 2013) in the second and third years. The incongruences triggered the reframing process. The teachers used examples from the compulsory-school level to introduce the figurative scheme, while the teachers in the compulsory schools moved from examples without words to more complex word examples in order to develop the students’ ability to use the operations in different situations. One possible explanation for the different ways of using examples is that the iterative cycles of testing and refining the intended object of learning enabled the teachers to enhance examples to clarify the sub-goal structure (Atkinson et al. 2000). To do this, the teachers adopted a new approach, namely analysing the reasoning and solutions (Swan 2005, 2011) that would help the students to develop generalisations of structures (Atkinson et al. 2000). The upper secondary school teachers’ experience was that even upper secondary school students could make persistent errors in understanding and solving algebraic equations, while the students were more accurate with the word examples. When all the word examples were found to be difficult for most students, the teachers reflected that figurative schemes could aid performance across example complexity and students’ math proficiency (e.g. T3, upper secondary school).

In regard to the possibility of supporting teachers’ choice or construction of examples, the results showed that reflection-for-action (Farrell 2013) was the vital component in the teachers’ decision-making process. It gave the teachers an opportunity to focus on variation and the results of the lessons, which in turn improved the teachers’ future decision-making strategies. The use of the figurative method generally supported teachers in increasing their use of word examples to convey generality and invariance, to explain and justify notations and conventions and to connect mathematical concepts to real-life experiences (Zaslavsky 2010). The results show that, for the teachers, reflection-for-action was another form of learning that grew out of experience and was connected to students’ discernment of aspects of the object of learning.

In summary, the current study extends previous research on reflection-of-action, providing more powerful indications of what teachers should think about so they can improve or change their own practice. The use of concrete representations (Fig. 2) in combination with a reflection about what varies and what is invariant gave the teachers the opportunity to choose or design examples in which patterns of variation were used. This gave students the opportunity to make connections between the literal meaning of the sentence and how to express this meaning mathematically. In addition, the use of a figurative scheme has the potential to give students an understanding of both the text in a word example and the mathematics connected to it.

An effective use of reflection-for-action in the teaching of mathematics requires a special understanding of the use of examples in mathematics. In choosing or designing examples, teachers need to reflect on different representations and to know what the essence of variation is. Examples should be designed so the key aspects are varied, allowing students to experience the effect of the variation. In addition, the use of patterns of variation gave the teachers clues as to what they should reflect on to improve or change their own practice.