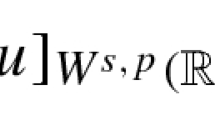On fractional Orlicz–Sobolev spaces

Abstract

Some recent results on the theory of fractional Orlicz–Sobolev spaces are surveyed. They concern Sobolev type embeddings for these spaces with an optimal Orlicz target, related Hardy type inequalities, and criteria for compact embeddings. The limits of these spaces when the smoothness parameter $s\in (0,1)$ tends to either of the endpoints of its range are also discussed. This note is based on recent papers of ours, where additional material and proofs can be found.

1 Introduction

One of the available notions of Sobolev spaces of fractional order calls into play the Gagliardo–Slobodeckij seminorm. Given an open set $\Omega \subset \mathbb R^n$, with $n \in \mathbb N$, and numbers $s\in (0,1)$ and $p \in [1, \infty )$, this seminorm will be denoted by $|\,\cdot \,|_{s,p,\Omega }$, and is defined as

$$\begin{aligned} | u|_{s,p,\Omega }=\bigg (\int _{\Omega } \int _{\Omega }\left( \frac{|u(x)-u(y)|}{|x-y|^s}\right) ^p\frac{\,dx\,dy}{|x-y|^n}\bigg )^{\frac{1}{p}} \end{aligned}$$

(1.1)

for a measurable function $u: \Omega \rightarrow \mathbb R$. The fractional Sobolev space $W^{s,p}(\Omega )$ is defined as the Banach space of those functions u for which the norm

$$\begin{aligned} \Vert u\Vert _{W^{s,p}(\Omega )} = \Vert u\Vert _{L^p(\Omega )} + |u|_{s,p,\Omega } \end{aligned}$$

(1.2)

is finite. Standard properties of the spaces $W^{s,p}(\Omega )$ are classical. The last two decades have witnessed an increasing number of investigations on these spaces because of their use in the analysis of nonlocal elliptic and parabolic equations, whose study has received an enormous impulse in the same period – see e.g. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22, 24,25,26,27, 31, 34, 35, 38,39,40, 43,44,54, 56, 57, 59, 60, 64].

The aim of this note is to survey a few recent results, contained in [1,2,3,4], on some aspects of fractional Orlicz–Sobolev spaces. They constitute an extension of the spaces $W^{s,p}(\Omega )$, in that the role of the power function $t^p$ is performed by a more general finite-valued Young function A(t), namely a convex function from $[0, \infty )$ into $[0, \infty )$, vanishing at 0. The fractional Orlicz–Sobolev space, of order $s\in (0,1)$, associated with a Young function A, will be denoted by $W^{s,A}(\Omega )$, and is built upon the Luxemburg type seminorm $|\,\cdot \,|_{s,A,\Omega }$ given by

$$\begin{aligned} | u|_{s,A,\Omega }= \inf \bigg \{\lambda >0: \int _{\Omega } \int _{\Omega }A\left( \frac{|u(x)-u(y)|}{\lambda |x-y|^s}\right) \frac{\,dx\,dy}{|x-y|^n}\le 1\bigg \} \end{aligned}$$

(1.3)

for a measurable function $u: \Omega \rightarrow \mathbb R$. The norm of a function u in $W^{s,A}(\Omega )$ is accordingly defined as

$$\begin{aligned} \Vert u\Vert _{W^{s,A}(\Omega )} = \Vert u\Vert _{L^A(\Omega )} + |u|_{s,A,\Omega }, \end{aligned}$$

(1.4)

where $\Vert u\Vert _{L^A(\Omega )}$ stands for the Luxemburg norm in the Orlicz space $L^A(\Omega )$. Definitions (1.3) and (1.4) have been introduced in [37], where some basic properties of the space $W^{s,A}(\Omega )$ are analyzed under the $\Delta _2$ and $\nabla _2$ conditions on A. Plainly, these definitions recover (1.1) and (1.2) when $A(t)=t^p$ for some $p \in [1, \infty )$.

Sobolev embeddings for the space $W^{s,p}(\Omega )$ have been long known. In particular, if $s\in (0,1)$ and $1\le p <\frac{n}{s}$, then there exists a constant C such that

$$\begin{aligned} \Vert u\Vert _{L^{\frac{np}{n-sp}}(\mathbb R^n)} \le C |u|_{s,p,\mathbb R^n} \end{aligned}$$

(1.5)

for every measurable function $u : \mathbb R^n\rightarrow \mathbb R$ decaying to 0 near infinity. A companion result holds if $\mathbb R^n$ is replaced by any bounded open set $\Omega$ with a sufficiently regular boundary $\partial \Omega$, for any function $u \in W^{s,p}(\Omega )$, provided that the seminorm $|u|_{s,p,\mathbb R^n}$ is replaced by the norm $\Vert u\Vert _{W^{s,p}(\Omega )}$.

Sharp extensions of these Sobolev type inequalities and ensuing embeddings to the spaces $W^{s,A}(\Omega )$ are presented in Sect. 3. For instance, the optimal Orlicz target space $L^B(\mathbb R^n)$ in the inequality

$$\begin{aligned} \Vert u\Vert _{L^{B}(\mathbb R^n)} \le C |u|_{s,A,\mathbb R^n}, \end{aligned}$$

for some constant C and every measurable function $u : \mathbb R^n\rightarrow \mathbb R$ decaying to 0 near infinity, is exhibited. Compact embeddings are also characterized. Here, we shall limit ourselves to consider target spaces of Orlicz type. However, inequalities and embeddings involving even stronger rearrangement-invariant norms are available. For these results we refer to [1, 4], where proofs of the material collected in this paper can also be found. Let us add that in those papers optimal embeddings for higher-order fractional spaces $W^{s,A}(\Omega )$ associated with any $s\in (0, n) {\setminus } \mathbb N$ are established as well.

A second issue that will be addressed concerns the limits as $s\rightarrow 1^-$ and $s\rightarrow 0^+$ of the space $W^{s,A}(\mathbb R^n)$. It is well known that setting $s=1$ in the definition of the space $W^{s,p}(\mathbb R^n)$ does not recover the first-order Sobolev space $W^{1,p}(\mathbb R^n)$. Moreover, the Lebesgue space $L^p(\mathbb R^n)$ cannot be obtained on choosing $s=0$ in the definition of $W^{s,A}(\mathbb R^n)$. Still, the seminorm $\Vert \nabla u\Vert _{L^p(\mathbb R^n)}$ and the norm $\Vert u\Vert _{L^p(\mathbb R^n)}$ of a function are reproduced as limits as $s\rightarrow 1^-$ and $s\rightarrow 0^+$, respectively, of the seminorm $|u|_{s,p,\mathbb R^n}$, provided that the latter is suitably normalized by a multiplicative factor depending on s, p and n.

Specifically, a version in the whole of $\mathbb R^n$ of a result by Bourgain-Brezis-Mironescu [9, 10] tells us that, if $p\in [1, \infty )$, then

$$\begin{aligned} \lim _{s\rightarrow 1^-} (1-s) \int _{\mathbb R^n} \int _{\mathbb R^n}\left( \frac{|u(x)-u(y)|}{|x-y|^s}\right) ^p\frac{dx\,dy}{|x-y|^n} = K(p,n) \int _{\mathbb R^n} |\nabla u(x)|^p\; dx\nonumber \\ \end{aligned}$$

(1.6)

for every function $u\in W^{1,p}(\mathbb R^n)$, where

$$\begin{aligned} K(p,n) = \frac{1}{p} \int _{\mathbb {S}^{n-1}} |\theta \cdot {e }|^p \; d{\mathcal {H}}^{n-1}. \end{aligned}$$

(1.7)

Here, $\mathbb {S}^{n-1}$ denotes the $(n-1)$-dimensional unit sphere in $\mathbb R^n$, ${\mathcal {H}}^{n-1}$ denotes the $(n-1)$-dimensional Hausdorff measure, ${e }$ is any point on $\mathbb {S}^{n-1}$, and the dot “$\; \cdot \;$” stands for scalar product in $\mathbb R^n$. Conversely, if $p\in (1,\infty )$, $u\in L^p(\mathbb R^n)$ and the limit (or even the liminf) on the left-hand side of (1.6) is finite, then $u \in W^{1,p}(\mathbb R^n)$. The case when $p=1$ is excluded from the latter result, but has a counterpart with $W^{1,1}(\mathbb R^n)$ replaced by $BV(\mathbb R^n)$, the space of functions of bounded variation in $\mathbb R^n$. A slight variant of these facts is proved in [62]. In the precise form appearing above, they follow as special cases of results of [3]. A version of Eq. (1.6) with $\mathbb R^n$ replaced by a bounded regular domain can be found in [32].

The limit as $s\rightarrow 0^+$ is the subject of a theorem by Maz’ya–Shaposhnikova [50], which ensures that

$$\begin{aligned} \lim _{s\rightarrow 0^+} s \int _{\mathbb R^n} \int _{\mathbb R^n}\left( \frac{|u(x)-u(y)|}{|x-y|^s}\right) ^p\frac{dx\,dy}{|x-y|^n} = \frac{2\,n \omega _n}{p} \int _{\mathbb R^n} |u(x)|^p\; dx \end{aligned}$$

(1.8)

for each $p \in [1, \infty )$, and for every function u decaying to 0 near infinity and making the double integral finite for some $s\in (0,1)$. Here, $\omega _n$ denotes the Lebesgue measure of the unit ball in $\mathbb R^n$. Equation (1.8) has to be interpreted in the sense that $u\in L^p(\mathbb R^n)$ if and only if the limit on the left-hand side if finite, and that, in the latter case, the equality holds.

Section 4 is devoted to counterparts, established in [3] and [2], of these results in the Orlicz framework. Namely, it deals with the limits

$$\begin{aligned} \lim _{s\rightarrow 1^-} (1-s) \int _{\mathbb R^n}\int _{\mathbb R^n} A\left( \frac{|u(x) - u(y)|}{|x-y|^s}\right) \; \frac{dx\,dy}{|x-y|^n}, \end{aligned}$$

(1.9)

and

$$\begin{aligned} \lim _{s\rightarrow 0^+} s \int _{\mathbb R^n}\int _{\mathbb R^n} A\left( \frac{|u(x) - u(y)|}{|x-y|^s}\right) \; \frac{dx\,dy}{|x-y|^n}. \end{aligned}$$

(1.10)

Interestingly, the conclusions about these limits share some features with those in (1.6) and (1.8), but also present some diversities. In particular, as shown by counterexamples, certain results can only hold under the additional $\Delta _2$-condition on A, or are affected by some restrictions in the general case.

2 Function spaces

A function $A: [0, \infty ) \rightarrow [0, \infty ]$ is called a Young function if it has the form

$$\begin{aligned} A(t) = \int _0^t a(\tau ) d\tau \qquad \quad \hbox {for}\quad t \ge 0, \end{aligned}$$

for some non-decreasing, left-continuous function $a: [0, \infty ) \rightarrow [0, \infty ]$ which is neither identically equal to 0 nor to $\infty$. Clearly, any convex (non trivial) function from $[0, \infty )$ into $[0, \infty ]$, which is left-continuous and vanishes at 0, is a Young function.

A Young function A is said to dominate another Young function B globally if there exists a positive constant C such that

$$\begin{aligned} B(t)\le A(C t) \qquad \text {for} \quad t \ge 0\,. \end{aligned}$$

(2.1)

The function A is said to dominate B near infinity if there exists $t_0> 0$ such that (2.1) holds for $t \ge t_0$.

The function B is said to grow essentially more slowly near infinity than A if

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{B(\lambda t)}{A(t)} =0 \end{aligned}$$

(2.2)

for every $\lambda >0$. Note that condition (2.2) is equivalent to

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{A^{-1}(t)}{B^{-1}(t)} =0. \end{aligned}$$

(2.3)

A Young function A is said to satisfy the $\Delta _2$-condition – briefly $A\in \Delta _2$ – globally if there exists a positive constant C such that

$$\begin{aligned} A(2t) \le C A(t) \end{aligned}$$

(2.4)

for $t \ge 0$. If A is finite-valued and there exists $t _0 >0$ such that inequality (2.4) holds for $t \ge t_0$, then we say that A satisfies the $\Delta _2$-condition near infinity.

Let $\Omega$ be a measurable subset of $\mathbb R^n$, with $n\ge 1$, having Lebesgue measure $|\Omega |$. Set

$$\begin{aligned} {\mathcal {M}}(\Omega )=\{u:\Omega \rightarrow \mathbb R: u \quad \hbox {is measurable}\}, \end{aligned}$$

and

$$\begin{aligned} {\mathcal {M}}_+(\Omega )=\{ u\in {\mathcal {M}}(\Omega ) : u \ge 0\}\,. \end{aligned}$$

The notation ${\mathcal {M}}_d(\Omega )$ is employed for the subset of ${\mathcal {M}}(\Omega )$ of those functions u that decay near infinity, according to the following definition:

$$\begin{aligned} {\mathcal {M}}_d(\Omega )=\{ u\in {\mathcal {M}}(\Omega ) : |\{|u|>t\}|<\infty \,\, \text {for every} \,\, t>0\}\,. \end{aligned}$$

Plainly, ${\mathcal {M}}_d(\Omega )= {\mathcal {M}}(\Omega )$ if $|\Omega |<\infty$. The Orlicz space $L^A (\Omega )$, associated with a Young function A, is the Banach space of those functions $u\in {\mathcal {M}}(\Omega )$ for which the Luxemburg norm

$$\begin{aligned} \Vert u\Vert _{L^A(\Omega )}= \inf \left\{ \lambda >0 : \int _{\Omega }A \left( \frac{|u(x)|}{\lambda } \right) dx \le 1 \right\} \, \end{aligned}$$

is finite. In particular, $L^A (\Omega )= L^p (\Omega )$ if $A(t)= t^p$ for some $p \in [1, \infty )$, and $L^A (\Omega )= L^\infty (\Omega )$ if $A(t)=0$ for $t\in [0, 1]$ and $A(t) = \infty$ for $t\in (1, \infty )$.

If A dominates B globally, then

$$\begin{aligned} \Vert u \Vert _{L^B(\Omega )} \le C \Vert u \Vert _{L^A(\Omega )} \end{aligned}$$

(2.5)

for every $u \in L^A(\Omega )$, where C is the same constant as in (2.1). If $|\Omega |< \infty$, and A dominates B near infinity, then inequality (2.5) continues to hold for some constant $C=C(A,B, t_0, |\Omega |)$.

The alternative notation $A(L)(\Omega )$ will also be employed, in the place of $L^A(\Omega )$, to denote the Orlicz space associated with a Young function equivalent to A.

The space $E^A(\Omega )$ is defined as

$$\begin{aligned} E^A(\Omega ) = \bigg \{u\in {{\mathcal {M}}} (\Omega ):\ \ \int _{\Omega }A \left( \frac{|u(x)|}{\lambda } \right) dx < \infty \,\,\hbox {for every} ~ \lambda >0\bigg \}\,. \end{aligned}$$

If A is finite-valued, then the space $E^A(\Omega )$ agrees with the closure in $L^A(\Omega )$ of the space of bounded functions with bounded support in $\Omega$. Trivially,

$$\begin{aligned} E^A(\Omega )\subset L^A(\Omega )\,. \end{aligned}$$

This inclusion holds as equality if and only if either $|\Omega |<\infty$ and $A\in \Delta _2$ near infinity, or $|\Omega |=\infty$ and $A\in \Delta _2$ globally.

Assume now that $\Omega$ is an open subset of $\mathbb R^n$. We denote by $V^{1,A}(\Omega )$ the homogeneous Orlicz–Sobolev space given by

$$\begin{aligned} V^{1,A}(\Omega ) = \left\{ u \in W^{1,1}_{\mathrm{loc}} (\Omega ):\, |\nabla u| \in L^A(\Omega )\right\} . \end{aligned}$$

Here, $\nabla u$ denotes the gradient of u. The notation $W^{1,A}(\Omega )$ is adopted for the classical Orlicz–Sobolev space defined by

$$\begin{aligned} W^{1,A}(\Omega ) = \left\{ u \in L^A(\Omega ): |\nabla u| \in L^A(\Omega )\right\} . \end{aligned}$$

The space $W^{1,A}(\Omega )$ is a Banach space equipped with the norm

$$\begin{aligned} \Vert u\Vert _{W^{1,A}(\Omega )} = \Vert u \Vert _{L^A(\Omega )} + \Vert \nabla u \Vert _{L^A(\Omega )}\,. \end{aligned}$$

By $W^1E^A(\Omega )$ we denote the space obtained on replacing $L^A(\Omega )$ with $E^A(\Omega )$ in the definition of $W^{1,A}(\Omega )$.

The space of functions of bounded variation on $\Omega$ is denoted by $BV(\Omega )$. It consists of all functions in $L^1(\Omega )$ whose distributional gradient is a vector-valued Radon measure Du with finite total variation $\Vert Du\Vert (\Omega )$ on $\Omega$. The space $BV(\Omega )$ is a Banach space, endowed with the norm defined as

$$\begin{aligned} \Vert u\Vert _{BV(\Omega )} = \Vert u\Vert _{L^1(\Omega )} + \Vert Du\Vert (\Omega ) \end{aligned}$$

for $u \in BV(\Omega )$.

Given a function $u\in BV(\Omega )$, we denote by $\nabla u$ the absolutely continuous part of Du with respect to the Lebesgue measure, and by $D^su$ its singular part. One has that

$$\begin{aligned} \Vert Du\Vert (\Omega ) = \int _\Omega |\nabla u|\, dx + \Vert D^su\Vert (\Omega ), \end{aligned}$$

where $\Vert D^su\Vert (\Omega )$ stands for the total variation of the measure $D^su$ over $\Omega$.

More generally, assume that A is a Young function with a linear growth near infinity, in the sense that

$$\begin{aligned} \lim _{t \rightarrow \infty }\frac{A (t)}{t} <\infty . \end{aligned}$$

(2.6)

Then a functional $J_{A,\Omega }$ associated with A can be defined on $BV(\Omega )$ as

$$\begin{aligned} J_{A,\Omega }(u) = \int _{\Omega } {A}\left( |\nabla u| \right) dx + a^\infty \Vert D^su\Vert (\Omega ) \end{aligned}$$

(2.7)

for $u \in BV(\Omega )$, where

$$\begin{aligned} a^\infty = \lim _{t \rightarrow \infty }\frac{A (t)}{t}. \end{aligned}$$

(2.8)

The functional $J_{A,\Omega }$ agrees on $BV(\Omega )$ with the relaxed functional of

$$\begin{aligned} \int _\Omega A(|\nabla u|)\, dx \end{aligned}$$

on $L^1(\Omega )$ with respect to convergence in $L^1_{\mathrm{loc}}(\Omega )$, which is defined as

$$\begin{aligned} \inf \bigg \{\liminf _{m\rightarrow \infty } \int _\Omega A(|\nabla u_m|)\, dx: \{u_m\}\subset C^1(\Omega ), \,\,u_m\rightarrow u \, \, \text {in}\,\,L^1_{\mathrm{loc}}(\Omega )\bigg \}. \end{aligned}$$

One has that the functional $J_{A,\Omega }$ is lower semicontinuous in $BV(\Omega )$ with respect to convergence in $L^1_{\mathrm{loc}}(\Omega )$. Moreover, for every function $u \in BV(\Omega )$, there exists a sequence $\{u_m\}\subset C^1(\Omega )$ such that

$$\begin{aligned} u_m\rightarrow u \, \, \text {in}\,\,L^1_{\mathrm{loc}}(\Omega ) \quad \text {and} \quad J_{A,\Omega }(u) = \lim _{m\rightarrow \infty } \int _\Omega A(|\nabla u_m|)\, dx. \end{aligned}$$

The homogeneous fractional Orlicz–Sobolev space $V^{s,A}(\Omega )$ is defined as

$$\begin{aligned} V^{s,A}(\Omega ) = \big \{u \in {\mathcal {M}} (\Omega ): |u|_{s,A, \Omega }<\infty \}\,, \end{aligned}$$

where $|\, \cdot \, |_{s,A, \Omega }$ is the seminorm given by (1.3).

The subspace of those functions in $V^{s,A}(\Omega )$ that decay near infinity is denoted by $V^{s,A}_d(\Omega )$. Namely

$$\begin{aligned} V^{s,A}_d(\Omega ) = V^{s,A}(\Omega ) \cap {\mathcal {M}}_d(\Omega ). \end{aligned}$$

If $|\Omega |< \infty$ and $s \in (0,1)$, we also define the space

$$\begin{aligned} V^{s,A}_\perp (\Omega ) = \left\{ u\in V^{s,A}(\Omega ): u_\Omega =0\right\} \,, \end{aligned}$$

where

$$\begin{aligned} u_\Omega = \frac{1}{|\Omega |}\int _\Omega u\; dx\,, \end{aligned}$$

the mean value of u over $\Omega$.

The fractional-order Orlicz–Sobolev space $W^{s,A}(\Omega )$ is defined as

$$\begin{aligned} W^{s,A}(\Omega ) = \left\{ u \in L^A(\Omega ):\, u \in V^{s,A}(\Omega )\right\} , \end{aligned}$$

and is a Banach space equipped with the norm given by (1.4). Clearly, $W^{s,A}(\Omega ) \rightarrow V^{s,A}_d(\Omega )$, and, as a consequence of Proposition 1, Sect. 3, $W^{s,A}(\Omega ) = V^{s,A}_d(\Omega )$ if $\Omega$ is bounded.

We conclude by mentioning a fractional-order Pólya–Szegő principle, which implies the decrease of the fractional Orlicz–Sobolev seminorm under symmetric rearrangement of functions u. Recall that the symmetric rearrangement $u^\bigstar$ of a function $u \in {\mathcal {M}}_d (\mathbb R^n)$ is defined as the radially decreasing function about 0 which is equidistributed with u.

Theorem 2.1

(Fractional Pólya–Szegő principle) Let $s \in (0,1)$ and let A be a Young function. Assume that $u\in {\mathcal {M}}_d (\mathbb R^n)$. Then

$$\begin{aligned} \int _{\mathbb R^n}\int _{\mathbb R^n} A\left( \frac{|u(x)-u(y)|}{|x-y|^{s}}\right) \frac{dx\,dy}{|x-y|^n} \ge \int _{\mathbb R^n}\int _{\mathbb R^n} A\left( \frac{|u^{\bigstar }(x)-u^{\bigstar }(y)|}{|x-y|^{s}}\right) \frac{dx\,dy}{|x-y|^n}.\nonumber \\ \end{aligned}$$

(2.9)

In the case when A is a power, inequality (2.9) can be traced back to [5, 6]. The result for Young functions A satisfying the $\Delta _2$-condition and functions $u \in W^{s,A}(\mathbb R^n)$ is proved in [33]. The general version stated in Theorem 2.1 can be found in [1]. An earlier related contribution, dealing with functions of one-variable, is [42].

3 Sobolev type inequalities

Our first theorem provides us with the optimal – i.e. smallest possible – Orlicz target space in the Sobolev embedding for the space $V^{s,A}_d(\mathbb R^n)$. Such an optimal space is built upon the Young function $A_{\frac{n}{s}}$ associated with A, n and s as follows.

Let $s\in (0,1)$ and let A be a Young function such that

$$\begin{aligned} \int ^{\infty }\left( \frac{t}{A(t)}\right) ^{\frac{s}{n-s}}\,dt = \infty \end{aligned}$$

(3.1)

and

$$\begin{aligned} \int _{0}\left( \frac{t}{A(t)}\right) ^{\frac{s}{n-s}}\,dt < \infty . \end{aligned}$$

(3.2)

Then, $A_{\frac{n}{s}}$ is given by

$$\begin{aligned} A_{\frac{n}{s}} (t) = A(H^{-1}(t)) \quad \text {for} \ t\ge 0, \end{aligned}$$

(3.3)

where the function $H: [0, \infty ) \rightarrow [0, \infty )$ obeys

$$\begin{aligned} H(t) = \bigg (\int _0^t \bigg (\frac{\tau }{A(\tau )}\bigg )^{\frac{s}{n-s}} d\tau \bigg )^{\frac{n-s}{n}} \quad \text {for}\,\, t \ge 0. \end{aligned}$$

Theorem 3.1

(Optimal Orlicz target space) Let $s\in (0,1)$. Assume that A is a Young function satisfying conditions (3.1) and (3.2), and let $A_{\frac{n}{s}}$ be the Young function defined as in (3.3). Then

$$\begin{aligned} V^{s,A}_d(\mathbb R^n) \rightarrow L^{A_{\frac{n}{s}}}(\mathbb R^n), \end{aligned}$$

(3.4)

and there exists a constant $C=C(n,s)$ such that

$$\begin{aligned} \Vert u\Vert _{L^{A_{\frac{n}{s}}}(\mathbb R^n)} \le C |u|_{s,A,\mathbb R^n} \end{aligned}$$

(3.5)

for every function $u \in V^{s,A}_d(\mathbb R^n)$. Moreover, $L^{A_{\frac{n}{s}}}(\mathbb R^n)$ is the optimal target space in inequality (3.5) among all Orlicz spaces.

Remark 1

Assumption (3.2) on the Young function A cannot be dispensed with in Theorem 3.1. Actually, one can show that it is necessary for an embedding of the space $V^{s,A}_d(\mathbb R^n)$ to hold into any rearrangement-invariant space. Assumption (3.1) amounts to requiring that A has a subcritical growth with respect to the smoothness parameter s. It generalizes the condition $p<\frac{n}{s}$ required for the classical inequality (1.5).

Remark 2

The fractional Orlicz–Sobolev inequality (3.5) precisely matches the integer-order inequality established in [29] (see also [28] for an alternative form). Indeed, setting $s =1$ in formula (3.3) for the function $A_{\frac{n}{s}}$ recovers the Young function which defines the optimal Orlicz target space in the Orlicz–Sobolev inequality for $W^{1,A}(\mathbb R^n)$.

We now present an application of Theorem 3.1 to a family of Young functions whose behaviour near zero and near infinity is of power-logarithmic type. Although quite simple, these model Young functions enable us to recover results available in the literature and to exhibit genuinely new inequalities.

Example 1

Consider a Young function A such that

$$\begin{aligned} A(t) \,\,\text {is equivalent to}\,\, {\left\{ \begin{array}{ll} t^{p_0} (\log \frac{1}{t})^{\alpha _0} &{} \quad \text {near zero}\\ t^p (\log t)^\alpha &{} \quad \text {near infinity,} \end{array}\right. } \end{aligned}$$

(3.6)

where either $p_0>1$ and $\alpha _0 \in \mathbb R$, or $p_0=1$ and $\alpha _0 \le 0$, and either $p>1$ and $\alpha \in \mathbb R$, or $p=1$ and $\alpha \ge 0$. Here, equivalence is meant in the sense of Young functions.

Let $s\in (0,1)$. The function A satisfies assumption (3.1) if

$$\begin{aligned} \text {either} \ 1\le p< \frac{n}{s} \ \text {and} \ \alpha \ \text {is as above, or} \ p=\frac{n}{s} \ \text {and} \ \alpha \le \frac{n}{s} -1, \end{aligned}$$

(3.7)

and satisfies assumption (3.2) if

$$\begin{aligned} \text {either} \ 1\le p_0< \frac{n}{s} \ \text {and} \ \alpha _0 \ \text {is as above, or} \ p_0=\frac{n}{s} \ \text {and} \ \alpha _0 > \frac{n}{s} -1. \end{aligned}$$

(3.8)

Then, by Theorem 3.1, embedding (3.4) and inequality (3.5) hold, where

$$\begin{aligned} A_{\frac{n}{s}}(t)\,\, \text {is equivalent to}\,\, {\left\{ \begin{array}{ll} t^{\frac{n{p_0}}{n-s{p_0}}} (\log \frac{1}{t})^{\frac{n\alpha _0}{n-s{p_0}}} &{} \quad \text { if} \ 1\le {p_0}< \frac{n}{s}\\ e^{-t^{-\frac{n}{s(\alpha _0 +1)-n}}} &{} \quad \,\, \text {if}\ {p_0}=\frac{n}{s} \,\text {and}\, \alpha _0 > \frac{n}{s} -1 \end{array}\right. } \,\, \text {near zero,} \end{aligned}$$

and

$$\begin{aligned} A_{\frac{n}{s}}(t) \,\, \text {is equivalent to} \,\, {\left\{ \begin{array}{ll} t^{\frac{np}{n-sp}} (\log t)^{\frac{n \alpha }{n-sp}} &{} \quad \text { if} \,1\le p< \frac{n}{s} \\ e^{t^{\frac{n}{n-(\alpha +1)s}}}&{} \quad \,\text {if} p=\frac{n}{s} \, \text {and}\, \alpha < \frac{n}{s} -1 \\ e^{e^{t^{\frac{n}{n-s}}}} &{} \quad \,\text {if} p=\frac{n}{s} \, \text {and}\, \alpha = \frac{n}{s} -1 \end{array}\right. } \quad \text {near infinity.}\nonumber \\ \end{aligned}$$

(3.9)

Furthermore, the target space in the resultant embedding and inequality is optimal among all Orlicz spaces.

In particular, if

$$\begin{aligned} p={p_0}<\tfrac{n}{s} \quad \text { and} \quad \alpha =\alpha _0 =0, \end{aligned}$$

(3.10)

this result reproduces inequality (1.5). In the limiting case when

$$\begin{aligned} p={p_0}=\tfrac{n}{s}, \quad \alpha =0 \quad \text {and} \quad \alpha _0 > \tfrac{n}{s} -1, \end{aligned}$$

we obtain a fractional embedding of Pohozhaev-Trudinger-Yudovich type [55, 61, 63] – see also the recent paper [54] with this regard.

The next result amounts to a Hardy type inequality for fractional Orlicz–Sobolev spaces $V^{s,A}_d (\mathbb R^n)$. This inequality extends a theorem of Maz’ya–Shaposhnikova [50, Inequality (3)]. The relevant Hardy inequality is a central step in the Proof of Theorem 3.1 and of its augmented version with optimal rearrangement-invariant target norm established in [1, Theorem 6.2]. Its statement involves a new Young function ${{\widehat{A}}}$, associated with A, s and n according to the formula

$$\begin{aligned} {{\widehat{A}}} (t)=\int _0^t{{\widehat{a}}} (\tau )\,d\tau \quad \text {for} \ t\ge 0, \end{aligned}$$

(3.11)

where ${{\widehat{a}}}:[0, \infty ) \rightarrow (0, \infty )$ is the function whose inverse obeys

$$\begin{aligned} {{{\widehat{a}}}\,}^{-1}(r) = \left( \int _{a^{-1}(r)}^{\infty } \left( \int _0^t\left( \frac{1}{a(\varrho )}\right) ^{\frac{s}{n-s}}\, d\varrho \right) ^{-\frac{n}{s}}\frac{dt}{a(t)^{\frac{n}{n-s}}} \right) ^{\frac{s}{s-n}} \quad \text {for} \ r\ge 0. \end{aligned}$$

Theorem 3.2

(Fractional Orlicz–Hardy inequality) Let $s\in (0,1)$. Assume that A is a Young function satisfying conditions (3.1) and (3.2) and let ${{{\widehat{A}}}}$ be the Young function given by (3.11). Then there exists a constant $C=C(n,s)$ such that $\lim _{s\rightarrow 1^-}C(n,s)< \infty$ and

$$\begin{aligned} \left\| \frac{u(x)}{|x|^s}\right\| _{L^{{{\widehat{A}}}}(\mathbb R^n)} \le C |u|_{s,A,\mathbb R^n} \end{aligned}$$

(3.12)

for every function $u \in V^{s,A}_d (\mathbb R^n)$. Moreover,

$$\begin{aligned} \int _{\mathbb R^n}{{{\widehat{A}}}}\left( \frac{|u(x)|}{|x|^s}\right) \,dx \le (1-s) \int _{\mathbb R^n} \int _{\mathbb R^n} A\left( C\frac{|u(x)-u(y)|}{|x-y|^s}\right) \,\frac{dx\, dy}{|x-y|^n}\qquad \end{aligned}$$

(3.13)

for every function $u \in {\mathcal {M}}_d (\mathbb R^n)$.

Let us mention that a Hardy-type inequality for one-dimensional fractional Orlicz–Sobolev spaces has recently been established in [58].

Example 2

Let A be a Young function as in (3.6), and let $s\in (0,1)$. Assume that the parameters p, $p_0$, $\alpha$ and $\alpha _0$ satisfy assumptions (3.7) and (3.8). Theorem 3.2 implies that inequalities (3.12) and (3.13) hold, where

$$\begin{aligned} {{\widehat{A}}}(t)\,\, \text {is equivalent to}\,\, {\left\{ \begin{array}{ll} t^{p_0}(\log \frac{1}{t})^{\alpha _0} &{} \quad \text { if} \ 1\le {p_0}< \frac{n}{s}\\ t^{\frac{n}{s}} (\log \frac{1}{t})^{\alpha _0 - \frac{n}{s}} &{} \quad \,\text {if} \ {p_0}=\frac{n}{s} \ \text {and} \ \alpha _0> \frac{n}{s} -1 \end{array}\right. } \quad \text {near zero,} \end{aligned}$$

and

$$\begin{aligned} {{\widehat{A}}}(t) \,\, \text {is equivalent to} \,\, {\left\{ \begin{array}{ll} t^p (\log t)^\alpha &{} \quad \text {if }1\le p< \frac{n}{s} \\ t^{\frac{n}{s}} (\log t)^{\alpha - \frac{n}{s}} &{} \quad \text {if } p=\frac{n}{s} \text { and } \alpha < \frac{n}{s} -1 \\ t^{\frac{n}{s}} (\log t)^{-1} (\log (\log t))^{-\frac{n}{s}}&{} \quad \text {if } p=\frac{n}{s} \text { and } \alpha = \frac{n}{s} -1 \end{array}\right. } \quad \text {near infinity.} \end{aligned}$$

In particular, the choices ${p_0}=p<\tfrac{n}{s}$ and $\alpha _0 =\alpha =0$ yield ${{\widehat{A}}}(t) =t^p$, and inequalities (3.12) and (3.13) recover (apart from the specific form of the constant involved) [50, Inequality (3)].

A version of Theorem 3.1 holds even if $\mathbb R^n$ is replaced by an open set $\Omega \subset \mathbb R^n$, provided that the latter enjoys suitable regularity properties. For instance, it suffices to assume that $\Omega$ is a bounded Lipschitz domain. This is the subject of the next result, which, like the other results of this section dealing with subsets $\Omega$ of $\mathbb R^n$, is established in [4].

Theorem 3.3

(Optimal Orlicz target space on domains) Let $\Omega$ be a bounded Lipschitz domain in $\mathbb R^n$. Assume that $s\in (0,1)$ and that A is a Young function satisfying conditions (3.1) and (3.2). Then

$$\begin{aligned} W^{s,A}(\Omega ) \rightarrow L^{A_{\frac{n}{s}}}(\Omega ), \end{aligned}$$

(3.14)

and $L^{A_{\frac{n}{s}}}(\Omega )$ is the optimal Orlicz target space in (3.14). Moreover, there exists a constant $C=C(n,s,\Omega )$ such that

$$\begin{aligned} \Vert u\Vert _{L^{A_{\frac{n}{s}}}(\Omega )} \le C |u|_{s,A,\Omega } \end{aligned}$$

for every function $u \in V^{s,A}_\perp (\Omega )$.

Example 3

Let $\Omega$ be a bounded Lipschitz domain in $\mathbb R^n$ and let $s\in (0, 1)$. Consider a Young function A as in (3.6) under assumptions (3.7) and (3.8) on the parameters p, ${p_0}$, $\alpha$, $\alpha _0$. Owing to Theorem 3.3, embedding (3.14) holds with $A_{\frac{n}{s}}$ obeying (3.9). Let us notice that, since $|\Omega |<\infty$, only the behaviour near infinity of the function $A_{\frac{n}{s}}$ plays a role now. Therefore, embedding (3.14) takes the form

$$\begin{aligned} W^{s,A}(\Omega ) \rightarrow \,\, {\left\{ \begin{array}{ll} L^{\frac{np}{n-sp}} (\log L)^{\frac{n \alpha }{n-sp}} (\Omega )&{} \quad \text { if } 1\le p< \frac{n}{s}\\ \exp {L^{\frac{n}{n-(\alpha +1)s}}}(\Omega ) &{} \quad \text { if } p=\frac{n}{s} \text { and } \alpha < \frac{n}{s} -1\\ \exp \exp {L^{\frac{n}{n-s}}}(\Omega ) &{} \quad \text { if } p=\frac{n}{s} \text { and } \alpha = \frac{n}{s} -1, \end{array}\right. } \end{aligned}$$

(3.15)

the target spaces being optimal among all Orlicz spaces. Embedding (3.15) recovers or extends to the fractional case various results available in the literature. The case corresponding to (3.10) is classical. Integer-order Sobolev embeddings parallel to (3.15) are special instances of the general results of [30], which, in their turn, include various borderline cases established in [36, 41, 55, 61, 63]. In fact, the paper [36], and some sequel contributions by the same authors, also deal with fractional embeddings, but for spaces defined in terms of potentials instead of difference quotients.

Theorem 3.3 rests on Theorem 3.1 and on an extension result for fractional Orlicz–Sobolev spaces on Lipschitz domains. The dependence of the norm of the linear extension operator on the parameter $s\in (0,1)$ can be properly described on making use of an equivalent norm $\left| \left| \left| \cdot \right| \right| \right| _{W^{s,A}(\Omega )}$ on $W^{s,A}(\Omega )$, defined as follows. Call $A_\bullet$ the Young function given by $A_\bullet (t)= \min \{s,1-s\}A(t)$ for $t\ge 0$. Then, we set

$$\begin{aligned} \left| \left| \left| u \right| \right| \right| _{W^{s,A}(\Omega )} = \Vert u\Vert _{L^A(\Omega )} +|u|_{s, A_\bullet ,\Omega } \end{aligned}$$

for $u \in W^{s,A}(\Omega )$.

Theorem 3.4

(Extension operator for fractional Orlicz–Sobolev spaces) Let $\Omega$ be a bounded Lipschitz domain in $\mathbb R^n$. Assume that $s\in (0, 1)$ and let A be a Young function. Then there exist a linear extension operator ${\mathcal {E}}: W^{s, A}(\Omega ) \rightarrow W^{s, A}(\mathbb R^n)$ and a constant $C=C(\Omega )$ such that

$$\begin{aligned} {\mathcal {E}}(u) =u \quad \text {in}\;\; \Omega \, \end{aligned}$$

and

$$\begin{aligned} \left| \left| \left| {\mathcal {E}} (u) \right| \right| \right| _{{W}^{s,A}(\mathbb R^n)}\le C \left| \left| \left| u \right| \right| \right| _{{W}^{s,A}(\Omega )} \end{aligned}$$

for every function $u \in W^{s,A}(\Omega )$.

Moreover, there exists a constant $C{'}=C{'}(s,\Omega )$ such that

$$\begin{aligned} |{\mathcal {E}} (u)|_{s,A, \mathbb R^n}\le C{'} |u|_{s,A, \Omega } \end{aligned}$$

for every function $u \in V^{s,A}_{\perp }(\Omega )$.

The Poincaré type inequality stated in the next proposition, of independent interest, has a role in the Proof of Theorem 3.4.

Proposition 1

(Fractional Orlicz–Poincaré inequality) Let $\Omega$ be a bounded open set in $\mathbb R^n$. Assume that $s\in (0,1)$ and that A is a Young function. If $u \in V^{s,A}(\Omega )$, then $u \in L^A(\Omega )$. Moreover, there exists a constant $C=C(s, \Omega )$ such that

$$\begin{aligned} \Vert u- u_\Omega \Vert _{L^A(\Omega )} \le C |u|_{s,A, \Omega } \end{aligned}$$

for every function $u \in V^{s,A}(\Omega )$. Furthermore,

$$\begin{aligned} \int _\Omega A\big (\big |u(x)-u_\Omega \big |\big )\, dx \le \int _\Omega \int _\Omega A\left( C\frac{|u(x)-u(y)|}{|x-y|^s}\right) \frac{\,dx\,dy}{|x-y|^n} \end{aligned}$$

for every function $u \in V^{s,A}(\Omega )$.

The last result of this section is a criterion for the compactness of a fractional Orlicz–Sobolev embedding into an Orlicz space. A necessary and sufficient condition amounts to requiring that the Young function that defines the latter space grows essentially more slowly near infinity (in the sense of (2.2)) than the Young function that defines the optimal Orlicz target for a merely continuous embedding given by Theorem 3.1. This is the content of the following theorem.

Theorem 3.5

(Compact embeddings) Let $s\in (0, 1)$ and let A be a Young function fulfilling conditions (3.1) and (3.2). Let $A_{\frac{n}{s}}$ be the Young function defined by (3.3). Assume that B is a Young function. The following properties are equivalent.

• (i) B grows essentially more slowly near infinity than $A_{\frac{n}{s}}$, namely

  $$\begin{aligned} \lim _{t\rightarrow \infty } \frac{B(\lambda t)}{A_{\frac{n}{s}}(t)} =0 \end{aligned}$$

  for every $\lambda >0$.

• (ii) The embedding

  $$\begin{aligned} V^{s,A}_d(\mathbb R^n) \rightarrow L^B_{\mathrm{loc}}(\mathbb R^n) \end{aligned}$$

  (3.16)

  is compact.

• (iii) The embedding

  $$\begin{aligned} W^{s,A}(\Omega ) \rightarrow L^B(\Omega ) \end{aligned}$$

  is compact for every bounded Lipschitz domain $\Omega$ in $\mathbb R^n$.

The assertion that embedding (3.16) is compact means that every bounded sequence in $V^{s,A}_d(\mathbb R^n)$ has a subsequence whose restriction to E converges in $L^B(E)$ for every bounded measurable set E in $\mathbb R^n$. Let us notice that the equivalence of properties (i) and (ii) is not explicitly mentioned in [4]. Its proof follows, modulo minor variants, along the same lines as that of the equivalence of (i) and (iii).

Example 4

Assume that $\Omega$ is a bounded Lipschitz domain in $\mathbb R^n$. Let $s\in (0,1)$ and let A be a Young function as in (3.6), (3.7) and (3.8). From Theorem 3.5 and property (2.3) one infers that the embedding

$$\begin{aligned} W^{s,A}(\Omega ) \rightarrow L^B (\Omega ) \end{aligned}$$

is compact if and only if B is a Young function fulfilling

$$\begin{aligned} {\left\{ \begin{array}{ll} \lim _{t\rightarrow \infty }\frac{t^{\frac{n-sp}{np}}(\log t)^{-\frac{\alpha }{p}}}{B^{-1}(t)} =0 &{} \quad \text { if }1\le p< \frac{n}{s} \\ \lim _{t\rightarrow \infty }\frac{ (\log t)^{\frac{n-(\alpha +1)s}{n}}}{B^{-1}(t)} &{} \quad \text {if } p=\frac{n}{s} \text { and } \alpha < \frac{n}{s} -1 \\ \lim _{t\rightarrow \infty }\frac{ (\log \log t)^{\frac{n-s}{n}}}{B^{-1}(t)} &{} \quad \text {if } p=\frac{n}{s} \text { and } \alpha = \frac{n}{s} -1. \end{array}\right. } \end{aligned}$$

If A and B are as above, an analogous result holds for the embedding $V^{s,A}_d(\mathbb R^n) \rightarrow L^B_{\mathrm{loc}}(\mathbb R^n)$.

4 Limits as $s \rightarrow 0^+$ and $s \rightarrow 1^-$

Here we are concerned with the question of existence and values of the limits (1.9) and (1.10).

Let us begin by addressing the problem of the limit as $s\rightarrow 0^+$. A result from [2] tells us that, if the Young function A satisfies the $\Delta _2$-condition, and the function $u\in V^{s,A}_d(\mathbb R^n)$ for some $s\in (0,1)$, then the limit in (1.10) does exist, and equals the integral of a Young function of |u| over $\mathbb R^n$. Interestingly, such a Young function is not just a constant multiple of A in general. It is instead the Young function ${\overline{A}}$ given by the formula

$$\begin{aligned} {\overline{A}}(t) = \int _0^t\frac{A(\tau )}{\tau }\, d\tau \qquad \text {for} \ t\ge 0\,. \end{aligned}$$

Observe that the Young functions A and ${\overline{A}}$ are equivalent, since $A(t/2) \le {\overline{A}}(t) \le A(t)$ for $t \ge 0$, owing to the monotonicity of A(t) and A(t)/t. In particular, if $A(t)=t^p$ for some $p \ge 1$, then

$$\begin{aligned} {\overline{A}}(t)= \tfrac{1}{p} \,t^p \qquad \text {for} \ t \ge 0. \end{aligned}$$

(4.1)

Theorem 4.1

Let A be a Young function satisfying the $\Delta _2$-condition. Assume that $u \in \bigcup _{s\in (0,1)} V^{s,A}_d(\mathbb R^n)$. Then

$$\begin{aligned} \lim _{s\rightarrow 0^+} s\int _{\mathbb R^n} \int _{\mathbb R^n} A\left( \frac{|u(x)-u(y)|}{|x-y|^s}\right) \frac{dx\,dy}{|x-y|^{n}} = 2\,n \omega _n \int _{\mathbb R^n} {\overline{A}}(|u(x)|)\; dx\,. \end{aligned}$$

(4.2)

Plainly, owing to Eq. (4.1), Theorem 4.1 reproduces the Maz’ya–Shaposhnikova result (1.8) when $A(t)=t^p$ for some $p \ge 1$.

Let us mention that, under the additional $\nabla _2$-condition on A, an earlier partial result in this connection had been established in [23], where bounds for the $\liminf _{s\rightarrow 0^+}$ and $\limsup _{s\rightarrow 0^+}$ of the expression under the limit in (4.2) are given.

We emphasize that the $\Delta _2$-condition imposed on A in Theorem 4.1 is not just a technicality. The next result shows that its conclusion can indeed fail if the $\Delta _2$-condition is removed.

Theorem 4.2

There exist Young functions A, which do not satisfy the $\Delta _2$-condition, and corresponding functions $u:\mathbb R^n\rightarrow \mathbb R$ such that $u \in \ V^{s,A}_d(\mathbb R^n)$ for every $s\in (0,1)$ and

$$\begin{aligned} \int _{\mathbb R^n} {\overline{A}}(|u(x)|)\;dx \le \int _{\mathbb R^n} A(|u(x)|)\;dx <\infty \,, \end{aligned}$$

but

$$\begin{aligned} \lim _{s\rightarrow 0^+}\,s\int _{\mathbb R^n} \int _{\mathbb R^n} A \left( \frac{|u(x) - u(y)|}{|x-y|^s}\right) \; \frac{dx\, dy}{|x-y|^n} =\infty \,. \end{aligned}$$

We refer to the paper [2] for Proofs of Theorems 4.1 and 4.2. Let us just mention here that the Young functions A and the functions u announced in the statement of Theorem 4.2, that demonstrate the possible failure of Eq. (4.2), can be chosen with the following properties:

$$\begin{aligned} A(t)= e^{-\frac{1}{t^{\gamma }}} \quad \hbox {for large} \ t\,, \end{aligned}$$

and

$$\begin{aligned} u(x) = \frac{x_1}{\lambda |x| \log ^{\frac{1}{\gamma }} {(\kappa +|x|)} } \quad \text {for large} \ |x|, \end{aligned}$$

where $x=(x_1, \dots x_n)$, for suitably related constants $\gamma \ge 1$ and $\lambda \in (1,2)$.

We finally focus on the limit as $s\rightarrow 1^-$. As recalled in Sect. 1, in the case of standard Sobolev spaces associated with the exponent p, the result takes a different form depending on whether $p=1$ or $p\in (1,\infty )$. More precisely, whereas Eq. (1.6) holds under the assumption that $u\in W^{1,p}(\mathbb R^n)$ for every $p\in [1,\infty )$, the fact that $u\in L^p(\mathbb R^n)$ and the limit in (1.6) is finite ensure that $u\in W^{1,p}(\mathbb R^n)$ if $p\in (1,\infty )$, but just that $u\in BV(\mathbb R^n)$ if $p=1$. Also, under the latter assumption, Eq. (1.6) continues to hold with $\int _{\mathbb R^n}|\nabla u|dx$ replaced by $\Vert Du\Vert (\mathbb R^n)$ on the right-hand side.

A parallel phenomenon occurs in the ambient of Orlicz–Sobolev spaces. Similarly to the limit (1.10), the Young function to be applied to the modulus of the gradient to describe the limit (1.9) is not a mere multiple of A. The relevant function will be denoted by $A_\circ : [0, \infty ) \rightarrow [0, \infty )$, and is defined as

$$\begin{aligned} A_\circ (t) =\int _0^t \int _{\mathbb {S}^{n-1}} A(r \, |\theta \cdot {e }|) \; d{\mathcal {H}}^{n-1} (\theta ) \; \frac{dr}{r} \qquad \hbox {for}\;\; t\ge 0\,, \end{aligned}$$

(4.3)

where $e$ is any fixed vector in $\mathbb {S}^{n-1}$. One can show that $A_\circ$ is a Young function equivalent to A. Specifically, there exist constants $c_1=c_1(n)$ and $c_2=c_2(n)$ such that

$$\begin{aligned} A(c_1 t) \le A_\circ (t) \le c_2 A(t) \quad \text {for} \ t \ge 0. \end{aligned}$$

Observe that, if $A(t)=t^p$, then

$$\begin{aligned} A_\circ (t) = K(n,p) t^p \qquad \hbox {for} \, t\ge 0, \end{aligned}$$

where K(n, p) is the constant defined by (1.7).

Theorem 4.3

Let A be a finite-valued Young function. Assume that $u\in W^{1,A}(\mathbb R^n)$. Then there exists $\lambda _0>0$ such that

$$\begin{aligned} \lim _{s\rightarrow 1^-} (1-s) \int _{\mathbb R^n}\int _{\mathbb R^n} A\left( \frac{|u(x) - u(y)|}{\lambda |x-y|^s}\right) \; \frac{dx\,dy}{|x-y|^n}= \int _{\mathbb R^n} {A}_\circ \left( \frac{|\nabla u|}{\lambda }\right) \; dx\nonumber \\ \end{aligned}$$

(4.4)

for every $\lambda \ge \lambda _0$. If $u\in W^1E^A(\mathbb R^n)$, then Eq. (4.4) holds for every $\lambda >0$.

Remark 3

Let us emphasize that, unlike Theorem 4.1, the $\Delta _2$-condition is not required in Theorem 4.3, at the expense of replacing u by $u/\lambda$ for sufficiently large $\lambda >0$. This is consistent with the fact that, if A does not satisfy this condition, membership of $\nabla u$ in the Orlicz space $L^A(\mathbb R^n)$ only ensures that $\int _{\mathbb R^n} {A} \big (\frac{|\nabla u|}{\lambda }\big )\; dx$, and hence $\int _{\mathbb R^n} {A}_\circ \big (\frac{|\nabla u|}{\lambda }\big )\; dx$, is finite for sufficiently large $\lambda$. However, under the $\Delta _2$-condition on A, one has that $W^{1,A}(\mathbb R^n)=W^{1,A}(\mathbb R^n)$, and hence Eq. (4.4) holds for every $\lambda >0$, including $\lambda =1$.

In the framework of Orlicz spaces associated with a Young function A, an analogue of the distinction between $p=1$ and $p \in (1,\infty )$ for powers is properly formulated in terms of the limit at infinity and/or at 0 of the (non-decreasing) function A(t)/t. In particular, a converse to Theorem 4.3 holds under the superlinear growth condition on A near infinity

$$\begin{aligned} \lim _{t \rightarrow \infty }\frac{A (t)}{t}=\infty , \end{aligned}$$

(4.5)

and the sublinear decay condition at 0

$$\begin{aligned} \lim _{t \rightarrow 0^+}\frac{A (t)}{t}=0. \end{aligned}$$

(4.6)

Plainly, if $A(t)=t^p$, either of conditions (4.5) and (4.6) is equivalent to requiring that $p>1$.

Theorem 4.4

Let A be a finite-valued Young function. Assume that A fulfills conditions (4.5) and (4.6). If $u\in L^A(\mathbb R^n)$ is such that

$$\begin{aligned} \liminf _{s\rightarrow 1^-} \;(1-s) \int _{\mathbb R^n}\int _{\mathbb R^n} A\left( \frac{|u(x) - u(y)|}{\lambda |x-y|^s}\right) \; \frac{dx\,dy}{|x-y|^n} < \infty \end{aligned}$$

(4.7)

for some $\lambda >0$, then $u\in W^{1,A}(\mathbb R^n)$.

In the case when A has a linear growth near infinity or near 0, Theorems 4.3 and 4.4, respectively, have counterparts in the framework of functions of bounded variation.

Assume that A is a Young function for which equation (4.5) fails, and hence condition (2.6) holds. Since the function $A_\circ$ given by (4.3) is equivalent to A, Eq. (2.6) also holds if A is replaced by $A_\circ$. Let $a^\infty _\circ$ be the number defined as in (2.8), with A replaced by $A_\circ$, namely

$$\begin{aligned} a^\infty _\circ = \lim _{t \rightarrow \infty }\frac{A_\circ (t)}{t}. \end{aligned}$$

The following result tells us that, under (2.6), if $u\in BV(\mathbb R^n)$ then the limit in (4.4) equals the functional $J_{A_\circ , \mathbb R^n}(u)$ defined as in (2.7), namely the relaxed functional of $\int _{\mathbb R^n}A_\circ (|\nabla u|)\, dx$ with respect to convergence in $L^1_{\mathrm{loc}}(\mathbb R^n)$.

Theorem 4.5

Let A be a Young function fulfilling condition (2.6). Assume that $u\in BV(\mathbb R^n)$. Then,

$$\begin{aligned} \lim _{s\rightarrow 1^-} (1-s) \int _{\mathbb R^n}\int _{\mathbb R^n} A\left( \frac{|u(x) - u(y)|}{|x-y|^s}\right) \; \frac{dx\,dy}{|x-y|^n}= \int _{\mathbb R^n} {A}_\circ \left( |\nabla u| \right) dx +a^\infty _\circ \Vert D^su\Vert (\mathbb R^n). \end{aligned}$$

Suppose now that condition (4.6) does not hold, namely

$$\begin{aligned} \lim _{t \rightarrow 0^+}\frac{A (t)}{t} >0. \end{aligned}$$

(4.8)

From Eq. (4.7) one can conclude that $u \in BV(\mathbb R^n)$.

Theorem 4.6

Let A be a Young function fulfilling condition (4.8). Assume that $u\in L^1(\mathbb R^n)$ is such that

$$\begin{aligned} \liminf _{s\rightarrow 1^-} \;(1-s) \int _{\mathbb R^n}\int _{\mathbb R^n} A\left( \frac{|u(x) - u(y)|}{\lambda |x-y|^s}\right) \; \frac{dx\,dy}{|x-y|^n} < \infty \end{aligned}$$

for some $\lambda >0$. Then $u\in BV(\mathbb R^n)$.