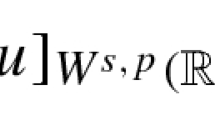On a new fractional Sobolev space with variable exponent on complete manifolds

Abstract

We present the theory of a new fractional Sobolev space in complete manifolds with variable exponent. As a result, we investigate some of our new space’s qualitative properties, such as completeness, reflexivity, separability, and density. We also show that continuous and compact embedding results are valid. We apply the conclusions of this study to the variational analysis of a class of fractional $p(z, \cdot )$-Laplacian problems involving potentials with vanishing behavior at infinity as an application.

1 Introduction

Let $(\mathcal{M}, \mathrm{g})$ be a smooth complete compact Riemannian n-manifold. The present paper is devoted to proving some qualitative properties of a new fractional Sobolev space with variable exponent in complete manifolds, as well as to studying the existence of weak solutions to the following problem as an application:

$$\begin{aligned} ( \mathcal{P} ) \quad \textstyle\begin{cases} ( - \Delta _{g} )_{p( z, \cdot )}^{s} \mathrm{u} ( z ) + \mathcal{V} ( z ) \vert \mathrm{u} ( z ) \vert ^{q( z ) - 2} \mathrm{u} = h( z, \mathrm{u} ( z )) & \text{in $ \mathcal{Q}$}, \\ \mathrm{u} |_{\partial \mathcal{Q}}= 0, \end{cases}\displaystyle \end{aligned}$$

where $\mathcal{Q} \subset \mathcal{M}$ is an open bounded set with a smooth boundary $\partial \mathcal{Q}, s \in (0, 1 ), p \in C( \mathcal{M} \times \mathcal{M}, ( 1; \infty ) )$ with $sp( z, y ) < n$, we assume that p is symmetric and satisfies the following conditions:

$$\begin{aligned} &1 < p^{-} = \min_{(z, y) \in \overline{M}^{2}} p(z, y) \leq p( z, y) \leq p^{+} = \max_{(z, y) \in \overline{M}^{2}} p(z, y), \end{aligned}$$

(1)

$$\begin{aligned} & p\bigl((z, y) - (x, x)\bigr) = p(z, y) \quad \forall x, y, z \in M^{3}, \end{aligned}$$

(2)

and we set

$$\begin{aligned} \hat{p} (z) = p(z, z), \quad \forall z \in \overline{M}, \end{aligned}$$

also $q: \overline{\mathcal{M}} \rightarrow (1, \infty )$ satisfies $1 < q^{-} \leq q^{+} < p^{-} \leq p^{+} < + \infty$, where $q^{+} = \sup_{z \in \overline{\mathcal{M}}} q( z ), q^{-} = \inf_{z \in \overline{\mathcal{M}}} q( z )$, and functions $h, \mathcal{V}$ satisfy some suitable conditions (see Sect. 4).

This type of operator has a significant role in many fields in mathematics, e.g., calculus of variations and partial differential equations, and it has also been used in a variety of physical and engineering contexts, e.g., fluid filtration in porous media, constrained heating, elastoplasticity, image processing, optimal control, financial mathematics, and elsewhere, see [8, 18, 37] and the references therein.

In recent years, wide research has been done on fractional partial differential equations with variable growth. For example, Bahrouni and Rădulescu [7] developed some qualitative properties on the fractional Sobolev space $W^{s, q( z ), p( z, y )} ( \mathcal{Q} )$ for $s \in ( 0, 1 )$ and $\mathcal{Q}$ being a bounded domain in $\mathbb{R}^{n}$ with a Lipschitz boundary. Moreover, they studied the existence of solutions to the following problem:

$$\textstyle\begin{cases} \mathcal{L} \mathrm{u}( z ) + \vert \mathrm{u} ( z ) \vert ^{q( z ) - 1} \mathrm{u}( z ) = \lambda \vert \mathrm{u}( z ) \vert ^{r( z ) - 1} \mathrm{u}( z ) & \text{in $ \mathcal{Q}$}, \\ \mathrm{u} = 0 & \text{in $ \partial \mathcal{Q} $}, \end{cases} $$

where

$$\begin{aligned} \mathcal{L} \mathrm{u}( z ) = p. v. \int _{\mathcal{Q}} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y ) - 2} ( \mathrm{u}( z ) - \mathrm{u}( y ) )}{ \vert z - y \vert ^{n + sp( z, y )}} \,dy, \end{aligned}$$

$\lambda > 0$, and $1 < r( z ) < p^{-} = \min_{( z, y )\in \mathcal{Q} \times \mathcal{Q}} p( z, y )$. Bahrouni [6] continued the study of this class of fractional Sobolev spaces with variable exponent and the related nonlocal operator. More precisely, he proved a variant of the comparison principle for $( - \Delta _{p( z )} )^{s}$. He gave a general principle of sub-supersolution method for the following problem:

$$\begin{aligned} ( \mathcal{P}_{1} ) \textstyle\begin{cases} ( - \Delta _{p( z )} )^{s} \mathrm{u} = f( z, \mathrm{u} ) & \text{in $ \mathcal{Q}$}, \\ \mathrm{u} = 0 & \text{in $ \mathbb{R}^{n} \backslash \mathcal{Q} $}, \end{cases}\displaystyle \end{aligned}$$

where $\mathcal{Q}$ is a smooth open bounded domain, $n \geq 3, s \in (0,1), p, f$ are continuous functions, and f satisfies the following assumption:

$$\begin{aligned} \bigl\vert f( z, t ) \bigr\vert \leq c_{1} + c_{2} \vert t \vert ^{r( z )- 1}, \quad \forall z \in \mathbb{R}^{n}, \forall t \in \mathbb{R}, \end{aligned}$$

where $r \in C( \mathbb{R}^{n}, \mathbb{R} )$ and $1 < r( z ) < p^{*} ( z ) = \frac{n p(z, z)}{n - sp(z, z)}, \forall z \in \mathbb{R}^{n}$.

Kaufmann, Rossi, and Vidal [32] proved a compact embedding theorem for fractional Sobolev spaces with variable exponents into variable exponent Lebesgue space and, as an application, they showed the existence and uniqueness of solutions to the following fractional $p( z, y )$-Laplacian equation:

$$\begin{aligned} \textstyle\begin{cases} \mathcal{L} \mathrm{u} ( z ) + \vert \mathrm{u} ( z ) \vert ^{q( z ) - 2} \mathrm{u}( z ) = f( z ) & \text{in $ \mathcal{Q}$}, \\ \mathrm{u} = 0 & \text{in $ \partial \mathcal{Q} $}, \end{cases}\displaystyle \end{aligned}$$

with $f \in L^{a( z )} ( \mathcal{Q} ), a( z ) > 1$.

In [31] the authors refined the fractional Sobolev spaces with variable exponents given in [6, 7, 32] and established fundamental embeddings of this space. In addition, they gave a sufficient condition for the exponent $p( \cdot, \cdot )$ on $\mathbb{R}^{n} \times \mathbb{R}^{n}$ for the iteration argument of De Giorgi type and proved global boundedness of weak solutions to the problem $( \mathcal{P}_{1} )$. Readers may refer to [1, 4, 5, 12–14, 19, 21–23, 27, 33, 34, 36, 38, 42] and the references therein for more ideas and techniques developed to guarantee the existence of weak solutions for a class of nonlocal fractional problems with variable exponents. When $p( \cdot, \cdot ) = p = \text{constant}$, we quote, for example, the relevant work of Vázquez [41], see also [2, 9–11, 15, 17, 20, 35] and the references therein. Various techniques have been proposed in the literature in order to recover the compactness in several circumstances. We refer to Tang and Cheng [40], who proposed a new approach to restore the compactness of Palais–Smale sequences, and to Tang and Chen [39], who introduced an original method to recover the compactness of minimizing sequences. A related approach has been developed by Chen and Tang [16] in the framework of Cerami sequences.

Before discussing our main results, we give a review of equations involving the fractional p-Laplace operator on Riemannian manifolds. As far as we know, there is only the work of Guo, Zhang, and Zhang [29] who proved the existence of solutions to the following p-Laplacian equations with homogeneous Dirichlet boundary conditions:

$$\begin{aligned} \textstyle\begin{cases} (- \Delta _{g} )^{s}_{p} \mathrm{u}( z ) = f( z, \mathrm{u}( x ) ) & \text{in $ \mathcal{Q}$}, \\ \mathrm{u} = 0 & \text{in $ M \backslash \mathcal{Q} $}, \end{cases}\displaystyle \end{aligned}$$

where $sp < n$ with $s \in ( 0, 1 ), p \in ( 1; \infty ), ( - \Delta _{g} )_{p}^{s}$ is the fractional p-Laplacian on Riemannian manifolds, $( M, g )$ is a compact Riemannian n-manifold, $\mathcal{Q}$ is an open bounded subset of M with a smooth boundary $\partial \mathcal{Q}$, and f is a Carathéodory function satisfying the Ambrosetti–Rabinowitz-type condition.

The motivation of this paper was, on the one hand, the work of Fu and Guo [24] who introduced the variable exponent function spaces on Riemannian manifolds in 2012, followed by Gaczkowski and Górka [25] who in 2013 examined the above space in the case of compact manifolds, and Guo [28] who in 2015 discussed the properties of the Nemytsky operator and obtained the existence of weak solutions for Dirichlet problems of nonhomogeneous $p(m)$-harmonic equations. Finally, in 2016 Gaczkowski, Górka, and Pons [26] studied the variable exponent function spaces on complete noncompact Riemannian manifolds. Furthermore, they proved the continuous embeddings results between Sobolev and Hölder function spaces, using classic assumptions on the geometry. In addition, they established the compact embeddings of H-invariant Sobolev spaces, where H is a compact Lie subgroup of the manifold group of isometries, and, as an application, they showed the existence of weak solutions to nonhomogeneous $q(z)$-Laplace equations. For further background, we recommend that readers consult [1, 12] and the references therein. On the other hand, we were also motivated by the work of Guo, Zhang, and Zhang [29] who established the theory of fractional Sobolev spaces on Riemannian manifolds.

The novelty of our work is in extending Sobolev spaces with variable exponents to cover the fractional case with complete manifolds. We prove some qualitative properties of this new space. Next, we study the existence of solutions to some nonlocal problems involving potentials allowed for vanishing behavior at infinity. However, the main difficulty is presented by the fact that the $p(z)$-Laplacian operator has a more complicated nonlinearity than the p-Laplacian operator. For example, it is nonhomogeneous. To the best of our knowledge, there is no known result along this line.

The outline of the paper is as follows. In Sect. 2, we collect the pertinent properties and notations of Lebesgue spaces with variable exponents and Sobolev–Orlicz spaces with variable exponents on a complete manifold. Moreover, we show the relation between the norm and the modular. In Sect. 3, we study the completeness, reflexivity, separability, and density of our new space. Furthermore, we prove a continuous and compact embedding theorem of this space into variable exponent Lebesgue spaces. In Sect. 4, we deal with a fractional $p(z)$-Laplacian problem involving potentials allowed for vanishing behavior at infinity as an application.

2 Preliminaries

In this section, we review some definitions and properties of spaces $W_{0}^{1, q( z )} ( \mathcal{Q})$, where $\mathcal{Q}$ is an open subset of $\mathbb{R}^{n}$, and $W_{0}^{1, q( z )} ( \mathcal{M})$, which are known as the Sobolev spaces with variable exponents and the Sobolev spaces with variable exponents on a complete manifold, respectively. For more background, we refer to [1, 3, 12, 21, 26, 28, 30] and the references therein.

2.1 Sobolev spaces with variable exponents

Suppose that $\mathcal{Q} \subset \mathbb{R}^{n}$ is a bounded open domain, with $n \geq 2$. Let $q(\cdot ): \mathcal{Q} \rightarrow (1, \infty )$ be a measurable function. We define real numbers $q^{+}$ and $q^{-}$ as follows:

$$\begin{aligned} q^{+} = \mathrm{ess}\sup \bigl\{ q( z ): z \in \mathcal{Q} \bigr\} \quad \text{and} \quad q^{-} = \mathrm{ess}\inf \bigl\{ q( z ): z \in \mathcal{Q} \bigr\} . \end{aligned}$$

Definition 2.1

([21])

We define the Lebesgue space with variable exponent $L^{q(\cdot )} ( \mathcal{Q} )$ as follows:

$$\begin{aligned} L^{q(\cdot )} ( \mathcal{Q} ) = \biggl\{ \mathrm{u}: \mathcal{Q} \rightarrow \mathbb{R}: \varrho _{q(\cdot )} ( \mathrm{u} ) = \int _{\mathcal{Q}} \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z )} \,dz < + \infty \biggr\} , \end{aligned}$$

and endow it with the Luxemburg norm

$$\begin{aligned} \Vert \mathrm{u} \Vert _{L^{q(\cdot )} ( \mathcal{Q} )} = \inf \biggl\{ \mu > 0: \varrho _{q(\cdot )} \biggl( \frac{\mathrm{u}}{\mu } \biggr) \leq 1 \biggr\} , \end{aligned}$$

if $q^{+} < + \infty$.

Proposition 2.1

([21])

$( L^{q(\cdot )} ( \mathcal{Q} ), \Vert \cdot \Vert _{L^{q(\cdot )} ( \mathcal{Q} )} )$ is a separable Banach space, and uniformly convex for $1 < q^{-} \leq q^{+} < +\infty$, hence reflexive.

Proposition 2.2

(Hölder inequality, [21])

$$\begin{aligned} \biggl\vert \int _{\mathcal{Q}} \mathrm{u} v \,dx \biggr\vert \leq \biggl( \frac{1}{q^{-}} + \frac{1}{( q^{\prime } )^{-}} \biggr) \Vert \mathrm{u} \Vert _{L^{q(\cdot )} ( \mathcal{Q} )} \Vert v \Vert _{L^{q^{\prime } ( \cdot )} ( \mathcal{Q} )}, \quad \forall \mathrm{u}, v \in L^{q( \cdot )} ( \mathcal{Q} ) \times L^{q^{\prime }(\cdot )} ( \mathcal{Q} ), \end{aligned}$$

with $\frac{1}{q( z )} + \frac{1}{q^{\prime } ( z )} = 1$.

Definition 2.2

([21])

We define the variable exponent Sobolev space by

$$\begin{aligned} W^{1, q( z )} ( \mathcal{Q} ) = \bigl\{ \mathrm{u:u} \in L^{q( z )} ( \mathcal{Q} ) \text{ and } \vert D \mathrm{u} \vert \in L^{q( z )} ( \mathcal{Q} ) \bigr\} , \end{aligned}$$

end endow it with the norm

$$\begin{aligned} \Vert \mathrm{u} \Vert _{W^{1, q( z )} ( \mathcal{Q} )} = \Vert \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{Q} )} + \Vert D \mathrm{u}\Vert _{L^{q( z )} ( \mathcal{Q} )}, \quad \forall \mathrm{u} \in W^{1, q( z )} ( \mathcal{Q} ) \end{aligned}$$

and set $W^{1, q( z )}_{0} ( \mathcal{Q} ): = \overline{C^{\infty }_{0} ( \mathcal{Q} )}^{ W^{1, q( z )} ( \mathcal{Q} )}$.

2.2 Sobolev spaces with variable exponents on complete manifolds

Let $(\mathcal{M}, \mathrm{g})$ be a smooth complete compact Riemannian n-manifold. We begin by recalling some background, more can be found in [1, 3, 26, 28, 30]. A chart of manifold $\mathcal{M}$ is a couple $( \mathcal{Q}, \varphi )$, where φ is a homeomorphism of the open set $\mathcal{Q}$ onto some open subset of $\mathbb{R}^{n}$. Furthermore, a collection of charts $( \mathcal{Q}_{i}, \varphi _{i} )_{i \in I}$ such that $\mathcal{M} = \bigcup_{i \in I} \mathcal{Q}_{i}$ is called an atlas on $\mathcal{M}$.

Remark 2.1

([30, page 9])

For any atlas $( \mathcal{Q}_{i}, \varphi _{i} )_{i \in I}$ on $\mathcal{M}$, there exists a partition of unity $( \mathcal{Q}_{j}, \varphi _{j}, \eta _{j} )_{j \in J}$ subordinate to the covering $( \mathcal{Q}_{i} )_{i \in I}$.

Now, we define a natural positive Radon measure.

Definition 2.3

([30, page 9)])

Let $\mathrm{u}: \mathcal{M} \to \mathbb{R}$ be continuous with compact support, and let $( \mathcal{Q}_{i}, \varphi _{i} )_{i \in I}$ be an atlas on $\mathcal{M}$, and set

$$\begin{aligned} \int _{\mathcal{M}} \mathrm{u}( z ) \,dv_{\mathrm{g}} ( z ) = \sum _{k \in J} \int _{\varphi _{k} ( \mathcal{Q}_{k} )} \bigl( \bigl( \det (\mathrm{g}_{ij} ) \bigr)^{\frac{1}{2}} \eta _{k} \mathrm{u} \bigr) o\varphi ^{-1}_{k} ( z ) \,dz, \end{aligned}$$

where $dv_{\mathrm{g}} = (\det ( \mathrm{g}_{ij} ) )^{\frac{1}{2}} \,dz$ is the Riemannian volume element on $( \mathcal{M}, \mathrm{g} )$, $\mathrm{g}_{ij}$ are the components of the Riemannian metric g in the chart, and dz is the Lebesgue volume element of $\mathbb{R}^{n}$.

Next, we define the Sobolev spaces $L_{k}^{q( \cdot )} ( \mathcal{M} )$ as the completion of $C^{q(\cdot )}_{k} ( \mathcal{M} )$ with respect to the norm $\Vert \mathrm{u} \Vert _{L^{q( \cdot )}_{k}}$, where

$$\begin{aligned} C^{q(\cdot )}_{k} ( \mathcal{M} ) = \bigl\{ \mathrm{u} \in C^{ \infty } ( \mathcal{M} ) \text{ such that } \forall j, 0 \leq j \leq k, \bigl\vert D^{k} \mathrm{u} \bigr\vert \in L^{q( \cdot ) } ( \mathcal{M} ) \bigr\} \end{aligned}$$

and

$$\begin{aligned} \Vert \mathrm{u} \Vert _{L^{q( \cdot )}_{k}} = \sum_{j = 0}^{k} \bigl\Vert D^{j} \mathrm{u} \bigr\Vert _{L^{q( \cdot )}}, \end{aligned}$$

with $| D^{k} \mathrm{u} |$ being the norm of the kth covariant derivative of u, defined in local coordinates by

$$\begin{aligned} \bigl\vert D^{k} \mathrm{u} \bigr\vert ^{2} = \mathrm{g}^{i_{1} j_{1}} \cdots \mathrm{g}^{i_{k} j_{k}} \bigl( D^{k} \mathrm{u} \bigr)_{i_{1} \dots i_{k}} \bigl( D^{k} \mathrm{u} \bigr)_{j_{1} \dots j_{k}}. \end{aligned}$$

Definition 2.4

([3])

Let $\zeta: [ \alpha, \beta ] \rightarrow \mathcal{M}$ be a curve of class $C^{1}$. The length of ζ is

$$\begin{aligned} \ell ( \zeta ) = \int _{\alpha }^{\beta } \sqrt{\mathrm{g} \biggl( \frac{d \gamma }{d s }, \frac{d \gamma }{d s} \biggr)} \,ds, \end{aligned}$$

and, for a pair of points $z, y \in \mathcal{M}$, we define the distance $d_{\mathrm{g}} ( z, y )$ between z and y by

$$\begin{aligned} d_{\mathrm{g}} ( z, y ) = \inf \bigl\{ \ell ( \zeta ): \zeta [ \alpha, \beta ] \rightarrow \mathcal{M} \text{ such as } \zeta ( \alpha ) = z \text{ and } \zeta ( \beta ) = y \bigr\} . \end{aligned}$$

Definition 2.5

([26])

A function $t: \mathcal{M} \rightarrow \mathbb{R}$ is log-Hölder continuous if there exists a constant C such that, for every pair of points $\{ z, y \}$ in $\mathcal{M,}$

$$\begin{aligned} \bigl\vert t( z ) - t( y ) \bigr\vert \leq C \biggl( \log \biggl( e + \frac{1}{d_{\mathrm{g}} ( z, y )} \biggr) \biggr)^{-1}. \end{aligned}$$

Let $\mathcal{P}^{\mathrm{log}} ( \mathcal{M} )$ be the set of log-Hölder continuous real functions on $\mathcal{M}$, which is linked to $\mathcal{P}^{\mathrm{log}} ( \mathbb{R}^{n} )$ by the following proposition:

Proposition 2.3

([3, 26])

Given $q \in \mathcal{P}^{\mathrm{log}} ( \mathcal{M} )$, let $( \mathcal{Q}, \phi )$ be a chart such that

$$\begin{aligned} \frac{1}{2} \delta _{i j } \leq \mathrm{g}_{i j} \leq 2 \delta _{i j } \end{aligned}$$

as bilinear forms, where $\delta _{i j}$ is the Kronecker delta symbol. Then $q\circ \phi ^{-1} \in \mathcal{P}^{\mathrm{log}} ( \phi ( \mathcal{Q} ) )$.

Definition 2.6

([3])

If the Ricci tensor of g, denoted by $Rc ( \mathrm{g} )$, satisfies $Rc ( \mathrm{g} ) \geq \lambda ( n - 1 ) \mathrm{g}$, for some λ and for all $z \in \mathcal{M}, \exists v > 0$ such that $| B_{1} ( z ) |_{\mathrm{g}} \geq v$, where $B_{1} ( z )$ are balls of radius 1 centered at some point z in terms of the volume of smaller concentric balls, then we say that the n-manifold $( \mathcal{M}, \mathrm{g} )$ has property $B_{vol} ( \lambda, v )$.

Proposition 2.4

([1, Proposition 2.17])

Let $\mathrm{u} \in L^{q( z )} ( \mathcal{M} ), \{ \mathrm{u}_{k} \}_{k \geq 0} \subset L^{q( z )} ( \mathcal{M} )$. Then

• (i) $\Vert \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )} < 1 \Longrightarrow \Vert \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )}^{q^{+}} \leq \varrho _{q( z )} ( \mathrm{u} ) \leq \Vert \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )}^{q^{-}}$,

• (ii) $\Vert \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )} > 1 \Longrightarrow \Vert \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )}^{q^{-}} \leq \varrho _{q( z )} ( \mathrm{u} ) \leq \Vert \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )}^{q^{+}}$,

where

$$\begin{aligned} \varrho _{q(z)} ( \mathrm{u} ) = \int _{\mathcal{M}} \bigl\vert \mathrm{u} (z) \bigr\vert ^{q(z)} \,dv_{g} (z). \end{aligned}$$

We now prove the following proposition.

Proposition 2.5

If $\mathrm{u}, \mathrm{u}_{k} \in L^{q( z )} ( \mathcal{M} )$ and $k \in \mathbb{N}$, then the following assertions are equivalent:

• (1) $\lim_{k \rightarrow + \infty } \Vert \mathrm{u}_{k} - \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )} = 0$,

• (2) $\lim_{k \rightarrow + \infty } \varrho _{q( z )} ( \mathrm{u}_{k} - \mathrm{u} ) = 0$,

• (3) $\mathrm{u}_{k} \rightarrow \mathrm{u}$ a.e. on $\mathcal{M}$ and $\lim_{k \rightarrow + \infty } \varrho _{q( \cdot )} ( \mathrm{u}_{k} ) = \varrho _{q( \cdot )} ( \mathrm{u} )$.

Proof

If $\Vert \mathrm{u}_{k} - \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )} \rightarrow 0$, then

$$\begin{aligned} \lim_{k \rightarrow +\infty } \int _{\mathcal{M}} \vert \mathrm{u}_{k} - \mathrm{u} \vert ^{q( z )} \,dv_{\mathrm{g}} ( z ) = 0. \end{aligned}$$

It is now easy to observe that $\mathrm{u}_{k} \rightarrow \mathrm{u}$ a.e. on $\mathcal{M}$. Thus $|\mathrm{u}_{k}|^{q( z )} \rightarrow |\mathrm{u}|^{q( z )}$ on $\mathcal{M}$ and the integrals of the functions $| \mathrm{u}_{k} - \mathrm{u} |^{q( z )}$ are absolutely equicontinuous on $\mathcal{M}$, and since

$$\begin{aligned} \vert \mathrm{u}_{k} \vert ^{q( z )} \leq 2^{q^{+} - 1} \bigl( \vert \mathrm{u}_{k} - \mathrm{u} \vert ^{q( z )} + \vert \mathrm{u} \vert ^{q( z )} \bigr), \end{aligned}$$

the integrals of the $|\mathrm{u}_{k}|^{q( z )}$ are also absolutely equicontinuous on $\mathcal{M}$, so, by the Vitali convergence theorem, we obtain that

$$\begin{aligned} \lim_{k \rightarrow + \infty } \varrho _{q( \cdot )} ( \mathrm{u}_{k} ) = \varrho _{q( \cdot )} ( \mathrm{u} ). \end{aligned}$$

Conversely, if $\mathrm{u}_{k} \rightarrow \mathrm{u}$ on $\mathcal{M}$, we can deduce that $|\mathrm{u}_{k} - \mathrm{u}|^{q( z )} \rightarrow 0$ on $\mathcal{M}$, and using the same techniques as in the above proof, and due to the fact that

$$\begin{aligned} \vert \mathrm{u}_{k} - \mathrm{u} \vert ^{q( z )} \leq 2^{q^{+} - 1} \bigl( \vert \mathrm{u}_{k} \vert ^{q( z )} + \vert \mathrm{u} \vert ^{q( z )} \bigr), \end{aligned}$$

and $\lim_{k \rightarrow + \infty } \varrho _{q( \cdot )} ( \mathrm{u}_{k} ) = \varrho _{q( \cdot )} ( \mathrm{u} )$, we obtain that $\lim_{k \rightarrow +\infty } \varrho _{q( \cdot )} ( \mathrm{u}_{k} - \mathrm{u} ) = 0$. □

Remark 2.2

The following relation will be used to compare the functionals $\Vert \cdot \Vert _{L^{q( \cdot )} ( \mathcal{M} )}$ and $\varrho _{q( \cdot )} ( \cdot )$:

$$\begin{aligned} \min \bigl\{ \varrho _{q( \cdot )} ( \mathrm{u} )^{\frac{1}{q^{-}}}, \varrho _{q( \cdot )} ( \mathrm{u} )^{\frac{1}{q^{+}}} \bigr\} \leq \Vert \mathrm{u} \Vert _{L^{q( \cdot )} ( \mathcal{M} )} \leq \max \bigl\{ \varrho _{q( \cdot )} ( \mathrm{u} )^{\frac{1}{q^{-}}}, \varrho _{q( \cdot )} ( \mathrm{u} )^{\frac{1}{q^{+}}} \bigr\} . \end{aligned}$$

Definition 2.7

([28])

The Sobolev space $W^{1, q( z )} ( \mathcal{M} )$ consists of all functions $\mathrm{u} \in L^{q( z )} ( \mathcal{M} )$ for which $D^{k} \mathrm{u} \in L^{q( z )} ( \mathcal{M} )$ $k = 1, 2, \dots, n$. The norm is defined by

$$\begin{aligned} \Vert \mathrm{u} \Vert _{W^{1, q( z )} ( \mathcal{M} )} = \Vert \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )} + \sum_{k = 1}^{n} \bigl\Vert D^{k} u \bigr\Vert _{L^{q( z )} ( \mathcal{M} )}. \end{aligned}$$

The space $W_{0}^{1, q( z )} ( \mathcal{M} )$ is defined as the closure of $C^{\infty } ( \mathcal{M} )$ in $W^{1, q( z )} ( \mathcal{M} )$.

Theorem 2.1

([1])

Let $\mathcal{M}$ be a compact Riemannian manifold with a smooth boundary or without boundary and $q( z ), p( z ) \in C( \overline{\mathcal{M}} ) \cap L^{\infty } ( \mathcal{M} )$. Assume that

$$\begin{aligned} q( z ) < n, \quad p( z ) < \frac{n q( z )}{n - q( z )} \quad \textit{for } z \in \overline{ \mathcal{M}}. \end{aligned}$$

Then

$$\begin{aligned} W^{1, q( z )} ( \mathcal{M} ) \hookrightarrow L^{p( z )} ( \mathcal{M} ) \end{aligned}$$

is a continuous and compact embedding.

Proposition 2.6

([3])

If $( \mathcal{M}, \mathrm{g} )$ is complete, then $W^{1, q( z )} ( \mathcal{M} ) = W^{1, q( z )}_{0} ( \mathcal{M} )$.

3 Fractional Sobolev space with variable exponent on a complete manifold

On a complete manifold, we introduce in this section a new fractional Sobolev space with variable exponent and state our mains results.

Definition 3.1

Let $p: \overline{\mathcal{M}} \times \overline{\mathcal{M}} \rightarrow (1; \infty )$ be a continuous variable exponent and let $s \in (0, 1)$. We define the modular

$$\begin{aligned} \varrho _{p( \cdot, \cdot )} ( \mathrm{u} ) = \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ). \end{aligned}$$

For $s \in (0, 1 )$, we introduce the variable exponent Sobolev fractional space on a complete manifold as follows:

$$\begin{aligned} W^{s, p( z, y )} ( \mathcal{M} ) ={}& \biggl\{ \mathrm{u}: \mathcal{M} \rightarrow \mathbb{R}: \mathrm{u} \in L^{\hat{p}( z )} ( \mathcal{M} ) \text{ such as}\\ &\int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) < \infty, \text{ for some } \lambda > 0 \biggr\} . \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert \mathrm{u} \Vert _{\varrho _{p( \cdot, \cdot )}} = \inf \biggl\{ \lambda > 0: \varrho _{p( \cdot, \cdot )} \biggl( \frac{\mathrm{u}}{\lambda } \biggr) \leq 1 \biggr\} = [ \mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )}. \end{aligned}$$

The modular $\varrho _{p( \cdot, \cdot )}$ has the following properties.

3.1 Lemmas

In this part, we will go through some of our new fractional space’s qualitative lemmas.

Lemma 3.1

Let $p \in C( \mathcal{M} \times \mathcal{M}, (1; \infty ) )$ be a continuous variable exponent. Then for any $\mathrm{u} \in W^{s, p( z, y )} ( \mathcal{M} )$, we get

• (1) $[\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )} \geq 1 \Longrightarrow [\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{-}} \leq \varrho _{p( \cdot, \cdot )} ( \mathrm{u} ) \leq [\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{+}}$,

• (2) $[\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )} \leq 1 \Longrightarrow [\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{+}} \leq \varrho _{p( \cdot, \cdot )} ( \mathrm{u} ) \leq [\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{-}}$.

Proof

(1) For all $\theta \in ( 0, 1 )$, we have

$$\begin{aligned} \theta ^{p^{+}} \varrho _{p(\cdot, \cdot )} ( \mathrm{u} ) \leq \varrho _{p(\cdot, \cdot )} ( \theta \mathrm{u} ) \leq \theta ^{p^{-}} \varrho _{p(\cdot, \cdot )} ( \mathrm{u} ). \end{aligned}$$

So, if $[\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )} > 1$, then $0 < \frac{1}{[\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )}} < 1$, thus we have

$$\begin{aligned} \frac{\varrho _{p( \cdot,\cdot )} ( \mathrm{u} )}{[\mathrm{u}]^{p^{+}}_{W^{s, p( z, y )} ( \mathcal{M} )}} \leq \varrho _{p(\cdot, \cdot )} \biggl( \frac{\mathrm{u}}{[\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )}} \biggr) \leq \frac{\varrho _{p( \cdot, \cdot )} ( \mathrm{u} )}{[\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{-}}}, \end{aligned}$$

and, since $\varrho _{p( \cdot, \cdot )} ( \frac{\mathrm{u}}{[\mathrm{u}]_{W^{s, p( z, y )} ( \mathcal{M} )}} ) = 1$, obtain our result. We proceed in the same way for (2). □

Remark 3.1

It is important to note that the results of Proposition 2.5 apply to $\varrho _{p( \cdot, \cdot )}$.

Lemma 3.2

If $( \mathcal{M}, \mathrm{g} )$ be a smooth complete compact Riemannian n-manifold, then $W^{s, p( z, y )} ( \mathcal{M} )$ is a Banach space.

Proof

Let $\{ \mathrm{u}_{n} \}$ be a Cauchy sequence in $W^{s, p( z, y )} ( \mathcal{M} )$. Since

$$\begin{aligned} \hat{p}( z ) < \hat{p}^{*}_{s} ( z ) = \textstyle\begin{cases} \frac{n \hat{p} ( z )}{n - s \hat{p}( z )} & \text{if $ s \hat{p}( z ) < n$}, \\ + \infty & \text{otherwise}, \end{cases}\displaystyle \end{aligned}$$

for any $z \in \overline{\mathcal{M}}$, it follows that for any $\eta > 0$, there exists $\mu _{\eta }$ such that, if $\ell, m \geq \mu _{\eta }$,

$$\begin{aligned} \Vert \mathrm{u}_{\ell } - \mathrm{u}_{m} \Vert _{L^{\hat{p}( z )} ( \mathcal{M} )} \leq \Vert \mathrm{u}_{\ell } - \mathrm{u}_{m} \Vert _{W^{s, p( z, y )} ( \mathcal{M} )} \leq \eta. \end{aligned}$$

(3)

Since $L^{\hat{p}( z )} ( \mathcal{M} )$ is complete (Lemma 2.5 in [28]), there exists $\mathrm{u} \in L^{\hat{p}( z )} ( \mathcal{M} )$ such that $\mathrm{u}_{\ell } \rightarrow \mathrm{u}$ strongly in $L^{\hat{p}( z )} ( \mathcal{M} )$ as $\ell \rightarrow + \infty$. Consequently, we may find a subsequence $\{ \mathrm{u}_{\ell _{t}} \}$ of $\{\mathrm{u}_{\ell } \}$ in $W^{s, p( z, y )} ( \mathcal{M} )$ such that $\mathrm{u}_{\ell _{t}} \rightarrow \mathrm{u}$ a.e. on $\mathcal{M}$.

Then, by the Fatou’s lemma and (3) with $\eta = 1$, we obtain

$$\begin{aligned} &\varrho _{p( \cdot, \cdot )} ( \mathrm{u} ) \\ &\quad= \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) \\ &\quad\leq \lim_{t \rightarrow + \infty } \inf \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}_{\ell _{t}} ( z ) - \mathrm{u}_{\ell _{t}} ( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) \\ &\quad \leq 2^{p^{+} -1} \lim_{t \rightarrow + \infty } \inf \biggl[ \int _{ \mathcal{M} \times \mathcal{M}} \frac{ \vert ( \mathrm{u}_{\ell _{t}} ( z ) - \mathrm{u}_{\mu _{1}} ( z ) ) - ( \mathrm{u}_{\ell _{t}} ( y ) - \mathrm{u}_{\mu _{1}} ( z ) ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) \\ &\qquad{} + \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}_{\mu _{1}} ( z ) - \mathrm{u}_{\mu _{1}} ( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{g} ( y ) \biggr] \\ &\quad\leq 2^{p^{+} -1} \Bigl[ \lim _{t \rightarrow + \infty } \inf \varrho _{p( \cdot, \cdot )} ( \mathrm{u}_{\ell _{t}} - \mathrm{u}_{\mu _{1}} ) + \varrho _{p( \cdot, \cdot )} ( \mathrm{u}_{\mu _{1}} ) \Bigr] \\ &\quad \leq 2^{p^{+} - 1} \Bigl[ \lim_{t \rightarrow + \infty } \inf \bigl( \Vert \mathrm{u}_{\ell _{t}} - \mathrm{u}_{\mu _{1}} \Vert _{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{+}} + \Vert \mathrm{u}_{\ell _{t}} - \mathrm{u}_{\mu _{1}} \Vert _{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{-}} \bigr) \\ &\qquad{}+ \bigl( \Vert \mathrm{u}_{\mu _{1}} \Vert _{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{+}} + \Vert \mathrm{u}_{\mu _{1}} \Vert _{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{-}} \bigr) \Bigr] \\ &\quad\leq 2^{p^{+} - 1} \bigl( 2 + \Vert \mathrm{u}_{\mu _{1}} \Vert ^{p^{+}}_{W^{s, p( z, y )} ( \mathcal{M} )} + \Vert \mathrm{u}_{\mu _{1}} \Vert _{W^{s, p( z, y )} ( \mathcal{M} )}^{p^{-}} \bigr) < + \infty. \end{aligned}$$

Hence, $\mathrm{u} \in W^{s, p( z, y )} ( \mathcal{M} )$. On the other hand, let $\ell \geq \mu _{\eta }$. Then, according to (3) and from Fatou’s lemma, we get

$$\begin{aligned} \varrho _{p( \cdot, \cdot )} ( \mathrm{u}_{\ell } - \mathrm{u} ) \leq \lim _{t \rightarrow + \infty } \inf \varrho _{p(\cdot, \cdot )} ( \mathrm{u}_{\ell } - \mathrm{u}_{\ell _{t}} ) \leq \frac{\eta ^{p^{+}} + \eta ^{p^{-}}}{2} = \eta ^{*}. \end{aligned}$$

Thus $\lim_{\ell \rightarrow + \infty } \varrho _{p( \cdot, \cdot )} ( \mathrm{u}_{\ell } - \mathrm{u} ) = 0$. Thanks to Remark 3.1, $\lim_{\ell \rightarrow + \infty } \Vert \mathrm{u}_{\ell } - \mathrm{u} \Vert _{W^{s, p( z, y )} ( \mathcal{M} )} = 0$. That is, $\mathrm{u}_{\ell } \rightarrow \mathrm{u}$ strongly on $W^{s, p( z, y )} ( \mathcal{M} )$ as $\ell \rightarrow + \infty$. □

Lemma 3.3

Let $(\mathcal{M}, \mathrm{g})$ be a smooth complete compact Riemannian n-manifold, and $p(z, y) \in C( \mathcal{M} \times \mathcal{M}, ( 1, \infty ))$ with $sp(z, y)< n$, for $z, y \in \overline{\mathcal{M}}$. Then $W^{s,p(z, y)}(\mathcal{M})$ is a separable and reflexive space.

Proof

Consider $\mathrm{u}, v \in W_{0}^{s, p(z, y)}(\mathcal{M})$ satisfying $\|\mathrm{u}\|_{W_{0}^{s, p(z, y)}(\mathcal{M})}=\|v\|_{W_{0}^{s, p(z, y)}(\mathcal{M})}=1$ and $\|\mathrm{u}-v\|_{W_{0}^{s, p(z, y)}(\mathcal{M})} \geq$ ε, where $\varepsilon \in (0,2)$.

Case $p(z, y) \geq 2$. By inequality (28) in [2], we have that

$$\begin{aligned} & \biggl\Vert \frac{\mathrm{u}+v}{2} \biggr\Vert _{W_{0}^{s, p(z, y)}( \mathcal{M})}^{p(z, y)} + \biggl\Vert \frac{\mathrm{u}-v}{2} \biggr\Vert _{W_{0}^{s, p(z, y)}(\mathcal{M})}^{p(z, y)} \\ &\quad\leq \biggl( \frac{1}{2} \biggr)^{\frac{p^{+}}{p^{-}}} \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}(z)-\mathrm{u}(y) \vert ^{p(z, y)}}{ (d_{\mathrm{g}}(z, y) )^{n + sp(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \\ &\qquad{}+ \biggl(\frac{1}{2} \biggr)^{\frac{p^{+}}{p^{-}}} \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert v(z)-v(y) \vert ^{p(z, y)}}{ (d_{\mathrm{g}}(z, y) )^{n + sp(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \\ &\quad< \frac{1}{2} \int _{ \mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}(z)-\mathrm{u}(y) \vert ^{p(z, y)}}{ (d_{\mathrm{g}}(z, y) )^{n + sp(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \\ &\qquad{}+\frac{1}{2} \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert v(z)-v(y) \vert ^{p(z, y)}}{ (d_{\mathrm{g}}(z, y) )^{n + sp(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \\ &\quad= \frac{1}{2} \Vert \mathrm{u} \Vert _{W_{0}^{s, p(z, y)}(\mathcal{M})}^{p(z, y)}+\frac{1}{2} \Vert v \Vert _{W_{0}^{s, p(z, y)}(\mathcal{M})}^{p(z, y)}=1. \end{aligned}$$

So, $\Vert \frac{\mathrm{u}+v}{2} \Vert _{W_{0}^{s, p(z, y)}( \mathcal{M})}^{p(z, y)} \leq 1-(\varepsilon / 2)^{p(z, y)}$. Taking $\delta =\delta (\varepsilon )$ such that $1-(\varepsilon / 2)^{p(z, y)}=(1-\delta )^{p(z, y)}$, we obtain $\Vert \frac{\mathrm{u}+v}{2} \Vert _{W_{0}^{s, p(z, y)}( \mathcal{M})} \leq (1-\delta )$.

Case $1< p(z, y)<2$. Letting $p^{\prime }(z, y) = \frac{p(z, y)}{(p(z, y)-1)}$, we have

$$\begin{aligned} \Vert \mathrm{u} \Vert _{W_{0}^{s, p(z, y)}(\mathcal{M})}^{p^{\prime }(z, y)}= \biggl[ \int _{\mathcal{M} \times \mathcal{M}} \biggl( \biggl( \frac{ \vert \mathrm{u}(z)-\mathrm{u}(y) \vert }{ (d_{\mathrm{g}}(z, y) )^{\frac{n}{p(z, y)}+s}} \biggr)^{p^{\prime }(z, y)} \biggr)^{p(z, y)-1} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \biggr]^{\frac{1}{p(z, y)-1}}. \end{aligned}$$

As a result of the Minkowski inequality (see Theorem 2.13 in [15]) and inequality (27) in [2], we obtain that

$$\begin{aligned} \begin{aligned}& \biggl\Vert \frac{\mathrm{u}+v}{2} \biggr\Vert _{W_{0}^{s, p(z, y)}( \mathcal{M})}^{p^{\prime }(z, y)}+ \biggl\Vert \frac{\mathrm{u}-v}{2} \biggr\Vert _{W_{0}^{s, p(z, y)}(\mathcal{M})}^{p^{\prime }(z, y)}\\ &\quad \leq \biggl\{ \int _{ \mathcal{M} \times \mathcal{M} } \biggl[ \biggl( \biggl\vert \frac{(\mathrm{u}(z)-u(y))+(v(z)-v(y))}{2 (d_{\mathrm{g}}(z, y) )^{\frac{n}{p(z, y)}+s}} \biggr\vert \biggr)^{p^{\prime }(z, y)} \\ & \qquad{}+ \biggl( \biggl\vert \frac{(\mathrm{u}(z)-\mathrm{u}(y))-(v(z)-v(y))}{2 (d_{\mathrm{g}}(z, y) )^{\frac{n}{p(z, y)}+s}} \biggr\vert \biggr)^{p^{\prime }(z, y)} \biggr]^{p(z, y)-1} \,dv_{ \mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \biggr\} ^{\frac{1}{p(z, y)-1}} \\ &\quad\leq \biggl(\frac{1}{2} \Vert \mathrm{u} \Vert _{W_{0}^{s, p(z, y)}(\mathcal{M})}^{p(z, y)}+ \frac{1}{2} \Vert v \Vert _{W_{0}^{s, p(z, y)}(\mathcal{M}))}^{p(z, y)} \biggr)^{p^{\prime }(z, y)-1}=1. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \biggl\Vert \frac{\mathrm{u}+v}{2} \biggr\Vert _{W_{0}^{s, p(z, y)}(M)}^{p^{ \prime } (z, y)} \leq 1- \frac{\varepsilon ^{p^{\prime } (z, y)}}{2^{p^{\prime } (z, y)}}. \end{aligned}$$

Taking $\delta =\delta (\varepsilon )$ such that $1-(\varepsilon / 2)^{p^{\prime }(z, y)}=(1-\delta )^{p^{\prime }(z, y)}$, from the Milman–Pettis theorem we obtain that $W_{0}^{s, p(z, y)}(\mathcal{M})$ is reflexive.

Now, we show that $W_{0}^{s, p(z, y)}(\mathcal{M})$ is a separable space. Define the operator

$$\begin{aligned} &T: W^{s, p(z, y)}(\mathcal{M}) \rightarrow L^{\hat{p}(z)}( \mathcal{M}) \times L^{p(z, y)}(\mathcal{M} \times \mathcal{M}), \\ & \mathrm{u} \mapsto T(\mathrm{u})= \biggl(\mathrm{u}(z), \frac{\mathrm{u}(z)-\mathrm{u}(y)}{d_{g}(z, y)^{\frac{n}{p(z, y)}+s}} \biggr). \end{aligned}$$

Then

• T is well defined.

• T is an isometry.

Indeed, for $\mathrm{u} \in W_{0}^{s, p(z, y)}(\mathcal{M})$, we obtain

$$\begin{aligned} \bigl\Vert T(\mathrm{u}) \bigr\Vert _{L^{\hat{p}(z)}(\mathcal{M}) \times L^{p(z, y)}(\mathcal{M} \times \mathcal{M})}&= \Vert \mathrm{u} \Vert _{L^{ \hat{p}(z)}(\mathcal{M})}+ \biggl\Vert \frac{\mathrm{u}(z)-\mathrm{u}(y)}{d_{\mathrm{g}}(z, y)^{\frac{n}{p(z, y)}+s}} \biggr\Vert _{L^{p(z, y)}(\mathcal{M}\times \mathcal{M})}\\ &= \Vert \mathrm{u} \Vert _{W_{0}^{s, p(z, y)}(\mathcal{M})}. \end{aligned}$$

So, $T(W_{0}^{s, p(z, y)}(\mathcal{M}))$ is a closed subspace of $L^{\hat{p}(z)}(\mathcal{M}) \times L^{p(z, y)}(\mathcal{M} \times \mathcal{M})$. Thanks to Proposition 3.17 in [15], we get that $T(W_{0}^{s, p(z, y)}(\mathcal{M}))$ is separable, therefore $W_{0}^{s, p(z, y)}(\mathcal{M})$ is also separable. □

Lemma 3.4

Suppose that $( \mathcal{M}, \mathrm{g} )$ satisfies property $B_{vol} ( \lambda, v )$ with finite volume, and (2) holds. Then $C_{0}^{\infty } ( \mathcal{M} )$ is dense in $W^{s, p( z, y )} ( \mathcal{M} )$.

Proof

Consider the following real-valued function:

$$\begin{aligned} f( t ) = \textstyle\begin{cases} 1 & \text{if $ t \leq 0$}, \\ 1 - t & \text{if $ 0 \leq t \leq 1 $}, \\ 0 & \text{if $ t \geq 1 $}. \end{cases}\displaystyle \end{aligned}$$

Let $\varphi \in C^{\infty } ( \mathcal{M} )\cap W^{s,p(z, y)}( \mathcal{M})$, and let y be a fixed point of $\mathcal{M}$ such that $\varphi _{\nu }(\alpha )=\varphi (\alpha )f(d_{\mathrm{g}}(y,\alpha )))$, where $d_{\mathrm{g}}$ is the Riemannian distance associated to g and $\nu \in \mathbb{N}$. We can easily see that $\varphi _{\nu }(\alpha )\in W^{s,p(z, y)}(\mathcal{M})$ for $\nu \in \mathbb{N}$. Then, since $\mathcal{M}$ is a compact Riemannian n-manifolds, it can be covered by a finite number of charts $(\mathcal{Q}_{k},\phi _{k})_{k=1,\ldots,m}$. Let $\eta _{k}$ be a smooth partition of unity subordinate to the covering $\mathcal{Q}_{k}$. We can see that $h=\eta _{k}\varphi _{\nu }\circ \phi _{k}^{-1}\in W^{s,p(z, y)}( \phi _{k}(\mathcal{Q}_{k}))$.

So, by Lemma 3.2 in [7], we can extract a subsequence $h_{t}\in C^{\infty } ( \mathbb{R^{n}} )$ such that $h_{t} \rightarrow h$ strongly in $W^{s,p(z, y)}(\phi _{k}(\mathcal{Q}_{k}))$ as $t \rightarrow \infty$. Thus, $h_{t}\circ \phi _{k}\in C^{\infty }(\mathcal{M})$ and $h_{t}\circ \phi _{k}$ converge strongly to $\eta _{k}\varphi _{\nu }$ in $W^{s,p(z, y)}(\mathcal{M})$ as $t \rightarrow \infty$. □

Remark 3.2

We can also prove the previous lemma, without assuming condition (2), by using the following method:

For $\mathrm{u} \in C_{0}^{\infty } ( \mathcal{M} )$, we need to prove that

$$\begin{aligned} \int _{\mathcal{M} \times \mathcal{M} } \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) < \infty. \end{aligned}$$

Notice that $\forall ( z, y ) \in \mathcal{M} \times \mathcal{M}$, we have

$$\begin{aligned} \bigl\vert \mathrm{u}( z ) - \mathrm{u}( y ) \bigr\vert \leq \Vert D \mathrm{u} \Vert _{L^{ \infty } ( \mathcal{M} )} \,d_{\mathrm{g}} ( z, y ), \qquad\bigl\vert \mathrm{u}( z ) - \mathrm{u}( y ) \bigr\vert \leq 2 \Vert \mathrm{u} \Vert _{L^{ \infty } ( \mathcal{M} )}. \end{aligned}$$

Thus,

$$\begin{aligned} \bigl\vert \mathrm{u}( z ) - \mathrm{u}( y ) \bigr\vert ^{p( z, y )} \leq \Vert D \mathrm{u} \Vert _{L^{\infty } ( \mathcal{M} )}^{p( z, y )} \bigl(d_{ \mathrm{g}} ( z, y ) \bigr)^{p( z, y )}, \quad\text{for all } ( z, y ) \in \mathcal{M} \times \mathcal{M}, \end{aligned}$$

and

$$\begin{aligned} \bigl\vert \mathrm{u}( z ) - \mathrm{u}( y ) \bigr\vert ^{p( z, y )} \leq 2^{p( z, y )} \Vert \mathrm{u} \Vert _{L^{\infty } ( \mathcal{M} )}^{p( z, y )}, \quad \text{for all } ( z, y ) \in \mathcal{M} \times \mathcal{M}. \end{aligned}$$

Hence,

$$\begin{aligned} &\bigl\vert \mathrm{u}( z ) - \mathrm{u}( y ) \bigr\vert ^{p( z, y )} \leq \bigl( \Vert D \mathrm{u} \Vert _{L^{\infty } ( \mathcal{M} )}^{p^{+}} + \Vert D \mathrm{u} \Vert _{L^{ \infty } ( \mathcal{M} )}^{p^{-}} \bigr) \bigl( d_{\mathrm{g}} ( z, y )\bigr)^{p( z, y )},\\ &\quad \text{for all } ( z, y ) \in \mathcal{M} \times \mathcal{M}, \end{aligned}$$

and

$$\begin{aligned} \bigl\vert \mathrm{u}( z ) - \mathrm{u}( y ) \bigr\vert ^{p( z, y )} \leq 2^{p^{+}} \bigl( \Vert \mathrm{u} \Vert _{L^{\infty } ( \mathcal{M} )}^{p^{+}} + \Vert \mathrm{u} \Vert _{L^{\infty } ( \mathcal{M} )}^{p^{-}} \bigr), \quad \text{for all } ( z, y ) \in \mathcal{M} \times \mathcal{M}. \end{aligned}$$

Hence

$$\begin{aligned} \bigl\vert \mathrm{u}( z ) - \mathrm{u}( y ) \bigr\vert ^{p( z, y )} \leq 2^{p^{+} - 1} \bigl( \Vert \mathrm{u} \Vert _{C^{1} ( \mathcal{M} )}^{p^{+}} + \Vert \mathrm{u} \Vert _{C^{1} ( \mathcal{M} )}^{p^{-}} \bigr) \min \bigl\{ 1, \bigl(d_{ \mathrm{g}} ( z, y )\bigr)^{p( z, y )} \bigr\} . \end{aligned}$$

Therefore, according to [30], we obtain

$$\begin{aligned} &\int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert ( \eta _{s} \mathrm{u} ) ( z ) - ( \eta _{s} \mathrm{u}) ( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) \\ &\quad\leq \mathrm{vol}( \mathcal{M}) 2^{p^{+} -1} \bigl( \Vert \mathrm{u} \Vert _{C^{1} ( \mathcal{M} )}^{p^{+}} + \Vert \mathrm{u} \Vert _{C^{1} ( \mathcal{M} )}^{p^{-}} \bigr) \\ &\qquad{} \times \int _{\mathcal{M} \times \mathcal{M}} \frac{ \min \{1, (d_{\mathrm{g}} ( z, y ))^{p( z, y )}\}}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) < \infty, \end{aligned}$$

where $( \eta _{s} )$ is a smooth partition of unity subordinate of the covering $B_{z_{k}} ( r )$ for any k, and $B_{z_{k}} ( r )$ denotes the Euclidean ball of $\mathbb{R}^{n}$ with center $z_{k}$ and radius r. Then we deduce that, for $\mathrm{u} \in C_{0}^{\infty } ( \mathcal{M} )$,

$$\begin{aligned} \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) < \infty. \end{aligned}$$

Thus $\mathrm{u} \in W^{s, p( z, y )} ( \mathcal{M} )$.

Now, we will extend an embedding result between $W^{1, p( z, y )} ( \mathcal{M} )$ and $W^{s, p( z, y )} ( \mathcal{M} )$ to manifolds.

Lemma 3.5

Suppose that the smooth complete compact Riemannian n-manifold $( \mathcal{M}, \mathrm{g} )$ has property $B_{vol} ( \lambda, v )$ for some $( \lambda, v ), p \in C( \mathcal{M} \times \mathcal{M}, ( 1, + \infty ))$, and $s \in (0, 1 )$. Then $\Vert \mathrm{u} \Vert _{W^{s, p( z, y )} ( \mathcal{M} )} \leq C \Vert \mathrm{u} \Vert _{W^{1, p( z, y )} ( \mathcal{M} )}$, where $C = C( n, s, \lambda, v, p^{+}, p^{-})$. In particular, $W^{1, p( z, y )} ( \mathcal{M} ) \sqsubseteq W^{s, p( z, y )} ( \mathcal{M} )$.

Proof

For the sake of convenience, let $[u]_{W^{1, p(z, y)} (\mathcal{M} )} = 1$ and set

$$\begin{aligned} C = \sup_{(z, y) \in \mathcal{M} \times \mathcal{M}} \bigl( d_{g} (z, y) \bigr)^{( 1- s ) p(z, y)}. \end{aligned}$$

Then

$$\begin{aligned} &\int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u} (z) - \mathrm{u} (y) \vert ^{p(z, y)}}{C(d_{g} (z, y))^{n + sp(z, y)}} \,dv_{g} (z) \,dv_{g} (y) \\ &\quad= \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u} (z) - \mathrm{u} (y) \vert ^{p(z, y)}}{(d_{g} ( z, y))^{n + p(z, y)}} \frac{(d_{g} ( z, y))^{(1 - s) p(z, y)}}{C} \,dv_{g} (z) \,dv_{g} (y) \\ &\quad \leq \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u} (z) - \mathrm{u} (y) \vert ^{p(z, y)}}{(d_{g} ( z, y))^{n + p(z, y)}} \,dv_{g} (z) \,dv_{g} (y) \\ & \quad\leq 1. \end{aligned}$$

Thus, $[u]_{W^{s, p(z, y)} (\mathcal{M})} \leq C [u]_{W^{1, p(z, y)} (\mathcal{M})}$.

Hence,

$$\begin{aligned} \Vert u \Vert _{W^{s, p(z, y)} (\mathcal{M})} \leq C \Vert u \Vert _{W^{1, p(z, y)} (\mathcal{M})}. \end{aligned}$$

 □

Remark 3.3

We can also prove the previous lemma using the same technique as that of [29, Lemma 2.6].

Theorem 3.1

Let $\mathcal{M}$ be a compact Riemannian manifold, $p\in C( \mathcal{M} \times \mathcal{M}, ( 1; \infty )), s \in ( 0, 1 )$ with $sp( z, y ) < n$ and $q \in C( \mathcal{M}, ( 1; \infty ))$. Assume that

$$\begin{aligned} 1 < q^{-} = \min_{z \in \mathcal{M}} q( z ) \leq q( z ) < \frac{n \hat{p}( z )}{n - s \hat{p}( z )} \quad \textit{for all } z \in \overline{\mathcal{M}}, \end{aligned}$$

then $W^{s, p( z, y )} ( \mathcal{M} ) \hookrightarrow L^{q( z )} ( \mathcal{M} )$ is a continuous and compact embedding.

Proof

The demonstration of this theorem is based on an idea introduced in [1, 21, 28, 29]. Let $\varphi: V \subset \mathcal{M} \rightarrow \mathbb{R}^{n}$ be an arbitrary local chart on $\mathcal{M}$, and $G \subset \mathcal{M}$ an open set with compact closure and contained in V. Take $\{ G_{l} \}_{l = 1, \dots, k}$ to be a finite subcovering of $\mathcal{M}$ such that $G_{l}$ is homeomorphic to the open unit ball $B_{0} ( 1 )$ of $\mathbb{R}^{n}$ and, for any l, the components $\mathrm{g}_{ij}^{l}$ of g in $( \mathrm{g}_{l}, V_{l} )$ satisfy

$$\begin{aligned} \frac{1}{\alpha \delta _{ij}} < \mathrm{g}_{ij}^{l} < \alpha \delta _{ij} \end{aligned}$$

as bilinear forms, for some constant $\alpha > 1$. Let $\{ \pi _{l} \}_{l = 1, \dots, k}$ be a smooth partition of unity subordinate to the finite covering $\{G_{l} \}_{l = 1, \dots, k}$. It is clear that if $\mathrm{u} \in W^{s, p( z, y )} ( \mathcal{M} )$, then $\pi _{l} \mathrm{u} \in W^{s, p( z, y )} ( G_{l} )$ and $( \varphi _{l}^{-1} )*(\pi _{l} \mathrm{u} ) \in W^{s, p( \varphi _{l}^{-1} ( z, y ))} ( B_{0} ( 1 ) )$ with $\mathrm{u} = \sum_{l = 1}^{k} \pi _{l} \mathrm{u}$. According to Lemma 3.5, the Sobolev embedding theorem [1, 21, 29], we get the continuous and compact embedding

$$\begin{aligned} W^{s, p( z, z )} ( G_{l} ) \hookrightarrow L^{q( z )} ( G_{l} ) \quad \text{for any } l = 1, \dots, k. \end{aligned}$$

Thus, we can conclude that $W^{s, p( z, y )} ( \mathcal{M} ) \subset L^{q( z )} ( \mathcal{M} )$, and the embedding is continuous and compact. □

4 Application

In this part, as an application, we give an existence result to the following problem:

$$\begin{aligned} ( \mathcal{P} )\quad \textstyle\begin{cases} ( - \Delta _{g} )_{p( z, \cdot )}^{s} \mathrm{u}( z ) + \mathcal{V}( z ) \vert \mathrm{u} ( z ) \vert ^{q( z ) - 2} \mathrm{u} = h( z, \mathrm{u}( z )) & \text{in $ \mathcal{Q}$}, \\ \mathrm{u} |_{\partial \mathcal{Q}}= 0, \end{cases}\displaystyle \end{aligned}$$

where $s \in (0, 1 ), p \in C( \mathcal{M} \times \mathcal{M}, ( 1; \infty ) )$ with $sp( z, y ) < n, q: \overline{\mathcal{Q}} \rightarrow (1, \infty )$ satisfy the following condition:

$$\begin{aligned} 1< q^{-} \leq q^{+} < p^{-} \leq p^{+} < \frac{n \hat{p}( z )}{n - s \hat{p}( z )}, \end{aligned}$$

(4)

$( \mathcal{M}, \mathrm{g} )$ is a smooth complete compact Riemannian n-manifold, $\mathcal{Q} \subset \mathcal{M}$ is an open bounded set with smooth boundary $\partial \mathcal{Q}, h: \mathcal{Q} \times \mathbb{R} \rightarrow \mathbb{R}$ is a Carathéodory function satisfying the following assumptions:

$(h_{1})$:

(AR-condition) There exist $\beta > p^{+}$ and some $I > 0$ such that, for each $|\alpha | > I$, we have

$$\begin{aligned} 0 < \int _{\mathcal{M}} H( z, \alpha ) \,dv_{\mathrm{g}} ( z ) \leq \int _{\mathcal{M}} h( z, \alpha ) \frac{\alpha }{\beta } \,dv_{ \mathrm{g}} ( z ) \quad\text{a.e. } z \in \mathcal{M}, \end{aligned}$$

where $H( z, \alpha ) = \int _{0}^{\alpha } h( z, \upsilon ) \,d \upsilon$ is the primitive of $h( z, \alpha )$,

$(h_{2} )$:

$h( z, 0 ) = 0$,

$(h_{3} )$:

$\lim_{|\alpha | \rightarrow 0} \frac{h( z, \alpha )}{|\alpha |^{q( z ) - 1}} = 0$ uniformly a.e. $z \in \mathcal{M}$,

and $( - \Delta _{\mathrm{g}} )_{p( z, \cdot )}^{s} \mathrm{u} ( z )$ is the fractional $p( z, \cdot )$-Laplace operator which (up to normalization factors) may be defined as

$$\begin{aligned} ( - \Delta _{\mathrm{g}} )_{p( z, \cdot )}^{s} \mathrm{u}( z ) = 2 \lim_{\epsilon \rightarrow o^{+}} \int _{M \backslash B_{\epsilon } ( z )} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y ) - 2} ( \mathrm{u}( z ) - \mathrm{u}( y ) )}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( y ), \end{aligned}$$

for $z \in \mathcal{M}$, where $B_{\epsilon } ( z )$ denotes the geodesic ball of $\mathcal{M}$ with center z and radius ϵ and $d_{\mathrm{g}} ( z, y )$ defines a distance on $\mathcal{M}$ whose topology coincides with the original one. The vanishing potential satisfies the following assumptions:

• (i) $\mathcal{V}: \mathcal{M} \rightarrow \mathbb{R}$ is a continuous function, and there exist $\theta >0, \gamma > 0$ such that $\mathcal{V}( z ) > \theta > 0$ for all $z \in \mathcal{M}$, and

  $$\begin{aligned} \int _{\mathcal{M}} \mathcal{V}( z ) \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z )} \,dv_{\mathrm{g}} ( z ) \leq \gamma \Vert \mathrm{u} \Vert _{W^{s, p( z, y )} ( \mathcal{M} )}^{q( z )}, \end{aligned}$$

  for all $\mathrm{u} \in W^{s, p( z, y )}_{0} ( \mathcal{M} )$.

• (ii) $\mathcal{V}( z ) \rightarrow + \infty$ as $| z | \rightarrow + \infty$.

Definition 4.1

A measurable function $\mathrm{u} \in W^{s, p( z, y )}_{0} ( \mathcal{M} )$ is said to be a weak solution of $( \mathcal{P} )$ if

$$\begin{aligned} & \int _{M \times M} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y ) - 2} ( \mathrm{u}( z ) - \mathrm{u}( y ) ) ( \varphi ( z ) - \varphi ( y ) )}{( d_{g} ( z, y ))^{n + sp( z )}} \,dv_{g} ( z ) \,dv_{g} ( y )\\ &\qquad{} + \int _{M} \mathcal{V}( z ) \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z ) - 2} u( x ) \varphi ( z ) \,dv_{g} ( z ) \\ &\quad = \int _{M} h\bigl( z, \mathrm{u}( z ) \bigr) \varphi ( z ) \,dv_{g} ( z ), \quad\text{for all } \varphi \in W^{s, p( z, y )}_{0} ( \mathcal{M} ). \end{aligned}$$

Theorem 4.1

Under assumptions $(h_{1} )$–$( h_{3} )$, (4) and (i)–(ii), if $( M, g )$ satisfies the property $B_{vol} ( \lambda, v )$, then problem $( \mathcal{P} )$ possesses at least one weak solution.

Proof

Consider the functional $E: W^{s, p( z, y )}_{0} ( \mathcal{M} ) \rightarrow \mathbb{R}$ defined by

$$\begin{aligned} E( \mathrm{u} ) = A( \mathrm{u} ) - B( \mathrm{u} ), \end{aligned}$$

where

$$\begin{aligned} A( \mathrm{u} ) = \int _{\mathcal{M} \times \mathcal{M}} \frac{1}{p( z, y )} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) + \int _{ \mathcal{M}} \frac{\mathcal{V}( z )}{q( z )} \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z )} \,dv_{\mathrm{g}} ( z ) \end{aligned}$$

and

$$\begin{aligned} B( \mathrm{u} ) = \int _{\mathcal{M}} H\bigl( z, \mathrm{u}( z ) \bigr) \,dv_{ \mathrm{g}} ( z ). \end{aligned}$$

 □

Lemma 4.1

Assume that the assumptions (i)–(iii) hold. Then $A \in C^{1} ( W^{s, p( z, y )}_{0} ( \mathcal{M} ) )$ and

$$\begin{aligned} \bigl\langle A'( \mathrm{u} ), \varphi \bigr\rangle ={}& \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y ) - 2} ( \mathrm{u}( z ) - \mathrm{u}( y ) ) ( \varphi ( z ) - \varphi ( y ) )}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) \\ &{} + \int _{\mathcal{M}} \mathcal{V}( z ) \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z ) - 2} \mathrm{u}( z ) \varphi ( z ) \,dv_{\mathrm{g}} ( z ), \end{aligned}$$

(5)

for all $\mathrm{u}, \varphi \in W^{s, p( z, y )}_{0} ( \mathcal{M} )$.

Proof

For $\mathrm{u} \in W^{s, p( z, y )}_{0} ( \mathcal{M} )$, we have

$$\begin{aligned} A( \mathrm{u} ) ={}& \int _{\mathcal{M} \times \mathcal{M}} \frac{1}{p( z, y )}. \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) + \int _{ \mathcal{M}} \frac{\mathcal{V}( z )}{q( z )} \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z )} \,dv_{\mathrm{g}} ( z ) \\ \leq{}& \frac{1}{p^{-}} \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) + \frac{1}{q^{-}} \int _{\mathcal{M}} \mathcal{V}( z ) \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z )} \,dv_{\mathrm{g}} ( z ) \\ \leq{}& \frac{1}{p^{-}} \bigl( \Vert \mathrm{u} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}^{p^{+}} + \Vert \mathrm{u} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}^{p^{-}} \bigr) + \frac{\gamma }{q^{+}} \bigl( \Vert \mathrm{u} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}^{q^{+}} + \Vert \mathrm{u} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}^{q^{-}} \bigr) \\ &\bigl(\text{using Lemma 3.1 and (i)}\bigr) \\ < {}&+ \infty. \end{aligned}$$

Hence, A is well defined.

To prove that $A \in C^{1} ( W^{s, p( z, y )}_{0} ( \mathcal{M} ) )$, we consider $\{ \mathrm{u}_{t} \} \subset W^{s, p( z, y )}_{0} ( \mathcal{M} )$ such that $\mathrm{u}_{t} \rightarrow \mathrm{u}$ strongly in $W^{s, p( z, y )}_{0} ( \mathcal{M} )$ as $t \rightarrow + \infty$. Then, we have

$$\begin{aligned} \lim_{t \rightarrow + \infty } \int _{\mathcal{M} \times \mathcal{M}} \biggl[ \frac{ \vert \mathrm{u}_{t} ( z ) - \mathrm{u}_{t} ( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y )^{n + sp( z, y )}} - \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y )^{n + sp( z, y )}} \biggr] \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) = 0. \end{aligned}$$

(6)

Without losing generality, we further assume that $\mathrm{u}_{t} \longrightarrow \mathrm{u} \text{ a.e. in } \mathcal{M} \text{ as } t \rightarrow + \infty$. Using (6), we get that

$$\begin{aligned} \biggl\{ \frac{ \vert \mathrm{u}_{t} ( z ) - \mathrm{u}_{t} ( y ) \vert ^{p( z, y )} ( \mathrm{u}_{t} ( z ) - \mathrm{u}_{t} ( y ) )}{( d_{\mathrm{g}} ( z, y ) )^{n + sp( z, y )}} \biggr\} _{t} \end{aligned}$$

is bounded in $L^{p( z, y )} ( \mathcal{M} \times \mathcal{M} )$ and, according to Brezis–Lieb lemma in [23], we obtain

$$\begin{aligned} \lim_{t \rightarrow + \infty } \int _{\mathcal{M} \times \mathcal{M} } \biggl( \frac{ \vert \mathrm{u}_{t} ( z ) - \mathrm{u}_{t} ( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} - \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} \biggr) \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) = 0. \end{aligned}$$

Similarly,

$$\begin{aligned} \lim_{t \rightarrow + \infty } \int _{\mathcal{M} } \mathcal{V}( z ) \bigl\vert \bigl\vert \mathrm{u}_{t} ( z ) \bigr\vert ^{q( z ) - 2} \mathrm{u}_{t} ( z ) - \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z ) - 2} \mathrm{u}( z ) \bigr\vert ^{q( z )} \,dv_{\mathrm{g}} ( z ) = 0. \end{aligned}$$

Hölder’s inequality now gives

$$\begin{aligned} &\bigl\Vert A'( \mathrm{u}_{t} ) - A'( \mathrm{u} ) \bigr\Vert _{( W^{s, p( z, y )}_{0} ( \mathcal{M} ) )'} \\ &\quad= \sup_{\varphi \in W^{s, p( z, y )}_{0} ( \mathcal{M} ); \Vert \varphi \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )} = 1} \bigl\vert \bigl\langle A'( \mathrm{u}_{t} ) - A'( \mathrm{u} ), \varphi \bigr\rangle \bigr\vert \rightarrow 0 \quad\text{as } t \rightarrow + \infty. \end{aligned}$$

Hence, $A \in C^{1} ( W^{s, p( z, y )}_{0} ( \mathcal{M} ) )$. Finally, we can easily verify that the functional A is Gâteaux differentiable on $W^{s, p( z, y )}_{0} ( \mathcal{M} )$ and (5) holds for all $\mathrm{u}, \varphi \in W^{s, p( z, y )}_{0} ( \mathcal{M} )$. □

Lemma 4.2

The functional E satisfies the mountain pass geometry in the sense that

• (i) $E( 0 ) = 0$.

• (ii) There exist $\zeta, \mu > 0$ such that $E( \mathrm{u} ) \geq \mu$ if $\Vert \mathrm{u} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )} > \zeta$.

• (iii) There exists u, with $\Vert \mathrm{u}\Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )} > \zeta$, such that $E( \mathrm{u} ) \leq 0$.

Proof

• (i) $E( 0 ) = 0$ is obvious.

• (ii) According to $(h_{1}), (i)$, Proposition 2.4, Lemma 3.1, and Theorem 3.1, we have

  $$\begin{aligned} E( \mathrm{u} ) ={}& \int _{\mathcal{M} \times \mathcal{M}} \frac{1}{p( z, y )} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ) \\ &{}+ \int _{ \mathcal{M}} \frac{\mathcal{V}( z )}{q( z )} \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z )} \,dv_{\mathrm{g}} ( z ) - \int _{\mathcal{M}} H\bigl( z, \mathrm{u}( z )\bigr) \,dv_{\mathrm{g}} ( z ) \\ \geq{}& \frac{1}{p^{+}} \varrho _{p( \cdot, \cdot )} ( \mathrm{u} ) + \frac{\theta }{q^{+}} \Vert \mathrm{u} \Vert _{L^{q( z )} ( \mathcal{M} )}^{q^{+}} - \frac{1}{\beta } \Vert \mathrm{u} \Vert ^{q^{-}}_{W^{s, p( z, y )}_{0} ( \mathcal{M} )}\\ \geq{}& \frac{1}{p^{+}} \Vert \mathrm{u} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}^{p^{+}} + \frac{\theta C^{q^{+}}}{q^{+}} \Vert \mathrm{u} \Vert ^{q^{+}}_{W^{s, p( z, y )}_{0} ( \mathcal{M} )} - \frac{1}{p^{+}} \Vert \mathrm{u} \Vert ^{q^{-}}_{W^{s, p( z, y )}_{0} ( \mathcal{M} )}. \end{aligned}$$

  Since $p^{+} > q^{+} \geq q^{-}$, we deduce that $E( \mathrm{u} ) > 0$.

• (iii) According to Lemma 3.1, $(h_{1}), (h_{3})$, and (i), we have for $t > 0$ and $\mathrm{u} \neq 0$,

  $$\begin{aligned} E( t \mathrm{u} ) ={}& \int _{\mathcal{M} \times \mathcal{M}} \frac{t^{p( z, y )}}{p( z, y )} \frac{ \vert \mathrm{u}( z ) - \mathrm{u}( y ) \vert ^{p( z, y )}}{( d_{\mathrm{g}} ( z, y ))^{n + sp( z, y )}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y )\\ &{} + \int _{ \mathcal{M}} \frac{\mathcal{V}( z )}{q( z )} t^{q( z )} \bigl\vert \mathrm{u}( z ) \bigr\vert ^{q( z )} \,dv_{\mathrm{g}} ( z ) - \int _{\mathcal{M}} H\bigl( z, t \mathrm{u}( z ) \bigr) \,dv_{\mathrm{g}} ( z ) \\ \leq{}& \frac{t^{p^{+}}}{p^{-}} \varrho _{p( \cdot, \cdot )} ( \mathrm{u} ) + \frac{\gamma t^{q^{-}}}{q^{-}} \Vert \mathrm{u} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}^{q^{-}} \\ \leq{}& \frac{t^{p^{+}}}{p^{-}} \Vert \mathrm{u} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}^{p^{-}} + \frac{\gamma t^{q^{-}}}{q^{-}} \Vert \mathrm{u} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}^{q^{-}}. \end{aligned}$$

  Since $q^{-} < p^{-}$, for t small enough, we infer that $E (t \mathrm{u} ) < 0$.

This completes the demonstration of the lemma. □

Lemma 4.3

Let $(\mathcal{M}, \mathrm{g})$ be a smooth complete compact Riemannian n-manifold and $p( \cdot ) \in C_{+}(\mathcal{M} \times \mathcal{M} )$. Assume that assumptions $(h_{1})$–$(h_{3} )$ and (i)–(ii) hold. Then the functional E satisfies the Palais–Smale condition.

Proof

Let $(\mathrm{u}_{m})_{m \in \mathbb{N}}\subset W^{s, p( z, y )}_{0} ( \mathcal{M} )$ be such that $J(\mathrm{u}_{m})$ is bounded and $J'(\mathrm{u}_{m}) \rightarrow 0$ as $m\rightarrow \infty$. Then there exists $C>0$ such that $dJ(\mathrm{u}_{m}, \mathrm{u}_{m}) \leq C\Vert \mathrm{u}_{m}\Vert _{W^{s, p( z, y )}_{0}}$ and $|J(\mathrm{u}_{m})|< C$. We prove that $(\mathrm{u}_{m})_{m\in \mathbb{N}}$ is bounded in $W^{s, p( z, y )}_{0}(\mathcal{M})$.

We prove the statement by the method of contradiction. Indeed, if the assertion were not true, up to a subsequence, $\Vert \mathrm{u}_{m}\Vert _{W^{s, p( z, y )}_{0}(\mathcal{M})} \rightarrow \infty$ as $m \rightarrow \infty$. From $(h_{1})$, we have

$$\begin{aligned} C+C \Vert \mathrm{u}_{m} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}\geq E( \mathrm{u}_{m})-\frac{1}{\beta } \bigl\langle E'( \mathrm{u}_{m} ), \mathrm{u}_{m} \bigr\rangle \geq \biggl( \frac{1}{p^{+}}-\frac{1}{\beta } \biggr) \Vert \mathrm{u}_{m} \Vert _{W^{s, p( z, y )}_{0} ( \mathcal{M} )}^{p^{+}}. \end{aligned}$$

This is a contradiction as $\Vert \mathrm{u}_{m}\Vert _{W^{s, p( z, y )}_{0}(\mathcal{M})} \rightarrow \infty$. Since $W^{s, p( z, y )}_{0}(\mathcal{M})$ is a reflexive Banach space, there exists $\mathrm{u} \in W^{s, p( z, y )}_{0}(\mathcal{M})$ such that, up to a subsequence,

$$\begin{aligned} &\mathrm{u}_{m} \rightharpoonup \mathrm{u} \quad\text{weakly in } W^{s, p(z, y)}_{0}(\mathcal{M}), \\ &\mathrm{u}_{m} \longrightarrow \mathrm{u} \quad\text{a.e. in } \mathcal{M},\\ &\mathrm{u}_{m} \rightarrow \mathrm{u} \quad\text{strongly in } L^{ \gamma (z)} (\mathcal{M} ) \text{ for }1 \leq \gamma (z) < p_{s}^{*}(z). \end{aligned}$$

Since $\mathrm{u}_{m}\longrightarrow \mathrm{u}$ a.e. in $\mathcal{M}$, we have that

$$\begin{aligned} \frac{ \vert \mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) \vert ^{p( z, y )-2} (\mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) )}{( d_{\mathrm{g}} ( z, y ))^{ (\frac{n}{p( z, y )}+s )(p( z, y )-1)}} \rightarrow \frac{ \vert \mathrm{u}(z)-\mathrm{u}(y) \vert ^{p( z, y )-2}(\mathrm{u}(z)-\mathrm{u}(y))}{(d_{\mathrm{g}}(z,y))^{ (\frac{n}{p( z, y )}+s )(p( z, y )-1)}} \end{aligned}$$

a.e. $(z, y) \in \mathcal{M} \times \mathcal{M}$. On the other hand, $\Vert \mathrm{u}_{m} \Vert _{W_{0}^{s, p( z, y )} ( \mathcal{M} )}$ is uniformly bounded and this implies that there exists a constant $C>0$ such that

$$\begin{aligned} \int _{\mathcal{M} \times \mathcal{M}} \biggl( \frac{ \vert \mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) \vert }{d_{\mathrm{g}}(z,y)^{\frac{n}{p(z, y)}+s}} \biggr)^{p(z, y)} \,d v_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \leq C \quad\text{for all } m \geq 1, \end{aligned}$$

that is,

$$\begin{aligned} \int _{\mathcal{M}\times \mathcal{M}} \biggl\vert \frac{ \vert \mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) \vert ^{p(z, y)-2} (\mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) )}{d_{\mathrm{g}}(z,y)^{ (\frac{n}{p(z, y)}+s )(p(z, y)-1)}} \biggr\vert ^{\frac{p(z, y)}{p(z, y)-1}} \,d v_{\mathrm{g}}(z) \,d v_{ \mathrm{g}}(y) \leq C. \end{aligned}$$

Therefore,

$$\begin{aligned} \frac{ \vert \mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) \vert ^{p(z, y)-2} (\mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) )}{d_{\mathrm{g}} (z,y)^{ (\frac{n}{p(z, y)}+s )(p(z, y)-1)}} \rightharpoonup \frac{ \vert \mathrm{u}(z)-\mathrm{u}(y) \vert ^{p(z, y)-2}(\mathrm{u}(z)-\mathrm{u}(y))}{d_{\mathrm{g}}(z,y)^{ (\frac{n}{p(z, y)}+s )(p(z, y)-1)}} \end{aligned}$$

weakly in $L^{p^{\prime }(z, y)} (\mathcal{M} \times \mathcal{M} )$ with $p^{\prime }(z, y)=\frac{p(z, y)}{p(z, y)-1}$. If $v \in W^{s, p(z, y)}_{0}(\mathcal{M})$, it follows that $\frac{v(z)-v(y)}{d_{\mathrm{g}}(z,y)^{\frac{n}{p( z, y )}+s}} \in L^{p( z, y )} (\mathcal{M} \times \mathcal{M} )$. As a result,

$$\begin{aligned} & \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) \vert ^{p(z, y)-2} (\mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) )(v(z)-v(y))}{d_{\mathrm{g}}(z,y)^{ (\frac{n}{p(z, y)}+s )(p(z, y)-1)} \,d_{\mathrm{g}}(z,y)^{\frac{n}{p(z, y)}+s}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \\ &\quad \rightarrow \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}(z)-\mathrm{u}(y) \vert ^{p(z, y)-2}(\mathrm{u}(z)-\mathrm{u}(y))(v(z)-v(y))}{d_{\mathrm{g}}(z,y)^{n+s p(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y). \end{aligned}$$

By Vitali’s theorem, we have $E'(\mathrm{u})=0$. We define the sequence $w_{n}=\mathrm{u}_{m} - \mathrm{u}$. Since $(\mathrm{u}_{m})_{m\in \mathbb{N}}$ is uniformly bounded and $\mathrm{u}_{m}\rightarrow \mathrm{u}$ a.e. in $\mathcal{M}$, thanks to Brezis–Lieb lemma in [23], we obtain that

$$\begin{aligned} &\int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) \vert ^{p(z, y)}}{d_{\mathrm{g}}(z,y)^{n+s p(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \\ &\quad = \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert w_{m}(z)-w_{m}(y) \vert ^{p(z, y)}}{d_{\mathrm{g}}(z,y)^{n+s p(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) \\ &\qquad{}+ \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert \mathrm{u}(z)-\mathrm{u}(y) \vert ^{p(z, y)}}{d_{\mathrm{g}}(z,y)^{n+s p(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) + o(1). \end{aligned}$$

Therefore, a straightforward computation yields

$$\begin{aligned} \lim_{m \rightarrow \infty } E(\mathrm{u}_{m}) = {}&\lim _{m \rightarrow \infty } \int _{\mathcal{M} \times \mathcal{M}} \frac{ \vert w_{m}(z)-w_{m}(y) \vert ^{p(z, y)}}{d_{\mathrm{g}}(z,y)^{n+s p(z, y)}} \,d v_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y)\\ &{}- \int _{\mathcal{M}} H\bigl(z, \mathrm{u}( z )\bigr) \,d v_{\mathrm{g}}(z)+ \int _{\mathcal{M}} \frac{\mathcal{V}(z)}{q(z)} \bigl\vert \mathrm{u}(z) \bigr\vert ^{q(z)} \,dv_{\mathrm{g}} ( z ) \\ &{}+ \int _{\mathcal{M} \times \mathcal{M}}\frac{1}{p(z, y)} \bigl\vert \mathrm{u}(z)- \mathrm{u}(y) \bigr\vert ^{p(z, y)}{d_{\mathrm{g}}(z,y)^{n+s p(z, y)}} \,dv_{\mathrm{g}} ( z ) \,dv_{\mathrm{g}} ( y ). \end{aligned}$$

Using $E'(\mathrm{u}_{m}) \rightarrow 0$ as $m \rightarrow \infty$, we have

$$\begin{aligned} &\int _{\mathcal{M} \times \mathcal{M}} \frac{1}{p(z, y)} \frac{ \vert w_{m}(z)-w_{m}(y) \vert ^{p(z, y)}}{d_{\mathrm{g}}(z,y)^{n+s p(z, y)}} \,d v_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y)\\ &\quad \rightarrow \int _{ \mathcal{M}} \mathcal{V}(z) \bigl\vert \mathrm{u}(z) \bigr\vert ^{q(z)}\,d v_{ \mathrm{g}}(z)- \int _{\mathcal{M}} h\bigl(z,\mathrm{u}( z )\bigr) \mathrm{u}( z ) \,dv_{\mathrm{g}}(z) \\ &\qquad{}+ \int _{\mathcal{M} \times \mathcal{M}} \frac{1}{p(z, y)} \frac{ \vert \mathrm{u}_{m}(z)-\mathrm{u}_{m}(y) \vert ^{p(z, y)}}{d_{\mathrm{g}}(z,y)^{n+s p(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y). \end{aligned}$$

As $E'(\mathrm{u})=0$, we have

$$\begin{aligned} \lim_{m\longrightarrow \infty } \int _{\mathcal{M} \times \mathcal{M}} \frac{1}{p(z, y)} \frac{ \vert w_{m}(z)-w_{m}(y) \vert ^{p(z, y)}}{d_{\mathrm{g}}(z,y)^{n+s p(z, y)}} \,dv_{\mathrm{g}}(z) \,dv_{\mathrm{g}}(y) =0. \end{aligned}$$

 □

So, finally, from Lemmas 4.2 and 4.3, we conclude that our problem $( \mathcal{P} )$ possesses a weak solution.