1 Introduction

Stability assessment is a fundamental aspect of the analysis and design of dynamic systems. The foundations of modern stability theory lie in Aleksandr M. Lyapunov’s work [1].

For nonlinear problems of the general form

$$\begin{aligned} \dot{{\textbf{x}}}&= {\textbf{f}}({\textbf{x}}, t), \end{aligned}$$
(1)

stability is a local property of a specific solution, the state vector \({\textbf{x}}(t)\), resulting from a corresponding set of initial conditions

$$\begin{aligned} {\textbf{x}}(t_0)&= {\textbf{x}}_0 , \end{aligned}$$
(2)

i.e., of a Cauchy problem.

A well-known special case is that of Linear, Time-Invariant (LTI) problems, i.e., those resulting from the linearization of the problem of Eq. (1) about a steady reference solution \(\bar{{\textbf{x}}}\), such that \({\textbf{0}} = {\textbf{f}}(\bar{{\textbf{x}}}, t)\), in the form

$$\begin{aligned} \dot{{\textbf{x}}}&= {\textbf{A}} {\textbf{x}} , \end{aligned}$$
(3)

matrix \({\textbf{A}} = \left. {\textbf{f}}_{/{\textbf{x}}} \right| _{\bar{{\textbf{x}}}}\) being the constant characteristic matrix of the problem. In this case, stability is a characteristic of the entire system rather than of a specific solution. In fact, the solution of Eq. (3) for the initial conditions of Eq. (2) is

$$\begin{aligned} {\textbf{x}}(t)&= \textrm{e}^{{\textbf{A}} (t - t_0)} {\textbf{x}}_0 \end{aligned}$$
(4)

which, considering a spectral decompositionFootnote 1 of matrix \({\textbf{A}} = {\textbf{V}} \textrm{diag}({\mathbf {\gamma }}) {\textbf{V}}^{-1}\), where the operator \(\textrm{diag}(\cdot )\) constructs a diagonal matrix from a vector, yields

$$\begin{aligned} {\textbf{x}}(t)&= {\textbf{V}} \textrm{e}^{\textrm{diag}({\mathbf {\gamma }}) (t - t_0)} {\textbf{V}}^{-1} {\textbf{x}}_0 . \end{aligned}$$
(5)

Equation (5) shows that the expansion or contraction characteristics of the solution only depend on the sign of the real part of the eigenvalues of matrix \({\textbf{A}}\), regardless of the initial conditions of Eq. (2).

It is worth noticing that Eq. (4) can be interpreted in terms of the state transition matrix (STM) \({\textbf{Y}}(t, t_0)\) for LTI problems, namely the matrix that describes the evolution of the state from time \(t_0\) to time t for independently unitary initial conditions, \({\textbf{Y}}(t, t_0) \overset{\textrm{LTI}}{=} \textrm{e}^{{\textbf{A}} (t - t_0)} = {\textbf{V}} \textrm{e}^{\textrm{diag}({\mathbf {\gamma }}) (t - t_0)} {\textbf{V}}^{-1}\).

In many applications associated with rotorcraft dynamics, and specifically in helicopter rotor aeromechanics, problems often need to—or can conveniently—be formulated as time-periodic. The periodicity in these problems usually results from the rotational motion of the rotor (or of the rotors). Whenever the symmetry of the equations of motion of the rotor is spoiled, a periodic dependence of the problem on the azimuthal position of each blade is introduced, which does not cancel when the contributions of all blades are summed. Examples can be found in the study of ground resonance when the motion of the hub center in a plane orthogonal to the rotation axis is considered (in this case, periodicity can still be eliminated by resorting to multiblade coordinates, but it is definitely lost when non-identical blades or blade lead-lag dampers are considered), in rotor aeromechanics when non-axial flow conditions are considered (e.g., helicopters in forward flight, tiltrotor in transitional flight or during whirl flutter, etc.), and in several other cases of great practical interest (see for example [3]).

Nonlinear periodic problems are often characterized by periodic equilibria, namely solutions in the form of periodic orbits \(\bar{{\textbf{x}}}(t)\), such that \(\bar{{\textbf{x}}}(t + T) \equiv \bar{{\textbf{x}}}(t)\), where T is the period. Linearization about such orbits yields Linear, Time-Periodic (LTP) problems of the form

$$\begin{aligned} \dot{{\textbf{x}}}&= {\textbf{A}}(t) {\textbf{x}} , \end{aligned}$$
(6)

with \({\textbf{A}}(t + T) \equiv {\textbf{A}}(t)\).

In this case, the stability of a periodic orbit can be evaluated using the Floquet-Lyapunov method [4], considering that the solution of Eq. (6) with the initial conditions of Eq. (2) is

$$\begin{aligned} {\textbf{x}}(t)&= {\textbf{P}}(t) \textrm{e}^{{\textbf{B}} (t - t_0)} {\textbf{x}}_0 , \end{aligned}$$
(7)

where matrix \({\textbf{B}}\) is constant, whereas matrix \({\textbf{P}}(t)\) is periodic, namely \({\textbf{P}}(t + T) \equiv {\textbf{P}}(t)\). Equation (7) can be interpreted in terms of the STM for LTP problems, namely, \({\textbf{Y}}(t, t_0) \overset{\textrm{LTP}}{=} {\textbf{P}}(t) \textrm{e}^{{\textbf{B}} (t - t_0)}\). As such, the solution after one period, for \(t = t_0 + T\), is \({\textbf{x}}(t_0 + T) = {\textbf{P}}(t_0 + T) \textrm{e}^{{\textbf{B}} T} {\textbf{x}}_0 = {\textbf{P}}(t_0) \textrm{e}^{{\textbf{B}} T} {\textbf{x}}_0\). Without loss of generality, the initial value of matrix \({\textbf{P}}\) can be arbitrarily chosen as \({\textbf{P}}(t_0) \equiv {\textbf{I}}\), yielding \({\textbf{x}}(t_0 + T) = \textrm{e}^{{\textbf{B}} T} {\textbf{x}}_0 = {\textbf{H}} {\textbf{x}}_0\), where \({\textbf{H}} = \textrm{e}^{{\textbf{B}} T}\) is the so-called “monodromy matrix” of the problem, the STM of the LTP problem over one period, T. The magnitude of its eigenvalues \(\Lambda _i\), called “characteristic coefficients,” indicates whether the solution over one period contracts regardless of \({\textbf{x}}_0\) (\(\left| \Lambda _i \right| < 1\) \(\forall i\)), or there are specific directions in the solution space that result in an expansion (at least one \(\Lambda _i\) such that \(\left| \Lambda _i \right| > 1\)), the case of one or more eigenvalues \(\left| \Lambda _i \right| \equiv 1\), with geometric multiplicity equal to the algebraic, corresponding to simple stability.

This approach was introduced in the rotorcraft aeromechanics community by Parkus, who first used it to analyze blade flapping aeromechanics in the late 1940s [5], but it was only after the advent of digital computers that the method could see a practical application. In the early 1970s, Peters and Hohenemser were the first to propose it for the periodic flapping motion arising from non-axial flow [6], followed by Biggers [7] and Friedmann and Silverthorn [8]. Hammond used the method to investigate the stability of the motion resulting from the loss of isotropy of rotor blade damping (i.e., just one blade damper inoperative) in ground resonance [9]. Bauchau and Nikishkov applied the method to the analysis of complex rotorcraft aeromechanics problems using multibody dynamics [10].

In general, however, when problems are nonlinear and subjected to non-(strictly) periodic time dependence, as may occur in many transient-related problems, the ability to evaluate the stability of generic, arbitrary reference trajectories can be extremely useful. The use of Lyapunov Characteristic Exponents (LCE), also referred to as Lyapunov Exponents (LE), in the field of rotorcraft aeromechanics has been proposed in recent work by this research group [11,12,13], with specific reference to studying their sensitivity [14,15,16,17], also in application of other aerospace-related problems [15], attempting to extend their application to problems formulated as differential-algebraic equations (DAEs) using the multibody approach [18] and to overcome issues associated with algebraic multiplicity greater than one [19].

In this study, an original idea is introduced for employing two nonlinear dynamics techniques to forecast the stability of rotorcraft modeled as nonlinear systems. By employing multibody dynamics, the intrinsically nonlinear aeromechanical system is simulated, generating time series data for the system’s degrees of freedom. Subsequently, LCEs are utilized to retrospectively assess the system’s quantitative stability parameters. This approach removes the requirement to explicitly define stability computations within the multibody dynamics simulation, thereby granting analysts the convenience of directly utilizing their simulation outcomes in the stability prediction of nonlinear time-dependent rotorcraft systems.

2 Lyapunov characteristic exponents

The LCEs indicate the rate of expansion or contraction of perturbations of a generic solution of the nonlinear differential problem of Eq. (1) along independent directions in the state space. As such, they describe the stability of the reference solution with respect to such directions.

Consider a state vector \({\textbf{x}}(t)\) that represents a solution of Eq. (1) for \(t \ge t_0\) (some authors refer to it as the ‘fiducial trajectory’), and another state vector \({_i {\textbf{x}}(t)}\) that represents the solution of the linear time-variant (LTV) problem

$$\begin{aligned} {_i \dot{{\textbf{x}}}}&= \left. {\textbf{f}}_{/{\textbf{x}}} \right| _{{\textbf{x}}(t), t} \, {_i {\textbf{x}}} ,&{_i {\textbf{x}}(t_0)}&= {_i {\textbf{x}}_0} \end{aligned}$$
(8)

obtained from the linearization of Eq. (1) about the fiducial trajectory \({\textbf{x}}(t)\), for an initial perturbation \({_i {\textbf{x}}_0}\) of arbitrary magnitude and direction. According for example to Dieci and Van Vleck [20], LCEs are defined as

$$\begin{aligned} \lambda _i&= \lim _{t \rightarrow +\infty } \frac{1}{t} \log \left\| _i {\textbf{x}}(t) \right\| , \end{aligned}$$
(9)

where \(\log (\cdot )\) is the natural logarithm function and \(\left\| \cdot \right\|\) denotes the Euclidean norm. Each \(\lambda _i\) is calculated from one of n linearly independent vectors of initial conditions \({_i {\textbf{x}}_0}\), the equivalent of the principal directions of an LTI problem. Since Eq. (8) is LTV, its solution can be expressed through the STM \({\textbf{Y}}(t, t_0)\) as

$$\begin{aligned} {_i {\textbf{x}}}(t) = {\textbf{Y}}(t, t_0) \, {_i {\textbf{x}}_0} . \end{aligned}$$
(10)

In fact, for a generic LTV problem, the STM \({\textbf{Y}}(t, t_0)\) of Eq. (10) is the solution to the problem \(\dot{{\textbf{Y}}} = \left. {\textbf{f}}_{/{\textbf{x}}} \right| _{{\textbf{x}}(t), t} {\textbf{Y}}\), with \({\textbf{Y}}(t_0, t_0) = {\textbf{I}}\), the previously reported LTI and LTP forms representing special cases of this general expression. Equation (9) is thus equivalent to

$$\begin{aligned} {\mathbf {\lambda }}&= \lim _{t \rightarrow +\infty } \frac{1}{t} \textrm{Re} \left( \log \left( \textrm{eig} \left( {\textbf{Y}}(t, t_0) \right) \right) \right) , \end{aligned}$$
(11)

where all \(\lambda _i \in {\mathbf {\lambda }}\) are simultaneously and independently evaluated. This result can be obtained by considering the spectral decomposition of the STM, \({\textbf{Y}}(t, t_0) = {\textbf{V}} \textrm{diag}({\mathbf {\Gamma }}) {\textbf{V}}^{-1}\). In this context, both matrix \({\textbf{V}}\) and vector \({\mathbf {\Gamma }}\) are time-dependent (their explicit dependence on time, t, is omitted for ease of notation), with the diagonal matrix \(\textrm{diag}({\mathbf {\Gamma }})\) containing the eigenvalues \(\Gamma _i\) of the STM at time t. The spectral decomposition of a time-dependent matrix does not need to be performed in practice (it would likely be impossible in cases of practical interest); it is considered only for explanatory purposes. Use it to reformulate Eq. (9) as

$$\begin{aligned} \lambda _i&= \lim _{t \rightarrow +\infty } \frac{1}{t} \log \left\| {\textbf{Y}}(t, t_0) \, {_i {\textbf{x}}_0} \right\| \end{aligned}$$
(12)

and, using the ith eigenvector \({\textbf{V}}_i\) for the arbitrary \({_i {\textbf{x}}_0} = {\textbf{V}}_i\), obtain

$$\begin{aligned} \lambda _i&= \lim _{t \rightarrow +\infty } \frac{1}{t} \log \left\| {\textbf{V}} \textrm{diag}({\mathbf {\Gamma }}) {\textbf{e}}_i \right\| \end{aligned}$$
(13)

with \({\textbf{e}}_i\) a vector of zeros, except for the ith element, of unit value, which extracts the ith eigenvalue from matrix \(\textrm{diag}({\mathbf {\Gamma }})\), namely \(\textrm{diag}({\mathbf {\Gamma }}) {\textbf{e}}_i = \Gamma _i\) and \({\textbf{V}} \textrm{diag}({\mathbf {\Gamma }}) {\textbf{e}}_i = {\textbf{V}}_i \Gamma _i\). The natural logarithm of the norm of vector \({\textbf{V}}_i \Gamma _i\), \(\log \left\| {\textbf{V}}_i \Gamma _i \right\|\), corresponds to the real part of the complex logarithm of the eigenvalue \(\Gamma _i\), plus a constant term associated with the norm of \({\textbf{V}}_i\), which is uninfluential when the limit for \(t \rightarrow +\infty\) is considered. In fact, \(\left\| {\textbf{V}}_i \Gamma _i \right\| \le \left\| \Gamma _i \right\| \left\| {\textbf{V}}_i \right\|\), the former corresponding to \(\lambda _i t\) for \(t \rightarrow +\infty\), and thus, \(\log \left\| {\textbf{V}}_i \Gamma _i \right\| = \log \left\| \Gamma _i \right\| + \log \left\| {\textbf{V}}_i \right\|\) (by the way, if the eigenvector \({\textbf{V}}_i\) is normalized for unit norm, then \(\log \left\| {\textbf{V}}_i \right\| \equiv 0\)). This operation can be independently repeated for all eigenvectors and eigenvalues of the STM.

When all LCEs are negative, the solution is exponentially stable. When at least one LCE is positive, the reference solution is unstable or leads to a chaotic attractor. When the largest LCE is zero, or the largest LCEs are zero, a limit-cycle oscillation (LCO) is expected; i.e., in the state space, there exists one direction, or multiple independent directions (as many as the number of zero-valued LCEs), along which the solution neither expands nor contracts, and converges to a self-sustained periodic motion. In case of multiple largest LCEs equal to zero, a higher order periodic or quasi-periodic attractor exists, e.g., a multi-dimensional torus.

The LCE definition corresponds to the real part of the eigenvalues of matrix \({\textbf{A}}\) in the case of LTI problems (for this reason, in Sect. 4, LCEs and real parts of eigenvalues obtained using Matrix Pencil Estimation (MPE) will be graphically compared). In fact, as anticipated, for those problems

$$\begin{aligned} {\textbf{Y}}(t, t_0)&\overset{\text {LTI}}{\equiv } \textrm{e}^{{\textbf{A}} (t - t_0)} , \end{aligned}$$
(14)

and thus, Eq. (11) yields

$$\begin{aligned} {\mathbf {\lambda }}&\overset{\text {LTI}}{=} \textrm{Re}(\textrm{eig}({\textbf{A}})) , \end{aligned}$$
(15)

considering the spectral representation \({\textbf{A}} = {\textbf{V}} \textrm{diag}({\mathbf {\gamma }}) {\textbf{V}}^{-1}\), which is a unitary transformation and thus preserves the eigenvalues \({\mathbf {\gamma }}\) of matrix \({\textbf{A}}\), and the definition of matrix exponential, \(\textrm{e}^{{\textbf{M}}} = \sum _{k=0}^{\infty } {\textbf{M}}^k / k!\) [21].

In the case of LTP problems, considering the generic solution of Eq. (7), and replacing t with nT in Eq. (11), one obtains

$$\begin{aligned} {\mathbf {\lambda }}&\overset{\text {LTP}}{=} \lim _{n \rightarrow +\infty } \frac{1}{n T} \textrm{Re} \left( \log \left( \textrm{eig} \left( {\textbf{Y}}(t_0 + n T, t_0) \right) \right) \right) \nonumber \\&= \frac{1}{T} \textrm{Re} \left( \log \left( \textrm{eig} \left( {\textbf{H}} \right) \right) \right) , \end{aligned}$$
(16)

where, instead of the continuous time t, a discrete time nT is considered, corresponding to sampling the continuous process once per period. As such, without loss of generality, matrix \({\textbf{P}}(t_0 + n T) \equiv {\textbf{I}}\) can be considered in Eq. (7), such that \({\textbf{Y}}(t_0 + n T, t_0) \equiv \textrm{e}^{{\textbf{B}} n T} = {\textbf{H}}^n\). The eigenvalues of matrix \({\textbf{B}}\) are the Floquet–Lyapunov exponents, namely \(\textrm{eig}({\textbf{B}}) = \log (\textrm{eig}({\textbf{H}}))/T\), their real part being the corresponding LCEs (as such, their real part will be also compared with LCEs in Sect. 4). In this sense, one may consider the LCEs as sort of the eigenvalues of matrix \({\textbf{f}}_{/{\textbf{x}}}\), appropriately averaged over time, with the exponents of LTI and LTP problems, respectively, from Eqs. (15) and (16), as special cases.

The LCEs are often called the ‘spectrum’ of the associated problem, much like the spectrum of LTI problems is represented by the eigenvalues of matrix \({\textbf{A}} = {\textbf{f}}_{/{\textbf{x}}}\).

In most cases, however, the definition of Eq. (11) cannot be used in practice, essentially for two reasons:

  • the limit for \(t \rightarrow +\infty\) needs to be truncated to a finite value, albeit large enough to achieve practical convergence, when LCEs are numerically estimated;

  • at least some of the elements of the STM usually contract to zero, in case of asymptotic stability of the solution, or expand to infinity, in case of instability, resulting in either under- or overflowing, or a mix of both.

As discussed in the work of Benettin et al. [22], practical LCE estimation requires one to exploit the re-orthogonalization of the local directions of evolution of the solution; otherwise, despite starting the estimation process from the previously mentioned linearly independent directions \({_i {\textbf{x}}_0}\), it would inevitably converge toward the \(\lambda _i\) of largest value.

Alternative approaches based on well-known orthogonal decompositions [the Singular Value Decomposition (SVD) and the QR factorization, respectively [2]] have been proposed [20, 22, 23], considering that

$$\begin{aligned} {\mathbf {\lambda }}&= \lim _{t \rightarrow +\infty } \frac{1}{t} \textrm{qr}({\textbf{Y}}) \end{aligned}$$
(17)
$$\begin{aligned} {\mathbf {\lambda }}&= \lim _{t \rightarrow +\infty } \frac{1}{t} \textrm{svd}({\textbf{Y}}), \end{aligned}$$
(18)

where \(\textrm{svd}(\cdot )\) are the singular values of the argument matrix, whereas \(\textrm{qr}(\cdot )\) are the diagonal coefficients of the upper triangular matrix \({\textbf{R}}\) that results from the QR factorization of the argument matrix, formulated to ensure the production of non-negative diagonal coefficients. Those formulations exploit the possibility to reformulate the corresponding LCE definition in manners that prevent over- and underflow.

3 Jacobian-less methods: Max LCE from time series

The estimation of LCEs using the above-mentioned methods requires the knowledge of the Jacobian matrix of the problem, and the ability to integrate the associated linear, time-dependent problem. Although one may legitimately be interested in evaluating the whole spectrum of the problem, the stability of the problem can be practically assessed by estimating the largest LCE, or Maximum LCE (MLCE), something that can also be done directly from time series, as those resulting from the direct time integration of the problem (or even from measurements).

This approach is rather interesting, because it can be used in conjunction with the results of numerical simulations performed using rather complex multibody models. This is the case, for example, of general-purpose multibody dynamics solvers, often used to analyze the dynamics and aeromechanics of complex aerospace systems like rotorcraft [24], as in the present case. In this work, the free, general-purpose multibody solver MBDynFootnote 2 [25] is used. MBDyn is a versatile multibody solver developed at the Aerospace Science and Technology Department of Politecnico di Milano and distributed as free software. It automatically formulates and solves the equations of motion for a collection of entities with degrees of freedom (nodes), interconnected through kinematic constraints and flexible components. Constraint equations are formulated as algebraic equations, the corresponding reaction forces being formulated through Lagrange multipliers, according to the redundant coordinate set approach. Consequently, the resulting problem is formulated as a system of Differential-Algebraic Equations (DAE).

The MLCE is the LCE associated with the least damped principal direction of the problem, which represents the most critical stability indicator. Among the algorithms proposed in the literature (see for example [26]), the one proposed by Rosenstein et al. [27] is used in this work to investigate the whirl-flutter stability of a tiltrotor.

The trajectory matrix, \({\textbf{Z}}\), is constructed from an N-point time series \(z_\ell\), \(\ell =1,\ldots ,N\) obtained from the generic scalar measurement \(z_\ell = z_\ell ({\textbf{x}}(t_\ell ), t_\ell )\), a function of the state \({\textbf{x}}(t)\) obtained from the process at time \(t_\ell = (\ell - 1) h\), using the time delay method. Each column \({\textbf{Z}}_k\) of matrix \({\textbf{Z}}\) is a phase-space vector, namely

$$\begin{aligned} {\textbf{Z}}&= \left[ \begin{array}{ cccc } {\textbf{Z}}_1&{\textbf{Z}}_2&\ldots&{\textbf{Z}}_m \end{array} \right] \end{aligned}$$
(19)

with

$$\begin{aligned} {\textbf{Z}}_k&= \left[ \begin{array}{ cccc } z_{1+(k-1)J}&z_{2+(k-1)J}&\ldots&z_{M+(k-1)J} \end{array} \right] ^\textrm{T}, \end{aligned}$$
(20)

where \(k=1,\ldots ,m\). The generic element of vector \({\textbf{Z}}_k\), \(z_{i+(k-1)J}\), is the value of the measurement z at time \(t_{i+(k-1)J}\). Thus, \({\textbf{Z}} \in {\mathbb {R}}^{M \times m}\), with M, N, m, and J related by

$$\begin{aligned} M&= N - (m - 1) J, \end{aligned}$$
(21)

where m is the embedding dimension, N is the length of the time series (\(t_N\) would be the last time in the available time series), and J represents the so-called reconstruction delay, obtained by estimating the average mutual information (AMI) [28]. The embedding dimension is usually estimated in accordance with Takens’ theorem, i.e., \(m > 2 n\), using the false nearest neighbor (FNN) algorithm [29]. After constructing the trajectory matrix, the algorithm locates the nearest neighbor, \({\textbf{Z}}_{{\hat{j}}}\), of each point on the trajectory. It is found by searching the point that minimizes the distance from each particular reference point, \({\textbf{Z}}_{j}\). The distance is expressed as

$$\begin{aligned} d_j(0)&= \min _{{\textbf{Z}}_{{\hat{j}}}} \left\| {\textbf{Z}}_{j} - {\textbf{Z}}_{{\hat{j}}} \right\| , \end{aligned}$$
(22)

where \(d_j(0)\) is the initial distance, i.e., \(d_j(t_\ell )\) for \(\ell = 1\), and thus, \(t_\ell = 0\), from the jth point to its nearest neighbor.

Nearest neighbors must have a temporal separation greater than the mean period (\({\bar{T}}\), the reciprocal of the mean frequency of the power spectrum, although it can be expected that any comparable estimate, e.g., using the median frequency of the magnitude spectrum, yields equivalent results) of the time series

$$\begin{aligned} \left| t_j - t_{{\hat{j}}} \right|&> {\bar{T}}. \end{aligned}$$
(23)

Thanks to this, each pair of neighbors can be considered as nearby initial conditions for different trajectories.

The largest Lyapunov exponent is then estimated as the mean rate of separation of the nearest neighbors. The jth pair of nearest neighbors diverge approximately at a rate given by the largest Lyapunov exponent

$$\begin{aligned} d_j(t_{\ell +1})&\approx C_j \textrm{e}^{\lambda _1 (\ell h)}, \end{aligned}$$
(24)

where \(C_j\) is the initial separation and h is the time step. By taking the logarithm of both sides

$$\begin{aligned} \log d_j(t_{\ell +1})&\approx \log C_j + \lambda _1 (\ell h), \end{aligned}$$
(25)

which represents a set of approximately parallel lines, for \(j = 1,\ldots ,M\), each with a slope roughly proportional to \(\lambda _1\). The largest Lyapunov exponent estimate is calculated using a least-squares fit to the “average” discrete time line of the form \(a_0 + \lambda _1 \ell\), defined by

$$\begin{aligned} y(t_{\ell +1})&= \frac{1}{h} \langle \log d_j(t_{\ell +1}) \rangle , \end{aligned}$$
(26)

where \(\ell\) is the discrete time variable, the constant \(a_0\) is irrelevant, and \(\langle \cdot \rangle\) denotes the average over all values of j; \(\lambda _1\) can be estimated for example using Matlab’s polyfit() function as polyfit(\(y(t_{\ell +1})\), \(\ell\), 1).

The value of j is randomly chosen within the elements of the time series. Once j is defined, \({\hat{j}}\) indicates the nearest point that satisfies the inequality of Eq. (23). The “randomness” of the choice of the value j is only apparent, as it only represents the starting point of a sequence of series of distances whose average is evaluated to obtain the estimate of the MLCE through Eq. (26), under the assumption of invariance of the dynamic state reached by the system. In this sense, each pair of neighbors can be considered as nearby initial conditions for different trajectories. In the state of invariant dynamics, the window of estimation does not change with the location. Therefore, assuming that the dynamics do not change, the time history is divided into pair of neighbors, with the distance between the neighbors of \(\left\| t_j - t_{{\hat{j}}} \right\| > {\bar{T}}\). The MLCE is estimated from a mean value of the distance, so a sufficient number of pair of neighbors should result in its convergence to a stable average at each iteration. In the literature, there is no indication of how many pairs are needed, so the proposed approach is to start with an initial guess and check the convergence of the estimated MLCE by increasing the number of pairs of neighbor points.

Other methods can be used for MLCE estimation, for example, the one proposed by Kantz [30]; it differs from Rosenstein’s in the way the distance between trajectories is defined. Not as an Euclidean norm but as an absolute-value norm, so the modulus of the difference in the embedding space. Moreover, this method uses all neighbor points within a certain neighborhood, which might reduce the statistical errors, especially in the presence of noise.

Another algorithm has been proposed by Wolf et al. [31]. Wolf’s algorithm is somewhat more complicated, since it compares directions, not only distances. Therefore, it requires more free parameters: the embedding dimension, an upper bound of the distances when one must choose a new neighboring trajectory, an angular threshold for the difference between the new and old directions of the new difference vector and, for noisy data, the minimal distance between the reference trajectory and its new neighbor. This yields higher statistical fluctuations in the results.

The algorithms proposed by Eckmann et al. [32] and Sano and Sawada [33] are also worth of mention. They differ from Rosenstein’s and Wolf’s, because they are based on the computation of the tangent map, which is obtained by estimating a linearized flow map of tangent space through the least-squares error algorithm. However, they still rely on the concept of time delay and an arbitrary choice of the sphere radius, epsilon, for calculating propagation in the possible directions. These algorithms suffer from high statistical fluctuations.

4 Numerical results

4.1 Introductory example: ground resonance

The first example is related to ground resonance, as illustrated in [34]. The problem of a 4-blade rotor mounted on a flexible support originally proposed by Hammond [9] is implemented in MBDyn. The multibody model differs from Hammond’s original problem in that it is defined as a collection of 8 rigid bodies, for a total of 96 first-order differential equations, representing the airframe, the hub, and the four blades of the simplified rotor, connected by ideal kinematic constraints that only allow the in-plane displacement of the hub center, restrained by linear springs and dampers, prescribe the angular velocity of the hub with respect to the airframe, and allow the lead-lag rotation of the blades, restrained by linear lead-lag dampers, for another 32 algebraic equations and 6 remaining degrees of freedom: the in-plane components of the hub displacement and the lead-lag rotation of the four blades. As such, the relative motion between the blades and the hub is described by their absolute motion rather than by small relative angles as in Hammond’s original work. Apart from this, the two models are kinematically and dynamically equivalent.

The proposed algorithm is applied according to Table 1.

Table 1 Example application of the proposed algorithm to the ground resonance problem
Full size table

When all dampers are operative and small perturbations about the nominal configuration are considered, the maximum LCE extracted using the proposed approach is identical to the real part of the corresponding eigenvalue of the system matrix when Hammond’s problem is written in LTI form using multiblade coordinates. The same holds when one damper is inoperative (i.e., the corresponding damping coefficient is set to zero), thus making the problem LTP, but the largest characteristic exponent resulting from the classical Floquet–Lyapunov analysis, namely \(\lambda _{\textrm{MFLCE}} \equiv \max (\textrm{Re}(\log (\Lambda _i))/T)\), is negative, indicating stability (Fig. 1, \(\Omega < 210\) rpm and \(\Omega > 300\) rpm). However, when the classical Floquet–Lyapunov analysis of the LTP problem yields a positive largest real part of the Floquet–Lyapunov characteristic exponents, the LCE analysis instead yields zero, indicating a limit cycle (Fig. 1, 210 rpm \(< \Omega < 300\) rpm). The convergence to a limit cycle, although of large amplitude (Fig. 2, where \(A_{\zeta _3}\) is the rotation amplitude of blade no. 3, the one with the failed damper, about its lead–lag hinge), is confirmed by visually inspecting the time history of the fiducial trajectory. Of course, from an engineering point of view an LCO, especially of such amplitude, is as unacceptable as an instability. However, a more accurate determination of the resulting phenomenon helps better understanding its nature and, at the same time, illustrates the potential of the proposed method in studying the stability of complex systems.

Fig. 1
figure 1

Maximum LCE estimated from the nonlinear model using the Jacobian-less method compared with the largest real part of Floquet–Lyapunov exponents from the linearized model for the ground resonance problem

Full size image
Fig. 2
figure 2

Amplitude \(A_{\zeta _3}\) of limit-cycle oscillation of the blade with failed damper, blade no. 3

Full size image

4.2 XV-15 tiltrotor whirl flutter

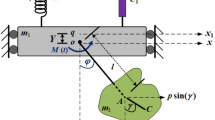
The aeroelastic simulation of the XV-15 tiltrotor is now considered. This analysis uses a highly sophisticated aeroservoelastic model that includes all the major structural components (Fig. 3). This represents a significant increase in complexity compared to the models studied in [35,36,37].

The airframe model now comprises the flexible wing, the rigid fuselage and empennages, the control surfaces (elevator, rudder, flaps, and flaperons), and the nacelle tilt mechanisms (Fig. 3a). The overall model, originally developed in [36], now also comprises the essential elements of the cockpit (a seat and the control inceptors—collective and cyclic) for rotorcraft–pilot couplings investigations.

The purpose of this model is to represent the fundamental frequencies and mode shapes of the complete aircraft, with a focus on the wing–nacelle portion. The proprotor is a 3-blade stiff-in-plane rotor with gimballed hub (Fig. 3b). It consists of three blades, the flexible yoke, and the detailed, geometrically exact pitch control chain.

An original geometrically exact, composite ready beam finite element model particularly suited for multibody dynamics, called ‘finite volume’ [38, 39], is used to model the flexibility of wing, rotor blades, and yokes of the two rotors.

The blade aerodynamics are based on the quasi-steady blade element model, with momentum theory for the averaged inflow (BEMT). The lift, drag, and moment aerodynamic coefficients are corrected for Mach number, stall, and three-dimensional flow. A similar aerodynamic model is also used for the wing. Although missing the capability to consider aerodynamic interactions, this model is considered adequate for high-speed stability analysis.

Fig. 3
figure 3

XV-15 model

Full size image
Table 2 Analyzed configurations
Full size table

To encompass the complete parameter range of the XV-15 tiltrotor, the six operational configurations presented in Table 2 were examined. Configuration #1 portrays the standard operating condition for the airplane mode, with the rotors spinning at 86% of the nominal RPM, trimmed for nominal thrust, and the downstop (the locking mechanism that blocks the nacelle in the airplane configuration when set to ON) locked. Configuration #2 deviates from the first by simulating an engine failure scenario, with the engines in idle condition, and windmilling rotors. Configurations #3 and #4 refer to the final portion of the conversion corridor, with the downstop activated and the rotors at helicopter RPM (100% of nominal), respectively, providing nominal thrust and in windmill condition, simulating engine failure. Configurations #5 and #6 differ from the preceding two in that the downstop mechanism is unlocked, as occurs during conversion, resulting in degraded stiffness of the wing–nacelle connection. The examination of these configurations provides valuable insight into the tiltrotor’s performance and stability in various operational scenarios, supporting its safe and effective operation.

To emphasize the response of the three main symmetric modes in the recorded data, namely wing flatwise (also called “beamwise”) and chordwise bending and wing torsion, three simulations are conducted for each configuration and speed, using different excitations. These specific modes are considered, because they appear to be the most critical for aeroelastic stability in the selected configurations; however, should other dynamics of the problem be characterized by a larger MLCE, they would surface from the response, provided that the excitation is sufficiently broadband to trigger them, and they are reachable through the selected input. The collective (1) and longitudinal (2) and lateral (3) cyclic pitch controls are symmetrically used (i.e., the collective and longitudinal cyclic controls of the two rotors receive identical input, whereas the lateral cyclic inputs are opposite) to produce the three independent excitations. The input signal is a sine modulated by a ramp, namely, \(\delta _i = a_i t \sin (\omega t)\), for \(0 \le t \le t_f\), and zero otherwise. The frequency, \(\omega\), is selected as the natural frequency of the aircraft’s normal mode one mainly wants to excite, which is obtained from an eigenanalysis of the structural model alone. The slope of the ramp, \(a_i\), is chosen to obtain about 20% of the range of the command after 10 cycles. The motion of the center of the hub is shown in the plots.

Each simulation consists of three distinct phases:

  1. (i)

    In the startup phase, the model is progressively driven toward the desired trim point using the procedure illustrated in [40].

  2. (ii)

    Excitation is critical in achieving satisfactory results during the identification process. Besides using a periodic signal with a fundamental frequency corresponding to the structural dynamic one wants to excite most, the amplitude of the input to be used during the excitations phase must be selected with care. Too small a value may result in noisier responses, increasing uncertainties in the identification process. On the contrary, too large an amplitude may cause convergence issues in the simulation, triggering unwanted transitions to other attractors than the desired trim points, something that may occur especially when the desired ones are only marginally stable. Furthermore, large inputs could impose excessive loads on the structure, although this aspect is more critical in experimental applications of the method.

  3. (iii)

    During the free response phase, after the system is perturbed, the simulation runs for a designated time period, whose duration must be carefully selected to be able to capture a sufficiently extended response. Such duration is crucial to obtain the necessary frequency resolution. Possible issues are discussed in the following, along with examples of numerical results. Difficulties can emerge with the reference identification method (Matrix Pencil Estimation (MPE), as discussed later) if the system response is non-negligibly nonlinear.

The simulations took between about 10 min and 15 min of CPU time for a simulated time of about 30 s on an AMD Ryzen 7 5800X 8-Core Processor.

The estimated MLCE was compared with the real part of the eigenvalues identified using the MPE, originally designed by Hua [41]. The MPE method is utilized to calculate the parameters of exponentially damped or undamped sinusoids in noise. The authors tested this approach on simplified issues, such as a signal comprised of two sinusoids and background white noise. The results indicated that the MPE method was less susceptible to noise when compared to the classical Prony method [42]. Pivetta et al. [43] later introduced a variant of the multiple input algorithm and applied it to more complex problems, such as tiltrotor whirl-flutter analysis. The MPE method can estimate the modal parameters of a system based on its free responses to an external input. However, it must be noted that the method can produce consistent outcomes only if the sampled response consists of a free decay and no unknown external forces are acting on the system.

Although the method is effective in capturing the free decay behavior, it encounters difficulties when the time series become more complex, particularly if only the exponential component is considered. In such cases, a low amplitude limit cycle that does not pose any issues can be mistaken as an exponential divergence if only the transient is considered.

Floquet–Lyapunov characteristic exponents could be used as well, but their straightforward evaluation would require an enormous computational effort to (a) reach a (stable) periodic trim configuration, (b) perturb one by one all the states of the problem and integrate their evolution over a period, to construct the monodromy matrix, and (c) compute its eigenvalues. The proposed method is intended to avoid such complexity. Alternative procedures, as the one proposed by Bauchau and Nikishkov in 2001 [10] and consisting of performing an implicit Floquet analysis on a subsystem obtained by projecting the original problem on a suitably chosen subspace using an Arnoldi algorithm, would require a substantial—if at all feasible—modification of the solver.

To identify the limit cycle, the maximum LCE approach is tested. Initially, the decay behavior is estimated to evaluate the accuracy of the method, followed by the analysis of the unstable part where the majority of parameter differences are observed. The validity and effectiveness of the method are verified by utilizing the free decaying exponent in the usable region. For this specific example, the time series are only considered for the same range as the MPE method. However, the underlying dynamics can manifest after a longer period. Discrepancies can also be observed in stable regions, which can be attributed to nonlinearity within the time series, or variations in the time window. This can result in fluctuations in the accuracy of the analysis, making it challenging to evaluate the dynamics of the system as shown later when discussing Configuration #6.

In the original formulation, the algorithm proposed by Rosenstein et al. is applied to a single time series, namely a scalar signal. In complex multivariable problems, the choice of a suitable signal can be critical, along with some parameters of the method, related to the duration of the signal and other factors discussed in the original paper. To overcome this critical aspect, a Proper Orthogonal Decomposition of the multiple signals resulting from the multibody dynamics simulation can be performed. Interesting results with this method have been obtained, for example, in [44] while analyzing the whirl flutter of a tiltrotor semispan wind-tunnel model. However, in the present work, the direct analysis of single signals was sufficient.

In the following, the six configurations of Table 2 are analyzed to give the reader an exhaustive evaluation of their estimated stability characteristics and to illustrate the issues that may surface when the proposed method is used and how can the corresponding results be interpreted. These configurations are considered the most critical for whirl flutter. Those in helicopter configuration (HP) exhibit the largest nominal angular velocity, as opposed to the lower angular velocity of the airplane configuration (AP), and thus larger rotor forces and moments. In addition, the configurations with the downstop disengaged (i.e. set to OFF), exhibit a substantially reduced torsional stiffness between the nacelle and its attachment at the wing tip. Other configurations, including intermediate nacelle angles comprised between 0 deg and 90 deg with non-zero forward flight speed, and thus a substantial transverse component of inflow, could also be of interest as they would produce a markedly periodic response. They are not considered in the following, because, according to the literature, they are not deemed critical for the aeroelastic stability of the vehicle, since such nacelle angles are permitted—or achievable in trimmed flight—only at much lower values of forward speed.

In Fig. 4, the MLCEs obtained using the proposed formulation from time series with different excitations are compared with the real part of the MPE-estimated eigenvalues of Configuration #1 (Power ON, AP mode, Downstop ON); they refer to response to a symmetric excitation. Flutter is estimated at \(U_{\infty } = 195.5\) m/s by linear interpolation.

The differences in the values obtained with stimulation in wing torsion are due to the MLCE’s inability to estimate very fast dynamics, because it is necessary to have several pairs of neighbors to obtain a consistent mean value. When damping is very high, the transients of interest are very fast, and the number of points is insufficient for a correct estimation. In this scenario, the MPE approach shows superior performances in estimation. If there are nonlinearities, as indicated in Fig. 4c, the MLCE can provide a more precise description of the decaying dynamics than the MPE. However, it makes little sense to use the MLCE in the case of a very fast, damped dynamical response of a linear system, as the point of strength of the method is in cases like the one in Fig. 4b, where an LCO takes place. In this case, the MLCE can estimate the stationary dynamics, while linear methods cannot describe limit cycles. The black dashed and dotted decaying lines shown in Fig. 4c result from torsional perturbation using the two corresponding \(\lambda _i\) from Fig. 4a, \(\lambda _\textit{MLCE}\) and \(\lambda _\textit{MPE}\).

Fig. 4
figure 4

MLCEs compared with real part of eigenvalues from MPE in Configuration #1 (Power ON, AP mode, Downstop ON). Flutter is estimated at \(U_{\infty } = 195.5\) m/s by linear interpolation (dashed red vertical line) and example time series

Full size image

In Fig. 5, the MLCEs are compared with the real part of the MPE-estimated eigenvalues of Configuration #2 (Power OFF, AP mode, Downstop ON), in response to symmetric excitation. Flutter is estimated at \(U_{\infty } = 187.6\) m/s by linear interpolation. The time series in Fig. 5(c) obtained with the chordwise bending perturbation at \(U_{\infty } = 185.2\) m/s shows how the methods differ, as the MPE produces a positive value for the real exponent in contrast to the MLCE, which goes to zero. The dynamical response leads to a limit cycle in this case. Because the MPE technique is unable to identify the limit cycle, it provides an incorrect estimation as unstable.

Fig. 5
figure 5

MLCEs compared with real part of eigenvalues from MPE in Configuration #2 (Power OFF, AP mode, Downstop ON). Flutter is estimated at \(U_{\infty } = 187.6\) m/s by linear interpolation (dashed vertical red line) and example time series

Full size image

In Fig. 6, the MLCEs are compared with the real part of the MPE-estimated eigenvalues of Configuration #3 (Power ON, HP mode, Downstop ON) and Configuration #4 (Power OFF, HP mode, Downstop ON). In those setups, flutter is not detected. Flutter does not develop due to the influence of the downstop (in these configurations, the locking mechanism is activated, resulting in the nacelle being blocked in the airplane configuration) and the lower cruising speed in this setup. It is possible to predict flutter if the region is expanded, as shown in Fig. 7, and flutter is estimated at \(U_{\infty } = 157.5\) m/s by linear interpolation. In these configurations, the flutter velocity is still lower because of the increased angular velocity of the rotor compared to Configurations #1 and #2. Because the dynamical response in the expanded region is significantly nonlinear, only the MLCE may be used. The MCLE and MPE remain at similar values throughout the estimation region except for Configuration #4’s estimation after \(U_{\infty } = 100\) m/s. The difference in the chordwise and wing torsion directions can be attributed to the nonlinearity in the response and the high damping after the excitation.

Fig. 6
figure 6

MLCEs compared with real part of eigenvalues from MPE in Configurations #3 and #4

Full size image
Fig. 7
figure 7

Extended MLCEs compared with real part of eigenvalues from MPE in Configuration #3 (Power ON, HP mode, Downstop ON). Flutter is estimated at \(U_{\infty } = 157.5\) m/s by linear interpolation (dashed vertical red line)

Full size image

In Fig. 8, the MLCEs are compared with the real part of the MPE-estimated eigenvalues of Configurations #5 (Power ON, HP mode, Downstop OFF) and Configuration #6 (Power OFF, HP mode, Downstop OFF). Both of those configurations show a flutter speed, Configuration #5 at around \(U_{\infty } = 123.5\) m/s and Configuration #6 at around \(U_{\infty } = 119.2\) m/s. Since the nacelle is not locked, as the downstop is inactive, this operating region was predicted to be the least stable. This is confirmed by a flutter velocity lower than that of the other configurations, also due to a rotor speed higher than that of Configurations #1 and #2. For example, it is worth noticing that the instability at \(U_{\infty } = 133.8\) m/s for wing torsion eventually leads to a limit cycle, as illustrated in Fig. 8c. The MLCE tends to zero, accurately estimating the asymptotic behavior type as an LCO, which cannot be recognized by the MPE. There is a noticeable difference in the results related to wing torsion between the methods; this is due to the initially highly damped response, which has a big impact on MLCE’s estimation capability, since the response quickly vanishes, whereas MLCE requires long time histories to recognize the true asymptotic behavior of the solution.

Fig. 8
figure 8

MLCEs of Configuration #5 and Configuration #6 compared with real part of eigenvalues from MPE

Full size image

5 Discussion

The analysis of the transients resulting from the solution of complex systems, like the tiltrotor aeroelastic model presented in this work, dominated by strong nonlinearities, can result in responses that can hardly be interpreted as the response of linear systems. This is especially true when, for example, the response evolves into a limit cycle or some higher dimensional attractor. Casting such responses into an equivalent linear behavior, essentially of an exponential time response type, to be interpreted as an equivalent damping factor for stability assessment may prove futile, as it strongly depends on the size and collocation of the observation window. On the contrary, LCEs represent a reliable way to consistently “average” the growth/decay characteristics of a system, in the vicinity of the solution of interest, into an aggregated, long-term stability indicator. In this context, extracting the MLCE from time series represents a minimally intrusive approach to directly operate on time series rather than having to develop ad hoc solvers. Moreover, the methodology can also be applied to experimental data.

The proposed methodology also presents shortcomings and needs to be applied with due care. Notably, (a) when problems are highly damped, transients vanish very quickly, leaving an insufficient number of data points for an accurate estimation of the MLCE, although in those cases stability is not at stake; (b) when the nonlinearity of the problem dominates its asymptotic behavior (e.g., leading to an LCO), MLCEs provide useful insight whereas other methods, like MPE, fail; (c) as long as the problem is not excessively damped, long time histories may be required for accurate MLCE estimation, leading to significant computational cost; on the one hand, the efficiency of the algorithm and of the underlying nonlinear simulation would improve the applicability of the method to problems of industrial interest; on the other, one needs to carefully weigh the advantages of using a full-featured nonlinear simulation to study the stability of the problem with the computational cost that the extensive coverage of configurations and operating conditions of interest may require.

6 Conclusions

This paper discusses the use of estimated Lyapunov Characteristic Exponents to evaluate the stability of complex mechanical systems. The reference application is the whirl-flutter study of a tiltrotor aeroelastic model. The problem is formulated without any a priori linearization or coordinate transformation to reduce the azimuthal dependence of the equations. Nonlinear phenomena, like limit-cycle oscillations, can be detected. By leveraging Jacobian-less methods, the Maximum LCE, i.e., the most critical one regarding stability, can be estimated from time series computed using general-purpose multibody formulations, without the need to modify existing solvers. The Maximum LCE method can detect limit cycle conditions; future work will focus on identifying the amplitude of the perturbation associated with instability or a limit cycle, and other estimators based on the same concept that also account for stochastic noise.