Abstract
Modern, high-agility aircraft configurations often suffer from tail buffeting at subsonic speeds and medium to high angles of attack. This structural dynamic excitation through the unsteady flow field can result in heavy structural damage and degraded handling qualities. A flexible wind tunnel half model was developed at the Chair of Aerodynamics and Fluid Mechanics of the Technical University of Munich in cooperation with the Department of Acoustics and Vibration of Airbus Defence and Space. To provide enough flexibility, the wing and horizontal tail plane (HTP) are 3D-printed from polylactide (PLA). The model is used to experimentally analyze buffeting and to validate computational buffeting prediction. The objective of the present work is to examine aeroelastic phenomena with the modular designed flexible wind tunnel model. The measurement campaign takes place at the Göttingen type wind tunnel A. The model is equipped with various sensors. For unsteady pressure measurements on the surface of the wing and the HTP, piezo-resistive Kulite pressure transducers are installed on the wing and on the HTP. In addition, the flow field is described on the basis of numerical simulation results. For analyzing the structural response resulting from buffeting, miniature accelerometers are installed at the tips of the wing and the HTP. Strain gauges are used for calculating bending strains. As a reference case, a fully aluminum model is equipped correspondingly, but without strain gauges. Dominant frequencies corresponding to the structural eigenmodes can be identified and are excited in the PLA-setup (Buffeting). The unsteady pressure fluctuations on the surfaces act as the aerodynamic excitation input (Buffet). The measured tip accelerations of wing and tail are compared to simulation results with a one-way coupling CFD-CSM simulation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Modern high-agility aircraft often suffer from tail buffeting effects. Especially at subsonic speeds and medium to high angles of attack, these aircraft generate complex vortex systems and large areas of flow separation. With increasing angle of attack, the vortex systems become increasingly unstable leading to the breakdown of the vortex structures. Downstream of vortex breakdown, the flow field shows high turbulent intensities and distinct frequency contents [1]. The resulting pressure fluctuations on the configuration’s surface lead to a structural excitation of the aircraft components. The structural response evoked by the excitation of the unsteady flow field is known as buffeting [2]. Buffeting often occurs on the wings and tail planes of modern high-agility aircraft and can lead to severe structural damage as well as degraded handling qualities.
Due to its relevance for high maneuverability aircraft tail buffeting has long been subject to numerical and experimental research. In numerical buffeting research, partitioned fluid-structural coupling (see for example Piperno et al. [3]) is among the most promising approaches to tackle the challenges of the complex phenomenon. Depending on the feedback of the structural vibration to the airflow there are one-way coupling approaches (e.g. Aquilini and Parisse [4] and Katzenmeier et al. [5, 6]) or two-way coupling approaches (e.g. Schuette et al. [7], Sheta and Huttsell [8] and Guillaume et al. [9]).
Despite the extensive developments in numerical buffeting prediction, experimental data from wind tunnel testing is still essential for the validation of new coupling methods and the investigation of basic coupling effects in buffeting. However, the development and investigation of flexible wind tunnel models is still challenging. In early developments, Davis Jr. and Huston described model damping, structural frequency requirements, model support in the wind tunnel as well as model instrumentation as the major challenges for such models [10]. Until the 1990s, the most common layout of flexible wind tunnel models used metal spars which were covered with balsa wood [11]. More advanced models were constructed with fiber-composite skins and honeycomb or foam inner structures. A recent example of such composite designs is presented by Stenfelt and Ringertz [12] and by Ringertz [13] for an aeroelastic flutter model.
In a cooperation between Airbus Defence and Space and the Chair of Aerodynamics and Fluid Mechanics at the Technical University of Munich, a flexible wind tunnel model for tail buffeting analysis using rapid prototyping material was developed and presented in Katzenmeier et al. [14]. The model uses an aluminum fuselage with 3D-printed wing and horizontal tail (HTP) from polylactide (PLA). PLA provides enough structural flexibility to highlight buffeting effects while at the same time providing sufficient strength to withstand the buffeting loads without damage. Furthermore, 3D-printing with PLA allows to quickly and accessibly manufacture complex parts and to tailor their structural characteristics to specific requirements. To investigate buffet and buffeting, the model is instrumented with different sensors in each case. The aerodynamic excitation is analyzed with piezo-resistive Kulite pressure transducers, the dynamic structural response with accelerometers and strain gauges. This measurement setup enables fully aeroelastic analyses of tail buffeting effects in low-speed wind tunnel tests which can be used for validation of numerical coupling methods. Furthermore, aluminum versions of wing and HTP can also be attached to the fuselage as an alternative to the PLA parts which allows to investigate details on quasi-rigid aerodynamic surface.
Katzenmeier et al. described the development process, manufacturing and preliminary experimental results of the model where the aerodynamic excitation in form of mean and root mean square (rms) values of transient pressures at one position each on the wing and on the HTP were shown [14]. In the present study, the instrumentation of the model is shown in detail along with more extensive aeroelastic measurement results of the model, including the analysis of both the aerodynamic excitation and the dynamic structural response using the above-mentioned sensors and additionally considering frequency spectra. To the best of the authors’ knowledge, wind tunnel measurements with PLA or similar rapid prototyping materials for aeroelastic buffeting analysis are a noval approach.
The paper is further organized as follows:
Section 2 describes the model development, the experimental setup, the testing conditions and the measurement techniques used for the presented experiments. The numerical setup of the CFD and FEM model is described in Sect. 3. In Sect. 4, first the flow field is explained using a DES simulation. Subsequently, the measurement results from transient pressure transducers and accelerometers are compared for the fully flexible version (PLA wing and PLA HTP) and the quasi-rigid reference version (aluminum wing and aluminum HTP) of the model and the results from strain gauges are considered for the flexible case. Surface pressures, structural accelerations and deformations are evaluated regarding their mean values, their root-mean-square values and their frequency spectra at different angles of attack. The tip acceleration spectra as well as the rms values of the tip accelerations are compared to numerical results. In Sect. 5, the results are summarized and an outlook is given.
2 Experimental setup
2.1 Design of the wind tunnel model
For the wind tunnel model, a half model was chosen rather than a sting mounted full model to introduce as little additional external dynamics into the system as possible. The model should also highlight aeroelastic coupling effects during tail buffeting. For this purpose, flexible lifting surfaces, 3D-printed from polylactide (PLA) with a Young’s modulus of \(E = 3.5\,\mathrm{GPa}\) [15], are used. Katzenmeier et al. presented computational buffeting results of the model, which supports the application of this material for aeroelastic buffeting wind tunnel models [14]. PLA is on the one hand strong enough to withstand the loads during the wind tunnel measurements, on the other hand flexible enough to be used for buffeting investigations. The flexible components are scaled with respect to a possible generic large-scale configuration considering structural elasticity, i.e. especially wing and HTP deformation, and structural dynamics regarding wing and HTP bending and torsion modes, cf. similarity rules [16,17,18]. Aluminum lifting surfaces with a Young’s modulus of \(E = 70\,\mathrm{GPa}\) [19], representing the quasi-rigid case, are used as a comparative configuration. Figure 1 illustrates the modular concept of the wind tunnel model with its interchangeable wing and horizontal tail plane (HTP).
Different HTP settings can be set via the adapter colored yellow in Fig. 1. Table 1 provides the deflection \(\delta _\mathrm{HTP}\) associated with the respective angle of attack \(\alpha\).
Figure 2 shows a schematic view of the wind tunnel model with the basic geometry parameters. Its values are listed in Table 2. The sweep angles of the double delta wing are \(\rho _{W,1} = 76^\circ\) and \(\rho _{W,2} = 40^\circ\). The sweep angle of the leading and trailing edge of the HTP is \(\rho _\mathrm{HTP,LE} = \rho _\mathrm{HTP,TE} = 40^\circ\). The half span related to the wing root length is \(s_{W}/c_{r,W} = 0.5\) for the wing and \(s_\mathrm{HTP}/c_{r,W} = 0.3\) for the HTP.
More information about the modular wind tunnel model and its design process can be found in Katzenmeier et al. [14].
2.2 Sensor integration
The wind tunnel tests are performed with a quasi-rigid and flexible configuration. The wind tunnel model is instrumented with transient pressure transducers (Kulite), accelerometers (ACC) and strain gauges (SG). Figure 3 shows the sensor positions on the wing and HTP of the wind tunnel model. Transient pressure transducers (Kulite LQ-32-064-5 psi D) determine the differential pressure on the surface relative to the reference atmospheric pressure outside the test section. They are placed at positions where high (pressure) fluctuations are expected. Furthermore, uniaxial accelerometers (PCB 352C22/NC) measure the wing tip accelerations for analyzing the structural response resulting from buffeting. Strain gauges (VPG CEA-06-125UNA-350) are located on the surfaces of the flexible airfoils to determine the strains at the respective locations, see Fig. 3. Four strain gauges, two at the lower and two at the upper side, build a full bridge to measure pure bending strain at the point of interest, which is located on the bending line of the wing or HTP.
Table 3 shows the x- and y- coordinates of the sensor positions depending on the root length \(c_{r,W}\) or halfspan \(s_W\) of the wing. The origin is located at the front nose of the fuselage at the level of the wing root. To obtain a realistic strain behavior of the flexible components, the strain gauges are not placed directly at the wing or HTP root connection but outside the rigid connection to the fuselage.
Figure 4 shows the wind tunnel model with the three different sensor types integrated in the flexible wing and the flexible HTP. In addition, two accelerometers are integrated on the fuselage to detect any dynamics transmitted between the wing and the HTP via the fuselage that do not result from the excitation of their specific eigenmodes. The wind tunnel model with all the sensors on the fuselage and the flexible wing and HTP integrated into the test section of the wind tunnel can be seen in Fig. 5. Figure 6 illustrates the measurement setup. The accelerometers are connected to a NI 9234 data acquisition card, the pressure sensors and the strain gauges to NI 9237 data acquisition cards. The NI cDAQ-9185 chassis allows a synchronization of the various measurements of all sensors and transfers the data to the LabView controlled computer.
2.3 Measurement conditions
The measurements were performed at the TUM-AER wind tunnel A, a Göttingen type wind tunnel. The cross section of the open test section of the wind tunnel is \(1.80 \, \mathrm{m}\) by \(2.40 \, \mathrm{m}\). The length of the test section is \(4.80 \, \mathrm{m}\) and the turbulence intensity in each coordinate direction less than \(0.4\%\). With an open test section, the maximum speed is \(65 \, \mathrm{m}/\mathrm{s}\). Table 4 summarizes the measurement conditions of the wind tunnel investigations.
The Reynolds number related to the freestream velocity is set to \(\mathrm{Re}_{1/m}= 3.2\times 10^6 \, 1/\mathrm{m}\), which results in a required freestream velocity of about \(U_\infty = 51 \, \mathrm{m}/\mathrm{s}\) and a Mach number of about \(\mathrm{Ma}_\infty = 0.15\). The considered angle of attack range is between \(10^\circ\) and \(35^\circ\), which can be adjusted via a turntable. The wind speed is measured with a Prandtl probe in the freestream of the nozzle outlet. The measurements are performed with a measurement time of \(10 \, \mathrm{s}\). The interesting range with the first structural modes is up to approximately \(f = 500 \, \mathrm{Hz}\). Thus a 10 times higher sampling frequency of \(f_\mathrm{s} = 5120 \, \mathrm{Hz}\) is used. To avoid aliasing, a lowpass filter, which is automatically included in the data acquisition cards, is applied at half the sampling frequency \(0.5 \times f_\mathrm{s}\).
3 Numerical setup
The buffeting loads on the wind tunnel model are also predicted using a stochastic one-way coupling approach between the Computational Fluid Dynamics (CFD) results and a Finite-Element Model (FEM) in a random response solver. The approach is outlined in detail in Katzenmeier et al. [6] and was already used in the development process of the presented wind tunnel model in Katzenmeier et al. [14].
A combined study regarding grid refinement and physical time step size based on the experiences of a comparable study of a simplified configuration (cf. [5, 6]) was performed. For this purpose three different hybrid grids with increasing level of surface and volume grid refinement (coarse: 55.6 M cells; medium: 77.9 M cells; fine: 122.5 M cells) and different time step sizes between \(\Delta t = 2.4\times 10^{-5}\,\mathrm{s}\) and \(\Delta t = 6.0\times 10^{-5}\,\mathrm{s}\) were used. Based on the analysis of the aerodynamic coefficients (\(C_\mathrm{L}\), \(C_\mathrm{D}\) and \(C_{My}\)) and the mean and rms values of the pressure coefficient (\(\overline{c}_{p}\) and \(c_{p,\mathrm{rms}}\)), the medium grid with 77.9 M cells and a time step size of \(\Delta t = 3.0\times 10^{-5}\,\mathrm{s}\) (leading to CFL\(=1.0\)) was chosen because it provides sufficient results. Some selected results of the combined study are shown in Fig. 7. The chosen unstructured, hybrid CFD grid is shown in Fig. 8 and consists of a triangulated surface grid, 35 prism cell layers with a stretching factor of 1.25 for resolving the boundary layer and tetrahedral elements for the remaining volume. With a first layer cell height of \(h = 1.0\times 10^{-3}\,\mathrm{mm}\) a value of \(y^{+} \le 0.8\) can be reached for the whole model for the investigated flow conditions. Based on the investigations of Katzenmeier et al. [5], an improved delayed detached eddy simulation (SA-IDDES, [20]) turbulence model with Spalart–Allmaras (SA) basis and rotation correction with dual time stepping and an implicit Backward-Euler scheme with Lower-Upper Symmetric Gauss-Seidel (LUSGS) algorithm is used. Good convergence can be obtained within 200 inner iterations per physical time step. For the Cauchy convergence criterion a control value of \(\Delta = 1\times 10^{-5}\) for lift, drag and pitching moment coefficients as well as the total kinetic energy and maximum eddy viscosity is used. A single-grid approach with a second-order central scheme with matrix dissipation serves for spatial discretization. For reducing the artificial damping of the resolved flow structures and improving the accuracy of the computation, low-dissipation low-dispersion (LD2) settings were set in the SA-IDDES simulation. Since such settings support the potential for numerical instabilities in the solver, a blending function was used to restrict the LD2-scheme to the Large-Eddy Simulation (LES) regions. The considered simulation time is \(0.5\,\mathrm{s}\). The simulations are performed with similar inflow conditions to those in the wind tunnel tests with an angle of attack of \(\alpha =15^\circ\), \(\alpha =25^\circ\) and \(\alpha =35^\circ\), a Reynolds number related to the freestream velocity of \(\mathrm{Re}_{1/m}= 3.2\times 10^6 \, 1/\mathrm{m}\) and a resulting freestream velocity of \(U_\infty = 51 \, \mathrm{m}/\mathrm{s}\) or Mach number of \(\mathrm{Ma}_\infty = 0.15\). The simulations are executed with the flow solver DLR-TAU [21].
The FE model of the wind tunnel model was created with Hyperworks Hypermesh. The computation of normal modes of the configuration is performed with MSC Nastran [22]. Wing and HTP with their connection elements to the fuselage are modeled using finite elements. The fuselage was modeled with CBAR elements connected to the wing, HTP and their connectors through CBUSH elements. The model parameters were adapted so that its overall mode shapes and frequencies matched the results of a ground vibration test (GVT) of the model. Details on the FE-model and its adaption to the GVT can be found in Katzenmeier et al. [14]. The FE model of the wind tunnel model is presented in Fig. 9.
The CFD solution at the fluid-structure interface of the desired physical time-span is transferred to the structural model. The random response solver then computes the response to the given aerodynamic excitation. The stochastic approach enables a straightforward estimation of maximum and minimum responses within specific confidence intervals. The linear dynamic equations of motion of the aeroelastic system can be written in modal space as
with the modal amplitudes \(\varvec{\xi }(\omega )\) and the modal matrix \(\varvec{\Phi }\). \(\mathbf {M}_\mathrm{gen} = \varvec{\Phi }^\mathrm{T}\mathbf {M}\varvec{\Phi }\) describes the generalized mass matrix, whereas \(\mathbf {D}_\mathrm{gen} = \varvec{\Phi }^\mathrm{T}\mathbf {D}\varvec{\Phi }\) and \(\mathbf {K}_\mathrm{gen} = \varvec{\Phi }^\mathrm{T}\mathbf {K}\varvec{\Phi }\) are the generalized damping and stiffness matrices, respectively. The self-induced generalized aerodynamic forces are defined as \(\mathbf {GAF}(\varvec{\xi }(\omega ))=\varvec{\Phi }^T\mathbf {F}_{SI}(\varvec{\xi }(\omega ))\).
From Eq. 1 the random response can be computed using
where \(\mathbf {H}(\omega )\) is the frequency response function of the system. Proper Orthogonal Decomposition (POD) is used in the stochastic buffeting prediction process to reduce the size and associated computational effort of the buffeting excitation (see Katzenmeier et al. [6]). The original buffet excitation signals can be expressed through a small number of POD-modes \(\varvec{\Phi }_\mathrm{POD}\) with limited losses of accuracy. As described in Katzenmeier et al. [6] the approach allows to use the full spectral density matrix of the reduced buffet excitation signals. The time dependent surface forces from the CFD computation \(\mathbf {F}_B(t)\) are decomposed with the POD to obtain \(\mathbf {F}_{B,\mathrm{POD}}(t)\) and the corresponding spectral density matrix \(\mathbf {S}_\mathrm{F_{B, \mathrm{POD}}}(\omega )\). As shown in Katzenmeier et al. [6] the integration of the reduced spectral density matrix into the random buffeting response equation (Eq. 2) is formulated as
The response loads can be computed using the mode displacement method (see Bisplinghoff et al. [23]) as
In the present simulation, 200 POD-modes were used based on the results presented in [6].
4 Results and discussion
4.1 Analysis of the aerodynamic parameters
4.1.1 Flow field
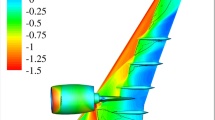
For a better interpretation of the sensor measurements, the flow field over the wing and HTP is of primary interest. To show this by way of introduction, a DES simulation is used. The results are presented in Fig. 10. More information about the simulation setup can be found in Sect. 3. Vortices formed at the leading edge of a delta wing are characterized by high axial velocities in the vortex core, low static pressure and lower total pressure due to high dissipation in the sub core [1]. Above a certain angle of attack, the phenomenon of vortex bursting occurs and with further increase of the angle of attack, the burst location moves upstream [1].
Figure 10a shows the iso-surface at a total pressure loss of \(3\%\) for an angle of attack of \(\alpha =25^\circ\). The colormap refers to the axial velocity component u normalized by the freestream velocity \(U_\infty\). The total pressure loss in the vortex core, which is typical for a vortex, makes both leading-edge vortices detectable. The first one is generated at the leading edge of the strake, while the second one forms at the lower-swept leading edge. Until the vortex bursting in the wing center area, high axial velocities can be seen in the strake vortex core. The vortex breakdown results in high (pressure) fluctuations, which are visualized in Fig. 10c in terms of the rms value of the pressure coefficient \(c_{p,\mathrm{rms}}\). As visualized, the Kulite sensors are located in areas of high (pressure) fluctuations on the wing and the HTP. High \(c_{p,\mathrm{rms}}\) values can also be found on the complete leading edge of the HTP as well as on its upper surface.
For a smaller angle of attack of \(\alpha =15^\circ\), Fig. 10b illustrates that due to the low \(c_{p,\mathrm{rms}}\) values the strake vortex remains stable over the wing area, whereas the vortex formed at the lower-swept leading edge has already burst. For high angles of attack such as \(\alpha =35^\circ\) it can be seen in Fig. 10d that, compared to \(\alpha =25^\circ\), the vortex burst point has moved significantly forward into the front strake region.
4.1.2 Surface pressures
The phenomena visible in the CFD simulation can also be observed in the experimental results. Figure 11 shows the mean pressure coefficient \(\overline{c}_{p}\) and the rms value of the pressure coefficient \(c_{p,\mathrm{rms}}\) of the wing and HTP at the Kulite position for different angles of attack between \(\alpha =10^\circ\) and \(\alpha =35^\circ\). The mean pressure coefficients of the flexible and rigid case in Fig. 11a show a similar curve over the complete angle of attack range for the wing and HTP. For the wing, the mean values of the flexible case tend to be slightly higher than for the rigid case. The mean pressure coefficient at the Kulite position of the wing decreases to approximately \(\alpha =25^\circ\) and subsequently increases. The increasing velocities at the upper surface of the wing caused by the leading edge vortices locally result in a high suction level [1]. Due to the shift of the vortex burst location at higher angles of attack, the burst point moves upstream in front of the Kulite position between \(\alpha =20^\circ\) and \(\alpha =25^\circ\), which leads to a drop in the local suction level at this point. The simulation results in Fig. 10 support these observations. It can be seen that the vortex burst point for \(\alpha =35^\circ\) is located further upstream from the Kulite position than for \(\alpha =25^\circ\), which results in a higher pressure level \(\overline{c}_{p}\) for \(\alpha =35^\circ\). At the HTP, \(\overline{c}_{p}\) increases marginally toward positive values, is zero at about \(\alpha =20^\circ\), and then continuously decreases slightly in the higher angle of attack range. The absolute values \(|\overline{c}_{p} |\) of the wing are significantly higher than those of the HTP over the entire angle of attack range. Figure 11b shows the pressure fluctuations on the surface of the wing and HTP at the Kulite position in terms of \(c_\mathrm{p,rms}\). For most angles of attack, the \(c_{p,\mathrm{rms}}\) values at the Kulite position of the rigid case are higher than those of the flexible case for both the wing and the HTP. In both cases, the shift of the strake vortex burst location in front of the wing’s Kulite position leads, as expected, to a significant abrupt increase of the \(c_{p,\mathrm{rms}}\) above \(\alpha =20^\circ\). Similar correlations can be found in the studies of Breitsamter [24]. The increase in pressure fluctuations between \(\alpha =10^\circ\) and \(\alpha =15^\circ\) in terms of \(c_{p,\mathrm{rms}}\) is due to the position of the vortex breakdown of the vortex formed at the lower-swept leading edge. Figure 10b illustrates that the bursted vortex already strongly influences the rms values of the pressure coefficient \(c_{p,\mathrm{rms}}\) at the Kulite position for \(\alpha =15^\circ\). While for the rigid wing the pressure fluctuations at the Kulite position increase up to \(\alpha =35^\circ\), for the flexible wing they increase up to \(\alpha =30^\circ\) and decrease slightly for \(\alpha =35^\circ\). At \(\alpha =30^\circ\), the local \(c_{p,\mathrm{rms}}\) value at the wing of the flexible case is minimally higher than that of the rigid case. For the HTP, the rms values of the pressure coefficient \(c_{p,\mathrm{rms}}\) at the Kulite position have a common minimum at \(\alpha =15^\circ\) for both the rigid and the flexible case, increasing subsequently in both cases up to an angle of attack of \(\alpha =25^\circ\). Between \(\alpha =25^\circ\) and \(\alpha =35^\circ\), both cases show a relatively constant level at the HTP. Figure 10 confirms the experimental results and illustrates that the level of pressure fluctuations \(c_{p,\mathrm{rms}}\) is very low for \(\alpha =15^\circ\) and is comparable for \(\alpha =25^\circ\) and \(\alpha =35^\circ\).
In general, it can be seen that the mean surface pressure values in terms of \(\overline{c}_{p}\) at the Kulite position are slightly lower for the rigid wing than for the flexible wing for most angles of attack, while they are very similar for the HTP. The pressure fluctuations in terms of \(c_{p,\mathrm{rms}}\) show differences between the two cases for both, the wing and the HTP. Thus, the flexibility of the wing and HTP seems to have an effect on the magnitude of the wing’s mean surface pressure values and on the magnitude of the pressure fluctuations on the wing’s and HTP’s surfaces.
4.2 Analysis of the pressure spectra
Figure 12 shows the power spectral densities (PSD) of the fluctuating pressure coefficients \(c_p'\) on the surface of the wing and HTP at the Kulite position for the rigid and the flexible case over several angles of attack. Based on the studies of Heckmeier et al. [25] a 1-D median filter of 1st order and a Savitzky-Golay finite impulse filter (FIR) of 1st order and a frame length of \(51\,Hz\) is used for denoising the initial averaged noisy signal in the frequency domain.
Figure 12a presents the power spectra of the rigid wing on the left-hand side and those of the flexible wing on the right hand side between \(\alpha =10^\circ\) and \(\alpha =35^\circ\). In the higher angle of attack range, a peak, the so-called buffet peak, can be seen in both cases, which moves toward lower reduced frequencies (\(k = f\times c_{r,W}/U_\infty\)) as the angle of attack increases.
Breitsamter explains this buffet peak shift by a growing cross-section of the burst vortex with increasing distance to the vortex burst location and thus with increasing angle of attack and the associated forward movement of the vortex burst station. With the cross section, the diameters of the fluid balls that follow the spiral motion increase and the narrow band energy concentration occurs at smaller frequencies. These frequency peaks are caused by the quasi-periodic pressure fluctuations downstream of vortex breakdown. They become more broadband with increasing distance to the vortex burst location [24].
In Fig. 12a, the peaks in the power spectral densities can especially be seen from \(\alpha =20^\circ\) upward for the flexible and the rigid wing. This is consistent with the observations regarding the \(c_{p,\mathrm{rms}}\) values in Fig. 11b, which increase significantly from \(\alpha =20^\circ\) due to vortex bursting. It can also be observed that the peaks become more narrow banded with increasing angle of attack.
In Fig. 12b, as in the case of the wing, the buffet peaks in the pressure spectra of the HTP can be identified especially for the angles upwards from \(\alpha =20^\circ\), but the peaks have a significantly higher bandwidth. The broader peaks could be explained by the greater distance of the measurement position at the HTP from the vortex breakdown point. A peak shift, as described in [1] for fin buffeting, can be observed and associated with smaller reduced frequencies than for the wing.
Figure 13a shows the fluctuating pressure spectra of the rigid and flexible wing for \(\alpha =25^\circ\) and \(\alpha =35^\circ\), visualized in a 2D single figure, and illustrates that the aerodynamic excitation input for buffeting effects is quite similar for the rigid and the flexible case. As in the case of the wing, Fig. 13b illustrates a similar PSD curve of \(c_p'\) for the rigid and flexible HTP for \(\alpha =25^\circ\) and \(\alpha =35^\circ\).
These local maxima in the PSD of the fluctuating pressure coefficients act as an aerodynamic excitation input and are responsible for the buffeting effects or structural response. Furthermore, it can be observed that the energy level of the buffet peak increases with increasing angles of attack at the wing and at the HTP.
4.3 Analysis of the structural dynamic parameters
For the analysis of the structural response from buffeting, the vertical tip accelerations of the wing and HTP of the rigid and flexible wing as well as the strains near the wing and HTP root are discussed in more detail.
4.3.1 Vertical tip accelerations
In contrast to the pressure fluctuations or the aerodynamic excitation input on the wing and the HTP, clear differences between the rigid and flexible cases can be observed in Fig. 14 for the structural dynamic response in terms of the vertical tip accelerations \(a_{z,\mathrm{rms}}\), normalized by the product of the inverse squared freestream velocity \(U_\infty ^2\) and the root length \(c_{r,W}\).
Over the complete angle of attack range, as expected, the \(a_{z,\mathrm{rms}}\) values for both the flexible wing and the flexible HTP are higher than for the rigid case, which serves as a quasi-rigid comparison model. For the flexible wing, a significantly higher excitation is observed at \(\alpha =25^\circ\) compared to the other angles of attack, which is not present for the rigid wing. This sudden increase can be explained by the vortex bursting above the wing from an angle of attack between \(\alpha =20^\circ\) and \(\alpha =25^\circ\). The unsteady pressure fluctuations resulting from vortex bursting lead to a strong increase in the structural excitation of the wing. The flexible wing thus reacts more sensitively to an aerodynamic excitation than the rigid wing. Between \(\alpha =30^\circ\) and \(\alpha =35^\circ\), the vertical accelerations on the wing remain almost constant in the flexible case or decrease slightly in the rigid case. For the HTP, however, the curve of both configurations increases significantly between the last two angles of attack compared to the previous trend at lower angles of attack. The \(a_{z,\mathrm{rms}}\) values at the HTP increase with increasing angle of attack in the completely considered angle of attack range.
In general, between the quasi-rigid and the flexible case at a comparable aerodynamic excitation, significant differences in the dynamic structural response can be seen. The flexible wing and HTP are thereby excited much more strongly and react more sensitively to occurring events in the aerodynamic excitation such as vortex bursting.
4.3.2 Analysis of the tip acceleration spectra of the flexible case
Due to the significantly higher rms values for the flexible lifting surfaces, the acceleration power spectral densities are discussed in more detail and are shown in Fig. 15.
In contrast to the spectra of \(c_p'\), simple averaging is used for denoising the initial averaged noisy signal of the tip accelerations in the frequency domain. To be able to assign the peaks in the PSD of \(a_z\) to the structural eigenmodes and thus to the structural response, the results of a ground vibration test (GVT) of the model installed in the wind tunnel are used. More information about the design of the GVT and its results can be found in Katzenmeier et al. [14].
In general, it can be observed that structural eigenmodes for all considered angles of attack are excited and the peaks in the spectra correlate very well with modes determined in the GVT. In Fig. 15a, the first three bending modes of the flexible wing are assigned to the reduced frequencies of \(k=0.64\), \(k=2.41\) and \(k=5.04\), the first two torsion modes to the reduced frequencies of \(k=2.19\) and \(k=4.43\). In Fig. 15b, the peaks in the spectrum of the HTP’s tip accelerations at \(k=0.48-0.53\) and \(k=4.15\) can be associated with the first and second bending mode. At an angle of attack of \(\alpha =10^\circ\), the bending mode is at \(k=0.53\) and moves with increasing angle of attack towards smaller reduced frequencies down to \(k=0.48\). A possible explanation for this is the excitation of a mode at about \(k=0.48\) (\(30\,\mathrm{Hz}\)), which could be identified in the GVT and correlates with the eigenmode of the connection of the HTP to the fuselage. As the angle of attack increases, the load on the connector increases as well and the excited mode becomes more dominant compared to the first bending mode of the HTP. The peak at \(k\approx 2.2\) cannot be associated with any eigenmode and lies in the range of the first torsion mode and second bending mode of the wing. Since it can also be detected in the power spectrum of the sensors attached to the fuselage, the peak at \(k=2.2\) at the HTP results from the transfer of dynamics from the wing via the fuselage to the HTP. Due to the fact that the wing and HTP are each mounted to the fuselage by frictional and positive connection and not with damping, vibrations can be transmitted between the individual components. A significant eigenmode of the fuselage at \(k=1.13\) causes the broadband lower peak in the spectrum of the wing and the HTP at this reduced frequency.
4.3.3 Bending strains of the wing and HTP
For the structural dynamics analysis, in addition to accelerometers, strain gauges are placed near the wing root of the flexible wing and HTP along the bending line to determine pure bending strains.
In Fig. 16, the mean and rms values, normalized by the product of Reynolds number related to the freestream velocity \(Re_\infty\) and the inverse root length \(c_{r,W}\), are plotted over a range of angles of attack between \(\alpha = 10^\circ\) and \(\alpha = 35^\circ\).
Figure 16a shows that for both the wing and the HTP, the mean values of the strain \(\overline{\varepsilon }\) increase with increasing angle of attack. The level on the wing is significantly higher than on the HTP. While the HTP shows only a slight increase between \(\alpha =10^\circ\) and \(\alpha =20^\circ\), the wing strains are characterized by the strongest increase in this range.
The differences in the rms values of the strains \(\varepsilon _{rms}\) at the SG position in Fig. 16b are much smaller between wing and HTP compared to the mean values. The values for the wing are higher than those for the HTP for all angles of attack except \(\alpha =15^\circ\), where they are on a comparable level despite a very low mean value.
4.3.4 Analysis of the strain spectra at the SG position of the flexible case
As with the spectra of the accelerations at the wing tips, the first two bending modes of the flexible wing at \(k=0.64\) and \(k=2.41\) in Fig. 17a and those of the flexible HTP at \(k=0.48-0.53\) and \(k=4.15\) in Fig. 17b can be identified for all considered angles of attack by the peaks in the strain spectra. Since the strain gauges are fixed along the bending line, the torsion modes in Fig. 17 cannot be identified. As with the HTP’s acceleration spectra, a shift to smaller reduced frequencies with an increasing angle of attack is evident in the first bending mode. Similarly, the strain spectra of the HTP show a peak at \(k\approx 2.2\) due to the dynamics transmitted by the wing. As with the tip accelerations, the peak at \(k=1.13\), which can be associated with an eigenmode of the fuselage, is seen in the bending spectra of the wing and the HTP.
4.4 Comparison to numerical results
The spectral contents of the wing and HTP tip accelerations from the numerical approach and experimental results are compared in Figs. 18, 19 and 20. The integrated response in the form of rms values of the tip accelerations are compared in Fig. 21.
The spectral contents match well for \(\alpha =15^\circ\) to \(\alpha =35^\circ\). The modal response in the numerical approach resembles the response in the experimental results. Minor shifts in frequency peaks result from limited adjustment of the FEM model to the GVT results for single modes over the whole frequency range.
For \(\alpha =15^\circ\), the numerical response amplitudes for the wing are larger than the experimental response for the 1st bending and 1st torsional mode, whereas they are smaller for the 2nd bending (Fig. 18). Due to the larger response amplitude of the 2nd bending the rms value of the experimental result is slightly higher than that of the simulation result (Fig. 21). For the HTP, the response amplitudes match well between simulation and experiment, leading to matching rms values.
The wing’s 1st bending response at \(\alpha =25^\circ\) matches more closely than for \(\alpha =15^\circ\) between simulation and experiment (Fig. 19). However, the 1st and 2nd torsion and 2nd and 3rd bending response are over-predicted by the simulation leading to much larger rms values for the simulation (Fig. 21). The spectral contents and rms values of the HTP response are similar in simulation and experiment for \(\alpha =25^\circ\) with slightly increased 1st bending response of the simulation, leading to slightly higher rms values of the simulation.
For \(\alpha =35^\circ\) the 1st bending response of the wing matches the experimental results (Fig. 20). The over-predictions for the 1st and 2nd torsion and 2nd and 3rd bending are also smaller than at \(\alpha =25^\circ\), leading to similar rms values of the wing response for simulation and experiment (Fig. 21). For the HTP the simulation predicts a larger rms value of the tip acceleration due to a larger response of the 1st bending mode of the HTP.
The over-predictions of the simulation mainly occur in the first torsion and second bending of the wing at \(\alpha =25^\circ\) and the HTP first bending mode at \(\alpha =35^\circ\). There are several possible reasons for the over-predictions in the numerical setup. Since the main response behavior over the whole frequency range is similar, the cause of the deviations can most likely not be found in the response solver and the structural solver but rather in one of the aerodynamic solvers. From first in-depth analyses of the data, sources of the over-predictions most likely are either (i) differences in the unsteady surface pressure distribution and levels, or (ii) differences in the motion-induced aerodynamic forces between simulation and experiment. Differences in the unsteady surface pressure can result from the numerical behavior of the DES simulation. Fig. 22 shows the mean and rms surface pressures at the Kulite positions as presented in Fig. 11 including the results from CFD. The mean surface pressures are predicted with high accuracy by the simulation for the wing and HTP over the angle of attack range. The simulation accurately predicts the unsteady surface pressures \(c_{p,rms}\) for the wing at \(\alpha =15^\circ\) and \(\alpha =35^\circ\) (Fig. 22). At \(\alpha =25^\circ\) the simulation predicts significantly higher pressure fluctuations at the wing’s Kulite position, which can be a first indication of the origin of the over-predictions of the structural response at \(\alpha =25^\circ\) as shown in Fig. 21. For the HTP, the simulation predicts the pressure fluctuations with high accuracy for \(\alpha =15^\circ\), while it predicts higher fluctuation levels for \(\alpha =25^\circ\) and \(\alpha =35^\circ\) (Fig. 22). The higher fluctuation levels can explain the larger structural responses in the simulations at these angles of attack compared to the experiment as shown in Fig. 21.
In addition, differences in the motion-induced aerodynamic forces can have a major impact on the structural response for specific modes. In the applied solver, these forces are provided by the DLM method. Försching [26] analyzed the experimental unsteady pressure distribution over an oscillating trapezoidal wing and compared the results to computational results of potential flow methods. It was found that, regarding the interaction of the wing oscillations with the separated flow field, the potential methods produced too little aerodynamic damping, which caused significant over-estimated vibrations. A similar effect could be the reason for the over-predictions in the presented data. In further analyses, the authors will investigate the aerodynamic damping of the first torsion and second bending of the wing at \(\alpha =25^\circ\) and the HTP first bending mode at \(\alpha =35^\circ\).
5 Conclusion
Wind tunnel tests were performed on a rigid and a flexible double delta wing configuration to investigate buffeting effects. Data analysis is performed for the wing and a horizontal tail plane. It could be shown that the setup described in this work is suitable for investigations of aeroelastic phenomena in low-speed wind tunnels.
The aerodynamic excitation (buffet) related to the pressure fluctuations, which are measured with piezo-resistive Kulite pressure transducers, only shows small differences for the rigid and flexible cases. The dynamic structural response (buffeting) is investigated with accelerometers and strain gauges. In contrast to the aerodynamic excitation, the subsequent dynamic structural response differs significantly between the two cases. The rms values of the accelerations at the tips are larger for the flexible lifting surfaces than for the quasi-rigid lifting surfaces. Consequently, the structural response of the flexible HTP is much more pronounced with comparable aerodynamic excitation. Furthermore, in the flexible case, the structural response to occurring events in the aerodynamic excitation such as vortex breakdown over the wing turns out to be much more sensitive. The spectral power peaks of the accelerations at the tips of the wing and HTP and of the strains at the flexible lifting surfaces correspond to the structural modes identified in a preceding GVT. When considering the spectra it must be taken into account that dynamics are introduced via the eigenmodes of the fuselage and that dynamics are transferred from the wing to the HTP via the fuselage.
The measured tip accelerations of wing and tail were compared to simulation results with a one-way coupling CFD-CSM simulation. The results show good agreement between experiment and simulation for the spectral contents and the rms values of the tip accelerations. Overpredictions of the rms values in the simulation were caused by overpredictions of the 1st torsion and 2nd bending for the wing and of the 1st bending for the HTP.
As a further step, PIV measurements will be performed to determine detailed flow field characteristics. In addition, the upstream and downstream effects of the flexible structures will be studied in more detail. The root bending moment will be determined from a correlation between simulations and measured strain at one single point.
References
Breitsamter, C.: Unsteady flow phenomena associated with leading-edge vortices. Progress Aerosp. Sci. 44(1), 48–65 (2008)
Mabey, D.G.: Some aspects of aircraft dynamic loads due to flow separation. Report, Advisory Group for Aerospace Research and Development (AGARD) (1988)
Piperno, S., Farhat, C., Larrouturou, B.: Partitioned procedures for the transient solution of coupled aroelastic problems part i: Model problem, theory and two-dimensional application. Comput. Methods Appl. Mech. Eng. 124(1), 79–112 (1995)
Aquilini, C., Parisse, D.: A method for predicting multivariate random loads and a discrete approximation of the multidimensional design load envelope. In: International Forum on Aeroelasticity and Structural Dynamics (IFASD) 2017, Como, Italy (2017)
Katzenmeier, L., Vidy, C., Benassi, L., Breitsamter, C.: Prediction of horizontal tail buffeting loads using URANS and DES approaches. In: International Forum on Aeroelasticity and Structural Dynamics (IFASD) 2019, Savannah, Georgia (2019)
Katzenmeier, L., Vidy, C., Breitsamter, C.: Using a proper orthogonal decomposition representation of the aerodynamic forces for stochastic buffeting prediction. J. Fluids Struct. 99 (2020)
Schütte, A., Einarsson, G., Raichle, A., Schöning, B., Mönnich, W., Orlt, M., Neumann, J., Arnold, J., Forken, T.: Numerical simulation of maneuvering aircraft by aerodynamic, flight-mechanics, and structural-mechanics coupling. J. Aircr. 46(1), 12 (2009)
Sheta, E.F., Huttsell, L.J.: Characteristics of F/A-18 vertical tail buffeting. J. Fluids Struct. 17(3), 461–477 (2003)
Guillaume, M., Gehri, A., Stephani, P., Vos, J., Mandanis, G.: F/A-18 vertical tail buffeting calculation using unsteady fluid structure interaction. Aeronaut. J. 115(1167), 285–294 (2011)
Davis Jr., D.D., Huston, W.B.: The use of wind tunnels to predict flight buffet loads. Report NACA Research Memorandum RM L57D25, NACA (1957)
Ricketts, R.H.: Experimental aeroelasticity history. Status and future in brief. Report, NASA Langley Research Center (1990)
Stenfelt, G., Ringertz, U.: Design and construction of aeroelastic wind tunnel models. Aeronaut. J. 119(1222), 1585–1599 (2015)
Ringertz, U.: Wing design for wind tunnel flutter testing. In: International Forum on Aeroelasticity and Structural Dynamics (IFASD) 2019, Savannah, Georgia (2019)
Katzenmeier, L., Vidy, C., Kolb, A., Breitsamter, C.: Aeroelastic wind tunnel model for tail buffeting analysis using rapid prototyping technologies. CEAS Aeronaut. J. 12, 633–651 (2021)
Farah, S., Anderson, D.G., Langer, R.: Physical and mechanical properties of PLA, and their functions in widespread applications—a comprehensive review. Adv. Drug Deliv. Rev. 107, 367–392 (2016)
John, H.: Critical review of methods to predict the buffet capability of aircraft. Report, Advisory Group for Aerospace Research and Development (AGARD) (1974)
Zan, S., Huang, X.Z.: Wing and FIN buffet on the standard dynamics model. Report Verification and Validation Data for Computational Unsteady Aerodynamics ADP010722, Defense Technical Information Center (2001)
Butoescu, V.A.J.: Similitude criteria for aeroelastic models. INCAS Bull. 7(Issue 1/2015), 37–50 (2015)
Wittel, H., Muhs, D., Jannasch, D., Voßiek, J.: Roloff/Matek Maschinenelemente. Springer, Wiesbaden (2015)
Shur, M.L., Spalart, P.R., Strelets, M.K., Travin, A.K.: A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 29(6), 1638–1649 (2008)
Schwamborn, D., Gardner, A.D., Von Geyr, H., Krumbein, A., Lüdeke, H., Stürmer, A.: Development of the DLR-TAU code for aerospace applications. In: International Conference on Aerospace Science and Technology (2008)
MSC.Software: MSC. Nastran version 68: basic dynamic analysis user’s guide. MSC.Software Corporation (2004)
Bisplinghoff, R.L., Ashley, H., Halfman, R.L.: Aeroelasticity. Dover Publications Inc, Mineola (1996)
Breitsamter, C.: Turbulente Strömungsstrukturen an Flugzeugkonfigurationen Mit Vorderkantenwirbeln. Doctoral Dissertation, Technical University of Munich, Munich (1997)
Heckmeier, F.M., Hayböck, S., Breitsamter, C.: Spatial and temporal resolution of a fast-response aerodynamic pressure probe in grid-generated turbulence. Exp. Fluids 62, 1–13 (2021)
Försching, H.W.: Unsteady aerodynamic forces on an oscillating wing at high incidences and flow separation. Report AGARD-CP-483, Aircraft Dynamic Loads due to Flow Separation, Sorrento (1990)
Acknowledgements
The funding of the presented investigations within the LUFO VI-1 project INTELWI (TUM: Experimental investigations and reduced-order models for the analysis of aeroelastic vibration effects at vortex dominated flows—FKZ: 20A1903D; Airbus Defence and Space: Investigation of vibration effects on flexible structures in vortex dominated flows—FKZ: 20A1903F) by the German Federal Ministry for Economic Affairs and Energy (BMWi) is gratefully acknowledged.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stegmüller, J., Katzenmeier, L. & Breitsamter, C. Horizontal tail buffeting characteristics at wing vortex flow impact. CEAS Aeronaut J 13, 779–796 (2022). https://doi.org/10.1007/s13272-022-00593-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13272-022-00593-3