1 Introduction

Since the first experimental observation by Hilton et al. [9], the buffet phenomenon has been investigated with various numerical and experimental approaches. Although researchers have tried to come up with a physical explanation for the phenomenon for decades, up to now there is no theoretical foundation explaining transonic buffet in its entirety. A thorough review of the developments in the field of transonic buffet research over the past decades has been presented by Giannelis [7].

An early attempt to explain the phenomenon in two dimensional flow included the bursting of a separation bubble reaching the trailing edge of the airfoil [17, 18]. However, this approach was disproved in a later study [4]. An important contribution in the explanation of shock buffet was Lee’s model [13] proposing a mechanism based on acoustic wave propagation. Although this model was supported by subsequent studies e.g. [6, 27], conflicting results were obtained as well [11] when predicting the buffet frequency.

Detailed experimental analyses of the 2D aspects of the buffet phenomenon were done on various airfoil geometries [3, 11, 16] identifying buffet frequencies in the Strouhal number range 0.06 to 0.07. Extending the investigations to three dimensional flow over swept wings, the buffet spectrum was found to be of a more broadband nature and of higher frequency content in the Strouhal number range 0.2–0.4 [22]. Subsequent studies by Steimle [25] and Dandois [5] support these findings. An explanation for the large difference in buffet frequency between 2D and 3D flow was given by Iovnovich and Raveh [10]. The authors described the spanwise development of so called buffet cells generated by pressure fluctuations originating from the lambda (\(\lambda\)) shock at the wing root propagating outboard. In recent studies it was proposed that these buffet cells can be linked to subsonic stall cells and that both phenomena actually represent the same flow instability [19, 20].

The research unit FOR2895 was put to work to expand the knowledge of the 3D buffet phenomenon. The initiative involves detailed numerical and experimental investigations of unsteady aerodynamic phenomena occurring at the border of the flight envelope [14]. One aspect of the research group is the investigation of lower wing surface buffet effects linked to aerodynamic engine/airframe interaction. While most of the studies investigating transonic buffet on aircraft configurations focus on cases at high incidences and shock induced separations on the wing upper surface, a similar phenomenon exhibiting unsteady shock/boundary layer interaction can also occur on the wing lower surface. A main driver for this phenomenon is the installation of engine nacelles with high bypass ratios and therefore large engine diameters mounted below the wing. Due to their size, the nacelles need to be coupled very closely to the wing to avoid additional adverse effects such as increased structural weight of the pylon or a longer landing gear. The close coupling of engine and airframe results in significant aerodynamic interference effects on the wing [23]. The surfaces of the nacelle, pylon, wing lower surface and fuselage form a half open channel in which the flow is accelerated. In addition, the flow is further accelerated by the jet of the engine passing under the wing. In transonic flight these effects result in local areas of supersonic flow and a corresponding shock occurs on the wing lower surface between the nacelle and the fuselage. Due to the interaction of the shock with the boundary layer of the wing, unsteady shock-induced separations can occur on the wing lower surface which are accompanied by an oscillation of the shock analogous to the known buffet phenomenon on the wing upper surface. The aforementioned effects may be relevant for the initiation of an emergency descent or for high speed dive conditions where the aircraft is pushed to very low angles of attack to reduce lift. Therefore, this study provides a new perspective on buffet phenomena around complex geometries adding to the already large knowledge base available for high speed high angle of attack conditions.

Within the scope of the research unit FOR2895, a UHBR (Ultra-High-Bypass-Ratio) nacelle was designed for the XRF1 wind tunnel model [24] with the aim to support a detailed assessment of these effects. Due to technical constraints, it was not feasible to construct a nacelle able to model the jet flow during the wind tunnel experiments, such as a turbine powered simulator. Therefore the design was executed as a through flow nacelle. It is acknowledged that the aforementioned additional flow acceleration due to the jet flow is therefore neglected in the study, nevertheless the formation of the half open channel and the flow acceleration due to displacement effects are accounted for.

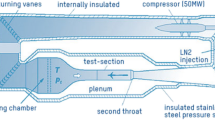
Within sub-project 3 of FOR2895, the lower wing buffet effects are to be assessed by means of highly sophisticated numerical simulations. Hybrid RANS-LES computations are about to be performed with the aim to locally resolve a region around the shock/boundary layer interaction by LES, while the rest of the aircraft configuration is modeled by unsteady RANS simulations including a Reynolds stress turbulence model. To validate these methods, high quality reference data is required. This data is obtained by performing wind tunnel tests at the cryogenic transonic wind tunnel facility ETW (European Transonic Windtunnel) [2, 8, 21]. The results of these tests are used in this study to assess the lower wing buffet phenomenon for the first time.

During the design of the new through flow nacelle for the XRF1 and the preparation of the wind tunnel tests, a variety of flight conditions were assessed with the aim to find flow conditions exhibiting lower wing buffet effects. These studies were conducted by means of RANS simulations under the assumption that strong shock induced separations occurring in these simulations will yield an indication for buffet. An example from these studies is shown in Fig. 1. The pressure distribution on the wing lower surface shows a strong shock inboard of the nacelle extending in the spanwise direction up to the fuselage. Behind the shock just inboard of the first flap track fairing the resulting flow separation is indicated by an area enveloped by a solid line. During these early stage simulations it was found that very low angles of attack are required to obtain this shock induced separation. It is noted that this configuration featuring a through flow nacelle misses the effect of additional flow separation due to the engine jet flow, therefore it is expected that a powered configuration will exhibit these effects at higher angles of attack.

Fig. 1
figure 1

Prediction of wing lower surface shock induced separation in a RANS simulation during early project stage, solid lines indicate \(c_{f,x}=0\), enveloped areas show local flow separations (\(Re=3.3\times 10^6, M=0.84, \alpha =-4^\circ\))

Full size image

2 Test setup

The experimental data shown and analyzed in this study was generated during the second wind tunnel test entry in the scope of the FOR2895 in December 2021. The XRF1 wind tunnel model [15] was used within the ETW cryogenic wind tunnel facility to study buffet phenomena at various conditions. The data analyzed in this study is part of a larger data set generated to analyze the buffet phenomena over a wide spectrum in high detail. In the following subsections, a short description of the wind tunnel test is given, but for brevity the focus is put on details relevant to the investigation of the lower wing buffet phenomena.

2.1 Model and instrumentation

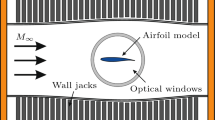
The XRF1 wind tunnel model is representative of a state of the art long range transport aircraft with a scale of 1 to 37 and was designed for high speed testing in cryogenic wind tunnel facilities. It is equipped with two UHBR through flow nacelles, a HTP and a VTP. The model is mounted to the ETW model cart by a rear sting protruding from the rear of the fuselage. The installation of the model inside the test section of ETW is depicted in Fig. 2. To ensure turbulent flow, the laminar turbulent transition location was fixed depending on the flow Reynolds number (see Table 1). The transition fixing was applied to the fuselage nose, the wing leading edges, and the HTP and VTP leading edges, as well as to the nacelle cowlings and core bodies.

Fig. 2
figure 2

XRF1 wind tunnel with UHBR through flow nacelles in the ETW test section during the MK2A test entry

Full size image

The model was mounted to a six-component strain gauge balance which measured the aerodynamic loads the model encountered during the test. The model itself is instrumented with 317 wing, 50 HTP, 18 nacelle and five fuselage surface static pressure tappings. The wing pressure tappings are installed on the upper surface of the starboard wing and the lower surface of the port wing in three primary spanwise stations. Various intermediate stations distributed between the primary spanwise sections complete the overall pressure port mapping of the wings. In addition to the static pressure tappings, dynamic pressure signals were recorded using 20 Kulite pressure transducers (Kulites) in the wing, 10 Kulites in the HTP, 4 Kulites in the nacelle and 10 Kulites in the pylon.

2.2 Pressure sensitive paint measurements

Steady and unsteady PSP (pressure sensitive paint) measurements were conducted during the test on the port upper surface and starboard lower surface of the wings. Several unsteady pressure transducers were installed on these wing surfaces. Therefore, the unsteady PSP data can be compared with the unsteady pressure transducer data directly. Both wings were coated with a thin layer of a special paint which changes its emitted luminescent intensity and lifetime under UV light depending on the local pressure. The thickness of the paint is considered to be below 5 µm. This PSP coating can be used for both steady and unsteady PSP measurements [28]. The steady PSP measurement was based on the lifetime method with a gated CCD sensor camera and pulsed UV LED units. Details of the PSP system used to capture steady pressure distributions can be obtained from [29]. The unsteady PSP measurement was based on the intensity method with a high-speed CMOS sensor camera and constant-power LED units [12]. The unsteady PSP system allows the capture of time-resolved PSP data with a sampling frequency of 1 or 2 kHz depending on the test conditions. A sampling rate of 2 kHz was used for tests conducted at temperatures of 180 K and above while 1 kHz sampling rate was used at 115 K because of lower PSP light intensity at lower temperature. The unsteady PSP system can only capture the temporal variations of relative pressure amplitude. This relative amplitude is a ratio of the absolute amplitude of the pressure signal and the time mean pressure. A reconstruction of the time-resolved absolute pressures was achieved by superposition of the steady PSP data and the unsteady PSP data in post-processing [30].

Two sets of masked data were delivered along with the PSP data depicted in Fig. 3. Mask 1 represents a minimal masking of the data, blanking only regions where no valid data could be obtained, e.g. the nacelle and the flap track fairings. Mask 2 is a more conservative mask blanking all areas that may contain doubtful data due to surface imperfections being present, e.g. screws, edges of cover plates or instrumentation. If not stated otherwise, mask 1 is used throughout the study simplifying the visibility of shocks and gradients on the surface pressure distribution.

Fig. 3
figure 3

Available masks for PSP data on the wing lower surface (dark areas indicate blanked data)

Full size image

2.3 Testing conditions

The wind tunnel test matrix for the UHBR induced lower wing buffet studies was defined based on preliminary RANS simulations. The test conditions relevant for lower wing buffet investigations shown in Table 1 were assessed during the test entry. Note that two Mach numbers were assessed except for \(Re=6.6\times 10^6\). Nevertheless, this study focuses on results obtained for \(M=0.84\) as the UHBR induced lower wing buffet phenomenon was most pronounced at these conditions.

Table 1 Testing conditions for lower wing buffet investigations
Full size table

3 Results

As mentioned above, early RANS simulations during the design phase of the UHBR through flow nacelle indicated a strong shock was expected to be present on the wing lower surface at the test conditions listed in Table 1. In Fig. 4 a first assessment of this shock based on experimental data is shown by means of steady PSP measurements of the wing lower surface pressure distribution. In the plot a shock of similar magnitude and at a similar location compared to Fig. 1 is visible. This shock extends in the spanwise direction from the fuselage up to the through flow nacelle. Although not the focus of this study, the outboard shock pattern also matches fairly well with the data from the RANS simulation in Fig. 1. For the sake of clarity, data extraction locations used throughout the study are marked in Fig. 4 as well.

Fig. 4
figure 4

Steady PSP data for the wing lower surface and data extraction locations (\(Re=3.3\times 10^6,\; M=0.84,\; \alpha =-4^\circ\))

Full size image

The wing pressure distribution at the inboard main pressure section of the XRF1 model at 23% span is shown in Fig. 5a. This section is located between the through flow nacelle and the fuselage inboard of the first flap track fairing (see Fig. 4). Due to the negative angle of attack, lower pressure coefficients are found on the wing lower surface. The shock induced by the presence of the nacelle is visible at around 23% chord. The agreement between the pressure tappings and the mean of the unsteady PSP measurements is excellent. Note that PSP data is only available for the wing lower surface in this case. In the background of Fig. 5a, time accurate pressure distributions from unsteady PSP measurements are shown to indicate the unsteady nature of the phenomenon and the elongation of shock movement. A strong increase in pressure fluctuation can be seen downstream of the shock indicating separated flow.

Fig. 5
figure 5

Local shock oscillation at \(y/s=0.23\) (\(Re=3.3\times 10^6,\; M=0.84,\; \alpha =-4^\circ\))

Full size image

The four vertical lines in Fig. 5a mark positions where the pressure time series for the first 100ms of the measurement shown in Fig. 5b were extracted. The extraction locations around the shock were aligned with the uPSP mean curve by placing one at the top of the shock, one at the foot of the shock and one in between them. For the most upstream position at \(x/c=0.21\) only small fluctuations in pressure can be seen for most of the time series because it is located at the top of the shock in the mean pressure distribution and the shock rarely reaches this position during its elongation. The most pronounced changes are visible for the position located at the center of the shock in the mean pressure distribution at \(x/c=0.23\). The pressure coefficient changes drastically within very short time while the shock moves back and forth over this position. The course of the pressure coefficient for the \(x/c=0.25\) position is similar, but of a reduced amplitude and at higher pressure levels. For the position far downstream of the shock at \(x/c=0.7\) small variations in pressure can be observed as well.

A first assessment of the spanwise extension of the phenomenon is shown in Fig. 6a. For three section cuts extracted at different spanwise stations on the inner wing, RMS (root mean square) values of the pressure coefficient are plotted. The locations of the moving shock exhibit the largest changes in pressure and the fluctuation levels downstream of the shock are significantly elevated for all sections. From Fig. 6a it is also evident that the shock location moves downstream with decreasing span as indicated in Fig. 4. Note that a secondary peak appears just downstream of the shock for the two most outboard sections. These peaks result from an optical artifact in the unsteady PSP data and do not represent actual surface pressure fluctuations. The artifacts stem from altered light refraction due to large density gradients of the test gas across compression shocks. If the optical path of the PSP camera system passes through a shock, as it is the case in this instance, the altered refraction results in a projection of the shock front being visible in the data. For the \(y/s=0.23\) section an additional increase in \(C_{p,RMS}\) is visible close to the trailing edge. This is an optical artifact as well although not originating from gas density gradients but rather from surface imperfection as this is a position where an insert for a few static pressure tappings is located (see Fig. 3; this artifact lies in the area blanked out by Mask 2).

Fig. 6
figure 6

Spanwise variation of buffet intensity and spectral content from unsteady PSP data (\(Re=3.3\times 10^6,\; M=0.84,\; \alpha =-4^\circ\))

Full size image

The positions of the maximum pressure fluctuations are marked P1 to P3. By using Welch’s method [26] PSD (power spectral density) spectra computed for these positions are shown in Fig. 6b . To non-dimensionalize the frequency content, the Strouhal number is computed with \(l_{\text {ref}}\) corresponding to the mean aerodynamic chord of the wind tunnel model as follows:

$$\begin{aligned} St = \frac{f \cdot l_{\text {ref}}}{U_{\infty }} \end{aligned}$$
(1)

Significant broadband signals can be identified for all of the three locations. Elevated PSD values can be seen in the Strouhal number ranges 0.1 - 0.14 and 0.18 - 0.33. Almost constant levels are observed for \(St<0.09\). The fact that these signals are present at various positions within the shock front gives an indication that the aerodynamic effects of shock movement are located within these frequency ranges. For Strouhal numbers above 0.33 the PSD decreases rapidly by an order of magnitude. The maximum Strouhal number observable is linked to the limited frame rate of the unsteady PSP camera of 2kHz.

3.1 Angle of attack dependency

During the wind tunnel tests various angles of attack were investigated with the unsteady PSP method. Results of this study are shown in Fig. 7. RMS values of the pressure coefficient are shown for the wing lower surface computed from 3600 images recorded with the unsteady PSP system. Increased RMS values due to the moving shock front located between the UHBR nacelle and the fuselage can be seen for all four angles of attack. It can be seen that the shock system is moving upstream with decreasing angle of attack and that the magnitude of the shock oscillation is increasing as well. This is also supported by the sectional \(C_{p,RMS}\) distribution shown in Fig. 8a.

From Figs. 7 and 8a it is evident that the chordwise elongation of the shock becomes larger for more negative angles of attack. This is explained by the increased (negative) circulation around the wing resulting in stronger flow accelerations and therefore an increase in shock strength similar to wing upper surface effects at positive angles of attack.

For angles of attack of \(-4^\circ\) and \(-4.5^\circ\), Fig. 7 shows increased pressure RMS values downstream of the shock extending up to the wing trailing edge. Taking into account preliminary accompanying simulations, these increased RMS values are caused by a shock induced separation and the associated vortex shedding originating from the shock/boundary layer interaction. The area of these increased RMS values resides in the same region where flow separation was predicted in the preliminary numerical study in Fig. 1.

Fig. 7
figure 7

RMS values of \(C_{p}\) for varying angles of attack computed from unsteady PSP measurements for the wing lower surface (\(Re=3.3\times 10^6,\; M=0.84\), Mask 2)

Full size image

In Fig. 8b, PSD spectra are shown at the locations of maximum \(C_{p,RMS}\) for each angle of attack. It is noticeable that the high frequency region for Strouhal numbers above 0.4 is not affected by a change in angle of attack. In contrast to this, deviations in PSD levels can be observed in the range of 0.1 to 0.4. A more negative angle of attack results in significantly increased PSD levels. The fact that an increase in \(C_{p,RMS}\) at the shock location is accompanied by increased spectral content in this frequency range together with the results of spanwise variation presented in Fig. 6 gives confidence that the lower wing buffet phenomena can be allocated to Strouhal numbers in the range 0.1 to 0.4.

Fig. 8
figure 8

Influence of angle of attack on buffet intensity and power spectrum at \(y/s=0.2\) extracted from unsteady PSP data (\(Re=3.3\times 10^6,\; M=0.84\))

Full size image

It is noted that increased RMS pressure values can be seen on the outboard wing in Fig. 7 as well indicating unsteady flow phenomena. Nevertheless, these are not analyzed in this study as the focus lies on the inboard UHBR induced buffet phenomenon.

3.2 Reynolds number dependency

As the buffet phenomenon by definition depends on the interaction of the shock with a boundary layer, its dependency on Reynolds number needs to be assessed. It is crucial to understand how the phenomenon translates from low Reynolds numbers to flight relevant Reynolds numbers. One reason for this is that numerical tools like LES or hybrid RANS-LES currently applied to further understand the buffet phenomenon are still limited to low Reynolds numbers due to limitations in computing power.

As can be seen in Table 1, the tests at varying Reynolds numbers also included a variation in the ratio of the dynamic pressure q (related to model loading) to the model’s Young’s modulus (a measure of model stiffness). The term q/E can thereby be interpreted as a measure of the model deformation. Differences in q/E usually imply the need to account for differences in model deformation. Nevertheless, preliminary investigations suggest that the variation in model deformation is insignificant for the inboard buffet effects at these conditions. Differences in the wing pressure distribution only start to be significant over the outer third of the span (see Appendix A).

Fig. 9
figure 9

RMS values of \(C_{p}\) for varying Reynolds number computed from unsteady PSP measurements for the wing lower surface (\(M=0.84,\; \alpha =-4^\circ\), Mask 2)

Full size image

In Fig. 9, RMS values of the local pressure are shown for the wing lower surface for all Reynolds numbers investigated. Due to the fact that the background noise of the unsteady PSP measurement system varies significantly with temperature, this noise had to be accounted for when computing the RMS levels. The details of this calibration method will be published in [30] in 2022.

The increased RMS values due to shock movement inboard of the nacelle can be seen for all Reynolds numbers investigated, indicating that the lower wing buffet phenomenon is present independent of Reynolds number. When comparing the plots it has to be noted that the maximum RMS levels observed for the highest Reynolds number case (\(Re=2.5\times 10^7\)) in the inboard area actually represent spurious values due to an optical artifact from the unsteady PSP measurements as described earlier. This effect is most severe for the highest Reynolds number case due to the high absolute density of the test gas at cold temperatures. Considering the sectional \(C_{p,RMS}\) distribution in Fig. 10a, the severity of this becomes evident. For the highest Reynolds number of \(2.5\times 10^7\), the RMS signal due to the artifact at \(x/c=0.4\) is much stronger than the actual surface pressure signal which coincides with the data for the other Reynolds numbers at \(x/c\approx 0.3\). Therefore the conclusion can be drawn that the location of the lower wing buffet phenomenon is not significantly altered by changes in Reynolds number.

Fig. 10
figure 10

Influence of Reynolds number on buffet intensity and power spectrum at \(y/s=0.2\) extracted from unsteady PSP data (\(M=0.84,\;\alpha =-4^\circ\))

Full size image

The spectral analyses of the Reynolds number dependency of lower wing buffet is given in Fig. 10b. Again, PSD levels are computed for the locations of maximum surface pressure fluctuations. Note that the maximum measurable Strouhal number for the highest Reynolds number case was limited to 0.709 due to fact that the camera frame rate had to be reduced to 1 kHz for technical reasons. The most striking observation from Fig. 10b is the overall reduced PSD levels for \(Re=3.3\times 10^6\). Nevertheless, the plateau observed for Strouhal numbers between 0.2 and 0.32 is also visible for \(Re=6.6\times 10^6\) and \(Re=1.29\times 10^7\), the latter two coinciding very well over the entire spectrum. In addition, the beginning of the decline of PSD levels at \(St=0.34\) coincides very well across the three lowest Reynolds numbers. For the highest Reynolds number of \(2.5\times 10^7\) very good agreement is observed with the data for \(Re=6.6\times 10^6\) and \(Re=1.29\times 10^7\) up to a Strouhal number of 0.34 from which point it fails to follow the decline of the curves towards higher frequencies. Instead, the \(Re=2.5\times 10^7\) spectrum shows an almost constant slope of PSD levels from low to high frequencies.

A deeper insight into the unsteady behavior of the flow field is given by the 2D spectrograms in Fig. 11. Here the frequency spectrum for the \(y/s=0.2\) section is shown over the entire chord length. This allows the identification of frequency bands in which coherent structures along the chord may be present. For all Reynolds numbers the shock location is visible at 30% chord as a dark horizontal line followed by signals stemming from the aforementioned optical artifacts just downstream. Vertical stripes can be identified in the Strouhal number range from 0.06 to 0.4 originating from the position of the shock and propagating downstream for the three lowest Reynolds numbers. These indicate that certain disturbances are excited at the shock location and are propagated up to the trailing edge of the wing. For the highest Reynolds number case in Fig. 11d the signal quality was not sufficient to identify any of these structures. The reason for this is on the one hand the poorer signal-to-noise ratio due to the low temperature and on the other the reduced camera frame rate, which worsens the spectral resolution.

Fig. 11
figure 11

Power spectral density plots at \(y/s=0.2\) (\(M=0.84,\; \alpha =-4^\circ\)) for all Reynolds numbers investigated

Full size image

For \(Re=3.3\times 10^6\) in Fig. 11a a sharp signal is visible for \(St \approx 0.2\) that stretches over almost the entire chord length. This is the only vertical line that is visible ahead of the shock front. Further analysis suggests that this signal is not related to the lower wing buffet phenomenon for multiple reasons. First, it is only visible at the lowest Reynolds number. Second, the signal is also present at various other spanwise positions on the wing, even far outboard of the through flow nacelle. In addition, a pressure wave cannot travel upstream through a supersonic region except in the thin subsonic shear layer close to the wall.

4 Conclusions

In this work a first assessment of a buffet phenomenon on the wing lower surface induced by the installation of a UHBR through flow nacelle was presented. Unsteady pressure sensitive paint measurement data recorded during wind tunnel testing under cryogenic conditions was used to perform the analysis. The wing lower surface buffet effect is caused by the formation of a half open channel between the nacelle, pylon, wing lower surface and fuselage. The resulting shock interacts with the viscous boundary layer on the wing lower surface resulting in a shock induced separation of unsteady nature. It was found that the amplitude of shock oscillation is increasing with decreasing angle of attack due to an increase in shock strength. Significant pressure fluctuations were found downstream of the shock indicating a large area of separated flow. The phenomenon was found to be present over a wide range of Reynolds numbers ranging from 3.3 to 25 million based on mean aerodynamic chord. A preliminary quantification of the buffet frequency ranges have been identified but further studies are required for confirmation. The frequency range and broadband nature of the buffet signal are in agreement with those found in previous studies for upper wing buffet effects at high angles of attack [1, 5, 22] indicating that a similar mechanism may be present. Nevertheless, more in-depth studies are needed to confirm these findings.

The shock induced separation predicted in early stage RANS simulations could be confirmed with experimental data. Although RANS simulations are unable to model the unsteady nature of the phenomenon, these findings give confidence that they are at least suited to give an indication of the presence of this type of buffet. Future work will include numerical investigations of the lower wing buffet by means of unsteady RANS simulations and hybrid RANS-LES methods. In addition, the unsteady PSP data will be analyzed in more detail using POD (proper orthogonal decomposition) and DMD (dynamic mode decomposition) methods to extract the dominant aerodynamic modes of the buffet and confirm the suspected buffet frequencies.