Numerical analysis of high-lift configurations with oscillating flaps

Abstract

This study presents two-dimensional aerodynamic investigations of various high-lift configuration settings concerning the deflection angles of droop nose, spoiler and flap in the context of enhancing the high-lift performance by dynamic flap movement. The investigations highlight the impact of a periodically oscillating trailing edge flap on lift, drag and flow separation of the high-lift configuration by numerical simulations. The computations are conducted with regard to the variation of the parameters reduced frequency and the position of the rotational axis. The numerical flow simulations are conducted on a block-structured grid using Reynolds Averaged Navier Stokes simulations employing the shear stress transport $k-\omega$ turbulence model. The feature Dynamic Mesh Motion implements the motion of the oscillating flap. Regarding low-speed wind tunnel testing for a Reynolds number of $0.5 \times 10^{6}$ the flap movement around a dropped hinge point, which is located outside the flap, offers benefits with regard to additional lift and delayed flow separation at the flap compared to a flap movement around a hinge point, which is located at 15 % of the flap chord length. Flow separation can be suppressed beyond the maximum static flap deflection angle. By means of an oscillating flap around the dropped hinge point, it is possible to reattach a separated flow at the flap and to keep it attached further on. For a Reynolds number of $20 \times 10^6$, reflecting full scale flight conditions, additional lift is generated for both rotational axis positions.

1 Introduction

To meet the ACARE Flightpath 2050 [8] reduction target emissions, it is necessary to increase aircraft efficiency. In addition to further developments in engine technology, improvements in reduced structural weight and aerodynamics are necessary. Weight optimization of flight-relevant systems such as flaps and high-lift devices are at the forefront. The advanced dropped hinge flap (ADHF), with its simple and light construction [26], stands in contrast to the complex flap systems used by previous generations of aircraft. For the present investigations the lift coefficient should be increased by means of oscillating flaps. Regarding constant lift at steady level flight flap dimensions can be reduced as the lift coefficient has been raised. The smaller flap size may lead to a reduced structural weight, which gives a margin for increasing the payload mass. Some additional weight related to the flap oscillating mechanism lowers the payload margin to some extent. In addition to increasing the lift coefficient, the flap oscillation is intended to excite the decay of the wake vortex system of the high-lift configuration. This study deals with the increase of lift by oscillating flaps.

Comprehensive investigations have already been carried out on the aerodynamics of oscillating airfoils and flaps. Cleaver, Wang, Gursul and Visbal [5,6,7] investigated the aerodynamic behavior of a vertically oscillating NACA-0012 airfoil at low Reynolds numbers with an already separated flow at the airfoil. An increase in lift was observed due to vortex separation at the leading edge. This vortex induces a negative pressure on the suction side of the airfoil. Local lift maxima were measured if the oscillation and vortex separation were in resonance. The lift increased approximately linearly with the oscillation frequency until a so-called mode-2 flow field occured. The leading edge vortex, created during the downward movement, dissipated by colliding with the airfoil already moving upwards again. This resulted in a reduction in lift. However, this had a positive effect on the drag with increasing frequency.

Miranda, Vlachos, Telionis and Zeiger [14] investigated how already separated flow can still be controlled by oscillating flaps. They used a symmetrical airfoil with sharp leading and trailing edges and a periodically moving flap. The oscillating flap was used to control the separated flow and the separated vortices. There was no need to hit a natural separation frequency of the flow structure. The method was particularly effective at angles of attack up to 20$^{\circ }$, whereas only slight increases in lift were observed at larger angles of attack.

Liggett and Smith [12] looked at an airfoil with flap and gap between flap and airfoil using numerical simulations with hybrid turbulence modelling. The flap oscillated with different frequencies. The influence of several parameters, like reduced frequency, angle of attack and gap size, on lift and drag was investigated. To a certain extent, it could be observed that the formation of trailing edge separation is prevented with increasing reduced frequency. In addition, the phase offset between the flap movement and the reaction of the aerodynamic forces increased within the angle of attack range of 6$^{\circ }$ to 16$^{\circ }$ with an increase in the reduced frequency. A larger gap spacing between flap and airfoil also increased the delay between flap movement and resulting aerodynamic response. At higher angles of attack and thus a separated flow, discontinuities were observed. So the oscillating flap favours the formation of vortices. Othman et al. [15, 23] investigated the transient lift behavior of a harmonic pitching NACA-0012 airfoil with CFD and static airfoil with oscillating flap by means of experiments. The results were compared with the transient theory according to Theodorsen (potential flow) [27] and with the Leishman method [11]. Leishman further developed Theodorsen’s theory by adding terms to include a moving trailing edge flap. In general, a good agreement with Theodorsen’s theory could be established. The amplitude of the lift decreased with low and medium reduced frequency and increased again with higher reduced frequency. The phase offset increased with increasing reduced frequency. The amplitude of the cumulative term showed the same progression as predicted by Theodorsen, although the simulations showed slightly lower values. With regard to the phase offset, the results of the simulation showed an overestimation in comparison to Theodorsen. The authors attributed this to the consideration of viscosity in CFD, which is not considered by potential flow modelling. The experimental investigations dealt with the effects of an oscillating flap on the transient lift behavior of an otherwise static profile. The Reynolds number was 21000, the fixed angles of attack were 0$^{\circ }$ and 10$^{\circ }$ with flap deflection angles of $\pm 5^{\circ }$, $\pm 8^{\circ }$ and $\pm 10^{\circ }$ at reduced frequencies from 0.023 to 0.12. In general, it could be observed that the experiments showed more pronounced lift peaks compared to theory. For small oscillations, it was found that there are only small differences in the time-averaged lift, most clearly with flap deflections of $\pm 8^{\circ }$ and $\pm 10^{\circ }$ and a reduced frequency of k $> 0.05$. At $\alpha = 10^{\circ }$, the lift increases at flap deflection angles of $\pm 5^{\circ }$ and $\pm 8^{\circ }$. Leishman’s method was less consistent at $\alpha = 10^{\circ }$, as it rather underestimated the lift gain.

In general, it was found that the harmonic movement of an airfoil can increase lift and delay flow separation. However, only Liggett and Smith [12] and Othman et al. [15] have investigated the case of a static main airfoil with dynamic trailing edge flap and its effect on the aerodynamic characteristics of the configuration. So, a rotational or translational motion of the flap or the airfoil was investigated.

In this paper, 2D high-lift configurations with oscillating slotted advanced dropped hinge flaps are considered by a CFD approach. On the one hand the time-averaged lift coefficient of the configuration should be increased by the oscillation and, on the other hand, the flow separation at the trailing edge flap should be shifted to higher deflection angles. A comparison between two different flap motion kinematics is shown. Also, a variation of the parameters reduced frequency and Reynolds number are included.

2 Geometry

In this section, the reference geometry of a transport aircraft LR-270 (Long Range-270) and the investigated high-lift geometry is presented. The reference geometry LR-270 was created within the project BIMOD (Influencing maximum lift and wake vortex instabilities by dynamic flap movement), which is conducted by the Institute of Aerospace Systems (RWTH Aachen), the Institute of Structural Mechanics (RWTH Aachen) and the Chair of Aerodynamics and Fluid Mechanics (TU Munich). In Sect. 2.1, the reference geometry LR-270 with its dimensions and data set is presented. By means of the reference geometry, a 2D high-lift configuration is derived in Sect. 2.2. The high-lift configuration is an advanced dropped hinge flap system at the trailing edge and a droop nose at the leading edge.

2.1 Reference geometry

A long-range aircraft with a maximum take-off mass of 270 t is designed (LR-270) with the aircraft design software MICADO [21] of the Institute of Aerospace Systems (RWTH Aachen). For the calculation various semi empirical methods such as described by Torenbeek [28], Raymer [18] and Howe [9] are used together with analytical tools to carry out the entire aircraft preliminary design under specification of a few top-level aircraft requirements. This paper gives a basic overview of the geometry LR-270 and further descriptions can be found in [25]. Table 1 gives the dimensions of the reference geometry LR-270.

Table 1 Dimensions of the reference geometry

The wing is divided into four segments (S1–S4). Figure 1 shows the span segments of the wing. Segment 1 ranges from y/s = 0.095 to y/s = 0.344, segment 2 from y/s = 0.344 to y/s = 0.665, segment 3 from y/s = 0.665 to y/s = 0.967 and segment 4 from y/s = 0.967 to y/s = 1. In spanwise direction a parameterized transonic NASA-SC2 airfoil is implemented. The sweep angle is defined at each segment as $\varphi _{25}$ = 30.08$^{\circ }$ (S1), $\varphi _{25}$ = 31.92$^{\circ }$ (S2), $\varphi _{25}$ = 32.23$^{\circ }$ (S3) and $\varphi _{25}$ = 34.25$^{\circ }$ (S4). The dihedral angle $\nu$ amounts at segment 1 $\nu$ = 9.41$^{\circ }$, segment 2 $\nu$ = 8.33$^{\circ }$, segment 3 $\nu$ = 10.95$^{\circ }$ and segment 4 $\nu$ = 8$^{\circ }$. The twist is not constant in the respective segments. Segment 1 starts with a twist angle of $\epsilon$ = 0.5$^{\circ }$ at y/s = 0.095 and decreases linearly to a value of $\epsilon$ = -1.5$^{\circ }$ at y/s = 0.344. In the same way, the twist angle in segment 2 decreases from $\epsilon$ = -1.5$^{\circ }$ to $\epsilon$ = -3$^{\circ }$. Segment 3 from $\epsilon$ = -3$^{\circ }$ to $\epsilon$ = -4$^{\circ }$ and segment 4 ends with $\epsilon$ = -4.7$^{\circ }$. The thickness ratio t/c_local decreases linearly in spanwise direction at segment 1 from t/c_local = 13.2% to t/c_local = 11%. Within segment 2 the thickness ratio changes from t/c_local = 11% to t/c_local = 9.4%. The thickness ratio stays constant in segment 3 at t/c_local = 9.4%. In segment 4, the thickness ratio varies from t/c_local = 9.4% to t/c_local = 9.5% (Table 2).

Fig. 1

Wing geometry of the generic aircraft LR-270

Table 2 Data set for the wing geometry

2.2 High-lift geometry

Based on the NASA-SC2 airfoil a high-lift configuration with variable droop nose deflection angle (DN), spoiler deflection angle (S) and flap deflection angle (F) is constructed. By means of numerical flow simulations and literature review [19, 20], the respective chord length of the high-lift devices are determined. The geometrical data of the high lift systems are simplified, first. No optimization is carried out. The geometry initially serves for trend studies. At this point reference should be made to literature which explicitly deals with droop nose devices [1, 4, 10, 16]. The design of the droop nose is based on the airfoil nose contour (Fig. 2). The hinge point of the droop nose is set to 0.1 c_local on the airfoil chord. At the range of 0 to 0.06 c_local the droop nose contour is a rigid body. From 0.06 c_local to 0.14 c_local the geometry is morphing by means of bending beam analogy. The chord length of the spoiler is c_S = 0.12 c_local. The hinge point of the spoiler is defined as the intersection of the upper side of the airfoil and the perpendicular direction to the airfoil chord at 0.76 c_local. The spoiler section is divided into a morphing and rigid part (Fig. 2). The flap chord length is set to c_F = 0.19 c_local. As a simplification, geometric data of the nose of the main airfoil is used for the trailing edge flap shape.

Fig. 2

Schematic drawing of the high-lift geometry with droop nose, spoiler and flap (ADHF-system) at y/s = 0.344 at $\epsilon$ = -1.5$^{\circ }$ and detail views of morphing droop nose and spoiler with definitions of gap and overlap

The droop nose is examined for the positions DN = [0$^{\circ }$; 15$^{\circ }$; 25$^{\circ }$]. The spoiler deflection angle takes the values S = [0$^{\circ }$; 4$^{\circ }$; 6.8$^{\circ }$; 8$^{\circ }$]. The trailing edge flap deflection angle is investigated, for a range of F = [15$^{\circ }$; 20$^{\circ }$; 25$^{\circ }$; 28$^{\circ }$; 29$^{\circ }$; 30$^{\circ }$; 34$^{\circ }$; 35$^{\circ }$]. For transient simulations with oscillating flap, two different rotation points are defined. The flap point (P_flap) is defined at P_flap = 0.15$\cdot$c_flap (see Fig. 3a) and the hinge point (P_hinge) is defined outside the geometry (see Fig. 3b). P_hinge is also the rotation point of the advanced dropped hinge flap (ADHF) system. The hinge point is designed as shown in [29]. The respective forms of the movement are explained in Sect. 3.2.

Fig. 3

Flap oscillation around the flap point P_flap (a) and the hinge point P_hinge (b)

3 Numerical setup

This section gives an overview on the applied computational mesh, the setup of the flow solver and the flow conditions. The prescribed flow conditions are summarized in Table 3.

Table 3 Flow conditions

3.1 Computational mesh

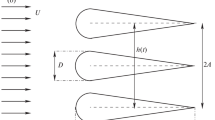
The generation of the computational mesh is conducted with ANSYS ICEMCFD. A block structured 2D mesh featuring quadrilateral elements is created. The boundary layer is resolved by choosing a dimensionless wall distance of y$^+ \le 1$ on the entire geometry. The computational domain and the applied boundary conditions are depicted in Fig. 4. The angle of attack $\alpha$ is defined by the boundary conditions. Depending on the sign of the angle of attack, the boundary conditions velocity inlet or pressure outlet are attributed to the boundaries.

Fig. 4

Computaional domain and boundary conditions

Convergence and mesh independency studies were conducted to determine a reasonable size of the computational mesh and to ensure low numerical errors caused by the spatial discretization. The mesh that is applied for the numerical investigations consists of approximately 150000 quadrilateral elements. The size of the domain guarantees no influence from the imposed boundary conditions on the flow field near the geometry.

3.2 Computational fluid dynamics

The numerical flow simulations are conducted with ANSYS FLUENT. The steady/unsteady Reynolds-averaged Navier-Stokes equations (U/RANS) are solved by means of a pressure based solver [2, 3]. For transient simulations with oscillating flaps a steady state solution is employed for the flow initialization. Turbulence modelling is performed by the shear stress transport $k-\omega$ SST turbulence model [13] and the turbulence properties at the boundaries are set in order to provide a turbulence intensity of Tu = 0.2% at the front of the geometry. The COUPLED algorithm [2, 3] treats the pressure-velocity coupling. The second-order pressure scheme is employed for the pressure interpolation and second-order upwind schemes are chosen for the spatial discretization of momentum, turbulent kinetic energy and specific dissipation rate. Moreover, a least squares cell-based formulation is used for the gradient calculation. A bounded second-order implicit scheme is selected for the temporal discretization [2, 3]. The time step size $\varDelta$t is selected by means of convergence studies, flow field analysis and frequency f of the flap motion:

$$\begin{aligned} \varDelta t = \frac{1}{f} \cdot \frac{1}{10^\text {N}} \quad \text {with}~ \text {N} = {1,2,3} \end{aligned}$$

(1)

In order to define the appropriate time step size, simulations with different time step sizes were carried out for N = [1; 2; 3]. A sufficient time step size resolution was achieved for N = 2. By means of the frequency f a reduced frequency k is defined as:

$$\begin{aligned} {k = \frac{\pi \cdot f \cdot c_{chord}}{U_{ref}}.} \end{aligned}$$

(2)

To model the flap motion an user defined function (UDF) is implemented. The flap motion function is defined as:

$$\begin{aligned} {g(t) = \varDelta \delta \cdot \sin\left(\frac{2k \cdot U_{ref}}{c_{chord}} \cdot t\right)}. \end{aligned}$$

(3)

If the equation is differentiated with respect to time, the velocity equation of the flap oscillation is obtained:

$$\begin{aligned} {g'(t) = \varDelta \delta \cdot \frac{2k \cdot U_{ref}}{c_{chord}} \cdot \cos\left(\frac{2k \cdot U_{ref}}{c_{chord}} \cdot t\right)}. \end{aligned}$$

(4)

Based on Eq. 4 the UDF is created. Parameters are the amplitude $\varDelta \delta$ , reduced frequency k and the location of the rotation point of the movement. A negative $\varDelta \delta$ corresponds to a reduction of the flap deflection angle and a positive $\varDelta \delta$ corresponds to an increase of the flap deflection angle. Figure 5 shows the plotted functions g(t) and $g'(t)$ for $\varDelta \delta$ = 2.5$^{\circ }$, f = 1 Hz, U_ref = 1 m/s and c_chord = 1 m.

Fig. 5

Flap kinematic functions g(t) and g’(t) with $\varDelta \delta = 2.5^{\circ }$, f = 1Hz, U_ref = 1 m/s, c_chord = 1 m

The flap position as a function of time is shown by g(t) while $g'(t)$ presents the angular velocity of the flap over time. The computational mesh must be adapted for each time step applying dynamic mesh motion methods, which include layering and smoothing [2].

4 Results

First, steady-state solutions of different high-lift configuration settings are presented (see Sect. 4.1). The investigations are conducted at two different Reynolds numbers. A Reynolds number attributed to full-scale conditions (Re = $20 \times 10^6$, Ma = 0.21) and a Reynolds number at wind tunnel conditions (Re = $0.5 \times 10^6$, Ma = 0.07) are defined. After an analysis of the steady-state results (lift and flow field) suitable solutions are selected for the transient simulations. The transient simulations are initialized by means of the steady-state solutions. Transient solutions are presented with regard to the influence of the reduced frequency k and the rotation point (see Sect. 4.2).

4.1 Steady state investigations

First, the results of the steady-state simulations on the full scale are evaluated at Re = $20 \times 10^6$ and Ma = 0.21. Here, the influences of the different high-lift devices, namely trailing-edge flap, spoiler and droop nose, on the lift coefficient and the flow field around the configuration are discussed and analyzed.

Trailing-edge deflection The flap deflection angle is adjusted by means of the hinge point (P_hinge). Figure 6 shows lift coefficient curves for flap deflection angles of F = [20$^{\circ }$; 25$^{\circ }$; 30$^{\circ }$] at Re = $20 \times 10^6$ and Ma = 0.21. The droop nose deflection angle and the spoiler deflection angle are set to DN = S = 0$^{\circ }$. The corresponding relativ gap g/c_local and overlap o/c_local (see Fig. 2) result to g/c_local = [0.01; 0.013; 0.015] and o/c_local = [0.016; 0.012; 0.008] for F = [20$^{\circ }$; 25$^{\circ }$; 30$^{\circ }$]. The parameter c_local represents the local chord length of the wing.

Fig. 6

Lift coefficient curves C_L($\alpha$) for high-lift configurations with variable flap deflection angle at Re = $20 \times 10^6$, Ma = 0.21

At a flap deflection of F = 30$^{\circ }$ (DN00S00F30), the flow at the flap is already separated at low angles of attack. This results in a downward shifted lift curve compared to the configurations DN00S00F25 and DN00S00F20. The lift curve of the configuration DN00S00F25 is shifted upwards with regard to the configuration DN00S00F20. As it can be expected, C_Lmax is increased for the configuration with flap deflection F = 25$^{\circ }$ compared to the configuration with flap deflection F = 20$^{\circ }$, but $\alpha _{\hbox {max}}$ is decreased. Figure 7 shows the normalized velocity magnitude and streamlines for the configuration with flap deflection angle of F = 25$^{\circ }$ (a) and F = 30$^{\circ }$ (b).

Fig. 7

Normalized velocity magnitude and streamlines for the high-lift configurations DN00S00F25 (a) and DN00S00F30 (b) at Re = $20 \times 10^6$, Ma = 0.21, $\alpha$ = 8$^{\circ }$

Spoiler deflection In order to avoid the flow separation at the trailing-edge flap, a spoiler deflection angle is applied. Increasing the spoiler deflection angle (mathematically negative) reduces the gap between spoiler and flap. This favours a reattachment of the flow to the trailing edge flap [24]. In addition, the flow is already diverted in the direction of the flap deflection by the spoiler. By increasing the spoiler deflection angle, the lift coefficient also increases. Figure 8 shows lift coefficient curves for spoiler deflection angles of S = [0$^{\circ }$; 4$^{\circ }$; 8$^{\circ }$], droop nose deflection of DN = 0$^{\circ }$ and flap deflection of F = 30$^{\circ }$ at Re = $20 \times 10^6$ and Ma = 0.21. This results to g/c_local = [0.015; 0.011; 0.006] and o/c_local = [0.008; 0.007; 0.006].

Fig. 8

Lift coefficient curves C_L($\alpha$) for high-lift configurations with variable spoiler deflection angle at Re = $20 \times 10^6$, Ma = 0.21

Fig. 9

Normalized velocity magnitude and streamlines for the high-lift configurations DN00S00F30 (a) and DN00S08F30 (b) at Re = $20 \times 10^6$, Ma = 0.21, $\alpha$ = 8$^{\circ }$

At larger spoiler deflection the non-linear course of the lift curve starts at lower angles of attack and the stall angle is also reduced [20]. Figure 9 shows the normalized velocity magnitude and streamlines for the configurations DN00S00F30 (a) and DN00S08F30 (b). For the configuration DN00S00F30 the flow around the flap is separated. To keep the flow attached the spoiler is deflected by S = 8$^{\circ }$ (DN00S08F30).

Fig. 10

Lift coefficient curves C_L($\alpha$) for high-lift configurations with variable droop nose deflection angle at Re = $20 \times 10^6$, Ma = 0.21

Fig. 11

Normalized velocity magnitude and streamlines for the high-lift configurations DN00S00F25 (a) and DN25S00F25 (b) at Re = $20 \times 10^6$, Ma = 0.21, $\alpha$ = 18$^{\circ }$

Fig. 12

Lift coefficient curves C_L($\alpha$) for high-lift configurations DN25S6.8F34 and DN25S6.8F35 at Re = $20 \times 10^6$, Ma = 0.21

Droop nose deflection Figure 10 shows lift coefficient curves with different droop nose deflections DN = [0$^{\circ }$; 15$^{\circ }$; 25$^{\circ }$] and fixed spoiler deflection S = 0$^{\circ }$ and flap deflection F = 25$^{\circ }$ at Re = $20 \times 10^6$ and Ma = 0.21.

By means of the droop nose, the maximum angle of attack $\alpha _{\hbox {max}}$ can be increased. Ultimately, it leads to a larger possible C_Lmax. But the curve of the lift coefficient is minimal shifted downward. This is achieved by reducing the over speeds at the leading edge. Thus, the positive pressure gradient is reduced, which has an advantageous effect on the separation behavior. Figure 11 shows the normalized velocity magnitude and streamlines for the configurations DN00S00F25 (a) and DN25S00F25 (b) at $\alpha$ = 18$^{\circ }$.

By means of a droop nose deflection the suction peak at the leading edge is reduced and two smaller suction peaks result (see Fig. 14). The adverse pressure gradient decreases. Consequently, the possibility of stall decreases. With regard to previous design studies on variable droop nose devices, the second suction peak could be avoided by a proper design of the variable droop nose. This issue is not emphasized in the context of the present study, as the main objective is on the oscillating trailing edge flap impact on lift coefficient trends.

Reference cases for dynamic lift impact Figure 12 shows the lift coefficient curves of the high-lift configuration DN25S6.8F34 and DN25S6.8F35 at a Reynolds number of Re = $20 \times 10^6$. The deflection angles of the droop nose and spoiler are fixed at DN = 25$^{\circ }$ and S = 6.8$^{\circ }$ for all transient investigations. The spoiler deflection angle is fixed at S = 6.8$^{\circ }$, since larger deflections cannot be realized for the lower Reynolds number (Re = $0.5 \times 10^6$) case, which is of relevance for low-speed small scale testing.

If the flap deflection is set to F = 35$^{\circ }$ the lift coefficient decreases for all angles of attack compared to a flap setting of F = 34$^{\circ }$. The reason for this is a flow separation at the trailing-edge flap (see Fig. 14).

Second, a lower Reynolds number case, Re = $0.5 \times 10^6$, Ma = 0.07, is considered which reflects typical low-speed wind tunnel conditions. In addition to the numerical simulations, experimental tests will be carried out in the course of the research project. Therefore, the full-scale model will be scaled to a wind tunnel dimension. For the lower Reynolds number, the high-lift devices have an analog influence on lift. However, due to the Reynolds number effect, for the lower Reynolds number $\alpha _{\hbox {max}} = 13^{\circ }$ and C_Lmax = 2.38 are reduced compared to the higher Reynolds number with $\alpha _{\hbox {max}} = 17^{\circ }$ and C_Lmax = 3.1. Figure 13 shows the lift coefficient curves of the high-lift configuration DN25S6.8F28 and the high-lift configuration DN25S6.8F29 at a Reynolds number of Re = $0.5 \times 10^6$ and Mach number of 0.07.

Fig. 13

Lift coefficient curves C_L($\alpha$) for high-lift configurations DN25S6.8F28 and DN25S6.8F29 at Re = $0.5 \times 10^6$, Ma = 0.07

Fig. 14

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F35 at Re = $20 \times 10^6$, Ma = 0.21, $\alpha = 8^{\circ }$ and pressure distribution

Fig. 15

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F29 at Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha = 12^{\circ }$ and pressure distribution

Fig. 16

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F35, flap motion around the flap point, k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $20 \times 10^6$, Ma = 0.21, $\alpha$ = 8$^{\circ }$ at t/T_p = [0.25; 0.5; 0.75; 1.00]

Fig. 17

Flap position at t/T_p = [0; 0.25; 0.5; 0.75; 1.00]

In a similar manner, the lift curve of the configuration DN25S6.8F29 at Re = $0.5 \times 10^6$ is shifted downward compared to the lift curve of the configuration DN25S6.8F28. Also here, a separation at the flap can be observed (see Fig. 15).

Now, an oscillating trailing-edge flap should provide an attached flow at the trailing-edge flap for both Reynolds number cases. For the higher Reynolds number (Re = $20 \times 10^6$) a “landing configuration” (DN25S6.8F35) is selected. Therefore, an angle of attack of $\alpha$ = 8$^{\circ }$ is chosen. For the configuration (DN25S6.8F29) with lower Reynolds number (Re = $0.5 \times 10^6$) an angle of attack of $\alpha$ = 12$^{\circ }$ is chosen, so that the lift coefficients of the two configurations are comparable. A 3D wind tunnel model is derived from the 2D numerical data in the course of the project. Since other effects are also to be investigated, a comparable lift coefficient between full scale and wind tunnel conditions is taken as a basis for the overall analysis. Figure 14 shows the pressure distribution, the normalized velocity magnitude and streamlines for the configuration DN25S6.8F35 at Re = $20 \times 10^6$.

Due to the droop nose, two suction peaks occur at the leading edge of the high-lift configuration. By means of the spoiler deflection angle, a suction peak is located at the spoiler hinge point. The flow at the trailing-edge flap is largely separated. Figure 15 shows the pressure distribution, the normalized velocity magnitude and streamlines for the configuration DN25S6.8F29 at Re = $0.5 \times 10^6$.

The minimum pressure coefficient at the leading edge is reduced compared to the configuration DN25S6.8F35 at Re = $20 \times 10^6$. The flow at the area of the spoiler is separated. Thereby, no suction peak is located at the spoiler hinge point. The flow at the trailing-edge flap is separated. The steady-state results of the configurations DN25S6.8F29 at Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha = 12^{\circ }$ and DN25S6.8F35 at Re = $20 \times 10^6$, Ma = 0.21, $\alpha = 8^{\circ }$ are the initial flow conditions for the transient investigations.

4.2 Transient investigations

Time accurate simulations varying the parameters reduced frequency k and rotation point are conducted. First, the configuration at the higher Reynolds number is examined. Figure 16 shows the contour plots of the normalized velocity magnitude and the streamlines of transient simulations at the normalized time steps t/T_p = [0.25; 0.5; 0.75; 1.00] for a flap motion around the flap point with k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, $\alpha$ = 8$^{\circ }$, Re = $20 \times 10^6$ and Ma = 0.21. As a reminder, Fig. 17 shows the respective position and angular velocity of the flap dependency on time.

As already mentioned, the transient simulation was initialized with the result from the steady state solution (see Fig. 14). The flow at the trailing-edge flap is attached at time t/T_p = 0.25. At time t/T_p = 0.50 the flap is in the initial position again and is moving downward. The flow around the flap is not separated like for the steady-state case. Furthermore, no separation can be located at time t/T_p = 0.75 (maximum flap deflection). The flow remains attached over the entire motion period.

Fig. 18

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F35, flap motion around hinge point, k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $20 \times 10^6$, Ma = 0.21, $\alpha$ = 8$^{\circ }$ at t/T_p = [0.25; 0.5; 0.75; 1.00]

Fig. 19

C_L and C_D as a function of t/T_p for DN25S6.8F35, flap and hinge kinematic, k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $20 \times 10^6$, Ma = 0.21, $\alpha$ = 8$^{\circ }$

Fig. 20

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F29 flap motion around flap point, k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$ at t/T_p = [0.25; 0.5; 0.75; 1.00]

Fig. 21

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F29 flap motion around hinge point, k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$ at t/T_p = [0.25; 0.5; 0.75; 1.00]

Fig. 22

C_L and C_D as a function of t/T_p for DN25S6.8F29, flap and hinge kinematic, k = 0.1, $\varDelta \delta = 2.5^{\circ }$, Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha = 12^{\circ }$

Figure 18 shows the contour plots of the normalized velocity magnitude and the streamlines of transient simulations at the normalized time steps t/T_p = [0.25; 0.5; 0.75; 1.00] for a flap motion around the hinge point with k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, $\alpha$ = 8$^{\circ }$, Re = $20 \times 10^6$ and Ma = 0.21. Here again, the transient simulation was initialized with the result from the steady state solution (see Fig. 14). The flow at the trailing-edge flap is attached at time t/T_p = 0.25 like for the kinematics around the flap point. Also at time t/T_p = 0.50 the flap is in the initial position again and is moving downward. The flow on the flap is not separated like for the steady state case. Furthermore, no separation can be located at time t/T_p = 0.75 (maximum flap deflection). Over the entire motion period the flow remains attached.

At first impression, there are no differences between the two forms of motion. But Fig. 19 shows the flow behavior of the different cases in the lift coefficient and the drag coefficient over three periods of time. The averaged lift coefficient and the drag coefficient (average of the third period) are nearly equal for both types of movement. The amplitude of the C_L curve of the hinge kinematics is lower compared to the flap kinematics. The lower variation of the lift coefficient would be advantageous because it would reduce the unsteady loads on the flap supports and thus reduce fatigue. Compared to the initial C_L and C_D values (DN25S6.8F35), the averaged lift coefficient is increased by 15.5% and the drag coefficient is decreased by 7.3%. Compared to the configuration DN25S6.8F34 (Fig. 12) the averaged lift coefficient is increased by 2.1% and the drag coefficient is increased by 6.6%. For a landing configuration these tendencies would be desirable, since a higher lift coefficient may reduce the approach speed and thus the length of the required runway. Furthermore, the higher drag coefficient allows for steeper approach glide path angles. Since the data under full-scale conditions are difficult to validate (no experimental data), numerical simulations are performed using wind tunnel conditions.

Therefore, the transient behavior for the lower Reynolds number is investigated. For the transient simulations under wind tunnel conditions, a completely different flow pattern is obtained. Compared to the configuration at high Reynolds number, a different behavior is present for the movement around the flap point at Re = $0.5 \times 10^6$. Figure 20 shows the contour plots of the normalized velocity magnitude and the streamlines of transient simulations at the normalized time steps t/T_p = [0.25; 0.5; 0.75; 1.00] for a flap motion around the flap point with k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, $\alpha$ = 12$^{\circ }$, Re = $0.5 \times 10^6$ and Ma = 0.07.

As already mentioned, the transient simulation was initialized with the result from the steady-state solution (see Fig. 15). The flow at the trailing-edge flap is separated at time t/T_p = 0.25. At time t/T_p = 0.50 the flap is in the initial position again and is moving downward. The flow at the flap is separated like for the steady-state case. Furthermore, a flow separation can be located at time t/T_p = 0.75 (maximum flap deflection). The flow remains separated over the entire period.

Figure 21 shows the contour plots of the normalized velocity magnitude and the streamlines of transient simulations at the normalized time steps t/T_p = [0.25; 0.5; 0.75; 1.00] for a flap motion around the hinge point with k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, $\alpha$ = 12$^{\circ }$, Re = $0.5 \times 10^6$ and Ma = 0.07. The flow at the trailing-edge flap is nearly attached at time t/T_p = 0.25. At time t/T_p = 0.50 the flap is in the initial position again and is moving downward. The flow around the flap is not separated like for the steady-state case. Furthermore, no separation can be located at time t/T_p = 0.75 (maximum flap deflection). The flow remains attached over the entire period. With regard to the flow separation behavior at the flap, the hinge point kinematics (case 2) is advantageous compared to the movement around the flap point (case 1).

Both flaps start to move in the mathematically positive direction of rotation. The flow at the flap for case 1 is still separated at t/T_p = 0.25. Furthermore, a separated flow at the trailing-edge flap can be observed over the entire simulation time of three periods. For case 2 the flow at the flap is nearly attached at t/T_p = 0.25. The flow at the flap remains attached for the further time steps. After a transient phase of three periods (t/T_p = 3), the flow at the flap is attached for the hinge point movement at any time step. The flow behavior of the different cases is reflected in the lift coefficient and the drag coefficient (see Fig. 22). Compared to case 1, case 2 exhibits an increase in the averaged lift coefficient of $\varDelta C_{\hbox {L}} = 12.6$%. The averaged drag coefficient is compared to case 1 lower by an amount of 4.4%. Compared to the configuration DN25S6.8F28 (Fig. 13) the averaged lift coefficient of case 2 is increased by 2.8% and the averaged drag coefficient is increased by 9.1%.

Now, various reasons for this behavior are explained. Figure 23 is a zoomed image section of the steady-state solution (Fig. 15) and shows the normalized velocity magnitude and streamlines at Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$. A large separation can be detected on the flap. This corresponds to the separation behavior of a non-moving wall. The position of the separation point is given by the fact that the wall shear stress $\tau _w$ becomes zero [22].

Fig. 23

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F29, flap motion around hinge point, k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$, at t/T_p = 0

Fig. 24

Alteration of the gap distance g/c of the configuration DN25S6.8F29 over the amplitude $\varDelta \delta$

Fig. 25

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F29, flap motion around hinge point, k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$ at t/T_p = [0.25; 0.5; 0.75; 1.00]

Now, the flap is actuated. The gap and overlap distance between spoiler and flap changes over time for both cases (see Fig. 24). This behavior is frequency independent. The change of the gap distance for case 2 is significantly higher compared to case 1.

For case 2, the gap distance decreases up to t/T_p = 0.25. Furthermore, the effective angle of attack of the flap is reduced. Based on these aspects, the flow is nearly attached at t/T_p = 0.25 for a flap motion around the hinge point, k = 0.1, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $0.5 \times 10^6$, $\alpha$ = 12$^{\circ }$ (see Fig. 25). Although the gap increases from time t/T_p = 0.25 to time t/T_p = 0.5 (initial start position), the flow at the flap still remains attached (see Fig. 25).

The separation process under unsteady flow conditions is different to steady flow conditions. A zone of reversed flow detached from the wall with attached flow on the surface underneath (wake burst) is formed between the flap flow and the airfoil flow instead of a steady-state separation at the flap like at time t/T_p = 0.00. This is reminiscent of the separation behavior of a downstream moving wall in flow direction [17]. In addition, an attached flow at the flap is detected at time t/T_p = 0.75 (see Fig. 25). At time t/T_p = 0.75 the maximum deflection of the flap is reached. As the effective angle of attack of the flap increases, the stagnation point at the flap lower side is shifted downstream from time t/T_p = 0.25 to t/T_p = 0.75. For this reason, the axial velocity on the suction side of the flap increases, although the gap is getting larger. These are aspects which increase the risk of flow separation. However, as there is still a relatively large overlap between flap and airfoil, the spoiler prevents flow separation at the flap.

Even for an upstream moving flap, the flow around the flap will remain attached. The reversed flow between flap flow and airfoil flow for the upstream moving flap differs from the reversed flow of the downstream moving flap. This indicates a transient flow behavior dependent on an upward or downward moving flap. However, this flow behavior during one period is frequency-dependent. Figure 26 shows the frequency dependency of the averaged lift coefficient in flap kinematics around the hinge point at $\varDelta \delta$ = 2.5$^{\circ }$, Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$.

Fig. 26

Averaged lift coefficient as function of the reduced frequency k, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$, kinematic around hinge point

Fig. 27

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F29, flap motion around hinge point, k = 0.05, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$, at t/T_p = [0.25; 0.5]

Fig. 28

Normalized velocity magnitude and streamlines for the high-lift configuration DN25S6.8F29, flap motion around hinge point, k = 0.4, $\varDelta \delta$ = 2.5$^{\circ }$, Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$ at t/T_p = [0.25; 0.5]

As already mentioned, for a steady flap deflection (k = 0) a separation is detected at the flap for DN25S6.8F29 at Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$. For a reduced frequency of k = 0.1, the lift coefficient increases slightly up to a reduced frequency of k = 0.3. The flow behavior in this frequency range is as shown in Fig. 25. For a reduced frequency of k = 0.05 the flow behavior is quasi-steady and the flow separates at t/T_p = 0.50 again. Figure 27 shows the normalized velocity magnitude and streamlines at Re = $0.5 \times 10^6$, Ma = 0.07, $\alpha$ = 12$^{\circ }$, k = 0.05, $\varDelta \delta$ = 2.5$^{\circ }$ at t/T_p = [0.25; 0.50]. At time t/T_p = 0.25 an attached flow can be observed at the flap. But at time t/T_p = 0.50 a flow separation at the flap is detected again. Even at the times t/T_p = [0.50-1.00] the flow remains separated. In contrast, at a frequency of k = 0.4 (and k = 0.5) the flow is separated at time t/T_p = 0.25 as well as at time t/T_p = 0.50 (see Fig. 28). The flow is separated at any time. The flap oscillates so fast that the fluid momentum transport cannot react to the movement of the flap. Ligget and Smith [12] list the dependence of the lift coefficient on the reduced frequency k in their study. Also here, it is shown that the effect for an increase of the lift coefficient by oscillating flaps hardly occurs at too low and too high reduced frequencies. Although the present study is difficult to compare with the results of Ligget and Smith (different Mach number, Reynolds number, geometrical properties, hybrid numerical approach), it is possible to recognize similarities in terms of the order of magnitude of the reduced frequency, for which an increase in the lift coefficient is obtained. This study is aimed to preliminary methods.

5 Conclusion

The enhancement of high-lift characteristics by oscillating flaps was investigated. Based on a NASA-SC2 airfoil a 2D advanced dropped hinge flap high-lift system was examined. A droop nose, a spoiler and a trailing-edge flap were integrated as high-lift devices. Based on the high-lift geometry a numerical setup was created. A block-structured mesh was built and a suitable numerical model was chosen. Steady-state simulations of different deflection angles of the high-lift devices (droop nose deflection = [0$^{\circ }$; 15$^{\circ }$; 25$^{\circ }$], spoiler deflection = [0$^{\circ }$; 4$^{\circ }$; 6.8$^{\circ }$; 8$^{\circ }$], flap deflection = [15$^{\circ }$; 20$^{\circ }$; 25$^{\circ }$; 28$^{\circ }$; 29$^{\circ }$; 30$^{\circ }$; 34$^{\circ }$; 35$^{\circ }$]) were investigated. Based on the steady-state solutions, appropriate configurations were determined for the transient calculations. The transient simulations with oscillating trailing-edge flaps were performed aiming at increasing the high-lift performance by dynamic flap movement. Two different Reynolds numbers (Re = $20 \times 10^6$ and Re = $0.5 \times 10^6$) were investigated. In particular, the dependence of lift and drag coefficient on the parameters reduced frequency and the center of rotation were examined. For the higher Reynolds number, reflecting a full-scale flight case, an increased lift and drag coefficient could be generated for both flap movement forms. The averaged lift and drag are nearly similar for both forms of movement. Differences can be seen in lift/drag amplitude of the oscillation. The averaged lift can be increased by 2.1% and the averaged drag by 6.6% compared to a steady-state configuration which is nearly at the maximum lift coefficient, i.e close to the stage of flow separation at the non-moving flap. With regard to lift, drag and flow behavior the kinematics around the hinge point exhibit better performance for the lower Reynolds number. This Reynolds number case refers to low-speed wind tunnel testing. By means of an oscillation around the flap point the flow at the flap remains separated. However, with an oscillation around the hinge point, an attached flow can be generated at the flap. Compared to a steady-state configuration at nearly maximum lift coefficient for the non-moving flap the averaged lift can be increased by 2.8% and the averaged drag by 9.1%. Furthermore, an advantage of the kinematics around the hinge point can be seen. But this behavior is frequency dependent. For a reduced frequency k = 0.05 no permanent attached flow can be generated at the flap. For the frequencies k = [0.1; 0.2; 0.3] an attached flow can be obtained and thus an increase of the lift coefficient can be achieved. For the frequencies k = [0.4; 0.5] the flow at the flap remains separated for the entire period. Based on the 2D preliminary data obtained, a generic 3D model will be built by means of the reference geometry LR-270 (Long Range 270). After the construction of the model, numerical and experimental investigations will be carried out in order to confirm trends of the 2D approach.