Advanced aeroelastic robust stability analysis with structural uncertainties

Abstract

Robust flutter analysis described in this paper is based on the robust control theory framework. Therefore, a time-domain linear fractional transformation representation of the perturbed aeroelastic system is modeled. Then, the robust stability is analyzed by means of the structured singular value $\mu$, which is defined as an alternative measure of robustness. Robust flutter analysis deals with aeroelastic (or aeroservoelastic) stability analysis taking structural dynamics, aerodynamics and/or unmodeled system dynamics uncertainties into account. Flutter is a well-known dynamic aeroelastic instability phenomenon caused by an interaction between structural vibrations and unsteady aerodynamic forces, whereby the level of vibration may trigger large amplitudes, eventually leading to catastrophic failure of the structure. The primary motivation of the robust flutter analysis is that this method allows the computation of the worst-case flutter velocity which can support, for example, the flight test program by a valuable robust flutter boundary. This paper addresses the issue of an approach for aeroelastic robust stability analysis with structural uncertainties with respect to physical symmetric and asymmetric stiffness perturbations on the wing structure by means of tuning beams.

1 Introduction

The primary aim of this paper is to investigate the impact of the stiffness uncertainties of the wings in spanwise direction and handle each wing separately in case of symmetric and especially asymmetric stiffness distribution. The asymmetric stiffness perturbation is mentioned in [3] within the robust flutter analysis for aeroelastic systems as an important issue for future investigations. It is quite possible that poor levels of precision with respect to manufacturing capabilities a small difference of bending and/or torsional stiffness may occur between the two wing structures which -in worst-case scenario- can be significant enough to cause an unpredictable coupling between symmetric and asymmetric modes. Therefore, it is essential to model such an asymmetry by means of an adequate uncertainty in physical stiffness model for each wing separately.

This paper starts with a brief mathematical introduction on the LFT representation of uncertain systems and provides an understanding of the definition and interpretation of $\mu$ within the robust stability analysis.

2 Linear fractional transformation and $\mu$ -analysis

The linear fractional transformation is a common framework for robust stability analysis of complex systems based on the small gain theorem [1]. An LFT is an interconnection of operators arranged in a feedback manner. Using a linear complex partitioned operator

$$\begin{aligned} \mathbf {P} = \begin{bmatrix} \mathbf {P_{11}} &{} \mathbf {P_{12}} \\ \mathbf {P_{21}} &{} \mathbf {P_{22}} \end{bmatrix} \quad \in \quad \mathbb {C}^{(o_{1} + o_{2}) \; x \; (i_{1} + i_{2})} , \end{aligned}$$

(1)

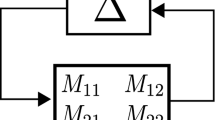
the LFT, $\mathbf {F_{u}}(\mathbf {P},\Delta )$ is defined as the closed-loop transfer matrix from system input u to system output y as the upper-loop LFT of system $\mathbf {P}$ closed by the norm-bounded structured matrix of perturbations $\Delta$ (Fig. 1):

$$\begin{aligned} \mathbf {F_{u}}(\mathbf {P},\Delta ) = \mathbf {P_{22}} \; + \; \mathbf {P_{21}} \Delta ( \mathbf {I} - \mathbf {P_{11}} \Delta )^{-1} \mathbf {P_{12}} . \end{aligned}$$

(2)

Fig. 1

Diagram representation of $\mathbf {F_{u}}(\mathbf {P},\Delta )$

An equivalent expression $\mathbf {F_{l}}(\mathbf {P},\Delta )$ is defined as the closed-loop transfer matrix from system input u to system output y as the lower-loop LFT of system $\mathbf {P}$ closed by $\Delta$ as illustrated in Fig. 2:

$$\begin{aligned} \mathbf {F_{l}}(\mathbf {P},\Delta ) = \mathbf {P_{11}} \; + \; \mathbf {P_{12}} \Delta ( \mathbf {I} - \mathbf {P_{22}}\Delta )^{-1} \mathbf {P_{21}} . \end{aligned}$$

(3)

Fig. 2

Diagram representation of $\mathbf {F_{l}}(\mathbf {P},\Delta )$

It can be seen from the Eq.  (2) that $\mathbf {P_{22}}$ denotes the transfer function (matrix) from input u to output y of the nominal plant while $\mathbf {P_{11}}$, $\mathbf {P_{12}}$ and $\mathbf {P_{21}}$ content the information how the perturbation is embedded in the nominal plant. After the uncertainty block $\Delta$ is extracted from the nominal plant, the system can be described as a nominal plant with an artificial feedback-loop. From the Eq.  (2) it becomes apparent that the LFT is well-posed if and only if the inverse of $(\mathbf {I} - \mathbf {P_{11}}\Delta )$ exist [4] (Fig. 3).

3 Structured singular value $\mu$

The structured singular value $\mu$ is an exact indicator of robust stability for systems with structured uncertainties (perturbations). It is a function of the complex transfer function matrix $\mathbf {P}$ and $\bar{\sigma }(\cdot )$ denotes the maximum singular value of the argument [2]

$$\begin{aligned} \mu (\mathbf {P}) = \frac{1}{\underset{\Delta \in {\varvec{\Delta }}}{\min }\{\bar{\sigma }(\Delta ) \; : \; \mathrm {det}(\mathbf {I}-\mathbf {P}\Delta ) \; = \; 0 \}} . \end{aligned}$$

(4)

$$\begin{aligned} \forall \Delta \in \varvec{\Delta } \quad \text {such that} \ \mathrm {det}(\mathbf {I}-\mathbf {P}\Delta ) = 0 \quad \text {otherwise} \; \mu = 0 . \end{aligned}$$

Fig. 3

LFT system for robust stability analysis using $\mu$-Framework

In this context $\mathbf {P}$ is robustly stable with respect to $\varvec{\Delta }$ which is norm-bounded by scalar $\beta \in {\mathbb {R}}$ such that $\Vert \Delta \Vert _{\infty } \le \beta , \; \forall \Delta \in \varvec{\Delta }$ if and only if $\mu (\mathbf {P}) \le \frac{1}{\beta }$. In the $\mu$-framework the model $\mathbf {P}$ is usually weighted to normalize the norm-bounded uncertainty set $\Delta$ to unity

$$\begin{aligned} \Vert \Delta \Vert _{\infty } \le 1, \; \forall \Delta \in \varvec{\Delta } \quad \text {if and only if} \quad \mu (\mathbf {P}) \le 1 . \end{aligned}$$

(5)

For $\mu \le 1$ there is no perturbation within exists that will destabilize the system. This state depicts that the true system dynamics are stable, assuming the nominal model dynamics with its set of uncertainty operators (modeling errors) are able to capture the dynamic behaviour of the true system.

4 Aeroelastic model

In this paper a condensed FE model of the FLEXOP demonstrator aircraft [5] for the numerical demonstration of the robust flutter analysis is used. The full FE model ($>600000$ nodes) comprises the wing, fuselage and empennage. The wing is modeled by a high-fidelity FE model comprising beam, surface and solid elements. The condensation of the FE model has been performed by the Guyan-reduction, also known as static condensation. The reduced model consists of 303 structural nodes and 1818 degrees of freedom (DoF). The aerodynamic model is based on vortex lattice method (VLM) [11] for steady aerodynamics and doublet lattice method (DLM) [10] for unsteady aerodynamics. A detailed overview of both the structural and aerodynamic model of the aircraft (Fig. 4) is described in [5].

Fig. 4

Aerodynamic panel model of the FLEXOP aircraft and structural nodes of condensed FE model

4.1 Equations of motion for the aeroelastic system

The equations of motion for the nominal aeroelastic system in time domain can expressed in a matrix form as

$$\begin{aligned} \mathbf {M}\ddot{x}(t) + \mathbf {C}\dot{x}(t) + \mathbf {K}x(t)\,= \, & {} \frac{1}{2} \rho V^{2}{\mathbf {Q}}(\bar{s},Ma)x(t)\nonumber \\\,= \, & {} P^{\,\mathrm {aero}}(t) \end{aligned}$$

(6)

which describes a system of N linear ordinary differential equations (ODEs) with N degrees of freedom (DoF) in the FE model where x(t) is the displacement vector with translational and rotational DoFs of the nodes, $\mathbf {M}$, $\mathbf {K}$ and $\mathbf {C} \in {\mathbb {R}}^{N\;x\;N}$are physical mass, stiffness and viscous damping matrices respectively belonging to the structural dynamics part of the equation. The right hand side of the Eq.  (6) denotes the unsteady aerodynamic forces where $\rho$ is the density of atmosphere, V is the flight speed and ${\mathbf {Q}}(\bar{s},Ma)$ is the unsteady aerodynamic influence coefficient (AIC) matrix which is a function of the nondimensional Laplace variable $\bar{s}$ and the Mach number Ma. The AIC matrix can be computed by several aerodynamic theories, such as DLM. In this paper, the subsonic unsteady aerodynamic forces have been modeled by means of DLM. Based on small disturbance hypothesis, DLM solves the linearized potential flow equation and obtains the aerodynamic forces under the assumption that aerodynamic surfaces oscillate harmonically. The nondimensional Laplace variable $\bar{s}$ is denoted $\bar{s} = g + ik$ where g is the damping and k is the reduced frequency. On the assumption of harmonic aerodynamic loads the nondimensional Laplace variable $\bar{s}$ becomes:

$$\begin{aligned} \bar{s}=s\frac{c_{\mathrm {ref}}}{2V} = i\omega \frac{c_{\mathrm {ref}}}{2V} = ik \end{aligned}$$

(7)

where $\omega$ is the frequency of vibration and $c_{\mathrm {ref}}$ the reference chord. Note that the dependence on the Mach number of the AIC matrix will be omitted from now on for conciseness. Using mode displacement method the physical displacement vector x(t) can be represented as a linear combination of m linearly independent vectors (mode shapes) leading to the approximation

$$\begin{aligned} x(t) = \varvec{\Phi }\eta \; , \quad \varvec{\Phi }=\begin{bmatrix} \Phi _{1}&\Phi _{2}&\ldots \Phi _{m} \end{bmatrix} \; \in \; {\mathbb {R}}^{N\;x\;m} \end{aligned}$$

(8)

where m is the number of eigenvectors. Combination of the Eqs. (6), (7) and (8) results in the following reduced-order dynamics

$$\begin{aligned} \mathbf {M}_{m}\ddot{\eta }(t) + \mathbf {B}_{m}\dot{\eta }(t) + \mathbf {K}_{m}\eta (t)\,= \, & {} \frac{1}{2} \rho V^{2}{\mathbf {Q}}_{m}(ik)\eta (t)\nonumber \\\,= \, & {} P_{m}^{\,\mathrm {aero}}(t) \end{aligned}$$

(9)

with

$$\begin{aligned} \mathbf {M}_{m}&= \varvec{\Phi }^{T}\mathbf {M}\varvec{\Phi } \end{aligned}$$

(10)

$$\begin{aligned} \mathbf {B}_{m}&= \varvec{\Phi }^{T}\mathbf {C}\varvec{\Phi } \end{aligned}$$

(11)

$$\begin{aligned} \mathbf {K}_{m}&= \varvec{\Phi }^{T}\mathbf {K}\varvec{\Phi } \end{aligned}$$

(12)

$$\begin{aligned} {\mathbf {Q}}_{m}(ik)&= \varvec{\Phi }^{T}{\mathbf {Q}}(ik)\varvec{\Phi } \end{aligned}$$

(13)

where $\mathbf {M}_{m}$ is the generalized mass matrix, $\mathbf {C}_{m}$ is the generalized viscous damping matrix, $\mathbf {K}_{m}$ is the generalized stiffness matrix and ${\mathbf {Q}}_{m}(ik)$ the generalized AIC matrix.

4.2 Rational function approximation

The generalized AIC matrix ${\mathbf {Q}}_{m}(ik) \in \mathbb {C}^{m\;x\;m}$ is a set of matrices which are calculeted for a set of suitable values of reduced frequency k. Thus, in order to compute AIC for any desired reduced frequency and perform time domain analysis (state-space representation), the AIC matrix in the frequency-domain has to be transformed into the Laplace domain and consequently into the time domain. One possible way is to fit the frequency dependent AIC matrix with rational functions in a least-squares sense. This method is called Rational Function Approximation (RFA). In this paper the Roger’s formulation [6] is used to approximate the AIC matrix ${\mathbf {Q}}_{m}(ik)$:

$$\begin{aligned} {\mathbf {Q}}_{m}(ik) = {\mathbf {Q}}_{m}(\bar{s}) \; \approx \; {\mathbf {Q}}_{m}^{0} + \bar{s}{\mathbf {Q}}_{m}^{1} + \bar{s}^{2}{\mathbf {Q}}_{m}^{2} \; + \; \sum \limits _{i=1}^{n_{p}} {\mathbf {Q}}_{m}^{L_{i}}\frac{\bar{s}}{\bar{s}+\beta _{i}} . \end{aligned}$$

(14)

The RFA Eq. (14) can be interpreted as a general two-part approach for aerodynamic loads based on quasi-steady and lag contributions. ${\mathbf {Q}}_{m}^{0}$, ${\mathbf {Q}}_{m}^{1}$ and ${\mathbf {Q}}_{m}^{2}$ are ${\mathbb {R}}^{m\;x\;m}$ real coefficient matrices representing the contribution of acceleration, velocity and displecement of the rigid and flexible degrees of freedom on the aerodynamic loads denoting the quasi-steady part of the approximation. The ${\mathbf {Q}}_{m}^{L_{i}} \in {\mathbb {R}}^{m\;x\;m}$ matrices with the predefined poles $\beta _{i},\; i=1,2,...,n_{p}$, are responsible for the lagging behavior of the unsteady flow. This is referred to time lag effect.

For time domain representation the equation system in (14) can be rearranged as follows [7]

$$\begin{aligned} {\mathbf {Q}}_{m}(\bar{s},Ma) \; \approx \; {\mathbf {Q}}_{m}^{0} + \bar{s}{\mathbf {Q}}_{m}^{1} + \bar{s}^{2}{\mathbf {Q}}_{m}^{2} + {\mathbf {D}}( \bar{s}\mathbf {I} - {\mathbf {R}} )^{-1}\mathbf {E}\bar{s} \end{aligned}$$

(15)

where

$$\begin{aligned} {\mathbf {D}}= & {} \begin{bmatrix} {\mathbf {Q}}_{m}^{L_{1}} \quad&{\mathbf {Q}}_{m}^{L_{2}} \quad \ldots \quad {\mathbf {Q}}_{m}^{L_{{{\rm n}_{\mathrm {p}}}}} \end{bmatrix} \; \in {\mathbb {R}}^{m\;x\;(m\cdot n_{p})} , \end{aligned}$$

(16)

$$\begin{aligned} {\mathbf {R}}= & {} \; \hbox {diag}\left( \begin{bmatrix} -\beta _{1} \mathbf {I} \quad -\beta _{2} \mathbf {I} \quad \ldots \quad -\beta _{n_{p}} \mathbf {I} \end{bmatrix}\right) \in {\mathbb {R}}^{(m\cdot n_{p})\;x\; (m\cdot n_{p})} , \end{aligned}$$

(17)

$$\begin{aligned} \mathbf {E}= & {} \begin{bmatrix} \mathbf {I} \quad \mathbf {I} \quad \ldots \quad \mathbf {I} \end{bmatrix}^{T} \; \in {\mathbb {R}}^{(m\cdot n_{p})\;x\; m} . \end{aligned}$$

(18)

For the lag states $x_L \in {\mathbb {R}}^{n_{lag}\;x\;1}$ the following ODE with $\dot{\eta }$ as input can be derived [7]:

$$\begin{aligned} \dot{x}_L \; = \; \left( \frac{V}{c_{\mathrm {ref}}/2}\right) {\mathbf {R}}x_{L} + \mathbf {E}\dot{\eta } \end{aligned}$$

(19)

The resulting generalized aerodynamic forces are then

$$\begin{aligned} P_{m}^{\mathrm {aero}}\,= \, & {} \frac{1}{2} \rho V^{2}{\mathbf {Q}}_{m}(ik)\eta (t) \approx \frac{1}{2}\rho V^{2}\left[ \vphantom {\left. \frac{c_{\mathrm {ref}}/2}{V}{\mathbf {Q}}_{m}^{1}\dot{\eta } \; + \; \left( \frac{c_{\mathrm {ref}}/2}{V}\right) ^{2}{\mathbf {Q}}_{m}^{2}\ddot{\eta } \; + \; {\mathbf {D}}x_{L} \right] }{\mathbf {Q}}_{m}^{0}\eta \; \right. \nonumber \\&+ \left. \frac{c_{\mathrm {ref}}/2}{V}{\mathbf {Q}}_{m}^{1}\dot{\eta } \; + \; \left( \frac{c_{\mathrm {ref}}/2}{V}\right) ^{2}{\mathbf {Q}}_{m}^{2}\ddot{\eta } \; + \; {\mathbf {D}}x_{L} \right] \end{aligned}$$

(20)

An alternative new approach for the generation of a generalized state-space aeroservoelastic model based on tangential interpolation is presented in [12]. Compared to RFA approach, this method enables a minimal order realization with interpolation of the unsteady aerodynamics by avoiding any selection of poles $\beta _{i}$ [12].

5 LFT model of the perturbed system

Consider again the generalized equations of motion for the aeroelastic response of the aircraft with unstaedy aerodynamics by combining the Eqs.  (9) and (20):

$$\begin{aligned}&\mathbf {M}_{m}\ddot{\eta }(t) + \mathbf {B}_{m}\dot{\eta }(t) + \mathbf {K}_{m}\eta (t) \nonumber \\&\quad = \frac{1}{2}\rho V^{2}\left[ \vphantom {\left. + \; \left( \frac{c_{\mathrm {ref}}/2}{V}\right) ^{2}{\mathbf {Q}}_{m}^{2}\ddot{\eta } \; + \; {\mathbf {D}}x_{L} \right] } {\mathbf {Q}}_{m}^{0}\eta + \frac{c_{\mathrm {ref}}/2}{V}{\mathbf {Q}}_{m}^{1}\dot{\eta } \; \right. \nonumber \\&\qquad \left. + \; \left( \frac{c_{\mathrm {ref}}/2}{V}\right) ^{2}{\mathbf {Q}}_{m}^{2}\ddot{\eta } \; + \; {\mathbf {D}}x_{L} \right] \end{aligned}$$

(21)

The state-space respresentation of the Eq. (21) is formulated with the generalized states $\eta$, $\dot{\eta }$ and the unsteady aerodynamic states $x_{L}$:

$$\begin{aligned} \begin{bmatrix} \dot{\eta } \\ \ddot{\eta } \\ \dot{x}_{L} \end{bmatrix} = \mathbf {A}_{\mathrm {V}} \begin{bmatrix} \eta \\ \dot{\eta } \\ x_{L} \end{bmatrix} \end{aligned}$$

(22)

where

$$\begin{aligned} \mathbf {A}_{\mathrm {V}}&= \begin{bmatrix} \mathbf {0} \quad &{} \mathbf {I} \quad &{} \mathbf {0} \\ -(\mathbf {M}^{Q}_{m})^{-1}\mathbf {K}^{Q}_{m} \quad &{} - (\mathbf {M}^{Q}_{m})^{-1}\mathbf {C}^{Q}_{m} \quad &{} \frac{1}{2}\rho V^{2}(\mathbf {M}^{Q}_{m})^{-1}{\mathbf {D}} \\ \mathbf {0} \quad &{} \mathbf {E} \quad &{} \frac{2V}{c_{\mathrm {ref}}}{\mathbf {R}} \end{bmatrix} \; , \end{aligned}$$

(23)

$$\begin{aligned} \mathbf {M}^{Q}_{m}&= \mathbf {M}_{m} - \rho \frac{c_{\mathrm {ref}}^{2}}{8}{\mathbf {Q}}_{m}^{2} \; , \end{aligned}$$

(24)

$$\begin{aligned} \mathbf {C}^{Q}_{m}&= \mathbf {C}_{m} - \frac{c_{\mathrm {ref}}}{4}\rho V{\mathbf {Q}}_{m}^{1} \; , \end{aligned}$$

(25)

$$\begin{aligned} \mathbf {K}^{Q}_{m}&= \mathbf {K}_{m} - \frac{1}{2}\rho V^{2}{\mathbf {Q}}_{m}^{0} \; . \end{aligned}$$

(26)

5.1 Parametrization over flight speed

The $\mu$-framework determines the stability over a range of airspeed to specify the onset of flutter. The generalized equations of motion for the aeroelastic response (22) are a function of the flight speed V, such that perturbations of this parameter can be integrated into the system as a linear fractional transformation.

Consider an additive perturbation $\delta V$ on the nominal velocity $\overline{V}$

$$\begin{aligned} V = \overline{V} + \delta V \end{aligned}$$

(27)

Separate the terms in the system dynamics (22) that involve $\delta V$:

$$\begin{aligned} \begin{bmatrix} \dot{\eta } \\ \ddot{\eta } \\ \dot{x}_{L} \\ \hline z_{V} \end{bmatrix} = \left[ \begin{array}{c|c} \overline{\mathbf {A}} &{} \overline{\mathbf {B}}_{V} \\ \hline \overline{\mathbf {C}} &{} \overline{{\mathbf {D}}}_{V} \end{array} \right] \begin{bmatrix} \eta \\ \dot{\eta } \\ {x}_{L} \\ \hline w_{V} \end{bmatrix} \end{aligned}$$

(28)

where

$$\begin{aligned} \overline{\mathbf {A}} = \begin{bmatrix} \mathbf {0} &{} \mathbf {I} &{} \mathbf {0} \\ -(\mathbf {M}^{Q}_{m})^{-1} \widetilde{\mathbf {K}}_m &{} -(\mathbf {M}^{Q}_{m})^{-1}\widetilde{\mathbf {C}}_m &{} \frac{1}{2}\rho \overline{V}^{2}(\mathbf {M}^{Q}_{m})^{-1}{\mathbf {D}}\\ \mathbf {0} &{} \mathbf {E} &{} \frac{2\overline{V}}{c_{\mathrm {ref}}}{\mathbf {R}} \\ \end{bmatrix} \end{aligned}$$

(29)

with

$$\begin{aligned} \widetilde{\mathbf {K}}_m&= \mathbf {K}_{m} - \frac{1}{2}\rho \overline{V}^{2}{\mathbf {Q}}_{m}^{0}\; , \end{aligned}$$

(30)

$$\begin{aligned} \widetilde{\mathbf {C}}_m&= \mathbf {C}_{m} - \frac{c_{\mathrm {ref}}}{4}\rho \overline{V}{\mathbf {Q}}_{m}^{1}\; , \end{aligned}$$

(31)

$$\begin{aligned} \overline{\mathbf {B}}_{V}&= \begin{bmatrix} \mathbf {0} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \\ \overline{V}\mathbf {I} \; &{} \; \mathbf {0} \; &{} \; \overline{V}\mathbf {I} \; &{} \; \mathbf {I} \\ \mathbf {0} \; &{} \; \mathbf {I} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \end{bmatrix}\; , \end{aligned}$$

(32)

$$\begin{aligned} \overline{\mathbf {C}}&= \begin{bmatrix} \frac{1}{2}\rho (\mathbf {M}^{Q}_{m})^{-1}{\mathbf {Q}}_{m}^{0} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \\ \mathbf {0} \; &{} \; \mathbf {0} \; &{} \;\frac{2}{c_{\mathrm {ref}}}{\mathbf {R}} \\ \mathbf {0} \; &{} \; \mathbf {0} \; &{} \; \frac{1}{2}\rho (\mathbf {M}^{Q}_{m})^{-1}{\mathbf {D}} \\ \frac{1}{2}\rho \bar{V}(\mathbf {M}^{Q}_{m})^{-1}{\mathbf {Q}}_{m}^{0} \; &{} \; \frac{c_{\mathrm {ref}}}{4}\rho (\mathbf {M}^{Q}_{m})^{-1}{\mathbf {Q}}_{m}^{1} \; &{} \; \frac{1}{2}\rho \bar{V}(\mathbf {M}^{Q}_{m})^{-1}{\mathbf {D}} \end{bmatrix} \; , \end{aligned}$$

(33)

$$\begin{aligned} \overline{{\mathbf {D}}}_{V}&= \begin{bmatrix} \mathbf {0} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \\ \mathbf {0} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \\ \mathbf {0} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \; &{} \; \mathbf {0} \\ \mathbf {I} \; &{} \; \mathbf {0} \; &{} \; \mathbf {I} \; &{} \; \mathbf {0} \end{bmatrix} \; . \end{aligned}$$

(34)

The additional input and outputs signals

$$\begin{aligned} w_{V}&= [w_{1}, w_{2}, w_{3}, w_{4}]^{T}\; , \end{aligned}$$

(35)

$$\begin{aligned} z_{V}&= [z_{1}, z_{2}, z_{3}, z_{4}]^{T}\; , \end{aligned}$$

(36)

are introduced into the nominal aeroelastic system given in (22) to include the perturbation in velocity to the nominal dynamics in a feedback manner (Fig. 5):

$$\begin{aligned} z_{1}\,= \, & {} \frac{\rho }{2}\left( \mathbf {M}^{Q}_{m}\right) ^{-1}{\mathbf {Q}}_{m}^{0}\eta, \end{aligned}$$

(37)

$$\begin{aligned} z_{2}\,= \, & {} \frac{2}{c_{ref}}{\mathbf {R}}x_{L}, \end{aligned}$$

(38)

$$\begin{aligned} z_{3}\,= \, & {} \frac{\rho }{2}\left( \mathbf {M}^{Q}_{m}\right) ^{-1}{\mathbf {D}}x_{L}, \end{aligned}$$

(39)

$$\begin{aligned} z_{4}\,= \, & {} \frac{\rho }{2}\overline{V}\left( \mathbf {M}^{Q}_{m}\right) ^{-1}{\mathbf {Q}}_{m}^{0}\eta + \frac{c_{\mathrm {ref}}}{4}\rho \left( \mathbf {M}^{Q}_{m}\right) ^{-1}{\mathbf {Q}}_{m}^{1}\dot{\eta } \; \nonumber \\&+ \; \frac{\rho }{2}\overline{V}\left( \mathbf {M}^{Q}_{m}\right) ^{-1}{\mathbf {D}}x_{L} + w_{1} + w_{3}, \end{aligned}$$

(40)

$$\begin{aligned} w_{V}\,= \, & {} \varvec{\Delta }_V z_{V}. \end{aligned}$$

(41)

Fig. 5

Upper-LFT system for nominal stability analysis in $\mu$-framework with perturbation in-flight speed

The nominal flutter problem modeled by means of perturbation to flight speed V in Eq. (28) can be solved as a $\mu$-computation. The tranfer function matrix $\mathbf {P}(s)$ which relates the input signal $w_{V}$ to the output signal $z_{V}$ can be derived from the Eq. (28):

$$\begin{aligned} \mathbf {P}(s) = \mathbf {\overline{C}}\left( s\mathbf {I}-\overline{\mathbf {A}}\right) ^{-1}\mathbf {\overline{B}}_{V}+\mathbf {\overline{D}}_{V} \end{aligned}$$

(42)

To make the perturbation on flight speed $\delta V$ which has the same unit as $\overline{V}$, to unity norm-bound constraint $\Vert \delta V \Vert _{\infty } \le 1$, the transfer function matrix $\mathbf {P}(s)$ has to be scaled by a weighting $W_{\overline{V}}$, where

$$\begin{aligned} V = \overline{V} + \delta V\cdot W_{\overline{V}} , \quad \Vert \delta V \Vert _{\infty } \le 1 \end{aligned}$$

(43)

The scaled plant transfer function matrix $\mathbf {\overline{P}}(s)$ is given by:

$$\begin{aligned} \mathbf {\overline{P}}(s) = W_{\overline{V}}\mathbf {P}(s) \end{aligned}$$

(44)

and in frequency domain with $s=i\omega$

$$\begin{aligned} \mathbf {\overline{P}}(i\omega ) = W_{\overline{V}}\mathbf {P}(i\omega ) \; , \end{aligned}$$

(45)

where $\mathbf {\overline{P}}(i\omega )$ is also called the flutter loop transfer function matrix of the uncertain system (Fig. 6).

Fig. 6

Feedback loop representation of the uncertain flutter transfer function matrix

Now the nominal flutter speed $V_{\mathrm {flutter}}^{\,\mathrm{nom,} {\mu }}$ can be determined via $\mu$-computation by means of the following algorithm.

For $\mu < 1$ there is no perturbation within exists that will destabilize the closed-loop system. Beacuse of well-known difficulties of exact real/mixed $\mu$ computation, which poses an NP-hard problem, efficiently computable upper bound of $\mu$ is used within the analysis.

The algoritm set out above should therefore give an introduction into the $\mu$-framework. The nominal flutter speed $V_{\mathrm {flutter}}^{\,\mathrm {nom}}$ can also be calculated by means of standard flutter solution techniques such as ${p{-}k}$-method or $\textit{g}$-method. For example, the ${p{-}k}$-method [8] is widely used in flight flutter test campaigns. The $\textit{g}$-method proposed by Chen [9] promises a reliable damping prediction by including a first order of damping term in the flutter equation. For the robust aeroelastic stability analysis additional uncertainties such as in structural dynamics, aerodynamics and/or unmodelled system dynamics have to be defined and subsequently included in the linear system to introduce modeling errors between the numerical model and the physical aircraft (Fig. 7).

6 Tuning beams

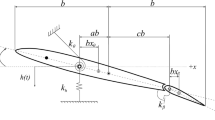
In this paper, account is taken of the uncertainties in the structural dynamics or, more explicitly, the structural stiffness model which has a significant impact within the lower frequency range and flutter analysis respectively. For the realization of the stiffness parameter variations tuning beams have been generated with respect to the condensed FE model. This approach is suitable for varying of stiffness parameters by only adjusting material properties of the tuning beams like bending and torisonal stiffness while avoiding a modification of the full FE model. The tuning beams are 3D beams and may also be called “space beam” elements [13].

Fig. 7

Arbitrarily oriented 3D beam element with 12 nodal degrees of freedom (DoF) in local and global coordinate system [13]

The beam element resists force in any direction and moment about any axis. The element stiffness matrix $\mathbf {K}_{el} \in {\mathbb {R}}^{12x12}$ of the 3D beam in local coordinate system is given by [13]:

$$\begin{aligned} \mathbf {K}_{el} = \begin{bmatrix} \mathbf {K}_{el}^{11} \; &{} \; \mathbf {K}_{el}^{12} \\ \mathbf {K}_{el}^{21} \; &{} \; \mathbf {K}_{el}^{22} \end{bmatrix} , \end{aligned}$$

(46)

where the submatrices $\mathbf {K}_{el}^{11}$, $\mathbf {K}_{el}^{12}$, $\mathbf {K}_{el}^{21}$ and $\mathbf {K}_{el}^{22}$ are defined as follows:

$$\begin{aligned} \mathbf {K}_{el}^{11}= & {} \begin{bmatrix} \frac{EA}{L} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{12EI_{zz}}{L^{3}} &{} \frac{12EI_{yz}}{L^{3}} &{} 0 &{} \frac{-6EI_{yz}}{L^{2}} &{} \frac{6EI_{zz}}{L^{2}} \\ 0 &{} \frac{12EI_{yz}}{L^{3}} &{} \frac{12EI_{yy}}{L^{3}} &{} 0 &{} \frac{-6EI_{yy}}{L^{2}} &{} \frac{6EI_{yz}}{L^{2}} \\ 0 &{} 0 &{} 0 &{} \frac{GI_{p}}{L} &{} 0 &{} 0 \\ 0 &{} \frac{-6EI_{yz}}{L^{2}} &{} \frac{-6EI_{yy}}{L^{2}} &{} 0 &{} \frac{4EI_{yy}}{L} &{} \frac{-4EI_{yz}}{L} \\ 0 &{} \frac{6EI_{zz}}{L^{2}} &{} \frac{6EI_{yz}}{L^{2}} &{} 0 &{} \frac{-4EI_{yz}}{L} &{} \frac{4EI_{zz}}{L} \end{bmatrix} , \end{aligned}$$

(47)

$$\begin{aligned} \mathbf {K}_{el}^{12}= & {} \begin{bmatrix} \frac{-EA}{L} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{-12EI_{zz}}{L^{3}} &{} \frac{-12EI_{yz}}{L^{3}} &{} 0 &{} \frac{-6EI_{yz}}{L^{2}} &{} \frac{EI_{zz}}{L^{2}} \\ 0 &{} \frac{-12EI_{yz}}{L^{3}} &{} \frac{-12EI_{yy}}{L^{3}} &{} 0 &{} \frac{-6EI_{yy}}{L^{2}} &{} \frac{6EI_{yz}}{L^{2}} \\ 0 &{} 0 &{} 0 &{} \frac{-GI_{p}}{L} &{} 0 &{} 0 \\ 0 &{} \frac{6EI_{yz}}{L^{2}} &{} \frac{6EI_{yy}}{L^{2}} &{} 0 &{} \frac{2EI_{yy}}{L} &{} \frac{-2EI_{yz}}{L} \\ 0 &{} \frac{-6EI_{zz}}{L^{2}} &{} \frac{-6EI_{yz}}{L^{2}} &{} 0 &{} \frac{-2EI_{yz}}{L} &{} \frac{2EI_{zz}}{L} \end{bmatrix} , \end{aligned}$$

(48)

$$\begin{aligned} \mathbf {K}_{el}^{21}= & {} \begin{bmatrix} \frac{-EA}{L} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{-12EI_{zz}}{L^{3}} &{} \frac{-12EI_{yz}}{L^{3}} &{} 0 &{} \frac{6EI_{yz}}{L^{2}} &{} \frac{-6EI_{zz}}{L^{2}} \\ 0 &{} \frac{-12EI_{yz}}{L^{3}} &{} \frac{-12EI_{yy}}{L^{3}} &{} 0 &{} \frac{6EI_{yy}}{L^{2}} &{} \frac{-6EI_{yz}}{L^{2}} \\ 0 &{} 0 &{} 0 &{} \frac{-GI_{p}}{L} &{} 0 &{} 0 \\ 0 &{} \frac{-6EI_{yz}}{L^{2}} &{} \frac{-6EI_{yy}}{L^{2}} &{} 0 &{} \frac{2EI_{yy}}{L} &{} \frac{-2EI_{yz}}{L} \\ 0 &{} \frac{6EI_{zz}}{L^{2}} &{} \frac{6EI_{yz}}{L^{2}} &{} 0 &{} \frac{-2EI_{yz}}{L} &{} \frac{2EI_{zz}}{L} \end{bmatrix} , \end{aligned}$$

(49)

and

$$\begin{aligned} \mathbf {K}_{el}^{22} = \begin{bmatrix} \frac{EA}{L} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{12EI_{zz}}{L^{3}} &{} \frac{12EI_{yz}}{L^{3}} &{} 0 &{} \frac{6EI_{yz}}{L^{2}} &{} \frac{-6EI_{zz}}{L^{2}} \\ 0 &{} \frac{12EI_{yz}}{L^{3}} &{} \frac{12EI_{yy}}{L^{3}} &{} 0 &{} \frac{6EI_{yy}}{L^{2}} &{} \frac{-6EI_{yz}}{L^{2}} \\ 0 &{} 0 &{} 0 &{} \frac{GI_{p}}{L} &{} 0 &{} 0 \\ 0 &{} \frac{6EI_{yz}}{L^{2}} &{} \frac{6EI_{yy}}{L^{2}} &{} 0 &{} \frac{4EI_{yy}}{L} &{} \frac{-4EI_{yz}}{L} \\ 0 &{} \frac{-6EI_{zz}}{L^{2}} &{} \frac{-6EI_{yz}}{L^{2}} &{} 0 &{} \frac{-4EI_{yz}}{L} &{} \frac{4EI_{zz}}{L} \end{bmatrix} . \end{aligned}$$

(50)

where E is elastic modulus, G is shear modulus, A is cross-sectional area, $I_{yy}$ and $I_{zz}$ are principal moments of inertia of A, $I_{p}$ is the torsional constant and L is the length of the 3D beam element. The assembly of global stiffness matrix of the tuning structure requires that each of the element stiffness matrix has to be transformed into the global coordinate system and subsequently integrated into the global stiffness matrix of the nominal FE model in the following way:

$$\begin{aligned} \mathbf {K}^{\,\mathrm {tuned}} = \overline{\mathbf {K}} + \sum _{i=1}^{n_{\mathrm {beam}}} \mathbf {K}_{i}^{\,\mathrm {beam}} \quad , \end{aligned}$$

(51)

where $\mathbf {K}^{\,\mathrm {tuned}}$ is the physical stiffness matrix of the tuned FE model, $\overline{\mathbf {K}}$ is the nominal physical stiffness matrix of the FE model and $\mathbf {K}_{i}^{\,\mathrm {beam}}$ is the physical stiffness matrix of the $i^{\,\mathrm {th}}$ tuning beam. This type of representation of the stiffness matrix in Eq. 51 by superposition of nominal model and the tuning structure is used for the uncertainty definition in the next section. The global stiffness matrix with its substructure components (nominal model and tuning structure) is visualized in Fig. 8.

Fig. 8

Visualization of the (assembled) global stiffness matrix

7 Uncertainty modeling

In this study, the wing structure is affected by the uncertainty of the physical stiffness matrix by means of tuning beams’ parameters. Two kinds of variations of physical stiffness characteristics have been defined. The first approach is characterized by symmetric variation of physical stiffness with respect to torsional rigidity ($GI_{p}$) and/or flexural rigidity (bending stiffness) ($EI_{yy}$), i.e. the tuning beams on the right and left wing structure have the same material properties to include symmetric uncertainties into the nominal model. The second approach denotes asymmetric variation of stiffness parameters of the tuning beams on the right and left-wing structure to represent asymmetric stiffness distribution in the nominal model.

Considering the perturbation of the physical stiffness matrix, the parametric additive uncertainties can be described as follows:

• I. Symmetric variation

  $$\begin{aligned} \mathbf {K}_{m}^{\,\mathrm {sym}} = \varvec{\Phi }^T \left[ \overline{\mathbf {K}} + \sum _{i=1}^{n_{\mathrm {beam}}/2} \delta _{i}^{W}\left( \mathbf {K}_{i}^{\,\mathrm {WR}} + \mathbf {K}_{i}^{\,\mathrm {WL}}\right) \right] \varvec{\Phi } \end{aligned}$$

  (52)

• II. Asymmetric variation

  $$\begin{aligned} \mathbf {K}_{m}^{\,\mathrm {sym}} = \varvec{\Phi }^T \left[ \overline{\mathbf {K}} + \sum _{i=1}^{n_{\mathrm {beam}}/2} \delta _{i}^{\,\mathrm {WR}}\mathbf {K}_{i}^{\,\mathrm {WR}} + \sum _{i=1}^{n_{\mathrm {beam}}/2} \delta _{i}^{\,\mathrm {WL}}\mathbf {K}_{i}^{\,\mathrm {WL}} \right] \varvec{\Phi } \end{aligned}$$

  (53)

where $n_{\mathrm {beam}}$ is the total number of tuning beams, $\overline{\mathbf {K}}$ is the nominal physical stiffness matrix of the aircraft, $\mathbf {K}_{i}^{\,\mathrm {WR}}$ and $\mathbf {K}_{i}^{\,\mathrm {WL}}$ are weigthing matrices which are in this case the physical stiffness matrices of the $i^{th}$ tuning beam with respect to the right wing (WR) and left wing (WL) structure, respectively. $\delta _{i}$, $\delta _{i}^{\,\mathrm {WR}}$ and $\delta _{i}^{\,\mathrm {WL}}$ are norm-bounded uncertainty operators with $\Vert \delta _{i}^{W}\Vert _{\infty } \le 1$, $\Vert \delta _{i}^{\,\mathrm {WR}}\Vert _{\infty } \le 1$ and $\Vert \delta _{i}^{\,\mathrm {WL}}\Vert _{\infty } \le 1$. It should be noted that $\varvec{\Phi }$ is the modal (eigenvector) matrix of the nominal system. This assumption is reasonable for small perturbations and can be validated by modal correlation analysis between nominal and perturbed system.

The extended LFT model of the new perturbed system, which includes feedback signals relating the perturbation to flight speed and uncertainties described in the Eqs. (52) and (53), may be defined analogous to the Eq. (28):

$$\begin{aligned} \begin{bmatrix} \dot{\eta } \\ \ddot{\eta } \\ \dot{x}_{L} \\ \hline z_{V} \\ z_{K} \end{bmatrix} = \left[ \begin{array}{c|c} \overline{\mathbf {A}} &{} \left[ \overline{\mathbf {B}}_{V} \; \overline{\mathbf {B}}_{K} \right] \\ \hline \begin{bmatrix} \overline{\mathbf {C}} \\ \overline{\mathbf {C}}_{K}\end{bmatrix} &{} \begin{bmatrix} \overline{{\mathbf {D}}}_{\mathrm {V}} &{} \overline{{\mathbf {D}}}_{\mathrm {V,K}} \\ \overline{{\mathbf {D}}}_{\mathrm {K,V}} &{} \overline{{\mathbf {D}}}_{\mathrm {K}}\end{bmatrix} \end{array} \right] \begin{bmatrix} \eta \\ \dot{\eta } \\ {x}_{L} \\ \hline w_{V} \\ w_{K} \end{bmatrix} \end{aligned}$$

(54)

where the new submatricest $\overline{\mathbf {B}}_{K} \in {\mathbb {R}}^{(2m+n_{\mathrm {lag}})\;x\;(m\cdot n_{\mathrm {beam}})}$ and $\overline{\mathbf {C}}_{K} \in {\mathbb {R}}^{(m\cdot n_{\mathrm {beam}})\;x\;(2m +n_{\mathrm {lag}})}$ are given as follows

$$\begin{aligned} \overline{\mathbf {B}}_{K}= & {} \begin{bmatrix} \mathbf {0}_{m} &{} \mathbf {0}_{m} &{} \cdots &{} \mathbf {0}_{m} \\ -\mathbf {I}_{m} &{} -\mathbf {I}_{m} &{} \cdots &{} -\mathbf {I}_{m} \\ &{} \mathbf {0}_{n_{\mathrm {lag}}\; x \; m\cdot n_{\mathrm {beam}}} &{} \end{bmatrix} \end{aligned}$$

(55)

$$\begin{aligned} \overline{\mathbf {C}}_{K}= & {} \begin{bmatrix} (\mathbf {M}^{Q}_{m})^{-1}\varvec{\Phi }^{T}\mathbf {K}_{1}^{\,\mathrm {WR}}\varvec{\Phi } &{}\quad \quad \mathbf {0}_{m} &{}\quad \quad \mathbf {0}_{m\; x\; n_{\mathrm {lag}}} \\ \vdots &{}\quad \quad \vdots &{}\quad \quad \vdots \\ (\mathbf {M}^{Q}_{m})^{-1}\varvec{\Phi }^{T}\mathbf {K}_{n_{\mathrm {beam}}/2}^{\,\mathrm {WR}}\varvec{\Phi } &{}\quad \quad \mathbf {0}_{m} &{}\quad \quad \mathbf {0}_{m\; x\; n_{\mathrm {lag}}} \\ (\mathbf {M}^{Q}_{m})^{-1}\varvec{\Phi }^{T}\mathbf {K}_{1}^{\,\mathrm {WL}}\varvec{\Phi } &{}\quad \quad \mathbf {0}_{m} &{}\quad \quad \mathbf {0}_{m\; x\; n_{\mathrm {lag}}} \\ \vdots &{}\quad \quad \vdots &{}\quad \quad \vdots \\ (\mathbf {M}^{Q}_{m})^{-1}\varvec{\Phi }^{T}\mathbf {K}_{n_{\mathrm {beam}}/2}^{\,\mathrm {WL}}\varvec{\Phi } &{}\quad \quad \mathbf {0}_{m} &{}\quad \quad \mathbf {0}_{m\; x\; n_{\mathrm {lag}}} \end{bmatrix} \end{aligned}$$

(56)

The submatrices $\overline{{\mathbf {D}}}_{\mathrm {V,K}} \in {\mathbb {R}}^{(3m+n_{\mathrm {lag}})x(3m+n_{\mathrm {lag}})}$, $\overline{{\mathbf {D}}}_{\mathrm {K,V}} \in {\mathbb {R}}^{(m\cdot n_{\mathrm {beam}})x(3m+n_{\mathrm {lag}})}$ and $\overline{{\mathbf {D}}}_{K} \in {\mathbb {R}}^{(m\cdot n_{\mathrm {beam}})x(m\cdot n_{\mathrm {beam}})}$ are zero matrices.

The robust flutter problem modeled by means of perturbation to flight speed V and stiffness model uncertainty in Eq. (54) can be solved by a $\mu$-computation. The tranfer function matrix $\mathbf {P}_{K}(s)$ which relates the input signals $w_{V}$ and $w_{K}$ to the output signals $z_{V}$ and $z_{K}$ can be derived from the Eq. (54):

$$\begin{aligned} \mathbf {P}_{K}(s) = \begin{bmatrix} \overline{\mathbf {C}} \\ \overline{\mathbf {C}}_{K}\end{bmatrix}\left( s\mathbf {I}-\overline{\mathbf {A}}\right) ^{-1}\left[ \overline{\mathbf {B}}_{V} \; \overline{\mathbf {B}}_{K} \right] + \begin{bmatrix} \overline{{\mathbf {D}}}_{\mathrm {V}} &{} \overline{{\mathbf {D}}}_{\mathrm {V,K}} \\ \overline{{\mathbf {D}}}_{\mathrm {K,V}} &{} \overline{{\mathbf {D}}}_{\mathrm {K}}\end{bmatrix} \end{aligned}$$

(57)

Once the transfer function matrix $\mathbf {P}_{K}(s)$ has been determined, the robust flutter speed $V_{\mathrm {flutter}}^{\,\mathrm {rob}}$ can be determined within the $\mu$-framework by means of the following algoritm.

8 Numerical results

For the numerical demonstration of the proposed uncertainty description 11 tuning beams for each wing ($n_{\mathrm {beam}}=22$) have been defined. Each wing consists of 60 structural nodes. The beams are placed within the nondimensional span range $\xi = [0.25,\; 0.75]$. For the modal model the first 15 modes ($m = 15$) have been considered within the frequency range of $2.9 \le f \le 35.6$  Hz. In this context, the considered frequency grid for $\mu$-computation must be sufficiently dense in order not to miss a critical frequency, which can lead to a prohibitive computational cost. For the following case studies, a frequency grid of 50 logarithmically spaced points between 3.0 and 12.0 Hz has been considered with regard to the nominal flutter results. The computed $\mu$ values are then interpolated within the same frequency range using linear interpolation with a step size of $\Delta f=0.05\; Hz$.

Fig. 9

Structural nodes of condensed FE model with tuning beams

Symmetric stiffness perturbations

• I Additive uncertainty of $10^{2} \frac{N}{m^{2}}$ with respect to bending stiffness $EI_{yy}$ for each tuning beam on the left and right wing structure

  • ${\varvec{\Delta }_\mathbf{K }^\mathbf{I }} = \mathrm {diag}\left( \delta _{1}^{W}\mathbf {I}_{m},\; \delta _{2}^{W}\mathbf {I}_{m},\; \ldots ,\; \delta _{n_{\mathrm {beam}}/2}^{W}\mathbf {I}_{m}\right)$ .

• II Additive uncertainty of $10^{2} \frac{N}{m^{2}}$ with respect to torsional stiffness $GI_{p}$ for each tuning beam on the left and right wing structure

  • ${\varvec{\Delta }_\mathbf{K }^\mathbf{II }} = \mathrm {diag}\left( \delta _{1}^{W}\mathbf {I}_{m},\; \delta _{2}^{W}\mathbf {I}_{m},\; \ldots ,\; \delta _{n_{\mathrm {beam}}/2}^{W}\mathbf {I}_{m}\right)$ .

• III Additive uncertainty of $10^{2} \frac{N}{m^{2}}$ with respect to both bending stiffness $EI_{yy}$ and torsional stiffness $GI_{p}$ for each tuning beam on the left and right wing structure

  • ${\varvec{\Delta }_\mathbf{K }^\mathbf{III }} = \mathrm {diag}\left( \delta _{1}^{W}\mathbf {I}_{m},\; \delta _{2}^{W}\mathbf {I}_{m},\; \ldots ,\; \delta _{n_{\mathrm {beam}}/2}^{W}\mathbf {I}_{m}\right)$ .

Asymmetric stiffness perturbations

• IV Additive uncertainty of $0.8\times 10^{2} \frac{N}{m^{2}}$ with respect to bending stiffness $EI_{yy}$ for each tuning beam on the left wing and $1.2\times 10^{2} \frac{N}{m^{2}}$ for each tuning beam on the right wing

  $$\begin{aligned} {\varvec{\Delta }_\mathbf{K }^\mathbf{IV }}&= \begin{bmatrix} {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WR}}} &{} \\ &{} {\varvec{\Delta }}_\mathbf{K }^{\,\mathrm {WL}} \end{bmatrix}\;\;\mathrm{where}\\ {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WR}}}&= \mathrm {diag}(\delta _{\mathrm {1}}^{\,\mathrm {WR}}\mathbf {I_{m}},\; \delta _{\mathrm {2}}^{\,\mathrm {WR}}\mathbf {I}_{m},\; \ldots ,\; \delta _{n_{\mathrm {beam}}/2}^{\,\mathrm {WR}}\mathbf {I}_{m})\;\;\mathrm{and}\\ {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WL}}}&= \mathrm {diag}(\delta _{\mathrm {1}}^{\,\mathrm {WL}}\mathbf {I_{m}},\; \delta _{\mathrm {2}}^{\,\mathrm {WL}}\mathbf {I}_{m},\; \ldots ,\; \delta _{n_{\mathrm {beam}}/2}^{\,\mathrm {WL}}\mathbf {I}_{m}). \end{aligned}$$

• V Additive uncertainty of $0.8\times 10^{2} \frac{N}{m^{2}}$ with respect to torsional stiffness $GI_{p}$ for each tuning beam on the left wing and $1.2\times 10^{2} \frac{N}{m^{2}}$ for each tuning beam on the right wing

  $$\begin{aligned} {\varvec{\Delta }_\mathbf{K }^\mathbf{V }}&= \begin{bmatrix} {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WR}}} &{} \\ &{} {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WL}}} \end{bmatrix}\;\;\mathrm{where}\\ {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WR}}}&= \mathrm {diag}(\delta _{\mathrm {1}}^{\,\mathrm {WR}}\mathbf {I_{m}},\; \delta _{\mathrm {2}}^{\,\mathrm {WR}}\mathbf {I}_{m},\; \ldots ,\; \delta _{n_{\mathrm {beam}}/2}^{\,\mathrm {WR}}\mathbf {I}_{m})\;\;\mathrm{and}\\ {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WL}}}&= \mathrm {diag}(\delta _{\mathrm {1}}^{\,\mathrm {WL}}\mathbf {I_{m}},\; \delta _{\mathrm {2}}^{\,\mathrm {WL}}\mathbf {I}_{m},\; \ldots ,\; \delta _{n_{\mathrm {beam}}/2}^{\,\mathrm {WL}}\mathbf {I}_{m}). \end{aligned}$$

• VI Additive uncertainty of $0.8\times 10^{2} \frac{N}{m^{2}}$ with respect to both bending stiffness $EI_{yy}$ and torisonal stiffness $GI_{p}$ for each tuning beam on the left and $1.2\times 10^{2} \frac{N}{m^{2}}$ for each tuning beam on the right wing

  $$\begin{aligned} {\varvec{\Delta }_\mathbf{K }^\mathbf{VI }}&=\begin{bmatrix} {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WR}}} &{} \\ &{} {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WL}}} \end{bmatrix} \;\;\mathrm{where}\\ {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WR}}}&= \mathrm {diag} \left( \delta _{\mathrm {1}}^{\,\mathrm {WR}}\mathbf {I_{m}},\; \delta _{\mathrm {2}}^{\,\mathrm {WR}}\mathbf {I}_{m},\; \ldots ,\; \delta _{n_{\mathrm {beam}}/2}^{\,\mathrm {WR}}\mathbf {I}_{m}\right) \;\;\mathrm{and}\\ {\varvec{\Delta }_\mathbf{K }^{\,\mathrm {WL}}}&= \mathrm {diag}\left( \delta _{\mathrm {1}}^{\,\mathrm {WL}}\mathbf {I_{m}},\; \delta _{\mathrm {2}}^{\,\mathrm {WL}}\mathbf {I}_{m},\; \ldots ,\; \delta _{n_{\mathrm {beam}}/2}^{\,\mathrm {WL}}\mathbf {I}_{m}\right) . \end{aligned}$$

Based on the above-defined cases, robust aeroelastic analyses have been carried out using Algorithm 2. Corresponding results are shown as $\mu$-f plots at various flight speeds in Figs. 9, 10, 11, 12, 13 and 14. The $\mu _{}$ values are taken from the upper bound calculation. The results for the nominal and robust flutter analysis are summarized in Table 1 (Fig. 15).

Table 1 Comparison of nominal and robust flutter analysis results

Fig. 10

$\mu$-Frequency plots of robust stability analysis for Case I

Fig. 11

$\mu$-Frequency plots of robust stability analysis for Case II

Fig. 12

$\mu$-Frequency plots of robust stability analysis for Case III

Fig. 13

$\mu$-Frequency plots of robust stability analysis for Case IV

Fig. 14

$\mu$-Frequency plots of robust stability analysis for Case V

Fig. 15

$\mu$-Frequency plots of robust stability analysis for Case VI

8.1 Analysis results

The numerical example demonstrates that even small stiffness parameter variations on the wing structures have a major impact on the onset of the flutter. There are considerable differences between flutter speeds with respect to bending and torsional stiffness variations. The impact of bending stiffness variations on the flutter margin is much stronger than the torsional stiffness uncertainties. This was to be expected due to the flutter results of the nominal model as shown in the graphic below (Fig. 16) where normalized modal participation factors of the flutter mode are plotted. The flutter mode involves a strong coupling between the first wing bending and the first wing torsion mode (critical modes) whereas the first wing bending mode at $f=2.93$ Hz dominates the motion at the flutter condition. Consequently, bending stiffness variations have a higher effect on the onset of the flutter condition.

Fig. 16

Modal participation factors of flutter mode at $V_{\mathrm {flut}} = 56.04 \; \frac{m}{s}$ of the nominal FE model

The defined uncertainty in Case I reduces the flutter speed by roughly $8 \%$ compared to the nominal flutter speed given in Table 1 whereas the symmetric uncertainty of the torsional stiffness defined in Case II leads to a reduction of the flutter speed by roughly $6.2 \%$. The Case III depicts a combination of the previous two cases and leads to a further reduction of the flutter speed by roughly $3.8 \%$ compared to the Case I. A further important point relating to key characteristics of the results refers to the asymmetry of the stiffness distribution as an uncertainty integrated into the nominal model. Comparison of the flutter speeds between Cases I and IV leads to the conclusion that an asymmetric bending stiffness uncertainty has an greater influence on the flutter margin then an assumption of symmetric bending stiffness uncertainty (reduction of flutter speed by $10.2 \%$), whereas the flutter speeds in Cases II and IV related to the symmetric and asymmetric torsional stiffness uncertainties remain relatively unchanged. Comparison of the results between Cases III and VI also reflects that a combination of asymmetric stiffness uncertainties related to bending and torsion parameters has a stronger effect on the flutter margin in comparison to the assumption of symmetric stiffness uncertainties in the model.

9 Conclusions

In this work a robust aeroelastic stability analysis within the $\mu$-framework has been carried out. Therefore, an LFT model of the perturbed aeroelastic system in state-space form parametrized over flight speed has been developed. Here, the account is taken of the uncertainties in the structural stiffness model which has a significant impact within the lower frequency range and flutter analysis respectively. For the realization of the stiffness parameter variations tuning beams have been generated with respect to the condensed FE model. This approach is suitable for varying of stiffness parameters by only adjusting material properties of the tuning beams avoiding to intervene in the full FE model. The study is limited to the wings of the aircraft and focussed on the investigation of physical stiffness uncertainties of the wings in spanwise direction and handle each wing separately in case of symmetric and especially asymmetric stiffness distribution which is widely underresearched scientifically with respect to robust aeroelastic analyses.