1 Introduction

Flutter is a self-excited instability in which aerodynamic forces on a flexible body couple with its natural vibration modes producing an undesired and often dangerous response of the system. Therefore, flutter analysis has been widely investigated and there are several techniques representing the state-of-practice (e.g. p-k method) [32]. These often assume that the model representing the system is linear, and the classic approach is to look at the smallest speed V such that the system features a pair of purely imaginary eigenvalues. This speed \(V_{\text {f}}\) is called flutter speed and is such that for \(V<V_{\text {f}}\) the aeroelastic system is stable.

One of the main issues related to flutter analysis using standard techniques arises from the sensitivity of this aeroelastic instability to small variations in parameter and modeling assumptions [31]. In addressing this aspect, in the last decades the so-called flutter robust analysis was proposed, which aims to quantify the gap between the prediction of the nominal stability analysis (model without uncertainties) and the worst-case scenario when a certain set of uncertainties is contemplated. The most well-known approaches, building on the linear fractional transformation (LFT) and \(\mu\) framework, are those from [3, 24]. More recent results have focused on LFT modeling strategies tailored to aeroelastic systems [19] and applications of \(\mu\) analysis to high fidelity models obtained with fluid-structure interaction solvers [18].

The main limitation of the aforementioned nominal and robust approaches lies in the fact that the analyzed system must be linear. While this assumption is often deemed acceptable, modern trends in the design of aerospace structures require a more realistic description of the system and this compels to consider cases where the linear hypothesis no longer holds [11]. In fact, structural deflections invalidating linearity assumptions can take place well below the flutter speed (and thus within the aircraft operating range) due to higher flexibility in modern (and envisioned) lightweight structures, thus analysis tools have to cope with a nonlinear description of the aircraft to make reliable aeroelastic predictions. While the study of nonlinear flutter for nominal (i.e. without uncertainties) systems has reached a certain degree of maturity and understanding [5, 8, 36], the case with uncertainties has received far less attention. Therefore, it is motivated the interest in the research community for strategies allowing an extension of the powerful robust flutter linear approaches to the nonlinear case.

Recent work by the authors [20] proposed an approach combining integral quadratic constraints and describing functions methods to address the robustness of the post-critical behaviour of an uncertain system subject to hard-nonlinearities (e.g. freeplay, saturation). While there the focus was on the deterioration of the response (characterized by amplitude and frequency) in the face of the uncertainties, the goal of this work is to provide robust stability margins for polynomial systems. That is, to provide a measure of the proximity of the nominal nonlinear system to the loss of stability.

The main idea is to use bifurcation theory [23] to define the conditions by which stability is lost. This technique has been amply used in the aerospace community [1, 7, 12] and its choice in this particular context is motivated by the fact that equilibria of nonlinear aeroelastic systems typically exhibit loss of stability in the form of limit cycle oscillations (LCO), which can be seen as a limited amplitude flutter. In fact, the onset of LCOs corresponds to a Hopf bifurcation point in the system [8], since the stable branch of equilibria (corresponding to the stable configuration of the system at low speeds) loses stability and meet a branch of periodic solutions. Taking the cue from this, the paper proposes numerical recipes, inspired by the LFT-\(\mu\) framework, to compute margins to Hopf bifurcations. The proposed bifurcation margins can therefore be interpreted as nonlinear analogs of the robust stability margins used in the context of robust (linear) flutter analysis [3, 19, 24].

Note finally, that previous works in the literature looked at the problem of computing perturbations to bifurcations. For example, in Ref. [9] an extension to multidimensional parameter spaces of standard methods for codimension-1 bifurcations was proposed. The central idea to determine locally closest bifurcations is to use normal vectors to hypersurfaces of bifurcation points. Both direct and iterative methods are proposed, with only the former, consisting of solving the full set of equations defining the bifurcation, applicable to the Hopf case (but deemed onerous, by the authors in Ref. [9], from a computational perspective). This approach was applied in Ref. [28] to the analysis of static bifurcations (namely transcritical and pitchfork) in flexible satellites, making, however, a number of simplifying assumptions, e.g., no dependence of the equilibrium on the uncertainties, system with Hamiltonian dynamics.

The layout of the article is as follows. Section 2 presents a cursory overview of the techniques employed in the work. In Sect. 3 the proposed approach to compute stability margins is detailed, whereas in Sect. 4 its application is demonstrated via a known case study from literature. Finally, Sect. 5 gathers the main conclusions of the work and future directions of researchFootnote 1.

2 Background

2.1 Notation and nomenclature

The symbol \(\hat{}\) is used for optimized quantities; the symbol \(\tilde{}\) is used for uncertain quantities.

\(\mathbb {R}^{n \times m}\), \(\mathbb {C}^{n \times m}\) =

Real and complex valued matrices with n rows and m columns

\(\bar{\sigma }(P)\) =

Maximum singular value of a matrix P

x =

Vector of \(n_x\) states

p =

Bifurcation parameter

f =

Nominal vector field

J =

Jacobian matrix of f

\(x_0\) =

Equilibrium point of f corresponding to \(p_0\)

\(x_{\text {H}}\) =

Equilibrium point of f corresponding to \(p_{\text {H}}\) at which a Hopf bifurcation occurs

\(\mathscr {F}_{u}(M,\Delta )\) =

Upper LFT of \(M \in \mathbb {C}^{n \times m}\) with respect to \(\Delta \in \mathbb {C}^{p \times r}\)

\(\Delta\) =

Structured uncertainty set associated to an LFT

\(\omega\)=

Real part of \(\nu\)

\(\delta\) =

Vector of \(n_{\delta }\) real uncertainties

\(\tilde{f}\) =

Uncertain vector field

\(\tilde{J}\) =

Jacobian matrix of \(\tilde{f}\)

\(\bar{p}_0\) =

Value of p for which the equilibrium point \(\bar{x}_0\) of f is stable

\(\bar{\delta }\) =

Worst-case perturbation for which \(\tilde{f}\) undergoes a Hopf bifurcation at \(\bar{p}_0\)

\(k_m\) =

Robust bifurcation margins

2.2 Bifurcation analysis and continuation methods

Bifurcation analysis studies qualitative changes in the features of a nonlinear system (e.g. number and type of steady-state solutions) when one or more parameters on which the dynamics depend are varied [23]. Consider an autonomous nonlinear system of the form:

$$\begin{aligned} \dot{x}=f(x,p), \end{aligned}$$
(1)

where \(x \in \mathbb {R}^{n_x}\) and \(p \in \mathbb {R}\) are, respectively, the vector of states and the bifurcation parameter, and \(f: \mathbb {R}^{n_x} \times \mathbb {R} \rightarrow \mathbb {R}^{n_x}\) is the vector field. In this work f is assumed to gather polynomial functions (\(f \in \mathscr {C}^{\infty }\)), thus the Jacobian matrix of the vector field \(\nabla _x f: \mathbb {R}^{n_x} \times \mathbb {R} \rightarrow \mathbb {R}^{n_x \times n_x}\), denoted here by J, is always defined.

The vector \(x_0\) is called a fixed point, or equilibrium, of the system given by (1) corresponding to \(p_0\) if \(f(x_0,p_0)=0\). Let us denote by \(n_{0}\) the number of eigenvalues of \(J(x_0,p_0)\) with zero real part. Then \(x_0\) is called a hyperbolic fixed point if \(n_{0}=0\), otherwise it is called nonhyperbolic.

Bifurcations of fixed points are concerned with the loss of hyperbolicity of the equilibrium as p is varied. Specifically, two scenarios can take place: static bifurcations and dynamic bifurcations. This work will focus on the latter case only, also referred to as Hopf bifurcation, at which branches of fixed points and periodic solutions meet. The Hopf bifurcation theorem, giving conditions for the occurrence of a dynamic bifurcation in a branch of equilibria, is a cornerstone result in dynamical systems theory and can be stated as follows. The reader is referred to the seminal monographs [16, 23] for thorough explanations of the profound concepts involved.

Theorem 1

[16] Suppose that the system \(\dot{x}=f(x,p)\), \(x \in \mathbb {R}^{n_x}\) and \(p \in \mathbb {R}\) has an equilibrium \((x_{\text {H}},p_{\text {H}})\) at which the following properties are satisfied:

  1. 1.

    \(J(x_{\text {H}},p_{\text {H}})\) has a simple pair of pure imaginary eigenvalues and no other eigenvalues with zero real parts. This implies, for the implicit function theorem, that there is a smooth curve of equilibria (x(p), p) with \(x(p_{\text {H}})=x_{\text {H}}\). The eigenvalues \(\nu (p)\), and \(\bar{\nu }(p)\) of J(x(p)), with \(\nu (p_{\text {H}}) = i \omega _0\), vary smoothly with p.

  2. 2.
    $$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} p} \left. ({\text {Re}} \nu (p))\right| _{p=p_{\text {H}}} \ne 0 \end{aligned}$$
    (2)

Then there is a unique three-dimensional center manifold passing through \((x_{\text {H}},p_{\text {H}})\) in \(\mathbb {R}^{n_x} \times \mathbb {R}\) and a smooth system of coordinates for which the Taylor expansion of degree 3 on the center manifold is given in polar coordinates \((\rho ,\theta )\) by:

$$\begin{aligned}&\dot{\rho }=(l_0 p + l_1 \rho ^2)\rho \nonumber \\&\dot{\theta }=\omega + l_2 p + l_3 \rho ^2 \end{aligned}$$
(3)

If \(l_1 \ne 0\), there is a surface of periodic solutions in the center manifold which has quadratic tangency with the eigenspace of \(\nu (p)\), \(\bar{\nu }(p)\). If \(l_1<0\), then these periodic solutions are stable limit cycles, while if \(l_1>0\), the periodic solutions are repelling.

Condition 1 of Theorem 1 requires that the Jacobian of the vector field has a pair of purely imaginary eigenvalues (and no other eigenvalues on the imaginary axis). Condition 2, also known as the transversality condition, prescribes that these eigenvalues are not stationary with respect to p at the bifurcation. A fundamental parameter determining the dynamic behavior in the neighborhood of a Hopf point is \(l_1\), also called first Lyapunov coefficient. Its value determines whether the Hopf bifurcation is subcritical or supercritical. The importance of this aspect in nonlinear flutter analysis will be commented in Sect. 4.

The computational tool of bifurcation analysis is numerical continuation, which provides path-following algorithms allowing to compute implicitly defined manifolds [23]. These schemes are based on the implicit function theorem, which guarantees, under the condition that J is non-singular at an initial point (\(x_0,p_0\)), that there exist neighbourhoods X of \(x_0\) and P of \(p_0\) and a function \(g:P \rightarrow X\) such that \(f(x,p)=0\) has the unique solution \(x=g(p)\) in X. Examples of numerical techniques to compute the implicit manifold g are Newton–Raphson, arclength, and pseudo-arclength continuation [15]. These are efficiently implemented in freely available software, such as AUTO [10] and COCO [6]. The latter will be used for all the continuation analyses performed in this work.

2.3 Linear fractional transformation and \(\mu\) analysis

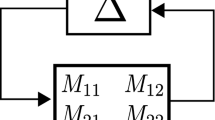
Linear fractional transformation (LFT) is the modeling paradigm in robust control theory for analysis and control design of uncertain systems. The central idea is to represent the original system in terms of nominal and uncertain components. To this aim, the unknown parts are pulled out of the system, so that the problem appears as a nominal system subject to an artificial feedback.

Let \(M\in \mathbb {C}^{(p_1+p_2)\times (q_1+q_2)}\) be a complex matrix partitioned as:

$$\begin{aligned} M= \begin{bmatrix} M_{11} &{} M_{12} \\ M_{21} &{} M_{22} \\ \end{bmatrix}, \end{aligned}$$
(4)

and let \(\Delta \in \mathbb {C}^{q_1 \times p_1}\) the uncertainty operator. The upper LFT of M with respect to \(\Delta\) is defined as the map \(\mathscr {F}_{u}:\mathbb {C}^{q_1\times p_1} \longrightarrow \mathbb {C}^{p_2 \times q_2}\):

$$\begin{aligned} \mathscr {F}_{u}(M,\Delta ) = M_{22} +M_{21} \Delta (I-M_{11} \Delta )^{-1}M_{12}. \end{aligned}$$
(5)

A crucial feature apparent in (5) is that the LFT is well posed if and only if the inverse of \((I-M_{11} \Delta )\) exists. Otherwise, \(\mathscr {F}_{u}(M,\Delta )\) is said to be singular.

Available toolboxes [25] allow to efficiently build up LFTs by providing the partitioned matrix M, which completely defines the map (5) along with the set \(\Delta\). In robust control this set typically gathers parametric and dynamic uncertainties affecting the system [38]. A general definition for this structured uncertainty set is:

$$\begin{aligned}&\Delta = \text {diag}(\delta _{i}I_{d_{i}}, \delta _{j} I_{d_{j}},\Delta _{D_k}) \nonumber \\&i=1,\ldots n_{R}; \quad j=1,\ldots ,n_{C}; \quad k=1,\ldots ,n_{D}; \end{aligned}$$
(6)

where the uncertainties associated with \(n_{R}\) real scalars \(\delta _{i}\), \(n_{C}\) complex scalars \(\delta _{j}\), and \(n_{D}\) unstructured (or full) complex blocks \(\Delta _{D_k}\) are listed in diagonal format. The identity matrices of dimension \(d_{i}\) and \(d_{j}\) take into account the fact that scalar uncertainties are generally repeated in \(\Delta\) when the LFT of the system is built up.

The structured singular value is a matrix function denoted by \(\mu _{ \Delta }(M)\), where \(\Delta\) is a structured uncertainty set. The mathematical definition is as follows:

$$\begin{aligned} \mu _{\Delta }(M) = \Bigg (\min _{\hat{\Delta } \in \Delta } \big (\bar{\sigma }(\hat{\Delta }) : \det ( I - M \hat{\Delta }) = 0 \big )\Bigg )^{-1}, \end{aligned}$$
(7)

if \(\exists \hat{\Delta } \in \Delta\) such that \(\det ( I - M \hat{\Delta }) = 0\) and otherwise \(\mu _{ \Delta }(M):=0\). Note that \(\bar{\sigma }(\hat{\Delta })\) denotes the maximum singular value of the matrix \(\hat{\Delta }\).

Equation (7) can then be specialized to the study of the robust stability (RS) of the system represented by \(\mathscr {F}_{u}(M,\Delta )\). At a fixed frequency \(\omega\), the coefficient matrix M is a complex valued matrix; in particular, \(M_{11}\) is known, and the RS problem can be formulated as a \(\mu\) calculation:

$$\begin{aligned} \mu _{\Delta }(M_{11}) = \Bigg (\min _{\hat{\Delta } \in \Delta } (\kappa :\det ( I - \kappa M_{11} \hat{\Delta }) = 0; \quad \bar{\sigma }(\hat{\Delta })\le 1)\Bigg )^{-1}, \end{aligned}$$
(8)

where \(\kappa\) is a real positive scalar. For ease of calculation and interpretation, the set \(\Delta\) is norm-bounded by scaling of M without loss of generality. The result can then be interpreted as follows: if \(\mu _{ \Delta } \le 1\) then there is no perturbation matrix inside the allowable set \(\Delta\) such that the determinant condition is satisfied, that is \(\mathscr {F}_{u}(M,\Delta )\) is well posed and thus the associated plant is robust stable within the range of uncertainties considered. On the contrary, if \(\mu _{ \Delta } \ge 1\) a candidate perturbation matrix (that belongs to the allowed set) exists which violates the well-posedness condition. In particular, the reciprocal of \(\mu\) (auxiliary notation is dropped for clarity) provides a measure (by means of its \(\Vert \cdot \Vert _{\infty }\) norm \(\kappa\)) of the smallest structured uncertainty matrix that causes instability. Due to this interpretation, the reciprocal of \(\mu\) is also referred to in the literature as robust stability margin of the system (see for example the Robust Control Toolbox [2]).

The calculation of the structured singular value is an NP-hard problem [4], thus all \(\mu\) algorithms work by searching for upper and lower bounds. The upper bound \(\mu _{\text {UB}}\) provides the maximum size perturbation \(\bar{\sigma } (\Delta ^{\text {UB}}) = 1/ \mu _{\text {UB}}\) for which RS is guaranteed, whereas the lower bound \(\mu _{\text {LB}}\) defines a minimum size perturbation \(\bar{\sigma } (\Delta ^{\text {LB}}) = 1/ \mu _{\text {LB}}\) for which RS is guaranteed to be violated. Along with this information, the lower bound also provides the critical perturbation matrix \(\Delta ^{\text {LB}}=\Delta ^{cr}_u\) determining singularity of the LFT.

Note also that \(\mu\) is evaluated in general on a discretized frequency range. This has the drawback of possibly missing critical frequencies and thus underestimating the value of \(\mu\). However, newly developed algorithms using Hamiltonian-based techniques [33] can also guarantee the validity of results over a continuum range of frequencies.

3 Computation of robust margins to Hopf bifurcations

3.1 Problem statement

The objective is to compute for polynomial systems margins of stable equilibria to the closest Hopf bifurcation. The starting point is the vector field f in (1), assumed to be subject to real parametric uncertainties denoted by:

$$\begin{aligned} \delta = [\delta _1; \ldots ; \delta _i; \ldots \delta _{n_{\delta }}], \quad \delta \in \mathbb {R}^{n_{\delta }}. \end{aligned}$$
(9)

This description allows to handle various sources of uncertainties, for example the lack of confidence on the values of model parameters or simplifying assumptions underlying the model. The expression for the uncertain vector field \(\tilde{f}\) and associated Jacobian \(\tilde{J}\) is:

$$\begin{aligned} \dot{x} = \tilde{f}(x,p,\delta ), \quad&\tilde{f}: \mathbb {R}^{n_x} \times \mathbb {R} \times \mathbb {R}^{n_{\delta }} \rightarrow \mathbb {R}^{n_x}, \quad \tilde{f} \in \mathscr {C}^{\infty } \end{aligned}$$
(10a)
$$\begin{aligned}&\tilde{J}: \mathbb {R}^{n_x} \times \mathbb {R} \times \mathbb {R}^{n_{\delta }} \rightarrow \mathbb {R}^{n_x \times n_x} . \end{aligned}$$
(10b)

Given a Hopf bifurcation point \((x_{\text {H}},p_{\text {H}})\) for the nominal system f, and a value of the bifurcation parameter \(\bar{p}_{0}\) associated with a stable fixed point \(\bar{x}_{0}\) of f, the goal is to determine the smallest perturbation \(\bar{\delta } \in \delta\) such that \(\tilde{f}\) undergoes at \(\bar{p}_{0}\) a Hopf bifurcation. In other words, the worst-case combination of parameters in \(\delta\) is sought such that the system experiences a Hopf bifurcation.

The goal stated above requires the adoption of a metric (for the magnitude of the perturbation) to formalize the concept of worst-case. To this aim, let us consider a generic uncertain parameter d, with \(w_{d}\) indicating the uncertainty level with respect to a nominal value \(d_0\) and a range \(\delta _{d}\in [-\,1,1]\) representing the normalized uncertainty. Note that \(d_0\) and \(w_{d}\) are typically fixed by the analyst based on the knowledge of the nominal value and dispersion of the parameter d, respectively. A multiplicative uncertain representation [38] of d is thus obtained as:

$$\begin{aligned} d=(1+w_{d}\delta _{d})d_0, \end{aligned}$$
(11)

where \(\delta _{d}=0\) corresponds to the nominal value of d, while \(\delta _{d}=\pm 1\) represents a perturbation at the extreme of the parameter range (e.g., a variation of \(\pm \, 20\%\) from \(d_0\) if \(w_{d}=0.2\)). Once the normalization (11) is applied to the uncertain parameters (9), a possible scalar metric (or norm) is the largest of the absolute values of the elements in \(\delta\). This can be equivalently expressed as \(\bar{\sigma }(\text {diag}(\delta ))\), i.e., the maximum singular value of the diagonal matrix with elements of \(\delta\) on the diagonal. This metric quantifies the deviation of the uncertain parameters from their nominal values along the direction of the parameter space where this is largest. In fact, \(k_{m}=\bar{\sigma }(\text {diag}(\delta ))\) can be regarded as a robust margin from bifurcation because \(k_{m} \le 1\) means that a candidate perturbation (i.e., within the allowed range of the uncertainty set) exists which determines a Hopf bifurcation. In the latter case, the equilibrium \(\bar{x}_{0}\) of the nominal vector field is said to be not robustly stable at \(\bar{p}_{0}\). On the contrary, if \(k_{m}\ge 1\) then there is no perturbation inside the allowed set capable of prompting a Hopf bifurcation. This is pictorially represented in Fig. 1, where on the x-axis is reported the bifurcation parameter and on the y-axis the margin \(k_{m}\) (note that the case \(p_0<p_{\text {H}}\) where a Hopf bifurcation is encountered by increasing p is assumed here without loss of generality). When the line \(k_{m}=1\) is crossed, the system is operated in a region where Hopf bifurcations can occur in the face of the uncertainties accounted for in the system (shaded area).

Fig. 1
figure 1

Concept of robust bifurcation margins

Full size image

Due to the definition of the metric used to formalize the concept of worst-case, the margin \(k_m\) has a direct relationship with the structured singular value \(\mu\). For a linear time-invariant system, \(k_m\) would coincide with \(\frac{1}{\mu }\), that is with the robust stability margin of the system [2]. This is also clear from the interpretation of \(k_m\) shown in Fig. 1. For a nonlinear system, it represents a natural extension of the robust stability margin where now the onset of a bifurcation (rather than the loss of stability) is considered.

3.2 Solution via nonlinear optimization

The fundamental idea behind the proposed approach is to exploit the versatility of the LFT paradigm to compute \(k_m\). Let us consider for a moment only Condition 1 of Theorem 1, which prescribes a pair of purely imaginary eigenvalues for the Jacobian. If \(\tilde{J}\) is interpreted as the uncertain state-matrix of the linear case, an LFT model of the former with respect to the uncertain parameters in \(\delta\) can be built up (numerically or even analytically [26]). This would be the starting point for the application of robust flutter analysis with \(\mu\) (see for example [19] for a detailed discussion on the derivation of LFT models for aeroelastic systems represented by state-space models). The main difference with the linear case is that typically \(\tilde{J}\) is also a function of the states of the system x, and this is reflected in the proposed definition of the LFT of the Jacobian \(\mathscr {F}_{u}(M_{\tilde{J}},\Delta _{\tilde{J}})\):

$$\begin{aligned}&\mathscr {F}_{u}(M_{\tilde{J}},\Delta _{\tilde{J}})=\mathscr {F}_{u}(\mathscr {F}_{u}(M_{\tilde{J}},\Delta ),\Delta _x), \end{aligned}$$
(12a)
$$\begin{aligned}&\Delta _{\tilde{J}} = \text {diag}(\Delta ,\Delta _x), \end{aligned}$$
(12b)
$$\begin{aligned}&\Delta = \text {diag}(\delta _{1}I_{d_{1}},\ldots ,\delta _{i}I_{d_{i}},\ldots ,\delta _{n_{\delta }}I_{d_{n_{\delta }}}), \end{aligned}$$
(12c)
$$\begin{aligned}&\Delta _x = \text {diag}(x_{1}I_{x_{1}},\ldots ,x_{j}I_{x_{j}},\ldots ,x_{n_{x}}I_{x_{n_{x}}}), \end{aligned}$$
(12d)

where the property that interconnections of LFTs can be rewritten as one single LFT [25] has been used in (12a). The structured set \(\Delta _{\tilde{J}}\) features \(\Delta\) (a particular instance of the set in Eq. (6) where only real parameters are considered) and \(\Delta _x\), which arises when performing the LFT modeling of \(\tilde{J}\) due to the states explicitly appearing in the Jacobian (and for which a similar representation to the one for \(\Delta\) is employed). Therefore, the final form of the two operators defining the LFT of the Jacobian \(\mathscr {F}_{u}(M_{\tilde{J}},\Delta _{\tilde{J}})\) are:

$$\begin{aligned}&M_{\tilde{J}}= \begin{bmatrix} M_{\tilde{J}_{11}} &{} M_{\tilde{J}_{12}} \\ M_{\tilde{J}_{21}} &{} M_{\tilde{J}_{22}} \\ \end{bmatrix}, \end{aligned}$$
(13a)
$$\begin{aligned}&\Delta _{\tilde{J}} = \text {diag}(\Delta ,\Delta _x), \end{aligned}$$
(13b)

where the sub-matrices of \(M_{\tilde{J}}\) are obtained via LFT modeling of the Jacobian, and \(\Delta _{\tilde{J}}\) has the structured form of the set defined in (6) and consist of uncertainty and states components which feature in the uncertain Jacobian \(\tilde{J}\).

Condition 1 can then be expressed as the singularity of \(\mathscr {F}_{u}(M_{\tilde{J}},\Delta _{\tilde{J}})\). Note that the partitioned matrix \(M_{\tilde{J}}\) is a function of the frequency \(\omega\) of the purely imaginary eigenvalues of \(\tilde{J}\). The standard approach in \(\mu\) analysis is to select a grid of frequencies and associate a margin to each of them. However, it is known that the dependency of \(M_{\tilde{J}}\) on the frequency is of LFT form [25, 38], that is \(\omega\) can be added to the set \(\Delta _{\tilde{J}}\) by appropriate manipulation of the sub-matrices of \(M_{\tilde{J}}\). This was shown explicitely in [19] when describing the state-space approach to LFT modeling of aeroelastic plant, and leverages the interpretation of LFT as a realization technique [25, 38]. As a result, it is possible to explicitly consider the critical frequency (corresponding to the closest bifurcation) as unknown of the problem by including it in the set \(\Delta _{\tilde{J}}\).

This ameliorates the issue of possibly missing critical values of \(\omega\), which can represent a concrete risk when analyzing flexible structures [13].

The discussion above paves the way for Program 1, which recasts the computation of \(k_m\) as a smooth nonlinear optimization problem.

Program 1

figure a
$$\begin{aligned} X=[x;\delta ;\omega ], \end{aligned}$$

where X is the vector of optimization variables including: the equilibrium point x; the uncertain parameters \(\delta\); and the frequency \(\omega\) (the symbol \(\hat{}\) will be used for solutions of the optimization). Let us examine the constraints of the program. Eq. (14a) guarantees that the solution \(({\hat{x}},{\hat{\delta }})\) corresponds to an equilibrium point for the system. Eq. (14b) ensures that \(\tilde{J}\) has a pair of complex eigenvalues \(\pm {\hat{\omega }}\), and Eq. (14c) bounds the size of the perturbation matrix. Off the shelf nonlinear optimization solvers can be employed to solve Program 1. Specifically, in this work interior point, active set, and sequential quadratic programming solvers have been tested. These are for example available with the MATLAB Optimization Toolbox [27]

3.3 General remarks

Program 1 can be regarded as a first attempt to extend the concept of \(\mu\) from the linear context to the nonlinear one. In fact, \(\mu\) computes by definition the worst-case perturbation matrix which makes an LFT ill-posed (same rationale used here) and employs the same metric (8) as the one used to define the robust bifurcation margin \(k_{m}\). Indeed, it follows immediately from the definitions that \(k_{m}=\bar{\sigma }(\text {diag}(\delta ))=\bar{\sigma }(\Delta )\)

The problem formulated in (14) is thus similar to that underlying the definition of \(\mu\) (8), but with two crucial differences: constraint (14a), and the addition of \(\Delta _x\) in the block \(\Delta _{\tilde{J}}\) of the LFT. Due to these differences, available algorithms for \(\mu\) cannot be applied to compute solutions of (14), and to overcome this the idea is to enforce singularity of the LFT by using directly the determinant condition (14b). In Ref. [34] this is listed among the known methods for the computation of \(\mu _{\text {LB}}\), and examples of related algorithms can be found in Refs. [17, 37]. The approaches presented in these references, however, are limited to the case of linear systems, i.e., they represent alternatives to well-established \(\mu\) lower bounds algorithms such as the power iteration [29] and the gain-based method [35].

An important remark is that Program 1 does not mathematically guarantee the onset of a Hopf bifurcation because it does not take into account the transversality condition (Condition 2 of Theorem 1). Note, however, that this framework will be applied to the study of aeroelastic systems where the bifurcation parameter p has a clear physical meaning (typically the speed V). The transversality condition is hence assumed to be automatically verified because p has a great effect on the spectrum of the Jacobian, and stationarity of the critical eigenvalues at the bifurcation point is deemed an unlikely scenario. These considerations were thoroughly assessed by extensive numerical campaigns using Program 1 to find worst-case perturbations. Dedicated continuation analyses, applied to the systems perturbed with the optimized vector of uncertainties \(\hat{\delta }\), confirmed the occurrence of a Hopf bifurcation at the expected value of the parameter \(\bar{p}_{0}\).

Another important observation on the proposed approach is that, since it is based on nonlinear optimization, there is no guarantee that the bifurcation found is the closest one. In other words, global minima might be missed and thus there could be a vector \(\bar{\delta }\) featuring a smaller norm than \(\hat{\delta }\) which causes a Hopf bifurcation. Local optima are a well-known issue in nonlinear optimization and, despite the large amount of research done on this topic, no standard solution is available [14]. Moreover, this issue is also common to previous works [9, 28] that aimed at computing closest bifurcation with different approaches.

Mitigation strategies depend on several aspects, including specific features of the program (e.g., type of constraints, objective functions) and adopted optimization algorithms. For this problem, the objective is to compute worst-case perturbations quantified by means of a scalar metric, thus a possible way to account for this issue is to estimate a guaranteed smallest magnitude of the perturbation for which the system is stable. This is the approach taken in \(\mu\) analysis, where the computation of \(\mu _{\text {LB}}\) (analog of \(k_m\)) is known to be prone to local minima and as a remedy upper bounds \(\mu _{\text {UB}}\) are proposed. Lower bounds on \(k_m\) (analogs of the upper bounds in \(\mu\) analysis) could then be a feasible approach.

A strategy which exploits the formulation of the optimization via LFT is to run Program 1 at a given frequency, i.e., \(\omega\) does not belong to the vector of optimization variables X but is fixed a priori (this can be easily done in the LFT modeling stage). The rationale behind this is twofold. From a mathematical point of view, the optimization is simplified by the fact that constraint (14b) does not depend on the frequency and this enhances the accuracy of the result. From a bifurcation perspective, fixing the frequency restricts the mechanisms by which the system can undergo a Hopf bifurcation when subject to uncertainties, which reduces the number of feasible solutions in the first place, and as a result makes it also more likely to detect the optimal one. A value of \(k_m\) can be associated with each discrete frequency, and the smallest of these values can be regarded as the most critical (similarly to what is done in \(\mu\) analysis). An example of this will be given in Sect. 4.3.

4 Application to robust nonlinear flutter

The concept of robust bifurcation margins is applied to a nonlinear aeroelastic case study with the aim to quantify the influence of parametric uncertainties on the onset of LCO in the system. Following the notation in Sect. 3.1, let us denote by \(V_{\text {H}}\) the speed at which the nominal system undergoes a Hopf bifurcation. Given a subcritical speed \(\bar{V}_0\) (such that \(\bar{V}_0<V_{\text {H}}\) corresponds to a stable equilibrium) and the definition of a vector \(\delta\) of parametric uncertainties, then the distance in the parameter space of the equilibrium at \(\bar{V}_0\) from the closest Hopf bifurcation is computed by means of the robust bifurcation margin \(k_m\).

4.1 System description and linear flutter

The system, sketched in Fig. 2 and commonly referred to as typical section, consists of a rigid airfoil with lumped springs simulating the 3 structural degrees of freedom (DOFs): plunge h, pitch \(\alpha\) and trailing edge flap \(\beta\). The position of the elastic axis (EA), center of gravity (CG) and aerodynamic center (AC), and the convention for the signs of the DOFs are marked in Fig. 2.

Fig. 2
figure 2

Typical section sketch

Full size image

The parameters in the model are: \(K_h\), \(K_{\alpha }\) and \(K_{\beta }\) –respectively, the plunge, pitch and control surface stiffness; half chord distance b; dimensionless distances a, c (from the mid-chord to, respectively, the elastic axis and the hinge location), and \(x_{\alpha }\) and \(x_{\beta }\) (respectively, the distance from elastic axis to airfoil center of gravity and from hinge location to control surface center of gravity); wing mass per unit span \(m_s\); moment of inertia of the section about the elastic axis \(I_{\alpha }\); and the moment of inertia of the control surface about the hinge \(I_{\beta }\). Based on these parameters, the structural mass \(M_s\) and stiffness \(K_s\) matrices (damping is assumed null) are defined as:

$$\begin{aligned}&M_s = m_s b^2 \left[ \begin{array}{ccc} 1 &{} x_{\alpha } &{} x_{\beta }\\ x_{\alpha } &{} r^2_{\alpha } &{} r^2_{\beta }+x_{\beta }(c-a)\\ x_{\beta } &{} r^2_{\beta }+x_{\beta }(c-a) &{} r^2_{\beta }\\ \end{array} \right] \nonumber \\&K_s= \left[ \begin{array}{ccc} K_h &{} 0 &{} 0\\ 0 &{} K_{\alpha } &{} 0\\ 0 &{} 0 &{} K_{\beta } \\ \end{array} \right] , \end{aligned}$$
(15)

where \(r_{\alpha } = \sqrt{\frac{I_{\alpha }}{m_s b^2}}\) and \(r_{\beta } = \sqrt{\frac{I_{\beta }}{m_s b^2}}\) are, respectively, the dimensionless radius of gyration of the section and of the control surface.

Theodorsen’s unsteady formulation is employed to model the aerodynamics [22]. This provides the aerodynamic operator as a transfer matrix Q representing transfer functions between the elastic degrees of freedom and the aerodynamic load components:

$$\begin{aligned} Q = \bigg (M_{nc}\bar{s}^2 + \big (B_{nc}+C(\bar{s})R_1 \cdot S_2\big )\bar{s}+ K_{nc}+C(\bar{s})R_1 \cdot S_1\bigg ), \end{aligned}$$
(16)

where: \(\bar{s}=\frac{s b}{V}\) (s is the Laplace variable); \(M_{nc}\), \(B_{nc}\), \(K_{nc}\), \(R_1\), \(S_{1}\), \(S_{2}\) are real coefficients matrices depending on the dimensionless distances a and c [22]; and \(C(\bar{s})\) is the Theodorsen function, which is a complex scalar depending on modified Bessel and Hankel functions depending on \(i \bar{s}\) [22]. Due to the motion assumptions underlying Theodorsen theory (purely harmonic), the expression in (16) has to be evaluated at \(\bar{s} = i\frac{\omega b}{V} = ik\), where k is called the reduced frequency. Since Q has a non-rational dependence on s, and a state-space representation of the aerodynamic forces is sought to describe the section with a system of ordinary differential equations of the type of (1), a rational approximation is computed via the Minimum State method [22]:

$$\begin{aligned} Q \approx A_{2} \bar{s}^2 +A_{1}\bar{s}+A_{0} + \bar{D} \begin{bmatrix} \frac{1}{\bar{s}+\gamma _{1}} &{} \ldots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \ldots &{} \frac{1}{\bar{s}+\gamma _{n_{a}}} \\ \end{bmatrix} \bar{E} \bar{s}. \end{aligned}$$
(17)

\(A_{2}\), \(A_{1}\) and \(A_{0}\) are real coefficient matrices modelling the quasi-steady contribution to the aerodynamic loads; \(\bar{D}\) and \(\bar{E}\) are real coefficient matrices capturing, with the lag roots \(\gamma _{i}\), the memory effect of the wake, which results in a phase shift and magnitude change with respect to the instantaneous loads. The aerodynamic rational approximation entails the addition of augmented states \(x_a\) equal in number to the number of roots \(n_a\).

By defining the vector of structural states \(x_s=[\frac{h}{b}; \alpha ; \beta ]\), the system can then be described in matrix form as:

$$\begin{aligned} \dot{x}=\left[ \begin{array}{c} \dot{x}_s \\ \ddot{x}_s \\ \dot{x}_a \\ \end{array}\right] = \left[ \begin{array}{ccccc} 0 &{} &{} I &{} &{} 0 \\ -M^{-1}K &{} &{} -M^{-1}B &{}&{} M^{-1}D \\ 0 &{} &{} \bar{E} &{}&{} R \\ \end{array}\right] \left[ \begin{array}{c} x_s \\ \dot{x}_s \\ x_a \\ \end{array}\right] =\mathscr {A}x, \end{aligned}$$
(18)

where (\(\rho _{\infty }\) is the air density):

$$\begin{aligned}&M = M_{s}-\frac{1}{2}\rho _{\infty }b^2 A_{2} \nonumber \\&B = -\frac{1}{2}\rho _{\infty }b V A_{1} \nonumber \\&K = K_{s}-\frac{1}{2}\rho _{\infty } V^2 A_{0} \nonumber \\&R=\left[ \begin{array}{ccc} -\frac{V}{b}\gamma _{1} &{} 0 &{} 0 \\ 0 &{} \ddots &{} 0 \\ 0 &{} 0 &{} -\frac{V}{b}\gamma _{n_{a}} \\ \end{array} \right] \nonumber \\&D = \frac{1}{2}\rho _{\infty } V^2 \bar{D}. \end{aligned}$$
(19)

M, B and K are, respectively, the aeroelastic inertial, damping and stiffness matrices. They include the structural terms (respectively \(M_s\) and \(K_s\) from Eq. 15) plus the aerodynamic quasi-steady matrices \(A_i\).

The case study is taken from [22] and the parameters defining the structural model and the geometry are provided in Table 1. It is remarked that this is a notional aeroelastic example and does not mean to be representative of any realistic configuration.

Table 1 Parameters of the linear typical section cas study [22]
Full size table

The total size \(n_x\) is 9 (six structural and three aerodynamic). The interested reader is referred to [19] for further details on the aeroelastic modeling of this system, including a discussion on different aerodynamic approximations and their impact on robust flutter analysis.

Linear flutter of this case study (both with and without uncertainties) was investigated in Ref. [19]. Nominal flutter analysis revealed that the system exhibits a flutter mechanism featured by a merging of the plunge and pitch frequencies (binary flutter) just before the instability occurs at the flutter speed \(V_{\text {f}}=302.7\) m/s with a flutter frequency \(\omega _{\text {f}}=70.7\) rad/s. \(\mu\)-based robust linear flutter analysis was then performed to investigate the effect of different combinations of parametric uncertainties at the subcritical speed \(V=270\) m/s \(<V_{\text {f}}\). The analysis taking into account perturbations in the coefficients of the structural matrices is briefly commented here. The uncertainty definition consists of a range of variation of 10% from the nominal value for the coefficients \(M_{{s}_{11}}\), \(M_{{s}_{22}}\), \(K_{\alpha }\) and of 5% for \(M_{{s}_{12}}\) (note that the mass matrix is symmetric, hence \(M_{{s}_{21}}\) is affected by the same uncertainty) and \(K_{h}\) (15). By recalling the definition of the mass matrix \(M_s\) in (15), it can be noted that the uncertainty on the mass takes into account possible inaccuracies in the knowledge of: the total section mass (\(M_{{s}_{11}}\)), the moment of inertia of the section about the elastic axis (\(M_{{s}_{22}}\)); the offset of elastic axis and the center of gravity (\(M_{{s}_{12}}\)). The resulting structured uncertainty set is:

$$\begin{aligned} \Delta =\text {diag}(\delta _{K\alpha },\delta _{Kh},\delta _{Ms11}, \delta _{Ms12} I_2, \delta _{Ms22}). \end{aligned}$$
(20)

In Fig. 3 the upper \(\mu _{\text {UB}}\) (UB) and lower \(\mu _{\text {LB}}\) (LB) bounds of the structured singular value \(\mu\) are shown. The balanced form algorithm was used to compute \(\mu _{\text {UB}}\), whereas for \(\mu _{\text {LB}}\) the gain-based algorithm [35] was employed (both from the Robust Control Toolbox in MATLAB R2015b [2]). Since the values of the bounds are very close, the actual value of \(\mu\) is well predicted. In particular, it can be concluded from this plot that the system is not robustly stable within the allowed uncertainty range because the peak value is \(\mu \cong 1.38\) (at \(\omega \cong 72\) rad/s). Therefore, the system is flutter-free only for structural uncertainties up to approximately 70% (\(\approx\) \(\frac{1}{1.38}\)) of the assumed size.

Fig. 3
figure 3

Robust linear analysis with \(\mu\) for the case of structural uncertainties

Full size image

Due to the accurate estimation of the lower bound, it is also possible to extract the smallest perturbation matrix \(\Delta _{u}^{cr}\) capable of causing instability, which corresponds to the peak in Fig. 3:

$$\begin{aligned} \Delta _{u}^{cr}&=\text {diag}(\delta _{K\alpha },\delta _{Kh},\delta _{Ms11}, \delta _{Ms12} I_2, \delta _{Ms22}) \nonumber \\&= \text {diag}(-0.7213, 0.6460,-0.7245, 0.7245 I_2, 0.71). \end{aligned}$$
(21)

From examining the signs and values of the above worst-combination it is noted that the structural parameters have opposite perturbations if grouped according to the affected degrees of freedom (i.e. plunge and pitch). Specifically, the plunge equilibrium sees a reduction in \(M_{s11}\) and an increase in \(K_{h}\), while the pitch equilibrium sees an increase in \(M_{s22}\) and a reduction in \(K_{\alpha }\). This corresponds to getting the plunge and pitch natural frequencies closer, which is known to be detrimental in systems prone to binary flutter.

4.2 Nonlinear problem definition and nominal analysis

Nonlinearities in the structural parameters are considered in this work. Specifically, hardening cubic stiffness terms for the plunge and pitch degrees of freedom are assumed, and the matrix \(K_s\) is rewritten accordingly:

$$\begin{aligned}&K_s= K_s^{\text {L}}+K_s^{\text {NL}}=\left[ \begin{array}{ccc} K_h^{\text {L}} &{} 0 &{} 0\\ 0 &{} K_{\alpha }^{\text {L}} &{} 0\\ 0 &{} 0 &{} K_{\beta } \\ \end{array} \right] \nonumber \\&\quad +\left[ \begin{array}{ccc} K_h^{\text {NL}} K_h^{\text {L}} \big (\frac{h}{b}\big )^2 &{} 0 &{} 0\\ 0 &{} K_{\alpha }^{\text {NL}} K_{\alpha }^{\text {L}} \alpha ^2 &{} 0\\ 0 &{} 0 &{} 0\\ \end{array} \right] , \end{aligned}$$
(22)

where the linear \(K_s^{\text {L}}\) and nonlinear \(K_s^{\text {NL}}\) structural stiffness matrices have been introduced. As per usual practice [8], the coefficients of the nonlinear terms are assumed proportional to the corresponding linear ones (which are those defined in Table 1) through the coefficients \(K_{h}^{\text {NL}}\) and \(K_{\alpha }^{\text {NL}}\).

When the nonlinear stiffness matrix \(K_s\) (22) is used in (19) to define the aeroelastic matrix K, the dynamics are given in the form of the generic vector field (1), and thus the following description holds:

$$\begin{aligned}&\dot{x}=f(x,V)=\mathscr {A}^{\text {L}}(V)x+f^{\text {NL}}(x) \nonumber \\&J(x,V) = \mathscr {A}^{\text {L}}(V) + \nabla _x f^{\text {NL}}(x), \end{aligned}$$
(23)

where:

$$\begin{aligned}&\mathscr {A}^{\text {L}} = \begin{bmatrix} 0 &{} I &{} 0 \\ -M^{-1}\big [K_{s}^{\text {L}}-\frac{1}{2}\rho _{\infty } V^2 A_{0}\big ] &{} -M^{-1}B &{} M^{-1}D \\ 0 &{} E &{} R \\ \end{bmatrix};\nonumber \\&f^{\text {NL}} = \begin{bmatrix} 0 &{} 0 &{} 0 \\ -M^{-1}K_{s}^{\text {NL}} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{bmatrix}x. \end{aligned}$$
(24)

In the above definition, the bifurcation parameter p is the speed V (which is a typical choice for flutter analysis), but other options could also be considered.

Numerical continuation can thus be applied to (23) after having specified the value of the trim state \(x_t\). Two trim conditions are considered to show the different effect on the results. The first corresponds to a zero trim state, i.e., \(x_t=0\), whereas the second has a non-zero value \(\alpha _t=1^{\circ }\) for the angle of attack of the section. In the case where the typical section is meant to represent the main wing of an aircraft, this can be physically motivated by the presence of a positive lift, e.g. needed to counterbalance gravitational forces of the body directed downwards. In a conventional aircraft configuration, one could also think of modeling the tailplane as a typical section and the non-zero value of the trim state would be justified by the need for a static equilibrium about the aircraft’s centre of gravity. In that case, the nonzero state entry would be that of the elevator deflection \(\beta _t\). More refined descriptions for \(x_t\) could consider a dependence of \(x_t\) on speed or the presence of a predeformed shape (with non-zero values for all the displacements), but this is not done here since the present description is sufficient to illustrate the role played by \(x_t\).

To present an overview of the possible nonlinear responses of the system, four scenarios are considered. These arise from considering, for each trim state \(x_t\), two possible stiffness cases with only plunge nonlinear stiffness, i.e. \(K_{\alpha }^{\text {NL}}=0\), and with only pitch nonlinear stiffness, i.e. \(K_{h}^{\text {NL}}=0\). The results are presented in Table 2, where, for each scenario (s#, with \(\#=1,\ldots ,4\)), the speed \(V_{\text {H}}\) at which the Hopf bifurcation occurs the frequency of the associated imaginary eigenvalues \(\omega _{\text {H}}\), and the type of bifurcation (sub for subcritical and super for supercritical) are reported. The latter refers to the fact that in general two situations can arise at \(V_{\text {H}}\) when the system undergoes a Hopf bifurcation. If the bifurcation is supercritical, then for \(V>V_{\text {H}}\) a stable LCO exists featured by an amplitude gradually increasing with speed V (benign LCO). Moreover, the phenomenon is reversible and by reducing the speed below \(V_{\text {H}}\) the stable branch of equilibria is recovered. Viceversa, if the bifurcation is subcritical, then for \(V<V_{\text {H}}\) an unstable LCO exists and this often transitions into a stable one featured by higher amplitudes. This is a far more dangerous scenario since the system will suddenly jump to this LCO branch for V slightly larger than \(V_{\text {H}}\), and the absence of oscillations cannot be recovered by simply decreasing V, because of hysteresis [12, 36].

Figure 4 shows the corresponding bifurcation diagrams with V on the x-axis and the normalized plunge DOF \(\frac{h}{b}\) on the y-axis (in case of branches of LCO, this is the maximum value over a period). The usual convention of representing stable steady-states (equilibria and LCOs) with solid line and unstable ones with dashed line is adopted in here.

Table 2 Hopf bifurcations of the nominal system for different combinations of nonlinearities and trim states
Full size table
Fig. 4
figure 4

Bifurcation diagram of the nominal system for different combinations of nonlinearities and trim states

Full size image

The first important observation from Fig. 4 is that when \(x_t=0\) the branch of equilibria is \(x=0\) regardless of V. This implies that \(J=\mathscr {A}^{\text {L}}\), and thus the occurrence of the Hopf bifurcation is independent of the nonlinear terms. This is in accordance with the results from Table 2, where for s1 and s2 it holds \(V_{\text {H}}=V_{\text {f}}\) and \(\omega _{\text {H}}=\omega _{\text {f}}\), i.e., the results of the linear case [19] are retrieved. Nonlinear terms, however, do have an effect on the type of bifurcation (indeed s1 is subcritical whereas s2 is supercritical).

When \(\alpha _t=1^{\circ }\), it can be seen that the branch of equilibria has a non-zero (speed dependent) value. Moreover, different values of \(V_{\text {H}}\) and \(\omega _{\text {H}}\) are registered depending on the nonlinearity affecting the system. This is due to the fact that the linearization of the Jacobian is now affected by the nonlinear term of the vector field \(f^{\text {NL}}\), thus there is an effect from the type of nonlinearity on the onset of the Hopf bifurcation. A consequence of the nonlinear terms is thus also that different values of \(\alpha _t\) (in general \(x_t\)) will correspond to different \(V_{\text {H}}\). This behaviour is not surprising since the dependence of flutter speed on the angle of attack is a known feature of nonlinear flutter [30].

Another important trend, independently of the trim state, is that a subcritical bifurcation occurs for the cases of plunge nonlinearity, whereas for the case of pitch nonlinearity the bifurcation is supercritical. This aspect is in agreement with the discussion in [8], where the concept of intermittent flutter based on the instantaneous natural frequencies of the underlying linear system is used to qualitatively explain the mechanisms prompting different LCOs.

4.3 Nonlinear flutter robust margins

The initial step to compute robust bifurcation margins is the definition of the nominal system and of the uncertainty set. The former is described by the vector field (23) analyzed in Sect. 4.2, while for the latter the set (20) consisting of 5 structural parameters is considered. It is then possible to provide an expression for the uncertain vector field as:

$$\begin{aligned} \dot{x}=\tilde{f}(x,V,\delta )&=\tilde{\mathscr {A}}^{\text {L}}(V,\delta )x+\tilde{f}^{\text {NL}}(x,V,\delta ) \end{aligned}$$
(25a)
$$\begin{aligned} \tilde{J}(x,V,\delta )&= \tilde{\mathscr {A}}^{\text {L}}(V,\delta ) + \nabla _x \tilde{f}^{\text {NL}}(x,V,\delta ). \end{aligned}$$
(25b)

The speed V will be fixed to a value \(\bar{V}_0\) associated with a stable equilibrium. In order to allow for a comparison with the linear robust analysis performed in Sect. 4.1, \(\bar{V}_0=270 \frac{m}{s}\) is selected. Note that this is smaller than all the Hopf bifurcation speeds \(V_{\text {H}}\) for the nominal nonlinear system (Table 2), hence it is a valid choice according to the discussion in Sect. 3.1.

All the cases reported in Table 2 are considered and Program 1 is applied with an initialization provided by the nominal values of the unknowns. Results are reported in Table 3 in terms of the robust stability margin \(k_m\), frequency \(\hat{\omega }\) of the imaginary eigenvalues at \(\bar{V}_0\), and type of Hopf bifurcation (as predicted by the continuation solver employed to analyse the perturbed system).

Table 3 Robust bifurcation margins at \(\bar{V}_0=270\) m/s for different combinations of nonlinearities and trim states
Full size table

Note that the \(x_t=0\) cases, s1 and s2, present identical robust margins and frequencies. Recall that for these scenarios the branch of equilibria \(x=0\) was found in the nominal cases (Fig. 4), and observe (from Eq. (24) and the definition of the uncertainties) that \(\tilde{f}^{\text {NL}}(0,\cdot ,\cdot )=0\), that is, \(x=0\) are also equilibria of the uncertain vector field. Therefore, \(\nabla _x \tilde{f}^{\text {NL}}\equiv 0\) and the determination of \(k_m\) is equivalent to the problem solved by \(\mu\) in the linear case, i.e., finding the smallest perturbation matrix such that \(\tilde{\mathscr {A}}^{\text {L}}\) is neutrally stable. Hence, the margin \(k_m\) should not depend on the nonlinear terms. This is an interesting result, which complements the discussion in Sect. 4.2 concerning the effect of \(x_t\) on nonlinear flutter. While the role played by \(x_t\) on (nominal) nonlinear flutter is better understood, its effect on robustness is relatively unexplored and should be considered when making the simplifying assumption of zero trim states [36]. Note also that the margin \(k_m\) for these two scenarios is within less than 1% from the maximum singular value of the absolute magnitude of the perturbation matrix in (21). This is very important, since \(\mu _{\text {LB}}\) and \(\mu _{\text {UB}}\) were shown to be close around the peak of Fig. 3, indicating that at least for this case, the proposed Program 1 is able to detect the global minimum of the optimization. The vector \(\hat{\delta }\) found by the optimizer is:

$$\begin{aligned} \hat{\delta } =&\, [K_{\alpha }^{\text {L}};\,K_h^{\text {L}};\,M_{s_{11}}; \,M_{s_{12}};\, M_{s_{22}}] \nonumber \\ =&\, [-\,0.7328;\,0.7328;\,-\,0.7328;\,0.5027;\,0.7328]. \end{aligned}$$
(26)

Note that this vector features the same sign-grouping as those in (21), thus the same physical mechanism of instability commented before is predicted by the solver. It is also worth remarking that Program 1 has the frequency \(\omega\) as decision variable, whereas \(\mu\) was applied at discrete frequencies (Fig. 3) because this is the available implementation for the standard algorithms [2].

As for the cases with \(x_t \ne 0\), s3 and s4, note that these cannot be analyzed with \(\mu\) because \(\tilde{J}\) is now also a function of the nonlinear terms due to non zero values for the equilibria (which are in turn a function of the uncertainties). The results using Program 1 show that for both a Hopf bifurcation can occur within the allowed range of uncertainties since \(k_m<1\) in Table 3. Also, note that the values of \(k_m\) are consistent with the analyses in Table 2, for which s3 presented a smaller \(V_{\text {H}}\) than s4. Thus, since \(\bar{V}=270\) m/s is closer to the nominal bifurcation speeds for s3, it is also expected that this scenario will have a smaller bifurcation margin. Another important information available from Table 3 is that the predicted worst-case Hopf bifurcations are of the same nature (subcritical or supercritical) as the corresponding ones in nominal conditions. That is, the considered set of uncertainties can determine a Hopf bifurcation at smaller speeds but are not able to change the type of bifurcation.

The plunge and pitch nonlinear stiffness coefficients are given, respectively by \(K_{h}^{\text {NL}}K_{h}^{\text {L}}\) and \(K_{\alpha }^{\text {NL}} K_{\alpha }^{\text {L}}\) (22). Thus, uncertainty in the linear stiffness coefficients, considered so far, affect also the nonlinear stiffness matrix \(K_{s}^{\text {NL}}\). However, the proportional coefficients \(K_{h}^{\text {NL}}\) and \(K_{\alpha }^{\text {NL}}\) have been assumed fixed (and equal to 100, see Table 2). To account for the known uncertainty regarding the determination of their values, \(K_{h}^{\text {NL}}\) and \(K_{\alpha }^{\text {NL}}\) will be allowed to vary within \(20\%\) from their nominal values. That is, each nonlinear coefficient is given by the multiplication of two independent uncertain parameters. In addition, uncertainties in two aerodynamic parameters are added to the set of uncertain parameters. Specifically, the terms \(A_{0,12}\) and \(A_{0,22}\) of the steady aerodynamic matrix \(A_{0}\) (17) are also allowed to vary within \(20\%\) from their nominal values.

This new more complex case, consisting of nine total parametric uncertainties, is analysed for the case when the system has both plunge and pitch nonlinear stiffness. The vector \(\hat{\delta }\) found by Program 1 is:

$$\begin{aligned}&\hat{\delta } =[K_{\alpha }^{\text {L}};\,K_h^{\text {L}};\,M_{s_{11}}; \,M_{s_{12}}; M_{s_{22}};\,K_{\alpha }^{\text {NL}};\,K_h^{\text {NL}};\,A_{0,22};\,A_{0,12}] \nonumber \\&\quad = [-0.2432;\,0.2432;\,-\,0.2432; \nonumber \\&\qquad -0.2432;\,0.2432;\,-\,0.2432;\,0.2432;\,0.2432;\,-\,0.2432]. \end{aligned}$$
(27)

By numerical continuation, it is found that the system undergoes a supercritical Hopf bifurcation at \(\bar{V}=270\) m/s when the perturbation in (27) are used to modify the values of the associated parameters. It can be observed that \(k_m\approx 0.24\), which is drastically smaller than all the margins reported in Table 3 as a consequence of the additional uncertainty introduced into the model. The robust bifurcation margin \(k_m\) allows the degradation of robustness to be quantitatively identified.

Figure 5 shows the reciprocal of the robust bifurcation margin as a function of the frequency. As discussed in Sect. 3.3, this can be performed by applying Program 1 at a given frequency on a grid of frequencies, i.e., without including \(\omega\) in the vector of optimization variables (like usually done in \(\mu\) analysis).

Fig. 5
figure 5

Frequency representation of the reciprocal of the robust bifurcation margin

Full size image

When \(\frac{1}{k_m} \ge 1\), a perturbation in the allowed range of uncertainties exist such that an Hopf bifurcation is experienced by the system when perturbed. In this regard, Fig. 5 features a pronounced peak approximately larger than 4, corresponding to a margin of 0.24 (which equals the result in Eq. 27 obtained without frequency gridding). The representation in Fig. 5 resembles those typically employed in linear robust analysis with \(\mu\) (recall for example Fig. 3). This points out that this new framework for robustness analysis can yield something more than a simple binomial-type prediction (that is, whether the system is stable or not in the face of the defined uncertainties). Indeed, the additional information in terms of frequency content and parameters sensitivity that are available when applying \(\mu\) have been recently illustrated, with application to the body freedom flutter problem, in Ref. [21]. For example, in this case, the analyses confirm that the closest supercritical Hopf bifurcations take place in the range of frequencies where the pitch and plunge modes coalesce, which is the binary flutter mechanism already ascertained in nominal conditions.

5 Conclusions

This work investigates a methodology inspired by the robust control techniques \(\mu\) and LFT to study the effect of parametric uncertainties on the stability of polynomial nonlinear systems. The approach is formulated in the framework of bifurcation theory and thus aims to quantify (by means of robust bifurcation margins) the distance of a nominally stable uncertain system from qualitative changes in its steady-state behaviour. The determination of the bifurcation margins is posed as a nonlinear smooth optimization problem which can be solved with off the shelf algorithms. The approach is then applied to a standard case study from the aeroelastic literature. A numerical example is first introduced with an overview on nominal and robust linear flutter analysis, and then distinctive features of the nonlinear flutter problem are commented. Notably, for the case of zero trim state the proposed approach is able to reproduce results obtained with \(\mu\) analysis standard algorithms, whereas for the case of non-zero trim state (where \(\mu\) analysis can no longer be applied) new results, verified via numerical continuation, are obtained. When further uncertainties are added, the framework allows the quantification of robustness degradation of the stability of the system and provides important insights as the worst-case perturbation and a frequency-wise interpretation of the loss of stability.