Simulation of the aerodynamic interaction between rotor and ground obstacle using vortex method

Abstract

The mutual aerodynamic interaction between rotor wake and surrounding obstacles is complex, and generates high compensatory workload for pilots, degradation of the handling qualities, and performance, and unsteady force on the structure of the obstacles. The interaction also affects the minimum distance between rotorcrafts and obstacles to operate safely. A vortex-based approach is then employed to investigate the complex aerodynamic interaction between rotors and ground obstacle, and identify the distance where the interaction ends, and this is also the objective of the GARTEUR AG22 working group activities. In this approach, the aerodynamic loads of the rotor blades are described through a panel method, and the unsteady behaviour of the rotor wake is modelled using a vortex particle method. The effects of the ground plane and obstacle are accounted for via a viscous boundary model. The method is then applied to a “Large” and a “Wee” rotor near the ground and obstacle, and compared with the earlier experiments carried out at the University of Glasgow. The results show that predicted rotor induced inflow and flow field compare reasonably well with the experiments. Furthermore, at certain conditions, the tip vortices are pushed up and re-injected into the rotor wake due to the effect of the obstacle resulting in a recirculation. Moreover, contrary to without the obstacle case, peak and thickness of the radial outwash near the obstacle are smaller due to the barrier effect of the obstacle, and an upwash is observed. In addition, as the rotor closes to the obstacle, the rotor slipstreams impinge directly on the obstacle, and the upwash near the obstacle is faster, indicating a stronger interaction between the rotor wake and the obstacle. In addition, contrary to the case without the obstacle, the fluctuations of the rotor thrust, and rolling and pitching moments are obviously strengthened. When the distance between the rotor and the obstacle is larger than 3R, the effect of the obstacle is small.

1 Introduction

Helicopters are frequently operating close to obstacles, such as buildings, ships, and mountains, for search, rescue, and transportation due to their hover, low-speed flight, vertical landing, and take-off capabilities. Nevertheless, the aerodynamic interactions between rotorcraft wake and obstacles not only produce unsteady forces on the obstacles, but also degrade the rotorcraft performance and handling qualities. Furthermore, pilots may experience high workloads when operating near the obstacles. This situation may endanger helicopters as shown in the International Helicopter Safety Team reports (IHST) [1]. Therefore, understanding the aerodynamic interaction between helicopters and obstacles is an important research subject.

The work presented in this paper stems out of the activities of the GARTEUR AG22 working group that is investigating the interaction of helicopter wakes with the ground obstacles. This GARTEUR group brings together researchers performing measurements of helicopter wake at model scale with numerical analysts aiming to deliver high-fidelity simulations of the complex interactions taking place in these flows. The GARTEUR group is also touching on important operational issues observed by pilots during search and rescue missions, medevac operations, or operations in confined areas like restricted helipads on top of buildings or inside compounds.

In the past, several experimental investigations [2,3,4,5,6,7,8] have been carried out to study the influence of the obstacles on the flow field and the performance of rotors. The flow recirculation phenomena for rotors operating near the ground and obstacles were first studied by Timm through flow visualization [2]. Forces and moments of rotors near the ground or walls were then tested [3]. Furthermore, the effects of wake of a large upstream object to a nearby rotorcraft was also conducted at the Fluid Mechanics Laboratory (FML), NASA Ames Research Center, and focused on basic fluid mechanics of the aerodynamic interaction between a rotor and a wake [4]. Moreover, the flow field in the vicinity of a helicopter hovering near a hangar was studied at the National Research Council (NRC) Flight Research Laboratory (FRL) [5]. More recently, the effect of the confined area geometry on the aerodynamic performance of a hovering rotor was investigated [6]. Pressure measurements on the obstacle and particle image velocimetry surveys of a rotor near it were implemented to investigate the interference effects of the building model on the helicopter performance under the GARTEUR Action Group 22 [7]. As partly it, an experimental survey, including the rotor induced inflow and flow field between the rotors and the obstacles, was carried out at the University of Glasgow [8]. The experiments showed that the obstacle had a strong influence on the rotor flow field.

To date, numerical investigations [3,4,5, 9,10,11,12], ranging from simple blade element vortex methods to Navier–Stokes-based CFD, have been employed to study the aerodynamic interaction between rotorcraft wake and obstacles. The aim of the numerical simulation is to find the best method that one can use for simulating such flow. A blade element vortex method (BEV), coupled with a simple prescribed wake contraction model, a mirror-imaged ground model, and a linear wake skew estimation, was implemented by Quinliven [4] to deliver efficient results. However, the BEV method was based on flow superposition, and did not predict the recirculation region found in experiments. This was because the aerodynamic interaction is non-linear, and it was difficult to simulate complex interactional phenomena using simple methods [3]. Therefore, CFD methods coupled with a simpler model for the rotor were developed to revisit the problem. A fully coupled helicopter/ship dynamic interface tool had been established by coupling the CFD code (PUMA2) and the flight dynamics simulation (GENHEL) to study the interaction between a helicopter wake and a large aircraft hangar structure [9]. It was shown that when the helicopter was operating close to the solid structures the rotor wake significantly affected the oncoming airwake, and the situation became more severe when the rotorcraft moved closer to the ground and hangar. In addition, a CFD solver coupled with a blade loading model based on Galerkin’s method was proposed to study the helicopter–building interaction [3]. The results indicated that the phenomenon of aerodynamic interference intensely disturbed the flow around the helicopter. Moreover, the CFD solver Cobalt, used with the monotone integrated large eddy simulation (MILES) approach, was employed to study flow field in the vicinity of a helicopter hovering near a vertical face [5]. It was shown that the helicopter downwash dominated the flow field, but including the flow over and around the hangar structure was important.

More recently, within the GARTEUR AG22 group, several methods had so far been assessed. These included pure Eulerian, grid-based methods, ROSITA [10] and HMB [11], coupled with actuator disk and unsteady actuator disk models, that could resolve with good accuracy the loads on the rotor blades and the near-field of the helicopter but required large grids and CPU time to propagate the helicopter wake away from the rotor. Other methods, like pure Langrangian methods, including the unsteady panel method (UPM), that was based on the potential flow equation for representing the blade loads and on free-wake models for resolving the far-wake of the helicopter [12]. Such methods also faced difficulties with the required mirror boundary condition and required a certain degree of empiricism in determining the vortex core radius and roll-up. In addition, viscous effects were not usually taken into account.

Given the importance of the problem at hand, there is a need for efficient and accurate methods that do not suffer from the aforementioned problems but can be used by engineers routinely to find out safe distances to be kept between helicopters and buildings and support guidelines for pilots regarding the effects of the wake on the surrounding infrastructure. Such methods may need to be developed further if a complete analysis of the wake/obstacle interaction is needed. Here, a vortex particle method, coupling with a viscous boundary model, is developed to numerically investigate the interference between a building, simplified as a cubic box, and a helicopter. In this method, the aerodynamics of the rotor is described through an UPM, and the unsteady behaviour of the vortices near the ground and obstacle is modelled through the viscous vortex particle method [13]. The viscous effects of the ground and obstacle are accounted for by the viscous boundary model satisfying the no-slip and non-penetration boundary conditions. This is implemented by generating a vortex sheet on the ground and obstacle surface and diffusing the vortex into flow field. The flow field between the rotor and the obstacle is then computed and compared with the experimental data to validate the present method. The result compared well with the Glasgow University data [8]. The numerical results are performed to investigate the physical interpretation of the aerodynamic interaction between the rotor and the ground obstacles, and further explored to the minimum distance from the obstacle to minimize the effect of the obstacle, which is smaller than the clearance, three rotor diameters, from taxiing helicopter in the currently established guidance CAP 493 [14].

2 Computational method

2.1 Aerodynamic model of rotor

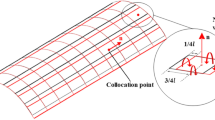
A helicopter has a distinct trailed wake with its own characteristics near the ground and obstacles. This is because the flow field, especially at low height, is dominated by the wake of rotors. Furthermore, successful aerodynamic analysis of rotorcraft near the ground and obstacles requires accurate modelling of blade airloads and their vortices. The aerodynamics of the rotor is first represented by the UPM [13]. Based on this method, the velocity potential of the rotor is defined in a global reference system (X, Y, Z) in Fig. 1, which shows the position of the rotor hub center with respect to the ground and the obstacle, as follows:

Fig. 1

Schematic of a rotor, ground, and obstacle

$$\phi (x,y,z,t)=\frac{1}{{4\pi }}\int_{{{S_{\text{r}}}}} {\mu {\mathbf{n}}\, \cdot \,\nabla \left( {\frac{1}{r}} \right)} {\text{d}}S - \frac{1}{{4\pi }}\int_{{{S_{\text{r}}}}} {\sigma \left( {\frac{1}{r}} \right)} {\text{d}}S{\kern 1pt} +\frac{1}{{4\pi }}\int_{{{S_{{\text{rw}}}}}} {\mu {\mathbf{n}}\, \cdot \,\nabla \left( {\frac{1}{r}} \right)} {\text{d}}S,$$

(1)

where σ and µ are the source and doublet distributions placed on the rotor blades (S_r) and on the wake surface (S_rw). n denotes the outward unit normal vector of surfaces, and r is the position vector (x, y, z) between the point of the velocity potential and center of a panel on the rotor blades or the wake surface.

The wake surface (S_rw) is determined by the shed-wake doublet panels, which are composed of two rows of panels in the present method. The first row leaves the trailing-edge (T.E.) at a median angle of the T.E., and travel to the next time step with local velocity. The strengths of those panels are determined through the T.E. Kutta condition. The second row is generated from the first row in the next time step, and the second-row panels are transformed into vortex particles. More details can be found in Ref. [13].

The boundary conditions for the rotor require that the velocity component normal to the blades is zero. The boundary conditions at infinity require flow disturbances to decrease to zero. Both can then be expressed as follows:

$$\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial \phi }}{{\partial n}} - {{\mathbf{v}}_{\text{r}}}\,\cdot\,{\mathbf{n}}=0}&{\quad {\text{rotor}}\;{\text{surface}}} \\ {\lim \nabla {\phi _{r \to \infty }}=0}&{\quad {\text{far-field}}\;{\text{boundary,}}} \end{array}} \right.$$

(2)

where v_r is the velocity of a point on the rotor surface S_r.

The boundary condition at infinity is automatically fulfilled through Green’s function [13]. According to the Neumann boundary condition and the trailing-edge Kutta condition, the surface boundary conditions are transformed to algebraic equations that are solved for the source and doublet distributions. The flow field of the rotor is then determined, and based on the panel method, the unsteady pressure on the rotor blade surfaces can be calculated using the velocity potential and flow velocity through Bernoulli’s equation. Thus, the non-dimensional form of the blade unsteady pressure is then given as follows:

$${C_p}=\frac{{p - {p_{{\text{ref}}}}}}{{\left( {1/2} \right)\rho {{({{\mathbf{v}}_{{\text{ref}}}})}^2}}}=1 - \frac{{{{({\mathbf{v}})}^2}}}{{{{({{\mathbf{v}}_{{\text{ref}}}})}^2}}} - \frac{2}{{{{({\mathbf{v}}_{{{\text{ref}}}}^{{}})}^2}}}\frac{{\partial \phi }}{{\partial t}},$$

(3)

where p_ref and ρ are the far-field referenced pressure and air density; ${\mathbf{v}}$, $p$, and ${\mathbf{v}}_{{{\text{ref}}}}^{{}}$ are the local fluid velocity, local pressure, referenced velocity, respectively, at each section of the rotor. $\phi$ is the velocity potential.

The aerodynamic forces on the panels of the rotor can then be computed as follows:

$$\Delta {{\mathbf{F}}_k}= - {C_{pk}}{\left( {\rho {\mathbf{v}}_{{{\text{ref}}}}^{2}/2} \right)_k}\Delta {S_k}{{\mathbf{n}}_k},$$

(4)

where ΔF_k is the aerodynamic load on the panel, ΔS_k is the panel area, and n_k is its normal vector.

2.2 Wake model of the rotor

The tip vortex emanating from the blade needs to be preserved for over long periods of time to capture the interaction with the ground and the obstacle. Therefore, the wake of the rotor is modelled based on the viscous vortex particle method [13] which solves the Navier–Stokes equation with velocity–vorticity (u, ω) in Lagrangian frame using vector-valued particles:

$$\frac{{\partial {\mathbf{\omega }}}}{{\partial t}}+{\mathbf{u}}\, \cdot \,\nabla {\mathbf{\omega }}=\nabla {\mathbf{u}}\, \cdot \,{\mathbf{\omega }}+\nu {\nabla ^2}{\mathbf{\omega }},$$

(5)

where ν is the kinematic viscosity, and ${\mathbf{\omega }}=\nabla \times {\mathbf{u}}$ is the vorticity field associated with the velocity field.

The second term on the left-hand side describes the vortex particle convection which is solved using the fourth-order Runge–Kutta scheme with the Biot–Savart law. The right-hand side includes the vortex particle stretching and viscous diffusion effects. Viscous diffusion ($\nu {\nabla ^2}{\mathbf{\omega }}$) is simulated through the particle strength exchange (PSE) which suggests that the Laplacian operator ${\nabla ^2}$ can be replaced by an integral operator [15, 16] as follows:

$${\nabla ^2}{\mathbf{\omega }} \approx \frac{2}{{{\varepsilon ^2}}}\int_{V} {{\zeta _\varepsilon }({\mathbf{x}} - {\mathbf{y}})[{\mathbf{\omega }}({\mathbf{x}}) - {\mathbf{\omega }}({\mathbf{y}})]{\text{d}}{\mathbf{y}}} ,$$

(6)

where ζ_ε is a kernel function with Gaussian distribution and ε is the smoothing radius.

Vortex stretching ($\nabla {\mathbf{u}} \cdot {\mathbf{\omega }}$) is represented by a direct scheme where the velocity gradient can be expressed as a product of the kernel function gradient and the position gradient [17]. Thus, the particle velocity gradient in Eq. (5) can be expressed as follows:

$$\nabla {\mathbf{u}}\left( {{\mathbf{x}},t} \right)= - \sum\limits_{{j=1}}^{N} {\nabla [{K_\varepsilon }(\rho )({\mathbf{x}} - {{\mathbf{x}}_j})]} \times {{\mathbf{\alpha }}_j},$$

(7)

where K_ε is the Biot–Savart kernel for velocity evaluation; x_j and α_j are the position and vector-valued vorticity, respectively.

Vortices are shed from the blade surfaces via the applied Neumann boundary condition and by converting shed-wake doublet panels to vorticity. In addition, those vortex particles that interpenetrate into the solid boundary condition are reflected to the flow based on the mirror method in Ref. [13] to satisfy the conservation of vorticity.

2.3 Viscous model of the ground and obstacle

It is believed that having the no-slip and non-penetration boundary conditions is critical to the aerodynamic computation of rotorcraft near the ground and the obstacle. Therefore, a viscous boundary model, suitable for complex geometries, such as ground and buildings, is developed by considering the no-slip and non-penetration boundary conditions based on a vorticity sheet concept [18,19,20].

When a set of bodies, such as the ground and the obstacle, is immersed in a flow, their effect can be summarized in two expressions of the boundary conditions: the flow cannot go through solid walls, which is a non-penetration boundary condition, and the tangential velocity of the flow on wall is zero, which is a no-slip boundary condition. They are expressed as follows:

$$\left\{ {\begin{array}{*{20}{l}} {{\mathbf{u}}({\mathbf{x}})\,\cdot\,{\mathbf{n}}=0}&{\quad {\text{non-penetration}}\;{\text{boundary}}\;{\text{condition}}} \\ {{\mathbf{u}}({\mathbf{x}})\,\cdot\,{\mathbf{t}}=0}&{\quad {\text{no-slip}}\;{\text{boundary}}\;{\text{condition,}}} \end{array}} \right.$$

(8)

where ${\mathbf{u}}$ is velocity, ${\mathbf{n}}$ represents unit vector normal to the body boundary, and ${\mathbf{t}}$ represents unit vector tangential to the body boundary in the direction of integration.

In addition, there is a free-stream velocity at the far-field which is written as follows:

$${\mathbf{u}}\left| {_{{{\mathbf{x}} \to \infty }}=} \right.{{\mathbf{u}}_\infty }.$$

(9)

Based on the Poincaré’s formula [17], a Fredholm equation of the second kind that justifies the no-slip condition can be written as follows:

$$\frac{{{\mathbf{\gamma }} \times {\mathbf{n}}}}{2} - \int_{{\text{S}}} {K({\mathbf{x}} - {{\mathbf{x}}^\prime }) \times {\mathbf{\gamma }}({{\mathbf{x}}^\prime }){\text{d}}S} ={{\mathbf{u}}_{{\text{slip}}}},$$

(10)

where u_slip is the total induced velocity from the vorticity in the flow field. ${\mathbf{\gamma }}$ is bound vortex sheet which enforces the no-slip condition, and $K$ is written as follows:

$$K\left( {{\mathbf{x}},{{\mathbf{x}}^\prime }} \right)=\nabla G\left( {{\mathbf{x}},{{\mathbf{x}}^\prime }} \right)= - \frac{1}{{4\pi }}\frac{1}{{{{\left| {{\mathbf{x}} - {{\mathbf{x}}^\prime }} \right|}^3}}}.$$

(11)

Equation (10) defines the vortex sheet on the ground surface and the obstacle which is used to generate vorticity into flow field and satisfy the no-slip condition and boundary condition in Eq. (8). Since ${\mathbf{u}}=\nabla \times \psi$ and ${\mathbf{\omega }}=\nabla \times {\mathbf{u}}=\nabla \times \left( {\nabla \times \psi } \right)$ with the definition that $\psi$ is the stream function related to vorticity inside obstacle ${\mathbf{\omega }}$, the equation

$$\int_{{{\Omega _i}}} {\psi \, \cdot \,\left[ {\nabla \times (\nabla \times \psi )} \right]{\text{d}}V} =\int_{{{\Omega _i}}} {{{\left| {\nabla \times \psi } \right|}^2}{\text{d}}V} - \int_{{\partial {\Omega _i}}} {\psi \, \cdot \,\left[ {(\nabla \times \psi ) \times {\mathbf{n}}} \right]{\text{d}}S} ,$$

(12)

can be rewritten as follows:

$$\int_{{{\Omega _i}}} {\psi \, \cdot \,{\mathbf{\omega }}\,{\text{d}}V} =\int_{{{\Omega _i}}} {{{\left| {\mathbf{u}} \right|}^2}{\text{d}}V} - \int_{{\partial {\Omega _i}}} {\psi \, \cdot \,\left( {{\mathbf{u}} \times {\mathbf{n}}} \right){\text{d}}S} .$$

(13)

For a non-rotating obstacles, ω = 0 everywhere inside it. Therefore, the left-hand side of Eq. (13) vanishes. If u × n, the tangential velocity is also zero at the wall, then Eq. (13) becomes $\int_{{{\Omega _i}}} {{{\left| {\mathbf{u}} \right|}^2}{\text{d}}V} =0$. This means that ${\mathbf{u}}\, \cdot \,{\mathbf{n}}$ vanishes at the boundary. The tangential and normal velocity conditions are satisfied for the non-rotating ground and obstacle based on the stream function related to the vorticity field. The vector sheet, ${\mathbf{\gamma }}$, is parallel to the body surface based on a vorticity sheet concept [18,19,20], and hence, only two vorticity components need to be determined. By dividing the body surface into vortex sheet panels, integration on the surfaces using Eq. (10) can be equivalently written as the superposition of integrations on the panels constituting those surfaces. Quadrilateral geometry and constant-strength panels are used in the current study. Therefore, the viscous boundary conditions are transformed to algebraic equations that provide the vector vortex sheet distribution.

In a viscous flow, the presence of a solid boundary affects the flow by forcing the fluid to decelerate to zero velocity at the wall. In other words, the solid body is a source of vorticity, and this can be modelled by a flux of vorticity on the body surface [18,19,20,21,22]. Therefore, after a vortex sheet on the boundary is obtained, transferring the vorticity of the vortex sheet to the nearby particles in the fluid domain is carried out. This is accomplished by solving a diffusion equation with the correct boundary conditions:

$$\begin{aligned} \frac{{\partial {\mathbf{\omega }}}}{{\partial t}} - \nu \Delta {\mathbf{\omega }} & =0{\kern 1pt} \\ {\mathbf{\omega }}\left( {t - \delta t} \right) & =0{\kern 1pt} {\kern 1pt} \\ \nu \frac{{\partial {\mathbf{\omega }}}}{{\partial n}} & =\frac{{ - {\mathbf{\gamma }}(s)}}{{\delta t}}{\kern 1pt} . \\ \end{aligned}$$

(14)

The solution of Eq. (14) can be computed in integral form [18]:

$${\mathbf{\omega }}\left( {{\mathbf{x}},t} \right)=\int_{0}^{t} {\int_{{\text{S}}}^{{}} {{G_{\text{h}}}\left( {{\mathbf{x}},t;{\mathbf{s}},\tau } \right){\mathbf{\gamma }}\left( {\xi ,\tau } \right){\text{d}}s{\text{d}}\tau } } ,$$

(15)

where G_h is the three-dimensional heat kernel, with $\tau <t$:

$${G_{\text{h}}}\left( {{\mathbf{x}},t;{\mathbf{s}},\tau } \right)={(4\pi \nu (t - \tau ))^{ - 3/2}}\exp \left( { - \frac{{{{\left| {{\mathbf{x}} - {\mathbf{s}}} \right|}^2}}}{{4\nu (t - \tau )}}} \right).$$

(16)

This flux must be emitted during a time $\Delta t$. In effect, the vortex sheet ${\mathbf{\gamma }}$ must be distributed to neighbouring particles by discretizing Green’s integral for the inhomogeneous Neumann problem corresponding to the diffusion equation. Then, a particle receives, from that panel, an amount of “vorticity × volume” given by the following:

$$\Delta {{\mathbf{\alpha }}_i}=\int_{0}^{{\Delta t}} {\frac{{{\text{d}}{{\mathbf{\alpha }}_i}}}{{{\text{d}}t}}{\text{d}}t} ,$$

(17)

where

$$\frac{{{\text{d}}{{\mathbf{\alpha }}_i}}}{{{\text{d}}t}}=\int_{{{x_i} - {h_{xi}}/2}}^{{{x_i}+{h_{xi}}/2}} {\int_{{{y_i} - {h_{yi}}/2}}^{{{y_i}+{h_{yi}}/2}} {\int_{{{z_i} - {h_{zi}}/2}}^{{{z_i}+{h_{zi}}/2}} {\frac{{{\text{d}}{\mathbf{\omega }}}}{{{\text{d}}t}}} } } \,{\text{d}}x\,{\text{d}}y\,{\text{d}}z,$$

(18)

where (x_i, y_i, z_i) and (h_xi, h_yi, h_zi) are the positions of the particles and the size of the integration cuboid, respectively.

The rate of change of the vorticity, ${\text{d}}{\mathbf{\omega }}/{\text{d}}t$, due to the rectangular panel of uniform strength ${\mathbf{\gamma }}$ and size b × f, is shown in Fig. 2, and is equal to:

Fig. 2

Vortex sheet panel diffusion to particle

$$\frac{{\text{d}}}{{{\text{d}}t}}{\mathbf{\omega }}\left( {{\mathbf{x}},t} \right){\kern 1pt} =\frac{{\Delta {\mathbf{\gamma }}}}{{\Delta t}}\frac{1}{{2\sqrt \pi }}\frac{1}{{\sqrt {4\nu t} }}\exp \left( { - \frac{{{z^2}}}{{4\nu t}}} \right) \times \left( {\left[ {{\text{erfc}}} \right]_{{\left( {x - b/2} \right)/\sqrt {4\nu t} }}^{{\left( {x+b/2} \right)/\sqrt {4\nu t} }}} \right) \times \left( {\left[ {{\text{erfc}}} \right]_{{\left( {y - f/2} \right)/\sqrt {4\nu t} }}^{{\left( {y+f/2} \right)/\sqrt {4\nu t} }}} \right).$$

(19)

Then

$$\begin{aligned} \frac{{{\text{d}}{{\mathbf{\alpha }}_i}}}{{{\text{d}}t}} & =\frac{{\Delta {\mathbf{\gamma }}}}{{\Delta t}}\left( {\left[ {{\text{erfc}}} \right]_{{\left( {{z_i}+{h_{zi}}/2} \right)/\sqrt {4\nu t} }}^{{\left( {{z_i} - {h_{i,l}}/2} \right)/\sqrt {4\nu t} }}} \right) \times \frac{1}{2}\sqrt {4\nu t} \left[ {\left( {\left[ {{\text{ierfc}}} \right]_{{\left( {\left( {{x_i} - b/2} \right) - {h_{xi}}/2} \right)/\sqrt {4\nu t} }}^{{\left( {\left( {{x_i} - b/2} \right)+{h_{xi}}/2} \right)/\sqrt {4\nu t} }}} \right) - \left( {\left[ {{\text{ierfc}}} \right]_{{\left( {\left( {{x_i}+b/2} \right) - {h_{xi}}/2} \right)/\sqrt {4\nu t} }}^{{\left( {\left( {{x_i}+b/2} \right)+{h_{xi}}/2} \right)/\sqrt {4\nu t} }}} \right)} \right] \\ & \quad \times \frac{1}{2}\sqrt {4\nu t} \left[ {\left( {\left[ {{\text{ierfc}}} \right]_{{\left( {\left( {{y_i} - f/2} \right) - {h_{yi}}/2} \right)/\sqrt {4\nu t} }}^{{\left( {\left( {{y_i} - f/2} \right)+{h_{yi}}/2} \right)/\sqrt {4\nu t} }}} \right) - \left( {\left[ {{\text{ierfc}}} \right]_{{\left( {\left( {{y_i}+f/2} \right) - {h_{yi}}/2} \right)/\sqrt {4\nu t} }}^{{\left( {\left( {{y_i}+f/2} \right)+{h_{yi}}/2} \right)/\sqrt {4\nu t} }}} \right)} \right], \\ \end{aligned}$$

(20)

where $\left[ {{\text{erfc}}} \right]$ is the complementary error function and $\left[ {{\text{ierfc}}} \right]$ is the integral of error function complement.

The time integral in Eq. (17) is evaluated numerically using a Gauss quadrature with four points.

3 Numerical results and discussion

3.1 Induced inflow of the rotor–ground–obstacle

The experimental campaign of Zagaglia et al. [8] conducted at the University of Glasgow is used for the verification of the method. The experimental campaign consisted of a set of tests reproducing rotor hover conditions at different positions with respect to a simplified obstacle with a cubic shape. The large rotor is modelled with four untwisted rectangular blades of NACA0012 airfoil sections, and is used to compute rotor induced inflow under the interaction of the ground and the obstacle as shown in Fig. 3 and Table 1. The computational rotor is modelled with 4800 panels composed of 60 panels in the chordwise direction and 20 panels in the spanwise direction, and the azimuthal angle step is 5.0°. The ground plane and the cubic obstacle are resolved using 7600 panels of 5 m × 3 m and 1 m × 1 m, respectively. The rotor is moved with the global reference system (X, Y, Z) which defines the position of the rotor hub center with respect to the obstacle shown in Fig. 3. The origin of the global reference system is fixed and placed on the ground plane at the obstacle mid-span. The rotor reference system (x, y, z) corresponds to the load-cell axes in the experiment, and the rotor inflow along the rotor x and y axes, 4 cm (4%D) above the rotor plane, are predicted by the present method and measured by means of a Dantec 2D FiberFlow two-component Laser Doppler Anemometry (LDA) system in the experiment.

Fig. 3

Model of the rotor, the ground plane, and the obstacle

Comparisons of the induced velocity profiles along X- and Y-directions at various rotor positions (A–G), X/R = − 1.0, 0.0, 1.0, 1.5, 2.0, 4.0, Z/R = 1.5, 3.0, and no-obstacle, with the experiments are shown in Figs. 4 and 5. It is shown that the predicted induced velocities have the similar trend to the experiments, and the predicted peak values are found to match very well with the experiment data. Furthermore, the rapid change of downwash near the blade tip (Figs. 4, 5) is well predicted, suggesting that the effect of tip vortices is captured by the present method. However, the velocity at the root of the blade is over-predicted, since the rotor hubs and the shafts of the test rigs are not modelled in the present work. It should be noted that, even if there are small discrepancies, the overall comparison of the induced velocity prediction with the experiments is still very good.

Fig. 4

Induced velocity 4% D above the rotor plane in X- and Y-directions. The rotor in c–h are located at stations D (X = 1.5R, Z = 1.5R), E (X = 2R, Z = 1.5R), and G (X = 4R, Z = 1.5R), respectively

Fig. 5

Induced velocity 4%D above the rotor plane in X- and Y-directions. The rotor in c–h is located at stations A (X = − 1R, Z = 3R), B (X = 0R, Z = 3R), and C (X = 1R, Z = 3R), respectively

The influence of the rotor position on the time-averaged induced velocity is shown in Fig. 6 that provides some insight into the interaction between the rotor and the ground obstacle. Contrary to the no-obstacle case, the peak of the induced velocity of X = 1.5R and Z = 1.5R is clearly larger. This is because the rotor wake impinges upon the obstacle and re-enters the rotor resulting in a recirculation which is confirmed later in Fig. 19. Furthermore, the peak-induced velocity decreases with increasing the distance between the rotor and the obstacle, since this weakens the interaction. However, as opposed to the Z = 1.5R case, the peak-induced velocity at Z = 3.0R increases with increasing the X due to the different variation range of X and the different wake interaction. The induced velocity at X=-1.0R is smaller than that of the no-obstacle case shown in Fig. 6b. This is because the rotor is above the obstacle, and its wake impinges upon the top surface of the obstacle, and the effect of the obstacle is similar to the effect of the ground as confirmed in Fig. 7a. Contrary, the rotor is above the ground at X = 1.0R, and the rotor wake convects downstream in the region A of the obstacle, as shown in Fig. 7f. As a result, the effect of the obstacle is weakened, and the peak-induced velocity is larger than that of X = − 1.0R.

Fig. 6

Influence of the rotor position on the induced velocity 4%D above the rotor in X-direction

Fig. 7

Wake structure of the rotor–ground–obstacle

The wake structure under the interaction of the ground and the obstacle at Z = 3.0R is plotted in Fig. 7. It is shown that, at X = − 1.0R, Fig. 7b, the rotor tip vortices first contract radially and then expand as they approach the top surface of the obstacle, twine around the obstacle, and finally expand again as they approaching the ground. Furthermore, those vortices convect away from the four sides of the obstacle after impinging upon its top surface. The blade root vortices are pushed up producing a fountain. Like the previous case, when the rotor is located at X = 0R, the tip vortices on the side A expand as they approach the top surface of the obstacle and convect far away from the obstacle, as shown in Fig. 7d. However, contrary to the previous case, the tip vortices on the side B contract radially, convect downstream as out of ground effect, and then expand as they approach the ground plane. Consequently, the rotor wake surrounds part of the obstacle. Clearly, as opposed to the previous two cases, since the rotor is located in the upper right, X = 1.0R, the rotor wake does not expand around the obstacle in Fig. 7f. The tip vortices on the side A contract radially, convect downstream, and stay in the area between the obstacle and the ground. Nevertheless, the vortices on the side B expand away from the obstacle as they approach the ground plane and result in a wall jet.

3.2 Flow field of the rotor–ground–obstacle

The flow field under the interaction between the rotor and the ground obstacle is computed based on the “Wee” rotor rig, as shown in Table 2 and Fig. 3. The flow field in the region between the obstacle and the rotor was investigated with the Stereoscopic PIV [8].

Table 1 Main features of the “Large” rotor rig

Table 2 Main features of the “Wee” rotor rig

The “Wee” rotor is modelled with two untwisted rectangular blades of NACA0012 airfoil sections. The rotor blade is modelled using 2400 panels composed of 60 panels in the chordwise direction and 20 panels in the spanwise direction, and the azimuthal angle step is 5.0°. The ground plane and the cubic obstacle are modelled using 1900 panels of 0.6 m × 1.65 m and 0.3 m × 0.3 m, respectively.

The predicted velocity contours for the rotor at Z = 2.0R, X = 1.5R are shown and compared with the experimental data in Fig. 8. The comparison demonstrates excellent correlation between the computational predictions and the experimental measurements of the flow field in terms of peak and corresponding position of peak. In addition, the peak velocity within the wake boundary and the radial outward expansion of the rotor-induced flow are predicted correctly. Furthermore, a recirculation region near the obstacle is also observed. However, the predicted recirculation region is smaller than that of the experiment. This is because the radial velocity is slightly under-predicted and the predicted rotor wake impinges directly on the obstacle with lower height. In addition, the test rig is not modelled in the simulation.

Fig. 8

In-plane velocity magnitude contours of the rotor at Z = 2.0R and X = 1.5R

A more quantitative validation of the present method compares the time-averaged radial and vertical velocity profiles at different locations (X = 0.06 m, 0.1 m, and 0.19 m, Z = 0.09 m, 0.1 m, 0.3 m, 0.18 m, 0.24 m, and 0.3 m) with the experimental data, as shown in Fig. 9. The comparisons are at the rotor plane, contraction, expansion, outwash, downwash, and recirculation regions.

Fig. 9

Lines of the velocity parallel and normal to the ground

The extracted horizontal velocities at various downstream distances, Z = 0.09 m, 0.1 m, and 0.3 m, parallel to the ground for this configuration are shown in Fig. 10. In addition, experimental data are used to validate the present approach. At the Z = 0.09 and 0.1 m, where the flow intensely expands, the predicted horizontal velocity distribution is found to match very well with the experiments. Furthermore, even though the position corresponding to the peak velocity is slightly over-predicted, the peak of the outwash velocity is accurately predicted by the present method. Moreover, at the Z = 0.3 m, the rotor plane, the peak, and its corresponding span of inflow are predicted correctly.

Fig. 10

Comparison of V_X velocity distribution parallel to the ground

Comparisons of the vertical component of the downwash velocity above the ground plane with the experiments are shown in Fig. 11. The predicted peak of the downwash velocity and the peak position agree well with the measurements. Furthermore, the rapid changes of the downwash near X = 0.1 m (Fig. 11) show that the effect of the tip vortex is also captured well. It is worth noting that the upwash velocity near the obstacle (X = 0.0–0.075 m), Fig. 11a, caused by the effect of the obstacle also correlates well with the measured data, indicating that the recirculation region is captured by the present method.

Fig. 11

Comparison of V_Z velocity distribution parallel to the ground

The predicted radial and vertical velocity components, V_r and V_Z, are plotted against the normal distance from the ground at several radial stations and compared with the experimental data in Figs. 12 and 13. It can be seen that, in general, the predicted outwash velocity profiles have a similar trend as the experiment measurements. Furthermore, although the distance above the ground plane corresponding to the peak radial velocity is under-predicted (53.2% difference), the peak radial velocity near the obstacle is predicted reasonably well, which indicates that the outwash due to the ground and the obstacle is captured. In addition, there is good agreement between the computational downwash velocity profiles and the experiments. The downwash velocity at X = 0.06 m and 0.1 m is slightly over-predicted, while it, at X = 0.16 m, is under-predicted. Even though there are small discrepancies, the simulation shows acceptable agreement with the test data.

Fig. 12

Comparison of V_r velocity profiles normal to the ground

Fig. 13

Comparison of V_Z velocity profiles normal to the ground

3.3 Difference of flow field on both sides of the rotor

Figure 14 shows the time average flow field at the XY plane on both sides of the rotor. At the rotor plane and near the ground, the inflow and outwash in the regions A and B are similar, as shown in Fig. 14a. However, as opposed to the region B, near the obstacle, the V_x changes from negative to positive indicating a recirculation. Furthermore, contrary to the region B, the positive vertical velocity is greater, suggesting upwash near the obstacle, as shown in Fig. 14b.

Fig. 14

Time-averaged flow field of the rotor with the obstacle

Comparisons of the vertical velocity in the regions A and B at two distances above the ground are plotted in Fig. 15. At the rotor plane, the velocity in the region A is identical to that of the region B. This is because the obstacle has small effect on the rotor plane. However, the velocity near the obstacle (r/R = 1.5) in the region A is greater than that of the region B. This is a result of the recirculation produced by the interaction between the rotor wake and the obstacle.

Fig. 15

V_Z velocity distribution parallel to the ground in the both regions

The comparison of the radial and vertical velocities at different locations in the regions A and B, as shown in Fig. 16, provides some insight into the effect of the obstacle. At r = 0.433R, the radial and vertical velocity profiles in the region A show similar trend as that of the region B, as shown in Fig. 16c. However, At r = 1.1R and r = 0.833R, the peak and corresponding height of the radial velocity in the region A (back line) are smaller than that of the region B (blue line) due to the barrier effect of the obstacle. Furthermore, because the interaction between the rotor wake and the obstacle yields a recirculation, the peak vertical velocity in the region A (brown line) is greater than that of the region B (read line), as shown in Fig. 16a. In addition, compared with the region B, the vertical velocity in the region A at the Z < 0.05 m is larger due to the induced downwash of the recirculation.

Fig. 16

Radial and vertical velocity profiles normal to the ground on the both regions

Flow visualizations on the XZ and YZ planes are shown in Fig. 17. As expected, similar to a single rotor in ground effect, snapshots of the predicted rotor wake on the YZ plane in Fig. 17b show the characteristic formation of the tip vortices and vortex sheet structures in the wake below the rotor. In addition, a wall jet above the ground plane produced by the expansion of the rotor wake is shown in Fig. 16a. However, as opposed to the YZ plane, a recirculation region is clearly observed on the XZ plane. The tip vortices are pushed up under the effect of the obstacle.

Fig. 17

Flow visualization of the rotor wake

The time-averaged flow field near the ground plane at Z = 0.03 m (XY plane) in Fig. 18 provides further insight into the effect of the obstacle on the rotor wake. Compared with the region D, the radial velocity in the region C is smaller due to the blocking effect of the obstacle, as shown in Fig. 18a, while the tangential velocity is larger, as shown in Fig. 18b. Also worth noticing is that, Fig. 18b, the tangential velocity near the north and south surfaces of the obstacle is positive and negative, respectively, indicating that the flow moves toward to the obstacle. Furthermore, contrary to the flow leaving from the obstacle as shown in Fig. 18c, the velocity in the X-direction close to the obstacle is faster due to the swirl resulting from the rotation. Moreover, the stagnation region on the surface of the obstacle is shown in Fig. 18d. This is also confirmed in Fig. 18a, c.

Fig. 18

Time-averaged flow field at Z = 0.03 m

3.4 Differences of the flow field with different rotor positions

The predicted velocity contours of the rotor at different positions are shown and compared with the experiment data in Figs. 19, 20, 21, and 22 to disclose the main features of the flow field. The comparison demonstrates clearly the correlation between the predictions and the measurements. In addition, the velocity within the wake boundary and the radial outward expansion of the rotor-induced flow are predicted reasonably well for a range of rotor positions, and the expansion is caused by the effect of the ground plane. Moreover, in all four cases, it is obvious that the rotor-induced flow on the starboard side of the flow field is forced to expand radially outward as a wall jet. However, as expected, the wall jet near the obstacle is deflected by both the ground plane and the obstacle result in a recirculation region. This recirculation region is caused by the fact that the rotor wake, once deflected by the ground, is re-deflected again by the obstacle. In addition, it is deeply dependent on both the rotor height and distance from the obstacle.

Fig. 19

Velocity magnitude contours of the rotor at Z = 1.5R, X = 1.5R

Clearly, as opposed to the rotor at Z = 2.0R shown in Fig. 20, the recirculation region due to the interaction between the wake and the obstacle is more prominent and the layer is thicker and faster at Z = 1.5R shown in Fig. 19. In addition, the rotor wake impinges upon the ground plane before being deflected by the obstacle at X = 2.0R and 3.0R shown in Figs. 21 and 22. However, the rotor slipstreams at X = 1.5R shown in Fig. 20 does impinge directly upon the obstacle rather than the ground plane. This is because the expansion flow of the rotor wake is closed to the obstacle. Furthermore, the layer that goes upwards close to the obstacle is faster as the position of the rotor decreasing, indicating a stronger interaction.

Fig. 20

Velocity magnitude contours of the rotor at Z = 2.0R and X = 1.5R

Fig. 21

Velocity magnitude contours of the rotor at Z = 2.0R and X = 2.0R

Fig. 22

Velocity magnitude contours of the rotor at Z = 2.0R and X = 3.0R

Figure 23 shows wake structure of the rotor operating at different positions with respect to the obstacle. Compared to the X = 3R, the rotor wake at the X = 1.5R shown in Fig. 23b twines around the obstacle and stretches more intensely. In addition, as the rotor position in X-direction increases, the interaction between the vortex and the obstacle, and the stretching of vortices are weakened. The predicted flow visualization of the rotor wake under the interaction of the ground plane and the obstacle is shown in Fig. 24 to highlight the structures found within the wake near the obstacle in Fig. 23. Snapshots of the predicted flow field show that the tip vortices near the obstacle are clearly reflected and pushed upward by the obstacle and the ground plane resulting in vortex pairing and a recirculation in all cases. By Comparing the height of involved tip vortices of the rotor at Z = 2.0R shown in Fig. 24b, the positions of the reflected tip vortices are higher than the rotor plane at Z = 1.5R shown in Fig. 24a, indicating that the interaction between the tip vortices and the obstacle is intense and the recirculation is strengthened. However, the height of the involved tip vortices will decrease with increasing the rotor X-direction shown in Fig. 24b–d. This is because the tip vortices will be first reflected by the ground plane and then re-deflected again by the obstacle. As a result, the recirculation region is smaller and the interaction of vortex-obstacle is weakened.

Fig. 23

Wake structure of the rotor at different positions with respect to the obstacle

Fig. 24

Flow visualization of the rotor wake at different positions with respect to the obstacle

3.5 Differences of the rotor force with different rotor positions

Figure 25 shows the rotor thrust, rolling, and pitching moments for the rotor at different positions with respect to the obstacle (Z = 2.0R). Even though the rotor is running without the obstacle, there is a fluctuation of the rotor thrust, rolling and pitching moments. This is because the flow filed is also unsteady due to the effect of the ground. However, contrary to the case without obstacle, the fluctuations of the rotor thrust, rolling, and pitching moments under the effect of the obstacle are obviously strengthened, since the flow field of the rotor is affected by the obstacle. Furthermore, as the distance between the rotor and the obstacle increases, the peak-to-peak value of the thrust, and the average and peak-to-peak value of the rolling and pitching moment decrease, while the average of the thrust increases, indicating that the effect of obstacle is weakened. It is shown that when the position is larger than 3R in X-direction, the variation of the thrust, rolling, and pitching moment is similar to that of no-obstacle.

Fig. 25

Thrust, rolling, and pitching moments for the rotor at different positions with respect to the obstacle (Z = 2.0R)

The thrust, rolling, and pitching moments, which are referred to the XYZ reference, for the rotor at different distances above the ground (X = 2.0R) are plotted in Fig. 26. The results are shown on a 90° interval to explain the variations of force and moment when the blade is vertical and parallel to the obstacle. Like the out of ground effect case (OGE), the variation of the rotor thrust, rolling, and pitching moments at Z = 4.0R are small, since the obstacle has weak influence on the flow field of the rotor. Furthermore, similar to the previous cases at different positions (Z = 2.0R), when the distance above the ground is larger than 3R, the variation of the thrust, rolling, and pitching moment is similar to the OGE. However, as opposed to the OGE, the fluctuation of the thrust, rolling, and pitching moments at Z = 1.0R and 1.5R are clearly strengthened. The average of the thrust and rolling moment increases, while the average of the pitching moment obviously decreases. The negative value of the pitching moment indicates that the rotor is nose down, suggesting that the rotor will be pushed close to the obstacle. This is because the effect of ground increases the rotor thrust, and the effect of the obstacle will generate recirculation and increase the velocity near the obstacle, resulting in a negative value of the pitching moment and a stronger fluctuation of the thrust, rolling, and pitching moments.

Fig. 26

Thrust, rolling, and pitching moments for the rotor at different positions with respect to the obstacle (X = 2.0R)

The distribution of the rotor thrust and pitching moments for the hub center of the rotor at different positions in Fig. 27 provides further insight into the effect of the obstacle. In the area B, the average of the rotor thrust is strengthened and larger than the OGE by 27.2%, since the presence of the ground reduces the induced velocity in the plane of the rotor. In the area C, it also increases by 18.1% due to the effect of the obstacle. This is because the rotor tip vortices first contract radially and then expand as they approach the top surface of the obstacle, and finally expand again as they approaching the ground, as shown in Fig. 7b. Like the effect of the ground, the obstacle reduces the induced velocity of the rotor resulting increase of the rotor thrust, as shown in Fig. 6b. Furthermore, compared with the area B, the average of the thrust in the area C is smaller, because the rotor wake twines around the obstacle after impinging upon its top surface and expands again as they approaching the ground as shown in Fig. 7a, b. However, contrary to both the area B and C, the thrust in the area A obviously decreases, and is smaller than the OGE by 16.0%. The reason for the difference can be understood by comparing the inflow in Figs. 19 and 22. There is a strong recirculation between the rotor and the obstacle at X = 1.5R and Z = 1.5R, which obviously decreases the angle of attack and thrust of the blade closing to the obstacle. As a result, the average of the rotor thrust decreases, suggesting that the performance of the rotor will be degraded. In other words, the rotorcraft may be difficult to take off in this case due to the effect of the obstacle. Moreover, the pitching moment clearly decreases, as shown in Fig. 27c, suggesting that the rotor is nose down and pushed toward to the obstacle. In addition, the peak-to-peak values of the rotor thrust and the pitching moment in the area A, compared to others areas, are obviously greater, as shown in Fig. 27b, d, indicating that a stronger vibration in rotor will be yielded. This is due to the unsymmetrical flow field of the rotor, as shown in Fig. 19, and the influence of the recirculation induced by the obstacle. In addition, when the position is larger than 3R in X- and Z-direction, the variations of the thrust and pitching moment are small, which suggests that the effect of the obstacle is small.

Fig. 27

Distribution of the thrust and pitching moments for the rotor at different positions

4 Conclusion

A vortex-based approach is used here to predict the flow field of a rotor operating near the ground and obstacle. The aerodynamics of the rotor is modelled using an UPM, and the unsteady behaviour of the rotor wake is taken into account through the employed vortex particle method. The effect of the ground and the obstacle are modelled by a viscous boundary model. The present approach is applied to a scaled-rotor, including a “Large” configuration and a “Wee” configuration, running near the ground and obstacle. Experiments by the University of Glasgow were used, and some conclusions can be drawn as follows:

• 1. The predicted rotor-induced inflow and flow field under the aerodynamic interaction between the rotor and the ground obstacle are compared reasonably well with the experiment, and the peak velocity of the radial outwash and vertical downwash is predicted correctly.

• 2. The tip vortices are pushed up and re-injected into the rotor wake resulting in the recirculation region between the rotor wake and obstacle.

• 3. Contrary to without the obstacle, peak and thickness of the radial outwash near the obstacle are smaller due to the barrier effect of the obstacle, and an upwash is also appear.

• 4. As the rotor closes to the obstacle, the rotor slipstreams impinge directly on the obstacle. The upwash near the obstacle is faster as the position of the rotor decreasing, indicating a stronger interaction between the rotor wake and the obstacle.

• 5. Contrary to the case without obstacle, the fluctuations of the rotor thrust, rolling, and pitching moments are obviously strengthened. When the distance between the rotor and the obstacle is larger than 3R, the effect of the obstacle is small.