Explicit numerical study of unsteady hydromagnetic mixed convective nanofluid flow from an exponentially stretching sheet in porous media

Abstract

A numerical investigation of unsteady magnetohydrodynamic mixed convective boundary layer flow of a nanofluid over an exponentially stretching sheet in porous media, is presented. The transformed, non-similar conservations equations are solved using a robust, explicit, finite difference method (EFDM). A detailed stability and convergence analysis is also conducted. The regime is shown to be controlled by a number of emerging thermophysical parameters i.e. combined porous and hydromagnetic parameter (R), thermal Grashof number (G _r ), species Grashof number (G _m ), viscosity ratio parameter (Λ), dimensionless porous media inertial parameter (∇), Eckert number (E _c ), Lewis number (L _e ), Brownian motion parameter (N_b) and thermophoresis parameter (N_t). The flow is found to be accelerated with increasing thermal and species Grashof numbers and also increasing Brownian motion and thermophoresis effects. However, flow is decelerated with increasing viscosity ratio and combined porous and hydromagnetic parameters. Temperatures are enhanced with increasing Brownian motion and thermophoresis as are concentration values. With progression in time the flow is accelerated and temperatures and concentrations are increased. EFDM solutions are validated with an optimized variational iteration method. The present study finds applications in magnetic nanomaterials processing.

Introduction

Magnetohydrodynamic (MHD) boundary layer flows with heat and mass transfer from a continuously stretching surface with a given temperature distribution moving in an otherwise quiescent fluid medium have stimulated considerable interest in recent years. Magnetic fields can be used to manipulate thermal or mechanical energy in flowing electrically conducting polymers and can yield significant cost savings in manufacturing processes (Garnier 1992). Many robust applications of MHD materials processing have been developed including micro-structural modification by heat transfer control (Asai 2012), induction heating of ceramic metal matrix composites (Garnier 1996), liquid metal stirring operations (Fautrelle et al. 2009) and boundary-layer separation control via Lorentzian forces (Ishikwa et al. 2007). Transport phenomena in stretching sheet flows are of particular relevance to boundary layer modeling (Abdou and Soliman 2012). After the pioneering mathematical studies of Sakiadis (1961) and Crane (1970), several researchers further investigated stretching sheet boundary layer flows for different types of stretching velocity. Magyari and Keller (2000) considered the steady boundary layer heat and mass transfer flow from an exponentially stretching continuous surface with an exponential temperature distribution, deriving solutions which exhibited an exponential dependence on the temperature distribution in the direction parallel to that of the stretching. Partha et al. (2005) studied the effect of viscous dissipation on the mixed convective boundary layer heat transfer from an exponentially stretching surface. Elbashbeshy (2001) considered wall transpiration (suction) effects on heat transfer in boundary layer flow from an exponentially continuous stretching surface. Khan (2006) studied non-Newtonian (viscoelastic) boundary layer fluid flow over an exponentially stretching sheet. Sanjayanand and Khan (2006) considered viscoelastic heat and mass transfer from an exponentially stretching sheet. A numerical simulation of boundary layer flow over an exponentially stretching sheet with thermal radiation was undertaken by Bidin and Nazar (2009). The exponential stretching sheet scenario is important both for practical reasons and also for mathematical treatment. In real polymer stretching systems, Stastna et al. (1991) have shown that relaxational processes in polymer systems can be characterized by a relaxation function which exhibits a stretched exponential behaviour. By stretching polymer sheets at exponential rates, the relaxation of elastic stresses is overcome and a homogenous material distribution is achieved. Analytically exponential sheet models have also been studied by Elbashbeshy (2001) who obtained similarity solutions based on the exponential stretching velocity distribution in the stretching direction. Therefore, exponential stretch rates are both physically relevant and also allow mathematical similarity analysis. Although the original study by Ishikwa et al. (2007) considers only linear stretching, quadratic stretching has been investigated by Kumaran and Ramanaiah (1996). A generalized form of stretching can also be achieved and indeed has been formulated by Weidman and Magyari (2010) for continuous surfaces stretching with arbitrary polynomial velocities, designated as “super-stretching”. In the context of actual materials processing operations, the exponential model for stretching achieves the best efficiency (Bataller 2008).

Convective transport in porous media also has extensive applications in industrial systems including energy storage, filtration of liquids, drying processes, etc. Gorla and Zinolabedini (1987) investigated free convective heat transfer from a vertical surface to a saturated porous medium with an arbitrary varying surface temperature. Bég et al. (2009) obtained non-similar solutions for hydromagnetic transport in a porous medium from a stretching sheet with cross-diffusion effects.

In recent years, a fundamental new development in thermo-fluid mechanics has been the introduction of nanofluids. Choi (1995) described such fluids as being suspensions comprising nanometer-sized metallic particles strategically deployed in common working fluids (air, water) which achieve highly enhanced thermal properties. Kang et al. (2006) presented an experimental study of nanofluid thermal conductivities. Crainic et al. (2003, 2007) identified the significant magnetohydrodynamic properties of specific nanofluids which are exploitable in their manufacture. The performance-enhancing characteristics of magnetic nanofluids in industrial MHD pumps used in materials processing have also been emphasized by Shahidian et al. (2011). Boundary layer flows of nanofluids in either non-porous (purely fluid) and porous media, have also received significant attention following the study of Kuznestov and Nield (2010) in which buoyancy effects were considered. This study highlighted that Brownian motion and thermophoresis are significant mechanisms in nanofluid performance. Bég and Tripathi (2012) further showed the substantial role of Brownian motion and thermophoresis in augmenting heat transfer in peristaltic nanofluid transport. Khan and Pop (2010, 2011) studied, respectively, the laminar boundary layer flow of a nanofluid past a stretching sheet and also free convection boundary layer nanofluid flow in a porous medium. Hamad and Pop (2011) addressed the stagnation-point nanofluid boundary layer flow on a permeable stretching sheet in a porous medium in the presence of a heat sink or source. Bég et al. (2012) studied the free convection nanofluid boundary layer from a spherical body to a porous medium using a homotopy analysis method and a Darcian drag force model. Rana et al. (2012) employed a variational finite element method to study natural convection nanofluid boundary layer flow from a tilted surface in porous media. Magnetohydrodynamic nanofluid boundary layer flows have also recently garnered interest. Hamad et al. (2011) used a group theoretical approach and shooting quadrature to study magneto-nanofluid natural convection boundary layer flow from a vertical plate. Khan et al. (2011) analyzed numerically the thermal radiative flux effects on hydromagnetic nanofluid boundary layer flow from a stretching surface. Recently Rana et al. (2013) studied using a finite element technique, the transient magnetohydrodynamic boundary layer flow in an incompressible rotating nanofluid over a stretching continuous sheet, showing that both Brownian motion and thermophoresis enhance wall mass transfer rates (Sherwood number). Very recently Abbasbandy and Ghehsareh (2012) used the Hankel–Padé expansion method to study nanofluid hydromagnetic boundary-layer flows.

The vast majority of nanofluid boundary layer flow models have been steady-state in nature. In the present article we therefore simulate the transient MHD dissipative mixed convective boundary layer nanofluid flow over an exponentially stretching sheet adjacent to a non-Darcian porous medium. The governing equations are transformed into dimensionless, strongly coupled, non-linear partial differential equations featuring a number of thermophysical parameters. An explicit finite difference computational algorithm is employed to yield solutions. Elaboration of the stability and convergence characteristics is also included. The present study is relevant to the manufacturing of magnetic nanofluids (Baron et al. 2007) and chemical engineering operations involving electro-conductive nanofluid suspensions (Stephens et al. 2010) and has not been, to the authors’ knowledge, thus far reported in the literature.

Mathematical model

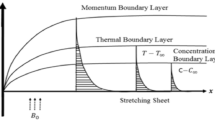
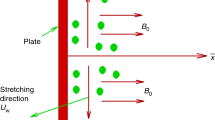
Consider the time-dependent (unsteady) two-dimensional flow of an incompressible viscous and electrically conducting nanofluid induced by a stretching sheet in a porous medium saturated with quiescent ambient nanofluid. The sheet uniform temperature and species concentration are raised to $T_{w} ( > T_{\infty } )$ and $C_{w} ( > C_{\infty } )$ respectively, which are thereafter maintained constant, where $T_{w} ,\,C_{w}$ are temperature and species (nanoparticle) concentration at the wall and $T_{\infty } ,\,C_{\infty }$ are temperature and species concentration far away from the sheet, respectively. The x-axis is orientated along the exponentially stretching sheet in the direction of the motion and y-axis is perpendicular to it. A variable strength magnetic field, B(x) is applied normal to the sheet and induced magnetic field is neglected, which is justified for MHD flow at small magnetic Reynolds number. The physical configuration and coordinate system are shown in Fig. 1. Under the above assumptions and usual boundary layer approximation, the transient MHD mixed convective nanofluid transport is described by the following equations, which extend the earlier formulation of Kuznetsov and Nield (2010) to consider magnetic field and inertial porous medium drag effects:

Fig. 1

Physical model and coordinate system

Mass conservation

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(1)

Momentum conservation

$$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} \,=\, \tilde{\nu }\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{v}{K}u - c^{*} \varepsilon^{2} u^{2} - \frac{{\sigma B^{2} }}{\rho }u + g\beta_{\text{T}} (T - T_{\infty } ) + g\beta_{c}^{*} (C - C_{\infty } )$$

(2)

Energy conservation

$$\frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} \,=\, \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} \,+\, \frac{{\tilde{\nu }}}{{c_{p} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \,+\, \frac{{(\rho c)_{p} }}{{(\rho c)_{\text{f}} }}\left\{ {D_{\text{B}} \left( {\frac{\partial T}{\partial y}.\frac{\partial C}{\partial y}} \right) \,+\, \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right\}$$

(3)

Species (nano-particle concentration) conservation

$$\frac{\partial C}{\partial t} + u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }}$$

(4)

where u and v are the velocities in the x- and y-directions, respectively, t is time, ρ is the fluid density, $\nu$ the kinematic viscosity, $\tilde{\nu }$ the reference kinematic viscosity, K the permeability of the porous regime, c _p the specific heat at constant pressure, T and C the fluid temperature and concentration in the boundary layer, $c^{*} \varepsilon^{2}$ is the inertia parameter, α is the thermal diffusivity, $(\rho c)_{p}$ is effective heat capacity of the nanofluid, $(\rho c)_{\text{f}}$ is heat capacity of the fluid, D_B is the species diffusivity and D_T is the thermophoresis diffusion coefficient. In Eq. (2) (Newton’s second law), the first term on the left hand side is the temporal velocity gradient, the second and third terms are the convective acceleration terms. The first term on the right hand side denotes viscous shear, the second represents the Darcian porous media drag (linear), the third designates second order Forchheimer porous media drag, the fourth is the magnetohydrodynamic Lorentz body force, the fifth is the thermal buoyancy term and the last term on the right hand side of Eq. (2) is the species buoyancy force. In Eq. (3) which is a statement of Fourier’s law of heat conservation, the first term on the left hand side denotes the transient temperature gradient and the second and third terms on the left hand side represent the convective heat transfer terms. The first term on the right hand side signifies thermal diffusion, the second term is viscous heating, and the last dual component term denotes Brownian motion and thermophoresis contributions. In Eq. (4), which is a statement of Fick’s law of mass (species) diffusion, the first term on the left hand side is the transient concentration gradient, and the second and third terms are the convective mass transfer terms. The first term on the right hand side denotes the species diffusion and the last term is the relative contribution of thermophoresis to Brownian motion.

The relevant initial and boundary conditions are:

$$\begin{gathered} \begin{array}{ll} {t = 0,\,u = 0,\,v = 0,\,T = T_{\infty } ,\,C = C_{\infty } } & {\text{everywhere}} \\ {t \ge 0,\,u = 0,\,v = 0,\,T = T_{\infty } ,\,C = C_{\infty } } & {{\text{at}}\,x = 0} \\ \end{array} \hfill \\ u = u_{w} = U_{0} {\text{e}}^{x/L} ,\,v = 0,\,T = T_{w} ,\,T_{\infty } + T_{0} {\text{e}}^{2x/L} ,\,C = C_{w} = C_{\infty } + C_{0} {\text{e}}^{2x/L} \quad {\text{at}}\,y = 0 \hfill \\ u = 0,\,v = 0,\;T \to T_{\infty } ,\,C \to C_{\infty } \quad {\text{at}}\,y \to \infty \hfill \\ \end{gathered}$$

(5)

where U₀ is the reference velocity, $T_{0} ,\,C_{0}$ the reference temperature and concentration, respectively, and L is the reference length. To obtain similarity solutions, it is assumed that the magnetic field B(x) and the variable thermal conductivity K* are of the form:

$$B = B_{0} {\text{e}}^{\frac{x}{2L}}$$

(6)

$$K = K_{0} {\text{e}}^{\frac{x}{L}}$$

(7)

where $B_{0}$ denotes constant magnetic field and $K_{0}$ is the constant thermal conductivity. This exponential formulation has also been adopted by several other researchers in magnetohydrodynamics, as elaborated by Yakovlev et al. (2013) who have also adopted exponential magnetic field relations. Sadooghi and Taghinavaz (2012) have also explained the validity of employing exponentially decaying functions of magnetic field. Exponential decay in thermal conductivity has also been related to energy transport in nanomaterials, as elaborated by Wang (2012). Furthermore the formulations adopted in Eqs. (6), (7) in addition to being physically valid, also provide an elegant simplification in the mathematical complexity of the non-dimensional transport equations, as will be demonstrated now. Introducing the following non-dimensional variables;

$$\begin{aligned}X & = \frac{{xU_{0} }}{\nu }{\text{e}}^{\frac{x}{L}} ,\,Y =\frac{{yU_{0} }}{\nu }{\text{e}}^{\frac{x}{L}} ,\,U =\frac{u}{{U_{0} }}{\text{e}}^{-\frac{x}{L}} ,\,V = \frac{v}{{U_{0}}}{\text{e}}^{-\frac{x}{L}}, \\ \,\tau & = \frac{{tU_{0}^{2}}}{\nu }{\text{e}}^{\frac{2x}{L}} ,\,\bar{T} = \frac{{T - T_{\infty} }}{{T_{w} - T_{\infty } }},\,\bar{C} = \frac{{C - C_{\infty }}}{{C - C_{\infty } }}. \\ \end{aligned}$$

(8)

From the above transformations the, non-linear, coupled partial differential Eqs. (1)–(4) become non-dimensional as follows:

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial y} = 0$$

(9)

$$\frac{{\partial U}}{{\partial \tau }} + U\frac{{\partial U}}{{\partial X}} + V\frac{{\partial U}}{{\partial Y}} = \wedge\frac{{\partial ^{2} U}}{{\partial Y^{2} }} - \frac{1}{{R_{e}}}\left( {RU + \Delta U^{2} - G_{r} \bar{T} - G_{M} \bar{C}}\right)$$

(10)

$$\frac{{\partial \bar{T}}}{\partial \tau } + U\frac{{\partial \bar{T}}}{\partial X} + V\frac{{\partial \bar{T}}}{\partial Y} = \frac{1}{{P_{r} }}\left( {\frac{{\partial^{2} \bar{T}}}{{\partial Y^{2} }}} \right) + \wedge E_{c} \left( {\frac{\partial U}{\partial Y}} \right)^{2} + N_{\text{b}} \left( {\frac{{\partial \bar{T}}}{\partial Y}.\frac{{\partial \bar{C}}}{\partial Y}} \right) + N_{\text{t}} \left( {\frac{{\partial \bar{T}}}{\partial Y}} \right)^{2}$$

(11)

$$\frac{{\partial \bar{C}}}{\partial \tau } + U\frac{{\partial \bar{C}}}{\partial X} + V\frac{{\partial \bar{C}}}{\partial Y} = \frac{1}{{L_{e} }}\left[ {\frac{{\partial^{2} \bar{C}}}{{\partial Y^{2} }} + \left( {\frac{{N_{\text{t}} }}{{N_{\text{b}} }}} \right)\frac{{\partial^{2} \bar{T}}}{{\partial Y^{2} }}} \right].$$

(12)

The non-dimensional boundary and initial conditions transform to:

$$\begin{array}{*{20}c} {\tau \le 0,\,U = 0,\,V = 0,\,\bar{T} = 0,\,\bar{C} = 0} & {\text{everywhere}} \\ {\tau > 0,\,U = 0,\,V = 0,\,\bar{T} = 0,\,\bar{C} = 0} & {{\text{at}}\,{\text{X = 0}}} \\ \end{array}$$

(13)

$$\begin{array}{*{20}c} {U = 1,\,V = 0,\,\bar{T} = 1,\,\bar{C} = 1} & {{\text{at}}\,Y{ = 0}} \\ {U = 0,\,V = 0,\,\bar{T} = 0,\,\bar{C} = 0} & {{\text{at}}\,Y \to \infty } \\ \end{array}$$

(14)

where the notation primes denote differentiation with respect to η and the parameters are defined as follows: $R = \left( {\frac{\nu L}{{K_{0} U_{0} }} + \frac{{\sigma B_{0}^{2} L}}{{\rho U_{0} }}} \right)$ is the combined porous and magnetic parameter, $\wedge = \frac{{{\nu }}}{v}$ is viscosity ratio parameter, $\nabla = c^{*} \varepsilon^{2} L$ is dimensionless porous media inertia parameter, $G_{r} = \frac{{g\beta T_{0} L}}{{U_{0}^{2} }}$ is thermal Grashof number, $G_{m} = \frac{{g\beta C_{0} L}}{{U_{0}^{2} }}$ is species Grashof number, $P_{r} = \frac{\upsilon }{\alpha }$ is Prandtl number, $E_{c} = \frac{{U_{0}^{2} }}{{c_{p} T_{0} }}$ is Eckert number, $N_{\text{B}} = \frac{{(\rho c)_{p} D_{\text{B}} (C_{w} - C_{\infty } )}}{{\nu (\rho c)_{\text{f}} }}$ is Brownian motion parameter, $N_{\text{t}} = \frac{{(\rho c)_{p} D_{\text{T}} (T_{w} - T_{\infty } )}}{{\nu T_{\infty } (\rho c)_{\text{f}} }}$ is thermophoresis parameter, $L_{e} = \frac{\nu }{{D_{\text{B}} }}$ is the Lewis number and $R_{{e_{x} }} = \frac{{LU_{0} {\text{e}}^{\frac{x}{L}} }}{v}$ is the local Reynolds number.

Explicit numerical solutions

In order to solve the non-similar unsteady coupled non-linear partial differential equations (9)–(12), under boundary conditions (13, 14), an explicit finite difference method (EFDM) algorithm, as described by Carnahan et al. (1969) has been developed. Finite difference algorithms are still employed widely in unsteady multi-physical materials processing flows and generally yield very accurate and stable solutions and can easily accommodate time variables. Finite difference simulations have been conducted recently by, for example, Mohiddin et al. (2010) who studied transient double-diffusive non-Newtonian convection form a cone. Further studies using difference methods include Prasad et al. (2011) who analyzed unsteady viscoelastic natural convection boundary layer flow from a vertical surface and Prasad et al. (2011) who studied radiative-convective non-Newtonian flow from a cone. An extensive review of applications of finite difference (and other numerical) methods in hydromagnetic materials processing flows has recently been conducted by Bég (2012). In the explicit approach, a rectangular region of the flow field is chosen and the region is divided into a grid of lines parallel to the X and Y axes, where X-axis is taken along the sheet and the Y-axis is normal to the sheet, as depicted in Fig. 2.

Fig. 2

Finite difference space grid

Here the sheet of height $X_{\hbox{max} } ({=}100)$ is considered i.e. X varies from 0 to 100 and assumed $Y_{\hbox{max} } ({=}25)$ as corresponding to $Y \to \infty$ i.e. Y varies from 0 to 25. There are $m_{\hbox{max} } ({=}125)$ and $n_{\hbox{max} } ({=}125)$ grid spaces in the X and Y directions, respectively (Fig. 2). It is assumed that $\Updelta X,\,\Updelta Y$ are constant mesh sizes along the X and Y directions, respectively, and are prescribed as follows: $\Updelta X = 0.8(0 \le X \le 100)$ and $\Updelta Y = 0.2(0 \le Y \le 25)$ with the smaller time-step, $\Updelta \tau = 0.005$. Let $U^{\prime},\,V^{\prime},\,\bar{T}^{'}$ and $\bar{C}^{'}$ denote the values of $U,\,V,\,\bar{T}$ and $\bar{C}$ at the end of a time-step, respectively. Using the explicit finite difference approximation, the following system of finite difference equations is obtained:

$$\frac{{U_{i,j}^{'} - U_{i - 1,j}^{'} }}{\Updelta X} + \frac{{V_{i,j} - V_{i,j - 1} }}{\Updelta Y} = 0$$

(15)

$$\begin{aligned} \frac{{U_{i,j}^{'} - U_{i,j} }}{\Updelta \tau } + U_{i,j} \frac{{U_{i,j} - U_{i - 1,j} }}{\Updelta X} + V_{i,j} \frac{{U_{i,j + 1} - U_{i,j} }}{\Updelta Y} & = \wedge \frac{{U_{i,j + 1} - 2U_{i,j} + U_{i,j - 1} }}{{(\Updelta Y)^{2} }} \\ & \quad - \frac{1}{{R_{e} }}(RU_{i,j} + \nabla U_{i,j}^{2} - G_{r} \bar{T}_{i,j} - G_{m} \bar{C}_{i,j} ) \\ \end{aligned}$$

(16)

$$\begin{aligned} \frac{{\bar{T}_{i,j}^{'} - \bar{T}_{i,j} }}{\Updelta \tau } + U_{i,j} \frac{{\bar{T}_{i,j} - \bar{T}_{i - 1,j} }}{\Updelta X} + V_{i,j} \frac{{\bar{T}_{i,j + 1} - \bar{T}_{i,j} }}{\Updelta Y} & = \frac{1}{{P_{r} }}\left( {\frac{{\bar{T}_{i,j + 1} - 2\bar{T}_{i,j} + \bar{T}_{i,j - 1} }}{{(\Updelta Y)^{2} }}} \right) + \wedge E_{c} \left( {\frac{{U_{i,j + 1} - 2U_{i,j} + U_{i,j - 1} }}{{(\Updelta Y)^{2} }}} \right) \\ & \quad + N_{\text{b}} \left( {\frac{{\bar{T}_{i,j + 1} - \bar{T}_{i,j} }}{\Updelta Y}.\frac{{\bar{C}_{i,j + 1} - \bar{C}_{i,j} }}{\Updelta Y}} \right) + N_{\text{t}} \left( {\frac{{\bar{T}_{i,j + 1} - \bar{T}_{i,j} }}{\Updelta Y}} \right)^{2} \\ \end{aligned}$$

(17)

$$\frac{{\bar{C}_{i,j}^{'} - \bar{C}_{i,j} }}{\Updelta \tau } + U_{i,j} \frac{{\bar{C}_{i,j} - \bar{C}_{i - 1,j} }}{\Updelta X} + V_{i,j} \frac{{\bar{C}_{i,j + 1} - \bar{C}_{i,j} }}{\Updelta Y} = \frac{1}{{L_{e} }}\left[ {\left( {\frac{{\bar{C}_{i,j + 1} - 2\bar{C}_{i,j} + \bar{C}_{i,j - 1} }}{{(\Updelta Y)^{2} }}} \right) + \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\left( {\frac{{\bar{T}_{i,j + 1} - 2\bar{T}_{i,j} + \bar{T}_{i,j - 1} }}{{(\Updelta Y)^{2} }}} \right)} \right]$$

(18)

with initial and boundary conditions:

$$\begin{gathered} U_{i,j}^{0} = 0,\,V_{i,j}^{0} = 0,\,\bar{T}_{i,j}^{0} = 0,\,\bar{C}_{i,j}^{0} = 0 \hfill \\ U_{0,j}^{n} = 0,\,V_{0,j}^{n} = 0,\,\bar{T}_{0,j}^{n} = 0,\,\bar{C}_{0,j}^{n} = 0 \hfill \\ \end{gathered}$$

(19)

$$\begin{gathered} U_{i,0}^{n} = 1,\,V_{i,0}^{n} = 0,\,\bar{T}_{i,0}^{n} = 1,\,\bar{C}_{i,0}^{n} = 1 \hfill \\ U_{i,L}^{n} = 0,\,V_{i,L}^{n} = 0,\,T_{i,L}^{n} = 0,\,C_{i,L}^{n} = 0,\,{\text{where}}\,L \to \infty . \hfill \\ \end{gathered}$$

(20)

Here the subscripts i and j designate the grid points with X and Y coordinates, respectively, and the superscript n represents a value of time, $\tau = n \cdot \Updelta \tau$ where n = 0, 1, 2, …

Stability and convergence analysis

Since an explicit procedure is being employed, a discussion of the stability and convergence aspects of the finite difference scheme is warranted. For constant mesh sizes the stability criteria of the scheme may be established as follows. Equation (15) will be ignored since $\Updelta \tau$ does not feature in it. The general terms of the Fourier expansion for U, $\bar{T}$ and $\bar{C}$ at a time arbitrarily called τ = 0 are all ${\text{e}}^{i\alpha X} {\text{e}}^{i\beta X}$, apart from a constant, where $i = \sqrt { - 1}$. At a time τ, these terms become:

$$\begin{gathered} U:\psi (\tau ){\text{e}}^{i\alpha X} {\text{e}}^{i\beta Y} \hfill \\ \bar{T}:\theta (\tau ){\text{e}}^{i\alpha X} {\text{e}}^{i\beta Y} \hfill \\ \bar{C}:\phi (\tau ){\text{e}}^{i\alpha X} {\text{e}}^{i\beta Y} \hfill \\ \end{gathered}$$

(21)

After the time-step these terms will become:

$$\begin{gathered} U:\psi^{'} (\tau ){\text{e}}^{i\alpha X} {\text{e}}^{i\beta Y} \hfill \\ \bar{T}:\theta^{'} (\tau ){\text{e}}^{i\alpha X} {\text{e}}^{i\beta Y} \hfill \\ \bar{C}:\phi^{'} (\tau ){\text{e}}^{i\alpha X} {\text{e}}^{i\beta Y} \hfill \\ \end{gathered}$$

(22)

Substituting (21) and (22) into Eqs. (16)–(18), regarding the coefficients U and V as constants over any one time-step, we obtain the following equations upon simplification,

$$\begin{aligned} \frac{{\psi^{'} (\tau ) - \psi (\tau )}}{\Updelta \tau } + U\frac{{\psi (\tau )(1 - {\text{e}}^{i\alpha \Updelta X} )}}{\Updelta X} + V\frac{{\psi (\tau )({\text{e}}^{i\beta \Updelta Y} - 1)}}{\Updelta Y} & = \wedge \left\{ {\frac{2\psi (\tau )(\cos \beta \,\Updelta Y - 1)}{{(\Updelta Y)^{2} }}} \right\} \\ & \quad - \frac{R}{{R_{e} }}\psi (\tau ) - \frac{\nabla U}{{R_{e} }}\psi (\tau ) + \frac{{G_{r} }}{{R_{e} }}\theta^{'} + \frac{{G_{m} }}{{R_{e} }}\varphi^{'} \\ \end{aligned}$$

(23)

$$\begin{aligned} \frac{{\theta^{'} (\tau ) - \theta (\tau )}}{\Updelta \tau } + U\frac{{\theta (\tau )(1 - {\text{e}}^{ - i\alpha \Updelta X} )}}{\Updelta X} + V\frac{{\theta (\tau )({\text{e}}^{i\beta \Updelta Y} - 1)}}{\Updelta Y} & = \frac{1}{{P_{r} }}\frac{2\theta (\tau )(\cos \beta \Updelta Y - 1)}{{(\Updelta Y)^{2} }} \\ & + \wedge E_{c} U\psi (\tau )\left( {\frac{{{\text{e}}^{i\beta \Updelta Y} - 1}}{\Updelta Y}} \right)^{2} + N_{b} \bar{C}\theta \left( \tau \right)\left\{ {\frac{{\left( {e^{i\beta \Updelta Y} - 1} \right)}}{\Updelta Y}} \right\}^{2} + N_{t} \bar{T}\theta \left( \tau \right)\left\{ {\frac{{\left( {e^{i\beta \Updelta Y} - 1} \right)}}{\Updelta Y}} \right\}^{2} \\ \end{aligned}$$

(24)

$$\begin{aligned} & \frac{{\phi^{'} (\tau ) - \phi (\tau )}}{\Updelta \tau } + U\frac{{\phi (\tau )(1 - {\text{e}}^{-i\alpha \Updelta X} )}}{\Updelta X} + V\frac{{\phi (\tau )({\text{e}}^{i\beta \Updelta Y} - 1)}}{\Updelta Y} \\ & \quad = \frac{1}{{L_{e} }}\left[ {\left\{ {\frac{{2\phi (\tau )\left( {\cos \beta \Updelta Y - 1} \right)}}{{(\Updelta Y)^{2} }}} \right\} + \left( {\frac{{N_{\text{t}} }}{{N_{\text{b}} }}} \right).\left\{ {\frac{2\theta (\tau )(\cos \,\beta \Updelta Y - 1)}{{(\Updelta Y)^{2} }}} \right\}} \right] \\ \end{aligned}$$

(25)

The Eqs. (23)–(25) can be written in the following form:

$$\psi^{'} = A\psi + B\theta^{\prime} + C\phi^{'}$$

(26)

$$\theta^{\prime} = D\psi + E\theta$$

(27)

$$\phi^{'} = F\theta + G\phi$$

(28)

where

$$A = 1 - U\frac{\Updelta \tau }{\Updelta X}(1 - {\text{e}}^{ - ia\Updelta X} ) - V\frac{\Updelta \tau }{\Updelta Y}({\text{e}}^{i\beta \Updelta Y} - 1) + \frac{2\Updelta \tau }{{(\Updelta Y)^{2} }} \wedge (\cos \beta \Updelta Y - 1) - \frac{R}{{R_{e} }}\Updelta \tau - \frac{\nabla U}{{R_{e} }}\Updelta \tau$$

(29)

$$B = \frac{{G_{r} }}{{R_{e} }}\Updelta \tau$$

(30)

$$C = \frac{{G_{m} }}{{R_{e} }}\Updelta \tau$$

(31)

$$D = \frac{\Updelta \tau }{{(\Updelta Y)^{2} }} \wedge E_{c} U({\text{e}}^{i\beta \Updelta Y} - 1)^{2}$$

(32)

$$\begin{aligned} E & = 1 - U\frac{\Updelta \tau }{\Updelta X}(1 - {\text{e}}^{-i\alpha \Updelta X} ) - V\frac{\Updelta \tau }{\Updelta Y}({\text{e}}^{i\beta \Updelta Y} - 1) + \frac{1}{{P_{r} }}\frac{2(\cos \beta \Updelta Y - 1)}{{(\Updelta Y)^{2} }}\Updelta \tau \\ & \quad + N_{\text{b}} \bar{C}\left\{ {\frac{{({\text{e}}^{i\beta \Updelta Y} - 1)}}{\Updelta Y}} \right\}^{2} \Updelta \tau + N_{\text{t}} \bar{T}\left\{ {\frac{{{\text{e}}^{i\beta \Updelta Y} - 1}}{\Updelta Y}} \right\}^{2} \Updelta \tau , \\ \end{aligned}$$

(33)

$$F = \frac{1}{{L_{e} }}\left( {\frac{{N_{\text{t}} }}{{N_{\text{b}} }}} \right)\frac{2\Updelta \tau }{{(\Updelta Y)^{2} }}(\cos \beta \Updelta Y - 1)$$

(34)

and

$$G = 1 - U\frac{\Updelta \tau }{\Updelta X}(1 - {\text{e}}^{-i\alpha \Updelta X} ) - V\frac{\Updelta \tau }{\Updelta X}({\text{e}}^{i\beta \Updelta Y} - 1) + \frac{1}{{L_{e} }}\frac{2\Updelta \tau }{{(\Updelta Y)^{2} }}(\cos \beta \Updelta Y - 1).$$

(35)

Again using Eqs. (27) and (28) in (26):

$$\psi ' = H\psi + I\theta + J\phi$$

(36)

where,

$$\begin{gathered} H = A + BD, \hfill \\ I = BE + CF\,{\text{and}} \hfill \\ J = CG \hfill \\ \end{gathered}.$$

(37)

Therefore Eqs. (26)–(28) can be expressed as:

$$\psi ' = H\psi + I\theta + J\phi$$

(38)

$$\theta = D\psi + E\theta$$

(39)

$$\phi ' = F\theta + G\phi$$

(40)

Furthermore the Eqs. (38)–(40) can be expressed in matrix–vector form as follows:

$$\left[ {\begin{array}{*{20}c} {\psi '} \\ {\theta '} \\ {\phi '} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} H & I & J \\ D & E & 0 \\ 0 & F & G \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \psi \\ \theta \\ \phi \\ \end{array} } \right]$$

(41)

that is, $\eta ' = T\eta$ where

$$\eta ' = \left[ {\begin{array}{*{20}c} {\psi '} \\ {\theta '} \\ {\phi '} \\ \end{array} } \right],T = \left[ {\begin{array}{*{20}c} H & I & J \\ D & E & 0 \\ 0 & F & G \\ \end{array} } \right]\quad{\text{and}}\quad\eta = \left[ {\begin{array}{*{20}c} \psi \\ \theta \\ \phi \\ \end{array} } \right]$$

(42)

To determine the stability condition, it is necessary to evaluate the eigenvalues of the amplification matrix T but this task is very difficult since all the elements of T are different. Hence the problem requires that the Eckert Number E _c is assumed to be very small and tends to zero. With this consideration $D = 0$ and the amplification matrix becomes:

$$T = \left[ {\begin{array}{*{20}c} H & I & J \\ 0 & E & 0 \\ 0 & F & G \\ \end{array} } \right]$$

(43)

Hence the problem requires that after simplification of the matrix T, we get the following eigenvalues, $\lambda_{1} = H,\,\lambda_{2} = E\,\,{\text{and}}\,\,\lambda_{3} = G$. For stability, each of the eigenvalues $\lambda_{1} ,\lambda_{2}$ and $\lambda_{3}$ must not exceed unity in modulus. Hence the stability condition is $\left| H \right| \le 1,\,\left| E \right| \le 1$ and $G \le 1$, for all $\alpha ,\beta$ Now we assume that U is everywhere non-negative and V is everywhere non-positive. Details for this assumption are given in Carnahan et al. (1969) and are required for well-posedness of the boundary value problem and to ensure the elimination of spurious modes of oscillation. The assumption is founded on numerical analysis, and is more a computational aspect than a physical one. It follows that, $H = A + BD = A$; since $D = 0$.

$$\begin{gathered} \therefore \,H = 1 - U\frac{\Updelta \tau }{\Updelta X}( {1 - {\rm e}^{ - i\alpha \Updelta X} }) - V\frac{\Updelta \tau }{\Updelta Y}( {{\rm e}^{i\beta \Updelta Y} - 1} ) + \frac{2\Updelta \tau }{{( {\Updelta Y} )^{2} }} \wedge ( {\cos \beta \Updelta Y - 1} ) - \frac{R}{{R_{e} }}\Updelta \tau - \frac{\nabla U}{{R_{e} }}\Updelta \tau \hfill \\ \Rightarrow H = 1 - 2\left[ {a + b + 2 \wedge c - \frac{R}{{2R_{e} }}\Updelta \tau - \frac{\nabla U}{{2R_{e} }}\Updelta \tau } \right] \hfill \\ \end{gathered}$$

(44)

where $a = U\frac{\Updelta \tau }{\Updelta X},\,b = | V|\frac{\Updelta \tau }{\Updelta Y}$ and $c = \frac{\Updelta \tau }{{( {\Updelta Y} )^{2} }}$. The coefficients a, b and c are all real and non-negative. We can demonstrate that the maximum modulus of H occurs when $\alpha \Updelta X = m\pi$ and $\beta \Updelta Y = n\pi$, where m and n are integers and hence H is real. The value of $|H|$ is greater when both m and n are odd integers. To satisfy the $|H| \le 1$, the most negative allowable value is $H = - 1$. Therefore, the first stability condition is:

$$2\left[ {a + b + 2 \wedge c - \frac{R}{{2R_{e} }}\Updelta \tau - \frac{\nabla U}{{2R_{e} }}\Updelta \tau } \right] \le 2$$

(45)

$$\therefore \left[ {U\frac{\Updelta \tau }{\Updelta X} + \left| V \right|\frac{\Updelta \tau }{\Updelta Y} + 2 \wedge \frac{\Updelta \tau }{{\left( {\Updelta Y} \right)^{2} }} - \frac{R}{{2R_{e} }}\Updelta \tau - \frac{\nabla U}{{2R_{e} }}\Updelta \tau } \right] \le 1$$

(46)

Likewise, the second stability condition$\left| E \right| \le 1$ requires that;

$$\therefore \left[ {U\frac{\Updelta \tau }{\Updelta X} + \left| V \right|\frac{\Updelta \tau }{\Updelta Y} + 2\frac{\Updelta \tau }{{\left( {\Updelta Y} \right)^{2} }}\left( {\frac{1}{{P_{r} }} + N_{\rm b} \bar{C} + N_{\rm t} \bar{T}} \right)} \right] \le 1$$

(47)

Similarly the third stability condition$|G| \le 1$ requires that;

$$\left[ {U\frac{\Updelta \tau }{\Updelta X} + \left| V \right|\frac{\Updelta \tau }{\Updelta Y} + \frac{2}{{L_{e} }}\frac{\Updelta \tau }{{\left( {\Updelta Y} \right)^{2} }}} \right] \le 1$$

(48)

Therefore, the stability conditions of the method are;

$$U\frac{\Updelta \tau }{\Updelta X} + \left| V \right|\frac{\Updelta \tau }{\Updelta Y} + 2 \wedge \frac{\Updelta \tau }{{\left( {\Updelta Y} \right)^{2} }} - \frac{R}{{2R_{e} }}\Updelta \tau - \frac{\nabla U}{{2R_{e} }}\Updelta \tau \le 1$$

(49)

$$U\frac{\Updelta \tau }{\Updelta X} + \left| V \right|\frac{\Updelta \tau }{\Updelta Y} + 2\frac{\Updelta \tau }{{\left( {\Updelta Y} \right)^{2} }}\left( {\frac{1}{{P_{r} }} + N_{\rm b} \bar{C} + N_{\rm t} \bar{T}} \right) \le 1$$

(50)

$$U\frac{\Updelta \tau }{\Updelta X} + \left| V \right|\frac{\Updelta \tau }{\Updelta Y} + \frac{2}{{L_{e} }}\frac{\Updelta \tau }{{\left( {\Updelta Y} \right)^{2} }} \le 1.$$

(51)

From the initial condition, $U = V = \bar{T} = \bar{C} = 0$ at $\tau = 0$ and the consideration due to stability and convergence analysis is $R \ge 0.5\,{\text{and}}\,R_{e} \ge 0.5$. Hence the convergence criteria of the method are $\wedge \le 4.01,\,P_{r} \ge 0.25\,{\text{and}}\,L_{e} \ge 0.25.$

Validation with variational iteration method

To verify the EFDM solutions, the present non-linear boundary value problem has also been solved with an optimized He variational iteration method (VIM). VIM is also a very powerful semi-analytical/numerical technique developed by He (1999). This procedure was originally developed for environmental chemical engineering pollution problems and approximate solutions for the problem of seepage flow in a porous medium with fractional derivatives were obtained (Anwar Bég 2013). VIM has been subsequently successfully applied to variety of other fluid dynamic phenomena including shallow water hydrodynamics (Tari et al. 2007), bio-thermal tissue treatment simulations (Elsayed 2013), electro-thermal thruster simulation for spacecraft (Anwar Bég 2013), brain tissue chemo-mechanics (Anwar Bég 2013), Von Kármán swirling flows in porous regimes (Shahmohamadi et al. 2012). VIM is a robust method therefore in obtaining exact and approximate solutions of linear and non-linear differential equations. In this method, general Lagrange multipliers are introduced to construct correction functionals for the problem. The multipliers can be identified optimally via the variational theory. There is no need for linearization or discretization, and excessive computational work and round-off errors are thereby avoided. Time is easily accommodated as a third dimension to the two spatial dimensions (X, Y). VIM demonstrates exceptional stability, exponential convergence and accuracy and is ideal for non-linear transport phenomena encountered in chemical engineering problems. For readers not familiar with this procedure, we provide here a brief overview. Consider the following non-linear differential equation:

$$Lu + Nu = g(t),$$

(52)

where $L,$$N$ and $g(t)$ are the linear operator, the non-linear operator and a heterogeneous term, respectively. VIM uses a correction functional (He 1999) and for Eq. (52) this can be written as:

$$u_{n + 1} (t) = u_{n} (t) + \int_{0}^{t} \lambda \,[Lu_{n} (\tau ) + N\,\tilde{u}_{n} (\tau ) - g(\tau )]\,{\text{d}}\tau \quad n \ge 0,$$

(53)

The successive approximations, $u_{j}$, $j \ge 0$ can be established by determining $\lambda ,$ a general Lagrangian multiplier, which can be identified optimally via the variational theory. The function $\tilde{u}_{n}$ is a restricted variation which means $\delta \,\tilde{u}_{n} = 0.$ Therefore, we first determine the Lagrange multiplier $\lambda$ that will be identified optimally via integration by parts. The successive approximations $u_{n + 1} (t),\,\,n \ge 0$ of the solution $u(t)$ will be readily obtained upon using the obtained Lagrange multiplier and by using any selective function $u_{0} .$ When $\lambda$ has been determined, then several approximations $u_{j} (t),$$j \ge 0,$ follow immediately. Consequently, the exact solution may be obtained by using:

$$u = \mathop { \lim }\limits_{{{\text{n}} \to \infty }} u_{n} .$$

(54)

We therefore construct correction functionals and thereafter apply the variational iteration formula. Very lengthy algebraic expressions result from the functionals and are omitted here for brevity. The series expansions are evaluated in a purpose-built Matlab-based code, TRANSNANOVIM (Anwar Bég 2013), developed for transient nanofluid dynamic flows. Computations on a dual-processor Unix workstation are achieved in tens of seconds. Comparison of the EFDM and VIM solutions are documented in Tables 1, 2, 3, for the velocity, temperature and nanoparticle concentration fields, for various combinations of the governing thermofluid parameters and different time steps. In all cases excellent agreement is obtained, testifying to the accuracy of the EFDM computations, the latter being used to present all graphical solutions in the next section. Confidence in the EFDM results is therefore justifiably very high. In fact both methods demonstrate exceptional accuracy, stability and fast convergence characteristics and show excellent promise in simulating non-linear problems in nanophysical flows. It is also evident from the current simulations that these methods are an elegant alternative to other popular but computationally intensive methods for nonlinear boundary value problems e.g. Chebyschev spectral collocation methods (Anwar Bég et al. 2013) which are also popular for electrical transport phenomena simulations.

Table 1 EFDM and VIM computations compared for velocity field (U) with  = 5, R = 4.0, G _r  = 3.0, G _m  = 2.0, Λ = 1.5, ∇ = 1.0, E _c  = 0.01, L _e  = 5.0, N_b = N_t = 0.1, P _r  = 1.0, R _e  = 0.5, X = 10.0

Table 2 EFDM and VIM computations compared for temperature field ($\bar{T}$) with  = 20, R = 4.0, G _r  = 4.0, G _m  = 2.0, Λ = 1.5, ∇ = 1.0, E _c  = 0.01, L _e  = 5.0, N_b = N_t = 0.3, P _r  = 1.0, R _e  = 0.5, X = 10.0

Table 3 EFDM and VIM computations compared for nanoparticle concentration field ($\bar{C}$) with τ  = 60, R = 4.0, G _r  = 4.0, G _m  = 2.0, Λ = 1.5, ∇ = 1.0, E _c  = 0.01, L _e  = 5.0, N_b = N_t = 0.1, P _r  = 1.0, R _e  = 0.5, X = 10.0

Results and discussion

Extensive numerical solutions have been obtained for the system governing Eqs. (15)–(18) under boundary conditions (19) and (20), with the EFDM algorithm. The values of the governing parameters are chosen to be physically representative of actual nanofluids (Kuznetsov and Nield 2010; Khan et al. 2011; Rana et al. 2013; Abbasbandy and Ghehsareh 2012). Non-dimensional velocity, temperature and species concentration are computed for different values of combined porous and hydromagnetic parameter (R), thermal Grashof number(G _r ), species Grashof number (G _m ), viscosity ratio parameter (Λ), dimensionless porous media inertial parameter (∇), Eckert number (E _c ), Lewis number (L _e ), Brownian motion parameter (N_b), thermophoresis parameter (N_t) and Prandtl number (P _r ) and local Reynolds number (R_e). To obtain the steady-state solutions, the calculations are executed for a range of non-dimensional times, $\tau = 5\,{\rm to}\,80$. Velocity, temperature and concentration profiles do not exhibit any subsequent variation after $\tau = 60$. Therefore, the solution for $\tau \ge 60$ is taken as the steady-state solution. The distributions of the flow variables are illustrated in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. In all cases, X is prescribed a value of 10.

Fig. 3

Thermal Grashof number $( {G_{r} })$ effect on velocity profiles

Fig. 4

Species Grashof number $( {G_{m} })$ effect on velocity profiles

Fig. 5

Combined porous and magnetic parameter effect on velocity profiles

Fig. 6

Viscosity ratio parameter $\left( \wedge \right)$ effect on velocity profiles

Fig. 7

Thermophoresis and Brownian motion parameter $\left( {N_{\rm t} \, {\rm and} \,N_{\rm b} } \right)$ effect on velocity profiles

Fig. 8

Thermophoresis and Brownian motion parameter $\left( {N_{\rm t} \, {\rm and} \,N_{\rm b} } \right)$ effect on temperature profiles

Fig. 9

Prandtl number $( {P_{r} } )$ effect on temperature profiles

Fig. 10

Viscosity ratio parameter $\left( \wedge \right)$ effect on temperature profiles

Fig. 11

Lewis number effect on nanoparticle concentration profiles

Fig. 12

Thermophoresis and Brownian motion parameter effect on nanoparticle concentrations

Fig. 13

Prandtl number effect on nanoparticle concentration profiles

Figure 3 represents the evolution of dimensionless velocity $(U)$ with Y for different values of $G_{r}$ and non-dimensional times, τ. An increase in thermal Grashof number clearly enhances velocity i.e. induces a strong acceleration in the flow. A distinct velocity shoot arises for all profiles near the sheet surface (Y = 0) and this is accentuated with increasing thermal Grashof number. With increasing thermal Grashof number the thermal buoyancy force is increased which aids in momentum development in the boundary layer. Velocity boundary layer thickness is therefore increased with increasing G _r . With greater elapse of time, τ, the velocity is also found to be enhanced substantially.

Figure 4 illustrates the distribution of dimensionless velocity distribution $(U)$ with transverse coordinate, Y for various species (mass) Grashof numbers, $G_{m}$ and non-dimensional times, τ. Again a significant elevation in velocity is observed with progressively greater velocity shoots near the stretching sheet, as species Grashof number is increased. Greater values of G _m imply a greater species buoyancy force associated with the mass diffusion of nanoparticles in the regime. With greater values of τ the nanofluid flow is also strongly accelerated.

Figure 5 displays the dimensionless velocity profiles $(U)$ versus Y for different values of combined porous media drag and hydromagnetic drag parameter, R, and non-dimensional time, τ. A marked deceleration is witnessed in the vicinity of exponentially stretching sheet with increasing R. In the dimensionless momentum equation (10), the components of $R = \left( {\frac{\upsilon L}{{K_{^\circ } U_{^\circ } }} + \frac{{\sigma B_{^\circ }^{2} L}}{{\rho U_{^\circ } }}} \right)$ both serve to inhibit the momentum development in the boundary layer. The first term i.e. Darcian linear drag causes greater impedance to the flow of the nanofluid. The second term i.e. Lorentzian hydromagnetic drag, acts transverse to the magnetic field i.e. in the negative X-direction and also retards the flow considerably. For R = 0.5, 2.5 a velocity shoot is still present near the sheet surface; however, this vanishes for R = 5.0. With increasing time, τ, velocity is again found to be enhanced. Progression in time therefore once again accelerates the flow in the porous regime.

Figure 6 presents the dimensionless velocity distributions $(U)$ versus Y for different values of the viscosity ratio parameter, Λ and also non-dimensional time, τ. The parameter Λ features both in the momentum conservation Eq. (10) and also the energy conservation Eq. (11), where it is associated with the momentum diffusion term and viscous heating term, respectively. Close to the stretching sheet, an increase in Λ, causes a notable rise in velocity magnitudes, however, further from the sheet surface this trend is reversed and the flow is slightly decelerated. The contribution of viscosity is progressively reduced from the sheet surface (wall) towards the free stream. Momentum boundary layer thickness is therefore found to be increased closer to the sheet surface. In all cases a velocity shoot is computed in close proximity to the wall. With progression in time, τ, the velocity is strongly accelerated. However, with greater time values, there is a more gradual decay in velocity from the near-wall regime to the free stream.

Figure 7 depicts the response in dimensionless velocity profiles $(U)$ through the boundary layer, transverse to the sheet surface for different values of thermophoresis parameter, N_t, and Brownian motion parameter, N_b, and also with various non-dimensional times, τ. Thermophoresis serves to warm the boundary layer and simultaneously exacerbates nanoparticle deposition away from the fluid regime (on to the surface). This effectively accentuates momentum development in the regime and elevates the velocity, as observed in Fig. 6. A similar effect is induced with increasing Brownian motion parameter values i.e. the flow is accelerated. The presence of smaller nanoparticles, which corresponds to higher N_b values, implies a stronger contribution from Brownian motion. This assists the boundary layer flow and increases velocity boundary layer thickness. Similar trends have been observed by, among others, Kuznetsov and Nield (2010) and also Khan and Pop (2010, 2011). As in the other velocity distributions, an increase in time is again shown to significantly accelerate the flow throughout the boundary layer.

Figure 8 displays the evolution of dimensionless temperatures $( {\bar{T}} )$ with transverse coordinate, Y for different values of thermophoresis parameter, N_t, Brownian motion parameter, N_b, and various non-dimensional times, τ. As expected, the boundary layer profiles exhibit similar patterns to those for regular heat transfer fluids i.e. base fluids. The temperature in the boundary layer increases with an increase in both the thermophoresis and Brownian motion parameters. In numerous studies reported in the literature e.g. (Choi 1995; Kang et al. 2006), various mechanisms have been proposed to account for the thermal conduction enhancement in nanofluids. These explanations include interfacial ordering of liquid molecules on the surface of nanoparticles, ballistic transport of energy carriers within individual nanoparticles and between nanoparticles that are in contact, as furthermore the geometrical nanoparticle networking. A popular explanation is the direct contribution of nanoparticles which transport thermal energy since nanoparticles are often in the form of agglomerates and/or aggregates. As elucidated earlier, for larger nanoparticles, Brownian motion is weak and the parameter N_b will have small values, and vice versa for smaller nanoparticles. A greater concentration of smaller nanoparticles is therefore expected to enhance thermal conduction more effectively than a smaller concentration of larger nanoparticles. The influence of Brownian motion on thermal fields is generally very strong and tends to thicken thermal boundary layers as does the thermophoresis effect. The temperatures are also generally enhanced with an increase in time for all values of Y. Thermal boundary layer thickness is therefore increased with elapse in time.

Figure 9 illustrates dimensionless temperature distribution $( {\bar{T}} )$ versus Y for different values of Prandtl number, $P_{r}$ and non-dimensional time, τ. Prandtl number signifies the relative contribution of momentum diffusion to thermal diffusion in the boundary layer regime. For P _r  > 1, momentum diffusion rate exceeds thermal diffusion rate. As a result the temperatures in the nanofluid regime will be decreased with a rise in P _r from 3, through 5 to 10. Thermal boundary layer thickness will also be markedly decreased. With increasing time, temperatures are again observed to be strongly enhanced throughout the regime i.e. for all values of Y from the sheet surface through to the free stream.

Figure 10 shows the dimensionless temperature profiles $( {\bar{T}} )$ versus Y for different values of viscosity ratio parameter, Λ and non-dimensional time, τ A strong increase in temperature accompanies a rise in viscosity ratio, and this pattern is sustained for all distances into the boundary layer. Thermal boundary layer thickness is therefore enhanced with increasing viscosity ratio. With greater values of time, τ, nanofluid temperatures are also elevated.

Figures 11, 12, 13 present the response of nanoparticle concentration profiles for various Lewis number, Brownian motion and thermophoresis numbers, and Prandtl numbers, respectively. In all plots the effect of non-dimensional time, τ, is also studied. An increase in Lewis number significantly reduces the nanoparticle concentration values (Fig. 11) in the regime. Lewis number defines the ratio of thermal diffusivity to mass (nanoparticle species) diffusivity. It is used to characterize fluid flows where there is simultaneous heat and mass transfer by convection. Effectively it is also the ratio of Schmidt number and the Prandtl number. For L _e  > 1, thermal diffusion rate exceeds species diffusion rate and nanoparticle concentrations are therefore suppressed. Concentration boundary layer thickness is also reduced with increasing L _e values. Conversely an increase in Brownian motion and thermophoresis parameters (Fig. 12) acts to enhance nanoparticle concentration values. These two mechanisms therefore assist the diffusion of nanoparticles in the boundary layer and elevate the concentration boundary layer thickness. Similarly increasing Prandtl number (Fig. 13) is also found to initially boost the nanoparticle concentration values (closer to the sheet surface); however, further from the sheet surface (wall) this behaviour is reversed and an increase in Prandtl number is observed to marginally decrease concentration values. In all cases (Figs. 11, 12, 13) an increase in time, τ, generally enhances concentration values.

Conclusions

A mathematical model for transient hydromagnetic mixed convection boundary layer flow of an electrically conducting, nanofluid over an exponentially stretching sheet embedded in an isotropic, homogenous porous medium has been developed. The non-dimensionalized conservation equations have been solved with a robust, EFDM, with details of the stability and convergence characteristics included. Validation has been obtained with an optimized transient VIM algorithm. A detailed study of the effects of several key thermophysical parameters controlling the flow characteristics has been conducted. The computations have shown that:

• 1. Velocity and momentum boundary layer thickness are enhanced with increasing thermal Grashof Number, species Grashof number, Brownian motion parameter and thermophoresis parameter, whereas they are decreased with increasing Darcian porous media drag parameter, hydromagnetic parameter and viscosity ratio parameter.

• 2. Nanofluid temperature and thermal boundary layer thickness are elevated with increasing thermophoresis, Brownian parameter and viscosity ratio parameter, whereas they are suppressed with increasing Prandtl number.

• 3. Nanoparticle concentration and concentration boundary layer thickness are both increased with increasing thermophoresis, Brownian parameter and Prandtl number, whereas they are reduced with increasing Lewis number.

• 4. Increase in time generally accelerates the flow i.e. increases momentum boundary layer thickness, increases temperatures and enhances nanoparticle concentration values in the boundary layer regime.

The resent study has demonstrated the excellent accuracy and stability of the explicit finite difference numerical approach in non-linear unsteady two-dimensional magnetohydrodynamic nanofluid transport simulation in porous media. Future studies will consider the application of this method to bio-convection nanofluid flows, of interest in microbial fuel cell technology (Anwar Bég et al. 2013) and will be communicated in due course.