Aggregation kinetics and shear rheology of aqueous silica suspensions

Abstract

The kinetics of aggregation of silica nanoparticle solutions as a function of NaCl and silica concentrations is studied experimentally and theoretically. Silica nanoparticles form fractal aggregates due to the collapse of the electrical double layer at high salt concentrations and resulting reduction in stabilizing repulsive force. We propose a convenient model to describe the aggregation of silica nanoparticles and the growth of their aggregate size that depends on particle size and concentration and salt concentration. The model agrees well with experimental data. The aggregation of silica nanoparticles also affects the rheology of the suspension. We propose an equilibrium approach for sediment volume fraction to determine the maximum effective packing fraction. The results for the relative viscosity of silica aggregates agree well with the proposed viscosity model, which also collapses onto a single master curve.

Introduction

The potential application of nanoparticle dispersions as formation stimulation agents, contrast agents or simply as tracers in upstream oil and gas industry requires knowledge of the dispersion properties of these nanoparticles. Silica nanoparticles are commonly used because of their low cost for fabrication and surface modification. The control of the stability of nanoparticle dispersions is crucial under reservoir salinity and temperature, which are often quite severe. Transport of nanoparticles to target zones in the reservoir is the key in achieving the goal of improved recovery. Therefore, transport properties such as the mobility of nanoparticles and the dispersion rheology are very important. These properties depend on several things such as particle size and concentration. Therefore, determining the rate of change in the size of aggregates formed by nanoparticles is essential for an effective displacement of unstable suspensions of nanoparticles in reservoir rock.

The aggregation kinetics of colloidal particles is commonly modeled by fractal dimension, stability ratio theories (Smoluchowski 1916, 1917; Fuchs 1934), or population balance models (Hounslow et al. 1988). Aggregation rate is the main parameter that needs to be determined in these methods. The absolute rates of fast or slow aggregation regimes can be experimentally determined by turbidity or size measurements, or numerically calculated using stability ratio approach. The confirming experiments must be performed in such a way that the data correspond to the early stage of aggregation, because these methods take into account only the early time of aggregation where single particles collide and form doublets. Under such conditions, the selection of particle size and concentration and electrolyte type and concentration becomes challenging, especially when using nanoparticles, because of their size and relatively small light scattering properties.

Aqueous suspensions of silica nanoparticles have been studied for their aggregation behavior by light scattering (Aubert and Cannell 1986; Schaefer and Martin 1984; Lin et al. 1990; Dietler et al. 1986; Schaefer and Martin 1984; Martin 1987) and x-ray scattering Schaefer and Martin (1984). Fractal dimensions for slow and fast aggregation regimes are calculated by these authors. Schaefer et al. (1984) observed a power–law behavior of aggregation which was claimed to be a signature of fractal structures. They proposed that the structure of fast aggregating clusters could change and become more compact after a long time to approach a fractal dimension of 2.12. Aubert and Cannell (1986) also observed a restructuring to a fractal dimension from 1.75 to 2.08 for rapid aggregation. Giordano-Palmino et al. (1994) studied the effect of an adsorbed layer of nonionic surfactant in silica suspensions on the dispersion stability and aggregation kinetics. Rapid flocculation was observed by a drastic increase in UV–vis absorbance data. The authors suggested that bridging of surface micelles were responsible for the aggregation of these particles. Gorrepati et al. (2010) showed how silica precipitation proceeded under very acidic conditions (below pH 0) below silica’s isoelectric point and at low temperature, 5 °C. The authors modified Smoluchowski equation by incorporating a geometric population balance to simulate the aggregation of particles. An exponential increase in particle size was observed experimentally and also predicted by their simulation study.

In our previous work (Metin et al. 2011a), we defined the critical salt concentration (CSC) below which the silica nanoparticles stay well dispersed in solution. In this paper, we focus on how the aggregation of silica nanoparticles evolves in time in the presence of NaCl above the CSC. We present a systematic study of the aggregation of silica nanoparticle dispersions and their rheological behavior under the pH and NaCl conditions in hydrocarbon reservoirs. The effect of the size of the primary silica nanoparticles, NaCl, and particle concentration on the aggregation kinetics of silica is determined by measuring the change in aggregate size as a function of time. We propose a new model to describe the aggregation kinetics and use experimental data or theory to determine the model parameters. Our proposed model is very convenient to use and provides a framework to collapse all the data onto a single curve using dimensionless numbers. The rheology of unstable silica suspensions is modeled using the effective maximum packing fraction concept coupled with effective aggregate volume fraction.

Materials and experimental methods

The materials under study are aqueous dispersions of silica nanoparticles provided by 3M, Co. The mean diameters of the primary particles are 5, 25 and 75 nm, they have an unmodified (bare) surface. The particles are monodisperse in aqueous solution. The shape of silica nanoparticles is spherical as determined by images of a scanning transmission electron microscope (STEM). The silica nanoparticles are electrostatically stabilized in an aqueous medium with a zeta potential of around −45 mV at pH = 9. Stock dispersions containing 16–41 % by weight silica nanoparticles were diluted with deionized water up to a desired silica concentration. In the absence of electrolyte, the silica nanoparticles were well dispersed and did not aggregate as determined by size measurements. Analytical grade NaCl was added to silica nanoparticle dispersions to study the aggregation kinetics and the rheology of silica nanoparticle aggregates in dispersion. The respective critical salt concentrations (CSC) for 5, 25, and 75 nm diameter silica nanoparticles are 0.5, 1, and 1 wt% NaCl, respectively. The isoelectric point and the zeta potential plot as a function of pH can be found in detail in Metin et al. (2011a).

We used a Delsa Nano dynamic light scattering (DLS) instrument from Beckman Coulter to study the effective diameter of silica nanoparticle aggregates as a function of time. Effective diameter is the hydrodynamic diameter calculated from Stokes–Einstein equation using the average diffusion coefficient determined by the autocorrelation function and cumulants method. Autocorrelation function is one method of analyzing time dependent signals such as the random intensity fluctuation (Delsa Nano User’s Manual 2012). The experiments were carried out at 25 °C.

A strain controlled TA Instruments ARES LS-1 rheometer with double-wall Couette fixture was used to determine the rheology of the silica aggregates in suspension at different shear rates at 25 °C. We evaluated the effect of shear rate, aggregate size, and effective volume fraction on the shear viscosity.

Results and discussions

Aggregation kinetics

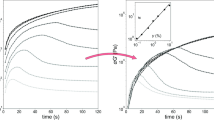
The aggregation of silica nanoparticles takes place at salt concentrations greater than the CSC as discussed in detail in our previous study (Metin et al. 2011a). Figure 1 represents the effect of NaCl concentration on the aggregation kinetics of silica nanoparticles at concentrations greater than the CSC. An S-shape curve on a semi-logarithm of time scale occurs for all samples. As the NaCl concentration increases, the rate of aggregation of the silica nanoparticles increases as does the maximum effective diameter of the aggregate.

Fig. 1

Effect of NaCl concentration on the rate of aggregation expressed as diameter growth as measured by DLS. The samples are at 25 °C and contain 1 wt% of 25 nm diameter primary silica nanoparticles. The solid lines correspond to the model proposed in Eq. 6

The effect of NaCl on this aggregation behavior could be explained by considering the interaction potential between two charged spherical nanoparticles as described by DLVO theory (Derjaguin and Landau 1941; Verwey and Overbeek 1948; Hunter 2001). The repulsion energy, which is a function of electrical double layer thickness, κ⁻¹, (m), decreases as electrolyte concentration increases. Therefore, the total interaction energy changes as a function of electrolyte concentration. The maximum total interaction energy or the energy barrier, V_Tmax, (J), decreases as the electrolyte concentration increases. Reerink and Overbeek (1954) showed that the aggregation rate is proportional to the exponential of energy barrier as shown by Eq. 1. This theory was first developed by Fuchs (1934).

$$ W \approx \frac{1}{2\kappa a}e^{{\left( {\frac{{V_{\text{Tmax}} }}{{k_{\text{B}} T}}} \right)}} = \frac{{k_{\text{fast}} }}{{k_{\text{s}} }} $$

(1)

In Eq. 1, a is the particle radius (m), k_B, (J/K), the Boltzmann constant, and T (K) is the temperature. The stability ratio, W, is the ratio of fast aggregation (k_fast, m³/s) to slow aggregation (k_s, m³/s) rates. The aggregation kinetics of colloidal suspensions divides into two regimes: fast and slow aggregation. In the fast aggregation regime, the absence of potential energy barrier occurs because large concentrations of electrolyte are present in the solution and the double layer thickness is suppressed. Therefore, each collision between particles becomes successful, and the rate of attachment is limited only by the rate of diffusion of the particles toward each other. On the other hand in the slow aggregation regime, the presence of a potential barrier decreases the number of successful collisions between particles, and hence, the magnitude of this potential barrier controls the kinetics of aggregation. The aggregation rate constant k_fast is in the fast aggregation regime and derived by von Smoluchowski (1916, 1917) (see also Hunter 2001) as $k_{\rm fast} = \frac{{8k_{\rm B} T}}{3\eta }$.

In other words, k_fast is the aggregation rate constant in the absence of an energy barrier, and is reduced by the stability ratio W in the presence of the barrier. For the slow aggregation regime, where the presence of an energy barrier decreases the number of successful collisions between particles, the actual aggregation rate constant, k_s, can be estimated from Eq. 1. The aggregation rate constant k_fast was calculated from the von Smoluchowski expression given above. The energy barrier, V_Tmax, was determined by using the DLVO curves presented in a previous study (Metin et al. 2011a). Then, k_s was estimated from Eq. 1. The data shown in Fig. 1 corresponds to the slow aggregation regime, and we can compare the rate constant in Eq. 1 to experimentally determined k_s. The latter was obtained from the rate of change of effective particle diameter (hydrodynamic diameter) in DLS measurements at early time of aggregation (Schudel et al. 1997) by $\left. \frac{{\rm d}D}{{\rm d}t} \right|_{t \to 0} = k_{\rm s} N_{0}$ as presented in Fig. 2. Here, N₀, the initial particle number concentration (#particles/m³), can be calculated from initial particle weight concentration, c₀, using the correlation $N_{ 0} = c_{ 0} \frac{3}{{4\pi a^{ 3} \rho }}$, where ρ is the density of silica.

Fig. 2

Effective particle diameter as a function of time as measured by DLS for 25 nm diameter primary particles at early aggregation times. Lines correspond to a linear fit to experimental data

Figure 3 presents k_s as a function of NaCl concentration. As NaCl concentration increases, the rate constant k_s also increases as discussed above. At NaCl concentration smaller than 5 wt%, we obtained a good agreement between the values of k_s determined experimentally and calculated from the theory presented in Eq. 1 for 3.5 and 4 wt% NaCl. However, the theory overestimates k_s for 3 wt%. The concentration of NaCl is used for the calculation of electrical double layer thickness and the maximum total interaction energy in Eq. 1. The double layer thickness is calculated to be 0.44 nm for 1 wt% silica with 3 wt% NaCl sample. At 5 wt% NaCl concentration, the aggregation is fast and the early data of aggregate size are limited by the resolution of DLS in time. At high ionic strengths, non-DLVO repulsion may come into play such as silica hairs (Iler 1971; Vigil et al. 1994; Israelachivili et al. 1996). These thin silica hairs on the surface could push the double layer repulsion out to extend further than van der Waals attraction and also generate an additional short-range steric repulsion.

Fig. 3

Comparison of the slow aggregation rate constant, k_s, in Eq. 1 and experimental results

Figure 4, the effect of silica concentration on aggregation kinetics is similar to the effect of NaCl in the sense that increasing particle concentration accelerates aggregation, Fig. 3. However, the physics behind this increase in aggregation rate is different for each effect. From an equilibrium perspective, we have shown that the CSC is independent of particle concentration, but we cannot explain our observations from the concept of CSC because it is not a kinetic parameter.

To understand the effect of particle concentration on aggregation kinetics, we take a close look at how these nanoparticles come in contact and how aggregation develops. The particles must travel a certain distance with a certain diffusivity to come close to each other, and then form an aggregate with a probability of sticking that depends on the extent of the energy barrier, V_Tmax. For a fixed electrolyte concentration, the extent of the energy barrier and, hence, the sticking probability are fixed. However, the mean distance that particles travel before each collision will be small at large particle concentrations, which in turn will increase aggregation rates. Therefore, we argue that the effect of separation distance between particles is significant on the aggregation behavior of silica nanoparticles at different concentrations. Note that the largest nanoparticle concentration we studied is 5 wt%, for which the diffusion coefficient may be same as that of a more dilute concentration, 1 wt% .

Fig. 4

Effect of silica concentration on the kinetics of aggregation. The samples are at 25 °C and contain 3 wt% NaCl. The primary particle diameter is 25 nm. The lines are from the model proposed in Eq. 6

To model the experimental observations on the aggregation kinetics of silica nanoparticle dispersions not only at the early time of aggregation but also at late time, we propose a model for the growth of an aggregate size as a function of time. We assume that there are enough particles in the vicinity of the aggregate and, hence, the growth is not diffusion limited (see Fig. 5). The mass of the aggregate scales as $m \propto \alpha D^{{d_{\text{f}} }}$. The fractal dimension of silica aggregates was studied in detail by Aubert and Cannell (1986), Schaefer and Martin (1984), Lin et al. (1990), Dietler et al. (1986), and Martin (1987). The values reported agree well with each other and are 2.05 for slow aggregation and 1.75 for fast aggregation. In our experiments, the aggregation data belong to the slow aggregation regime mostly. Therefore, we assume that the fractal dimension, d_f, is 2.05. Then, we can simplify the equation above as m ≈ αD².

Fig. 5

Schematic for the growth of an aggregate of diameter D in a cell of volume β

We write a mass balance assuming mass is conserved and single particles attach to the aggregate that already exists in a unit volume. The rate of change in mass of the aggregate is then given as

$$ \frac{{{\text{d}}m}}{{{\text{d}}t}} = 4\pi m_{\text{p}} k\left( \frac{D}{2} \right)^{2} n_{1} $$

(2)

where m is the mass of an aggregate (kg), m_p the mass of a single particle (kg), k a new rate constant (m/s) for this particular process, and n₁ (#/m³) the number concentration of single particles in a unit volume β (m³) of the dispersion. The rate of change of the number concentration of single particles can then be expressed as

$$ \frac{{{\text{d}}n_{1} }}{{{\text{d}}t}} = - \frac{1}{{m_{p} \beta }}\frac{{{\text{d}}m}}{{{\text{d}}t}} = - \frac{k\pi }{\beta }D^{2} n_{1} = - k_{2} D^{2} n_{1} $$

(3)

where the rate constant k₂ is simple kπ/β. The mass of an aggregate, m, can be expressed in terms of diameter of the aggregate, D (m), by the correlation m ≈ αD², Eq. 4 so that

$$ \frac{{{\text{d}}D}}{{{\text{d}}t}} = \frac{{m_{\text{p}} k\pi }}{2\alpha }Dn_{1} = k_{1} n_{1} D $$

(4)

where the rate constant k ₁ is m _p kπ/2α. At the early time of aggregation, where n₁ can be assumed constant, Eq. 4 has an analytical solution with an exponential growth term for the diameter. This equation explicitly shows why such an exponential growth is observed experimentally in the aggregation study of silica nanoparticle solutions.

We can express Eq. 4 as a function of diameter by dividing Eq. 4 by Eq. 3, and solving the resultant equation with the condition at infinite time that n₁ = 0 and D = D_eq, so that

$$ \frac{{\rm d} D}{{\rm d}t} = - \frac{{k_{2} }}{2}D\left( {D^{2} - D_{\rm eq}^{2} } \right) $$

(5)

For the early time of aggregation of nanoparticles, where D ≪ D_eq, Eq. 5 reduces to $\frac{{{\text{d}}D}}{{{\text{d}}t}} = \frac{{k_{2} D_{\text{eq}}^{2} }}{2}D$ with an analytical solution of D(t) = D₀e^st where $s = \frac{{k_{2} D_{\rm eq}^{2} }}{2}$. This equation is same as the class-II exponential growth model in reaction limited aggregation (RLA) regime (or slow aggregation regime).

Eq. 5 has an analytical solution in the following form with the initial condition of D = D₀, the diameter of the primary particles at the beginning of the aggregation stage at t = 0.¹

$$ \frac{D(t)}{{D_{\text{eq}} }} = \frac{1}{{\left\{ {\left[ {\left( {\frac{{D_{\text{eq}}^{2} }}{{D_{0}^{2} }} - 1} \right)e^{{ - k_{2} tD_{\text{eq}}^{2} }} } \right] + 1} \right\}^{1/2} }} $$

(6)

We use the model in Eq. 6 to fit our experimental data for aggregate size as a function of time, as measured by DLS. Then, we determine the model parameter, k₂ (m⁻² s⁻¹). The results are shown in Figs. 1 and 3 for different NaCl and silica concentrations, respectively.

We present the fitting parameter k₂ as a function of NaCl and nanoparticle concentration in Fig. 6. As discussed previously, an increase in the aggregation rate occurs as NaCl or nanoparticle concentration increases.

Fig. 6

The model parameter, k₂, in Eq. 6 as a function of NaCl and silica concentration for 25-nm diameter primary particles

At the beginning of the aggregation, our model represents well the change in aggregate diameter in time. However, as D approaches D_eq, the model in Eq. 6 deviates slightly from experimental data. In the proposed model, we did not allow aggregates to collide with each other unless they grow big enough that adjacent aggregates become a part of a network. In other words, the model takes into account that adjacent aggregates become a part of a network. On the other hand, in the experiments, aggregate-to-aggregate collisions occur and D_eq is reached earlier than prediction.

At late time aggregation, a limiting value for aggregate diameter is reached. In this period, the model in Eq. 6 slightly underestimates the growth of aggregates. If individual aggregates grow large enough, they may undergo significant sedimentation before aggregates collide with each other and span the space. The ratio of gravitational force to Brownian diffusion is expressed as a gravitational Peclet number, Pe_g as follows (Poon and Haw 1997)

$$ Pe_{\text{g}} = \frac{{2\pi \Updelta \rho ga^{4} }}{{9k_{\text{B}} T}}\left( {\frac{D}{{D_{0} }}} \right)^{{d_{\text{f}} + 1}} $$

(7)

where ∆ρ is the density difference between the particles and dispersion medium. We can also express a maximum size that an aggregate could reach depending on particle concentration. The aggregates grow and span space at this critical size, D_c, which is a function of particle volume fraction, ϕ₀ and fractal dimension, d_f as follows (Poon and Haw 1997)

$$ D_{\text{c}} \approx 2a\phi_{0}^{{1/(d_{\text{f}} - 3)}} $$

(8)

If this critical size occurs when Pe_g < 1, then D_c is the limiting length scale for D_eq. Otherwise, gravitational force will limit D_eq. In our experiments, Pe_g is smaller than 1 for silica concentrations ≥2 wt%. Within that range of silica concentration, our experimental results show that D_eq is almost same as D_c from Eq. 8. Therefore, we can predict the maximum aggregate size reached before sedimentation becomes prevalent. Note that D_c decreases as nanoparticle concentration increases.

The parameters in Eq. 6, the rate constant $s = \frac{{k_{2} D_{\text{eq}}^{2} }}{2}$ and the equilibrium diameter D_eq, are presented as a function of silica and NaCl concentrations in Figs. 7 and 8 for 25-nm silica nanoparticles. A power–law relationship occurs between the rate constant and NaCl or silica concentrations. However, the equilibrium diameter seems to be much less sensitive to NaCl concentration than silica concentration. The comparison between D_eq and D_c is in Fig. 8 as a function of silica concentrations. A good agreement again occurs between these two parameters for silica concentrations >3 wt%, where Pe_g is <1.

Fig. 7

The equilibrium diameter and comparison between the rate constant, $s = \frac{{k_{2} D_{\rm eq}^{2} }}{2}$, in Eq. 6 as a function of NaCl concentration at 1 wt% silica particles of 25 nm primary diameter

Fig. 8

The equilibrium diameter and comparison between the rate constant, $s = \frac{{k_{2} D_{\rm eq}^{2} }}{2}$, in Eq. 6 as a function of silica concentration at 3 wt% NaCl. The primary silica particles are of 25 nm in diameter

Once we determine the rate constant, s, in our model, we investigate the parameters constituting s, $s = \frac{{k_{2} D_{\text{eq}}^{2} }}{2}$, where k₂ is

$$ k_{2} = \frac{k\pi }{\beta } $$

(9)

We can estimate β and k from postulating Eqs. 10 and 11 by dimensional grouping of terms.

$$ k \approx \left( {\frac{{D_{\text{iff}} }}{l}} \right)\frac{1}{2\kappa a}\exp \left( { - \frac{{V_{\text{Tmax}} }}{{k_{\text{B}} T}}} \right) $$

(10)

where l is the width of the secondary minimum in the DLVO curve. The diffusion coefficient, D_iff, is calculated from Einstein-Stokes equation as $D_{\text{iff}} = \frac{{k_{\text{B}} T}}{6\mu \pi a}$

$$ \beta = \frac{n}{{n_{0} }} = \left( {\frac{{D_{\rm eq} }}{{0.8D_{0} }}} \right)^{{d_{\rm f} }} \left( {\frac{{D_{0}^{3} \pi }}{{6\phi_{0} }}} \right) $$

(11)

where β is the volume of the cell depicted in Fig. 5, ϕ₀ is the initial volume fraction of particles, n is the number of single particles forming an aggregate of size D_eq, and n₀ is the initial number of single particles per total volume. The multiplier of 0.8 comes from the relation between the hydrodynamic radius (effective diameter D_eq) and the radius of gyration in the calculation of n. We calculate β from Eq. 11 and compare with that obtained from Eq. 9. The values for β shows a length scale of around 2,000 nm which is reasonable when we look at the size of aggregate, D_eq, formed in a unit cell. We calculate k from Eq. 10 and k₂ from experimental data. The values for β agree well for various silica concentrations at 3 wt% NaCl, Fig. 9. However, we observe a deviation between the values obtained by these two approaches for NaCl concentrations at 4 and 5 wt% with 1 wt% nanoparticle concentration. Similarly, we can determine k from Eq. 10 and compare it with Eq. 9, where β is calculated from Eq. 11. The results are in the same order of magnitude (Fig. 9).

Fig. 9

The comparison of parameter β obtained by Eqs. 9–10 with Eq. 11 as a function of silica concentration at 3 wt% NaCl. The primary silica particles are 25 nm in diameter

The effect of primary particle size on the aggregation growth of silica nanoparticles is in Fig. 10. Both attractive and repulsive interaction potentials are functions of particle size, and enhanced colloidal stability occurs at larger particle sizes (He et al. 2008). As particle size increases, the maximum in the interaction potential (energy barrier to aggregation) also increases. While 5 and 25 nm particles show similar aggregation kinetics at 4 wt% NaCl, the sediment volume fraction is almost 1 for small particles (5 nm diameter) at the end of aggregation at equilibrium. Although the aggregation times for the 5 and 25 nm particles at 4 wt% NaCl are similar, the sediment volume fraction is almost 1 for small particles (5 nm diameter) at the end of aggregation at equilibrium. However, bigger particles (25 nm diameter) formed a sediment with a volume fraction <0.5, after the aggregates settled. The size measurements by DLS are evaluated for homogeneous turbid phase before the aggregates sediment out of the suspension. The time frame of measurements was short enough compared to aggregation time to collect representative data of aggregates.

Fig. 10

Effect of particle size on the kinetics of aggregation at 25 °C. The samples contain 4 wt% NaCl for the samples with the primary particle diameter of 5 and 25 nm and 5 wt% NaCl for those with 5 and 25 nm diameter. The change in aggregate diameter, measured by DLS in time is presented. The lines are from the model in Eq. 6

Shear rheology of silica suspensions

Our previous study (Metin et al. 2011b) developed a model for the rheology of stable silica nanoparticle dispersions. Our unified model could collapse all the data onto a single curve using the concept of maximum effective packing fraction. We showed that the viscosity of silica nanoparticle dispersions is a strong function of particle volume fraction. Here, we extend our study to understand and model the rheology of unstable silica dispersions.

The aggregation of silica nanoparticles affects the rheology of the suspension because the size of the aggregate changes in time. In suspensions undergoing significant aggregation, the volume fraction of the aggregate becomes the effective solid volume fraction. We present our results on the shear rheology of unstable silica nanoparticle suspensions of primary particle size 5, 25 and 75 nm. Figure 11 shows the viscosity of 1 wt% 25 nm primary silica nanoparticles as a function of shear rate at various aggregate sizes. The aggregation rate is slow compared to the time required to take steady shear viscosity measurements, thus we can assume equilibrium during each steady shear rate measurement. Newtonian behavior is observed within the shear rate ranges studied.

Fig. 11

Viscosity of 1 wt% unmodified silica nanoparticle with 3 wt% NaCl at different aggregation stages as presented by the effective diameter of the aggregate in Fig. 1

The viscosity of the suspension changes in time (Fig. 12) with respect to the aggregate size. To model the rheology of unstable dispersions, we must determine the effective volume fraction of the aggregates, ϕ_Agg, from Eq. 12.

Fig. 12

Evolution of average viscosity over the range of shear rates from 1–300 s⁻¹ of 1 wt% unmodified silica nanoparticle with 3 wt% NaCl in time. The line is from Eq. 13 combined with Eqs. 6 and 12

$$ \phi_{\text{Agg}} = \phi_{0} \left( {\frac{D}{{D_{0} }}} \right)^{{3 - d_{\text{f}} }} $$

(12)

The size of the aggregate at a specific time during the aggregation stage can be estimated using the models, we proposed above. We modified our model for relative viscosity, η_r, to take into account the effective volume fraction of the aggregate as follows:

$$ \eta_{\text{r}} = \left[ {1 + 0.75\frac{{\phi_{\text{Agg}} }}{{\left( {\phi_{\hbox{max} }^{\text{eff}} - \phi_{\text{Agg}} } \right)}}} \right]^{2} $$

(13)

where ϕ ^eff_max is the maximum effective packing fraction and is a function of particle size for stable nanoparticle dispersions, where the extent of electrical double layer or steric layer is important (Metin et al. 2011b). However, for the unstable unmodified silica nanoparticle suspensions, the thickness of electrical double layer is reduced significantly because of the presence of electrolytes, and the aggregates can be assumed as hard spheres in terms of interactions. We can estimate the maximum effective packing fraction by an equilibrium approach. The phase behavior of 25 nm unmodified silica nanoparticles at 3 wt% NaCl for 0.5–3 wt% silica concentration is presented in Fig. 13. As the nanoparticle concentration increases, the aggregate volume or the sediment volume fraction increases as well.

Fig. 13

Test tubes containing 3 wt% NaCl and 0.5–3 wt% silica nanoparticles of 25 nm diameter. As silica concentration increases the sediment height also increases

Let us assume that n single silica particles form one aggregate. At equilibrium, all the single particles become part of aggregates and there is no free single particle in the supernatant (Eq. 14).

$$ \begin{gathered} nP \to A_{(s)} \hfill \\ C_{\text{P}}^{\text{T}} = nC_{\text{A}} \hfill \\ C_{\text{P}}^{\text{T}} = n\phi_{\hbox{max} }^{\text{eff}} C_{\text{sed}} v \hfill \\ \end{gathered} $$

(14)

where C ^T_P is the total concentration of single silica particles (# single particles/m³), C_A is the concentration of aggregates (# aggregates/m³), ϕ ^eff_max is the maximum effective packing fraction of aggregates in the sediment (m³ aggregate/m³ sediment), C_sed is the concentration of sediment (m³ sediment/m³), and v is the reciprocal of the volume of a single aggregate (1/m³ aggregate). The number of particles, n, (# single particles/aggregate), forming the aggregate is determined from $n = \left( {\frac{{D_{\text{eq}} }}{{0.8D_{0} }}} \right)^{{d_{\text{f}} }}$where D_eq is the equilibrium aggregate diameter as described by the aggregation kinetics model. From our equilibrium approach, we can determine the volume fraction of aggregates in the sediment by simply plotting C ^T_P versus nC_sedv = Y as shown in Fig. 13. The slope corresponds to ϕ ^eff_max equals to 0.68. This result is close to a cubic packing of aggregates within a sediment, and indicates that the structure of the sediment is the same for silica concentrations studied (Fig. 14).

Fig. 14

The determination of the aggregate volume fraction by the proposed equilibrium approach. The slope of the line corresponds to the aggregate volume fraction, ϕ ^eff_max  = 0.68

Once we determine the maximum effective packing fraction, we can estimate the relative viscosity of the unstable silica aggregates from Eq. 13 and collapse all the data onto a single curve regardless the size of primary particles or electrolyte concentration as shown in Fig. 15. The data presented in Fig. 15 correspond to a homogeneous turbid phase of the aggregation.

Fig. 15

Comparison of the proposed model with experimental data of relative viscosity of silica nanoparticle dispersions

Conclusions

We have studied the aggregation kinetics of unmodified silica nanoparticles of 5 and 25 nm primary diameters as a function of particle and NaCl concentration above the CSC. The aggregation kinetics is strongly influenced by initial particle size and particle and salt concentrations. Our proposed model is very convenient to use and successfully described the aggregation kinetics. The model parameters: equilibrium diameter and rate constant were determined using experimental data and also estimated independently assuming DLVO theory. The early time of aggregation follows an exponential growth that is a characteristic of the slow aggregation regime. This behavior is successfully captured by the proposed model. The parameters in our proposed model are shown to be calculable independently from the proposed equations.

Maximum effective packing fraction is estimated from an equilibrium approach model of sediment volume fraction to be 0.68. The results for the relative viscosity of silica aggregates in turbid phase agree well with the proposed viscosity model and collapse onto a single curve. Unstable particle suspensions exhibit Newtonian behavior, which could be predicted by our viscosity model developed for stable dispersions.