Introduction

The investigation of rock mechanical parameters holds paramount importance throughout various stages in the life cycle of oil and gas wells. These applications encompass predicting pore pressure, assessing wellbore stability, ensuring well integrity, optimizing drilling operations, and enhancing hydraulic fracturing (Moose et al. 2003; Klimentos 2005; Fjaer et al. 2008; Kholsravantain et al. 2016; Germay et al. 2017; Hussain et al. 2020). Among these parameters, rock strength emerges as a fundamental characteristic. As defined by Fjaer et al. (2008), rock strength signifies the stress level at which rocks undergo failure. Rock failure poses a prevalent challenge in the oil and gas industry, leading to complications like sand production and reservoir compaction, detrimentally impacting well productivity. These repercussions encompass reduced formation permeability, diminished reservoir pressure, and decreased production rates (Settari and Walters 2001; Boutt et al. 2011; Najibi et al. 2017).

Uniaxial/unconfined compressive strength (UCS) and tensile strength (T0) stand out as primary indicators of rock mechanical properties, gaining widespread utilization in fields such as mining and petroleum industries (Parsajoo et al. 2021; He et al. 2020). The determination of UCS can be executed directly through standardized procedures outlined by the International Society of Rock Mechanics (Ulusay and Hudson 2007) and the American Society for Testing and Materials (Standard ASTM 2010). Meanwhile, Tensile Strength is often identified as the highest stress–strain curve point, typically around 0.1 of the UCS value, especially in proximity to excavation areas, where it tends to be notably lower than compressive strength (Perras and Diederichs 2014). Both UCS and tensile strength testing, however, necessitate meticulously prepared samples, incurring expenses, consuming time, and inducing destruction (Kalantari et al. 2018). Consequently, alternative techniques have emerged for assessing rock UCS, including block punch, scratch, point load strength (PLS), and Schmidt hammer tests (SHT) (Palassi and Emami 2014; He et al. 2019, 2020). Additionally, the Brazilian tensile strength (BTS) test is a commonly employed method for evaluating tensile strength (Heidari et al. 2012; Mahdiyar et al. 2019).

Numerous empirical relationships have been established to infer UCS and tensile strength from these indirect methodologies, predominantly employing straightforward multiple regression and statistical approaches, as highlighted by A. Mahmoodzadeh et al. (2021a, b). For instance, Kahraman et al. (2005) unveiled a direct connection between UCS and PLS, while Madhubabu et al. (2016) employed linear correlations involving compressive strength, porosity, PLS, and Poisson's ratio, especially concerning carbonate rocks. In addition, several research investigations have explored the correlation between UCS and compressional wave velocity. These correlations have been modeled both exponentially (Moradian and Behnia 2009a, b; Nefeslioglu 2013; Mishra and Basu 2013) and linearly (Yilmaz and Yuksek 2009; Dehghan et al. 2010; Armaghani et al. 2016; Heidari et al. 2018a, b; Celik 2019). Furthermore, a multitude of empirical relationships have been devised to relate tensile strength to BTS, incorporating various rock index tests such as block punch and point load testing (Nazir et al. 2013; Haung et al. 2019; Harandizadeh et al. 2020; Parsajoo et al. 2021). Additionally, diverse studies have endeavored to establish connections between UCS and BTS for different rock types (Altındağ and Güney 2010; Comakli and Cayirli 2019). Nevertheless, these investigations have indicated that the precision of these empirical correlations is constrained, typically yielding average coefficients of determination (R2) in the range of 0.4–0.7. This underscores the demand for a high degree of precision when predicting BTS during the initial formulation of these equations. Moreover, the scarcity of data or limited laboratory measurements might lead scientists to employ these correlations without scrutinizing their underlying assumptions (Azimian et al. 2014; Hassanvand et al. 2018).

In contemporary times, artificial intelligence (AI) has emerged as a superior alternative to human reasoning when it comes to establishing connections between strength parameters and the available field or laboratory measurements. As pointed out by Fjaer et al. (2008), machine learning (ML) techniques offer a way to surmount several challenges and uncertainties associated with imprecisions, data deficiencies, and the intricacies of drilling operations, as emphasized in studies by Al-Abduljabbar et al. (2020), Mahmoud et al. (2020), Ahmed et al. (2019), and others. The integration of machine learning into the processing of logging data has brought about a transformative impact in the realm of petroleum engineering and reservoir characterization.

Machine learning methodologies, including neural networks, decision trees, and support vector machines, have clearly demonstrated their effectiveness in gleaning valuable insights from extensive and intricate logging datasets. These algorithms exhibit the capability to swiftly discern patterns, anomalies, and correlations within the data, thereby empowering geoscientists and engineers to make well-informed decisions concerning reservoir properties, fluid compositions, and lithology classifications. Furthermore, machine learning models exhibit proficiency in managing substantial volumes of historical and real-time logging data, rendering them indispensable tools for the optimization of well drilling, production strategies, and reservoir management, as highlighted in studies conducted by Ali et al. (2020, 2021, 2023) and Ashraf et al. (2021).

Numerous studies in the existing body of literature have undertaken the task of predicting unconfined compressive strength (UCS) using a variety of artificial intelligence techniques, often drawing on core data as their foundation (Rabbani et al. 2012). Take, for instance, the work of Heidari et al. (2018a, b), which leveraged a dataset comprising 109 data points encompassing parameters like p-wave velocity, Is50, and block punch index BPI. In their study, they employed the fuzzy inference system (FIS) to estimate UCS, and the precision of their model was meticulously evaluated using the R2 statistic, yielding an impressive score of 0.91. Additionally, artificial neural network (ANN) methodologies have gained significant traction among researchers as a powerful tool for UCS prediction, consistently achieving accuracy levels exceeding 0.9 in various studies (Mohamed et al. 2015; Torabi-Kaveh et al. 2015; Madhubabu et al. 2016; Ferentinou and Fakir 2017; Sharma et al. 2017; Mahmoodzadeh et al. 2021a, b). Furthermore, the prognosis of Brazilian Tensile Strength (BTS) has been successfully carried out using ANN approaches, incorporating diverse rock parameters such as grain size, rock type, and mineral ratios, as exemplified by the work of Singh et al. (2001). Notably, several studies have embraced alternative input variables including density, Schmidt hammer readings, and Is50 (Mahdiyar et al. 2019; Haung et al. 2019; Parsajoo et al. 2021), consistently delivering superior predictive accuracy when compared to traditional multiple regression techniques. For a comprehensive overview of the latest advancements in machine learning (ML) applications for the prediction of UCS and tensile strength (T0) across diverse lithologies, please refer to Table 1.

Table 1 the previous ML models for UCS and BTS prediction
Full size table

Despite the advancements in this area of research, most of the existing studies used a relatively small number of data points, limiting the model’s accuracy. In addition, most of the inputs used for the training and testing of the AI models were collected from core logs and lab measurements. The objective of this work is to utilize a large set of logging data, approximately 2600 data points, acquired from an actual field in the middle east for UCS and T0 Prediction using two ML techniques, decision tree (DT) and random forest (RF) and compare them to find the most accurate technique. The data is comprised of gamma-ray (GR), Sonic time compressional (DTC) and Shear (DTS) times, rock bulk density (RHOB), and neutron porosity. According to the literature RF and DT have been used in the oil and gas industry, with little work for tensile strength and UCS prediction from Well Logs. This will overcome the difficulties associated with lab measurements as well as provide a fast tool for measuring these parameters during the early stage of well development using well-logging data.

Methodology

In this study, we employed a comprehensive methodology that harnessed the power of decision trees (DT) and random forest (RF) algorithms to predict two critical parameters, uniaxial compressive strength (UCS) and tensile strength (T), crucial for characterizing reservoir rock types. Our approach commenced with rigorous data preprocessing, including feature selection and normalization, to ensure the quality and consistency of the dataset. Subsequently, we utilized decision trees to create individual predictive models for UCS and T. These models were further integrated into a random forest ensemble, leveraging the strengths of multiple decision trees to enhance predictive accuracy. The following sections discuss the data description and preprocessing, details about the used ML methods and their advantage, and the input parameters importance and selection.

Data description

The dataset employed in this investigation comprises well logging data sourced from carbonate reservoirs situated in the Middle East. This logging dataset encompasses 2670 records, encompassing critical parameters, such as gamma-ray (GR), compressional time (DTC), shear time (DTS), bulk density (ROHB), and neutron porosity (NPHI). According to pertinent literature sources, these parameters hold significant relevance in predicting the rock's strength properties (Madhubabu et al. 2016; Matin et al. 2018; Mahmoodzadeh et al. 2021a, b). The tensile strength of the rock is contingent upon various factors, including mineralogical composition, texture, and porosity. For instance, gamma-ray (GR) logs can be leveraged to estimate mineralogical composition and clay content, critical in gauging rock strength. Additionally, compressional time (DTC) and shear time (DTS) logs facilitate the estimation of P-wave and S-wave velocities, pivotal for determining Young's modulus and Poisson's ratio. Furthermore, bulk density (ROHB) and neutron porosity (NPHI) logs prove invaluable in assessing porosity density, thereby aiding in the prediction of mechanical properties, such as Young's modulus, Poisson's ratio, and UCS.

To ensure the robustness of the predictive models, a validation dataset comprising 638 data points from an alternate well was incorporated. The collected data was subjected to random division into training and testing sets, with varying ratios ranging from 60:40 to 85:15. Remarkably, the optimal model performance was achieved when employing a 70:30 ratio. Figure 1 provides a representative depiction of the dataset employed in this study, showcasing well logging tracks for various logging parameters alongside their associated UCS and T values.

Fig. 1
figure 1

example of logging track for the different well logs

Full size image

Table 2 shows the statistical parameters of the training data, including the minimum and maximum value, the range of the data, the mean, and the standard deviation. The GR values range from 3.338 API to 85.799 API, DTC ranges from 44.899 us/ft to 66.124 us/ft, while the bulk density ranges from 2.325 g/cc to 3.045 g/cc.

Table 2 Statistical parameters of the training data set
Full size table

Decision trees (DT)

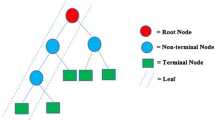
Decision trees are a concept drawn from the structure of ordinary trees, featuring nodes, a root, branches, and leaves (Ali et al. 2012). As elucidated by Zhao and Zhang (2008), decision trees manifest as a manifestation of supervised classification. The typical orientation for a Decision Tree, as noted by Ali et al. (2012), involves its construction from left to right, commencing at the root node and progressing downward. The initial node of the tree, where this journey commences, is aptly referred to as the root node, while the terminal point of the tree's branches is termed a leaf. Furthermore, each node within the tree represents distinct characteristics, with the range of values being depicted through branches extending from internal nodes, functioning as partition points for the respective sets of values associated with the given characteristic (Ali et al. 2012). A visual representation of this Decision Tree architecture can be observed in Fig. 2.

Fig. 2
figure 2

Decision tree structure

Full size image

Random forest (RF)

Random Forest, originally conceived by Breiman (2001), comprises an ensemble of unpruned regression or classification trees, as outlined in Breiman's work in 2001. According to insights from Ali et al. (2012), Random Forest leverages a set of L tree-structured base classifiers {h(Xɵn), n = 1, 2, 3…L}, with X representing the input and {ɵn} denoting a family of dependent, identically distributed random vectors. Importantly, the data undergoes random selection for each Decision Tree, allowing the creation of a Random Forest through the randomized sampling of either a feature subset and/or a training data subset for every Decision Tree. Furthermore, features are subject to random selection at each decision split, thereby enhancing prediction accuracy by mitigating correlations between trees, achieved through the randomized feature selection. Thus, as elucidated by Ali et al. (2012), the growth of each tree follows these steps:

  • N is subject to random sampling. This sample serves as a training dataset, drawn with replacement from the original data when the training dataset contains N cases.

  • M signifies the total number of inputs. At each node, a variable m is chosen, exceeding M. Additionally, m variables are randomly selected from the pool of M variables, with the optimal split based on these m variables used for node division. Moreover, the value of m remains constant throughout the forest's growth.

  • Pruning is not applied during the expansion of each tree, allowing them to reach their maximal extent.

Input parameters importance

In this investigation, it was imperative to explore the connection between the input and output parameters in order to identify the significant factors affecting the prediction process. This analysis also illustrates how sensitive the output parameters are to variations in the input parameters. To accomplish this, we employed the Pearson correlation coefficient (R), as calculated by Eq. 1, which spans from − 1, indicating a strong negative relationship, to 1, indicating a strong positive relationship.

$$R=\frac{\sum \left({x}_{i}- \right)\left( {y}_{i}- {\mu }_{y}\right) }{ {\sigma }_{x}{\sigma }_{y}}$$
(1)

where, R is the correlation coefficient, yi is the dependent parameter, xi is the independent parameter,\({\sigma }_{x}\mathrm{ and }{\sigma }_{y}\), are the standard deviations of independent and dependent parameters, \({\mu }_{x}\) and \({\mu }_{y}\), are the mean of the independent and dependent parameters. The correlation coefficient between the UCS and the input parameters were found to be 0.54, − 0.93, − 0.92, 0.15, − 0.95 for GR, DTC, DTS, RHOB, NPHI, respectively. In addition, by studying the effect of each parameter, it was found that the highest relation observed between the output and the input parameter was when the gamma-ray and DTC, and ROHB were used for the analysis as shown in Table 3. Although other parameters were tested, their significance was minuscule as the reduction in the R-value was inconsequential.

Table 3 Sensitivity analysis between inputs and output parameters
Full size table

Consequently, the decision was made to build the models using these three parameters, GR, DTC, and RHOB Moreover, the testing data was found to fall in the same range as the training data, which was observed from its statistical parameters shown in Table 4. This step added more confidence to the models making the data unbiasedly selected and representative of the original data set. Furthermore, in addition to Pearson correlation, the absolute average percentage error (AAPE) in Eq. 2, was used to assess the quality of the model. The lower the percentage, the better the prediction method.

$$\mathrm{AAPE}=(\frac{ \sum |(\mathrm{Measured}-\mathrm{Predicted})/\mathrm{Measured} |}{ n})100$$
(2)

where n is the number of data points

Table 4 Statistical parameters of the testing data
Full size table

Result and discussion

Decision tree (DT)

DT model optimum parameters were adjusted to improve the accuracy of the model as shown in Table 5. It was found that the Maximum Depth of the tree is “11” and “6” for T0 and UCS respectively, while the maximum feature was “sqrt” for tensile strength prediction and “auto” for UCS predictive model. The ‘maximum feature’, represents the size of the random subsets considered while splitting a node. Thus, when ‘Max-Feature’ is “auto”, it means that the random forest is a bagged ensemble of ordinary regression trees while “sqrt” means the subset size is considered sqrt(n-features), where n_features represents the number of features in data.

Table 5 Models optimum hyperparameters
Full size table

Figures 3 and 4 depict a comparison between the actual and predicted strength parameters throughout both the training and testing phases. These results aptly demonstrate the DT model's impressive capacity to forecast UCS and T0 with remarkable precision based on the well logging data. Notably, during the training phase, the T0 predictions achieved an R value of 0.99 and 0.93 for testing, accompanied by AAPE scores of 0.45% and 1.4%, respectively. Additionally, the linear relationship between forecasted UCS values and actual measurements was notably strong, registering R values of 0.99 and 0.97, while the AAPE amounted to 0.56% and 0.97% during training and testing, respectively.

Fig. 3
figure 3

DT model tensile strength result. a Training, b Testing

Full size image
Fig. 4
figure 4

DT model UCS prediction result. a Training, b testing

Full size image

Random forest (RF)

RF optimum parameters were found through sensitivity analysis and summarized in Table 5. The maximum feature was “auto” for UCS and T0 predictive models. The Number of estimate N, which was found to greatly affects the accuracy of the model was found 100 and 150 for the T0 and UCS models respectively. The results displayed in Fig. 5 show that RF was able to predict tensile strength with R values of 0.99 for training and 0.98 for testing, while the AAPE values were less than 1% during the training and testing stage.

Fig. 5
figure 5

RF Tensile strength result. a Training, b testing

Full size image

Mirroring the outcomes observed in the prediction of tensile strength, the RF model exhibited a remarkable capacity for accurately predicting UCS. This proficiency is underscored by the one-to-one correspondence between the predicted and actual UCS values, wherein R values of 0.99 and 0.98 were recorded, accompanied by AAPE scores of 0.28% and 0.59% during the training and testing phases, respectively (see Fig. 6).

Fig. 6
figure 6

RF UCS prediction results. a Training, b Testing

Full size image

Validation of the DT and RF models

The validation process for both models involved a separate dataset collected from well-2, comprising approximately 600 data points, with their respective statistical characteristics outlined in Table 6. The remarkable congruity between the predicted and actual UCS and T0 values underscores the precision and reliability of these models in forecasting strength parameters based on well-logging data. The evaluation of this correspondence employed the correlation coefficient (R) to gauge the relationship between predicted and measured values, while model quality was assessed using AAPE, as illustrated in Fig. 7. For the tensile strength models, R values were determined to be 0.93 and 0.97 for DT and RF, respectively, affirming RF's superiority as a predictive model. This superiority was further substantiated by the AAPE scores of 0.65% for RF and 1.4% for DT. Figure 8 exhibits the linear correlation between measured and predicted UCS values for DT and RF, revealing an R-value of 0.97. However, the corresponding AAPE figures were 0.65% for RF and 0.78% for DT.

Table 6 Statistical parameters of validation data
Full size table
Fig. 7
figure 7

Tensile strength models validation. a RF, b DT

Full size image
Fig. 8
figure 8

UCS models validation. a RF, b DT

Full size image

Across the study's three stages—training, testing, and validation—DT and RF consistently demonstrated their capacity to deliver high-quality and accurate predictive models for both tensile strength and unconfined compressive strength, as derived from well logs. This performance, notably, surpassed existing models in the literature (as shown in Table 1). Moreover, this study's use of actual well logging profiles eliminated the uncertainties tied to lab measurements of input parameters, and the substantial dataset employed further contributed to the models' robustness and precision.

Figures 9 and 10 summarize the performance indicators for RF and DT models to predict UCS and T. RF model showed a superior performance with R values higher than 0.98 in predicting UCS and T for the different datasets with AAPE less than 0.7%. DT model showed slightly lower performance as the AAPE increased to 1.4% in predicting the T for the testing and validation datasets.

Fig. 9
figure 9

Summary of the developed models’ performance for predicting UCS in different datasets. a R values, b AAPE

Full size image
Fig. 10
figure 10

Summary of the developed models’ performance for predicting T in different datasets. a R values, b AAPE

Full size image

Future developments for this study encompass the exploration of advanced machine learning algorithms. More advanced machine learning algorithms beyond decision trees (DT) and Random Forests (RF) including ANN, ANFIS, GBR, and others in order to improve the prediction accuracy and robustness. In addition, future work includes continuous refinement of feature engineering, potential data augmentation, and real-world application testing. Collaborative efforts with experts from geology and materials science will refine models and their practicality.

Conclusions

The investigation harnessed the power of Random Forest (RF) and Decision Tree (DT) machine learning (ML) techniques to forecast unconfined compressive strength (UCS) and Tensile strength (T0) from a well-logging dataset encompassing gamma-ray (GR), compressional time (DTC), shear time (DTS), bulk density (ROHB), and Neutron porosity (NPHI). The key findings are summarized below.

  • Both DT and RF models exhibited remarkable proficiency in predicting strength parameters throughout the formation with exceptional precision.

  • The RF model showcased superior prediction accuracy when compared to DT.

  • The study underwent validation using data from well-2, affirming the robustness of both models, with R-values exceeding 0.93.

Leveraging these two models presents an economical and expeditious solution for the industry to anticipate mechanical parameters using well-logging data, characterized by an extraordinary degree of precision and reliability. Notably, it's crucial to acknowledge that this study's scope was confined to carbonate reservoirs, and further experimentation across diverse geological formations is imperative for the broad applicability of these findings.