Abstract
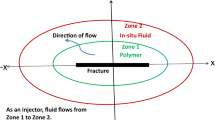
During polymer flooding into the reservoir using shear-thinning non-Newtonian fluids, an interface exists between the in situ Newtonian crude oil in the reservoir and the injected polymer solution. This paper examines the application of non-Newtonian well test analysis techniques to develop an analytical solution to non-Newtonian/Newtonian fluids with different flow index composite reservoirs for estimating the interface boundary conditions in such reservoirs. Mathematical models were presented and solved analytically using the Laplace transform. The solution was inverted to real domain with the Stehfest algorithm (Stehfest Commun ACM, 1970). Solutions were obtained for three boundary conditions that are infinite acting, constant pressure and no-flow boundaries. New pressure and pressure derivative type curves are developed for naturally fractured reservoirs. A general solution was obtained, which is adaptable to the case of non-Newtonian/Newtonian fluid interface. Numerical examples are used to estimate the radius of investigation, reservoir and power-law flow parameters using type curve matching and Tiab’s direct synthesis technique.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Enhanced oil recovery (EOR) encompasses processes of improving the recovery of hydrocarbons from oil reservoirs after primary production has declined. Among chemical-based enhanced oil recovery processes, polymer flooding is a highly practiced process in conventional oil reservoirs. Polymer flooding utilizes the injection of polymer solutions into oil reservoirs (Manrique et al. 2017). The presence of a polymer in water increases the viscosity of the injected fluid, which upon injection reduces the water-to-oil mobility ratio and the permeability of the porous media, thereby improving oil recovery. The net result is the increase in oil displacement, reservoir sweep efficiencies, and pressure gradient, especially in heterogeneous oil reservoirs (Manzoor 2020).
Well test analysis is often carried out before, during, and after polymer flooding to obtain an accurate reservoir description and to evaluate fluid mobilities within the project area (Huh and Snow 1985). Many field applications of polymer flooding have been reported as technically and economically successful. However, Non-Newtonian power-law behavior of polymer solutions such as lack of a simple proportionality relation between shear stress and rate of shear, non-uniform polymer distribution within the reservoir, and the decrease of apparent viscosity with increasing shear rates (Tariq Fariss Al-Fariss 1984) has led to various setbacks during polymer flooding. As a result, different works have been done to investigate how to maximize the oil recovery during polymer flooding. Manzoor (2020) studied the effect of injection pressure and polymer concentration on flooding performance.
During polymer flooding, the reservoir is often made up of two or more regions and, as such, is regarded as a composite reservoir. Most times, the two regions, which might be oil and polymer solution/water regions, have different rock and fluid properties. Ikoku and Ramey (1979) derived a linearized partial differential equation for describing the radial flow of a slightly compressible non-Newtonian power-law fluid through a homogeneous porous medium. They obtained approximate analytical solutions to the equation by considering constant rate injection in an infinitely large radial flow system. The solutions provided a new method of well test analysis for non-Newtonian fluids injected into reservoirs. However, they did not consider the discontinuity of fluid in the reservoir at the interface. Lund and Ikoku (1981) addressed this neglect through numerical method by extending the flow of non-Newtonian fluids through a porous media onto composite reservoirs containing non-Newtonian and Newtonian fluids.
Ertekin et al. (1987) studied the pressure transient behavior of non-Newtonian/Newtonian composite fluid flow in a porous media. Their work employed numerical method and primarily focused on a porous media with a finite-conductivity vertical fracture. Gencer and Ikoku (1984) analyzed injectivity and falloff test data during two-phase flow of non-Newtonian (power-law) and Newtonian fluids to determine the saturation gradients that can develop. They considered simultaneous (multiphase) flow of oil and water, and effects of relative permeability characteristics of the porous media, finite radius of the skin region, skin factor, injection time, viscosity of the Newtonian fluid, and rock compressibility on the pressure response.
Katime-Meindl and Tiab (2001) applied Tiab’s direct synthesis (TDS) technique to the case of flow of non-Newtonian fluid through porous media. Pressure and pressure derivative data of a well test data in a homogeneous reservoir are interpreted without the use of type curve matching or regression analysis. The analysis considered the effect of skin factor and wellbore storage, and equations for calculating mobility and radius from wellbore to the nearest boundary were obtained.
Escobar et al. (2010) utilized the pressure derivative curve in interpreting well test data in reservoirs with non-Newtonian power-law fluids. They obtained equations to estimate the permeability, skin factor and non-Newtonian bank radius. The characteristic features found on the pressure and pressure derivative curves enabled the application of Tiab’s direct synthesis (TDS) technique to their work. No analytical mathematical model developed to describe the pressure behavior in composite reservoir with non-Newtonian/Newtonian fluids.
In this study, we developed a general analytical solution to describe pressure transient behavior in a reservoir with two immiscible different non-Newtonian fluids having different flow indexes. Figure 1 represents the physical description of the composite reservoir. TDS technique is used for the analysis.
Mathematical model
The linearized partial differential equation for naturally fractured reservoir (NFR) as presented by Omosebi and Igbokoyi (2015) is:
All the dimensionless variable and derivation are in “Appendix”.
The assumptions used in developing this model are: (1) fluid flow in the reservoir is radial, (2) laminar and Darcy’s flow is valid, (3) isothermal, single phase and slightly compressible fluid with constant properties, (4) homogenous and isotropic system, (5) pseudoplastic (shear-thinning) fluid obeys Ostwald–de Waele power-law relationship and (6) steady-state effective viscosity. The mathematical model also assumed there is no transition region.
The approximate long-time solution at the wellbore when rD is unity is:
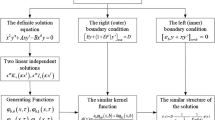
The solutions to Eq. 1 in Laplace space with various boundary conditions are presented in “Appendix”. Solution with the dimensionless wellbore storage CD and skin S is:
Type curve
Apart from the flow index, interporosity transfer and storativity ratio, two key parameters are used to characterize the type curve. They are alpha and theta (see Eqs. 38 and 59 in “Appendix”).
and
While alpha is a function of diffusivity ratio D, theta is a function of mobility ratio M. Therefore,
The effect of mobility and diffusivity ratios is demonstrated in Figs. 2 and 3 as in the work of Ambastha (1988).
Figure 4 is the curve generated for the three outer boundary conditions.
Figures 5 and 6 show the condition when the inner region is Newtonian and the outer region is non-Newtonian. This is to replicate a case when the pressure measurement is taking place at the producer of the Newtonian fluids; for example, crude oil that exhibits Newtonian behavior. The early pressure derivative is 0.5, while the late pressure derivative exhibits non-Newtonian behavior.
Figure 7 is a reversed behavior of Fig. 5. However, the non-Newtonian flow regime in the inner region has a strong influence in the outer region with Newtonian flow.
Odeh and Yang (1979) derived the expression for the radius of investigation in non-Newtonian fluid flow in porous media. This expression is simplified to:
Ikoku and Ramey (1979) also used a similar approach to arrive at their formula for radius of investigation as:
Equations 14 and 15 are used in this study to compute the polymer front. Equation 14 gives radius of investigation in centimeter, while Eq. 15 gives it in meter. Ikoku and Ramey (1979) also presented the formula for estimating the effective viscosity of the polymer fluid as:
where the effective viscosity is not given, Eq. 16 is used to estimate the effective viscosity.
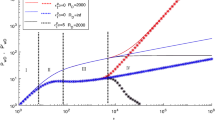
The main purpose of this work is to get a general solution for a composite reservoir with two regions having different properties with non-Newtonian fluid flow in porous media. The result of the general solution for case of m = 0.9 in the outer region is shown in Fig. 8. This type of solution is particularly useful for heavy crude that exhibits non-Newtonian behavior and being displaced by polymer fluid for increased recovery.
Applications to numerical examples
The two numerical examples used to verify the mathematical models are from Lund and Ikoku’s (1981) work. The numerical examples are for homogeneous system with storativity ratio ω equal to 1.0.
Type curve method
Injection test
The match in Fig. 9 was obtained with a flow index n of 0.9 (Table 1).
We estimated the effective viscosity with Eq. 16. The value of the effective viscosity with n of 0.6 is 0.0000402 Pas, while n equals 0.9 giving 0.00424 Pas. The effective viscosity of the polymer cannot be less than that of the Newtonian fluid in the formation; hence, we have confidence in the match with 0.9 as the value of n, and therefore, the value of the polymer effective viscosity used in this work is 0.00424 Pas.
We used pressure derivative plot to estimate the time at the interface. Lund and Ikoku (1981) used the plot of ΔP against tv to estimate the time at the interface. The pressure derivatives give better estimate of point of discontinuity. From Fig. 10, we estimated the interface to be at the time t = 931 s. Lund and Ikoku’s time at interface is 7100 s. This is already in the transition region (Table 2).
The alpha (α) value for both match is 0.003 and theta (θ) is 0.00135.
The effective compressibility in the polymer zone, which is region I, is estimated from the value of alpha and time match.
From the time match:
From the value of alpha:
Falloff test from the same numerical model.
The Agarwal equivalent time is used for all the plots in the falloff test (Figs. 11, 12).
The same values of alpha and theta were used (Table 3).
From the time match:
From the value of alpha:
Tiab’s direct synthesis method
Interporosity flow parameter is obtained by substituting the co-ordinates of the minimum point of the trough, tmin and (t x ΔP′)min according to Tiab et al (2006). At that point,
For storage capacity ratio, the method of calculation is obtained using the pressure derivative co-ordinate of the minimum point and the radial flow regime line, according to Tiab et al (2006). It is given as:
At the infinite-acting radial flow regime of non-Newtonian fluid, the log–log plot of the pressure derivative versus time will give a straight line with slope, v. The value of n can then be determined from the slope. By substituting the dimensionless pressure equations into the pressure derivative equation, the mobility ratio (effective permeability–viscosity ratio) is calculated by Igbokoyi and Tiab (2007) as:
At tIARF = 1 s,
For the skin factor, the following equation from Omosebi and Igbokoyi (2015) is obtained:
Wellbore storage is computed with the usual equation.
Permeability in region II and the skin factor can be computed with the following equations presented by Tiab (1995).
Calculate the interporosity flow parameter using Eq. 17
Define R as:
Calculate the storage ratio;
or
TDS method
Injection test
From Fig. 10, at \(t = 931\,{\text{s}}\), \((\Delta P_{ws} ) = 3610000\,{\text{Pa}}\), and \(\left( {t*\Delta P^{\prime}_{w} } \right) = 724063\,{\text{Pa}}\)
From fluid and reservoir parameters,
Therefore, permeability:
Using the Newtonian region (region II) with average pressure derivative \(\left( {t \times \Delta P^{\prime}} \right)_{{{\text{IARF2}}}} = 275618\,{\text{Pa}}\,{\text{and}} \Delta P_{{{\text{IARF2}}}} = 6730000\,{\text{Pa}}, t_{r2} = 63.9\,{\text{h}}\)
With Newtonian fluid viscosity of 0.003 Pas, the permeability is 97 md.
Skin factor S using non-Newtonian formula:
Skin factor S using Newtonian formula:
Falloff test
From Fig. 10, at \(t = 3088\,{\text{s}}\), \((\Delta P_{ws} ) = 4530000\,{\text{Pa}}\), and \(\left( {t*\Delta P^{\prime}_{w} } \right) = 882286\,{\text{Pa}}\)
Using the Newtonian region (region II) with average pressure derivative \(\left( {t \times \Delta P^{\prime}} \right)_{{{\text{IARF2}}}} = 268582\,{\text{Pa}}\,{\text{ and}} \Delta P_{{{\text{IARF2}}}} = 7060000\,{\text{Pa}}, t_{r2} = 143.62\,{\text{h}}\)
With Newtonian fluid viscosity of 0.003 Pas, the permeability is 99 md (Tables 4, 5).
Skin factor S using non-Newtonian formula:
Skin factor S using Newtonian formula:
Discussion of the results
The new analytical model developed was used to analyze simulated data from the work of Lund and Ikoku. The major differences between Lund and Ikoku, and this study results are the value of flow index n in region I and the polymer front. The analytical method for estimating radius of investigation developed by Ikoku and Ramey could not confirm the polymer front estimated by Lund and Ikoku. While Lund and Ikoku used the plot of ΔP versus tv to estimate the polymer front, we used pressure derivative curve to estimate the polymer front, which should be more accurate. Moreover, we used Odeh and Yang’s method to estimate the polymer front, and the results are in good agreement with this study’s. Permeability estimated from both type curve and TDS methods for injection and falloff tests is consistent. Therefore, the new analytical method developed is considered valid.
Conclusions
A general solution for a composite reservoir with two regions in a radial system is developed. The solution is applicable to both non-Newtonian and Newtonian composite reservoirs in two-region radial system.
The model was applied to solve simulated numerical examples of injection and falloff tests. Type curve and Tiab’s direct synthesis methods were used to analyze the numerical data, and consistent results were obtained.
The radius of investigation for non-Newtonian derived by Ikoku and Ramey, and Odeh and Yang is based on the same assumptions. However, Odeh and Yang’s method gives more accurate results.
Availability of data and materials
Available.
Code availability
Available.
Abbreviations
- B :
-
Formation volume factor, rm3/stm3
- C D :
-
Dimensionless wellbore storage
- c t :
-
Total compressibility Pa−1
- h :
-
Formation thickness, m
- H :
-
Consistency index (power-law parameter) Pa sn
- k :
-
Formation permeability, m2
- m, n :
-
Flow behavior index (power-law parameter), dimensionless
- P D ′ :
-
Dimensionless wellbore pressure derivative
- P D :
-
Dimensionless wellbore pressure drop
- P i :
-
Initial pressure, Pa
- P wD :
-
Dimensionless wellbore flowing pressure
- \(\underline {P}\) D :
-
Dimensionless pressure drop in Laplace space
- q :
-
Volumetric flow rate, m3/s
- r :
-
Radial distance, m
- r D :
-
Dimensionless radial distance at any point, (r/rw)
- R eD :
-
Dimensionless radial distance at boundary conditions (external)
- r w :
-
Wellbore radius, m
- S :
-
Skin factor, dimensionless
- t :
-
Time, s
- t*ΔP′:
-
Pressure derivative, Pa
- t D :
-
Dimensionless time
- Γ(x):
-
Gamma (factorial) function
- ΔP :
-
Pressure drop
- φ :
-
Porosity, fraction of bulk volume
- λ :
-
Interporosity flow parameter, dimensionless
- μ :
-
Viscosity, Pas
- θ :
-
Effective mobility ratio for a two-region composite reservoir
- ω :
-
Storage capacity ratio, dimensionless
- π :
-
3.142
- 1:
-
Referring to region 1, inner region
- 2:
-
Referring to region 2, outer region for a two-region composite reservoir
- D:
-
Dimensionless quantity
References
Al-Fariss TF (1984) Non-Newtonian oil flow through porous media, PhD Dissertation, University of British Columbia
Ambastha AK (1988) Pressure transient analysis for composite system. Study done at Stanford University, Stanford
Ertekin T, Adewumi MA, Daud ME (1987) Pressure transient behaviour of non-Newtonian/Newtonian fluid composite systems in porous media with a finite conductivity vertical fracture. Soc Pet Eng J. https://doi.org/10.2118/17053-PA
Escobar FH, Martinez J, Montealegre-Madero M (2010) Pressure and pressure derivative analysis for a well in a radial composite reservoir with a non-Newtonian/Newtonian interface. CT&F – Ciencia Technologia y Futura 4(2):33–42
Gencer CS, Ikoku CU (1984) Well test analysis for two-phase flow of non-newtonian power-law and newtonian fluids. ASME J Energy Resour Technol 106:295–305
Huh C Snow TM (1985) Well testing with a non-newtonian fluid in the reservoir. SPE 14453-MS. https://doi.org/10.2118/14453-MS
Igbokoyi AO, Tiab D (2007) New type curves for the analysis of pressure transient data dominated by skin and wellbore storage—non-Newtonian fluid. Soc Pet Eng J. https://doi.org/10.2118/106997-MS
Ikoku CU, Ramey HJ (1979) Transient flow of non-Newtonian power-law fluids in porous media. Soc Pet Eng J 19(3):164–174. https://doi.org/10.2118/7139-PA
Katime-Meindl I, Tiab D (2001) Analysis of pressure transient test of non-newtonian fluids in infinite reservoir and in the presence of a single linear boundary by the direct synthesis technique. Soc Pet Eng J. https://doi.org/10.2118/71587-MS
Lund O, Ikoku CU (1981) Pressure transient behaviour of non-Newtonian/Newtonian fluid composite reservoirs. Soc Pet Eng J. https://doi.org/10.2118/9401-PA
Manrique E, Ahmadi M, Samani S (2017) Historical and recent observations in polymer floods: an update review. CT&F – Ciencia Technologia y Futura 6(5):17–48
Manzoor AA (2020) Modeling and simulation of polymer flooding with time-varying injection pressure. ACS Omega 2020(5):5258–5269. https://doi.org/10.1021/acsomega.9b04319
Odeh AS, Yang HT (1979) Flow of non-Newtonian power-law fluids through porous media. SPEJ 19(3):155–163. https://doi.org/10.2118/7150-PA
Omosebi O, Igbokoyi A (2015) Analysis of pressure falloff tests of non-Newtonian power-law fluids in naturally-fractured bounded reservoirs. Petroleum 1(2015):318–341. https://doi.org/10.1016/j.petlm.2015.10.006
Stehfest H (1970) Algorithm 368: numerical inversion of laplace transforms [D5]. Commun ACM. https://doi.org/10.1145/361953.361969
Tiab D, Restrepo DP, Igbokoyi A (2006) Fracture porosity of naturally fractured reservoirs. Soc Pet Eng J. https://doi.org/10.2118/104056-MS
Vongvuthipornchai S, Raghavan R (1987) Pressure falloff behavior in vertically fractured wells: non-Newtonian power-law fluids. SPEFE 2(4):573–589. https://doi.org/10.2118/13058-PA
Funding
No funding was received to assist with the preparation of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Mathematical derivations
Appendix: Mathematical derivations
The general partial differential equation (Ikoku & Ramey 1979) is:
For region II, we have:
where
Outer boundary condition
Infinite system
Closed (no-flow) boundary system
Constant pressure boundary system
Inner boundary condition
and,
Therefore,
Equation 47 is formerly established by Vongvuthipornchai and Raghavan (1987) in equation B-8 of their paper.
And flow equation for non-Newtonian fluid (flow index m) is:
But,
Adapting Eq. (12) in Lund and Ikoku (1981) to non-Newtonian/Newtonian fluid flow, at interface RD (i.e., rates are equal at the interface):
where
Therefore,
Set
Therefore,
If we assume that permeability, compressibility and porosity are approximately the same in both regions, then
From Eq. 6, at the interface;
If m = n,
A general Laplace solution for the dimensionless pressure drop for region I is:
Laplace solution for the dimensionless pressure drop in infinite (non-Newtonian) flow for region II is:
At interface,\(r_{D} = R_{D} , \underline {P}_{D1} = \underline {P}_{D2}\)
Therefore,
Set:
where:
Combining Eqs. 69 and 70, we have:
At wellbore condition, \(r_{D} = 1:\)
Combine Eqs. 77 and 79, we have:
Laplace solution for the dimensionless pressure drops for constant pressure boundary system for region II is
Since \(\underline {P}_{D2} = 0 @ R_{eD} ,\)
At interface RD, \(\frac{{\partial \underline {P}_{D2} }}{{\partial r_{D} }} = - \frac{\theta }{{sR_{D}^{m} }}\) and \(\underline {P}_{D1} = \underline {P}_{D2}\).
Therefore,
Also,
Set
From Eq. (78),
Laplace solution for the dimensionless pressure drops for closed (no-flow) boundary system for region II is
At interface RD, \(\frac{{\partial \underline {P}_{D2} }}{{\partial r_{D} }} = - \frac{\theta }{{sR_{D}^{m} }}\) and \(\underline {P}_{D1} = \underline {P}_{D2}\)
Set
Similarly, we have:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ukwuigwe, O.C., Igbokoyi, A.O. Analytical solution to pressure transient analysis in non-Newtonian/Newtonian fluids in naturally fractured composite reservoirs. J Petrol Explor Prod Technol 11, 4277–4293 (2021). https://doi.org/10.1007/s13202-021-01292-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-021-01292-1