Introduction

In situ stress consists of three main components of vertical (SV), minimum horizontal (Shmin), and maximum horizontal (SHmax) stresses that are applied perpendicularly to rock at a certain depth. Drilling operation changes the equilibrium condition of in situ stress and creates a disturbed in situ stress state around the wellbore (Jaeger and Cook 1979). Such a stress disturbance around the wellbore wall creates some problems such as wellbore instability, tight hole, drilling-induced tensile fractures, breakout in the wellbore, and creep of salt layers toward the wellbore. Among the advantages of determining the in situ stress before and after drilling are the estimation of the optimum mud weight, optimum directional drilling trajectory to minimize risk level and lower maintenance costs, studying casing collapse and shear, wellbore stability analysis, designing a proper drilling bit for further drilling, selecting suitable casings, preventing sand production, selecting efficient strategies for well completion, and determining the optimum exploitation from the oil reservoir. Drilling-induced tensile fracture and breakouts are both the precursors of wellbore instability, which occur when the stress concentration on the wellbore wall is higher than the mechanical strength of the wellbore wall rock (Cao et al. 2016; Ju et al. 2018; Taherynia et al. 2016). Besides, drilling-induced tensile fracture and breakouts occur when the stress magnitude on the wellbore wall is larger than the tensile and compressive strengths of the rock, respectively (Bell and Gough 1979; Cao et al. 2016; Horn et al. 2016; Taherynia et al. 2016; Ju et al. 2018). Directions of drilling-induced tensile fracture and breakouts show the minimum horizontal stress (Shmin) and maximum horizontal stress (SHmax), respectively (Bell and Gough 1979). Breakouts in wellbore wall can be detected and investigated using the image logs and caliper measurements while drilling-induced tensile fractures are only identified using the image logs (Peška and Zoback 1995; Brudy and Zoback 1993; Lund and Zoback 1999; Cao et al. 2016; Horn et al. 2016). Sedimentary rocks, in which oil field drilling occurs, are porous and contain some fluids. Pore pressure is generally referred to as the fluid content of the formations. Normal pore pressure (Pfn) at a depth H is the weight of fluid column above that depth, which is defined as:

$$P_{{\rm fn}} = \int_{0}^{H} {\rho_{{\rm f}} } (z)g{\text{d}}z.$$
(1)

The fluid density for seawater is within the range of 1.03–1.07 g/cm3. Thus, normal pore pressure indicates a ~ 10 MPa increase with a 1-km increase in depth (10 MPa/km or 0.45 psi/ft). In many important cases, the pore pressure deviates from the normal value and results in abnormal pore pressures (Fjaer et al. 2008).

Tests such as leak-off test (LOT), extended leak-off test (ELOT), micro-fracture test, and hydraulic fracturing can be applied to determine Shmin. All these tests are carried out in situ at a certain depth. To perform these tests, the fluid pressure is increased at a certain depth until the fracture initiated and/or the pre-existing fracture reopened in the formation. The pressure recorded at the moment of fracture initiation presents the pressure needed to overcome rock strength, i.e., Shmin (Jandakaew 2007; Dehghan et al. 2015a, b, 2016, 2017, Dehghan and Khodaei 2017).

One of the most frequently used methods for determining the domain of SHmax is to apply the stress polygon method. To determine the lower and upper bounds of SHmax using this method, we should have Biot coefficient, Poisson’s ratio, wellbore azimuth, mud pressure difference, sliding friction, internal friction, pore pressure, uniaxial compressive strength (UCS), wellbore deviation, the azimuth of SHmax, and breakout width (WBO). In this study, magnitude of in situ stress around the Marun Oil Field’s failed wells was determined based on the field data and using the empirical equations and different methods.

Stress distribution in salt formations

Salt is one of the evaporite rocks, which is highly deformable with temperature and applied stresses. Stress state is highly complicated and varying in salt formations. Under the effect of in situ stress, this rock can show long-term viscoplastic and time-dependent (creep) behaviors (Jandakaew 2007). Allemandou and Dusseault (1996) conducted some triaxial creep tests on salt and identified the considerable role of octagonal shear stress and deviatoric stress on its creeping behavior. In this regard, creep tests were carried out under different temperature and pressure conditions on 10 core samples extracted from salts of the Gachsaran Formation, and their viscoplastic behavior was proved. Because of the role of evaporite cap rocks in hydrocarbon reservoirs and preventing oil escape, salt formations are suitable places for disposal of atomic waste and hydrocarbon storage (Winterle et al. 2012).

Due to the very low porosity and permeability of salt, an increase in the stress value is accompanied by its low compressibility and thus it starts to have a plastic movement. This phenomenon is attributed to the high Poisson’s ratio of salts, according to which when a certain stress is applied to the salt, its stress state becomes almost hydrostatic due to its incapability to keep deviatoric stresses. Stress in salts reaches a relaxation state and finally turns into the hydrostatic state. However, by moving from the salt toward non-salt formations, the hydrostatic stress condition and magnitude are disturbed and the vertical and horizontal stress values are changed (Fredrich and Fossum 2002).

Since the salt rocks are viscous and flow slowly at all nonzero shear stress states, it can be assumed that SV = SHmax = Shmin = \(\bar{\gamma } \cdot z\), where \(\bar{\gamma }\) is the mean overburden bulk density. Isotropic stress state is seen only in viscous rocks and very soft mud. Assuming an isotropic stress state of salts, the horizontal stress would be almost equal to overburden. So, the term under-balance is commonly addressed in drilling of a salt formation, according to which mud pressure is less than the vertical stress (Dusseault et al. 2004).

Marun Oil Field and casing collapse phenomenon

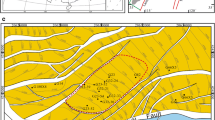
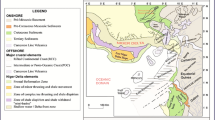
Marun Oil Field was discovered in 1963 through the seismic exploration technique. This oil field neighbors Kupal field in the north, Aghajari in the east, and Ahvaz City in the northwest. This field is in the eastern part of huge Dezful subsidence. By now, about 400 oil wells have been drilled in this oil field. Marun Oil Field has a NW–SE direction from its western to central part and a NE–SW direction in its eastern part. The length and the width of this field are 65 km and 7 km, respectively. The distance between the reservoir crest and the deepest level of water–oil contact is the Asmari Formation is about 2000 m. The field has a fault with a similar name (i.e., Marun Fault), which is in the northwest of Aghajari Fault in Faulted Zagros Belt. The length of this NE–SE fault is about 50 km. The thrust fault has been thrust on the sediments of neighboring plain due to the performance of Marun Anticline. The evaporitic Gachsaran Formation consists of seven members with sequence of anhydrite, marl, and salt layers. The first member (the lowest one) which is made up of anhydrite is known as the cap rock of the Asmari carbonate reservoir, the most famous hydrocarbon reservoir in Iran.

According to the report of National Iranian South Oil Company (NISOC) and Schlumberger Oil Company in 2005 about the casing collapse problem in this field, 48 out of 267 wells (17.5%) drilled since the first oil production from this field (1950) until 2005 had shown casing collapse problem (Rolf et al. 2006). Most of these failures have occurred in members 4–2 of the Gachsaran Formation, which consists of salt and associated a small portion of interlayers of marl and anhydrite with a varying thickness. The reason for the difference in thickness of this formation is the effect of tectonic of plastic materials that make the Gachsaran Formation. Considering the lithology and creep behavior with time, when the stress generated by the creeping movement of the Gachsaran salts applied on casing exceeds the collapse resistance of casing, it would definitely collapse (Rolf et al. 2006). Accordingly, it is necessary to determine in situ stress for the analysis and study of creep movements in the Gachsaran Formation Salts in the Marun Oil Field’s failed wells. Marun Anticline has an NW–SE direction. As can be seen from the focal mechanism map of earthquakes in the southwestern part of Iran (Fig. 1), SHmax has an azimuth of 40–45°.

Fig. 1
figure 1

Stress distribution map for Iran (general azimuth of SHmax based on earthquake focal data) (Rolf et al. 2006)

Full size image

Determination of in situ stress in Marun 42, 130, and 133 wells

Determination of vertical stress (SV)

Vertical stress (SV) component is calculated from surface for the given depth using the density log of the wells (Fjaer et al. 2008):

$$S_{{\rm V}} = \int_{0}^{z} \rho (z)g{\text{d}}z \cong \bar{\rho }gz$$
(2)

where g is gravitational acceleration, \(\bar{\rho }(z)\) is density at depth z, and \(\bar{\rho }\) is the mean overburden density. The density of sedimentary rocks varies with a range of 2–3 g/cm3, with the mean density being 2.5 g/cm3. At higher depths (overburden) of the reservoir, for which density logs are not available, density of rocks can be estimated for each lithology using geological graphic well logs or daily drilling reports. Since the reservoir is overlain by the Gachsaran Formation, density log was not available for estimating the SV. However, as mentioned earlier, SV can be estimated by averaging the densities of the existing lithologies (Zoback et al. 2003). Using the sonic logs and laboratory tests, the density of marl, anhydrite, and salt was estimated to be 2.55, 2.96, and 2.29 g/cm3, respectively, which can be averaged to 2.6 g/cm3. Accordingly, gradient of vertical stress in the Gachsaran Formation is 0.026 MPa/m. According to Eq. (2), SV at failure depths in Marun 42, 130, and 133 wells was calculated as 85.3, 88.86, and 86.58 MPa, respectively. The failure depths for these three wells were 3281, 3418, and 3330 m, respectively.

Determination of minimum horizontal stress (Shmin)

Due to a lack of hydraulic fracturing and leak-off test data in the Gachsaran Formation of the Marun Oil Field, to calculate minimum horizontal stress, mud losses information of the formation was used. Thus, if the mud weight leads to the fracture initiation and/or reopening the pre-existing fractures in the formation, the total mud weight can be considered equivalent to the minimum horizontal stress (Zoback 2010; Ward and Andreassen 1997; Serdyukov et al. 2016; Wang and Mi 2016). Based on mud weight information in the daily drilling reports, pore pressure in member 4 of the Gachsaran Formation up to the cap rock (member 1) in the Marun Oil Field would be about 0.022 MPa/m. This value implies the presence of a large amount of saline water at this depth and thus overpressure of the Formation. In this way, pore pressure at failure depths of Marun 42, 130, and 133 wells was estimated to be 66.8, 73.44, and 71.55 MPa, respectively. Drilling in members 4–2 of the Gachsaran Formation in Marun 133 well shows that mud weight has increased up to 145 pcf, which was declined to 140 pcf by the mud loss of 22 barrels. The mud column weight pressure (i.e., well pressure at the depth of failure) was calculated to be 75.85 MPa. Since fracture gradient of the Gachsaran Formation was 0.024 MPa/m, due to the pre-existing fractures, the 145 pcf mud weight can initiate or propagate fracturing at the failure depth. Since the fracturing induced by mud weight increase up to the formation strength must occur along the direction of horizontal stress, by converting mud weight unit (pcf) to pressure unit (MPa), it is seen that mud column weight at failure depth is almost equivalent to Shmin. At failure depth of Marun 130 well, mud weight increased up to 150 pcf, by which the well pressure was increased to 80.54 MPa, while mud weight was declined to 146 pcf.

At failure depth of the Marun 42 well, mud weight was increased up to 145 pcf, which was reduced to 135 pcf. At this moment, well pressure at failure depth was 74.74 MPa.

Moreover, Eq. (3) proposed by Hubbert and Willis (1972) was also used in the present work. This relation was prepared by conducting a set of hydraulic fracturing tests and analyses. Later on, Zoback and Healy (1984) showed that the constant 0.5 is associated with friction faulting theory in which sliding friction coefficient can be considered as 0.6 (Zoback and Healy 1984). Thus, the Shmin in the Marun 42, 130, and 133 wells was estimated to be 76.05, 81.15, and 79.06 MPa, respectively.

$$S_{{{\text{hmin}}}} = 0.5(S_{{\rm V}} - P_{{\rm p}} ) + P_{{\rm p}} .$$
(3)

Also, Breckels and van Eekelen (2008) used hydraulic fracturing results in several points and extracted a relationship between horizontal stress and depth. They incorporated the effect of the existing abnormal pressures in this equation and proposed Eqs. (4) and (5) (Fjaer et al. 2008). Also, Eaton (1969) proposed Eq. (6) for this purpose (Eaton 1969):

$$S_{{{\text{hmin}}}} = 0.0053H^{1.145} + 0.46(P_{{\rm p}} - P_{{\rm fn}} ) \, \quad {\text{ For}}\;H < 3500$$
(4)
$$S_{{{\text{hmin}} }} = 0.026H - 31.7 + 0.46(P_{{\rm p}} - P_{{\rm fn}} )\quad {\text{ For }}\;H > 3500$$
(5)
$$S_{{{\text{hmin}}}} = \frac{\upsilon }{1 - \upsilon }(S_{{\rm V}} - P_{{\rm p}} ) + P_{{\rm p}}$$
(6)

where H is depth (m), PP is pore pressure (MPa), Pfn is normal pore pressure (with respect to a gradient of 10.5 MPa/km), and \(\upsilon\) is a Poisson’s ratio. Equations (4), (5), and (6) and stress polygon were used to estimate Shmin.

Determination of maximum-horizontal-stress domain (SHmax)

Although in salt cross sections SV, Shmin, and SHmax are considered to be equal, stress polygon method was employed to prove this assumption. In the Marun Oil field, in none of the damaged wells, there are no image logs in order to observe the drilling-induced tensile fractures, breakouts, or natural fractures in the wellbore.

Through the studies performed by petroleum geomechanical engineers around the world, it has been reported that drilling-induced tensile fractures and breakouts in wellbores are not related to lithology. In other words, these discontinuity planes can occur in any lithology in the well drilling path. In this regard, image well logs such as ultrasonic borehole imager (UBI) and fullbore formation microimager (FMI) can be used to identify and analyze the magnitude of Shmin and SHmax. To determine SHmax using the stress polygon, it is necessary to have an azimuth of SHmax and breakout width (WBO). Due to not having these two parameters, even having SV, Shmin, UCS, pore pressure, and well pressure, it is not possible to accurately estimate SHmax in these wells. Figures 2, 3, and 4 illustrate stress polygons obtained from the Mohr–Coulomb failure criterion for the Marun 130, 133, and 42 wells, respectively. This criterion is one of the shear failure criteria in rock engineering studies that can consider the low permeability of Gachsaran Formation.

Fig. 2
figure 2

Stress polygon based on the Mohr–Coulomb failure criterion for Marun 130 well

Full size image
Fig. 3
figure 3

Stress polygon based on the Mohr–Coulomb failure criterion for Marun 133 well

Full size image
Fig. 4
figure 4

Stress polygon based on the Mohr–Coulomb failure criterion for Marun 42 well

Full size image

In Figs. 2, 3, and 4, the information required for plotting stress polygons is presented. As can be seen, parameters including WBO and the azimuth of SHmax are not available, which can both be extracted from image well log analyses. Based on earthquake focal data (Fig. 1), WBO and azimuth of SHmax were considered to be 0° and 45°, respectively. The red parallel lines in the figure demonstrate contours of UCS, which were determined to be 22 MPa for the Gachsaran Formation salts. Moreover, the Poisson’s ratio for this formation was estimated to be 0.45 (Farsimadan 2011). Steep blue parallel lines, on the other hand, illustrate contours of tensile strength, which are within the range of − 1 to − 2 MPa (Farsimadan 2011). By applying these two values and their intersection on stress polygon, we acquire an area (green shade) to calculate Shmin as well as upper and lower bounds of SHmax. The red and blue shades also represent the range of compressive and tensile strengths for the Gachsaran Formation salts in the different wells, respectively (Figs. 2, 3, and 4).

Interpretation of obtained in situ stress

The in situ stress was determined for all depths of the Gachsaran Formation in Marun 42, 130, and 133 wells, and their gradients along with gradients of normal pore pressure, pore pressure, and well pressure are presented in Figs. 5, 6, and 7. As can be seen in these figures, from a depth of 3000 m SHmax and SV values become very close to each other, but they are both greater than Shmin. One explanation for this observation is the high pore pressure that results in a convergence of stress in the stress polygon. The failure depths in these figures are denoted by arrows.

Fig. 5
figure 5

In situ stress determined for Marun 130 well

Full size image
Fig. 6
figure 6

In situ stress determined for Marun 133 well

Full size image
Fig. 7
figure 7

In situ stress determined for Marun 42 well

Full size image

It is worth mentioning that the difference of Shmin, SHmax, and SV (for an assumed hydrostatic condition) for all three wells can be due to lack of complete information, the use of empirical equations, and more importantly the presence of marl and anhydrite layers at failure depths. Another noteworthy point in the failure zone is the increased Shmin compared to fracture pressure gradient of the Gachsaran Formation. Table 1 summarizes the in situ stress results for Marun 42, 130, and 133 wells. The error values obtained for estimating Shmin and SHmax relative to SV by the different methods are shown with a +/− sign in Table 1.

Table 1 The in situ stress results for Marun 42, 130, and 133 wells
Full size table

Conclusion

The main conclusions of the present study can be summarized as follows:

  1. 1.

    At studied failure depths, due to the lithology of salt (and its viscoplasticity property) and high pore pressure, the values of estimated in situ stress are very close to each other, and the stress state can be considered as hydrostatic.

  2. 2.

    The Shmin in Marun 130 well at failure depth obtained using the stress polygon was estimated as 79.37 MPa, which is slightly different from the 80.54 MPa stress estimated using the mud loss information. In addition, in this well, SV is 88.86 MPa, while the lower and upper bounds of SHmax are, respectively, 88.56 and 90.64 MPa. Considering that SV is smaller than the upper bound of SHmax but greater than its lower bound, the faulting stress regime can be considered as a combination of normal and strike slip modes.

  3. 3.

    Shmin obtained using stress polygon for Marun 133 well at failure depth is 76.66 MPa, which is slightly different from the 75.85 MPa stress, obtained from mud loss of the formation. The upper and lower bounds of SHmax were, respectively, 84.15 and 86.09 MPa, while the SV was 86.58 MPa. Since SV is slightly larger than the upper bound of SHmax, it can be stated that the faulting regime is normal.

  4. 4.

    Shmin obtained using stress polygon for Marun 42 well at failure depth is 73.09 MPa, which is slightly different from the 74.73 MPa stress, obtained from mud loss of the formation. Also, SV at failure depth is 85.3 MPa that is slightly higher than the 84.1 MPa SHmax stress. Hence, a normal faulting mechanism can be considered for this well.

  5. 5.

    Based on the determined in situ stress, the overall faulting regime of the study area was determined to be normal/strike slip.

  6. 6.

    The SV and Shmin values at failure depth estimated using the relation proposed by Eaton (1969) are closer (because of the parameters used in this equation). Therefore, it is recommended for the estimation of Shmin.