Introduction

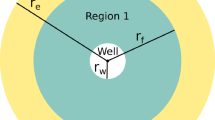
Perforation and completion of the wellbore might either impair or stimulate flow around the wellbore, forming a region with modified permeability. Hence, an additional pressure change occurs. Properties inside this damaged region are grouped in a parameter called mechanical skin factor, which is defined as (Hawkins 1956):

$$\begin{aligned} S=\left( \frac{k}{k_{\mathrm{skin}}}-1\right) \ln\left( \frac{r_{\mathrm{skin}}}{r_{{\rm w}}}\right) , \end{aligned}$$
(1)

where k stands for the reservoir permeability, \(r_{{\rm w}}\) represents the wellbore radius, \(k_{\mathrm{skin}}\) and \(r_{\mathrm{skin}}\) denote the damaged zone permeability and radius, respectively.

As shown in Eq. (1), an infinite number of radius–permeability combinations yield the same skin factor.

Even though conventional analysis techniques are able to determine the reservoir skin factor (Gao 1987; Ehlig-Economides and Joseph 1987; Banerjee et al. 1998; Peres et al. 2004), they cannot provide estimates for skin zone permeability and radius. Multilayer reservoirs present an additional setback, since skin zone properties may not be the same in all layers. Thus, additional information must be obtained from the pressure transient test, so that the damaged region properties can be determined.

During an injectivity test, the pressure derivative profile presents a characteristic signature, associated with the development of the flooded region (Peres and Boughara 2004; Barreto et al. 2011; Bela et al. 2019). Thereby, pressure derivative profile indicates the time when the waterfront overcomes the damaged zone in single-layer reservoirs. Skin radius, then, may be estimated using Buckley–Leverett theory (Buckley and Leverett 1941).

In this context, the first contribution of this work is to develop a technique to determine the skin zone radius in single-layer reservoirs. Then, skin zone permeability may also be computed, provided that an estimation for the mechanical skin factor is available.

Furthermore, an attempt was made to extend the proposed method to evaluate individual layer permeability, skin factor and damaged zone properties in multilayer reservoirs. Computation of individual layer properties was developed by assuming that layer flow-rates are decoupled. The discussion over the validity of this hypothesis is perhaps the most relevant novelty in this work.

In “Mathematical model” section, we present a brief overview on the existing analytical model for water injection in a reservoir composed of any number of layers. “Determining skin zone properties in single-layer reservoirs” section depicts the suggested technique to compute damaged zone properties in single-layer reservoirs, while the formulation for multilayer systems is described in “Computing the reservoir skin factor in multilayer reservoirs” and “Estimating individual layer properties” sections. The proposed method was applied on a set of cases, whose results are displayed in “Results and discussion” section. Finally, the main conclusions of this work may be seen in “Conclusions” section.

Mathematical model

Pressure change during an injectivity test can be understood as the sum of two terms: one related to the single-phase oil displacement throughout the reservoir and another that comes from the mobility differences between water and oil (Bela et al. 2019). During the injection period, pressure change in reservoirs without formation damage is given by Barreto et al. (2011):

$$\begin{aligned} \Delta P_{\mathrm{wf}}(t) = \Delta P_{\rm o}(t) + \frac{q_{\mathrm{in}j}}{\sum\limits_{j=1}^{n}A_j^{-1}(t)} \end{aligned}$$
(2)

The \(\Delta P_{\rm o}(t)\) term is evaluated by the line source solution (Peres et al. 2004). At late times, it can be estimated by the following logarithmic approximation (Banerjee et al. 1998):

$$\begin{aligned} \Delta P_{\rm o}(t)=\frac{\alpha _p q_{\mathrm{in}j} }{2 k_{\mathrm{eq}}h_{{\rm T}} \hat{\lambda }_{{\rm o}}} \ln\left( \frac{4\alpha _t k_{\mathrm{eq}} \hat{\lambda }_{{\rm o}} }{e^\gamma \phi c_{{\rm t}} r_{{\rm w}}^2}t\right) \end{aligned}$$
(3)

Equation (3) assumes that porosity and total compressibility are the same in all layers. If that is not the case, the \(\phi c_{{\rm t}}\) product may be replaced by a thickness-averaged porosity–compressibility product.

The \(A_j(t)\) coefficient is a weighting variable that encompasses the mobility contrast between oil and water in a given layer j (Barreto et al. 2011):

$$\begin{aligned} A_j(t)=\frac{\alpha _p }{k_{j} \hat{\lambda }_{{\rm o}} h_j}\int \limits _{r_{{\rm w}}}^{r_{{{\rm F}}j}(t)} \left( \frac{\hat{\lambda }_{{\rm o}}}{\lambda_{\rm t}}-1\right) \frac{{\rm d}r}{r} \end{aligned}$$
(4)

Buckley–Leverett theory is applied to compute the waterfront radius \(r_{{{\rm F}}j}\) (Buckley and Leverett 1941):

$$\begin{aligned} r_{{{\rm F}}j}(t)=\sqrt{\frac{q_{j}f'_{{\rm w}}t}{24\pi \phi h_j}+r_{{\rm w}}^2} \end{aligned}$$
(5)

In reservoirs with formation damage, an additional term must be added to account for the mechanical skin:

$$\begin{aligned} \Delta P_{\mathrm{wf}}(t) = \Delta P_{\rm o}(t) + \frac{q_{\mathrm{in}j}}{\sum\limits_{j=1}^{n}A_j^{-1}(t)} + \Delta P_{\mathrm{skin}} \end{aligned}$$
(6)

The \(\Delta P_{\mathrm{skin}}\) term depicts how the skin zone affects the single-phase oil flow. It is defined as:

$$\begin{aligned} \Delta P_{\mathrm{skin}}=\frac{\alpha _p q_{\mathrm{in}j}}{k_{\mathrm{eq}}h_{{\rm T}} \hat{\lambda }_{{\rm o}}}S \end{aligned}$$
(7)

In multilayer reservoirs, the skin factor is given by a weighted average of individual layer skin factors (Gao 1987), which are computed according to Eq. (1):

$$\begin{aligned} S=\frac{\sum\limits_{j=1}^{n}q_j S_j}{q_{\mathrm{in}j}} \end{aligned}$$
(8)

Although layer mechanical skins are constant, layer flow-rates may vary in time (Gao 1987; Barreto et al. 2011). Thus, according to Eq. (8), the reservoir skin factor can also change in time. That is, it accounts for the flow-rate transient effects.

The damaged zone also influences the two-phase flow that occurs within the flooded region. Thereby, the expression for the \(A_j(t)\) coefficient changes and depends on whether or not the flooded region has overcome the skin radius. While the waterfront is within the damaged zone,

$$\begin{aligned} A_j(t)=\frac{\alpha _p }{k_{j_{\mathrm{skin}}} \hat{\lambda }_{{\rm o}} h_j}\int \limits _{r_{{\rm w}}}^{r_{{{\rm F}}j}(t)} \left( \frac{\hat{\lambda }_{{\rm o}}}{\lambda_{\rm t}}-1\right) \frac{{\rm d}r}{r} \end{aligned}$$
(9)

Otherwise,

$$\begin{aligned} \begin{aligned} A_j(t)&=\frac{\alpha _p}{k_{j}h_j\hat{\lambda }_{{\rm o}}} \left[ \int \limits _{r_{{\rm w}}}^{r_{{{\rm F}}j}(t)}\left( \frac{\hat{\lambda }_{{\rm o}}}{\lambda_{\rm t}}-1\right) \frac{{\rm d}r}{r} \right. \\&\quad +\left. \left( \frac{k_j}{k_{j_{\mathrm{skin}}}}-1\right) \int \limits _{r_{{\rm w}}}^{r_{j_{\mathrm{skin}}}}\left( \frac{\hat{\lambda }_{{\rm o}}}{\lambda_{\rm t}}-1\right) \frac{{\rm d}r}{r}\right] \end{aligned} \end{aligned}$$
(10)

Determining skin zone properties in single-layer reservoirs

In single-phase well testing, the mechanical skin factor is determined from the difference between the observed pressure at a given time and the pressure change that would be expected if there were no formation damage (Gao 1987). Pressure change for the zero skin case is estimated by Eq. (3).

In injectivity tests, besides the mechanical skin due to the formation damage, there is also an apparent skin that reflects the mobility contrast between oil and water. Hence, the procedure described above yields a total skin factor, which encompasses both mechanical and apparent skins (Peres and Boughara 2004). Thus,

$$\begin{aligned} S_{{\rm t}}(t)=\frac{kh\hat{\lambda }_{{\rm o}}}{\alpha _p q_{\mathrm{in}j} }\left( \Delta P_{\mathrm{wf}}(t)-\Delta P_{{\rm o}}(t)\right) \end{aligned}$$
(11)

The relation between total, apparent and mechanical skin is given by (Peres and Boughara 2004):

$$\begin{aligned} S_{{\rm t}}(t)=S_{\mathrm{ap}}(t)+\frac{S}{\hat{M}} \end{aligned}$$
(12)

In Eq. (12), \(\hat{M}\) stands for the endpoint mobility ratio. It measures the relative easiness of water and oil to flow throughout the reservoir and is defined as the ratio between water and oil endpoint mobilities:

$$\begin{aligned} \hat{M}=\frac{\hat{\lambda }_{{\rm w}}}{\hat{\lambda }_{{\rm o}}} \end{aligned}$$
(13)

The mechanical skin depends only on the damaged zone properties, which do not vary in time. Thus, the mechanical skin remains constant in time. The apparent skin, in its turn, depends on the waterfront radius, which increases as injection goes on:

$$\begin{aligned} S_{\mathrm{ap}}(t)=\int \limits _{r_{{\rm w}}}^{r_F(t)}\left( \frac{\hat{\lambda }_{{\rm o}}}{\lambda_{\rm t}}-1\right) \frac{{\rm d}r}{r} \end{aligned}$$
(14)

Therefore, the apparent skin changes in time, hence, so does the total skin factor, as displayed in Eq. (12).

Equations (11) to (14) portray how the mechanical skin is determined. Nevertheless, Eq. (1) shows that, for a given skin factor, there are infinite possible combinations of skin zone radius and permeability. Thereby, estimates for skin zone properties have been unachievable so far.

Pressure derivative behavior, however, can help to accomplish this task. As depicted in “Mathematical model” section, the formulation to compute the \(A_j(t)\) coefficient changes according to the waterfront radius. As the flooded region reaches the skin zone radius, Eq. (9) is no longer valid and Eq. (10) must be used to compute the pressure change.

Fig. 1
figure 1

Pressure and derivative data for case A

Full size image

This causes a characteristic signature in the derivative profile. A sharp shift in pressure derivative is identified when the waterfront overcomes the skin radius. Figure 1 illustrates the time when a blunt drop in pressure derivative is observed, in a reservoir with endpoint mobility ratio lower than 1. Reservoir properties are the same as case A, depicted in Table 1.

Thereby, the time required for the waterfront to reach the damaged zone radius (from now on denoted as \(t_s\)) may be obtained from the pressure derivative profile. Once \(t_s\) has been identified, skin zone radius may be estimated using Buckley–Leverett theory (Buckley and Leverett 1941):

$$\begin{aligned} r_{\mathrm{skin}}=\sqrt{\frac{q_{\mathrm{in}j}f'_{{\rm w}}t_s}{24\pi \phi h}+r_{{\rm w}}^2} \end{aligned}$$
(15)
Fig. 2
figure 2

Pressure and derivative data for case B

Full size image

In cases where flow is favorable to water, there might occur a pressure drop after the waterfront overcomes the damaged region. Pressure derivative, then, decreases and may even assume negative values. Besides, the shift in pressure derivative behavior may not be so easily identifiable because the water saturation profile is smoother. Figure 2 shows the pressure and pressure derivative behavior for case B, from Table 1, which is an example with mobility ratio favorable to water. In these cases, the time when pressure derivative attains its minimum value should be assigned as \(t_s\).

After the well is shut, the waterfront remains stationary (Peres and Boughara 2004; Bela et al. 2019). Therefore, no derivative shift is observed during falloff. For this reason, the proposed technique is only applicable during the injection period.

Lastly, skin zone permeability might be determined through Eq. (1), applying the previously computed values for the mechanical damage and skin radius. Reservoir permeability, which is also required by Eq. (1), is estimated from the constant pressure derivative level (Banerjee et al. 1998; Bela et al. 2019):

$$\begin{aligned} k=\frac{1.151\alpha _pq_{\mathrm{in}j}}{h\hat{\lambda }_fm_f}, \end{aligned}$$
(16)

where f denotes either water or oil and \(m_f\) is the constant pressure derivative level associated with phase f.

Computing the reservoir skin factor in multilayer reservoirs

The procedure depicted in “Determining skin zone properties in single-layer reservoirs” section may be applied to evaluate the reservoir skin factor in multilayer reservoirs, with some suitable adjustments.

Assuming that oil properties are the same in all layers, total skin factor is computed by using the reservoir equivalent permeability and total thickness in Eq. (11):

$$\begin{aligned} S_{{\rm t}}(t)=\frac{k_{\mathrm{eq}}h_{{\rm T}}\hat{\lambda }_{{\rm o}}}{\alpha _p q_{\mathrm{in}j} } \left( \Delta P_{\mathrm{wf}}(t)-\Delta P_{{\rm o}}(t)\right) \end{aligned}$$
(17)

The computation of the apparent skin as depicted in Eq. (14) requires a waterfront radius. This radius may be obtained using the total injection flow-rate and the reservoir total thickness in Eq. (5), provided that all layers present the same relative permeability curves:

$$\begin{aligned} r_F(t)=\sqrt{\frac{q_{\mathrm{in}j}f'_{{\rm w}}t}{24\pi \phi h_{{\rm T}}}+r_{{\rm w}}^2} \end{aligned}$$
(18)

The mechanical skin, then, may be evaluated through Eq. (12).

Fig. 3
figure 3

Waterfront propagation in each layer

Full size image

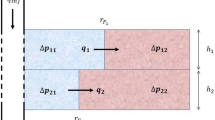
It is important to notice, though, that the waterfront may propagate differently in each layer, as shown in Fig. 3. Therefore, the waterfront radius from Eq. (18) does not necessarily correspond to the waterfront in any given layer.

Instead, it is a theoretical radius, which is required to set the integral limit in Eq. (14). Since relative permeability curves are assumed to be the same in all layers, this theoretical waterfront radius allows the determination of the reservoir apparent skin, as described in Eq. (14), without further concerns.

Estimating individual layer properties

An attempt is also made to estimate individual layer properties. Here, a crucial hypothesis is that flow is decoupled with respect to each layer, and flow-rates stabilize at a level proportional to layer flow capacities after a short transient period. For single-phase flow in commingled systems, it is known that this condition holds (Ehlig-Economides and Joseph 1987; Spath et al. 1994).

Under the assumption that injection in each layer is independent of the others, reservoir properties in Eq. (17) should be replaced by the respective layer properties to estimate total skin in a given layer j:

$$\begin{aligned} S_{{\rm t}_j}(t)=\frac{k_{j}h_j\hat{\lambda }_{{\rm o}}}{\alpha _p q_{j}} \left( \Delta P_{wf}(t)-\Delta P_{{\rm o}_j}(t)\right) \end{aligned}$$
(19)

Since flow is assumed to be decoupled in each layer, the \(\Delta P_{{\rm o}_j}\) term in Eq. (19) should be evaluated using the properties from layer j:

$$\begin{aligned} \Delta P_{{\rm o}_j}(t)=\frac{\alpha _p q_{j} }{2 k_{j}h_j \hat{\lambda }_{{\rm o}}} \ln\left( \frac{4\alpha _t k_{j} \hat{\lambda }_{{\rm o}} }{e^\gamma \phi c_{{\rm t}} r_{{\rm w}}^2}t\right) \end{aligned}$$
(20)

The decoupled flow-rate hypothesis enables the estimation of layer permeability as well. The suggested computation derives directly from the determination of the reservoir equivalent permeability:

$$\begin{aligned} k_{j}=\frac{1.151\alpha _pq_{j}}{h_j\hat{\lambda }_fm_f} \end{aligned}$$
(21)

Layer apparent skin is computed through Eq. (14), using the waterfront radius foreseen by Eq. (5). After total and apparent skin in a given layer has been computed, the mechanical skin will be evaluated, once again, by Eq. (12). One should notice that Eqs. (12) and (14) are not affected by the decoupled flow-rate hypothesis.

To estimate layer skin zone radius, the value of \(t_s\) should be defined in an analogous way to the single-layer case. Then, skin zone radius is determined by applying the identified value of \(t_s\) in Eq. (5).

In multilayer reservoirs, it is important to notice that there might occur more than one sharp shift in the pressure derivative profile. This signs that layer skin zone properties are remarkably different and, therefore, it takes more time for the damaged region in one layer to be overcome by the waterfront than in another layer. In these cases, more than one value of \(t_s\) might be identified. In a field example, where layer properties are unknowns to be determined, it is impracticable to identify which blunt shift is related to which layer.

Assessing the validity of the decoupled flow-rate hypothesis

Equations (19) and (21) highlight that the estimates for layer skin factor and permeability, which are constant, depend on layer flow-rate, which may vary in time.

In fact, the reservoir mechanical skin defined by Eq. (8) indicates that layer flow-rates are indeed coupled. Moreover, the formulation for the injection period in multilayer reservoirs under two-phase flow, developed by Barreto et al. (2011), also suggests that flow in each layer is indeed dependent of the other layers:

$$\begin{aligned} q_j(t)=\frac{\Delta P_{\mathrm{wf}}(t)-\Delta P_{{\rm o}}(t)-\Delta P_{\mathrm{skin}}}{A_j(t)} \end{aligned}$$
(22)

Whenever the decoupled flow-rate hypothesis is valid, Eq. (22) must yield the expected steady-state flow-rate according to layer flow capacities.

Thus, replacing Eq. (6) in Eq. (22):

$$\begin{aligned} q_j(t)=\frac{1}{A_j(t)}\frac{q_{\mathrm{in}j}}{\sum\limits_{i=1}^{n}A_j^{-1}(t)} \end{aligned}$$
(23)

The goal is to study the conditions required for flow-rates in all layers to stabilize at a level proportional to its flow capacity. For this reason, it is more relevant to understand flow-rate behavior after the waterfront has overcome the damaged zone in all layers. Thereby, applying Eq. (10) in expression (23):

$$\begin{aligned} \begin{aligned} q_j(t) = \frac{1}{\frac{\alpha _p}{k_{j}\hat{\lambda }_{{\rm o}}h_j}b_j}\frac{q_{\mathrm{in}j}}{\sum\limits_{i=1}^{n}\left[ \frac{\alpha _p}{k_{i}\hat{\lambda }_{{\rm o}}h_i}b_i\right] ^{-1}} \end{aligned} \end{aligned}$$
(24)

In Eq. (24), \(b_j\) is a coefficient that encompasses both integral terms in the definition of \(A_j(t)\):

$$\begin{aligned} \begin{aligned} b_j=S_{\mathrm{ap}j} +\left( \frac{k_j}{k_{j_{\mathrm{skin}}}}-1\right) \int \limits _{r_{{\rm w}}}^{r_{j_{\mathrm{skin}}}}\left( \frac{\hat{\lambda }_{{\rm o}}}{\lambda_{\rm t}}-1\right) \frac{{\rm d}r}{r} \end{aligned} \end{aligned}$$
(25)

In “Mathematical model” section, oil properties and relative permeability curves have been assumed to be the same in all layers. Applying this assumption in Eq. (24):

$$\begin{aligned} \begin{aligned} q_j(t)=\frac{1}{\frac{b_j}{k_jh_j}}\frac{q_{\mathrm{in}j}}{\sum\limits_{i=1}^{n}\frac{k_ih_i}{b_i}} \end{aligned} \end{aligned}$$
(26)

Hence, if the \(b_j\) term is the same in all layers, Eq. (26) may be rewritten as:

$$\begin{aligned} q_j(t)=q_{\mathrm{in}j}\frac{k_jh_j}{\sum\limits_{i=1}^{n}k_ih_i}=q_{ss_j} \end{aligned}$$
(27)

Equation (27) shows that, under the assumptions made, flow-rate in a given layer remains constant after the waterfront in every layer has overcome the skin radii. Layer flow-rate, then, stabilizes at a level proportional to layer flow capacity, as would be expected in a single-phase flow (Ehlig-Economides and Joseph 1987; Spath et al. 1994). This flow-rate is denoted as \(q_{ss_j}\).

Therefore, the decoupled flow-rate hypothesis is applicable whenever \(b_j\) is approximately the same in all layers. In other words, the method portrayed in this section yields good estimates for individual layer properties whenever layer properties are not remarkably different, specially within the damaged region.

If that is not the case, then layer flow-rate may stabilize at a level completely different than \(q_{ss_j}\). The reason for that is found at the expression to compute \(b_j\). Using the definition for layer mechanical skin [Eq. (1)], Eq. (25) may be rewritten as:

$$\begin{aligned} \begin{aligned} b_j=S_{\mathrm{ap}_j} +\frac{S_j}{\ln \left( \frac{r_{j_{\mathrm{skin}}}}{r_{{\rm w}}}\right) }\int \limits _{r_{{\rm w}}}^{r_{j_{\mathrm{skin}}}}\left( \frac{\hat{\lambda }_{{\rm o}}}{\lambda_{\rm t}}-1\right) \frac{{\rm d}r}{r} \end{aligned} \end{aligned}$$
(28)

Applying Eq. (8) in Eq. (28):

$$\begin{aligned} b_j=S_{\mathrm{ap}_j}+ \frac{q_{\mathrm{in}j}S}{q_j\ln \left( \frac{r_{j_{\mathrm{skin}}}}{r_{{\rm w}}}\right) } \int \limits _{r_{{\rm w}}}^{r_{j_{\mathrm{skin}}}}\left( \frac{\hat{\lambda }_{{\rm o}}}{\lambda_{\rm t}}-1\right) \frac{{\rm d}r}{r} \end{aligned}$$
(29)

Thus, Eqs. (26) and (29) evidence that layer flow-rates are in fact coupled when layer properties are different enough so that the \(b_j\) term may not be assumed to be approximately equal in all layers.

A possible alternative to overcome this setback could be achieved by using the rate-normalized pressure change to estimate individual layer properties. This technique was presented by Ehlig-Economides and Joseph (1987) for multilayer commingled reservoirs under conventional well testing.

Table 1 Single-layer cases properties
Full size table

However, to apply their formulation, there must be a flow-rate change during the test, so that two different nonzero flow-rates occur. Parameters, then, are computed based on the rate-normalized pressure change. In injectivity tests, a variable flow-rate would imply in great difficulties to compute waterfront radii. Thereby, their method is not easily adapted to injectivity tests.

Table 2 Estimated skin zone properties of the single-layer cases
Full size table

Results and discussion

The techniques described in “Determining skin zone properties in single-layer reservoirs” to “Estimating individual layer properties” sections were applied on a set of cases in order to assess their accuracy. The formulation depicted in “Mathematical model” section was implemented on a code that yielded the pressure transient data used to perform the proposed method. For all cases, water viscosity was set as 0.52 cP, which is the typical water viscosity at the reservoir temperature. It was considered an injection time of 96 h (or 4 days), followed by a falloff time of 96h. Falloff pressure data were used to determine reservoir and layer permeabilities. Wellbore radius was 0.108m. Relative permeability curves, rock and fluid compressibilities were extracted from Bela et al. (2019).

Single-layer cases

Table 1 presents the reservoir features for the single-layer tested cases, while Table 2 shows the results obtained applying the proposed method in these cases. In both tables, the skin zone radii denote the damaged zone extension beyond the wellbore.

Cases A to F consist of cases where flow around the wellbore is impaired; that is, skin factor is positive. Cases G and H, in their turn, represent reservoirs where flow around the wellbore is stimulated. This might happen, for example, in some carbonate reservoirs.

Fig. 4
figure 4

Pressure and derivative data for case G

Full size image

The suggested technique was able to provide estimates for skin zone properties in all cases, except case G. In this case, the mobility ratio is favorable to water. This means that the waterfront shape is smoother and, hence, the pressure derivative shift is softened. Besides, positive mechanical skins also impair the detection of \(t_s\). For those reasons, no noticeable pressure derivative shift was observed in case G. Thus, skin zone radius was not computed. Pressure and pressure derivative profile for this case are displayed in Fig. 4. It is interesting to observe, though, that the mobility ratio in case H was favorable enough to oil so that \(t_s\) could be identified. In all other cases, the value of \(t_s\) could be identified from the pressure derivative profile as depicted in “Determining skin zone properties in single-layer reservoirs” section.

Case B presented the highest error for the skin radius estimate. There are two main causes for that. The first is the mobility ratio. As explained regarding case G, mobility ratios favorable to water imply in a smoother waterfront profile. This means that the shift in pressure derivative is not so easily identified. Additionally, higher mobility ratios imply that the waterfront will overcome the damaged region faster. Thereby, the detection of \(t_s\) in cases with mobility ratio favorable to water is more sensitive to the time discretization.

Table 3 Multilayer cases properties
Full size table

Furthermore, the shorter the skin zone radius, the faster the waterfront will overcome the damaged region. This means that shorter skin radii increase the method sensitivity to the time discretization as well. These two reasons also explain why skin radii presented higher errors in cases C and E.

On the other hand, cases A, D, F and H presented either a mobility ratio favorable to oil or longer skin zone radius or both. As a result, errors associated with skin zone estimates were lower in these cases.

Regardless the issues related to the skin radii computation, permeability inside the damaged region was accurately estimated in all cases. The reason for this fact is given by how skin permeability is evaluated. As shown in Eq. (1), the estimation of skin zone permeability depends not only on the skin radius, but also on the mechanical skin factor and reservoir permeability. Thus, even in cases where skin radius error was more relevant, the estimates for \(k_{\mathrm{skin}}\) were computed with good accuracy due to the reservoir skin factor and permeability.

Multilayer cases

Reservoir properties of the multilayer cases are displayed in Table 3. Table 3 also shows the expected steady-state flow-rate in each layer (\(q_{ss_j}\)), evaluated according to layer flow capacities, as proposed by Spath et al. (1994). Estimates for layer properties are reported in Table 4, while the computed reservoir skin factors may be seen in Table 5. Permeability inside the damaged region was estimated using the computed values for \(k_j\) and \(r_{j_{\mathrm{skin}}}\) in Eq. (1). Once again, skin zone radii denote the damaged zone extension beyond the wellbore radius. Actual reservoir skin factors were determined through Eq. (8), applying the last measured flow-rate in each layer (which may be observed in Table 4).

Table 4 Estimated layer properties of the multilayer cases
Full size table
Table 5 Estimated reservoir mechanical skin for the multilayer cases
Full size table

In the multilayer examples, each case presented some particular features that deserve a more detailed comment. For this reason, a brief analysis regarding each case can be made:

Case I in this example, both layers present the same properties, except for the formation damage, which affects only layer 1. For this reason, layer flow-rates stabilize at a level that do not correspond to their respective steady-state values. Difference between measured and expected steady-state flow-rates is directly reflected in the errors presented by estimated layer permeabilities: The difference between \(q_j\) and \(q_{ss_j}\) is approximately equal to the layer permeability error for both layers. This result indicates that the decoupled flow-rate hypothesis is more sensitive to skin zone properties than to layer permeabilities. It is interesting to notice, though, that the proposed method was able to compute the skin factor for layer 1 with good accuracy and yielded a low skin factor for layer 2, which actually presents no skin. The reservoir mechanical skin was also estimated with low error.

As depicted in “Computing the reservoir skin factor in multilayer reservoirs” section, the value identified for \(t_s\) was applied to determine the skin zone radius in both layers. Since layer 2 presents no formation damage, it was expected that the estimated skin zone permeability in this layer would be very close to the actual layer permeability, implying that \(S_2\simeq 0\). However, the estimated skin zone properties for both layers showed a significant error. In layer 1, the estimation of skin zone radius is subjected to the same issues as the single-layer cases. Once again, time discretization plays an important role. Accuracy of skin zone permeability, in its turn, depends not only on the skin zone radius, but also on layer permeability and skin factor. As mentioned, layer permeability could not be evaluated with a good accuracy, and the error propagated to the skin zone permeability. This explains the error observed in layer 2 as well.

Case J This example clearly highlights the limitations of the proposed technique for layer properties determination. Here, both layers present the same properties, except for the skin zone permeability (and, hence, the mechanical skin). As a result, layer flow-rates remained during all test far from their expected flow capacity level. Thus, no layer property could be estimated with an acceptable error. This reinforces that, whenever layer skin factors are remarkably different, layer flow-rates are coupled and the suggested method is no longer applicable. Yet, the reservoir mechanical skin was estimated with good accuracy, showing once more that the method described in “Computing the reservoir skin factor in multilayer reservoirs” section is independent of layer flow-rate history.

Case K This example presented the best results from all multilayer tested cases. This better accuracy derives from the flow-rate history. The values for \(q_{ss_j}\) and \(q_{j}\) in Tables 3 and 4 evidence that layer flow-rates converged to the level associated with layer flow capacities. Thus, layer skin factors and permeabilities were evaluated with good accuracy. The reservoir skin factor was also estimated with little error. These results also suggest that layer skin zone properties are more relevant to the decoupled flow-rate hypothesis than layer permeabilities, which is consistent with cases I and J.

Pressure derivative in this example, portrayed in Fig. 5, presented two blunt shifts. Since the reservoir presents two layers, both pressure derivative drops were used to assign two values of \(t_s\). The first time was applied to compute the skin zone radius for the second layer, because this layer presents higher skin zone permeability and, hence, it should take a shorter time for the waterfront to overcome the damaged zone in this layer. The estimated values for \(r_{j_{\mathrm{skin}}}\) indicate that this assumption was correct and the first derivative drop is indeed related to the second layer. However, in a practical case, it is impossible to state with certainty that a given derivative shift is associated with a given layer, due to the fact that an infinite number of skin zone radius–permeability combinations yield the same skin factor, as depicted by Eq. (1).

Fig. 5
figure 5

Pressure and derivative data for case K

Full size image

Case L This stimulated example yielded good results for layer permeabilities. Again, this is explained by layer flow-rate history, which stabilized at the level foreseen by layer flow capacities. Here, only one sharp shift was observed in the pressure derivative profile. Thereby, the skin zone radii for both layers were estimated using the same value for \(t_s\). The results suggest that the waterfront overcomes the damaged zones approximately at the same time and, thus, the derivative shifts associated with each layer overlap one another. Therefore, estimates for skin zone properties presented relevant errors.

Case M This example also consists of a reservoir where only one layer presents formation damage. But here, layers present distinct permeabilities and thickness. Flow-rate history as displayed in Fig. 6 evidences that all layer flow-rates stabilize at a level which is completely different than what would be expected according to the flow capacity in each layer. This flow-rate profile is explained by the difference between layer skin factors.

Fig. 6
figure 6

Layer flow-rate history for case M

Full size image

As a result, layer properties in this case were estimated with relevant error. Computed mechanical skins for layers 2 and 3 indicate that the damaged region in those layers is significantly stimulated, although they do not present any formation damage in fact. These results strengthen that the proposed method relies on the fact that layer flow-rate must have reached the level foreseen by its flow capacity.

The computation of the reservoir skin factor, in its turn, was close to the actual value. This indicates that, although the proposed technique for layer properties estimation is sensitive to flow-rate transient effects (depicted in “Estimating individual layer properties” section), the same does not hold when it comes to determine the reservoir skin factor (reported in “Computing the reservoir skin factor in multilayer reservoirs” section).

Case N Analysis of this case is much similar to case M. The reservoir mechanical skin was computed with good accuracy, despite the fact that, once again, layer flow-rates stabilized at a level that is not related to layer flow capacity. On the other hand, this case exhibited an interesting feature regarding the determination of \(t_s\).

Figure 7 shows the pressure and pressure derivative profile for case N. Two distinct sharp drops in pressure derivative profile may be clearly identified in Fig. 7 as in case K. However, since the reservoir consists of three layers, the third shift must be partially or totally overlapped with one of the two observed drops. As it is impossible to state a priori which shift is related to each layer, all skin zone radii were computed using the time of the first derivative drop as \(t_s\). The results suggest that this value of \(t_s\) is associated with the third layer. Nevertheless, it is important to remind that in a real-field case, one cannot assure which layer matches the pressure derivative shift.

Fig. 7
figure 7

Pressure and derivative data for case N

Full size image

Conclusions

Based on the analytical formulation for the injection period, an interpretation method was developed to estimate the skin zone radius in single-layer reservoirs. Damaged zone permeability may also be computed, provided that the reservoir mechanical skin has been determined.

The proposed technique was applied on a set of cases and presented good results. The suggested method was more accurate for greater skin radii and lower endpoint mobility ratios.

For multilayer commingled reservoirs, a means for determining the reservoir mechanical skin was achieved. Assuming that layer flow-rates are decoupled, an attempt was also made to estimate individual permeabilities and layer skin factors. The results indicate that, whenever the estimated layer skin factors are similar, the decoupled flow-rate hypothesis holds. Otherwise, individual layer properties computed from the proposed method are not reliable.

In multilayer systems, the blunt pressure derivative shifts associated with each layer may be overlapped. Besides, in a practical case, it is not possible to state with certainty which shift is associated with which layer. Thus, the estimated skin zone properties presented significant errors.