Introduction

The injection of water into oil reservoirs in order to extract relevant information regarding the characteristics of the reservoir has become an interesting alternative to conventional well testing, given that it has many advantages. In addition to bringing greater safety to the procedure, the method helps to reduce \(\text {CO}_2\) emissions to the environment, since there is no need to gas/oil flaring which happens in a conventional well testing. However, it brings a new parameter to the problem since the system changes from a single-phase flow to a two-phase flow.

Operationally, the conventional and injectivity tests are completely different; however, the injectivity well testing presents enough information to perform the pressure behavior analysis. Therefore, it is possible to obtain different reservoir properties according to what it is requested or necessary to the study of the reservoir (Neto et al. 2020a). The method consists of injecting water at a constant rate during a period of time. After that, the well is shut in and then it is possible to analyze the pressure curves to estimate properties of the reservoir.

Solutions for injectivity test in the real field applied to a single layer and a multilayered reservoir have already been developed (Bela et al. 2019). Prats and Vogiatzis (1999) consider a injectivity study applied to a multilayered reservoir. However, their work relies only on the flow of a single fluid. Therefore, to the best of our knowledge, this is the first time a solution for two-phase flow in a multilayered reservoir developed in the Laplace domain is presented.

Previous studies showed that the fluid flow in multi-zone porous media is a nonlinear process, which is governed by the diffusivity equation, an equation describing the nonlinearities resulting from the dependence of fluid and medium properties on pressure (Wang et al. 2013). Hence, the pressure solution was obtained using a system of equations built in Laplace domain and brought to the real field using Stehfest’s Algorithm (Stehfest 1970) including the boundary and coupling conditions adopted to this model.

This work extends the single-layer solution in the Laplace domain to injectivity test developed by (Neto et al. 2020b) to multilayered reservoirs and the behavior observed in the curves of pressure and pressure derivative was analyzed in different cases considering a variation of properties in the layers of the reservoir. Also, a computational model was built to compare the results obtained.

Conceptual model

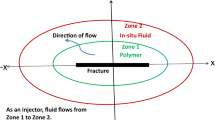
The formulation of the problem considers a reservoir with two layers both with two regions, where the outer radius is the same in both layers and there is no formation crossflow. The well is assumed to be at the center of a circular zone in a cylindrical model (Nie et al. 2012; Wang et al. 2013). In this geometry, there is a radial change in properties between the two distinct regions guided by the investigation radii. In radially composite reservoirs, the pressure response reflects the properties of both regions (Nie et al. 2019).

A schematic illustration of the physical model is shown in Figs. 1 and 2.

Fig. 1
figure 1

Schematic illustration of the side view of the reservoir model

Full size image
Fig. 2
figure 2

Schematic illustration of the top view of the reservoir model

Full size image

The external boundary is considered infinite acting. Region 1 represents the flooded zone and region 2 corresponds to the oil region, both considered homogeneous. In addition, the interface of the regions is flat and it has no thickness. The fluid mobility (k/\({\mu }\)) and compressibility are different on each side, and layer thicknesses are constant. Also, there is no resistance to flow between the two reservoir regions.

In the actual reservoir, a variation of properties around the wellbore at the interface of the regions can be observed due to the rock–fluid interaction. However, those alterations were not considered in the model presented here.

For the mathematical formulation, the following hypotheses are considered:

  1. 1.

    Two-phase flow without interaction between the fluids and a piston-like fluid displacement in which the water pushes the oil completely.

  2. 2.

    Isothermal flow with negligible gravitational forces and ignoring the impact of capillary forces.

  3. 3.

    Same initial pressure (\({p_i}\)) in all layers and small pressure gradients.

  4. 4.

    Reservoir is considered isotropic along each layer.

  5. 5.

    Single vertical injection well.

  6. 6.

    Constant flow rate during injection time.

  7. 7.

    Constant thickness (h) and porosity (\({\phi }\)) on each layer.

  8. 8.

    No flow considered in \({\theta }\) and z-directions.

  9. 9.

    The well is fully perforated along its extension.

Mathematical formulation

Considering the reservoir model described in “Conceptual model” section, a system of linear equations in Laplace domain is built to represent the differential equations of the water and oil phases, as well as the boundaries and coupling conditions.

The initial condition (IC) reflects the pressure distribution at the initial time along the reservoir. The internal boundary (IBC) indicates how the water is injected during the test, which, in this case, will be a constant flow rate. The external boundary condition (EBC) is relative to the flow behavior at the reservoir extreme limit. As it is considered a laterally infinite reservoir, that is, the reservoir boundaries, represented by the EBC, will not affect the well pressure response during the test time. The mathematical formulation was developed based on a consistent unit system.

Considering a piston-like fluid displacement, the fluid mobility (\(\hat{\lambda _i}\)), hydraulic diffusivity (\(\eta _i\)) and the derived fractional flow (\(f'_w\)) are defined by:

$$\begin{aligned} \eta _{ji}&= \frac{k_jk_{rji}}{\phi \mu _{ji}c_t} \end{aligned}$$
(1)
$$\begin{aligned} \hat{\lambda }_{ji}&= \frac{k_jk_{rji}}{\mu _{ji}} \end{aligned}$$
(2)
$$\begin{aligned} f'_w&= \frac{1}{1-S_{\mathrm{or}}-S_{\mathrm{wi}}} \end{aligned}$$
(3)

The layer properties will be indicated by indices ji, where j represents the layer and i the region. Therefore, \(k_j\) is the layer permeability, and \(k_{rji}\) is the relative permeability of the fluid.

Using the Buckley-Leverett formulation (Buckley and Leverett 1942), the water front radius (\(r_\mathrm{F}\)) is defined by:

$$\begin{aligned} r_{\mathrm{F}j}(t)=\sqrt{(r_w)^2+\frac{v_{\mathrm{inj}_j}(t)}{24\phi h_j}f'_w} \end{aligned}$$
(4)

where \(v_{\mathrm{inj}_j}\) is the water volume injected into each layer.

$$\begin{aligned} v_{\mathrm{inj}_j}(t)=\int _{0}^{t} q_{\mathrm{inj}}(t') \,\mathrm{d}t' \end{aligned}$$
(5)

Thus, the following equations model the problem:

Region 1:

PDE:

$$\begin{aligned} \frac{\partial }{\partial r} \bigg ( r\frac{\partial p_{j1}(r,t)}{\partial r} \bigg ) = \frac{1}{\eta _{j1}}\frac{\partial p_{j1}(r,t)}{\partial t} \end{aligned}$$
(6)

IC:

$$\begin{aligned} p_{j1}(r,t=0)=p_i \end{aligned}$$
(7)

IBC:

$$\begin{aligned} q_{j1}=-2\pi \hat{\lambda }_{j1}h_j \bigg (r \frac{\partial p_{j1}(r,t)}{\partial r} \bigg ) \bigg |_{r=r_w} \end{aligned}$$
(8)

Region 2:

PDE:

$$\begin{aligned} \frac{\partial }{\partial r} \bigg ( r\frac{\partial p_{j2}(r,t)}{\partial r} \bigg )= \frac{1}{\eta _{j2}}\frac{\partial p_{j2}(r,t)}{\partial t} \end{aligned}$$
(9)

IC:

$$\begin{aligned} p_{j2}(r,t=0)=p_i \end{aligned}$$
(10)

EBC:

$$\begin{aligned} \lim _{r \rightarrow \infty }p_{j2}(r,t) = p_i \end{aligned}$$
(11)

The relations between the regions and layers are expressed by the coupling conditions. The pressure and flow-rate equalities in each region at the interface between them, that is, at the water front radius (\(r_\mathrm{F}\)), represent the coupling conditions by region (CCR) (Nie et al. 2011, 2019). This condition is defined as:

CCR:

$$\begin{aligned} \left\{ \begin{matrix} p_{j1}(r_{\mathrm{F}j},t)= p_{j2}(r_{\mathrm{F}j},t) \\ q_{j1}(r_{\mathrm{F}j},t)=q_{j2}(r_{\mathrm{F}j},t) \end{matrix}\right. \end{aligned}$$
(12)

Applying Darcy’s law to compute the flow-rate in each region:

$$\begin{aligned} 2\pi \hat{\lambda }_{j1} h_j\left( r\frac{\partial p_{j1}}{\partial r}\right) \bigg |_{r=r_{\mathrm{F}j}}=2\pi \hat{\lambda }_{j2}h_j\left( r\frac{\partial p_{j2}}{\partial r}\right) \bigg |_{r=r_{\mathrm{F}j}} \end{aligned}$$
(13)

As one can see, both, water and oil rates are considered the same; however, it is only an approximation that can be applied in a piston-like problem.

Therefore,

$$\begin{aligned} \left( r\frac{\partial p_{j1}}{\partial r}\right) \bigg |_{r=r_{\mathrm{F}j}}=\frac{\hat{\lambda }_{j2}}{\hat{\lambda }_{j1}}\left( r\frac{\partial p_{j2}}{\partial r}\right) \bigg |_{r=r_{\mathrm{F}j}} \end{aligned}$$
(14)

Equations (13) and (14) refer only to the flow-rate CCR (12).

Since the considered reservoir model assumes that layers have no connection to each other except by the wellbore, the coupling condition by layers (CCL) is given by the pressure equality and the principle of mass conservation at this same point as shown below:

CCL:

$$\begin{aligned} \left\{ \begin{matrix} p_{j,1}(r_w,t)= p_{j+1,1}(r_w,t) \\ q_{\mathrm{inj}}=\sum \limits _{j=1}^{n}q_{j1}(r_w,t) \end{matrix}\right. \end{aligned}$$
(15)

Bringing the equations to Laplace domain:

Region 1:

PDE:

$$\begin{aligned} \frac{1}{r}\frac{\partial }{\partial r} \left( r\frac{\partial \bar{p}_{j1}}{\partial r} \right) = \frac{1}{\eta _{j1}}(u\bar{p}_{j1}(r,u)-p_{j1}(r,t=0)) \end{aligned}$$
(16)

Applying the Laplace transform in Eqs. (6) to (11) and applying the IC (given by Eqs. (7) and (10)), the following ordinary differential equation for Region 1 is obtained:

ODE:

$$\begin{aligned} \frac{\partial ^2 \bar{p}_{j1}(r,u)}{\partial r^2}+\frac{1}{r}\frac{\partial \bar{p}_{j1}(r,u)}{\partial r}=\frac{1}{\eta _{j1}}(u\bar{p}_{j1}(r,u)-p_i) \end{aligned}$$
(17)

IBC:

$$\begin{aligned} \bigg (r \frac{\partial \bar{p}_{j1}(r,t)}{\partial r} \bigg ) \bigg |_{r=r_w}=\frac{-2\hat{\lambda }_{j1}h_j}{q_{j1}}\frac{1}{u} \end{aligned}$$
(18)

Region 2:

ODE:

$$\begin{aligned} \frac{\partial ^2 \bar{p}_{j2}(r,u)}{\partial r^2}+\frac{1}{r}\frac{\partial \bar{p}_{j2}(r,u)}{\partial r}=\frac{1}{\eta _{j2}}(u\bar{p}_{j2}(r,u)-p_i) \end{aligned}$$
(19)

EBC:

$$\begin{aligned} \lim _{r \rightarrow \infty }\bar{p}_{j2}(r,u)=\frac{p_i}{u} \end{aligned}$$
(20)

The pressure change in Laplace domain may be defined as \(\varDelta \bar{p}(r,u)=\frac{p_i}{u}-\bar{p}(r,u)\) and \(\frac{\partial \bar{p}}{\partial r}=-\frac{\partial \varDelta \bar{p}}{\partial r}\). Thus, applying this definition for pressure change in Eqs. (16) to (20), the following equations are obtained:

Region 1:

ODE:

$$\begin{aligned} \frac{\partial ^2 \varDelta \bar{p}_{j1}}{\partial r^2}+\frac{1}{r}\frac{\partial ^2 \varDelta \bar{p}_{j1}}{\partial r}-\frac{u}{\eta _{j1}}\varDelta \bar{p}_{j1}=0 \end{aligned}$$
(21)

IBC:

$$\begin{aligned} \bigg (r \frac{\partial \varDelta \bar{p}_{j1}}{\partial r} \bigg ) \bigg |_{r=r_w}=\frac{-q_{j1}}{2\pi \hat{\lambda }_{j1}h_j}\frac{1}{u} \end{aligned}$$
(22)

Region 2:

ODE:

$$\begin{aligned} \frac{\partial ^2 \varDelta \bar{p}_{j2}}{\partial r^2}+\frac{1}{r}\frac{\partial ^2 \varDelta \bar{p}_{j2}}{\partial r}-\frac{u}{\eta _{j2}}\varDelta \bar{p}_{j2}=0 \end{aligned}$$
(23)

EBC:

$$\begin{aligned} \lim _{r \rightarrow \infty }\varDelta \bar{p}_{j2}(r,u)=0 \end{aligned}$$
(24)

Besides that, the coupling conditions in the Laplace domain are shown as:

CCR:

$$\begin{aligned} \left\{ \begin{matrix} \varDelta \bar{p}_{j1}(r_{\mathrm{F}j},u)=\varDelta \bar{p}_{j2}(r_{\mathrm{F}j},u) \\ \left( r\frac{\partial \varDelta \bar{p}_{j1}}{\partial r}\right) \bigg |_{r=r_{\mathrm{F}j}}=\frac{\hat{\lambda }_{j2}}{\hat{\lambda }_{j1}}\left( r\frac{\partial \varDelta \bar{p}_{j2}}{\partial r}\right) \bigg |_{r=r_{\mathrm{F}j}} \end{matrix}\right. \end{aligned}$$
(25)

CCL:

$$\begin{aligned} \left\{ \begin{matrix} \varDelta \bar{p}_{j,1}(r_w,u)=\varDelta \bar{p}_{j+1,1}(r_w,u) \\ \frac{q_{\mathrm{inj}}}{2\pi u\sum \limits _{j=1}^{n}\hat{\lambda }_{j1}h_j}=-\sum \limits _{j=1}^{n}\left( r\frac{\partial \varDelta \bar{p}_{j1}}{\partial r}\right) \bigg |_{r=r_w} \end{matrix}\right. \end{aligned}$$
(26)

The pressure solution for any layer j and region i in Laplace domain is:

$$\begin{aligned} \varDelta \bar{p}_{ji}=A_{ji}K_0\left( r\sqrt{\frac{u}{\eta _{fj}}}\right) +B_{ji}I_0\left( r\sqrt{\frac{u}{\eta _{fj}}}\right) \end{aligned}$$
(27)

where \(A_{ji}\) and \(B_{ji}\) are coefficients to be determined. It is also known by the Bessel functions properties (Abramowitz and Stegun 1964) that:

$$\begin{aligned}&\lim _{r \rightarrow \infty }K_0(r)=0 \end{aligned}$$
(28)
$$\begin{aligned}&\lim _{r \rightarrow \infty }I_0(r)=\infty \end{aligned}$$
(29)

Thus, to satisfy the external boundary condition of Region 2 given by Eq. (24), \(B_{j2}\) must be zero. Consequently, the pressure solution for i = 2 is:

$$\begin{aligned} \varDelta \bar{p}_{j2}=A_{j2}K_0\left( r\sqrt{\frac{u}{\eta _{j2}}}\right) \end{aligned}$$
(30)

By the IBC (22) and the flow-rate CCL (26):

$$\begin{aligned} \sum \limits _{j=1}^{n}\bigg (r \frac{\partial \varDelta \bar{p}_{j1}}{\partial r} \bigg ) \bigg |_{r=r_w}=-\frac{q_{\mathrm{inj}}}{2\pi \sum \limits _{j=1}^{n}(\hat{\lambda }_{j1}h_j)}\frac{1}{u} \end{aligned}$$
(31)

Thus, deriving the Eq. (27) with respect to \(r=r_w\) may be combined with Eq. (31):

$$\begin{aligned}&\sum \limits _{j=1}^{n} \sqrt{\frac{u}{\eta _{j1}}}\left( A_{j1}K_1\left( r_w\sqrt{\frac{u}{\eta _{j1}}}\right) -B_{j1}I_1\left( r_w\sqrt{\frac{u}{\eta _{j1}}}\right) \right) \nonumber \\&\quad =\frac{1}{r_w}\frac{q_{\mathrm{inj}}}{2\pi \sum \limits _{j=1}^{n}(\hat{\lambda }_{j1}h_j)}\frac{1}{u} \end{aligned}$$
(32)

Replacing the pressure solutions for Region 1 (27) in the corresponding CCL (26):

$$\begin{aligned}&A_{j1}K_0\left( r_w\sqrt{\frac{u}{\eta _{j1}}}\right) +B_{j1}I_0\left( r_w\sqrt{\frac{u}{\eta _{j1}}}\right) \nonumber \\&\quad =A_{j+1,1}K_0\left( r_w\sqrt{\frac{u}{\eta _{j+1,1}}}\right) +B_{j+1,1}I_0\left( r_w\sqrt{\frac{u}{\eta _{j+1,1}}}\right) \end{aligned}$$
(33)

On the other hand, from Eqs. (25) and (27), the following expression for the flow-rate CCR is obtained:

$$\begin{aligned}&A_{j1}K_1\left( r_{\mathrm{F}j}\sqrt{\frac{u}{\eta _{j1}}}\right) -B_{j1}I_1\left( r_{\mathrm{F}j}\sqrt{\frac{u}{\eta _{j1}}}\right) \nonumber \\&\quad =\frac{\hat{\lambda }_{j2}}{\hat{\lambda }_{j1}}\sqrt{\frac{\eta _{j1}}{\eta _{j2}}}A_{j2}K_1\left( r_{\mathrm{F}j}\sqrt{\frac{u}{\eta _{j2}}}\right) \end{aligned}$$
(34)

The last condition to be applied to this model is the pressure CCR (25). Therefore, combining the pressure solutions (27) and (30):

$$\begin{aligned} A_{j1}K_0\left( r_{\mathrm{F}j}\sqrt{\frac{u}{\eta _{j1}}}\right) +B_{j1}I_0\left( r_{\mathrm{F}j}\sqrt{\frac{u}{\eta _{j1}}}\right) =A_{j2}K_0\left( r_{\mathrm{F}j}\sqrt{\frac{u}{\eta _{j2}}}\right) \end{aligned}$$
(35)

The equations of hydraulic diffusivity, boundary conditions and coupling conditions of each region and layer provide a linear system that models this problem in the Laplace domain. The following equality represents this system:

$$\begin{aligned} M\left[ \begin{array}{cc} A_{11} \\ B_{11} \\ A_{12} \\ A_{21} \\ B_{21}\\ A_{22} \end{array}\right] =\left[ \begin{array}{cc} \frac{1}{r_w}\frac{q_{\mathrm{inj}}}{2\pi \sum \limits _{j=1}^{2}(\hat{\lambda }_{j1}h_j)}\frac{1}{u} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}\right] \end{aligned}$$
(36)

where M is a linear system in matrix form composed of Eqs. (32), (33), (34) and (35). Equation (32) represents the coefficients of the well pressure equation. Equation (33) expresses the coupling condition between layers and Eqs. (34) and (35) express, respectively, the flow-rate and pressure coupling conditions between regions of both layers.

For a better understanding, the matrix M was divided into two parts, as shown below. The first part consists of its first three columns and the second one by its last three.

$$\begin{aligned} \left| \begin{array}{c c c} \sqrt{\frac{u}{\eta _{11}}}K_1\left( r_w\sqrt{\frac{u}{\eta _{11}}}\right) &{} -\sqrt{\frac{u}{\eta _{11}}}I_1\left( r_w\sqrt{\frac{u}{\eta _{11}}}\right) &{} 0\\ \\ K_0\left( r_w\sqrt{\frac{u}{\eta _{11}}}\right) &{} I_0\left( r_w\sqrt{\frac{u}{\eta _{11}}}\right) &{} 0\\ \\ K_1\left( r_{\mathrm{F}1}\sqrt{\frac{u}{\eta _{11}}}\right) &{} -I_1\left( r_{\mathrm{F}1}\sqrt{\frac{u}{\eta _{11}}}\right) &{} -\frac{\hat{\lambda }_{12}}{\hat{\lambda }_{11}}\sqrt{\frac{\eta _{11}}{\eta _{12}}}K_1\left( r_{\mathrm{F}1}\sqrt{\frac{u}{\eta _{12}}}\right) \\ \\ K_0\left( r_{\mathrm{F}1}\sqrt{\frac{u}{\eta _{11}}}\right) &{} I_0\left( r_{\mathrm{F}1}\sqrt{\frac{u}{\eta _{11}}}\right) &{} -K_0\left( r_{\mathrm{F}1}\sqrt{\frac{u}{\eta _{12}}}\right) \\ \\ 0 &{} 0 &{} 0\\ \\ 0 &{} 0 &{} 0 \end{array}\right| \end{aligned}$$
(37)

Thus, the last three columns of matrix M are represented by:

$$\begin{aligned} \left| \begin{array}{c c c} \sqrt{\frac{u}{\eta _{21}}}K_1\left( r_w\sqrt{\frac{u}{\eta _{21}}}\right) &{} -\sqrt{\frac{u}{\eta _{21}}}I_1\left( r_w\sqrt{\frac{u}{\eta _{21}}}\right) &{} 0 \\ \\ -K_0\left( r_w\sqrt{\frac{u}{\eta _{21}}}\right) &{} -I_0\left( r_w\sqrt{\frac{u}{\eta _{21}}}\right) &{} 0\\ \\ 0 &{} 0 &{} 0\\ \\ 0 &{} 0 &{} 0\\ \\ K_1\left( r_{\mathrm{F}2}\sqrt{\frac{u}{\eta _{21}}}\right) &{} -I_1\left( r_{\mathrm{F}2}\sqrt{\frac{u}{\eta _{21}}}\right) &{} -\frac{\hat{\lambda }_{22}}{\hat{\lambda }_{21}}\sqrt{\frac{\eta _{21}}{\eta _{22}}}K_1\left( r_{\mathrm{F}2}\sqrt{\frac{u}{\eta _{22}}}\right) \\ \\ K_0\left( r_{\mathrm{F}2}\sqrt{\frac{u}{\eta _{21}}}\right) &{} I_0\left( r_{\mathrm{F}2}\sqrt{\frac{u}{\eta _{21}}}\right) &{} -K_0\left( r_{\mathrm{F}2}\sqrt{\frac{u}{\eta _{22}}}\right) \end{array}\right| \end{aligned}$$
(38)

Therefore, once the coefficients \(A_{11}\) and \(B_{11}\) were determined, it is concluded that in Laplace domain, the well pressure solution is calculated by:

$$\begin{aligned} \varDelta \bar{p}_{wf}=A_{11}K_0\left( r_w\sqrt{\frac{u}{\eta _{11}}}\right) +B_{11}I_0\left( r_w\sqrt{\frac{u}{\eta _{11}}}\right) \end{aligned}$$
(39)

The well pressure profile given by Eq. (39) is then converted to real domain through Stehfest Algorithm (Stehfest 1970).

Results

The accuracy of the analytical model detailed in “Conceptual model” section was determined by comparison with a commercial flow simulator (von Hohendorff Filho 2004). The curves of pressure (\(\varDelta P\)) and pressure derivative with respect to the natural logarithm of time (\(\varDelta P'\)) were plotted on log-log graphs functions of time. After the proposed solution was validated, a sensitivity study was performed, evaluating the influence of oil viscosity and injection flow-rate in the computed pressure response.

Model validation

The endpoint mobility ratio is a ratio between the mobility of the fluids under discussion. It is a critical factor to influence flooding efficiency of the water in the reservoir. When the endpoint mobility ratio is greater than one, it means the water is more mobile than oil. Otherwise, it means the water is less mobile than oil, leading to a better sweep efficiency. Thus, the mobility ratio is defined by:

$$\begin{aligned} {\hat{M}}=\frac{\hat{\lambda }_{w}}{\hat{\lambda }_{o}} = \frac{\mu _o}{\mu _w} \end{aligned}$$
(40)

The results are divided into two cases, considering different mobility ratios. However, despite being different, for each case, the fluid viscosities do not change in time, so the fluid mobility remains constant. In addition, as the model assumes a piston-like fluid displacement, the fluid mobility behind and ahead of \(r_\mathrm{F}\) is equal to the water and oil mobility, respectively.

The reservoir properties for both cases as well as the injection flow-rate are shown in Table 1. Meanwhile, the fluid viscosities for Cases 1 and 2 can be seen in Tables 2 and 3, respectively. Also, it was considered a 96-h flow period on both cases and the value of the water front radii \(r_{\mathrm{F}1}\) and \(r_{\mathrm{F}2}\) at the last time step were both equal to 21.65 m. It should be noted that the viscosity and permeability do not appear in Eq. (4), and as the only difference between Cases 1 and 2 is the oil viscosity, as well as the only difference between layers is the permeability, the water front radii is the same for all situations.

Table 1 Input data for both cases
Full size table
Table 2 Fluid properties in Case 1
Full size table
Table 3 Fluid properties in Case 2
Full size table

In Case 1, a 5 cP oil viscosity was tested, leading to a high mobility ratio and a better movement of the water, although not a great sweep efficiency in moving the oil along the radius of the reservoir. In Case 2, a lower oil viscosity was tested, leading to a mobility ratio lower than in Case 1 and consequently a better scenario to the sweep efficiency.

Figures 3 and 4 show the pressure and derivatives curves considering both the analytical solution and numerical data for Cases 1 and 2. A slight deviation between the curves at the short time can be observed due to the simulation grid refinement causing this line spacing can be observed. Besides that, in both cases, it is possible to notice the proximity of the results showing a good agreement between the models.

Fig. 3
figure 3

Pressure and pressure derivative data for Case 1

Full size image
Fig. 4
figure 4

Pressure and pressure derivative data for Case 2

Full size image

In addition, this refinement problem appears to be more sensitive in Case 1, even for a long time. It can be explained by the water front behavior, i.e., piston-like and due to its mobility ratio, since it is higher than one and greater than Case 2, leading to a more unstable displacement.

It is also observed that the derivative starts at a certain level and then stabilizes at another one, which is the same for both cases, even though the oil viscosity is different. This can be explained by the fact that in an injectivity test, the first level of the pressure derivative curve represents the oil mobility, while the second represents the water mobility. Thus, since the properties of the injected water are the same for Cases 1 and 2, the second derivative level is expected to be the same in both graphs.

Sensitivity analysis

In order to analyze the proposed solution with different scenarios, the pressure and pressure derivative over time were plotted, in five different oil viscosities (maintaining the injection rate at 1400 \(\text {m}^3\text {/day}\)) as shown in Fig. 5.

The pressure derivatives for different oil viscosities in Fig. 5 converge to the same level, as well as Figs. 3 and 4. The reason behind this behavior is the same as mentioned in “Model validation” section. As the oil viscosities are different for each curve and the first level of the pressure derivative curves represents the oil mobility, their initial level is not the same. However, as the properties of the injected water remain the same, the second level of all curves converges to a single threshold.

It is also possible to notice that the pressure curves rise as the oil viscosity increases. This is due to the fact that the higher the oil viscosity, the more distant it is from the water viscosity, and therefore, it departs from the 0.5 cP level. When oil and water viscosities are the same, pressure derivative remains constant during the entire test, since there is no difference between fluid mobilities.

Fig. 5
figure 5

Pressure and pressure derivative for different oil viscosities

Full size image

Figure 6 displays the variation of injection rate maintaining the same oil viscosity as Case 1. Figure 7, on the other hand, enables easy visualization of the difference between the behavior of each scenario, once it shows the normalized pressure and pressure derivative data. The normalized pressure is given by each pressure divided by its injection rate versus time. Thus, pressure derivative is also normalized by the injection flow-rate.

Fig. 6
figure 6

Pressure and pressure derivative for different injection flow-rates

Full size image
Fig. 7
figure 7

Normalized pressure and pressure derivative data for different injection flow-rates

Full size image

The drop of the pressure derivative curves indicates the transition between the oil properties region and the water properties region. Thus, looking at those same curves in Fig. 7, it is noticed that as the injection flow-rate changes, the pressure drop speed behavior behaves differently. This is due to the fact that with a lower injection rate, it takes longer for the water bank around the wellbore to become relevant, which means that pressure change will reflect water properties. However, considering the normalized pressure derivative data, all curves achieve the same level once the transition regime is over.

Fig. 8
figure 8

Region 1 composite radii data for different injection flow-rates

Full size image

As mentioned in “Mathematical formulation” section, the water front radius is defined by Eq. 4. Figure 8 presents the resulting curves for one layer varying the injection rate and maintaining the data from Case 1. For a specific moment, it is expected a greater advance in the water front radius as the flow-rate increases, since the fluid occupies a larger volume in less time. Furthermore, it is understood that for two or more layers with equal properties and injection rate, the behavior of the curves must be the same.

Conclusion and further discussions

Based on the solution for pressure change during injectivity tests in single-layer reservoir, it was possible to develop a formulation to a multilayered reservoir. The proposed multilayer solution uses coupling conditions between layers and between regions to build the linear system that must be solved to determine the pressure change.

The comparison between the numerical model and the analytical model developed in this work shows the proximity of the results and accuracy of the solution, once both tested cases obtained a good agreement with the numerical simulator.

The sensitivity study was done comparing the results considering different oil viscosities and injection flow-rates. From this sensitivity study, it was possible to notice how these parameters influence the pressure response and pressure derivative.

Thereby, this work presents a new and accurate solution for pressure response during a water injection well testing in a way that is possible to evaluate the wellbore pressure response.

Although the work presents the application in a reservoir with two layers, the solution may be extended to an arbitrary number of layers. This interpretation was possible considering an infinite reservoir with the boundary conditions not affecting the pressure behavior. However, the model can be adapted to different boundary conditions, for that the definition made on EBC (11) must be modified.

It is also possible to consider the skin distribution by adding a new region into the model. Thereby, it will be considered a model with three regions in which the first one, closest to the well, will be the skin region. The solution follows the one previously presented; in this regard, there will be a hydraulic diffusivity equation (\(\eta _s\)) and a fluid mobility (\(\lambda _s\)) for the skin region.

Furthermore, a wellbore storage coefficient (C) may be added to the model in order to include this phenomenon using the following relation (Everdingen and Hurst 1949; Ehlig-Economides and Joseph 1987):

$$\begin{aligned} \varDelta {\bar{p}}_{wf} = \frac{\varDelta \bar{p}_{wf}(u,C=0)}{1+u^2C\varDelta {\bar{p}}_{wf}(u,C=0)} \end{aligned}$$
(41)