Introduction

Every year, numerous hazardous dyes are released into the environment from a variety of sectors, which modifies the physicochemical characteristics of surface water, impedes the process of photosynthesis by lowering the permeability of sunlight, thus affecting aquatic eco-systems. Due to the complicated molecular structures and limited biodegradability of the dyes, treating dye effluent from the textile and dyestuff industries considered difficult. The negative impact does only involve the environment but also extends to humain health with reported carcinogenic and mutagenic properties (Sheshdeh et al. 2014; Lellis et al. 2019; Yang et al. 2021). Consequently, before wastewater was released, it was required to reduce or remove these dyes.

Basic Red 46 dye (BR 46) was an industrial dye and more used in textile industry. Consequently, before wastewater was released, it was required to reduce or remove these dyes. Additionally, several methods for color removal from wastewater included membrane separation, plasma technology, thermal and catalytic oxidation with potential heat recovery. (Özcan et al. 2006). The adsorption techniques, on the other hand, were the most successful methods due to their ease of use, affordability, and toxicity-insensitivity (Tanyildizi 2011). Furthermore, they don't affect the water's quality and don't produce degrading pollutants (Mittal 2006).

In recent years, several adsorbents have been employed to extract BR 46 from wastewater such as: olive–pomace (Graba et al. 2022), pomegranate peels (Akkari et al. 2022, 2023), active clay (Elhadj et al. 2020), moroccan clay (Karim et al. 2009), carbon and silica based composite(Małgorzata Wisniewska 2022), natural clay (Paredes-Quevedo et al. 2021), raw and purified clay (Karim et al. 2017), rough and treated algerian natural phosphates (Graba et al. 2015), crude P.mutilus biomass (Yeddou Mezenner et al. 2013), nickel oxidenanoparticlesmodified diatomite (Samarghandi et al. 2020), gypsum (Deniz and Saygideger 2010), biocharramatstraw (Yang et al. 2021). Unfortunately, these adsorbents often have low adsorption capabilities. Finding novel, readily accessible, and affordable adsorbents was therefore necessary (Srinivasan and Viraraghavan 2010).

A significant amount of waste or by-product containing P.mutilus biomass was produced by the antibiotic fermentation factory in Algeria and was burned and dumped into the ecosystem. After receiving the proper treatments, this surplus burned byproduct biomass was employed to remove BR 46 from an aqueous solution.

The purpose of this study was to investigate the ability of pyrolyzed by-product biomass to enhance the remediation dye-laden waters, particularly BR 46. This technique could be extended to other biomasses to increase their dye adsorption capacity.The pyrolyzed by-product biomass was firstly well characterized, and then a research how the operational parameters affected the BR 46 adsorption capacity by the pyrolyzed by-product biomass. Kinetic and adsorption isotherm tests were carried out. This study also included a thermodynamic analysis.

Materials and methods

Adsorbent preparation

From the SAIDAL antibiotic manufacturing complex in Medea(Algeria), biomass containing P. mutilus was obtained as a by-product. This by-product was properly cleaned twice: once with tap water and once with distilled water. It was then dried for 24 h at 60 °C in an oven. Biomass pyrolysis tests were carried out beforehand for a fixed time of 4 h and at a variable temperature sous atmosphere d’azote until a constant mass of adsorbent is obtained. Under these conditions, the time (4 h) and temperature (350 °C) were chosen for the pyrolysis of our biomass after the pyrolyzed by-product was manually ground, sieved and ground to a size range of 100–200 µm.

Specific area of the pyrolyzed by-product biomass

The specific area of the pyrolyzed by-product biomass was measured using HORIBA Laser scatteringparticle size distribution analyzer(LA-960). The density was identified with gas Pycnometer -MICROMETRICS (Accupyc II 1340).

S is the pyrolyzed by-product biomass specific area (m2/g).

ρ is the density (g/cm3)

with ρ = 2.42 g/cm3 and S = 0.26 m2/g

Table 1 is a summary of the physicochemical characteristics of the adsorbent.

Table 1 Physico-chemicalcharacteristics of the adsorbent
Full size table

BR 46 stock solution preparation

BR 46 used in this study was obtained from local textile factory(Algiers, Algeria) and was of commercial quality. The structure of BR46 and their properties was given in Table 2. To obtain suitable concentrations, stock solutions of 1 g/L of BR 46 in distillated water were prepared.

Table 2 Properties of BR 46
Full size table

Adsorbent characterization

Pyrolyzed by-product biomass (adsorbent) analysis

The FEI Quanta 600 (scanning electron microscopy (SEM)), in conjunction with the energy-dispersive X-ray (EDX) (Software: xTm version 3.0.13), was used to examine the adsorbent surface and as certain its chemical composition.

Micro-X-ray fluorescence (µXRF) (HORIBA, model: XGT5000 (Voltage:50 kV, Resolution:100 µm)) was used to analyze the element identification of pyrolyzed by-product biomass.

The most important chemical groups present at the pyrolyzed biomass surface were identified using a Shimadzu spectrophotometer model (FTIR-84004 cm−1 resolution in the frequency range 400–4000 cm−1. The samples were made into pellets using KBr.

Using a Setaram TG-ATD Labsysthermique and static air, the by-product biomass was put through to a thermal gravimetric analysis (TGA).

Determination of zero point charge

The pHzpc(zero charge point) was obtained when positively and negatively charged centers were equally distributed across the particle external surface. In order to obtain pHzpc,0.1 g of adsorbent has been introduced to 50 mL solution of KNO3 (0.01 M) and the initial pH of the KNO3-adsorbent solution was varied with 0.1 M HCl or 0.1 M NaOH solutions. At room temperature, the container was closed and agitated for 48 h and the final pH measured. The zero charge point(pHzpc) was the pH value at which the pHinitial–pHfinal = f (pHinitial) curve crosses the axis carrying pHinitial(Gorgievski et al. 2013; Blanes et al. 2016).

Batch adsorption experiment

The adsorption experiments were conducted in a batch system. A constant quantity of adsorbent (PS:150 µm) was added to 50 ml of dye solution in an erlenmeyer flask at room temperature (20 °C) for each adsorption test and agitated with a mechanical shaker (Fisher Scientific, heating magnetic stirrer) at 250 rpm. Solution pH value was kept constant during the entire experiments. NaOH or HCl (0.1 M) were used to adjust solution pH. At the end of the experiments, the mixtures have been centrifuged at 2500 rpm for 15 min. The supernatant were then filtered through 0.45 µm filters. The dye concentrations samples were measured using a UV–visible spectrophotometer (UV mini-1240) at 530 wavelengths.

The solution pH effect on the adsorbed quantity was determined by varying the solution pH between 2 and 10 under the following operating conditions (adsorbent concentration 1 g/L, BR46 concentration 20 mg/L, contact time 180 min).

By varying the concentration of our pyrolyzed by-product biomass at 0.2, 0.5, 1, 2, 3, 4, 5, 6, 7, and 10 g/L and under the following conditions, optimum pH of 7.5, BR 46 initial concentration of 20 mg/L and contact time of 180 min the impact of the adsorbent concentration has been examined,

The kinetic analysis was done using the prescribed conditions (BR 46 intial concentration = 20 mg/L, optimal pH = 7.5, optimal pyrolyzed by-product biomass concentration = 1 g/L). Experiments were conducted at various contact times: 5, 10, 20, 30, 40, 50, 60, 90, 120, 150, and 180 min in order to determine the optimal contact time to achieve BR 46 adsorption equilibrium.

To achieve the adsorption isotherm, the BR 46 concentration was changed between 5 and 400 mg/L under the following conditions: optimized pH = 7.5, optimized pyrolyzed by-product biomass concentration = 1 g/L, and contact period 180 min. The effect of the initial BR 46 concentration on the BR 46 adsorption capacity by pyrolyzed by-product biomass was assessed.

Utilizing an isothermal water bath set at 20 °C, 30 °C and 40 °C under the following conditions (optimal pH = 7.5, optimal pyrolyzed by-product biomass concentration = 1 g/L, BR46 initial concentration = 20 mg/L, contact time = 180 min), the temperature influence on the pyrolyzed by-product biomass adsorption capacity was studied.

Three repeats of each test were conducted. The average results were given. The BR46 quantity adsorbed by the adsorbent qt (mg/g) at specified time interval (t) was determined using the following Eq. (1):

$$q_{{\text{t}}} = \left( {C_{0} {-}C_{{\text{t}}} } \right)/\left( {C_{{\text{b}}} } \right)$$
(1)

where

Co is the initial BR46 concentration (mg/L)

Ct is the B46 concentration at time t (mg/L)

Cb is the pyrolyzed by-product biomass or adsorbent concentration (g/L)

qt is the instantaneous adsorption capacity (mg/g)

Equation below was used to get the dye adsorption capacity at equilibrium qe (mg/g):

$$q_{{\text{e}}} \, = \,\left( {C_{0} {-}C_{{\text{e}}} } \right)/\left( {C_{{\text{b}}} } \right)$$
(2)

where

Ce is the BR46 concentration at equilibrium (mg/L).

qe is the adsorption amount at equilibrium (mg/g).

Biosorption kinetic models

Four kinetic models pseudo-first-order, Elovich, pseudo-second-order and Ritchie have been used to describe the experimental kinetic data.

Pseudo-first order (PFO)

The pseudo-first-order (PFO) model was shown in its nonlinear version by the equation below: (Labiod et al. 2022).

$${q}_{{\text{t}}}={q}_{{\text{e}}1}\left[1-{\text{exp}}\left({k}_{1}t\right)\right]$$
(3)

k1 is the PFO rate constant (min−1) and qe1 is the adsorption amount (mg/g) at equilibrium obtained from the PFO model.

Pseudo-second order (PSO)

A pseudo-second-order (PSO) equation's in nonlinear form was given by the relationship below (Labiod et al. 2022).

$${q}_{{\text{t}}}=\frac{{q}_{{\text{e}}2}^{2}\bullet {k}_{2}t}{\left[{k}_{2}\bullet \left({q}_{{\text{e}}2}\right)\bullet t+1\right]}$$
(4)

where k2 is the rate constant(g/mg.min) and qe2 is the the adsorption amount (mg/g) at equilibrium obtained from the PSO model.

Elovich kinetic model

The Elovich kinetic model was applied to the study of the removal of contaminants from aqueous solutions as well as the chemisorption of gases onto heterogeneous surfaces and solid systems (Yuan et al. 2015). Although it shows second-order kinetics under the assumption that the solid surface contains heterogeneous energy, no adsorption mechanism was suggested. This model was utilized like (Qiu et al. 2009).

$$q\mathrm{t }=\frac{1}{\beta }{\text{ln}}(1 + \alpha \beta t)$$
(5)

In the Elovich model, α is the first rate constant (mg/g min) and β is the desorption constant throughout each experiment (mg/g).

Intraparticle diffusion model

The principal rate-controlling phase in the intraparticle diffusion model is intraparticle diffusion, which considers that film diffusion is negligible, especially in a batch reactor that is quickly agitated. The kinetic model below has been proposed by Weber and Morris to analyze intraparticle diffusion (Aravindhan et al. 2009).

$${q}_{{\text{t}}}={K}_{{\text{p}}}{{\text{t}}}^{1/2}+p$$
(6)

where:

kp is the rate of intraparticle diffusion constant (mg/g min1/2).

p is a constant that is related to the thickness of the boundary layer(mg/g).

Biosorption isotherms models

Different isotherm models (Temkin, Freundlich, Khan and Langmuir models) were explored in order to determine the most appropriate model fitting the equilibrium data.

Freundlich model

This model assumes that different energies will be used in adsorption process at various points of a heterogeneous surface of the adsorbent(Labiod et al. 2022). The Freundlich model's nonlinear Eq. (7) was written as follows:

$${q}_{{\text{e}}}={K}_{{\text{F}}}{{{\text{C}}}_{{\text{e}}}^\frac{1}{n}}$$
(7)

KF is the constant directly correlated with bonding energy (L/mg).

n is the factor of heterogeneity.

Langmuir model

Adsorption only occurs at specific localized spots on a material's surface. Based on the Langmuir model, only one molecule or atom can stay in each site, and saturation coverage corresponds to entire colonization of these sites. The energy distribution at the surface is uniform, and adsorbed molecules or atoms were adjacent to one another and do not come into contact(Labiod et al. 2022). The Langmuir model's nonlinear Eq. (8) was written as follows:

$${q}_{{\text{e}}}=\frac{{q}_{{\text{max}}}\bullet {K}_{{\text{L}}}\bullet {C}_{{\text{e}}}}{1+{K}_{{\text{L}}}\bullet {C}_{{\text{e}}}}$$
(8)

KL is the proportional constant to the adsorption energy (L/mg).

qmax is the maximum amount for adsorption (mg/g).

Temkin model

Indirect reactions between adsorbent and adsorbate were included in Temkin isotherm model. It is well known that as the system's surface area increases, the adsorption heating for each molecule in the layer decreases linearly (Labiod et al. 2022; Sahnoun et al. 2022). The Temkin model's nonlinear Eq. (9) was written as follows:

$${q}_{{\text{e}}}=\frac{{\text{RT}}}{{b}_{{\text{t}}}}\left({\text{ln}}{K}_{{\text{T}}}{C}_{{\text{e}}}\right)$$
(9)

bt is the factor related to adsorption heat (J/mol);

KT:is the isotherm constant (L/g);

T is the absolute temperature (K).

R is the ideal gas constant (8.314 J/mol K).

Khan model

For the adsorbate adsorption from pure solutions, the Khan model was a developed version of both the Freundlich and Langmuir models. This three-parameter isotherm model was created for adsorption processes for both single- and multi-component systems. The maximum adsorption values in this model may be accurately determined at very high correlation coefficients (Syafiuddin et al. 2018). The Khan model's nonlinear equation (Eq. (10)) was written as follows:

$${q}_{{\text{e}}}=\frac{{q}_{{\text{max}}}\bullet {K}_{{\text{k}}}\bullet {C}_{{\text{e}}}}{{\left(1+{K}_{{\text{K}}}\bullet {C}_{{\text{e}}}\right)}^{{n}_{k}}}$$
(10)

where the theoretical isotherm saturation capacity was represented by qmax (mg/g), the Khan isotherm model constant was denoted by KK, and the exponent of the Khan isotherm model was denoted by nK.

Thermodynamic study

The following equation can be used to relate the free energy of adsorption(\(\Delta\) G) to the equilibrium constant Keq (Liu 2009).

$$\Delta G= -RT {\text{ln}} {K}_{{\text{eq}}}$$
(11)

where Keq (dimensionless) is mathematically equivalent to KD (L/mol), the constant of the Langmuir model.

The formulas for calculating the change in entropy (\(\Delta\)S), change in enthalpy (\(\Delta\)H), and change in free energy (\(\Delta\)G) were given below.

$${\text{ln}}{K}_{{\text{eq}}} = (-\Delta H/{\text{RT}}) +(\Delta S/R )$$
(12)
$$\Delta G= \Delta H-T\times \Delta S$$
(13)

Statistic error functions

Nonlinear regression was used in this work to evaluate all model applicability. The statistical equations were utilized to assess the fit of the equation to the experimental data.

The statistical equations or functions used in this study were as follows

$${\mathrm{Chi square}(\chi }^{2})=\sum_{{\text{i}}=1}^{n}\frac{{\left({x}_{{\text{exp}}}-{x}_{{\text{model}}}\right)}_{i}^{2}}{{x}_{{\text{exp}}}}$$
(14)
$${\mathrm{Determination coefficient }(R}^{2})=\frac{\sum_{{\text{i}}=1}^{n}{\left({x}_{{\text{exp}}}-{\overline{x} }_{{\text{exp}}}\right)}_{i}^{2}-\sum_{i=1}^{n}{\left({x}_{{\text{exp}}}-{x}_{{\text{model}}}\right)}_{i}^{2}}{\sum_{{\text{i}}=1}^{n}{\left({x}_{{\text{exp}}}-{\overline{x} }_{{\text{exp}}}\right)}_{i}^{2}}$$
(15)
$$\mathrm{Residual Mean Squared Error }({\text{RMSE}})=\sqrt{\frac{1}{m-2}\sum_{i=1}^{n}{\left({x}_{{\text{exp}}}-{x}_{{\text{model}}}\right)}_{i}^{2}}$$
(16)
$$\mathrm{Average Relative Error}({\text{ARE}})=\frac{100}{m}\sum_{i=1}^{n}{\left|\frac{{x}_{{\text{exp}}}-{x}_{{\text{model}}}}{{x}_{{\text{exp}}}}\right|}_{{\text{i}}}$$
(17)

The experimental data's observation count is m.

xmodel is the value calculated from the model, xexp is the value obtained from the experimental data and \({\overline{x} }_{{\text{exp}}}\) is the experimental data's average value. The low value of RMSE and \(\chi 2\) and ARE and high value of R2 related to the model confirm the better the curve fitting.

Results and discussion

Characteristics of pyrolyzed by-product biomass

Scanning electron microscopy (SEM) and energy-dispersive X-ray (EDX) analysis of by-product biomass and pyrolyzed by-product biomass

SEM image of by-product biomass and pyrolyzed by-product biomass for (10 µm)of magnification (Fig. 1a and b) shows that the surfaces were smooth and had a lot of different-sized holes, which is an indication of the dye molecules being well absorbedAdditionally, the surface of the pyrolyzed by-product biomass (Fig. 1b) shows certain fractures and fissures that cause holes to develop, making the structure loose and boosting the phenomenon of diffusion toward the active areas.

Fig. 1
figure 1

SEM by-product biomass (a) and pyrolyzed by-product biomass (b)

Full size image

In general, pores are traps for pollutants present in water. These figures show the presence of pores, not their size. Other types of analysis are necessary to deduce the distribution of pore sizes present on the adsorbent and to be able to compare them with the size of the dye molecule. SEM analysis of our adsorbent after adsorption will not provide any further information on the adsorption mechanism.

The SEM–EDX analysis of the pyrolyzed by-product biomass showed the existence of magnesium,oxygen, calcium,chlore, sodium, and phosphore as well as the metallic elements (Si, Al, and Fe) (Table 2 and Fig. 2).The four macronutrients (P, Na, K and Ca) were typically found in mushrooms (Romanovskii and Martsul 2009; Zaker et al. 2019). The filtering agent used to remove Pleuromutilin, which contains silica from diatomaceous earth, is likely what caused the high quantity of silicium to be present.

Fig. 2
figure 2

SEM–EDX analysis of the pyrolyzed by-product biomass

Full size image

In addition, SEM–EDX analysis of the pyrolyzed by-product biomass (Table 3) illustrates that O and Si were the main elements of the pyrolyzed by-product biomass. We may make recommendations that the pyrolyzed by-product biomass was composed mainly of silica.

Table 3 SEM–EDX analysis of the pyrolyzed by-product biomass
Full size table

Thermogravimetric analysis

Figure 3 illustrates the thermogravimetric analysis of the biomass obtained as a by-product.

Fig. 3
figure 3

Thermogravimetric analysis of by-product biomass

Full size image

Figure 3 shows that the degradation of the by-product biomass takes place at temperatures between 25 and 350 °C. According to the breakdown of separate elements, The figure indicates four important stages. Rapid dehydration occurred during the first phase, which lasted from 25 to 150 °C. The second phase, which lasted from 150 to 200 °C, was accompanied by a loss of both free water and chemically bound water, which caused the organic components to dehydrate (Romanovskii and Martsul 2009). In the third stage, a modest quantity of light volatile chemical components are released when the by-product biomass's chemical structure starts to depolymerize and soften (200 °C–270 °C). Most reactive organic decomposition occurs in the third stage, sometimes referred to as the active stage. (Zaker et al. 2019). A severe decomposition of organic components was a characteristic of the fourth stage, which occurred between 270 °C and 350 °C degrees Celsius. After 350 °C, the mass loss plateau indicated that no substantial weight loss had occurred. (Yuvaraja et al. 2018).

We may estimate that the by-product biomass includes 98.1% mineral stuff, 1.4% water, and 0.5% organic matter.

MicroX-ray fluorescence (µXRF) of the pyrolyzed by-product biomass

Table 4 provides a summary of the analysis's (XRF) results.

Table 4 µXRF analysis of pyrolyzed by-product biomass both after and before BR 46 adsorption
Full size table

The table shows that pyrolysis does not affect the composition of the elements initially present in the biomass.

These Figs. 4 and 5 showed the µXRF analysis of pyrolyzed by-product biomass after and before adsorption.

Fig. 4
figure 4

µXRF analysis of pyrolyzed by-product biomass before adsorption

Full size image
Fig. 5
figure 5

µXRF analysis of pyrolyzed by-product biomass after adsorption

Full size image

(P, Si, Ti, Ca, K, Fe) may be found in the pyrolyzed by-product biomass as a result of these elements also being present in the by-product biomass. The fermenter's solution was filtered to recover this by-product biomass. The additives component that were introduced to the fermenter were based on these elements.

Point of zero charge (pHzpc)

Figure 6 illustrates the determination of the pHzpc. It has been found to be at 6.80.

Fig. 6
figure 6

Estimation of the pHzpc of the pyrolyzed by-product biomass

Full size image

Above pH 6.80, the surface of the pyrolyzed by-product biomass will be negatively charged, and below this pH, positively charged.

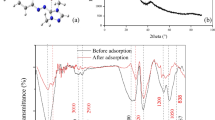
FTIR spectroscopy

The FTIR analysis was conducted with pyrolyzed by-product biomass before and after BR 46 adsorption to identify functional groups responsible of the BR 46 adsorption (Fig. 7).The band at 3500 cm−1 and 1500 cm−1 were due to (–OH) groups stretching band of the surface of silanolgroups(Wang et al. 2009) and of the adsorbed water molecules, respectively. The bands at 1100 cm−1 referred to siloxane vibrations of (SiO)n (Bois et al. 2003). It can be noted that the band located at 800 cm−1 and 500 cm−1 corresponds to Si–O–Si stretching band and the Si–O–Si bending band(Silva et al. 2009), respectively, attest the presence of silica.

Fig. 7
figure 7

Infrared spectrum of the pyrolyzed by-product biomass before and after BR 46 adsorption

Full size image

Figure 8 shows that there was no discernible difference in the FTIR spectra of the pyrolyzed by-product biomass before and after BR 46 adsorption. We may infer that the pyrolyzed by-product biomass' porosity structure and surface charge must be the most crucial factors in BR 46 adsorption.

Fig. 8
figure 8

pH effect on BR 46 adsorption (C0 = 20 mg/L,Cb = 1 g/L, T = 20 ± 2 °C, Contact time = 180 min, \(\omega\) = 250 rpm, PS: 150 µm)

Full size image

pH effect on the pyrolyzed by-product biomass adsorption capacity

The pH of the solution was one of the most significant variables affecting the adsorption phenomena. The influence of pH on the adsorption process was tested over a pH range of 2–10. Figure 8 shows that the amount of dye adsorbed on the pyrolyzed by-product biomass was closely related to the variation of the pH of the medium. BR46 elimination begin with a modest percentage and low pH levels, and then an increase in the amount adsorbed was observed with increasing pH, in excess of a maximum pH of 7.5. The maximum adsorbed amount at pH = 7.5 was about 17.5 (mg/g) of BR 46 per gram of pyrolyzed by-product biomass. Furthermore, The link between pH and the adsorption capacity of BR 46 may also be explained by the zero charge point (pHzpc) of the adsorbent. The zero charge point (pHzpc) of pyrolyzed by-product biomass was determined to be 6.8 (Fig. 6). When pH < pHzpc, we note that the surface of the pyrolyzed by-product biomass was positively charged and for pH > pHzpc it was negatively charged. Electrostatic attraction of the negatively charged pyrolyzed by-product biomass surface and positively charged dye ions can be used to explain the adsorption mechanism.

Mechanism of BR46 adsorption is presented in Fig. 9.

Fig. 9
figure 9

Proposed mechanism of BR 46 adsorption onto pyrolyzed by-product biomass

Full size image

Pyrolyzed by-product biomass concentration effect

Figure 10 shows that the elimination of BR46 rises in fact as the concentration of pyrolyzed by-product biomass increases until it reaches a limit value, equal to 1 g/L, where the number of sites starts to stabilize. Secondly, several authors (Wu et al. 2014; Aoulad El hadj Ali et al. 2022) have demonstrated that the BR 46 cations may readily access the adsorption sites when there is a little amount of adsorbent added to the BR 46 solution. Adsorbent addition often results in an increase in the number of adsorption sites; however, this increase may also cause the adsorbent to accumulate, which results in a reduction of the surface area of the adsorbent and consequently the number of sites for adsorbing the cationic dye molecules (Gupta et al. 2010; Li et al. 2013).

Fig. 10
figure 10

Concentration effect of pyrolyzed by-product biomass on BR46 adsorption (C0 = 20 mg/L, pH = 7.5, T = 20 ± 2 °C, contact time = 180 min, \(\omega\) = 250 rpm, PS: 150 µm)

Full size image

Contact time effect

As demonstrated in Fig. 11, the adsorption of BR 46 on biomass from pyrolyzed by-products rises with contact time and achieves equilibrium in 5 min. 17.5 mg/g was the highest adsorption capacity attained. The increase in adsorption capacity of the pyrolyzed by-product biomass can be explained by the presence or abundance of active sites on the outer layer of the adsorbent (Sawasdee et al. 2017; Aoulad El hadj Ali et al. 2022). At the slowest stage, adsorption becomes less efficient, this resulted from a decrease in the number of active sites on the adsorbent's surface.

Fig. 11
figure 11

Contact time effect on the adsorbed amount of BR 46 (Cb = 1 g/L,pH = 7.5, T = 20 ± 2 °C, C0 = 20 mg/L, \(\omega\) = 250 rpm, PS: 150 µm)

Full size image

Adsorption kinetics

Experimental kinetic results adjusted by pseudo-second-order, pseudo-first-order, Elovich and Ritchie kinetic models are illustrated in Fig. 12.

Fig. 12
figure 12

Application of all models to kinetic experiment results

Full size image

Table 5 summarizes all parameters of kinetic models which were calculated.

Table 5 Kinetic model parameters values generated from BR46 adsorption onto pyrolyzed by-product biomass
Full size table

Table 5 demonstrates that the Ritchie model was described the most accurate experimental results.

In fact, the intraparticle diffusion coefficient may be estimated using the slope of the plot of squareroot of time (min0.5) vs. the quantity of BR46 adsorbed (mg/g) (Fig. 13) (Sun and Yang 2003). The intraparticle diffusion phase of the adsorption process was demonstrated by the graph of qt vs t0.5 in Fig. 13, which illustrates one-linearity. The slope of the plot's first linear segment was used to establish the intraparticle diffusion parameter Kp (mg/g min0.5). A value of 7.54 was determined for the intraparticle coefficient Kp (mg/g min0.5).

Fig. 13
figure 13

Intraparticle diffusion plot for adsorption of BR46 onto pyrolyzed by-product biomass

Full size image

Equilibrium isotherm

Figure 14 shows the experimental equilibrium data of BR46 adsorption on pyrolyzed by-product biomass.

Fig. 14
figure 14

Adsorption isotherm of BR46 onto pyrolyzed by-product biomass. (contact time = 180 min, Cb = 1 g/L, pH = 7.5, T = 20 ± 2 °C, \(\omega\) = 250 rpm, PS: 150 µm)

Full size image

In Fig. 15, Freundlich, Langmuir, Khan, and Temkin isotherm models were applied to experimental equilibrium data.

Fig. 15
figure 15

Application of all isotherm models to experimental equilibrium data

Full size image

The parameters of several isotherm models were compiled in Table 6.

Table 6 Equilibrium isotherm models parameters values for BR46 adsorption onto pyrolyzedby-product biomass
Full size table

Table 6 demonstrates that Langmuir's model well predicts the experimental equilibrium data.

The average free energy by adsorption (bt) was calculated to be 0,037 kJ/mol. Therefore, the adsorption mechanism was physical in nature.

Table 7 provides a summary of the effectiveness of BR46 adsorption on various adsorbents. It was found that pyrolyzed by-product biomass had a significant BR46 adsorption capacity.

Table 7 Maximum quantity of BR46 adsorbed by different adsorbents
Full size table

This value is still lower than the obtained value using permanganate peels (akkari 23) as an adsorbant has a large specific surface area compared with the other type of adsorbant

Thermodynamic study

BR 46 adsorption isotherms on the adsorbent at different temperatures were obtained under the following operating conditions: BR 46 initial concentrations ranging from 5 to 400 mg/L, adsorbent concentration Cb = 1 g/L, solution pH = 7.5, contact time t = 180 min, temperature T = 20 °C, 30 °C, 40 °C and solution volume Vsolution = 50 mL.

By applying the nonlinear Langmuir isotherm model to the experimental equilibrium data at various temperatures (Fig. 16), the Langmuir equilibrium constants KL (L/mg) at different temperatures can be deduced. The conversion of the constant KL (L/mg) to the constant KD (L/mol) can be achieved by using the following expression:

$${K}_{D}= {K}_{L} . M. 1000$$
(19)

where M is the molar mass of BR46 (= 401.3.g/mol).

Fig. 16
figure 16

Application of Langmuir model to experimental equilibrium data at different temperatures

Full size image

Keq (dimensionless) were numerically identical to KD (L/mol).

The KD, KL and Keqvalues obtained at different temperatures are shown in Table 8.

Table 8 KD, KL and Keqvalues obtained from nonlinear Langmuir model at different temperatures
Full size table

Parameters values of ∆S, ∆H and ∆G were deduced from the plot of ln Keq vs 1/T (Fig. 17) and are shown in Table 9. All values of ∆G are negative, indicating that the BR 46 adsorption process was spontaneous. The BR 46 adsorption was exothermic and physical in nature, as indicated by the negative value of ∆H (∆H < 20 kJ/mol). In addition, negative values of (∆S) indicate a decrease in disorder at the solid/solution interface (Małgorzata Wisniewska 2022).

Fig. 17
figure 17

Evaluating the thermodynamic parameters for BR46 adsorption on the biosorbent using a plot of lnKeq vs. 1/T

Full size image
Table 9 Thermodynamic parameters values for BR46 adsorptiononto adsorbent
Full size table

Conclusion

The feasibility of eliminating dyes like Basic Red46 from aqueous solutions using pyrolyzed by-product biomass from the SAIDAL antibiotic manufacturing complex in Medea (Algeria) was investigated through a series of adsorption studies. After only 5 min, the BR46 adsorption by the pyrolyzed by-product biomass reached equilibrium. The pH value of 7.5 and the adsorbent content of 1 g/L were optimized for the removal of the color from the water solution. The greatest adsorption capacity of BR46 utilizing pyrolyzed by- product biomass was 135 mg/g.

Based on a recent study, the pyrolyzed by-product biomass may be utilized as a cheap adsorbent to successfully remove BR46 from a range of contaminated water sources. It can also be easily employed to remove other cationic dyes.

In perspective,the suggested investigation has to be more thorough in order to assess the effects of other dye competition and anionic dye adsorption, test regeneration of the adsorbent and study the pyrolyzed by-product biomass behaviour on a complex effluent, etc.