Introduction

Water pollution due to the release of various toxic chemicals and dyes from industrialization and urbanization is a global problem [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Arsenic occurs naturally in the earth’s crust, and much of its dispersion in the environment stems from mining and commercial uses. In industry, arsenic is a byproduct of the smelting process (separation of metal from rock) for many metal ores such as zinc, lead and cobalt. It cannot be destroyed once it has entered the environment, so that the amounts that we add can spread and cause health effects to humans and animals. The effects of arsenic exposure include discoloration of the skin, gangrene, intestinal problems, and carcinogenic effects include skin, lung, liver, kidney, and bladder cancers and ultimately death [32]. To reduce the health risks of human beings, the U.S. Environmental Protection Agency (USEPA) revised the maximum contaminant level (MCL) for arsenic in drinking water from 50 to 10 μg/L [33].

Arsenic occurs in the environment in several oxidation states such as − 3, 0, + 3 and + 5. Inorganic arsenic is generally found as trivalent arsenite or pentavalent arsenate form in the aqueous solution. As(III) is a hard acid and preferentially complexes with oxides and nitrogen. Whereas As(V) behaves like a soft acid, forming complexes with sulfides [34]. The speciation of arsenic in water is usually controlled by redox conditions, pH, biological activity, and adsorption reactions [35, 36]. As(III) is more toxic than As(V) and it is very difficult to remove from water. As a result of heightened guideline of arsenic toxicity and regulatory changes, prompting innovative research efforts towards efficient removing arsenic from contaminated water is of critical importance.

Many technologies such as coagulation [37], ion exchange [38], membrane filtration [39, 40], and precipitation [41] have been employed for the removal of metal ions from aqueous solutions and effluents. However, these methods can prove to be too costly, impractical to apply over large scales, or unable to remove trace quantities of the metalloid. To overcome these drawbacks, adsorption is a good alternative to remove metal ions from aqueous environment. Different types of adsorbents [42,43,44,45,46,47,48,49] have been used for the removal of a variety of pollutants from water. Recently, the application of nanomaterials, nanoadsorbents has come forth as a fascinating area of interest for the removal of metallic and dye pollutants from water [50,51,52,53]. A variety of nanoparticles titanium dioxide suspensions [54], chitosan nanoparticles [55], zinc oxide nanoparticles [56], Nickel/nickel boride nanoparticles-coated resin [57], zirconium oxide nanoparticles [58], MnFeO4 and CoFe2O4 [59] have been used for the removal of metal ions from water. Nanoparticles are having high adsorption capacity due to its large surface area. In this connection, utilization of nanoparticles has greater attention in metal ion removal process. As per the literature survey, there are no studies on the adsorption of As(III) using ZnO nanorods. Therefore, in the present study, ZnO nanorods have been used for the removal of As(III) from aqueous solution.

The goal of this work is to investigate the sorption capacity of ZnO nanorods as an adsorbent for the removal of As(III) from aqueous environment. The effects of varying parameters such as pH, dose, initial metal concentration, contact time and temperature on the adsorption process were examined. To clarify the sorption kinetics of As(III) by ZnO nanorods, Lagergren’s pseudo-first-order, pseudo-second-order and intraparticle diffusion models were applied to the experimental data. The isotherms of adsorption have been studied and various isotherm models, such as Langmuir, and Freundlich models, have been tested. In addition, thermodynamic parameters including the change in free energy (ΔGo), enthalpy (∆Ho) and entropy (∆So) were calculated to evaluate the thermodynamic behavior of the biosorption process.

Materials and methods

Materials

All the reagents were of analytical grade with a purity of 99% and used as received without further purification. ZnSO47H2O (S. D. Fine chemicals limited), KOH (Qualigens fine chemicals) tetraethyl orthosilicate (Sigma Aldrich). The glassware used was soaked in 10% HNO3 overnight before use and cleaned repeatedly with double distilled water. The stock solutions of As(III) were prepared by dissolving As2O3 in double distilled water. Fresh dilutions were used for each study. The initial pH of each solution was adjusted with 0.1 M HCl and NaOH.

Synthesis of ZnO nanorods

ZnO nanoparticles were prepared by drop by drop addition of 0.3 M of KOH (19.03 g/100 mL) from a burette to 0.017 M solution of ZnSO47H2O (5 g/100 mL) with constant stirring (500 rpm). The reaction mixture was stirred at room temperature. Then, tetraethyl orthosilicate (capping agent) was added in a certain amount to the reaction mixture to inhibit the growth of zinc hydroxide crystallite during the course of the precipitation. The solution becomes milky white under the constant stirring. The precipitate is separated by the filtration. After that, it washed several times with distilled water and absolute methanol until the impurities are free from precipitate. Finally, it was dried in hot air oven for 1 h at 353 k. The ZnO nanorods were stored in airtight containers and kept in desiccators until further use.

Apparatus

The crystallinity and phase identification of adsorbent powders were determined by X-ray diffraction (XRD) using a Rigaku Ultima III system equipped with a Cu sealed tube (λ = 1.54178°A). FT-IR spectra of the pure, As(III) loaded ZnO nanorods were measured with an FT-IR spectrophotometer (Thermonicolet-200 series, Germany) under ambient conditions. The spectra were recorded from (4000 to 500 cm−1) using a KBr pellet. The surface morphology of the samples was observed Scanning electron micrographs (Carl Zeiss, EVO MA 15, England). The pH of the As(III) solution is measured with a digital pH meter (Digisum D1-7007, India). Thermal gravimetric analysis (TGA) was carried out using on a Linseis L81-I TG–DTA instrument with a heating rate of 10 °C min−1 under an N2 atmosphere.

Batch adsorption studies

To obtain the performance of sorbent material, batch experiments were conducted. The pH of the solutions was adjusted by adding 0.1 M HCl and NaOH. A total of 0.4 g of adsorbent (ZnO nanorods) was mixed with 50 mL of As(III) solution in 125 mL of Erlenmeyer flasks. The pH of the solutions was adjusting by 0.1 M of HCl or NaOH. Then, the flasks were shaken at room temperature (303 K) for 2 h to reach equilibrium in shaking incubator. After that the samples were withdrawn from the shaking incubator and filtered through whatman filter paper 41 to remove As(III) from the solution. The amount of As(III) ions in the filtered solution was estimated.

$$q_{\text{e}} = \frac{{(C_{\text{i}} - C_{\text{e}} )V}}{M}$$
(1)

where qe (mg/g) was the adsorption capacity at equilibrium, Ci and Ce are initial and equilibrium concentration (mg/L) of As(III) in the aqueous phase, respectively, M (g) is the biosorbent dosage, and V (L) is the volume of the aqueous phase.

Results and discussion

Characterization of the adsorbent material

XRD analysis

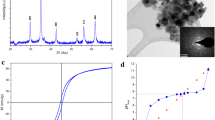
XRD spectra of pure and As(III) loaded ZnO nanorods are shown in Fig. 1. The peaks were seen at 31.96, 34.62, 36.44, 47.74, 56.79 and 63.05, which can be assigned to diffraction from (100), (002), (101), (102), (110) and (103) planes, respectively. This revealed that the resultant nanoparticles were of pure zinc oxide with a hexagonal structure.

Fig. 1
figure 1

X-RD spectra of pure ZnO nanorods

Full size image

FT-IR analysis

The functional groups of the synthesized ZnO nanorods were analyzed using the FT-IR spectrum. FT-IR spectra of pure and As(III) loaded ZnO nanorods are shown in Fig. 2. The major bands for the ZnO nanorods can be assigned as follows: The broad and strong bands at 3378 cm−1 (are due to the overlapping of –OH and –NH2 stretching vibrations), 1659 cm−1 (–NH2 bending vibrations), 1370 cm−1 (–CH symmetric bending vibrations in ZnO–OH), 1019 cm−1 (–CO stretching vibration in –COH). In addition, a broad absorption peak about 400–590 cm−1was assigned to the inorganic Zn–O stretching band. After As(III) loaded, the broad band at 3415 cm−1 which is concerned with –OH and –NH2 stretching vibrations increases after sorption process. This may be attributed to the deformation of –OH and –NH2 bands as a result of interaction between the functional groups and metal ions. The intensity of the band at 1659 cm−1 is substantially decreased to 1618 cm−1 after As(III) loaded. The shift of the peak from 1019 to 1032 cm−1 suggests the involvement of the C–O group in binding As(III).

Fig. 2
figure 2

FT-IR spectra of a pure ZnO nanorods and b As(III)-loaded ZnO nanorods

Full size image

SEM analysis

Surface morphology of the adsorbent is the most important one and the adsorption capacity mainly depends on the surface structure and surface porosity. Figure 3 shows the SEM images of (a) ZnO nanorods and (b) As(III)-loaded ZnO nanorods. From Fig. 3a, it is clearly observed that the pure ZnO nanorods are formed. After As(III) loaded (Fig. 3b), the nanorods are fully covered with the metal. It can be observed that the surface morphologies of ZnO are different before and after As(III) loaded.

Fig. 3
figure 3

SEM images of a pure ZnO nanorods, b As(III)-loaded ZnO nanorods

Full size image

TGA analysis

The TGA graph (Fig. 4) shows weight loss up to 450 °C and after this point there was no significant weight loss detected. The first weight loss occurred at 120 °C, representing the dehydration of samples due to desorption of physically adsorbed water molecules on the surface of ZnO nanorods. The second weight loss occurred between 250 and 350 °C, indicating the loss of OH− and CO32−.

Fig. 4
figure 4

TGA graph of ZnO nanorods

Full size image

Influence of solution pH

The pH of the solution is considered to be one of the most important factors affecting the biosorption process. The pH affects not only the solution chemistry of the metals but also the ionization state of the functional groups present on the surface of the sorbent. The effect of initial pH on the biosorption of As(III) onto ZnO nanorods was evaluated within the pH range of 2–9 (Figure not shown). At low pH values, protons occupy most of the sorption sites on the sorbent surface and less As(III) could be sorbed because of electrostatic repulsion. When the pH values increased, adsorbent surfaces were more negatively charged and the sorption of metal ions (positive charge) increased and reached maximum at pH 7.0 for As(III). Decreased sorption at higher pH (pH > 7.0) was due to the formation of soluble hydroxylated complexes of the metal ions and their competition with the active sites, and as a consequence, the retention had been decreased again. For this reason, the optimum pH was selected to be 7.0 for further experiments.

The effect of pH can also be explained in terms of pHpzc of the biosorbent. The pHPZC is an important characteristic for adsorbents to determine the pH at which the surface has net electrical neutrality. The initial pH of each solution was adjusted with 0.1 M HCl and NaOH. At pH < PZC, the surface charge of the adsorbents is positive which results in low As(III) sorption. At pH > PZC, the surface charge of the adsorbents is negative and the As(III) ions in solution were attracted to the surface to a greater extent. The PZC value of the ZnO nanorods is found to be 6.5.

Effect of agitation speed

The agitation speed experiments were undertaken with different agitation speeds of (30, 60, 90, 120, 150, 180, and 210) rpm keeping constant the other process variables. The amount of As(III) adsorption increases with an increase of the agitation speed from (30 to 210) rpm and the highest amount of As(III) (96% removal and the figure was not shown) was obtained with an agitation speed of 180 rpm. Lower speeds probably caused inefficient dispersion of adsorbent particles in water that led to agglomeration of particles. At higher agitation speed (> 180 rpm), the As(III) amount decreases. Hence, the optimum speed of 180 rpm has been selected for further study.

Influence of adsorbent dose

The amount of the adsorbent is an important parameter because it determines the adsorption capacity of an adsorbent for a given initial concentration of the adsorbate. The effect of adsorbent dose has been studied with various amounts of sorbent (0.1–0.6 g), while keeping all the other parameters constant at their optimum values (i.e., pH, agitation speed, temperature and contact time). From results (Fig. 5), the removal percentage of As(III) increases with increasing higher dosages. This is attributed to the increased adsorbent surface area and more available adsorption sites or functional groups because of the increase in adsorbent quantity. Beyond 0.4 g, there was no appreciable increase in the percentage adsorption, which indicates the saturation of the active adsorption sites in the biopolymer composite. An adsorbent content of 0.4 g was selected for all further experiments because of the high adsorption efficiency and acceptable adsorption capacity at this value.

Fig. 5
figure 5

Effect of adsorbent dose for the removal of As(III) from aqueous environment

Full size image

Influence of initial metal ion concentration and contact time

Contact time is one of the important parameters for successful biosorption application. To examine the effect of the initial metal concentration, the biosorption experiments were carried out at different initial metal concentrations (30, 50, 70, and 90 mg/L) at the optimum temperature and pH. The initial As(III) ion concentration was varied (30–90 mg/L) with varying contact times (15–120 min). The removal percentage increases with increasing the metal ion concentration (Figures not shown) and then it remained unchanged by further increase in initial metal ion concentrations. These results suggest that the available sites on the biosorbent are the limiting factor for the As(III) adsorption. It was observed that the sorption process reached equilibrium at 105 min. Afterwards, there were no significant changes in As(III) onto ZNO nanorods. Hence, the contact time of 105 min is selected for As(III) ions for further studies.

Kinetic models

Adsorption kinetics is important from the point of view that it controls the efficiency of the process and the models correlate the adsorbate uptake rate with its bulk concentration.

To analyze the adsorption rate, pseudo-first-order [60], pseudo-second-order [61] and intraparticle diffusion models [62] were used to investigate the adsorption kinetics of As(III) onto the ZnO nanorods.

The linear form of pseudo-first-order rate equation is generally expressed as follows:

$$\log \left( {q_{\text{e}} - q_{\text{t}} } \right) = \log q_{\text{e}} - \frac{{K_{1} }}{2.303}t$$
(2)

where qe (mg/g) and qt (mg/g) are the amounts of As(III) sorbed at equilibrium and at time t. K1 (min−1) is the rate constant of first-order biosorption process. The pseudo-first-order kinetic constants were determined from slope of the plot of log (qe − qt) versus t (Figure not shown) and the values are shown in Table 1.

Table 1 Kinetic parameters for the removal of As(III) onto ZnO nanorods at different As(III) concentrations
Full size table

The pseudo-second-order kinetic model of McKay and Ho can be expressed as:

$$\frac{t}{{q_{\text{t}} }} = \frac{1}{{K_{2} q^{2}_{\text{e}} }} + \frac{1}{{q_{\text{e}} }}t$$
(3)

where qe and qt are the amount of the As(III) removal per unit mass of biosorbent (mg/g) at equilibrium and at time t (min), and K2 (g/mg.min) is the pseudo-second-order rate constant. The biosorption rate constant (K2) is obtained from linear plot of t/qt versus t (Figure not shown) and the values are included in Table 1. As shown in Table 1, the R2 values for pseudo-second-order kinetic model at all the concentrations studied are higher than pseudo-first-order model. It was suggested that the pseudo-second-order model is more suitable for describing the sorption of As(III) onto ZNO nanorods.

The intraparticle diffusion model is based on the theory proposed by Weber and Morris

$$q_{\text{t}} = K_{\text{id}} t^{0.5} + c$$
(4)

where qt (mg/g) is the amount adsorbed at time t (min), Kid is the intraparticle diffusion rate constant (mg/g min−0.5) and C is the intercept that gives an idea about the thickness of the boundary layer. The intraparticle diffusion model coefficient values are calculated from the plot of qt versus t0.5 (Figure not shown) and are given in Table 1. It can be deciphered that these plots of qt versus t0.5 have three distinct regions. The initial region of the curve relates the adsorption on the external surface. The second region corresponds to the gradual uptake, which reflects the intraparticle diffusion as the rate-limiting step. The final plateau region indicates the equilibrium uptake. It denotes that the intraparticle diffusion is not the only rate-controlling step.

In addition, the sum of square error (SSE) test was carried out to predict the best fit.

$${\text{SSE}} = \sum \frac{{(q_{\text{t,e}} - q_{\text{t,m}} )^{2} }}{{q_{\text{t,e}}^{2} }}$$
(5)

where qt,e and qt,m are the experimental biosorption capacities of metal ions (mg/g) at time t and the corresponding values that are obtained from the kinetic models. SSE values for all kinetic models are calculated and are summarized in Table 1. Pseudo-second-order model has the lowest SSE values when compared with the pseudo-first-order and intraparticle diffusion models. Based on the low SSE values, it can be concluded that biosorption As(III) onto ZNO nanorods follows pseudo-second-order model.

Equilibrium isotherms

The capacity of an adsorbent can be described by sorption isotherms, which can help to explore the adsorption mechanism much more thoroughly. The sorption data have been subjected to different sorption isotherms, namely the Langmuir [63] and Freundlich [64].

The Langmuir model assumes that the uptake of metal ions occurs on a homogeneous surface by monolayer adsorption without any interaction between adsorbed ions. The linearized form of this isotherm can be expressed as:

$$\frac{1}{{q_{\text{e}} }} = \frac{1}{{q_{\text{m}} K}}\left[ {\frac{1}{{C_{\text{e}} }}} \right] + \frac{1}{{q_{\text{m}} }}$$
(6)

where qe is the equilibrium metal ion concentration on the sorbent (mg/g), Ce is the equilibrium metal ion concentration in the solution (mg/L), qm is the monolayer biosorption capacity of the sorbent (mg/g), and K is the Langmuir constant related to the free energy of sorption.

As seen from Table 2 the R2 values indicates that the Langmuir isotherm model fits well to the experimental data. The maximum adsorption capacity qmax was calculated from the Langmuir equation indicating the qmax of As(III) with ZnO nanoparticles 52.63 mg/g, respectively. For the Langmuir isotherm, a dimensionless separation factor can be expressed by the following equation:

Table 2 Langmuir and Freundlich isotherm constants and correlation coefficients for the removal of As(III) onto ZnO nanorods at different temperatures
Full size table
$$R_{\text{L}} = \frac{1}{{(1 + bC_{0} )}}$$
(7)

where b is the Langmuir constant (L/mg) and Co is the initial biosorbent concentration of As(III) ions (mg/L). The value of RL indicates the shape of isotherm to be either unfavorable (RL > 1), Linear (RL = 1), Favorable (0 < RL < 1), or irreversible (RL = 0). In this study, the RL values lie between 0 and 1. This indicates that the biosorption of As(III) onto ZNO is favorable.

The Freundlich isotherm is used for modeling the biosorption of metal ions on heterogeneous surfaces and the linearized form of the isotherm is as follows:

$$\log q_{\text{e}} = \log K_{\text{f}} + \frac{1}{n}\log C_{\text{e}}$$
(8)

where Kf (mg/g) is a constant relating the biosorption capacity and 1/n is an empirical parameter relating the biosorption intensity. The values of Freundlich constants Kf and 1/n are included in Table 2. The values of Freundlich constants Kf and 1/n were obtained from the plots of log Ce versus log qe (Figure not shown) and the values are included in Table 2. It is clear that the R2 values are not closer to unity compared to Langmuir model. This value indicates the degree of non-linearity between solution concentration and adsorption as follows: if n = 1, then adsorption is linear; if n < 1, then adsorption is a chemical process; if n > 1, then adsorption is a physical process. The n value in Freundlich equation was found to be 2.12, 1.96, and 1.62 for ZnO nanorods at three different temperatures (303, 313 and 323 K). Since n lie between 1 and 10, this indicates the physical adsorption of As(III) onto ZnO nanorods.

Chi square (χ 2) analysis

Chi square (χ2) test was adopted to find the suitability of an isotherm that fits best the experimental data. The Chi square (χ2) statistics is basically the sum of the squares of the difference between the experimental and calculated data from models, with each squared difference divided by corresponding data obtained by calculation. The equation for evaluating the best fit model is as follows:

$$\chi^{2} = \sum {\frac{{(q_{\text{e}} - q_{\text{e,m}} )^{2} }}{{q_{\text{e,m}} }}}$$
(9)

where qe,m is the equilibrium capacity obtained from the model (mg/g) and qe is the experimental equilibrium capacity (mg/g). From Table 2, lower χ2 values of Langmuir isotherm model show that the experimental data correlate well with the Langmuir isotherm than the Freundlich isotherm.

Effect of temperature

Temperature plays key roles on the biosorption process. Biosorption experiments were conducted at 303, 313 and 323 K to investigate the effect of temperature, with initial As(III) concentration of 125–225 mg/L, adsorbent dosage of 0.4 g/L, pH 7 and contact time of 105 min. It was observed that the maximum adsorption capacity of As(III) ion reached up to 52.63 mg/g at 323 K. The sorption capacity increased when temperature of the solution was increased, indicating that the process was endothermic. This may be a result of an increase in the mobility of As(III) ions with increasing temperature. An increasing number of molecules may also acquire sufficient energy to undergo an interaction with active surface sites of the adsorbent.

Thermodynamic parameters, such as of Gibbs free energy change (ΔGo), enthalpy change (∆Ho) and entropy change (∆So), were used to evaluate the thermodynamic feasibility of the process and to confirm the nature of the biosorption process. The parameters were determined using the following equations:

$$\Delta G^{o} = - {\text{RT}}\ln K_{\text{L}}$$
(10)
$$\ln K_{\text{L}} = - \frac{{\Delta H^{o} }}{\text{RT}} + \frac{{\Delta S^{o} }}{R}$$
(11)

where R is the universal gas constant (8.314 J/mol K), T is the temperature (K) and K is obtained by multiplying Langmuir constant b and qm. The negative values (− 5.741, − 5.342 and − 4.538 kJ/mol) of ΔGo indicate the spontaneous nature the adsorption of AS(III) at (303, 313, 323 K), respectively. The positive ΔHo value (13.75 kJ/mol) suggested that the AS(III) adsorption is endothermic in nature. The positive ΔSo value (0.0616 J/mol K) reveals the increase in randomness at the solid-solution interface during the fixation of the antimony ion on the active sites of the adsorbent.

Comparison of ZnO with other adsorbents

Table 3 shows a comparison of the maximum adsorption capacity of different materials reported in the literatures [17, 65,66,67,68,69,70] as adsorbents for As(III) from aqueous media under different experimental conditions. The qmax (52.63 mg/g) value of for ZnO nanorods was much higher than those materials used for removing As(III) ions. Also, it is concluded that ZnO is a novel sorbent for the removal of As(III) from aqueous solutions.

Table 3 Comparison of adsorption capacity of various adsorbents for As(III) ions from aqueous solution
Full size table

Conclusion

ZnO nanorods have been successfully synthesized from zinc acetate using KOH as a reducing agent at room temperature. The morphological studies were conducted using SEM indicating that the As(III) adsorption was done on the surface of the adsorbent. Pseudo-first-order, pseudo-second-order and intraparticle diffusion kinetic models were used to describe the kinetic data and the rate constants were evaluated. The result of the kinetic study shows that the adsorption of As(III) could be described by the pseudo-second-order equation. The equilibrium behavior of As(III) with a stronger affinity toward ZnO nanorods could be fitted very well by the Langmuir isotherm. The thermodynamic functions were calculated, and it can be concluded that the adsorption of As(III) over ZnO nanorods is an endothermic and spontaneous process. Hence, it may be concluded that ZnO nanorods exhibit as a good adsorbent for the treatment of aqueous solutions containing As(III) ions.