Performance comparison of IHACRES, random forest and copula-based models in rainfall-runoff simulation

Abstract

In this study, two models of Random Forest and copula-based simulation were used to evaluate the accuracy and efficiency of the IHACRES rainfall-runoff model in simulating the daily discharge of the Siminehroud River in the south of Lake Urmia basin, Iran. A trivariate copula-based model was created using discharge, rainfall and temperature data on a daily scale in the period 1992–2018. Vine family models and their conditional densities were used to implement the copula-based model. By calibrating the IHACRES model and also selecting the tree sequence in accordance with the data, rainfall-runoff simulations were performed in the study area. The accuracy and efficiency of the studied models were evaluated using RMSE and NSE criteria, and also violin plot and Taylor diagram. The results of comparing the error rate of rainfall-runoff simulation in the study area showed that the vine-based model reduces the RMSE statistics by about 14.5 and 16.5%, respectively, compared to the IHACRES and Random Forest models. According to the presented diagrams, the efficiency and certainty of IHACRES and copula-based simulation models are acceptable. While the Random Forest model does not have acceptable accuracy and efficiency in the study area. The copula-based simulation model has a good performance due to the unique tree sequence as well as involving the marginal distributions fitted to the data. Although the copula-based simulation model has increased the efficiency of the model in simulating the daily discharge by about 5% compared to the IHACRES model, it is not significant compared to the mathematical complexity of the copula-based model.

Introduction

So far, many models have been developed for rainfall-runoff simulation, each with its own advantages and limitations. Data-driven models have made great strides in this area in recent years. A combination of different models has also been used in this regard. Among these, the IHACRES model is one of the most important models for rainfall-runoff simulation. Croke and Jakeman (2004) described a new version of the nonlinear module in the IHACRES rainfall-runoff model. The basic model uses a nonlinear loss module to calculate effective rainfall and a linear routing module to convert effective rainfall to flow discharge. They stated that this model was developed to help estimate flow discharge in unmeasured basins where the observed evapotranspiration data are available. The new module has only 3 parameters and has significantly less correlation between the parameters.

Carcano et al. (2008) compared two models of feedforward multilayer perceptron and Jordan recurrent neural network in two small basins with irregular and flood regimes with the IHACRES model. The results showed that when good input data is not available, metric models perform better than conceptual models, and in general, it is difficult to justify the basic concept of the complex processes. Abushandi and Merkel (2013) used HEC-HMS and IHACRES rainfall-runoff models to simulate a flow event in the Wadi Dhuliel dry basin on an hourly scale. Both models were validated using observational flow datasets. By comparing the simulated and observed values, the results showed that the IHACRES model performs poorly in some areas, while the observed values are well consistent with the flow data simulated by HEC-HMS. Ahmadi et al. (2019) used three models SWAT, IHACRES and ANN in three timescales of daily, monthly and annual in a basin in the west of Tehran, Iran to simulate rainfall-runoff. The results showed that the performance of the three models is generally suitable for simulating the rainfall-runoff process, but the ANN model has a better performance for simulating daily, monthly and annual discharge than the other two models.

Esmali et al. (2021) compared the performance of IHACRES and SWAT rainfall-runoff models in three catchments with different climates including arid, semi-arid and semi-humid. The results showed that the SWAT model in arid, semi-arid and semi-humid basins has a better performance than the IHACRES model. Although the performance of both models is acceptable in semi-arid and semi-humid basins, but in arid basin, IHACRES model performed poorly compared to SWAT. Mohammadi et al. (2021) investigated the performance of two Hydrologiska Byråns Vattenbalansavdelning and Non Recorded Catchment Areas models in simulating the river flow in four basins in Indonesia compared to artificial intelligence models. The results of their research showed that the hybrid models based on artificial intelligence compared to Hydrologiska Byråns Vattenbalansavdelning and Non Recorded Catchment Areas simulate the river flow with higher accuracy. They stated these methods can be a suitable alternative to hydrological models. Fattahi et al. (2022) estimated the outflow of 19 sub-basins in northern Iran by using the IHACRES model. They used data-driven models based on artificial intelligence to compare the accuracy of considered models. The results showed that on average, the hybrid of IHACRES and data-driven model increases the efficiency of modeling compared to the individual use of IHACRES model. According to the Nash–Sutcliffe efficiency coefficient, the hybrid model had acceptable performance in six sub-basins, in which the IHACRES model had poor performance in estimating the river flow. They stated that the integration of the IHACRES model with a data-driven model (GMDH model) could improve the simulation results in all studied sub-basins. Mohammadi et al. (2022) used IHACRES, GR4J and MISD models to rainfall-runoff simulation in a basin in Switzerland. They also used other effective parameters such as wind speed, temperature, relative humidity, and snow depth in the simulations. They stated that the incorporation of meteorological variables in hydrological models increases the accuracy of models in rainfall-runoff simulation.

A review of the literature shows that different data-driven models have been used for rainfall-runoff simulation. One of the models that has been used recently for the simulation purposes is the copula-based model that has been studied in various studies (Nazeri Tehroudi et al., 2022b). Khashei et al. (2021) used copula-based models in Birjand meteorological station to present an approach to simulate potential evapotranspiration. The results showed that the values of Kendall’s tau in both simulation and observational modes are close to each other and are almost similar. Also, the simulation results of evapotranspiration showed a potential efficiency of 92%.

Nazeri Tehroudi et al. (2022a) examined and compared two efficient approaches (support vector regression and copula-based model) to simulate two variables of river discharge and monthly rainfall in the Lake Urmia basin, Iran. The simulation results showed that the copula-based model is more accurate than the support vector regression model. The results showed a 36% improvement in RMSE statistics by the copula-based model compared to the optimal support vector regression model in simulating river discharge on a monthly scale. Dastorani and Nazeri Tehroudi (2022) investigated the relationship between pumping time and groundwater level drawdown for two pumping tests with a constant flow discharge of 26.6 and 28.8 L per second and a pumping time of 220 min using two-dimensional copula functions. Type curves were obtained to estimate the groundwater level drawdown at different pumping times with different probabilities. The results of frequency analysis in the study area showed that for each unit of increase in pumping flow in the pumping well, a decrease of 0.32 m in the observation well is conceivable. Ahmadi et al. (2022) used a random forest model to estimate the monthly inflow (Q) to the Maroon Dam reservoir in Iran. To compare the results, they proposed two different types of hybrid models by pairing random forest with complete ensemble empirical mode decomposition and wavelet analysis. The obtained results confirmed the superiority of the proposed hybrid models over the classical random forest for estimating the monthly inflow of the reservoir.

The copula-based model, due to its multivariate nature, incorporates various parameters in the simulations which can be used as an efficient model to predict various phenomena. This model can increase the accuracy of the results by using the conditional density of the copula functions, tree sequence and marginal distributions of observational data. Therefore, in this study, we have tried to examine the potential and efficiency of this model in rainfall-runoff simulation according to the input values of IHACRES model. One of the most important objectives of this study is to compare the performance of the vine-based model, random forest model and common IHACRES model in rainfall-runoff simulation in the Siminehroud basin in northwest Iran.

Material and methods

Case study

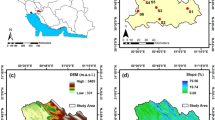
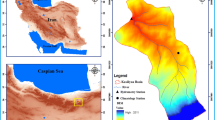
The Siminehroud River is located in the West Azarbaijan province in northwestern Iran and south of the Lake Urmia basin. The length of Siminehrood is 200 km and the area of its catchment at Dashband hydrometric station is 2090 square kilometers. In this study, daily discharge (m³/s), daily rainfall (mm) and daily temperature of Siminehrood basin measured at the Dashband station in the period of 1992–2018 were used. The total annual rainfall in this station is about 425 mm, and the mean annual discharge and temperature are about 11 m³/s and 11.7 °C, respectively. Figure 1 shows the location of the Dashband hydrometric station in the Lake Urmia basin.

Fig. 1

Location map of Siminehroud basin and Dashband station in Iran

IHACRES model

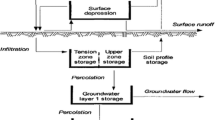
This model is a continuous rainfall-runoff model first developed by Jakeman and Hornberger (1993) for use in temperate basins, and then improved for temporary rivers (Jakeman and Hornberger 1993; Post and Jakeman 1999). The IHACRES rainfall-runoff model is developed simultaneously by hydrologists at the ICAM Watershed Management and Evaluation Center OF National University of Australia, Canberra, and CEH Ecology and Hydrology Center of British Environmental Research Association (Jakeman and Hornberger 1993; Post and Jakeman 1999). In the present study, the IHACRES software package developed by Croke et al. (2005a, b) has been used to simulate rainfall-runoff in the Siminehroud basin. The model requires two sets of rainfall and temperature data as input, as well as observational discharge data to calibrate the model and check the accuracy of the simulation results. The IHACRES model, like other models, has two parts (Astatkie and Watt 1998):

(a) A section that converts rainfall at the time base k (r_k) into effective rainfall (u_k) and excess rainfall which is eventually eliminated by evapotranspiration (assuming the watershed is impenetrable).

(b) A linear conversion function (or unit hydrograph, UH) that converts the effective rainfall into the discharge (x_k), which are called the loss section and the conversion function section (unit hydrograph), respectively).

The loss fraction for all rainfall-runoff processes at the watershed scale is considered nonlinear, while the conversion part is based on the theory of linear systems (Box and Jenkins 1970). The IHACRES model has six parameters, three of which are related to the nonlinear loss section (τw, 1/c, and f, which are the moisture storage capacity of the basin, the length of time it takes for the basin to dry, and the flood factor), and the three parameters related to the linear conversion function (τ^(q) and τ^(s) are part of the time it takes for reduce the discharge quickly and slowly, and v^(s) is the volume of the slow flow that shown the creation of a participatory river flow). Figure 2 shows the general structure of the used model.

Fig. 2

Model structure and conceptual dynamic response characteristics (Littlewood et al. 2007)

The equations used in the nonlinear reduction modulus to convert total rainfall into effective rainfall are as follows (Littlewood et al. 2007).

$$u_{k} = s_{k} \times r_{k} \,\,\,\,\,s_{0} = 0$$

(1)

$$S_{k} = C \times r_{k} + \left( {1 - \frac{1}{{\tau_{w} (t_{k} )}}} \right)S_{k - 1} ,\,\,\,\,\tau_{w} (t_{k} ) > 1$$

(2)

$$\tau_{w} (t_{k} ) = \tau_{w} \exp \,(f(R - t_{k} ))$$

(3)

$$x_{k} = \left[ {\left( {\frac{{b_{0}^{(q)} }}{{1 + a_{1}^{(q)} z^{ - 1} }}} \right) + \left( {\frac{{b_{0}^{(s)} }}{{1 + a_{1}^{(s)} z^{ - 1} }}} \right)} \right]u_{k - \delta }$$

(4)

$$x_{k} = \left( {\frac{{b_{0} + b_{1} z^{ - 1} }}{{1 + a_{1} z^{ - 1} + a_{2} z^{ - 2} }}} \right)u_{k - \delta }$$

(5)

where z⁻¹ is the backward shift operator, i.e. z⁻¹ x_k = x_k-1.

Parameter C in the loss module is calculated to balance the water between the effective rainfall and the observed discharge during the model calibration period, so it must start and end at a low flow of similar magnitude to change the amount of water stored in the basin at that period is minimized. Conceptually, 1/C can be considered as the depth (in millimeters) of a wet storage of basin (Post et al. 1998). The other parameters in Fig. 2 are also estimated as follows:

$$\tau^{(q)} = \frac{ - \Delta }{{\ln \left( { - a_{1}^{(q)} } \right)}}$$

(6)

$$\tau^{(s)} = \frac{ - \Delta }{{\ln \left( { - a_{1}^{(s)} } \right)}}$$

(7)

$$v^{(q)} = \left( {\frac{{b_{0}^{(q)} }}{{1 + a_{1}^{(q)} }}} \right)\left( \frac{1}{V} \right)$$

(8)

$$v^{(s)} = \left( {\frac{{b_{0}^{(s)} }}{{1 + a_{1}^{(s)} }}} \right)\left( \frac{1}{V} \right)$$

(9)

$$V = \left( {\frac{{b_{0}^{(q)} }}{{1 + a_{1}^{(q)} }}} \right) + \left( {\frac{{b_{0}^{(s)} }}{{1 + a_{1}^{(s)} }}} \right)$$

(10)

Analysis based on Vine copulas

Copula functions link the CDF of the marginal distributions of pair-variables to create joint distribution. These functions can provide a multivariate distribution given by univariate distributions. Copula functions at the first time introduced by Sklar (1959). Sklar (1959) showed how one-dimensional distribution functions can be combined into multivariate distributions. Copula functions are often used in bivariate mode. For dimensions higher than two, nested copulas or vine copulas can be used. Vine copulas include various states, the basis of which is the tree sequence. In this study, the frequency analysis and simulation based on vine copula is performed in trivariate mode. Vine copulas are presented in three general forms R (regular vine), C (canonical vine), and D (drawable vine), in which there is no difference between their tree sequences in the trivariate. In the R mode, the tree sequence is more varied than in the C and D ones. Due to their diverse structure, these copulas have the ability to model phenomena in high dimensions (Czado 2019). The tree sequence of vine copula in three dimensions is given as an example in Fig. 3. In three dimensions mode, there is no difference between the tree sequences of vine copulas, but the difference is in the internal copulas and the arrangement of variables, which can be seen in Fig. 3.

Fig. 3

Example of 3 dimensional copulas (Czado 2019)

In a C-vine tree, the dependence on a particular variable (as the first root of the node) is modeled by bivariate copulas for each pair. Given this variable, the dependencies of the paired series are chosen with respect to the second variable, which is called the second root of the node. Generally, one root of the node is selected in each tree and all pair dependencies are modeled according to this node and performed on all previous nodes. According to Czado (2019), this analysis changes the following to a multivariate density (Nazeri Tahroudi et al. 2021b):

$$\begin{gathered} f(x) = \prod\limits_{k = 1}^{d} {f_{k} } (x_{k} ) \times \prod\limits_{i = 1}^{d - 1} {\prod\limits_{j = 1}^{d - i} {c_{{i,i + j\left. {} \right|1:(i - 1)}} (F(x_{i} \left. \, \right|} } x_{1} ,...,x_{i - 1} ), \hfill \\ (F(x_{i + j} \left. \, \right|x_{1} ,...,x_{i - 1} )\left. \, \right|\theta_{{i,i + j\left. {} \right|1:(i - 1)}} \hfill \\ \end{gathered}$$

(11)

where $f_{k} ,k = 1,...,d$ is the marginal density and $c_{{i,i + j\left. {} \right|1:(i - 1)}}$ is the density of the bivariate copula with the $\theta_{{i,i + j\left. {} \right|1:(i - 1)}}$ parameters ($i_{k} ;i_{m}$ means: $i_{k} ,....,i_{m}$). The output is d-1 tree and i nodes, while the input to the pair of d-i copulas on each tree is i = 1, …, d-1. The performance function of the log-likelihood function of C-Vine copula with the θ_CV parameter is as follows:

$$l_{CV} (\theta_{CV} \left. \, \right|u) = \sum\limits_{k = 1}^{N} {\sum\limits_{i = 1}^{d - 1} {\sum\limits_{j = 1}^{d - i} {\log \left[ {c_{i,i + j|1:(i - 1)} (F_{i|1:(i - 1)} ,F_{i + j|1:(i - 1)} |\theta_{i,i + j|1:(i - 1)} )} \right]} } }$$

(12)

where $F_{{j|i_{1} :i_{m} }} = F(u_{k,j} |u_{{k,i_{1} }} ,...,uk,i_{m} )$ and the marginal distribution are also uniform.

D-vine provides an alternative method to select the order of these. At the first level of the tree, the dependencies of the first and second, second and third, third and fourth variables are used. This means that in a 5-dimensional Vine copula, at the first level of the tree, pairs (2;1), (3;2), (4;3), (5;4) are modeled. Whereas at the second level of the tree, the dependence of the first and third variables on the condition of the second variable (pair (1,3 | 2)), the second and fourth dependence on the condition of the third variable (pair (2,4 | 3)), etc. were modeled. In this method, the construction of the next level continues to the level of d-1. According to Czado (2019), the density of a D-vine is as follows:

$$\begin{gathered} f(x) = \prod\limits_{k = 1}^{d} {f_{k} } (x_{k} ) \times \hfill \\ \prod\limits_{i = 1}^{d - 1} {\prod\limits_{j = 1}^{d - i} {c_{j,i + i|(j + 1):(j + i - 1)} (F(x_{j} |} } x_{j + 1} ,...,x_{j + i - 1} ),(F(x_{j + i} |x_{j + 1} ,...,x_{j + i - 1} )\left. \, \right|\theta_{{j,j + i|x_{j + 1} ,...x_{j + i - 1} }} ) \hfill \\ \end{gathered}$$

(13)

where the output has more than d-1 tree, while the pair values in each tree are determined by the input. In order to obtain the conditional distribution functions F(x|v) for a vector v with the m dimensions, the following equation can be applied sequentially (Nazeri Tahroudi et al., 2022c):

$$h(x|v,\theta ): = F(x|v) = \frac{{\partial C_{{cv_{j} |v_{ - j} }} (F(x|v_{ - j} ),(F(\upsilon_{j} |v_{ - j} )|\theta )}}{{\partial F(\upsilon_{j} |v_{ - j} )}}$$

(14)

where $\upsilon_{j}$ is an arbitrary component of v and $v_{ - j}$ represents the (m-1) dimension vector with the exception of $\upsilon_{j}$. In addition, $C_{{cv_{j} |v_{ - j} }}$ is a bivariate copula distribution function with the specified parameter θ in the mth tree. The performance function of the log-likelihood of a D-Vine copula with the θ_DV parameter is as follows:

$$l_{DV} (\theta_{DV} \left. \, \right|\upsilon ) = \sum\limits_{k = 1}^{N} {\sum\limits_{i = 1}^{d - 1} {\sum\limits_{j = 1}^{d - i} {\log \left[ {c_{j,j + i|(j + 1)(j + i - 1)} (F_{j|(j + 1):(j + i - 1)} ,F_{j + i|(j + 1):(j + i - 1)} |\theta_{j,j + i|(j + 1):(j + u - 1)} )} \right]} } }$$

(15)

The R-vine is more flexible than the types C and D, because it can accommodate a wider range of structures. In order to increase the diversity of the structure, R-vine copulas introduce a new concept. For example, at the first level of the tree of 5-dimensional structure, the data are estimated as (1;2), (1,5), (1;3) and (3;4) pairs. Whereas at the second level of the tree, there are (2,3|1), (1,4|3) and (3,5|1) pairs. In the third tree there are (2,4|1,3) and (4,5|1,3) pairs and finally, in the fourth tree, there is (2,5|1,3,4) pair. Selecting the copula at the lower level affects the conditional copula at the upper level. Therefore, the choice of copula families influences each other. According to research by Dißmanna et al. (2013), we have:

$$f(x) = \prod\limits_{k = 1}^{d} {f_{k} } (x_{k} ) \times \prod\limits_{i = 1}^{d - 1} {\prod\limits_{{e \in E_{i} }}^{{}} {c_{{C_{e,a} ,C_{e,b} |D_{e} }} (F_{{C_{e,a} |D_{e} }} (x_{{C_{e,a} }} |} } x_{{D_{e} }} ),(F_{{C_{e,a} |D_{e} }} (x_{{C_{e,a} }} |x_{{D_{e} }} ))$$

(16)

where $e = a,b$ and $x_{{D_{e} }}$ is equal to $D_{e}$ and $x_{{D_{e} }} = x_{i} |i \in D_{e}$.

The log-likelihood function of the R-Vine copula with parameter $\theta_{RV}$ and $E_{1} ,E_{2} ,...,E_{d - 1}$ is as follows:

$$l_{RV} (\theta_{RV} \left. \, \right|\upsilon ) = \sum\limits_{k = 1}^{N} {\sum\limits_{i = 1}^{d - 1} {\sum\limits_{{e \in E_{t} }}^{{}} {\log \left[ {c_{j(e),k(e),D(e)} (F(u_{i,j(e)} |u_{i,D(e)} )|\theta_{j(e),k(e)|D(e)} )} \right]} } }$$

(17)

where $u_{i} = (u_{i,1} ,...,u_{i,d} )^{\prime} \in [0,1]^{d} ,i = 1,....,N.\,\,c_{j(e),k(e)|D(e)}$ equal to bivariate copula density with edge e and parameter $\theta_{j(e),k(e)|D(e)}$.

Conditional density in the 3D case

In this study, after selecting the copula function and its structure, the conditional density function used to estimate and evaluate the values of daily river flow (m³/s) given by daily precipitation (mm) and daily temperature (°C). The conditional density can be calculated as follows:

$$c(u_{3} |u_{1} ,u_{2} ) = \left. {\frac{{\partial^{3} C(u_{1} ,u_{2} ,u_{3} )}}{{\partial u_{1} \partial u_{2} \partial u_{3} }}} \right|_{{u_{1} ,u_{2} }}$$

(18)

where $u_{1} ,\,u_{2}$ and $u_{3}$ are daily flow rate (m³/s), daily precipitation (mm) and daily temperature (°C), respectively (Tahroudi et al. 2020; Nazeri Tahroudi et al. 2021a).

Vine-based simulation

To simulate a two-dimensional distribution function $F_{1,...,d}$ with conditional distribution functions $F_{j|1,...,j - 1} \left( { \cdot |x_{1} ,...,x_{j - 1} } \right)$ and their inversions $F_{j|1,...,j - 1}^{ - 1} \left( { \cdot |x_{1} ,...,x_{j - 1} } \right)$, for $j = 2,...,d$ iterative inverse probabilistic transformations can be used. In particular, a multivariate conversion introduced by Rosenblatt (1952) and studied in general form by Rüschendorf (1981) is used and reversed step by step. It is also called Rosenblatt conversion. The h function is used to determine the conditional distribution functions $C_{j|j - 1,...,1} ,\,\,j = 1,...,d$ that required for the structure of the pair-copula. This provides an iterative expression using the h functions for the optimal conditional distribution function, which can easily be reversed. More precisely, a notation $h_{1|2} \left( {u_{1} |u_{2} ;\theta_{12} } \right)$ is used for a function $h_{1|2}$ with parameters θ₁₂ from a specified bivariate copula C₁₂. For a bivariate copula $C_{ij} \left( {u_{i} ,u_{i} ;\theta_{ij} } \right)$ with parameter θ_{i j}, we define the h functions as follows (Ramezani et al. 2023):

$$h_{i\backslash j} \left( {u_{i} \backslash u_{j} ;\theta_{ij} } \right): = \frac{\partial }{{\partial u_{j} }}C_{ij} \left( {u_{i} ,u_{j} ;\theta_{ij} } \right)$$

(19)

$$h_{j\backslash i} \left( {u_{j} \backslash u_{i} ;\theta_{ij} } \right): = \frac{\partial }{{\partial u_{i} }}C_{ij} \left( {u_{i} ,u_{j} ;\theta_{ij} } \right)$$

(20)

For a parametric pair-copula $C_{{e_{a} ,e_{b} ;D_{e} }} \left( {w_{1} ,w_{2} ;\theta_{{e_{a} ,e_{b} ;D_{e} }} } \right)$ in a simplified regular vine corresponding to the edges $e_{a} ,e_{b} ;D_{e}$, the following symbol was introduced:

$$h_{{e_{a} ,e_{b} ;D_{e} }} \left( {w_{1} \backslash w_{2} ;\theta_{{e_{a} ,e_{b} ;D_{e} }} } \right): = \frac{\partial }{{\partial w_{2} }}C_{{e_{a} ,e_{b} ;D_{e} }} \left( {w_{1} \backslash w_{2} ;\theta_{{e_{a} ,e_{b} ;D_{e} }} } \right)$$

(21)

$$h_{{e_{a} \backslash e_{b} ;D_{e} }} \left( {w_{2} \backslash w_{1} ;\theta_{{e_{a} ,e_{b} ;D_{e} }} } \right): = \frac{\partial }{{\partial w_{1} }}C_{{e_{a} ,e_{b} ;D_{e} }} \left( {w_{1} ,w_{2} ;\theta_{{e_{a} ,e_{b} ;D_{e} }} } \right)$$

(22)

In this study, vine copulas and all common internal copulas and their rotational states were used to simulate the daily streamflow at the Dashband station.

Random forest algorithm

The random forest (RF) algorithm is proposed by Breiman (2001) as a cumulative learning method for regression and clustering problems based on decision tree development. A random forest is a collection of unpruned trees, each of them is obtained by a recursive segmentation algorithm. In other words, a random forest is a combination of several decision trees in which several self-organizing samples of data are involved (Freidman et al. 2001).

In order to create a regression tree, recursive segmentation and multiple regressions are used. The decision-making process is repeated at each internal node of the root node, according to the tree rule, until the predetermined stop condition is met. In the RF method, a random vector $X_{n}$ that is independent of random vectors $X_{1} ,X_{2} ,....,X_{n - 1}$ is generated for the nth tree. Also, all vectors follow the same distribution. Tree regression uses the training $X_{n}$ and calculated data sets to generate a set of trees equal to n as follows (Breiman 2001):

$$X_{n} = \left\{ {h_{1} (x),h_{2} (x),...,h_{n} (x)} \right\}$$

(23)

$$h_{n} = h(x,X_{n} ),x = \left\{ {x_{1} ,x_{2} ,...,x_{p} } \right\}$$

(24)

The above p-dimension vector forms a forest and the outputs for each tree are presented as follows:

$$y_{1} = h_{1} (x),y_{2} = h_{2} (x),...,y_{n} = h_{n} (x)$$

(25)

In the above equation, $y_{n}$ is the output of the nth tree. To obtain the final output, the average of all tree predictions is calculated (Breiman 2001).

Kendall’s tau correlation

Kendall's τ is defined as the probability of concordance minus the probability of discordance of the two random variables X₁ and X₂. The Kendall’s tau value between the continuous random variables X₁ and X₂ is defined as Eq. 26:

$$\tau (X_{1} ,X_{2} ) = P((X_{11} - X_{21} )(X_{12} - X_{22} ) > 0) - P((X_{11} - X_{21} )(X_{12} - X_{22} ) < 0)$$

(26)

where $(X_{11} - X_{12} )$ and $(X_{21} - X_{22} )$ are independent and uniformly distributed samples of $(X_{1} ,X_{2} )$ (Ramezani et al. 2019). Non-parametric estimates of the Kendall’s tau are presented in detail in Czado (2019). Specifically to estimate Kendall’s tau from a random sample {x_i1, x_i2, i = 1, …, n} of size n of the joint distribution of $(X_{1} ,X_{2} )$, consider all $\left( \begin{gathered} n \hfill \\ 2 \hfill \\ \end{gathered} \right) = \frac{{n\left( {n - 1} \right)}}{2}$ uncoordinated pairs $x_{i} : = \left( {x_{i1} ,x_{i2} } \right)$ and $x_{j} : = \left( {x_{j1} ,x_{j2} } \right)$ for i, j = 1,…, n (Czado 2019: Khozeymehnejad and Nazeri Tehroudi, 2020). If N_c is the number of concordance pairs, N_d is the number of discordance pairs, N₁ is the number of pairs x₁ and N₂ is the number of pairs x₂ of the random sample {x_i1, x_i2, i = 1, …, n} of the joint distribution $\left( {X_{1} ,X_{2} } \right)$, then the Kendall’s tau can be estimated as follows:

$$\hat{\tau }_{n}^{*} : = \frac{{N_{c} - N_{d} }}{{\sqrt {N_{c} + N_{d} + N_{1} } \sqrt {N_{c} + N_{d} + N_{2} } }}$$

(27)

To estimate τ in Eq. 27, Ginest and Favre (2007) used simple estimation assuming that there are no identical values. The Kendall’s tau estimation for a sample size of n without the same values is as follows:

$$\hat{\tau }_{n} : = \frac{{N_{c} - N_{d} }}{{\left( {\begin{array}{*{20}c} n \\ 2 \\ \end{array} } \right)}}$$

(28)

Both consistent estimates in the “absence of the same values” for the total number of unrated pairs are equal to the sum of N_c + N_d. If the observation rank is used instead of their values, both estimates do not change, so the estimates are based on rank.

Performance evaluation

In this study, in order to evaluate the performance of the studied models, two statistics including Nash–Sutcliffe (NSE) and the root mean square error (RMSE) were used as Eqs. 29 and 30, respectively. Also in this study, two graphic methods (i.e., Violin plot and Taylor diagram) were used in this regard.

$$NSE = 1 - \frac{{\sum\limits_{{{\text{i}} = {1}}}^{{\text{N}}} {(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Q}_{i} - Q_{i} )^{2} } }}{{\sum\limits_{{{\text{i}} = {1}}}^{{\text{N}}} {(Q_{i} - \overline{Q}_{i} )^{2} } }}.$$

(29)

$$RMSE = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Q}_{i} - Q_{i} )^{2} } }}{N}} .$$

(30)

where N and m are the number of data and number of parameters, respectively. $Q_{i}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Q}_{i}$ and $\overline{Q}_{i}$ are the observed, simulated and average of observed data, respectively (Nash and Sutcliffe 1970).

Results and discussion

IHACRES-based simulation

In order to simulate the daily discharge at Dashband station, the IHACRES model was first calibrated. In the meantime, the data for the period of 3/21/1992 to 8/22/2014 were used for the training and the data of the period for 8/23/2014 to 9/30/2018 were used to test the model. The calibration results of the model for simulation of rainfall-runoff in the region are presented in Table 1. One of the important parameters in this field is the value of v^s, which indicates the contribution of the base flow in the river discharge, which in the present study, according to the results presented in Table 1, indicates the existence of a medium base flow. Also, according to Table 1, it can be seen that the value of parameter c in the studied station is low, which indicates the rapid response of the studied basin to rainfall. This adds rainfall to the discharge with a low lag time. The correlation coefficient for the calibration stage of the IHACRES model on a daily scale was obtained 0.66, which indicates an acceptable accuracy of the model. Finally, according to the optimal parameters of the model, the discharge simulation at the Dashband station was performed on a daily scale. The results of the simulation of daily discharge at the Dashband station in training phase were presented in Figs. 4.

Table 1 The values obtained from the calibration process of IHACRES model

Fig. 4

a: The observed and simulated values of daily stream flow, b: Box plot of observed and simulated daily stream flow at Dashband station using IHACRES model in training phase

Based on the evaluation criteria (RMSE, NSE and R²) in Fig. 4a, the performance of the IHACRES model in simulating the river flow at Dashband station is acceptable that this is confirmed by the results presented in the box plot (Fig. 4b). According to Fig. 4a, a little underestimate can be seen at values less than 100 cubic meters per second. However, the maximum variation of the simulated values according to Fig. 4b corresponds to the maximum observational values. According to Fig. 4b, can be seen the major changes in the observed and simulated values, which are similar to each other.

Vine-based simulation

For vine-based simulation, first, the correlation between the studied paired variables was calculated using Kendall’s tau test and presented in Fig. 5. According to the results presented in Fig. 6, the correlation between pairs of temperature and discharge variables is higher than other paired variables. In order to simulate rainfall-runoff in the study area, dependent and Gaussian states of vine copulas were used. It should be mentioned that there is no difference among the tree sequences of vine copulas in the 3-D case. The only difference is the position of the three variables under the nodes. Considering different tree sequences based on different vine copulas, different structures were studied based on the Akaike information criterion (AIC), Bayesian information criterion (BIC) and Log-Likelihood criteria. The results of examining the various vine copulas are given in Table 2. The results of examining different tree sequences showed that according to the mentioned criteria, among the various copulas, the R-vine, C-vine and D-vine copulas had the same results and had the same function, which is conceivable due to the trivariate simulation. The C-, D- and R-vine copulas provided the same tree sequence with the same internal copulas. In the first tree, the Clayton and rotated version of the Clayton (90 degrees) copulas were selected and in the second tree, the 270 degrees Clayton copula was selected as the best-fitted copula. Rotational state of copulas actually help to cover the complete dependency in a data space, and the complete coverage of the dependency will increase the accuracy of the model. The selected tree sequence is shown in Fig. 6.

Fig. 5

Results of correlation of studied paired variables using Kendall’s tau test

Fig. 6

Tree sequence of the best vine copula in rainfall-runoff simulation at the Dashband station

Table 2 Results of the evaluation the different vine structures in simulating the rainfall-runoff at the Dashband station

Using the tree sequence of Fig. 6 and the selected copulas in Table 2, a rainfall-runoff simulation based on the vine copula was performed. The results of the rainfall-runoff simulation of Dashband station in Urmia Lake basin, northwest of Iran are presented in Fig. 7a. The results of this figure show the error rate (RMSE) of about 7 cubic meters per second on a daily scale in vine-based rainfall-runoff simulation. In addition, 95% confidence interval, 96% correlation, and 92% of Nash–Sutcliffe efficiency coefficient indicate the high accuracy of the vine-based model in rainfall-runoff simulation at Dashband station. Several cases are seen outside the simulation confidence intervals but are fewer than in the IHACRES model. The box plot of the observed discharge and the corresponding simulated values by the vine model is also shown in Fig. 7b. The range of variation of the simulated discharge values is similar to the observed values. According to Fig. 7b, a slight increase can be observed in the average of the simulated values compared to the observed values. The results showed that in comparison with the IHACRES model, applying the vine-based model led to a decrease in the error rate (RMSE) by about 16.5%, and an increase in the determination coefficient (R²) and model efficiency (NSE) to about 4.54 and 2.13 percent, respectively.

Fig. 7

a: The observed and simulated values of daily stream flow, b: Box plot of observed and simulated daily stream flow at Dashband station using vine-based model in training phase

Comparing the values of RMSE, NSE and R² statistics of IHACRES and vine-based models show that the vine-based model has higher accuracy and efficiency than the IHACRES model in simulating the daily streamflow at the Dashband station. Unlike the IHACRES model, as shown in Fig. 7a, there is not much overestimation and underestimation in the simulation results of the vine-based model. The efficiency of the model was about 92%, which has increased compared to the IHACRES model. A good match between the observed and simulated values can be seen in Fig. 7b.

Random forest-based simulation

The third model studied in this research is the random forest model. In this model, as well as two models, IHACRES and Copula-based simulation, the discharge values in the Dashband station were simulated using rainfall and temperature data on a daily scale. In this model, by drawing the PACF, the simulation with three lags was examined. The performance evaluation results of the random forest model in simulation of daily discharge at Dashband station are presented in Figs. 8a and b.

Fig. 8

a: The observed and simulated values of daily stream flow, b: Box plot of observed and simulated daily stream flow at Dashband station using Random Forest model in training phase

As can be seen from Fig. 8a, there are many simulated points outside the 95% confidence intervals. Underestimation and overestimation are observed in simulating the discharge of the Dashband station using the random forest model. According to Fig. 8b, it can be seen that the average simulated discharge values at the Dashband station is higher than the observed values. The random forest-based simulation presented an error rate (RMSE) of 12.11 m³/s and a Nash–Sutcliffe efficiency coefficient of 63% in simulating discharge at the Dashband station. Comparing the three examined models in this study indicates that the copula-based simulation model has higher accuracy than IHACRES and random forest models. The error rate of the copula-based model in simulating daily discharge in the Dashband station was 41.5% and 16.5%, lower than the random forest and IHACRES models, respectively. The efficiency of the copula-based simulation model has been improved by about 46% and 5%, respectively, compared to the random forest and IHACRES models. Comparing the results reveals that the difference between the random forest model and the other two models is too much. Therefore, it can be concluded that the random forest model has poorer performance than the other two models in simulating the daily river flow at Dashband station.

Visual comparison of rainfall-runoff models' performance

For a more detailed study and comparison of the three used models, the violin plot and the Taylor diagram were drawn and presented in Figs. 9 and 10, respectively. The results of the violin plot in Fig. 9 showed that both IHACRES and Copula-based simulation models are in good agreement with the observational data. According to the distributed form and shape of the observed and simulated values in Fig. 9, it can be expected acceptable performance from these two models, which according to the presented contents, the accuracy and certainty of both models are reliable. The results also show that the random forest model has a slightly underestimation in estimating the daily discharge, which has a lower performance than the two IHACRES and Copula-based models. Figure 10 shows a more accurate comparison of these three models. In the Taylor diagram, any model that is closer to the reference point (the hollow circle of the x-axis) is more reliable. According to Fig. 10, it can be seen that the copula-based model has a shorter distance to the reference point and as a result, has higher accuracy and performance. According to Fig. 10, the correlation of both Copula-based simulation and IHACRES models is in the range of 90%. The large distance from the reference point to the green point indicates the uncertainty and low accuracy of the Random Forest model in simulating the daily discharge of the Dashband station. Finally, the final results of the investigated models in rainfall-runoff simulation were presented in Fig. 11. According to Fig. 11, a good match can be seen between the observed values and the simulated values in IHACRES and Copula-based models.

Fig. 9

Violin plot of observed and simulated values of runoff in Dashband station

Fig. 10

Taylor diagram of observed and simulated values of runoff in Dashband station

Fig. 11

The final results of the investigated models in rainfall-runoff simulation

Discussion

Based on the evaluation criteria (RMSE, NSE and R²), the performance of the IHACRES model in simulating the river flow at Dashband station is acceptable, which is consistent with the results of Croke and Jakeman (2008). This is confirmed by the results presented in the box plot (Fig. 4b). On the other hand, Dye and Croke (2003) stated that the IHACRES model has a higher ability to simulate the discharge in small sub-basins. Since the Dashband sub-basin is considered to be a relatively small basin, the results can be considered in concordance with the results of Dye and Croke (2003). In addition, the IHACRES model is user-friendly and easy to use, it needs a low number of inputs, so it can be a suitable model for rainfall-runoff simulation in areas where little data is available. Also, input variables of this model are readily available from synoptic and hydrometric stations. But the RF model provided more error and less performance than the IHACRES and vine-based models, which did not provide satisfactory performance. The error rate of the RF model is 71% and 43% higher than the two models of vine-based and IHACRES, respectively. In general, the results show the superiority of the copula-based model in terms of three-variable rainfall-runoff simulation in the study area compared to the IHACRES and Random Forest models. The results of the copula-based model due to the use of appropriate margin distribution, conditional density and tree sequence appropriate to the input data, provided a satisfactory performance which is in accordance with the results of Tahroudi et al. (2020) in the copula-based simulation of discharge. Due to its flexible structure, this model has no geographical restrictions and is not dependent on the area of the study basin.

Conclusion

So far, many models have been developed to simulate the rainfall-runoff process. Selecting a suitable model for a basin is important to increase planning efficiency and improve water resources management. This requires evaluating the performance of different models to identify their capabilities and limitations in the studied basins. For this purpose, in this study, the performance of the IHACRES, random forest and vine-based model in simulating the rainfall-runoff phenomenon in the Dashband basin in the south of Lake Urmia was evaluated. The results of evaluating the IHACRES model using various statistical criteria and violin plot and Taylor diagram showed that this model had an acceptable performance and was able to model the entire range of changes in observational data. The efficiency of 88% in rainfall-runoff simulation in the study area is a reason to be confident in the performance of this model. The IHACRES model is based on three variables of discharge, rainfall and temperature data on a daily scale and it is a simple and user-friendly model. The results of the performance evaluation of the copula-based model in the simulation of Siminehroud river discharge indicated that this model has good accuracy and 92% efficiency (NSE). The high accuracy and performance of this model are due to the use of conditional density of copula functions, internal rotational copulas, and high capability of copula functions for the simulation purposes. According to the Taylor diagram, a correlation of more than 90% is visible for both copula-based and IHACRES models, but the standard deviation distance of the copula-based model is shorter than the IHACRES model. The copula-based model improves the simulation efficiency by about 4.5% compared to the IHACRES model. But the complexity of the copula-based model is greater than the IHACRES-based model. Due to ease of use, fewer inputs and reduced time spent according to the level of accuracy shown in this study, the IHACRES model can be used and recommended to simulate and predict river flow and rainfall-runoff simulation in the Lake Urmia Basin. However, if higher accuracy is required than the IHACRES model, a copula-based model is recommended. In the meantime, the results showed that the random forest model did not perform well in rainfall-runoff simulation in the study basin. The error rate of the random forest model in the rainfall-runoff simulation was 12.11 m³/s which is higher than the two other models. The difference of 46% efficiency of the random forest model with the vine copula model and the 40% difference in the efficiency of this model with the IHACRES model made the random forest model inappropriate for simulating the daily discharge at the Dashband hydrometric station. Due to the existence of heteroscedasticity in various parameters, in future studies, the accuracy of the proposed models can be challenged by adding conditional variance models such as ARCH models.