Skip to main content
SpringerLink
Log in

Evaluation of rainfall spatial correlation effect on rainfall-runoff modeling uncertainty, considering 2-copula

  • Original Paper
  • Published:
Arabian Journal of Geosciences Aims and scope Submit manuscript

Abstract

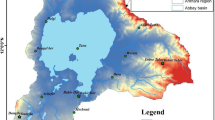
Lack of accuracy of rainfall-runoff simulation (RRS) remains critical for some applications. Among various sources of uncertainty, precipitation plays a particular role. Rainfall rates as the main input data of RRS are of the first factors controlling the accuracy. In addition to the depth, spatial and temporal distributions of rainfall impact the flood discharge. Most of the previous studies on RRS uncertainty have ignored rainfall spatial distribution, where in large catchments, it is necessary to be modeled explicitly. Karoon III is one most important basin of the Iran because of the Karoon III dam in the outlet. In the present work, effect of spatial correlation of rainfall on HEC-HMS (SMA) continuous RRS uncertainty is evaluated using 2variate copula (2copula). Monte Carlo simulation (MCS) approach was used to consider the rainfall spatial dependence. To reduce the computational expense, sampling efficiency and convergence for MCS, Latin hypercube sampling (LHS) was used. Copula functions consider wide range of marginal probability distribution functions (PDFs), eliminating limits of regular join PDFs. For this aim, two scenarios were investigated. In the first scenario, sub-basin rainfall was considered independent, and in the second scenario, 2copula was adopted to model spatial correlation of rainfall. Dimensionless rainfall depths were calculated for each sub-basin, and the PDFs were determined. The generated random dimensionless rainfalls were reweighted and multiplied by watershed’s mean rainfall value. Stochastic Climate Library was used to generate continuous daily rainfalls. Sampling from dimensionless rainfalls using LHS algorithm, 100 runs of calibrated model-simulated 100 flows for each day following MCS, and 80 % certainty bound was calculated. Results showed that considering dependence decreased 18 % of the maximum uncertainty bound width, so the methodology could be recommended for decreasing predicted runoff error.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

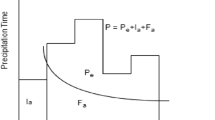
  1. \( \mathrm{Percent}\ \mathrm{error}\ \mathrm{in}\ \mathrm{peak}=100\left|\frac{q_s(peak)-{q}_o(peak)}{q_o(peak)}\right| \)

References

  • Bardossy A, Das T (2008) Influence of rainfall observation network on model calibration and application. Hydrol Earth Syst Sci 12:77–89

    Article  Google Scholar 

  • Bennett TH (1998) Development and application of a continuous soil moisture accounting algorithm for the Hydrologic Engineering Center Hydrologic Modeling System (HEC-HMS). MS thesis, Dept. of Civil and Environmental Engineering. University of California, Davis

    Google Scholar 

  • Berthet L, Andr’eassian V, Perrin C, Javelle P (2009) How crucial is it to account for the antecedent moisture conditions in flood forecasting? Comparison of event-based and continuous approaches on 178 catchments. Hydrol Earth Syst Sci 13:819–831

    Article  Google Scholar 

  • Cunderlik, J. M. and Simonovic, S.P. (2004a) Selection of calibration and verification data for the HEC-HMS hydrologic model, CFCAS project: assessment of water resources risk and vulnerability to changing climatic conditions, The University of Western Ontario, Department of Civil and Environmental Engineering, Project Report II.

  • Cunderlik, J. M. and Simonovic, S.P. (2004b) Calibration, verification and sensitivity analysis of the HEC-HMS hydrologic model, CFCAS project: assessment of water resources risk and vulnerability to changing climatic conditions, The University of Western Ontario, Department of Civil and Environmental Engineering, Project Report IV.

  • Cunge JA (1969) On the subject of a flood propagation computation method (Muskingum method). J Hydraul Res 7(7):205–230

    Article  Google Scholar 

  • Dupuis DJ (2007) Using copulas in hydrology: benefits, cautions, and issues. J Hydrol Eng 12(4):381–393

    Article  Google Scholar 

  • Favre A-C, El Adlouni S, Perreault L, Thiémonge N, Bobée B (2004) Multivariate hydrological frequency analysis using copulas. Water Resources Res 40(1):W01101

    Article  Google Scholar 

  • Flemming M, Neary V (2004) Continuous hydrologic modeling study with the hydrologic modeling system. J Hydrol Eng 9(3):175–183

    Article  Google Scholar 

  • Fontaine TA, Cruickshank TS, Arnold JG, Hotchkiss RH (2002) Development of a snowfall-snowmelt routine for mountainous terrain for the soil water assessment tool (SWAT). J Hydrol 262:209–223

    Article  Google Scholar 

  • Gabellani S, Boni G, Ferraris L, Handerberg JV, Provenzale A (2007) Propagation of uncertainty from rainfall to runoff: a case study with a stochastic rainfall generator. Advan Water Resour 30:2061–2071

    Article  Google Scholar 

  • Garcia A, Sainz A, Revilla JA, Alvarez C, Juanes JA, Puente A (2008) Surface water resources assessment in scarcely gauged basins in the north of Spain. J Hydrol 356:312–326

    Article  Google Scholar 

  • Genest C, Favre A-C (2007) Everything you always wanted to know about copula modeling but were afraid to ask. J Hydrol Eng 12(4):347–368

    Article  Google Scholar 

  • Genest C, MacKay RJ (1986) Copules archimédiennes et familles de lois bidimensionnelles dont les marges sont données. Can J Stat 14(2):145–159

    Article  Google Scholar 

  • Goda K (2010) Statistical modeling of joint probability distribution using copula: application to peak and permanent displacement seismic demands. Struct Saf 32:112–123

    Article  Google Scholar 

  • Golian S, Saghafian B, Elmi M, Maknoon R (2010) Derivation of probabilistic thresholds of spatially distributed rainfall for flood forecasting. Water Res Management 24(13):3547–3559

    Article  Google Scholar 

  • Golian S, Saghafian B, Elmi M, Maknoon R (2011) Probabilistic rainfall thresholds for flood forecasting: evaluating different methodologies for modelling rainfall spatial correlation (or dependence). Hydrol Process 25(13):2046–2055

    Article  Google Scholar 

  • Grimaldi S, Petroselli A, Nardi F (2012) A parsimonious geomorphological unit hydrograph for rainfall–runoff modelling in small ungauged basins. Hydrol Science J 57(1):73–83

    Article  Google Scholar 

  • Hwang Y, Clark MP, Rajagopalan B (2011) Use of daily precipitation uncertainties in stream flow simulation and forecast. Stoch Env Res Risk Asses 25:957–972

    Article  Google Scholar 

  • Joe H (1997) Multivariate models and dependence concepts. Chapman and Hall/CRC, Boca Raton

    Book  Google Scholar 

  • Kamali M, Ponnambalam K, Soulis ED (2007) Computationally efficient calibration of WATCLASS hydrologic models using surrogate optimization. Hydrol Earth Syst Sci Discuss 4:2307–2321

    Article  Google Scholar 

  • Mirzaei M, Huang YF, El-Shafie A, Chimeh T, Lee J, Vaizadeh N et al (2015) Uncertainty analysis for extreme flood events in a semi-arid region. Nat Hazards 78(3):1947–1960

    Article  Google Scholar 

  • Moulin L, Gaume E, Obled C (2009) Uncertainties on mean areal precipitation: assessment and impact on streamflow simulations. Hydrol Earth Syst Sci 13:99–114

    Article  Google Scholar 

  • Nelson, R.B. (2006) An introduction to copulas, Springer.

  • Schepsmeier, U. and Brechmann E.Ch. (2013) Statistical inference of C- and D-vine copulas, Package CDVine of R software.

  • Sklar A (1959) Fonctions de repartition an dimensions et leurs marges. Publications de l’Institut Statistique de l’Univ de Paris 8:229–231

    Google Scholar 

  • Sorooshian S, Duan Q, Gupta VK (1993) Calibration of rainfall-runoff models: application of global optimization to the Sacramento soil moisture accounting model. Water Resource Res 29:1185–1194

    Article  Google Scholar 

  • Srikanthan R, McMahon TA (2001) Stochastic generation of annual, monthly and daily climate data: a review. Hydrol Earth Syst Sci 5(4):653–670

    Article  Google Scholar 

  • Srikanthan, S., Chiew, F. And Frost, A. (2000) Stochastic Climate Library (SCL), User guide manual.

  • Sun X, Mein RG, Keenan TD, Elliott JF (2000) Flood estimation using radar and rain gauge data. J Hydrol 239:4–18

    Article  Google Scholar 

  • USACE (2000) Hydrologic Modeling System HEC-HMS, Technical reference manual. US Army Corps of Engineers, Hydrol. Eng. Center.

  • USACE (2010) Hydrologic Modeling System HEC-HMS, User’s manual, version 3.5. US Army Corps of Engineers, Hydrol. Eng. Center.

  • Vorechovskey M, Vovak D (2009) Correlation control in small-sample Monte Carlo type simulations I: a simulated annealing approach. Prob Eng Mech 24:452–462

    Article  Google Scholar 

  • Wang C, Chang N-B, Yeh G-T (2009) Copula-based flood frequency (COFF) analysis at the confluences of river systems. Hydrol Proces 23(10):1471–1486

    Article  Google Scholar 

  • Yu P-S, Yang TC, Chen SJ (2001) Comparison of uncertainty analysis methods for a distributed rainfall-runoff model. J Hydrol 244:43–59

    Article  Google Scholar 

  • Zahmatkesh A, Karamouz M, Nazif S (2015) Uncertainty based modeling of rainfall-runoff: combined differential evolution adaptive metropolis (DREAM) and K-means clustering. Advan Water Resour 83:405–420

    Article  Google Scholar 

  • Zhang GP, Savenije HHG (2005) Rainfall-runoff modelling in a catchment with a complex groundwater flow system: application of the representative elementary watershed (REW) approach. Hydrol Earth Syst Sci 9:243–261

    Article  Google Scholar 

  • Zhang L, Singh VP (2007) Bivariate rainfall frequency distributions using Archimedean copulas. J Hydrol 332(1–2):93–109

    Article  Google Scholar 

  • Zimmermann, H.J. (2001) Fuzzy set theory and its applications. Kluwer Academic Pub.

Download references

Author information

Authors and Affiliations

  1. Department of Water Engineering, College of Engineering, Marvdasht Branch, Islamic Azad University, Marvdasht, Iran

    Homa Razmkhah

  2. Department of Hydrology, College of Water Science and Engineering, Shahid Chamran University of Ahvaz, Ahvaz, Iran

    Ali Mohammad AkhoundAli & Fereydoun Radmanesh

  3. Department of Civil Engineering, College of Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran

    Bahram Saghafian

Authors
  1. Homa Razmkhah
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ali Mohammad AkhoundAli
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fereydoun Radmanesh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Bahram Saghafian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Homa Razmkhah.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Razmkhah, H., AkhoundAli, A.M., Radmanesh, F. et al. Evaluation of rainfall spatial correlation effect on rainfall-runoff modeling uncertainty, considering 2-copula. Arab J Geosci 9, 323 (2016). https://doi.org/10.1007/s12517-016-2392-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12517-016-2392-z

Keywords

Search

Navigation