Introduction

Since hydrological phenomena are usually described by more than one dependent variables, multivariate statistical and dependency analysis is required. The main subject of probabilistic multivariate analysis is to create a dependence structure for random variables. (Li and Zhang 2016). For multivariate modeling of different meteorological and hydrological values, multivariate distribution functions have been investigated in various studies (Salvadori and De Michele 2007). In multivariate hydrological analyses, mainly items such as showing the importance and framework of multivariate, fitting appropriate multivariate distribution and studying multivariate return periods are considered. (Chebana and Ouarda 2011). The most widely used copula cumulative joint distribution function (CDF) is Gaussian. To overcome it, a bivariate distribution with margins such as gamma bivariate distribution, exponential bivariate distribution and extreme values bivariate distribution was proposed (Adamson et al. 1999; Yue et al. 2001; Favre et al. 2002). Favre et al. (2004) summarized the drawbacks of this type of distribution: (1) marginal distribution should be from the same family, (2) for the case of more than two variables, it is not clear and expressive and (3) marginal distribution parameters are also used for dependency model between random variables. In order to overcome these deficiencies, copulas, which are the latest mathematical tools for analyzing multivariate phenomena, were used in hydrological analysis (Xiau et al. 2008). The advantages of using a copula distribution over joint distribution methods are: (1) flexibility in selection of appropriate marginal distribution and dependence structure; (2) Increase the dimension to more than two variables and (3) marginal distribution analysis and dependence structure (Serinaldi et al. 2009; Salvadori et al. 2007).

During the past years, copula functions have been used for analysis the multivariate hydrological time series. Favre et al. (2004) used bivariate copulas to describe the relationship between flood peak flow and flood volume. In another study, Shiau et al. (2006) used copula functions to investigate joint frequency of flood peak flow and flood volume. Zhang and Singh (2006) used Archimedean functions for two-dimensional distribution of flood characteristics (pair variables of peak flow and flood volume, pair variables of flood peak flow and flood duration, and pair variables of flood volume and flood duration). Also Grimaldi and Serinaldi (2006a, b) provided a three-dimensional distribution of flood variables using general and asymmetric Archimedean complex functions and performed extensive simulations to highlight differences. Salvadori and De Michele (2007) developed some hydrological modeling such as calculating joint probabilities and joint return periods of two different events by using copula functions. Zhang and Singh (2007a) used another model of Coppola called Gumbel–Hougaard to investigate the three-dimensional distribution of flood peak flow, volume, and flood duration. Kao and Govindaraju (2008) investigated the Plackett copula and used it for the temporal distribution of extreme rainfall.

The use of copula functions in water resources and hydrology can be named as follows: frequency analysis of rainfall (De Michele and Salvadori 2003; Grimaldi and Serinaldi 2006a; Kao and Govindaraju 2007; Kuhn et. al. 2007; Zhang and Singh 2007a; Keef et al. 2009), in field of frequency analysis of flood can be named study of Favre et al. (2004), Shiau et al. (2006), Renard and Lang (2007), and Zhang and Singh (2006 and 2007b). The use of copula function in field of frequency analysis of drought also can be named research of Shiau (2006), Serinaldi et al. (2009), Kao and Govindaraju (2010), and Song and Singh (2010). Also in field of analysis of sea storm, De Michele et al. (2007), in field of flow simulation, Chen et al. (2015), in field of multivariate analysis the characteristics of rainfall, Salvadori and De Michele (2007) and Zhang et al. (2013), in field of multivariate analysis the characteristics of drought, Salvadori and De Michele (2004), Mirakbari et al. (2010), Mirabbasi Najafabadi et al. (2013), Abdi et al. (2017), Ramezani et al. (2019) and Tahroudi et al. (2020a), in field of groundwater level simulation, Tahroudi et al. (2020b) and some field of multivariate extreme events can be named Salvadori et al. (2007) and Salvadori and De Michele (2010). Therefore, copula functions are effective tools for analyzing and simulating multivariate hydrological phenomena (Calvo and Savi 2009; Chen et al. 2014; Fan et al. 2016). Hydrological prediction is a non-structural measure to deal with floods and droughts and an essential principle for flood warning and reservoir operation (Zhang et al. 2015; Liu et al. 2016; Wu et al. 2017). Predictive models that have been widely used in recent years are mostly definitive.

However, a hydrological prediction model is only for simulating hydrological which is usually incomplete (Wetterhall et al. 2013; Ravines et al. 2008) that accept different hydrological and meteorological input and use the parameters of the conceptual model; and these complex factors are due to unreliability in hydrological predictions (Freer et al. 1996; Montanari and Grossi 2008; Montanari 2007). The principle of logical decision-making in uncertainty shows that when a definite prediction is wrong, the consequences are likely worse than in a situation where no prediction is available (Krzystofowicz 1999; Wetterhall 2013; Ramos et al. 2013). Therefore, the logical decision maker who wants to make the desired decisions should be explicitly predicted with uncertainty (Verkade and Werner 2011; Ramos et al. 2013). Hydrological prediction seeks to provide probabilistic prediction rather than definitive prediction. For example, Nazeri Tahroudi et al. (2021) attempted to flood routing via a copula-based approach. They used vine copulas to simulation the flood hydrographs. The results of their study showed that copula-based approach has acceptable accuracy and performance. Khashei-Siuki et al. (2021) used vine copulas to simulate the potential evapotranspiration. By introducing the best dependence structure and tree sequence, the results of simulation of potential evapotranspiration showed that the efficiency of C-vine copula in dependence analysis and simulation of potential evapotranspiration is good, which indicates the ability of vine copulas in multivariate analysis.

The researches on copula functions are limited to bivariate frequency analysis. Copula-based simulations have also been developed in recent years. But this study seeks to provide a copula-based approach to determining the three-variable return period. The aim of the present study, while analyzing the tree sequences of vine copulas in determining the joint return period and the joint probability of occurrence, is to model and simulate three-dimensional water resources signatures. In order to achieve this, C-, D- and R-vine copulas and their conditional density were used.

Materials and methods

Study area

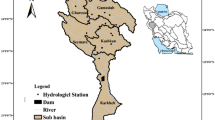
The study area in this study is Tapik basin located in the west of Lake Urmia basin. Lake Urmia is located 1267 m above sea level and directs runoff of heights around the basin. In this study, data on rainfall, river flow and groundwater level in Tapik basin during the statistical period of 1977–2019 have been used. Tapik aquifer is an unconfined aquifer. In the study basin, a rain gauge station was selected to indicate rainfall, a hydrometric station was selected to indicate river flow and a piezometric well was selected to show groundwater level changes. A summary of the statistical characteristics of the data studied in this study can be seen in Table 1 and the location of the study area as shown in Fig. 1.

Table 1 Statistical characteristics of the studied data at an annual scale
Full size table
Fig. 1
figure 1

Geographical location of Tapik basin in Iran and Lake Urmia basin

Full size image

Selection of indicator rain gauge station/piezometric well

In this study, to select indicator rain gauge station/piezometric well, the entropy theory was used. Since there are several rain gauge stations and piezometric wells in the study basin and their distribution is uniform throughout the basin, so instead of using thiessen polygon or weighted average, entropy theory was used. In this method, the rain gauge station/piezometric well that transfers more information with other stations is selected as the indicator rain gauge station/piezometric well. In this method, entropy indices are first calculated according to the probability tables and the interaction of the rain gauge stations/piezometric wells. The rain gauge stations/piezometric wells were classified and ranked according to entropy indices and finally based on information transfer index of entropy theory, introduced as the indicator rain gauge station/piezometric well. The rain gauge station/piezometric well that has the highest rank is selected as the indicator rain gauge station/piezometric well. In this study, Tapik rain gauge station/Nazloo piezometric well selected as the indicator rain gauge station/piezometric well in the basin. For more information on entropy theory, see Mogheir et al. 2006 and Tahroudi et al. 2019a.

Extraction of water resources signatures

The rainfall, river flow and groundwater level deficiencies, which are referred to as water resources signatures in this study, based on the proposed method of Tahroudi et al (2019b) are extracted for a 60-day duration. The values generated are hereinafter referred to as "signature".

The rainfall deficiency means deficiency for 1- to n-day consecutive durations of rainfall compared to its mean long-term which are extracted from the daily rainfall. At the first step, the mean individual daily long-term period (MIDLP) is calculated using Eq. (1) for every day of the year. In fact, the number of MIDLPs will be equal to the number of days in a year (365). (Besharat et al. 2014; Tahroudi et al. 2019b).

$$\begin{gathered} MIDLP = \frac{{Rainfall\,of\,Oct\,\,1^{st} ,\,1977 + ..... + Rainfall\,\,of\,Oct\,\,1^{st} ,\,\,2019}}{Number\,of\,years} \hfill \\ MIDLP = \frac{{Rainfall\,of\,Oct\,\,2^{nd} ,\,1977 + ..... + Rainfall\,\,of\,Oct\,\,2^{nd} ,\,\,2019}}{Number\,of\,years} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,: \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,: \hfill \\ MIDLP = \frac{{Rainfall\,of\,Dec\,\,31^{st} ,\,1977 + ..... + Rainfall\,\,of\,Dec\,\,31^{st} ,\,\,2019}}{Number\,of\,years} \hfill \\ \end{gathered}$$
(1)

In the next step, to obtain the new data, the daily rainfall data were subtracted from corresponding MIDLPs. The aim of present study is to find consecutive deficiency periods between 1 and n-day duration (Nazeri Tahroudi et al. 2019b). In this study, the above method was used to calculate river flow and groundwater level deficiency signatures.

Copula functions

The first topics related to copula functions and their application were introduced by Sklar (1959). Copulas are functions that connect the marginal distribution of one-dimensional variables to create a multivariate distribution (Nelson 2006). This function is able to show dependence structure between random variables and has recently emerged as a practical and efficient method for dependency modeling and dependency analysis of multivariate series. The results of studies by Joe (1997) and Kurowicka and Cooke (2007) indicated that a simple building block cascade called pair-copula can model multivariate series. Consider \(X = (X_{1} ,...,X_{n} )\) vector of random variables with \(f(x_{1} ,...,x_{n} )\) combined density function. This density is as follows:

$$f(x_{1} ,...,x_{n} ) = f_{n} (x_{n} ).f(x_{n - 1} |x_{n} ).f(x_{n - 2} |x_{n - 1} ,x_{n} )...f(x_{1} |x_{2} ,...,x_{n} )$$
(2)

this decomposition is unique until it reaches the reproduction of variables. Each joint distribution function implicitly includes the marginal behavior of individual variables and their dependence structure. The copula provides a way to isolate their dependence structure. A copula is the multivariate distribution C with the uniform distribution margins U (0,1) in [0,1]. Sklar theory states that any multivariate distribution F with margins F1(x1),…,F2(x2) can be written as follows:

$$F(x_{1} ,...,x_{n} ) = C\left\{ {F_{1} (x_{1} ),...,F_{n} (x_{n} )} \right\}$$
(3)

For some multidimensional (n-dimensional) C copulas, the above equation is actually corrected as follows.

$$C(u_{1} ,...,u_{n} ) = F\left\{ {F_{1}^{ - 1} (u_{1} ),...,F_{n}^{ - 1} (u_{n} )} \right\}$$
(4)

where \(F_{n}^{ - 1} (u_{n} )\) is the inverse of marginal distribution functions. According to the joint density function f, for incremental continuous F values, the continuous marginal densities F1,…,F2 are estimated using the following chain law for some n-variable copula densities \(c_{1...n} (.)\):

$$f(x_{1} ,...,x_{n} ) = c_{1...n} \left\{ {F_{1} (x_{1} ),...,F_{n} (x_{n} )} \right\}.f_{1} (x_{1} )...f_{n} (x_{n} )$$
(5)

For the bivariate example, Eq. (5) is simplified as follows:

$$f(x_{1} ,x_{2} ) = c_{12} \left\{ {F_{1} (x_{1} ),F_{2} (x_{2} )} \right\}.f_{1} (x_{1} ).f_{2} (x_{2} )$$
(6)

where \(c_{12} (.)\) is suitable pair-copula density for the pair of converted variables F1(x1) and F2(x2). For conditional density, the following can be done, which is the same for all pair-copulas.

$$f\left( {x_{1} |x_{2} } \right) = c_{12} \left\{ {F_{1} (x_{1} ),F_{2} (x_{2} )} \right\}.f_{1} \left( {x_{1} } \right)$$
(7)

For example, \(f(x_{n - 1} |x_{n} )\), the right of Eq. (2), can be decomposed into \(c_{(n - 1)n} \left\{ {F_{n - 1} (x_{n - 1} ),F_{n} (x_{n} )} \right\}\) pair-copula and \(f_{n - 1} (x_{n - 1} )\) marginal densities. For the random variables X1, X2 and X3, \(c_{12|3}\) suitable pair-copula can be written \(F(x_{1} |x_{3} )\) and \(F(x_{2} |x_{3} )\) for converted to values:

$$f\left( {x_{1} |x_{2} ,x_{3} } \right) = c_{12|3} \left\{ {F(x_{1} |x_{3} ),F(x_{2} |x_{3} )} \right\}.f\left( {x_{1} |x_{3} } \right)$$
(8)

Alternative decomposition is as follows:

$$f(x_{1} |x_{2} ,x_{3} ) = c_{13|2} \{ F(x_{1} |x_{2} ),F(x_{3} |x_{2} )\} .f(x_{1} |x_{2} )$$
(9)

where \(c_{13|2}\) differs from the pair-copula equation in (8). \(f(x_{1} |x_{2} )\) decomposition in Eq. (7) follows the following.

$$f(x_{1} |x_{2} ,x_{3} ) = c_{13|2} \{ F(x_{1} |x_{2} ),F(x_{3} |x_{2} )\} .c_{12} \{ F(x_{1} ),F(x_{2} )\} f_{1} (x_{1} )$$
(10)

where two pair-copulas are present.

It is now clear that any of the terms in Eq. (2) can be decomposed into several suitable pair-copulas and marginal densities using a general formula for a d-dimension vector v.

$$f(x|v) = c_{{xv_{j} |v_{ - j} }} \left\{ {F(x|v_{ - j} ),F(v_{j} |v_{ - j} )} \right\}.f(x|v_{ - j} )$$
(11)

where \(v_{j}\) is an optional component of v, \(v_{ - j}\) refers to the vector v that contains this component. As a result, under appropriate conditions, the multivariate conditional density, expressed as the product of the pair-copula, acts differently on various conditional probability distributions. Given that the structure is iterative, and according to a special classification, there are still many different parameters that the pair-copula structure includes F(x|v) marginal distribution functions. Joe (1997) showed that for each j:

$$f(x|v) = \frac{{\partial C_{{x,v_{j} |v_{ - j} }} \left\{ {F(x|v_{ - j} ),F(v_{j} |v_{ - j} )} \right\}}}{{\partial F(v_{j} |v_{ - j} )}}$$
(12)

where \(C_{ij|k}\) is the copula bivariate distribution function. For a special case where v is univariate:

$$f(x|v) = \frac{{\partial C_{cv} \left\{ {F(x),F(v)} \right\}}}{\partial F(u)}$$
(13)

\(h(x,v,\Theta )\) is also used to represent the conditional distribution function in cases where x and v are uniform. For example: F (x) = x and F (v) = v, then f (x) = f (v) = 1, in this case:

$$h(x,v,\Theta ) = F(x|v) = \frac{{\partial C_{x,y} (x,v,\Theta )}}{\partial v}$$
(14)

The second parameter of the expression h(.) has a perfect correspondence with the conditional variable and \(\Theta\) refers to the set of parameters of the joint distribution function x and v for the copula. In addition, \(h^{ - 1} (u,v,\Theta )\) the inverse of the function h, with respect to the first variable u or its equivalent, is equal to the inverse of the conditional distribution function.

In traditional multidimensional copulas, all series should have the same dependency. When the dimensions reach more, the accuracy of traditional methods is significantly reduced. Reciprocally, vine copulas allow all types of dependencies in different pairs. While a d-dimensional vine is made by d (d—1) a double copula as a tree. There are several ways to make a copula tree. C- and D-vine copulas are common types of trees. For example, in a C-vine tree, the dependency is modeled for a special variable (as the first root node) by bivariate copulas for each pair. According to this variable, the dependencies of the other pairs are selected according to the second variable. R-vine copula is more drawable than C or D type because it allows for a wider range of sequences. In order to increase sequence diversity, R-vine copula introduces a new concept. Two specific characteristics of vine tree were identified by Bedford et al. (2001). One of them is called drawable vine tree (D-vine) and the other is called canonical vine tree (C-vine). They are defined as follows:

A regular vine (R-vine) copula:

D-vine, if each node in T-1 tree has a maximum of two edges.

C-vine, if each tree in Ti has a special node with d-1 edge. The node with d-1 edge in Ti tree is called the root.

For higher dimension distribution, there is a significant number of possible pair-copula sequences. For example, there are 240 different sequences for the five-dimensional state (Aas et al. 2009). In order to help organize them, a graphical model called a regular vine was introduced. The regular copula class is very broad and includes a large number of possible pair-copulas. Each model offers a specific method for density analysis. C- and D-vine also belong to regular vines. Their characteristics may be in the form of, for example, a set of nested trees. Figure 2 shows characteristics of a five-dimensional vine that consists of four trees Tj, J = 1,…, 4. Tj tree has j-6 nodes and j-5 edges. Each edge with density belongs to the pair-copula and the edge label also belongs to the pair-copula density sample. For example, edge 14 | 23 belongs to the copula density C14|23(.). All analyses are defined by n (n-1) / 2 edge and marginal density of each variable. Tj tree node is only needed to determine the edge labels in Tj + 1 tree. As shown in Fig. 2, the two edges in Tj (which become nodes in Tj + 1) become one edge in Tj + 1 only if these edges have a common node in Tj. Note that a tree sequence is not absolutely necessary to apply the pair-copula method, but it does help to identify different pair-copula decompositions.

Fig. 2
figure 2

D-Vine with five variables, four trees and ten edges. Each edge may be associated with a pair-copula (Aas et al. 2009)

Full size image

Bedford and Cooke (2001) assigned the density of an n-dimensional distribution of regular copulas to C- and D-vine copulas. f(x1,…,xn) density of D-vine copula is written as follows:

$$\begin{gathered} f(x_{1} ,...x_{n} ) = \prod\limits_{k = 1}^{n} {f(x_{k} )} \prod\limits_{j = 1}^{n - 1} {\prod\limits_{i = 1}^{n - j} {c_{i,i + j|i + 1,.....,i + j - 1} } \left\{ {F\left( {x_{i} |x_{i + 1} ,...,x_{i + j - 1} } \right)} \right.} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\left. {F\left( {x_{i + j} |x_{i + 1} ,...,x_{i + j - 1} } \right)} \right\} \hfill \\ \end{gathered}$$
(15)

where j represents the trees that i runs around the edges of each tree. In D-Vine copula, no node in any of Tj trees is attached to more than two edges. In a regular vine copula, each Tj tree has a unique node attached to the n—j edge. Figure 3 shows C-vine copula with five variables. The next n density corresponding to C-vine copula is as follows:

$$\begin{gathered} f(x_{1} ,...x_{n} ) = \prod\limits_{k = 1}^{n} {f(x_{k} )} \prod\limits_{j = 1}^{n - 1} {\prod\limits_{i = 1}^{n - j} {c_{i,j + i|1,.....,j - 1} } \left\{ {F\left( {x_{j} |x_{1} ,...,x_{j - 1} } \right)} \right.} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\left. {F\left( {x_{j + i} |x_{1} ,...,x_{j - 1} } \right)} \right\} \hfill \\ \end{gathered}$$
(16)
Fig. 3
figure 3

C-vine copula with 5 variables, 4 trees and 10 edges (Aas et al. 2009)

Full size image

Knowing that C-vine copula is appropriate may be useful when a special variable is the key variable that governs the interaction in the data set. Such conditions, it may decide to replace this variable at the root of C-vine copula (as is shown in Fig. 3 in the first tree with variable number 1).

Trivariate state

The common definition for the structure of both 3-D C- and D-vine copulas is as follows:

$$\begin{gathered} f(x_{1} ,x_{2} ,x_{3} ) = f_{1} (x_{1} ).f_{2} (x_{2} ).f_{3} (x_{3} ).c_{12} \{ F_{1} (x_{1} ),F_{2} (x_{2} )\} . \hfill \\ c_{23} \{ F_{2} (x_{2} ),F_{3} (x_{3} )\} .c_{13|2} \{ F_{1} (x_{1} |x_{2} ),F_{2} (x_{3} |x_{2} )\} \hfill \\ \end{gathered}$$
(17)

There are six allowed methods for changing x1, x2, and x3 in Eq. (17), but only three methods have different decompositions. In addition, each of the three decompositions includes C- and D-vine copulas.

Conditional independence and pair-copula decompositions

Conditional independence can simplify analysis by reducing the level of pair-copula decompositions. Consider the three-dimensional process by decomposing the pair-copula in Eq. (2). For certain values of X1 and X3 with respect to X2, then, c13|2(F(x1|x2), F(x3|x2)) = 1. Therefore, pair-copula decomposition in this regard is simplified as follows.

$$f(x_{1} ,x_{2} ,x_{3} ) = f_{1} (x_{1} ).f_{2} (x_{2} ).f_{3} (x_{3} ).c_{12} \{ F_{1} (x_{1} ),F_{2} (x_{2} )\} .c_{23} \{ F_{2} (x_{2} ),F_{3} (x_{3} )\}$$
(18)

for any vector of V and two variables X and Y, they are conditionally independent (with respect to V) if:

$$c_{xy|v} \{ F(x|v),F(y|v)\} = 1$$
(19)

In hierarchical modeling, a model is simplified only if the common density factor uses the assumed conditional independence. For example, if the decomposition f(x1,x2,x3) = f(x2|x1,x3)f(x1|x3)f3(x3) is used in cases where X1 and X3 have conditional independence with X2, the existence of all pair-copulas is essential.

Confidence interval

Confidence interval for estimates xi are constructed using the standard error SE (xi). Lower and upper limit of the confidence interval for xi are calculated from (Apel 2004):

$$x_{i,U} = x_{i} + z_{1 - \alpha /2} .SE(x_{i} )$$
(20)
$$x_{i,L} = x_{i} - z_{1 - \alpha /2} .SE(x_{i} )$$
(21)
$$SE(x_{i} ) = \frac{{s_{x} }}{\sqrt n }\sqrt {1 + \frac{1}{2}z_{p}^{2} }$$
(22)

where z1–α/2 = –z α/2 is standard normal variable for levels corresponding to confidence interval 1 – α. where zp is standard normal variable corresponding to probability of nonexceedance p.

Results and discussion

Rainfall deficiency signature (RDS), river flow deficiency signature (FDS) and groundwater deficiency signature (GDS) were extracted using the desired method for a 60-day duration. The results of extracting the deficiency signatures for 10, 30 and 60-day durations are showed in Figs. 4, 5, 6.

Fig. 4
figure 4

Results of rainfall deficiency signature at Tapik rain gauge station for 10, 30 and 60-day durations in statistical period of 1977–2019

Full size image
Fig. 5
figure 5

Results of river flow deficiency signature at Tapik hydrometric station for 10, 30 and 60-day durations in statistical period of 1977–2019

Full size image
Fig. 6
figure 6

Results of groundwater level deficiency signature in Nazloo piezometric well for 10, 30 and 60-day durations in statistical period of 2004–2019

Full size image

The reason for choosing a 60-day duration is to consider the worst possible conditions for the study area. Because rainfall deficiency of more than 60 days not exist, this duration was selected as the final duration. As shown in the above Figures, concentration pattern distribution is the same for all three durations. As shown, the changes in rainfall deficiency signature have intensified in recent years. Due to changes in river flow in Lake Urmia basin mentioned in various studies including Khalili et al. (2016), Tahroudi et al. (2018) and Khozeymehnezhad and Tahroudi (2019), it is possible to observe the increasing trend of river flow deficiency signature. The change in the form of rainfall in recent years and the disappearance of snow reserves in the northern regions of Lake Urmia basin, as well as climate change, led to a reduction in rainfall and river flow. In recent years, river flow deficiency has changed the regime of rivers and permanent rivers have become seasonal rivers and even flood crossing. This will cause many problems for the West Azerbaijan Province of Iran and Lake Urmia, which are highly dependent on surface water. Reducing river flow and limiting the irrigation cycle of fields in this basin cause farmers to turn to groundwater and dig unauthorized wells, which causes serious damage to the aquifer. Inlet flow to Lake Urmia, in addition to surface water, includes groundwater. Reducing the inflow of surface water and groundwater to Lake Urmia increases its water salinity. This increase in salinity causes damage to the habitats of living things and aquatic animals. The results indicated that the groundwater deficiency signature has an increasing trend. Due to the shallow depth of groundwater in the study area, the rainfall and river flow have a direct effect on groundwater level and there is not much time delay between mentioned variables. With the increase of groundwater level deficiency and due to the size of the aquifer, a large volume of groundwater becomes unavailable, which is very difficult to compensate for the shortage of reservoir.

On the other hand, by increasing extreme values of rainfall and also groundwater level, the soil texture is gradually damaged, which is irreparable, and the soil structure gradually becomes irreversible, which will help increase the flood potential. In the next step, different marginal distributions are fitted to the data. The results of comparing the different distributions based on Kolmogorov–Smirnov and Anderson Darling goodness of fit tests are presented in Table 2.

Table 2 Results of fitting the marginal distribution on the studied signatures
Full size table

In this study, in order to obtain the best marginal distribution function, the common statistical distribution functions with two, three and four variables in hydrology were used. One of the important steps for applying copula functions is to discuss marginal distribution functions.

Trivariate analysis of groundwater deficiency signature affected by river flow and rainfall deficiency signatures for a 60-day duration

The studied signatures for 10, 30 and 60-day durations as well as rainfall, river flow and groundwater level were presented as shown in Fig. 7.

Fig. 7
figure 7

4-dimensional display of the studied signatures in Tapik basin (a: GDS, b: FDS and c: RDS)

Full size image

In this section, different vine copulas including C-, D- and R-vine copulas are investigated and the best copula is selected according to the criteria (AIC, BIC and Log likelihood). However, the use of vine copulas requires correlation between the studied signatures. Correlation is essential for using copula functions. If there is a poor correlation, copula functions will not be able to multivariate analysis. According to the results of Kendall’s tau, the correlation between the studied signatures is confirmed and the accuracy of multivariate analyses can be ensured. Various studies such as Zhang et al. (2018), Cooke et al. (2015), Kurowicka and Cooke (2007), Aas et al. (2009), Bezak et al. (2017), Bevacqua et al. (2017), Khan et al. (2019), Graler et al. (2013), Brunner et al. (2019) and Tahroudi et al. (2020a, b) also confirmed and recommended Kendall’s tau to investigate the correlation of pair-variables. The study results of correlation between the studied signatures in Tapik basin are presented in Fig. 8. In Fig. 8, the main diameter elements represent marginal histogram of copula data, top triangular elements represent pair-copula data, and lower triangular elements represent normalized empirical contour lines of copula data. The numbers presented indicate the correlation of Kendall’s tau between the studied signatures. In the next step, vine copulas are fitted.

Fig. 8
figure 8

Study of correlation of studied signatures using Kendall’s tau in Tapik basin

Full size image

Another noteworthy point is the selection of fitting trees. Rainfall and river flow will affect the groundwater level. In other words, river flow is affected by rainfall and on the other hand, the groundwater level is affected by river flow and rainfall. One of the important issues is the multiplicity of tree sequences in the use of vine copulas. In order to obtain the optimal copula, all the different tree sequence states created with C-, D- and R-vine copulas were analyzed and the results for Tapik basin are presented in Table 3, 4, 5, 6. Determining of copula parameters in this study was based on the maximum likelihood estimation (MLE( method.

Table 3 Study results of R-vine copula for selecting copula function and the type of tree in Tapik basin
Full size table
Table 4 Study results of Gaussian R-vine copula for selecting copula function and type of tree in Tapik basin
Full size table
Table 5 Study results of C-vine copula for selecting copula function and type of tree in Tapik basin
Full size table
Table 6 Study results of D-Vine copula for selecting copula function and type of tree in Tapik basin
Full size table

As shown in Tables above, no significant difference was between AIC, BIC and Log likelihood statistics. Therefore, according to the physics of the problem as well as the calculated statistical parameters, D-vine copula was selected as the best copula. Finally, the selected tree is described in Fig. 9. It should be noted, however, that in the three-dimensional state, no difference was between C- and D-vine copulas in terms of tree sequence. But their parameters are different. In different studies, the dependence structure and tree sequence of vine copulas including C-, D- and R-vine have been investigated and their accuracy has been different for different data (depending on the physics of the problem). The results also indicate the ability of R-vine copula to analyze data and investigate uncertainty. This has also been confirmed and recommended in a study by Cooke et al. (2015). These models are able to manage large amounts of data and maintain the correlation of all executed values. Of course, R-vine copula functions have drawable sequences, but they have high complexity, which is the case mentioned in a study by Aas et al. (2009). On the other hand, Khan et al. (2019) by investigating the correlation structure of climatic variables showed that the accuracy of the two C- and D-vine copulas is almost close to each other.

Fig. 9
figure 9

Final tree of D-vine copula in three-dimensional structure analysis of groundwater level deficiency signature in Tapik basin

Full size image

By introducing D-vine copula as the best copula for trivariate analysis of the studied signatures, the parameters of the internal copula functions for the joint analysis of the edges of pair-variables have also been calculated and presented. In the first tree, pair-variables, related copulas and edges are introduced and analyses are performed with selected copulas. In the second tree, according to the presented conditional structure, conditional and trivariate calculations are presented.

According to the selected sequences and edges, the analysis of the return period in "and" state of the groundwater deficiency signature affected by rainfall and river flow deficiency signatures was calculated and presented as shown in Fig. 10. The return period in "and" state is the state in which all three variables are less than a certain threshold. In the presented figures, the x-axis represents groundwater level deficiency signature, the y-axis represents rainfall deficiency signature, and the z-axis represents river flow deficiency signature. The color box to the right of the curves is also the 4th dimension. For example, increasing groundwater deficiency signature to about 0.5 m, which is affected by rainfall deficiency signature equal to 15 mm and river flow deficiency signature equal to 0.3 m3/s, has a return period of about 8 years.

Fig. 10
figure 10

Trivariate return period analysis of groundwater deficiency signature affected by river flow and rainfall deficiency signatures in "and" state for a 60-day duration

Full size image

For the study basin, different states can be observed, each of which has a special return period. The curve presented in this section can be used as a complete reference for water resources management in terms of changes in rainfall, river flow and groundwater level. This curve shows the changes in the studied values during different return periods, each of which can be estimated to occur. These curves are in fact the evolved state of two-dimensional analysis that show the effect of rainfall changes on the river flow and groundwater level. Given that in the last tree, RDS60 | GDS60, FDS60 is established, river flow deficiency signature for a 60-day duration also depends on rainfall deficiency signature for a 60-day duration. As a result, changes in river flow and groundwater deficiency signatures can be considered as affected by rainfall deficiency signature. The accuracy of the calculations is acceptable according to the statistics used to investigate the tree sequence of the copulas. Because using AIC, BIC and Log likelihood statistics, the accuracy of the copulas was evaluated and the best copula was selected.

In this study, in order to investigate the efficiency of vine copulas for modeling and simulating the copula values of the studied signatures, the combination of conditional values of the selected copulas was used. According to the aim of this study, groundwater deficiency signature was simulated in the study area and the results of Pearson correlation between pair-variables were presented as shown in Fig. 11. It should be noted that red values indicate Kendall’s tau of measured data and black values indicate Kendall’s tau between simulated data (groundwater deficiency signature) and other signatures.

Fig. 11
figure 11

Results of groundwater level deficiency signature simulation in Tapik basin on the copula scale

Full size image

The simulation was performed using vine copulas and selected internal copulas to evaluate the efficiency of the copulas for estimating the results. At this step, in order to estimate and determine the accuracy of the studied copulas, using conditional density of the copulas, the studied signatures were simulated for a 60-day duration. The other signature data were used to simulate the studied signatures. Thus, to simulate groundwater, river flow and rainfall deficiency signatures were used for a 60-day duration. Physically, in the case of groundwater level, it is possible to simulate groundwater level deficiency signature using rainfall and river flow deficiency signatures. But since groundwater level has no effect on river flow or rainfall, this simulation is physically rejected. However, simulation of rainfall and river flow deficiency signatures is presented only to investigate the accuracy of the copulas in the analyses. After simulating the studied signatures, the correlation of pair-signatures was investigated using Kendall’s tau test. The simulation results of studied pair-variables showed that correlation between rainfall and groundwater level deficiency signatures, and river flow and groundwater deficiency signatures at simulation stage reduced slightly. This reduction or increase in correlation values of the studied pair-copulas is not a reason for a reduction or increase in the accuracy of the copulas in the simulation of the studied signatures. RMSE and NSE statistics were used to investigate the accuracy and efficiency of the studied copulas in simulating the studied signatures. RMSE and NSE of the selected copulas for simulating groundwater deficiency signature for a 60-day duration due to rainfall and river flow deficiency signatures were 0.03 m and 70%, respectively. The results showed that vine copulas have high accuracy in simulating hydrological values. This has been the case mentioned and confirmed in various studies such as Aas et al. (2009) and Kurowicka and Cooke (2007). After simulating and confirming accuracy of the selected copula, joint frequency of the studied signatures was analyzed for a 60-day duration. The study results of the joint probability of occurrence of groundwater deficiency signature affected by rainfall and river flow deficiency signatures are presented in Fig. 12. For example, for this basin, the probability of increasing groundwater deficiency signature to more than 2.5 m, which is affected by rainfall deficiency signature equal to 300 mm and river flow deficiency signature equal to 2.5 m3/s, is about 90%.

Fig. 12
figure 12

Joint probability of occurrence of groundwater deficiency signature for a 60-day duration in Tapik basin

Full size image

The results of joint probability analysis of the studied signatures showed that the use of vine copulas as well as three-dimensional analysis can well show the changes in water resources signatures of the studied basin. The presented four-dimensional curves show the probability of occurrence of water resources signatures in the basin. Groundwater level in areas with surface water resources, such as Lake Urmia, is not dependent on rainfall as the only factor. For this reason, the use of trivariate analysis and the involvement of effective parameters such as rainfall and river flow deficiency signatures, increases the accuracy of groundwater deficiency signature estimation. Also, using the presented curves, the effect of each of rainfall and river flow deficiency signatures can be observed on groundwater level deficiency signature. This is also very important physically, because using the presented curves, the effect of rainfall can be directly and indirectly observed on groundwater level. The presented curves can be used as typical curves for water resources monitoring in the basin. The presented curves will act as a continuous monitoring system in the basin. Graler et al. (2013) in their studies on the multivariate flood return period showed that in the joint case, the probability of occurrence is closer to reality. On the other hand, the results of simulation also confirmed the performance of the selected copulas.

Conclusion

The combined, multivariate, or dependent events are multivariate extreme events that may not be limited in themselves, but their occurrence causes other events to occur. The conventional univariate statistical analysis in these cases cannot provide accurate information about the multivariate nature of these dependent events. Therefore, the risk associated with these events is not possible by univariate statistical analysis. Because the existing approaches are statistically different, from a scientific point of view, it is almost impossible to provide a suitable approach for estimating multivariate cases. Many practical models and approaches based on the concept of univariate return period have been proposed by researchers so far. But the multivariate return period has a different meaning. On the other hand, simulation using copulas is very helpful in investigating accuracy of selected copulas in the analyses performed. The results showed that in case of reduced rainfall in the study area, which is the first tangible factor in each basin, deficiency of other signatures can be estimated with different probabilities. This model is plotted using the many complexities that exist in terms of three-dimensional copula functions, parameter estimation, tree sequences, and conditional density. At later stages, future predictions can be very effective and there are no complexities in calculating curves. Given that each curve is specific to the relevant basin, these curves can be used as long as the changes in rainfall are not significant and there is no time of changing point in the data. These curves can be used to joint frequency analysis of water resources signatures in the study basin. For each rainfall deficiency signature (y axis), it is possible to observe river flow and groundwater level deficiency signatures affected by rainfall deficiency signature with different probabilities of occurrence. The results showed that by increasing rainfall deficiency signature, the joint probability of occurrence as well as groundwater level and river flow deficiency signatures increases. In the study basin, three-dimensional analysis of groundwater deficiency signature showed that with a reduction of more than 150 mm in rainfall, groundwater level increases significantly. In this case, river flow is reduced by about 2 m3/s. Groundwater level in this basin is highly dependent on rainfall changes. As rainfall deficiency signature in the study area increases, the decreasing trend of river flow increases. This is due to the seasonal rivers in this basin in recent years. The results showed that the probability of increasing groundwater level in trivariate state in the study basin is not less than 30%. The study results of the return periods of groundwater deficiency signature also showed that in the study basin, the increase in groundwater level every year is not far from expectation. In most cases, the return periods of groundwater deficiency signature in the basin are less than 5 years. 4-D curves of joint frequency analysis can be used in aquifer management, surface water and groundwater resources allocation, as well as water resources management in the basin.