Introduction

Spillways are major parts of dams for controlled and uncontrolled disposal of excess inflows to reservoirs, especially in flood conditions. Downstream of the spillways, at the point of contact of the jet with the riverbed, a hole is excavated into the soil and rocks due to the high energy of water. Therefore, for high-flow discharges, spillways are devised with energy dissipaters such as ski jumps to reduce the downstream scouring. There are many types of spillways, out of which the ski-jump bucket type is more commonly used. The energy dissipation in such a spillway is in the form of a jet of water leaving away from the bucket lip into the air, and then, falling into the plunge pool formed at the point of impact on the tailwater. To reduce heavy soil erosion and thereby dam failures, and to evaluate the stability of the dam and other hydraulic structures, accurate estimation of downstream scouring is very crucial.

In order to study erosion and scour downstream of hydraulic structures, physical hydraulic models such as Navier–stokes and associated equations by computational fluid dynamics (CFD) methods of finite element and finite volume have been widely applied (Zhang et al. 2014). However, these models due to their costs and complexities in design and analysis have become inefficient and time-consuming. Hence, researchers investigate other fast, easy, and accurate methods for scouring estimation in hydraulic studies. Recently, hydraulic experts employ soft computing techniques in estimating scouring in many studies (Muzzammil 2008; Guven et al. 2009; Adarsh 2010; Ebtehaj and Bonakdari 2013; Rikar et al. 2016; Najafzadeh et al. 2017; Parsaie et al. 2018; Abdollahpour et al. 2019). The main goal of prediction with AI techniques was following the recent developments to obtain the best model performances (Khatibi et al. 2017). In the last decade, artificial neural networks (ANN) as artificial intelligence (AI) techniques are widely employed in predicting hydraulic and other flow parameters (Muzzammil 2008; Emamgholizadeh 2012; Onen 2014; Raikar et al. 2016; Pourzangbar et al. 2017). However, due to many uncertainties in ANN modeling techniques, many attempts have been made by researchers to improve the model efficiency by applying optimization algorithms or developing other AI methods. The application of support vector regression (SVR) model in scour hole modeling has been significantly used in recent times (e.g., Goyal and Ojha 2011; Sharafi et al. 2016; Hoang et al. 2018; Sun et al. 2021). It is imperative to note that the dimensionality of the input space in the SVR model does not affect the computational complexity. Moreover, the models’ prediction accuracy is insensitive to the outliers in the datasets. The SVR model requires large datasets for model development; it suffers from dimensionality and it is computationally demanding too (Awad and Khanna 2015).

The advantage of hybrid models over stand-alone models is that it takes the strength of each model and neutralizes the weaknesses, which results in improving the overall performances of the developed models. Many researchers have taken the advantage of hybrid models in hydrologic and hydraulic problems. An application of a hybrid smart artificial firefly colony algorithm (SAFCA)-based support vector regression (SAFCAS) model in modeling scour depth near bridge piers is seen in the research work of Chou and Pham (2014). Through their work, the hybrid model integrates the firefly algorithm (FA), chaotic maps, adaptive inertia weight, Lévy flight, and SVR model for scour depth modeling. The model’s performances were compared and assessed with other numerical models and empirical models. Salih et al. (2020) ensemble enhanced binary particle swarm optimization (PSO) algorithm with SVR model (tBPSO-SVR) for submerged weir scour modeling. The comparison of the developed hybrid model with other machine learning models shows the outperformance of tBPSO-SVR model over other selected models.

Based on the literature, the efficiency of the optimization algorithm of innovative gunner (AIG) in soft computing hybrid models is less explored in water-related problems and hence needs further research to explore the effectiveness of its algorithm performance in the field of water resources problems. To the best of the authors’ knowledge, no studies have been carried out exploring the applicability of scour hole modeling using the hybrid model SVR-AIG. Hence, in this study, the effectiveness of the SVR-AIG hybrid model application over the stand-alone SVR model in scour depth modeling has been studied. Taylor diagrams, and scatter and Violin plots along with other measurement indices are used for checking the considerable improvements in SVR performance by employing the optimization AIG algorithm.

Methods and materials

Case study and data description

Conventionally, the scour depth downstream of the ski-jump buckets spillways (Fig. 1) has been estimated using various empirical equations derived from the experimental datasets. Veronese equation is among these equations, in which scour can be estimated as (Yildiz and Uzucek 1994):

$${d}_{S}=1.90{{H}_{1}}^{0.225}{q}^{0.54}$$
(1)

where ds is the vertical depth of scour below tailwater, H1 is the effective energy of the jet entering tailwater, and q represents specific discharge. Wu (1973) suggested another equation for estimating relative scour in ski-jump spillways as follows:

Fig. 1
figure 1

Schematic profile view of ski-jump spillway and variables (Azamathulla et al. 2008)

Full size image
$$\frac{{d}_{s}}{{H}_{1}}=2.11{(\frac{q}{\sqrt{q{H}_{1}^{3}}})}^{0.51}$$
(2)

Martins (1975) also proposed this equation for the estimation of scour depth:

$${d}_{s}=1.5{q}^{0.6}{{H}_{1}}^{0.1}$$
(3)

In the present work, the data of the previous experimental works, obtained from the mentioned and other traditional prediction formulae based on only q and H1, have been collected and compiled in Table 1 to investigate the usefulness of the SVR-AIG approach to predict scour depth at downstream of ski-jump spillways. To elaborate more, (\(\frac{{d}_{s}}{{H}_{1}}\)) is taken as dependent variable and \(\left(\frac{q}{g{H}_{1}^{3}}\right)\) as independent variable.

Table 1 Observed data of discharge intensity (q), head (H1), and scour depth (ds)
Full size table

Support vector regression (SVR)

The SVR model was first developed by Vapnik (1995) for regression and classification problems. The SVR model approach is considered a nonparametric approach, as it mainly relies on kernel functions. This model is developed based on statistical learning theory for structural risk minimization (Safavi and Esmikhani 2013). Also, this aims to decrease the learning machine's confidence interval and empirical risk for attaining a strong generalization capacity (Raghavendra and Deka 2015).

A set of training data, \({\left\{\left({x}_{i}+{d}_{i}\right)\right\}}_{i}^{N}\), is considered for model development, where \({x}_{i}\) is the input vector, \({d}_{i}\) is the target vector, and N is the number of observations. The regression function of SVM can be written as follows:

$$f_{x} = \omega_{i} \cdot \emptyset_{i} \left( x \right) + b$$
(4)

The variables are defined as: \({\omega }_{i}\) is a weight vector, b is a bias, and \({\varnothing }_{i}\) is a nonlinear transfer function that maps the input vectors into a high dimensional feature space, where a simple linear regression can deal with the complex nonlinear regression of the input space.

The SVR models minimize the e-insensitivity loss function to find a solution for the following equation:

(5)
(6)

where and represent the slack variables, which reduces the errors in the training process by the loss function over the error tolerance \(\varepsilon\); C is a positive trade-off parameter which represents the degree of the empirical error in the optimization problem and di is the desired or target value (Suryanarayana et al. 2014). Mathematical manipulations are adopted for transforming the objective function into the binary formulation. The dual problem is transformed into an objective function for quadratic coding, which was first employed to solve the SVR technique to guarantee a global minimum. During the training stage of the SVR model, the application and selection of the optimization algorithm are critical, as this determines the precision of optimization variables, training speed, and memory constraint. As a result, the following optimization is utilized and can be expressed as mentioned in Eq. 4 (Suryanarayana et al. 2014):

$$f_{x} = \mathop \sum \limits_{i = 1}^{i} \left( {a_{i} - a_{i}^{*} } \right)\left\langle {x_{i} ,x} \right\rangle + b$$
(7)

This is opted for solving linear regression problems, rather than nonlinear regression cases; a modified version of Eq. (4) is used and written as follows (Isazadeh et al. 2017):

$$f_{x} = \mathop \sum \limits_{i = 1}^{l} \left( {a_{i} - a_{i}^{*} } \right)k\left( {x_{i} ,x} \right) + b \;{\text{which}}\; k\left( {x_{i} ,x} \right) = \left\langle {\emptyset (x_{i} )\emptyset \left( x \right)} \right\rangle$$
(8)

where \(k\left( {x_{i} ,x} \right)\) represents the kernel function. The selection of suitable internal parameters is important for better prediction accuracy (Zounemat-Kermani et al. 2016). For the present study, a linear kernel is selected.

Some advantages and disadvantages of the SVR model are:

  1. (i)

    It is robust to the outliers.

  2. (ii)

    It can use multiple classifiers trained on the different types of data using the probability rules.

  3. (iii)

    It can improve prediction accuracy by measuring confidence in classification.

  4. (iv)

    SVR performs lower computation compared to other regression techniques.

  5. (v)

    It introduces an additional parameter ε.

  6. (vi)

    It calculates twice Lagrange multipliers (\({a}_{i}\), \({a}_{i}^{*}\), i.e., 2 for each).

  7. (vii)

    It uses all points in the model training (Ccoicca 2013).

Algorithm of innovative gunner (AIG)

The AIG is developed by Pijarski and Kacejko (2019) developed the AIG, which is considered as one of the quick metaheuristic optimization algorithms for solving many optimization problems. The other advantages include a high convergence rate and less time for optimization with high accuracy. It is evident from previous literature that this is one of the more efficient algorithms than other known swarm intelligence algorithms. Detailed information about the algorithm is given by Dehghani and Poudeh, (2021a, b).

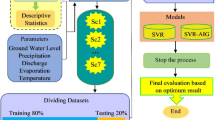
The overall steps involved in the model development of SVR-AIG are detailed in the flowchart shown in Fig. 2. The pseudo-code of the AIG algorithm is found in Roshni et al., (2022) also given in Fig. 3, which further elaborates the high-level working of the proposed scheme.

Fig. 2
figure 2

Flowchart of SVR-AIG model

Full size image
Fig. 3
figure 3

Pseudocode of AIG algorithm (Roshni et al. 2022)

Full size image

Both the SVR and hybrid SVR-AIG models were coded in MATLAB software.

Performance criteria

To validate the performance of the SVR-AIG model with respect to the standalone SVR model, three statistical score metrics were employed. These metrics can be described as:

I: Root mean square error (RMSE) expressed as:

$${\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {(P_{i} - O_{i} )^{2} } }$$
(9)

II: Mean absolute error (MAE) expressed as:

$${\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {\left( {P_{i} - O_{i} } \right)} \right|}$$
(10)

III: Correlation Coefficient (CC) expressed:

$${\text{CC}} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {O_{i } - \overline{{O_{i } }} } \right) \left( {P_{i } - \overline{{P_{i } }} } \right) }}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{N} \left( {O_{i } - \overline{{O_{i } }} } \right) \mathop \sum \nolimits_{i = 1}^{N} \left( {P_{i } - \overline{{P_{i } }} } \right) } }}$$
(11)

where Oi and Pi are the measured and estimated ith value of the scour depth (ds), \(\overline{{O }_{i}}\) and \(\overline{{P }_{i}}\) are the average of the measured and estimated scour depth value, respectively, and N is the number of data.

Results and discussion

In this research, the SVR model is used to predict the scour depth, and the performance is compared with the hybrid SVR-AIG model. The first stage of applying the models is to normalize the data and divide them for the training (70% of the whole data) and testing dataset (30% of the whole data). The experimental dataset including the head and discharge intensity was considered as the models’ input variables and the scour depth below the tailwater level was the output variable of the models. The parameters considered for constructing and developing the models’ structure are as presented in Tables 2 and 3.

Table 2 Parameters used in SVR modeling
Full size table
Table 3 Parameters used in SVR-AIG modeling
Full size table

The performance indices of root mean square error (RMSE), mean average error (MAE), and correlation coefficient (CC) are summarized in Table 4 for the training and testing phases. It is evident from Table 4 that the strategy of applying the AIG algorithm in the hybrid SVR-AIG model (with CC = 0.987, 0.991, RMSE = 2.839, 1.987, and MAE = 2.247, 1.201) has significantly improved the performances of the SVR model (with CC = 0.942, 0.975, RMSE = 5.686, 4.040, and MAE = 4.114, 3.201) at the training and testing phases based on all the performance indices. This proves the high ability of the AIG algorithm in improving the standalone SVR model.

Table 4 The values of the performance criteria of the models for training and testing stages
Full size table

The visual presentation of the test results for SVR and SVR-AIG models during the training and testing phase is shown in Fig. 4. It is observed from the time series plots that the predicted values are more aligned with the observed values for both the selected models. However, more accurate predictions of scour depth are evidently seen for the developed SVR-AIG model than SVR stand-alone model. The 1:1 correlation plots also show a significant correlation between the observed and the predicted values with R2 = 0.9742 for training and R2 = 0.9847 for testing phases for the SVR-AIG model.

Fig. 4
figure 4

Scatter plots and time series of the observed and predicted scour depth of the models for training and testing periods

Full size image

The error plots were prepared for both SVR and SVR-AIG models and the results are shown in Fig. 5. The relative error plot of the testing phase indicates that the error percentage varies from − 30% to + 15% in the SVR model and -30% to + 10% in the SVR-AIG model. It is interesting to note that the relative errors measured in the SVR-AIG model were less compared to the Model SVR in both the training and testing phases. It is also noteworthy that the SVR-AIG model results reduce the maximum relative error value by about 30%.

Fig. 5
figure 5

Relative error plots of the models for testing period

Full size image

Taylor diagrams (Fig. 6) visualize the variation of CC, standard deviation, and RMSE of the SVR and SVR-AIG outputs. The plot indicates that the hybrid SVR-AIG model outperforms the SVR model results in both the training and testing stages.

Fig. 6
figure 6

Taylor diagrams of the models at the training and testing periods

Full size image

Figure 7 shows the violin plots of the models for the training and testing phases. As can be seen from this figure, the shape of the violin of the SVR-AIG model is more similar to the observed shape at both the training and testing phases. This means that the predicted values of scour depth for the SVR-AIG model are more close to the observed/measured values at both the training and testing stages.

Fig. 7
figure 7

Violin plots of the models at the training and testing periods

Full size image

In general, the results of the evaluation of the statistical criteria and plots showed that the SVR-AIG model outperforms the SVR model in predicting the scour depth. This proves the high ability of the AIG optimization algorithm in improving the SVR performance and estimation of its optimal parameters. The results are in accordance with the results of Dehghani and Poudeh (2021a; b), who found that the hybridization of the AIG algorithm performs better than other optimization algorithms in improving the ANN models for hydrological modeling.

Conclusions

The focus of this research was to find the effectiveness of the SVR-AIG hybrid approach for scour depth estimation of the ski-jump spillways. The performance of the SVR-AIG hybrid models and the standalone SVR models in predicting the scour depth has been evaluated using statistical indicators. The performance indices (RMSE, MAE, and CC) and graphical indicators clearly indicated that the SVR-AIG method performs more precisely than the SVR standalone model results. The improved performance of the SVR may be attributed to the AIG algorithm that can solve complex nonlinear problems with greater accuracy than the standalone models. Therefore, to reduce heavy soil erosion, dam failures, and to evaluate the stability of the dam and other hydraulic structures it is recommended to apply the hybrid SVR-AIG model to predict scouring depth accurately. For future studies, it is recommended to develop the other hybrid models applying the AIG optimization algorithm and investigate its efficiency in improving the accuracy of the standalone models in estimating scour depth significantly.