Introduction

Soil erosion is an environmental, economic and social problem. Watersheds are taken as a unit to estimate the erosion problem. It is therefore important to monitor losses due to erosion in a watershed which is a planning unit for the sustainable development of natural resources (Meshram et al. 2017). Among many factors, water is the most important causative factor in soil erosion.

Soil attrition or erosion, excess water flow or runoff, changes in river geometry, degradation of streams, sediment accumulation in river and stream characters are related with morphometry (Meshram et al. 2018). This suggests that the morphometry of a basin is fundamental to the basin hydrology. In present time geo-morphometric analysis using a new technique i.e., Remote Sensing (RS) and Geographic Information Systems (GIS) being is utilized as this tool gives flexibility to analyze spatial data in a new manner (Gajbhiye et al. 2014; Meshram and Sharma 2017).

In this context, various approaches are available to analyze and prioritize sub-watersheds. These include Multi-Criteria Decision Analysis (MCDA) (Akay and Koçyiğit 2020; Chitsaz and Banihabib 2015; Dahmardeh Ghaleno et al. 2020; Sepehri et al. 2019), Soil and Water Assessment Tool (SWAT) (Mishra et al. 2007), Artificial Neural Network (ANN) (Dehghanian et al. 2020), Storm Water Management Model (SWMM) (Babaei et al. 2018), Support Vector Machine (SVM) (Tehrany et al. 2014; Fan et al. 2018) and The Hydrologic Modeling System (HEC-HMS) (Malekinezhad et al. 2017). Among the aforementioned methods, MCDA account takes priority due to its capability to handle nonlinear and complex problems and its usability to prioritize un-gaged watershed.

MCDA are the most usable methods which can be used to manage large amounts of data and solving decision-making under scale, quantitative, qualitative and conflict factors (Fernández and Lutz 2010; Mahmoud and Gan 2018). The Analytic Hierarchy Process (AHP) which was developed by Saaty (1980), due to some reasons such as cost-effectiveness, ease to use and understand has become one of the most popular methods among MCDA (Zou et al. 2013), which has been successful in various natural hazard studies such as landslides (Kayastha et al. 2013; Myronidis et al. 2016; Bahrami et al. 2020), flood magnitude (Sepehri et al. 2017; Swain et al. 2020; Lin et al. 2020), groundwater vulnerability (Sener and Davraz 2013; Abdullah et al. 2018; Das and Pal 2020).

In this regard, several methods were developed to reduce the number of pair-wise comparisons. In recent years, a new method was introduced by Rezaei (2015). This method is a more optimal version of AHP with the need of less compared data, resulting in more consistent results. However, the weak point of the BWM is related to the type of import data. This method just as the AHP, uses a limited 9-point table. In here, experts face a dilemma of choosing a point of initial weighting to factors causing inconsistency in the results. Therefore, it is better to use the fuzzy number instead of the limited 9-point table because it is more in line with actual situations and can obtain more convincing ranking results (Guo and Zhao 2017; Ali and Rashid 2019).

Rezaei (2015) introduced BWM as one of the most recent MCDM approaches. The premise of this strategy is to weight criteria using paired comparisons, such as AHP, with two obvious benefits: fewer pair wise comparisons and a greater consistency ratio. Traditional BWM compares clean values but fails to identify weights in an ambiguous context. As a result, fuzzy BWM was created (Guo and Zhao 2017; Hafezalkotob and Hafezalkotob 2017). Zhang et al. (2015) reported an enhanced fuzzy MCDM methodology for evaluating renewable electricity sources In Jiangsu Province, China. Photovoltaic energy was the top option in their study, followed by wind, biomass, and nuclear power facilities. Because fuzzy BWM inherits some distinguishing characteristics from BWM, it can produce weights of criteria using fuzzy numbers rather than crisp values. As a result, the uniqueness of weight data can be carefully preserved (Guo and Zhao 2017). Shojaei et al. (2017) evaluated Iranian airports using an integrated Taguchi loss function, VIKOR, and BWM method. Ahmed et al. (2017) used BWM to identify the most critical elements affecting gas supply sustainability.

The Gusru watershed in view of soil erosion and its related financial and ecological losses can be regarded as one of the most critical areas in central of India. However, no comprehensive and efficient works have been done to reduce the soil erosion. Thus the main objective of this study is to assess soil erosion based on the fuzzy best worse multi-criteria decision-making method of efficient prioritization of sub-watersheds. The outcomes of this study will be important for water resources management.

Materials and methods

Case study

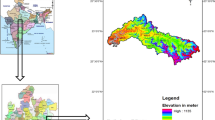
Gusru River watershed is situated in the Madhya Pradesh state lying Satna Panna districts, in India, and it lies between 80° 32′ 50.23' E and 80° 37′ 31.14′ E longitude, 24° 6′ 32.75′ and 24° 16′ 24.07′ N latitude (Fig. 1). It occupies an area of 155 km2 having an elevation range between 339 and 628 m above mean sea level. The Gusru River runs from east to west and confluences with Tons river at Sagwania village. In the eastern part of the watershed, there is a small check dam, which primarily serves as an irrigation outlet. There is no other source of water for irrigation; as a result, rainfed agriculture is primarily practiced. The soil structure in the watershed is primarily sandy loam. The soils under rainfed and irrigated conditions respond to a variety of crops and watershed management. Shale, sandstone and calcarious rocks are the dominant lithological units in the watershed. The study area descends from the plateau of Bhander and passes through the area between the escarpment of Bhander and the highlands of Kaimore.

Fig. 1
figure 1

Location map of the study area

Full size image

Methodology

The used procedure in this study can be summarized in the following stages:

  1. 1.

    Establishing morphometric parameters

  2. 2.

    Applying the Principal Component Analysis (PCA) for redundancy of parameter

  3. 3.

    Applying ensembles of the Fuzzy method and BWM to assigning weights to used indices based on importance of them on soil erosion.

Morphometric parameters

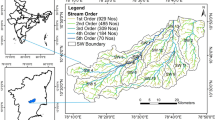
Stream network is a basic requirement of any morphometric study and the prioritization of watersheds (Meshram et al. 2022a). Digital Elevation Model (DEM) generated by Shutter Radar Topography Mission (SRTM) data is a common tool to define a stream network and sub-watershed map (Meshram et al. 2022b). Different drainage network parameters i.e., numbers and lengths and watershed area, perimeter, width and length were determined in GIS environment (Benzougagh et al. 2022; Meshram et al. 2022c). Then using standard formulae stream frequency, drainage density, circulatory ratio, form factor and elongation ratio were estimated. In order to do fuzzy-BWM analysis, we have adopted the morphometric parameters for the 14 sub-watershed of Gusru watershed from the previous studies of Sharma et al. (2011).

Principal component analysis

Most of the time there is relationship between the morphometric parameters such that some of the parameters share the same information. In performing component analysis, the co-ordinates axis is transformed to a new reference frame within the total variable space. This involves assigning new principal components to each variable either through an uncorrelated or an orthogonal transformation. These components are unique in that they consider the maximum variance between the variables (Gajbhiye et al. 2015a, b). The correlation matrix and principal components are thus obtained from the principal component analysis performed on the geomorphic variables. The analysis employs the first factor and rotated the factor loading matrices. The product of the square of a parameter’s loading and the percent of the rotated factor covariance give the order of importance of a parameter. Thus computation is derived from the most commonly used transformation technique involving rotated factor loading matrices based on the varimax criteria (Singh 2006; Ghoderao et al. 2022).

The proposed F-BWM model

Fuzzy sets and triangular fuzzy numbers

The subjective MCDA is sensitive to experts’ judgments, causing difficultly evaluating the weights when the experts uses natural language such as “very better,” “somewhat worse,” or “so much better” to express a kind of general preferences (Hafezalkotob and Hafezalkotob 2017). In mathematics, these natural languages are categorized as crisp sets. The concept of crisp sets only implied on full membership and non-membership, whereas in fuzzy set each elements can be partially membership (Sepehri et al. 2019; Chen et al. 2020). For the first time, the concept of fuzzy system was introduced and characterized using membership functions by Zadeh (1965) which grading membership between 0 and 1. In decision-making problems, the triangular fuzzy number (TFN) is one of the most used membership functions, which can be donated to triplet (\(l\), \(m\), \(u\)), where \(l<m<u\)(Dong et al. 2021; Guo and Zhao 2017; Omrani et al. 2018). The triangular fuzzy number is as follow:

$$\mu_{{\tilde{A}}} = \left\{ {\begin{array}{*{20}c} {0, x < l} \\ {\frac{x - l}{{m - l}}, l \le x \le m} \\ {\frac{u - x}{{u - m}}, m \le x \le u} \\ {0, x \ge u} \\ \end{array} } \right.$$
(1)

where \(l\), \(m\), \(u\) are the lower, median and upper numbers of à (for the basic mathematical calculations of two TFNs, can be referred to (Carlsson and Fullér 2001).

Fuzzy best–worst method (F-BWM)

Best–worst method (BWM) proposed by Rezaei (2015) is a new subjectively MCDA which can be used to derive optimal weights of criteria set \(\left\{{c}_{1},{c}_{1},\dots ,{c}_{j},\dots ,{c}_{n}\right\}\). In this content, it is necessity to determine the best (e.g., the most favorable) and the worst (e.g., the least favorable) of criteria by experts. Afterward, these criteria are compared relative to each other based on natural language (Mohtashami 2021). In F-BWM, it is necessity to transfer the natural language to fuzzy rating based on rules of transformation in Table 1 (Dong et al. 2021; Guo and Zhao 2017; Khanmohammadi et al. 2018). The fuzzy comparison can be showed as follows:

$$\tilde{A} = \left[ {\begin{array}{*{20}c} {\tilde{a}_{11} } & \cdots & {\tilde{a}_{1n} } \\ \vdots & \ddots & \vdots \\ {\tilde{a}_{n1} } & \cdots & {\tilde{a}_{nn} } \\ \end{array} } \right]$$
(2)

where each element of the matrix \(\tilde{A}\) represents the relative importance of criterion i to criterion j, \({a}_{ij}=(\mathrm{1,1},1)\) when \(i=j\). It must be noted that in BWM method, there is no need to n fuzzy performance comparison to obtain a completed matrix \(\tilde{A }\).

Table 1 Saaty’s 9-level linguistic scale
Full size table

In the current study, the details of F-BWM algorithm to calculate the fuzzy weights can be briefly described as follows (Dong et al. 2021; Guo and Zhao 2017; Ecer and Pamucar 2020):

  1. 1.

    Provide a set of desired criteria \(\left\{{c}_{1},{c}_{1},\dots ,{c}_{j},\dots ,{c}_{n}\right\}\), (\({c}_{1},{c}_{1},\dots ,{c}_{j},\dots ,{c}_{n}=\mathrm{morphometric parameter})\)

  2. 2.

    Determine the best \(\left({c}_{B}\right)\) and worst \(\left({c}_{W}\right)\) criterion

  3. 3.

    Provide \(\tilde{A}_{B}\) which shows fuzzy reference comparisons of \({c}_{B}\) over all the criteria.

    $$\tilde{A}_{B} = \left[ {\tilde{a}_{B1} ,\tilde{a}_{B2} , \ldots ,\tilde{a}_{Bn} } \right]$$
    (3)

    where \(\tilde{a}_{Bj}\) is the fuzzy preference of \({c}_{B}\) over \({c}_{j}\),\(\tilde{a}_{Bj} = \left( {a_{Bj}^{l} ,a_{Bj}^{m} ,a_{Bj}^{u} } \right)\), j = 1,2,…,n and \(\tilde{a}_{BB} = \left( {1,1,1} \right)\)

  4. 4.

    Provide \(\tilde{A}_{W}\) which shows fuzzy reference comparisons of all the criteria over \(c_{W}\).

    $$\tilde{A}_{W} = \left[ {\tilde{a}_{1W} ,\tilde{a}_{2W} , \ldots ,\tilde{a}_{nW} } \right]$$
    (4)

    where \(\tilde{a}_{jW}\) is the fuzzy preference of \(c_{j}\) over \(c_{B}\),\(\tilde{a}_{jW} = \left( {a_{jW}^{l} ,a_{jW}^{m} ,a_{jW}^{u} } \right)\), j = 1,2,…,n and \(\tilde{a}_{WW} = \left( {1,1,1} \right)\).

  5. 5.

    Determine the optimal fuzzy weight \(\tilde{w}^{*} = \left[ {\tilde{w}_{1}^{*} ,\tilde{w}_{2}^{*} , \ldots ,\tilde{w}_{n}^{*} } \right]\), where \(\tilde{w}_{j}^{*} = \left( {w_{j}^{*l} ,w_{j}^{*m} ,w_{j}^{*u} } \right)\) shows the optimal fuzzy weight of \({c}_{j}\) which is calculated using below model:

    $$\min \max_{j} \left\{ {\left| {\frac{{\tilde{w}_{B} }}{{\tilde{w}_{j} }} - \tilde{a}_{Bj} } \right|,\left| {\frac{{\tilde{w}_{j} }}{{\tilde{w}_{w} }} - \tilde{a}_{jw} } \right|} \right\}$$
    (5)
    $$s.t. \left\{ {\begin{array}{*{20}c} {\mathop \sum \limits_{j = 1}^{n} R\left( {\tilde{w}_{i} } \right) = 1} \\ {l_{j}^{w} \le m_{j}^{w} \le u_{j}^{w} } \\ {l_{j}^{w} \ge 0} \\ {j = 1,2, \ldots ,n} \\ \end{array} } \right.$$

where \(\tilde{w}_{B} = \left( {l_{B}^{w} ,m_{B}^{w} ,u_{B}^{w} } \right)\),\(\tilde{w}_{j} = \left( {l_{j}^{w} ,m_{j}^{w} ,u_{j}^{w} } \right)\), \(\tilde{w}_{W} = \left( {l_{W}^{w} ,m_{W}^{w} ,u_{W}^{w} } \right)\), \(\tilde{a}_{Bj} = \left( {l_{Bj}^{w} ,m_{Bj}^{w} ,u_{Bj}^{w} } \right)\),\(\tilde{a}_{jW} = \left( {l_{jW}^{w} ,m_{jW}^{w} ,u_{jW}^{w} } \right)\) and \(R\left( {\tilde{w}_{j} } \right) = 1/6\left( {w_{j}^{l} + 4w_{j}^{m} + w_{j}^{u} } \right)\).

The above model can be transferred as below optimization model which are based on consistency ratio (ξ) (next step).

$$\begin{array}{*{20}c} {\min \;\tilde{\xi }} \\ {s.t.\left\{ {\begin{array}{*{20}c} {\left| {\frac{{\tilde{w}_{B} }}{{\tilde{w}_{j} }} - \tilde{a}_{Bj} } \right| \le \tilde{\xi }} \\ {\left| {\frac{{\tilde{w}_{j} }}{{\tilde{w}_{W} }} - \tilde{a}_{jW} } \right| \le \tilde{\xi }} \\ {\mathop \sum \limits_{j = 1}^{n} R\left( {\tilde{w}_{j} } \right) = 1} \\ {l_{j}^{w} \le m_{j}^{w} \le u_{j}^{w} } \\ {l_{j}^{w} \ge 0} \\ {j = 1,2, \ldots ,n} \\ \end{array} } \right.} \\ \end{array}$$
(6)

where \(\tilde{\xi } = \left( {l^{\xi } ,m^{\xi } ,u^{\xi } } \right)\) and it can be assumed that \(\tilde{\xi }^{*} = \left( {k^{*} ,k^{*} ,k^{*} } \right) \le l^{\xi }\), then Eq. 6 can be transferred as:

$$\begin{array}{*{20}l} {\min \tilde{\xi }^{*} } \hfill \\ {s.t. \left\{ {\begin{array}{*{20}c} {\left| {\frac{{\left( {l_{B}^{w} ,m_{B}^{w} ,u_{B}^{w} } \right)}}{{\left( {l_{j}^{w} ,m_{j}^{w} ,u_{j}^{w} } \right)}} - \left( {l_{Bj} ,m_{Bj} ,u_{Bj} } \right)} \right| \le \left( {k^{*} ,k^{*} ,k^{*} } \right)} \\ {\left| {\frac{{\left( {l_{j}^{w} ,m_{j}^{w} ,u_{j}^{w} } \right)}}{{\left( {l_{W}^{w} ,m_{W}^{w} ,u_{W}^{w} } \right)}} - \left( {l_{jW} ,m_{jW} ,u_{jW} } \right)} \right| \le \left( {k^{*} ,k^{*} ,k^{*} } \right)} \\ {\mathop \sum \limits_{j = 1}^{n} R\left( {\tilde{w}_{i} } \right) = 1} \\ {l_{j}^{w} \le m_{j}^{w} \le u_{j}^{w} } \\ {l_{j}^{w} \ge 0} \\ {j = 1,2, \ldots ,n} \\ \end{array} } \right.} \hfill \\ \end{array}$$
(7)

By solving above model, the optimal fuzzy weight \(\left( {\tilde{w}_{1}^{*} ,\tilde{w}_{2}^{*} , \ldots ,\tilde{w}_{n}^{*} } \right)\) can be calculated.

Results and discussion

Morphometric parameters of Gusru watershed adapted from Sharma et al. (2011) are presented in Table 2. For redundancy of morphometric parameter, PCA has been applied. A hierarchical tree from the most effective morphometric results is used to prioritize the sub-watersheds.

Table 2 Sub-watershed wise morphometric parameters (Sharma et al. 2011)
Full size table

Fuzzy best worse method (F-BWM) was applied to establish the relative weights of parameters or criteria and for watershed prioritization.

The SPSS 22.0 software is employed to assess the inter-co-relationships of morphometric variables through a correlation matrix (Table 3). Very high correlations (R > 0.9) exist between the different morphometric parameters that is between; relief ratio (Rh) and relative relief (Rr); elongation ratio (Re) and farm factor (Rf), drainage density (Dd) and length of overland flow (Lo), and between the circulatory ratio (Rc) and compactness coefficient (Cc). In addition, moderately high correlations (R > 0.70) are observed between; RN and Rh/Rr/Dd/Lo and between Fs and Dd/T/Lo, Sa and Rh/Rr. Because there are no significant correlations between HI or Rb with any of the parameters under consideration, it is practically impossible to put the parameters into component groups. Therefore, the subsequent step makes use of the principal component analysis technique.

Table 3 Inter-correlation Matrix of the Geomorphic Parameters
Full size table

The correlation matrix obtained from the previous step is used to generate the first unrotated factor loading matrix (Table 4). The results show that about 81.76% of the total explained variance is attributed to the combination of the first three components with eigen values above one. It is observed that a strong correlation (R > 0.9) between RN and the first component (Table 5A). Relatively high correlations are also found between the first component and each of the variables; Dd, Lo, Rh, Fs, and Rr. On the other hand, Rc, Re, Rf and Cc have high correlations with second component. No significant correlations exist between the third component and any one of the parameters.

Table 4 Total Variance Explained
Full size table
Table 5 Varimax method of the first factor loading matrix (unrotated) and Rotated Factor Loading Matrix of fourteen geomorphic parameters
Full size table

Redistribution of the observed variance is performed so that better factor loadings can be obtained. This is done by carrying out analytical rotations those components whose eigen value exceeds one. The outcome of varimax rotation is shown in Table 5B.

The first component is very highly correlated with Fs and highly correlated with Dd, Lo and T. A strong correlation also exists between the second component with Rh and Rr, while moderately high correlations are obtained with RN and Sa. A very strong correlation is also apparent for the third component with Re and with Rf and at the same time moderately correlated with Cc and Rc.

Table 6 depicts the ordering of each parameter with respect to importance. The order of priority in descending order is given as Fs > Rr > Lo > Rh > Dd.

Table 6 Order of importance of parameters
Full size table

At the watershed scale, the sub-watersheds, based on their morphometric and hydrologic properties have different hydrological behavior regarding flood degree, erosion and sedimentation. Therefore, prioritization of sub-watersheds is a crucial step for watershed management strategies. Subjective MCDA is one of the mostly used methods for flood prioritization. These methods based on Smithson (2012) are categorized as knowledge-based methods, so that the results of a desired study are a function of experts’ decision, leading to high uncertainty of results. In this regard, BWM can be used as an efficiency method to reduce the number of subjective experts’ decisions (Rezaei 2015). However, the existence of qualitative judgments on BWM (i.e., 9-point table) can be considered as one of the main sources of uncertainty in this method, therefore, in this study we used TFN to nearly resolve the drawback of qualitative judgments (Bellman and Zadeh 1970a, b; Guo and Zhao 2017; Zhao and Guo 2014, 2015).

The statistical analysis of F-BWM has been used to prioritize sub-watersheds based on the degree of soil erosion. In this regard, five morphometric parameters i.e., Lo (C1), Fs (C2), Dd (C3), Rr (C4) and Rh (C5) were used. Based on experts’ knowledge and field survey, the Lo (C1) and Rh (C5) are considered as the best and worst criteria. Next, the fuzzy preferences to best criterion over other criteria (vector \(\tilde{A}_{B}\)) and all criteria over worst criteria (vector \(\tilde{A}_{W}\)) were determined. Then, based on step 5, the optimal fuzzy weight was done to obtain the weights (Table 7, Fig. 2).

Table 7 Prioritization of Micro-watersheds
Full size table
Fig. 2
figure 2

F-BWM weight to the most effective morphomeric parameter

Full size image

Figure 3 shows the results of F-BWM in watershed prioritization. Based on Table 7, the F-BWM weight of the sub-watershed 9 has the maximum value, so it is located as the first priority. On the contrary, sub-watershed 3 has been located in last rank (14) of the prioritization.

Fig. 3
figure 3

Soil erosion susceptibility map

Full size image

Conclusion

In the current study, five morphometric parameter i.e., Fs, Rr, Lo, Rh and Dd were used to watershed prioritization in the case study. In this regard, F-BWM as knowledge-based method was used to assigning initial weights to criteria. The conclusion can be drawn that the parameter Fs is the most important soil erosion related criterion, so that the sub-watersheds 9 and 3 which have first and last rank of prioritization, have the maximum and minimum value of F-BWM weight. In this state, the critical sub-watersheds can be better recognized for doing watershed management strategies.

In this study, there are various elements of improvement for the proposed method, as well as future research objectives. For enhanced input-based consistency ratio and constrained optimization equations, one of the defuzzification approaches is applied first. However, there are a variety of additional defuzzification strategies that can be used with the model, which could be a future study topic. Second, the primary goal of combining the views of several experts is to provide appropriate findings from pair wise comparison matrices. Each methodology has its own set of advantages and disadvantages, and future research might concentrate on the advantages and disadvantages of various aggregation methods.