Introduction

Drainage basins, catchments, and sub-catchments are the fundamental units for managing land and water resources and reducing the impact of natural disasters on sustainable development (Moore et al. 1994; Abdul Rahaman et al. 2015; Meshram et al. 2021a, b, c, d). Planning for the basin management highlights river erosion management techniques (Gajbhiye et al. 2015a, b). The assessment is also performed in sub-watersheds to assess the natural hazards and threats (soil erosion, floods, slide etc.). Watershed management recognizes the interdependence of land use, soil, and water, as well as the connectivity between uplands and downstream areas (Gajanan et al. 2015; Meshram et al. 2018). Soil erosion is the most common type of land degradation, and it is caused by the impact of land use/land cover on rain drops and runoff, resulting in soil detachment, movement, and deposition (Gajbhiye et al. 2015c; Kogo et al. 2020; Das et al. 2021). Water soil erosion is recognized as a major cause of earth deterioration throughout the world. Soil erosion in general, particularly in the Inaouene River watershed is not a recent problem in the country.

The theory of watershed management acknowledges the internships between upland, lowland, land use/land cover geomorphology, paths and soil connections. In the 1940's as well as the 1950's (Harinath and Raghu 2013), morphometric hydrological analysis work began. Mathematical analysis of the earth's surface structure and its soil form aspect are the analysis of morphometry (Clarke 1966; Agarwol 1998; Obi Reddy et al. 2002). The morphometry of the drains is connected with processes such as the rushing, soil erosion, river sedimentation, dries that alter the stream flow and bifurcation habit, catchment flow properties and the fulfillment and stability of the dam and reservoir if accessible within the reservoir (Prasad and Pani 2017; Gajbhiye and Sharma 2017; Al-Assadi 2020). The river and its flow, as well as the rivers bifurcation habits, affect the water. In understanding the geo-hydrological behavior of the catchment basin and channel network, a morphometric study of the catchment basin and channels reflects the dominant climate, geology, and structural history.

A review of the literature describes the several approaches developed for mapping and predicting soil erosion, such as: Universal Soil Loss Equation (USLE), Revised Universal Soil Loss Equation (RUSLE), Modified Universal Soil Loss Equation (MUSLE) and Morphometric Analysis (MA) (Chowdary et al. 2013; Jaiswal et al. 2014; Kumar and Joshi 2016; Meshram et al. 2020; Benzougagh et al. 2020). Because it benefits from rapid data processing, multi-criteria analysis and geographic information systems (GIS) have been successfully used in solving siting difficulties. To assess erosion vulnerability, a combination of GIS technologies and the multi-criteria decision method (MCDM) can be employed efficiently. In several previous case studies, it was confirmed that the combination of GIS tools and MCDM method in watershed and soil resource analysis, evaluation and vulnerability improves the decision-making process (Jaiswal et al. 2015; Haidara et al. 2019).

The present work integrates morphometric analysis (MA) model with the techniques of Spatial Remote Sensing (SRS) and Geographical Information System (GIS) to determine the critical soil erosion prone areas to prioritize watershed prioritization studies and to analyze various fields of catchment and watershed area morphometric parameters (Linear and Shape). In various works of literature, the compound parameter (Cp) model is a very precise way for evaluating earth surface attributes, particularly for the basin scale, and it is widely utilized for sustainable water resource management and scientific planning of sub-watersheds in data-scarce locations (Altaf et al. 2014; Benzougagh et al. 2016, 2017; Hembram and Saha 2020). Linear parameters have a direct relationship with erodibility; the higher the value, the higher is the erodibility. On the contrary, the shape parameters have an inverse relation to linear parameters, so the lower their value, the more the erodibility. For prioritization of micro-watersheds, the highest value of linear parameters was rated as rank 1, the second highest value was rated as rank 2, and so on, and the least value was rated last in rank. Thus, the lowest value of shape parameters was rated as rank 1, the next lowest value was rated as rank 2, and so on and the highest value was rated last in rank (Patel et al. 2012; Benzougagh et al. 2017).

Compound parameter (Cp) is calculated by summing all the ranks of linear parameters as well as shape parameters and then dividing by number of parameters. From the group of sub-watersheds, highest prioritized rank was assigned to sub-watershed having lowest compound factor and vice versa. It offers a dynamic environment and is an efficient tool for the analysis and manipulation of spatial data. This study is thus a valuable tool to measure, manage and plan conservation strategies for Inaouene catchment growth. But the priority principle is very useful for a better understanding of the fluvial and morphological characteristics of individual watersheds or sub watersheds, as well as the growth, in order to conserve the soil, and to collect water over a basin.

Study area

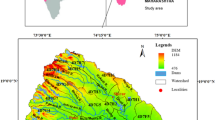
The North-East of Morocco lies the Inaouene Watershed. The area covers 3700 square kilometers and is located at the latitude between coordinates of 33°30' and 35°N and 3°30 ' and 5° W (Fig. 1). It is located between the domain Rif and the outcrops of the Middle Atlas.

Fig. 1
figure 1

Location map of study area

Full size image

This basin is described by a vast topographic (drop of 200–2500 m) and geologic complexity, which is suitable mainly to its geographic position (transition zone) between three structural domains which are from North to South: The Pre-Rif, the South-Rifa in corridor and the Middle Atlas. From the geological point of view, the basin is very heterogeneous, and it contains formations, ranging from the Paleozoic to the Quaternary. Numerous studies carried out on the risk of water erosion and the morphometry of rivers in a catchment area highlight the existence of a close relationship between, on the one hand, the shape of their longitudinal profiles and, on the other hand, the lithology of the land crossed and the tectonics. The evolution of erosion is controlled by several variables, notably the lithology of the land, the vegetation cover, the climate and the anthropic action which accelerates the process of risk and thus leads to the modification of the land use. The south-raif inadvertently controls the watershed on the left bank, which is characterized by the dominance of marl formations.

The basin’s geological environment includes a variety of morpho-structural and geological domains (Fig. 2):

  • The first anticlinal wrinkle of the folded Middle Atlas is formed by karstified limestones and dolomites of the Lias. It is affected by the major tectonic accident known as North Middle Atlas (ANMA).

  • The Hercynian massif of Tazekka occupies the upstream half of the basin and is presented in a buttonhole-oriented NE-SW. The Paleozoic terrains, of Cambrian, Ordovician and Visean ages, are varied and strongly metamorphosed (shales, pelites, sandstones, quartzites, basaltic and andesitic volcano-detrital rocks…). The purplish-green schists and the Cambrian sandstones (or Tazekka schists) are largely dominant. They are separated from the Ordovician pelites and olive-green shales by a tectonic contact marked by N40 fractures that dip to the SW (Hoepffner, 1978).

  • Permo-Triassic formations of red clay to basalt outcrop unconformably on the edges of the Paleozoic Tazekka massif.

  • The causes of Tahla and Chaâra are constituted by limestones and dolomites of the middle and lower Lias; the land is affected by a strong karstification (Tennevin 1978; Taous et al. 2009).

  • The South Rifian Corridor is a subsiding trench, dominated by the South Rifian thrust fault. It is formed by biocalcarenites and sandy marls of the upper Miocene. These rocks support the quaternary alluvium of the wadi Inaouene.

Fig. 2
figure 2

Map of geomorphological units and structural scheme of study area

Full size image

From the structural point of view (Fig. 2), the terrains of the SE part of the basin are affected by the North-Middle-Atlasic accident which takes the NE-SW direction. Toward the center of the basin, the Paleozoic terrain of the Tazekka massif is affected by a dense network of Hercynian and Alpine tectonic faults (thrusts, faults, fractures, etc.), generally oriented NE-SW and NW–SE (Charriere 1990; Hoepffner 1987). Some of these faults replayed as thrust faults and reverse faults, under a regime of compressive neotectonics stresses during the Pliocene and the early and recent Quaternary (Morel 1981; Sabaoui 1987). They probably controlled the organization of the hydrographic network and the drainage directions in the watersheds of the northern slope of the Middle Atlas (El Fellah 1983).

The structural data of the study area show that they are to be attributed to slope breaks (knick points) coinciding with the tectonic accidents that affect the land, although in some cases, the part of the influence of the lithology appears difficult to separate from that of the tectonics. Therefore, the existence of a strong relationship between the evolution of the processes of erosion risk and the tectonics of the region particularly is noted in the left bank of the watershed.

Subjected to an extreme erosion, these subtle lithological formations are contrary to the Tahla and Tazekka tablelands (Sibari et al. 2013). The watershed's climate in Inaouene is semiarid. The average yearly precipitation in the area is approximately 600 mm. The August and January temperatures rise to the highest averages; in August, a maximum average is 40 °C, and in January a minimum average is 5 °C.

Precipitation plays a key role in assessing the risk of water erosion. The aggressiveness of the rains is the potential risk of soil loss generated by a downpour on soil devoid of plant cover and any anti-erosion development. This erosivity is determined by calculating the climatic aggressiveness index. This index characterizes the effect of the impact of raindrops (splash effect) and the potential for runoff which are both associated with a downpour.

The figure below (Fig. 3) shows the superposition of the rainfall distribution zones and the geomorphological units of the study zone to identify and assess the zones vulnerable to the risk of erosion. Thus, to understand the competing forces responsible for soil erosion such as precipitation, geomorphology, lithologies, topography, plant cover, and anthropic action).

Fig. 3
figure 3

A rainfall map of the area overlaid upon structural units (a) and the detailed geology of the study area (b)

Full size image

Figure 3 depicts areas with high precipitation (620–950 mm) and friable lithology, as well as steep slopes, where the area’s most vulnerable to soil erosion are identified, particularly north and south of the watershed.

From a structural point of view, the Inaouene watershed is part of a junction zone between three structural domains. The effect of the tectonics combined with the lithology of the study area is individualized by the current installation of the dense and branched hydrographic network in this region (Benzougagh et al. 2020).

On the left bank of Inaouene river, tectonic measurements of the brittle deformation carried out within the marl layers, as well as cartographic surveys have allowed us to describe a tectonic system of conjugate normal faults N70 and N130 to N140. These faults affect the thick Miocene formations related to the synsedimentary subsidence. Microtectonic analyses and statistical treatment (Fig. 4) of the measurements allowed us to highlight a paleo stress field that is characterized by a sub-vertical and E-W to WNW-ESE-oriented maximum stress σ1. The normal play of these faults has caused the accentuation of the risk of water erosion. The combination of tectonics, friable lithology (predominance of marl) and precipitation accelerates the degree of erosion, which leads to the triggering of the risk of landslides.

Fig. 4
figure 4

Stereographic projection of tectonic measurements in the Inaouene watershed (Benzougagh et al. 2020)

Full size image

In addition to the factors mentioned above, we must take into account the action of mankind, which causes environmental disturbances and changes the land use/land cover through urban development and the destruction of nature. For a good governance of the watershed, the mapping of land use/land cover is necessary; for this reason the use of satellite images with high resolutions (IKONOS) is recommended for the mapping of roads, urban expansion, forests, etc. (Prudhvi Raju et al. 2008; Benzougagh et al. 2020, 2021).

Data and methodology

Drainage networks are needed for the morphometric analysis and priority of the Inaouene water bay. In this analysis, Advanced Space-borne Thermal Emission and Reflection Radiometer (ASTER) data were used to produce a geo-coded digital elevation model (DEM). The DEM was loaded from the site in Tagged Data file format with a ground resolution of 30 m (https:/search.earthdata.nasa.gov). In addition, in the first hydrographic network, the produced DEM has been processed and extracted from ASTER. However, the other parameters are calculated using the program QGIS (2.18.2), such as the number and length of streams in the different commands, the area of the catchment and the overall width and perimeter of the basin. Such parameters have been determined using drainage rate, drainage density, form factor, elongation ratio, and circulatory ratios. Consequently, Table 1 and Fig. 5 demonstrate the methods used for the estimation of morphometric parameters.

Table 1 Method of calculating Morphometric Parameters
Full size table
Fig. 5
figure 5

Flow diagram of methodology of work

Full size image

The morphometric parameters are also known as erosion risk assessment criteria of sub-watershed importance. The linear measure has a direct relationship with erodibility, based on research by Nookaratnam et al. (2005), Javeed et al. (2009) and Singh et al. (2013). The type calculation on the other hand has an inverse relation to erodibility. Consequently, first rank was given to the morphometric parameter having the high value, and so on. Inverse relationships with linear dimensions were shown in the regional aspects of characterization. Conversely, the areal aspects of the classification demonstrated an inverse relationship with the linear aspects. The first rank was given to the morphometric parameter having minimum value, and similarly the further ordering was done. After the ranking is rendered according to every single parameter, ranking values for each sub-basin are applied to achieve compound value (Cp) for all the linear and shape parameters of each sub-basin.

The compound parameter (Cp) was determined by a calculation of all the linear parameter ranks and type parameters and was then divided by the number of parameters. This is accomplished by following that morphometric parameter's evaluation. For each sub-basin, the value of each linear and shape parameter is applied to obtain a composition parameter (Cp) based on the mean value of these parameters for each sub-basin (Umak et al. 2017; Benzougagh et al. 2016, 2017; Umair and Syed 2014; Pawar-Patil and Mali 2013; Vandana 2013; Biswas et al. 1999). Nonetheless, highest priority was given to the sub-watershed with the lowest composite parameter value. The next higher value was the second priority, etc. In this particular sub-shift, the highest priority is the increased amount of soil erosion. Therefore, a possible area for soil conservation initiatives is considered.

Results and discussion

In morphometric analysis of the catchment basin, naming stream order is the first step. It is based, however, on the rank-finding suggested by Strahler (1964), which was used for 48 sub-watersheds in the current study (Fig. 6). Fundamental parameters were obtained from the sub-basin: area, perimeter, stream width, number of streams and basin size.

Fig. 6
figure 6

Sub-watersheds of the Inaouene River and their hydrographic network

Full size image

In this study, the descriptive description of Howard (1967) is used as a basis for hydrographic network analysis:

  • In the north, the watershed reveals that it is the Pre-rift zone, which is practically brittle with its materials. It was drained by an irregular ramification of tributaries and streams in many directions that joined the main channel (Fig. 6).

  • Two permeable lithologies can be found on the south shore: The Jurassic karstified carbonates (Tahla plateau) and the mio-plio quaternary detrital deposits (sandstones and conglomerates), and the Tazekka Paleozoic massif. This shore is marked by extensive fracking. This zone presents a mixture of two types of hydrographic networks: rectangular network with perpendicular disputes between the channels and sudden changes in the course of the drains and parallel-like network (Fig. 6). Morphometric analyses are carried out by measuring the river dimensions and areal aspects.

Linear characteristics of the drainage watersheds

As shown in Table 1, a linear function of a channel system is a stream order (U), a stream length (Lu) of each stream in each order (Nu), the average stream length (Lsm) and the stream length ratio (Rl).

Stream order (U)

Horton (1945) first put forward the concept of stream ordering, but Strahler (1964) made a few changes and suggested them later. The first stage of the quantitative analysis of the basin is stream ordering. The hierarchical relation between stream portions is expressed. The series is a flux branch in the water pool. The law of Horton was followed by a first-order stream of an unbranched stream. Therefore, it was known as a second order if two first-order streams were joined; two second-order streams join in the third order, etc. (Strahler 1964). The study of the drainage model for the change indicates that the region is under the tectonic structural influence. The river flow order is sixth (Fig. 7).

Fig. 7
figure 7

Number of each stream in each order of Inaouene watershed

Full size image

Stream number (Nu)

The stream number (Nu) refers to the entire number of stream portions of the order u according to Horton (1945) and Strahler (1964). In this analysis, the number of stream portions decreased as the order in all sub-watersheds increased (Fig. 7). Inaouene watershed was known as the fifth watershed of a total of 6997 separate stream segments. Number in the present paper region is dominated by the lower order flow segments.

The variation in the size and magnitude of the sub-watershed is due to the topographical, physiographic, geomorphological, and structural conditions of the region, as well as percolative capacities (Iqbal and Sajjad 2014; Umair and Syed 2014; Aher et al. 2014; Benzougagh et al. 2016). High first-order values mean an unintended floodwater is likely after heavy rainfall in downstream streams (Chitra et al. 2011; Chaitanya and Kanak 2017). Frequently this phenomenon is in the study area, especially in the rural municipality of Meknassia Charkia: 34°16′28″ N, 3°56′503 W (2010, 2015, 2017 and 03/2018).

Stream length (Lu)

Similar order stream lengths (Lu) are calculated by calculating the overall length of stream sections of the respective order and by counting the number of stream sections of different order (Horton, 1945). The maximum stream segment length is usually the maximum in first-order streams, and it decreases by increasing the stream series. The cumulative length of stream portions in first-order streams is expressed by all subsets and decreased when the current order increases. Departing from its common position, the terrain is characterized by high relief or moderately steep slopes, which are dominated by specific lithologies (Singh and Singh 1997). The total length of stream sections, in the first-order stream and in the sixth order, was evident in this field of study.

Stream length ratio (RL)

The stream length ratio is according to Horton law (1945) the ratio of the mid-length of one order (Lu) to the lower order (Lu-1), which appears to be constant in the following watershed orders. The flux-length ratio of different orders in the study area indicates shifts in the basin. This change is due to variability in topography and slope, which is an indicator of the late youth stage of geomorphic development in the study area flows. A difference in each sub-watershed can be found in the proportion of stream length between the streams of different order of the Inaouene basins. For sub-basins, RL values differ between 0.02 and 5.67. This change is due to changes in topography and slope, which suggest the late developmental youth period of the Inaouene drainage flows. The higher ratio of liquid length suggests high activity of erosion.

Bifurcation ratio (Rb)

The bifurcation ratio (Rb) of one to the next highest orders is defined as a number of flows. By the following formula, Schumm (1956) expressed the bifurcation ratio:

$$ R_{{\text{b}}} = \frac{{{\text{N}}_{{\text{u}}} }}{{{\text{N}}_{{{\text{u}} + 1}} }} $$
(1)

where Rb = bifurcation ratio, Nu = total number of stream segments of order u, Nu+1 = number segments of the next higher order.

The bifurcation ratio is a significant parameter that indicates the degree of ramification and the degree of dissection of the drainage system (Bharadwaj et al. 2014). Horton (1945) regarded the proportion of bifurcation as the relief and dissection scale. Strahler (1957) has shown that Rb displays only a slight variability in different regions, but not in tight geological regulation.

Rb for a given drainage density is controlled extensively by the form of a basin and shows a very small variation (from 3 to 5) in consistent basement from one area to the next (Chorley et al. 1984). Higher bifurcation levels are the characteristics of structurally less impaired drainage basins without any distortion (Nag 1998). The higher Rb levels suggest good structural regulation in this study (SBV12: Rb = 7), while the lower Rb values show that structural disturbances are not affected (SBV21-Rb = 0.2).

Linear aspects of the Inaouene River basin were studied in the present work. For sixth order flows in all of the sub-basins, the water flows connected to the drainage network are dendritic. The key linear parameters are stream length and bifurcation (Rb). The variations in the stream length ratio are sufficient for topographical and slope shifts. The lesser values indicate that structural changes are not affected, while the greater Rb values indicate that drainage patterns are strongly structurally regulated.

The bifurcation ratio therefore correlates favorably with the structural nature of the terrain. This allows for direct relations between linear parameters and erodibility. The relation between stream orders indicated the effect on drainage ramification of geology, structural control and relief. Therefore, the more the erodibility, the lower the cost.

Areal aspects of the drainage basin

Basin area is an important morphometric characteristic, because it is associated with the spatial distribution of a range of significant characteristics including drainage density, stream rate, drainage factor, circularity ratio and elongation, overland stream length, compactness rated, constant channel maintenance and infiltration number. All of these parameters are comprehensive.

Drainage density (Dd)

The watershed density indicates the similarity of the channel size, which provides the average channel width for the whole basin for a quantitative calculation. This can be found in the following units: km/km2 (Horton 1932; Chorley 1969). We have examined extensively the relationship between different environmental variables and drainage density and reported the principal findings below. It tests the rate of flood dissection and depends on a number of variables, including the climate (primarily rainfall), the topography (slopes), lithology, soil, geology and erosivity of the watershed, its vegetational cover, infiltration potential and water permeability.

Much research indicates that a high catch-density is caused by poor or impermeable material in the basement, while low catchment densities generally lead to the surface area with high resistance to or permitted subterranean substances (Strahler 1964; Melton 1957; Nag 1998; Thomas et al. 2011 and Benzougagh et al. 2016). Incidentally, the low density of the output contributes to crass texture and high input density to a perfect texture for drainage. Dd means a sluggish hydrogeological response to a poorly drained lake.

The region of highly resistant or permeable subsoil content usually results in the low drainage density [0–1.75]. The low and impermeable surface soil, scattered vegetation, and mountainous relief are responsible for a high drainage density (Dd > 3.50). This indicates a strongly divided catchment with relatively fast hydrological reactions to precipitation. The moderate Dd [1.75–3.50] suggests that the bottom and vegetative cover are highly permeable.

The drainage density is 0.77–2.22 km per square kilometer, which suggests low to medium drainage density in this study (Fig. 8).

Fig. 8
figure 8

Drainage density of 48 sub-watershed of Inaouene River

Full size image

Drainage texture (Dt)

The drainage texture has been defined by Horton (1945), as the total number of stream portions per perimeter of the area. The drainage structure displays the relative division of the canal into a divided fluvial terrain (Vincy et al. 2012), which counts on a number of natural factors such as precipitation, climate, soil and rock type, infiltrations, vegetation relief, and progression (Smith 1950). In Table 2, Smith listed the drainage texture in five classes:

Table 2 Classification of drainage texture
Full size table

The drainage texture of the basin in this study varies from 0.21 to SBV26 to 3.81 to SBV15. Therefore, 0.2 1 shows a very coarse texture drainage, and 3.81 shows a coarse texture drainage (Fig. 9).

Fig. 9
figure 9

Drainage texture of 48 sub-watershed of Inaouene River

Full size image

Stream frequency (Fs)

Horton (1932) has specified the basin's flux frequency (Fs) as the overall number of stream parts per unit area for all orders. The frequency of the flow is also called the level of drainage. The formula for calculating the flux frequency is according to Horton (1945):

$$ F_{{\text{S}}} = { }\frac{{{\text{N}}_{{\text{u}}} }}{{\text{A}}} $$
(2)

where Fs = drainage frequency, Nu = total number of stream segments of order U, A = basin area.

The density of streams primarily depends on the watershed lithology and shows the drainage system textures. This is an example of the different phases of landscape transition (Hajam et al. 2013). Fs was linked to permeability (rock structure), sloping, relief, rainfall nature and sum and water shield capacity of sub-surface material (Montgomery and Dietrich 1989). They find that Fs decreases in line with the increase in the stream number and is positively related to the basin catchment density values (Fig. 10).

Fig. 10
figure 10

Relationship between drainage density (Dd) and stream frequency (Fs) of 48 sub-watersheds of Inaouene River

Full size image

This paper shows a high 4.73-value stream rate in SBV26, due to a high level of infiltration and relief. High 0.26 in SBV15 shows the high runoff quality and raises the catchment density in the stream population.

Form factor (Ff)

In order to calculate the flux of a basin on a defined area, Horton (1932, 1945) proposed that this variable. In Ff, the proportion between the basin area and the basin length square is specified. The form factor illustrates the length and width relationship between the basin and is determined with the Horton formula (1932), as shown below:

$$ F_{{\text{f}}} = \frac{{\text{A}}}{{{\text{L}}_{{\text{b}}}^{2} }} $$
(3)

where A = area of basin (km2), Lb2 = square of the basin length.

Ff is always below 0.7854, because the shape of such a basin is not completely circular (Chopra et al. 2005; Iqbal and Sajjad 2014).

The form factor in this analysis ranges from 0.001 to 0.086 for all watersheds. The low value of the shape function means that the basin is bigger. The high shape factor vessel has a peak rate of short durations; the long, low shape sub-watershed has a lower peak level of long life (Umak et al. 2017). Flows of such stretch basins can be guided more easily than from the circular basin (Benzougagh et al. 2016).

Circularity ratio (Rc)

The circularity ratio is the proportion of the watershed region in a circle area that is the same distance as the circumference of the watershed, according to Miller (1953). In Miller's (1953) equation, the ratio is calculated as:

$$ R_{{\text{C}}} = \frac{{\text{A}}}{{{\text{A}}_{{\text{C}}} }}\,{\text{or}}\,R_{{\text{C}}} = 4{\uppi }\frac{{\text{A}}}{{{\text{P}}^{2} }} $$
(4)

where Rc: circularity ratio; A: basin area (km2); P: basin perimeter (km); \({\uppi } = {\text{Cts}} = 3.14\).

The circularity ratio's low, moderate, and high value are indicators of the young, intermediate and old phase of the tributaries ' life cycles (John Wilson et al. 2012). This governs climatic conditions, stream length and intensity, geological systems, the landscape and land use, the river relief and slope.

The Rc values for all watersheds in this paper indicate that the basins are nearly elongated. The diversity of the structural conditions, relief and pitch in these watersheds causes this anomaly.

Elongation ratio (Re)

The elongation ratio (Re) reflects the shape of the rivér basin. The elongation ratio is known, as it were, as the proportions between the circle diameter of the same area as the drainage basin and the total length of the basin, according to Schumn (1956). The equation is as follows:

$$ {\text{R}}_{{\text{e}}} = \left( {\frac{2}{{{\text{L}}_{{\text{b}}} }}} \right){*}\left( {\frac{{\text{A}}}{{\uppi }}} \right)^{0.5} $$
(5)

where A: the basin area (km2),\({\uppi }\) = 3.14, and Lb(km) is the basin length parallel to the principal drainage line.

The Re values for the expanded basin to 1.0 range from 0.6 to 1.0 for the circular basin, usually, according to, over a wide variety of climate and geology types. Drainage output in circular watersheds is greater than an extended watershed (Singh and Singh 1997). For areas of very low relief, the values of approx. 1.0 are typical; values in the range of 0.6 to 0.8 are usually related to high relief steep slope (Strahler 1964). The Re is divided into five categories (Table 3).

Table 3 Classification of elongation ratio
Full size table

The Re for watersheds is 0.56–0.75 in this journal. The most Re of the study area watersheds (79.17%) are aligned with the [0.5–0.7] elongated form and displays lower relief and steep slope. The less elongated shape of 20.83% of the watersheds is shown (Fig. 11).

Fig. 11
figure 11

Elongation ratio of sub-watersheds of Inaouene River

Full size image

Length of overland flow (Lg)

According to Horton (1945), overland flow (Lg), before it is concentrated to a definite flow channel, is the length of the water over the surface of the soil. The drainage density is equal to half (Dd), Lg = 1⁄2 Dd. Length of overland flow relates inversely to the average channel slope (Sunil et al. 2010; Umair and Syed 2014; Waikar and Nilawar 2014).

It also has a big effect on the development of a catchment basin physio-graphically, topographically and hydrologically. Compared to moderate sloping and flat land, the overland flow in the hilly terrain is small (Kumar 2017). It depends on the type of rock, climate, permeability, relief and vegetation, as well as the length of erosion.

The higher Lg value usually shows that the relief is low and the runoff process is slower. It was found in low pitch areas in which the erosion is not strong. It is usually linked to the development phase in the basin.

The overland flow time of these works varies between 0.13 and 2.37 for each basin of the Inaouene watershed. On the other side, Lg's low value shows high relief, higher drainage and lower relief.

Compactness coefficient (Cc)

The ratio of the compactness of a basin is the diameter of the basin to the radius of the circular region, which is proportional to the area of the basin, in line with Gravelius (1914).

$$ {\text{C}}_{{\text{C}}} = 0.2821\frac{{\text{P}}}{{{\text{A}}^{0.5} }} $$
(6)

Compactness coefficient (Cc) is used to describe a hydrological watershed's relation to the circular basin of a same area as the hydrological watershed. This is directly proportional to the risk assessment of erosion, meaning lower risk factor values mean that risk factors are less vulnerable, whereas higher values suggest the lower elongation and high erosion (great volunteer vulnerability), and the need for conservation calculation is expressed (Umak et al. 2017). The highest value contained in the sub-watershed is SBV09 (1.36), whereas for the sub-watershed the lowest value is SBV15 (0.04).

Constant channel maintenance (C)

The inverse catchment density (Horton 1945; Schumm 1956) can be defined as the constant maintenance channel (C). This shows the relative dimensions and genetic values of topography units in the catchment basin (Strahler 1957). The continuous maintenance of the channel thus defines the minimum restricting area needed for the creation of a drainage channel and tests the eroding potential in the watershed. The climate, permeability, lithology, the surface material's absorption potential and the covering of vegetation of the basin are considered. Due to the coarse texture and intensive drainage areas, most mini-watersheds are identical and low.

Constant maintenance for the channels ranges from 0.21 for SBV26 to 3.81 for SBV15 in this study. SBV26 (0.21) shows low values to maintain a constant flow, with high drainage network density and a reduced area needed to support 1 km of drainage and vice versa.

Infiltration number (If)

By multiplying the value of stream frequency with drainage density, the infiltration number of the basin is determined. The number of infiltrations has a significant influence on the characteristics of infiltration in the basin. The higher number of infiltrations indicates a lower infiltration and higher drainage quality. The result is that the drainage density is higher. Higher relief and impermeable lithology were thus illustrated by the infiltration characteristics of the watershed. Mini water basin infiltration number range from 0.07 to 22.42. Inaouene lake. The lower number of infiltrations is SBV15 (0.07), and the higher number of infiltrations is for SBV26 (22.42). The SBV15 basin has a higher level of infiltration in the alluvial plain.

The shape of the basin significantly affects the characteristics of flux discharge. For example, alternating flood discharge can be expected from an extended basin with a high bifurcation ratio. A round or circular basin with a lower bifurcation ratio may, however, have a strong water discharge on the other hand. Drainage and sediment movement are significantly affected by the shape of a lake. The form of the drainage tank also leads to the rate of entry of water into the river. The quantitative expression of the watershed may be defined in this paper by its form factor, compaction coefficient, circulation ratio, drainage rate, and elongation.

Land use and land cover

In addition to the morphometric analysis, the study of land use and land cover is another key factor in assessing the risk of erosion in a watershed. Climate, soil, slope, land use/ land cover (LULC), and soil management are all factors that influence erosivity (Khadse et al. 2015). Land use and land cover relate to man's utilitarian land operations, whereas land cover refers to natural vegetation, forest cover, and water bodies, among other things (Das et al. 2021). According to the Inaouene watershed land use/land cover categorization, seven different classes were identified, along with corresponding area. A substantial portion of the basin is under the cereal field (43.23%), followed by bare soil field (35.15%), which makes the study area vulnerable to the risks of soil degradation, followed by arboriculture field (7.61%), built-up area (4.62%), matorral-parcours (4.60%), forest cover (3.77%) and water (1.03%). The spatial distribution of the land uses and land cover of Inaouene watershed is shown in Fig. 12.

Fig. 12
figure 12

Land cover/land use map of the Oued Inaouene watershed

Full size image

Inter-correlation Matrix of Morphometric Parameters for Sub-watersheds of Inaouène River

The parameters of morphometric analysis are usually often correlated. The comparison indicates that some of the monitored information in one variable is also controlled in certain other residual variables. In particular, the first main element indicates that the linear combination of the original variables makes a maximum contribution to the total variance. The second major component, linked to the first, adds to the residual variance as much as possible, until the overall variance is analyzed (Table 3). The procedure, therefore, is most appropriate if all the variables are calculated in the same units (Sharma et al. 2014) as the total variance of the primary variabilities is dependent. It is therefore customary that the variables be expressed as normal, i.e., the unit for each measurement is to be chosen so that the sample variance is one. The analysis is then carried out on the correlation matrix, and the total variance is equivalent to n. The inter-correlation matrix (Table 4) was constructed from the 48 sub-watersheds of the Inaouene River using eleven chosen morphometric parameters (linear and areal).

Table 4 Correlation matrix of morphometric parameters for 48 sub-watersheds
Full size table

Initially, when these 12 morphometric variables were submitted to the matrix of correlation, there was found to be a high positive correlation between drainage densities with compactness coefficient (Cc) and infiltration number (If), surface drainage density ratio (T), form factor (Ff). There is also a strong negative association between texture ratio (T), shape factor (Ff), circularity ratio (Rc), overland flow length (Lg) and constant channel maintenance (C) with most morphometric parameters.

This demonstrates that there were high correlations between Dd and If, Fs and If (correlation coefficient greater than 0.9). In addition, between Dd, Dd and C, Dt and Fs, FS and C, Re and C strong correlations occurred (coefficient correlation of more than 0.74). The Dd and Cc, Dt and Rc, Fs and Cc, Ff and Lg, Rc and C are a few more slightly correlated parameters (relation coefficient more than 0.6). At this point, grouping parameters in components is very difficult and it gives no physical relevance since there was no meaningful association with any parameter such as T, Lg, Cc, and C (Table 5).

Table 5 Compound value and priority class for 48 sub-watersheds of Inaouène basin
Full size table

Correlation tests also show that the lowest drainage density (1) coefficient of correlation with infiltration (If) frequency (Fs) is the highest. The highest negative correlation with compactness coefficient (Cc) was shown by the elongation ratio (Re).

Prioritization of sub-watersheds

The morphometric parameter is also known as risk assessment parameters (Biswas et al. 1999), in particular the risk of erosion and of flooding, according to the prioritization based on morphometric analysis. Soil erodibility is directly related to linear parameters. The highest value for linear parameters was thus considered to be one, and the second highest priority was classified as two and so on for the priority setting of sub-basins.

Soil erodibility is related to shape parameters in reverse (Nookaratnam et al. 2005; Benzougagh et al. 2016, 2017). Less erodibility is the lower the price. The lowest value of the shape parameters was considered to be in the first position, then in the second place, and so on. The last in rank was the highest value. The sub-watershed ranking was thus calculated by giving highest priority/priority in linear parameters based on the highest value and lowest value in type parameters.

The classification was later carried out on the basis of all lone criteria. Therefore, the classification values for each of the 48 sub-basins have been applied to achieve a cumulative value for all dimensional and form parameters of each sub-basin. (Cp) The sub-basins were subsequently graded into five categories, based on compound value range, which are very low, low, moderate, high and high priority. Figure 13a and b displays the final priority chart for the region of research and priority rates for the Inaouene River sub-watersheds.

Fig. 13
figure 13

a: Prioritization map of 48 sub-watersheds; b: Percentage of sub-watersheds relative to priority rank of erosion risk in the Inaouene watershed

Full size image

Conclusions

The current study demonstrates the utility of remote sensing and geographic information system (GIS) techniques for morphometric analysis of sub-watersheds in the Inaouene watershed. The morphometric properties of distinct Sub-watersheds demonstrate their respective influence on hydrologic response of the sub-watersheds. The various morphometric parameters of each Sub-watershed were ranked based on their susceptibility to risk of soil erosion. Compound parameter (Cp)-based prioritization methods with the assist of GIS techniques identify sub-watersheds SBV1, SBV5, SBV9, SBV19, SBV20, SBV21, SBV37, SBV39, SBV47, and SBV48 as most vulnerable to high erosion hazard risk. This calls for setting up of immediate and viable remedial strategies for soil conservation and flood management. The present study further demonstrates the utility of Remote Sensing and GIS techniques in prioritization of watersheds, which may be helpful for taking the high priority implementation of soil and water conservation measures.