Introduction

Basin is an ideal unit to manage natural resources and reduce the impact on sustainable development from natural disasters (Abdul Rahaman et al. 2015). Planning for the basin management highlights river erosion management techniques (Gajbhiye et al. 2015a, b). The assessment was also performed in sub watersheds to assess the natural hazards and threats (soil erosion, floods, slide etc.). Water soil erosion is recognized as a major cause of earth deterioration throughout the world. Soil erosion in general, particularly in the Narmada River basin watershed is not a recent problem in the country. Environmental degradation is environmental degradation induced by the loss of resources such as air, water and soil; ecosystem destruction and the extinction of biodiversity. It is characterized as any changes or disruptions perceived to be deleterious or unwelcome to the environment. The issue of environmental degradation affects the countries of the world in general and the Narmada basin in particular.

Many additional threats to climate change emerge in this dynamic environment, including extreme land degradation and prolonged droughts. Unfortunately, these challenges, in conjunction with other environmental developments like as water and air pollution, are becoming increasingly important drivers of environmental degradation (Choudhary et al. 2015; Cramer et al. 2019). Among the examples of environmental degradation, the negative effect of risk of water erosion in the watershed. Land degradation is a complex series of processes in surfaces (Fadhil Al-Quraishi 2003) the example of land degradation in Narmada basin watershed is water erosion risk, which is a natural process. Defining the vulnerable field of soil erosion and identifying the key areas of erosion is critical for the prioritization and delineation of these areas of management.

The morphometric parameters represent nearly the entire watershed’s causative variables affecting rainfall-generated runoff and sediment, either directly or indirectly. Prior to using any sophisticated instrument to track watershed responses in relation to any of the hydrologic processes operating on it, the surface highlights are the most important analysis units. As a result, these criteria can be used to determine watershed planning goals in terms of proper soil and water management. An examination of silt load data from India and other parts of the world showed that not all watersheds are equally vulnerable to erosion (Nikam et al. 2014). As a result, in order to be handled on a priority basis, it is important to define a vital watershed. In this way, morphometric parameters combined with satellite-based land cover data of watersheds can be useful in prioritizing sub watersheds in the absence of extensive hydrological data.

The Remote Sensing (RS) and Geographic Information System (GIS) can serve as useful tools to monitor and assess land loss and soil erosion, helping to develop appropriate and reasonable strategies for management (Fadhil Al-Quraishi 2003). The watershed by its geographic position is vulnerable to several natural risks (flooding, landslide, drought, water erosion, forest fires, etc.). This study focus on the risk of ‘water erosion’. Several factors such as rainfall, lithology, slopes and plant cover must be prioritized, analyzed and treated by the approach of morphometric analysis. Morphometric mapping in combination with the Remote Sensing (RS) and Geographical Information System (GIS) which can serve as useful resources for monitoring and evaluating land loss and soil erosion, helping to establish appropriate and reasonable management strategies (Fadhil Al-Quraishi 2003; Benzougagh et al. 2020, 2022a, b; Meshram et al. 2022a, b). The morphometric analysis including linear, areal and drainage parameters. Morphometric watershed research is an important first step towards a clearer appreciation of watershed dynamic characteristics. Therefore, morphometric analysis is an important method for prioritizing sub-watershed growth and the management of natural resources (Biswas and Chakraborty 2016; Benzougagh et al. 2016, 2017). The results of the production of an erosion danger map are a powerful resource for planning to minimize the problems of soil erosion induced by potential and current sustainable growth programs in the research region as well as in other regions.

Recent studies have shown that remote sensing (RS) and geographic information system (GIS) tools and techniques are highly efficient and useful for improving and monitoring watersheds, as well as prioritizing sub-watersheds in soil and water management (Sarma and Saikia 2012; Ahmed and Rao 2015; Khadse et al. 2015; Makwana and Tiwari 2016; Khanday and Javed 2016; Farhan et al. 2017; Jharia et al. 2018; Kadam et al. 2019; Arefin et al. 2020). In the ongoing decades, numerous scientists have concentrated on deterministic or regression modeling. Koutsoyiannis (2001) proposed a system for coupling stochastic models of hydrologic measures applying to various time scales with the goal that the time arrangement produced by various model is reliable. Singh et al. (2001) created local stream span models for enormous number of un-checked Himalayan catchments. They announced that the factual methodology of quantile assessment performed acceptably in alignment just as in approval. Kumar and Rastogi (2005) analyzed hydrologic data for the year 1977–1985 for development of sub area routing model for estimation of sediment yield on storm basis from Gagas watershed, Ramganga reservoir catchment. Caissie et al. (2007) used a deterministic model to predict water temperatures in Miramichi River catchments (New Brunswick, Canada). When researching rivers of various sizes and thermal conditions, they concluded that deterministic water temperature models are useful tools for forecasting river water temperatures. Gupta and Singh (2010) multivariate statistical techniques were used to create dimensionally homogeneous and statistically optimal models for annual runoff and Sediment Production Rate (SPR) prediction from the Mahi catchment’s limited watersheds. The developed models can be used to forecast runoff and SPR in small un-gauged watersheds in the Mahi catchment that have similar physiographic characteristics. Singh et al. (2007) used deterministic modeling of annual runoff and sediment production rate for small watersheds of Chambal Catchment. Amoudry and Souza (2011) reviewed and discussed the deterministic coastal morphological and sediment transport modeling. Shojaeezadeh et al. (2018) introduced a parsimonious probabilistic model to describe the relationship between Suspended Sediment Load (SSL) and discharge volume. This model, rooted in multivariate probability theory and Bayesian Network, infers conditional marginal distribution of SSL for a given discharge level.

Watershed management is needed for the proper and efficient use of land and water resources. As a result, it is often preferable to begin management steps from the most sensitive sub-watershed. To make accurate predictions, comprehensive data are needed for proper scientific planning and management of the watershed. Many watersheds in India are not measured for such situations. Deterministic morphometric modeling is a fundamental method for studying a basin’s hydrologic activity. A deterministic model can be constructed using dimensionless morphometric characteristics and the sediment yield index. Models built in this way can be used to predict sediment yield in watersheds with similar physiographic conditions. Considering such approach the present study was undertaken. However, the basin’s understanding of the aforementioned facts has yet to be discussed, and no such scientific tests for a basin have been published thus far. As a result, the findings of this study are novel and significant to the water resource authorities concerned.

Material and methods description

Study area and data used

The Narmada is the Indian peninsula’s largest west-flowing river. It is one of India’s most powerful rivers. The Narmada River rises at an elevation of 1057 m above mean sea level in the Amarkantak Plateau of the Maikala range in the Shahdol district of Madhya Pradesh, at a latitude of 22° 40ʹ N and a longitude of 81° 45ʹ E. The river flows for 1312 km before crashing into the Gulf of Cambay in the Arabian Sea near Bharuch, Gujarat. The first 1079 km of its run are in Madhya Pradesh. The river forms the border between the states of Madhya Pradesh and Maharashtra for the next 35 km. It then forms the border between Maharashtra and Gujarat for the next 39 km (Gajbhiye et al. 2013a, b). The last length of 159 km lies in Gujarat. The Narmada basin covers 98,796 km2 and is located between longitudes 72° 32ʹ E and 81° 45ʹ E, and latitudes 21° 20ʹ N and 23° 45ʹ N. For model application, three watersheds were selected based on the availability of morphometric parameter and sediment yield index data, a brief description of which is given below:

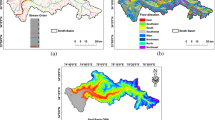
Bamhani watershed (Ba), Manot watershed (Ma), Mohgaon watershed (Mo) in Mandla district, India. In this research, morphometric parameter of 49 sub-watersheds across upper Narmada Basin Mandla, Madhya Pradesh State, India. The location map of the study watershed shown in Fig. 1.

Fig. 1
figure 1

Location map of the study area

Full size image

In order to develop morphometric deterministic model (MDM), we have taken the morphometric parameter and sediment yield index for the 49 sub-watershed (Ba, Ma, Mo) (Table 1) from the previous studies of Gajbhiye et al. (2014a, b).

Table 1 Morphometric parameter of the study area Gajbhiye et al. (2014a, b)
Full size table

Methodology

The used procedure in this study can be summarized in the following stages:

  1. 1.

    Establishing morphometric parameters and sediment yield index

  2. 2.

    Applying the principal component analysis (PCA) for redundancy of morphometric parameter

  3. 3.

    Develop morphometric deterministic model (MDM).

  4. 4.

    Parameter estimation.

  5. 5.

    Qualitative evaluation of model performance.

Morphometric parameters

Stream network is a basic requirement of any morphometric study and the prioritization of watersheds. Digital Elevation Model (DEM) (30*30 m) generated by Shutter Radar Topography Mission (SRTM) data is a common tool to define a stream network and sub-watershed map. Different drainage network parameters, i.e., numbers and lengths and watershed area, perimeter, width and length were determined in GIS environment (Meshram et al. 2019, 2020a, b, 2021). Then using standard formulae stream frequency, drainage density, circulatory ratio, form factor and elongation ratio were estimated. Sediment yield index is calculated using the AISLUS (1991) formulae.

Principal component analysis

Most of the time there is relationship between the morphometric parameters such that some of the parameters share the same information. In performing component analysis, the co-ordinates axis is transformed to a new reference frame within the total variable space. This involves assigning new principal components to each variable either through an uncorrelated or an orthogonal transformation. These components are unique in that they consider the maximum variance between the variables. The correlation matrix and principal components are thus obtained from the principal component analysis performed on the geomorphic variables (Gajbhiye et al. 2015c; Gajbhiye and Sharma 2017). The analysis employs the first factor and rotated the factor loading matrices. The product of the square of a parameter’s loading and the percent of the rotated factor covariance gives the order of importance of a parameter. Thus, computation is derived from the most commonly used transformation technique involving rotated factor loading matrices based on the varimax criteria (Singh 2006).

The proposed morphometric deterministic model

SPSS 16.0 software was used to create dimensionally homogeneous and statistically optimal models of the following linear (Eq. 1) and nonlinear (Eq. 2) form after redundancy of morphometric parameters into physically significant components.

$${\mathcal{Y}} = a_{0} + a_{1} x_{1} + a_{2} x_{2} + a_{3} x_{3} + ... + a_{n} x_{n}$$
(1)
$${\mathcal{Y}} = a_{0} x_{1}^{{a_{1} }} x_{2}^{{a_{2} }} x_{3}^{{a_{3} }} ...\;x_{n}^{{a_{n} }}$$
(2)

where \({\mathcal{Y}}\) is the dependent variable (Sediment yield index) and \(x_{1} ,x_{2} ,\;...,\;x_{n}\) are the independent variables (Morphometric parameter), \(a_{0} ,a_{1} ,\;...,a_{n}\) are the regression co-efficients.

Parameter estimation

The SPSS Statistical Package was used to analyze the data in Windows version 22.0. For multi-step regression, one-way multivariate analyses were used to depart from the morphometric parameter and SYI parameters. In the MDM, sediment yield index was dependent variable and morphometric parameter (most effective) was independent variables.

Evaluation of model performance

The accuracy of prediction models was evaluated using three error measures in this paper: Mean Absolute Error (MAE) (Chai and Draxler 2014) (Eq. 3), Nash–Sutcliffe Efficiency (NSE) (Nash and Sutclife 1970) (Eq. 4), and Willmott’s Index (WI) (Willmott 1981) (Eq. 5).

$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{{\text{n}}} \left| {{\mathcal{X}}_{i} - {\mathcal{Y}}_{i} } \right|$$
(3)
$${\text{NSE}} = \left| {1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{{\text{n}}} \left( {{\mathcal{Y}}_{i} - {\mathcal{X}}_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{{\text{n}}} \left( {{\mathcal{Y}}_{i} - \overline{{\mathcal{Y}}} } \right)^{2} }}} \right]} \right|$$
(4)
$${\text{WI}} = \left| {1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{{\text{n}}} \left( {{\mathcal{Y}}_{i} - {\mathcal{X}}_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{{\text{n}}} \left( {\left| {{\mathcal{X}}_{i} - \overline{{\mathcal{Y}}} } \right| + \left| {{\mathcal{Y}}_{i} - \overline{{\mathcal{Y}}} } \right|} \right)^{2} }}} \right]} \right|$$
(5)

where is the total number of data; i and i are the observed and predicted sediment yield index data; and, \(\overline{{\mathcal{Y}}}\) is the average of observed data.

Results and discussion

Morphometric parameters of upper Narmada basin watersheds adapted from Gajbhiye et al. (2014a, b) are presented in Table 1. For redundancy of morphometric parameter, PCA has been applied. A hierarchical tree from the most effective morphometric results is used to prioritize the sub-watersheds.

The SPSS 22.0 software is employed to assess the inter-co-relationships of morphometric variables through a correlation matrix (Table 2). Very high correlations (R > 0.9) exist between the elongation ratio (Re) and form factor (Rf); Lo and Dd. In addition, moderately high correlations (R > 0.70) are observed between; Rh and Rr; RN and Dd/Fs/T/Lo/Cc and between Dd and Fs/T/Cc, Fs and T/Lo; Rc and Cc; T and Cc; Lo and Cc. Because there are no significant correlations between Rr, Rb, Sa and HI with any of the parameters under consideration, it is practically impossible to put the parameters into component groups. Therefore, the subsequent step makes use of the principal component analysis technique.

Table 2 Inter-correlation matrix of the morphometric parameters
Full size table

The correlation matrix obtained from the previous step is used to generate the first unrotated factor loading matrix (Table 3). The results show that about 84.57% of the total explained variance is attributed to the combination of the first three components with eigen values above one. It is observed that a strong correlation (R > 0.9) between Cc and the first component (Table 4A). Relatively high correlations (R > 0.7) are also found between the first component and each of the variables; Lo, Dd, T, Fs, RN, Rc. On the other hand, Rh has high correlations with second component. Sa and HI have high correlation with third and fourth component correspondingly. No significant correlations exist between the Rb, Re, Rr and Rf with any one of the component.

Table 3 Total variance explained
Full size table
Table 4 Varimax method of the first factor loading matrix (unrotated) and rotated factor loading matrix of morphometric parameters
Full size table

Redistribution of the observed variance is performed so that better factor loadings can be obtained. This is done by carrying out analytical rotations those components whose eigen value exceeds one. The outcome of varimax rotation is shown in Table 4B.

The first component is very highly correlated with Fs and highly correlated with Dd, Lo, Fs and RN. The second component is very highly correlated with Rr, the third component is very highly correlated with Rf, Re and the fourth component is very highly correlated with HI. A strong correlation also exists between the first component with T and Cc, while second component with Rh. For the model development, we selected the morphometric parameter (Dd, Lo, Fs, RN, Rr, Rf, Re, HI) that’s very highly correlated (R > 0.90) with the component.

The sediment yield index models based on morphometric parameter were developed for the Narmada basin watersheds. The morphometric deterministic model (linear and nonlinear) was developed by considering the 34 sub-watershed dataset (Morphometric parameter and SYI). The linear and nonlinear MDM in form of Eq. 6 and 7 were derived on the basis of sub-watershed dataset. The value of coefficient of multiple regressions (R2) for linear MDM was (0.81). Whereas, R2 value for the nonlinear MDM was 0.89. This shows the applicability of morphometric deterministic models. The linear and nonlinear MDM developed by (34 sub-watershed) datasets are:

$$\begin{aligned} {\text{SYI}} & = 4391.73 + 61603.38\left( {R_{{\text{r}}} } \right) - 23.67\left( {R_{{\text{N}}} } \right) - 343.78\left( {D_{{\text{d}}} } \right) - 123.99\left( {F_{{\text{s}}} } \right) \\ & - 1080.08 \left( {R_{{\text{f}}} } \right) + 361.56\left( {R_{{\text{e}}} } \right) - 7618.15\left( {L_{{\text{o}}} } \right) - 86.30\left( {{\text{HI}}} \right) \\ R^{2} & = 0.81 \\ \end{aligned}$$
(6)
$$\begin{aligned} {\text{SYI}} & = 18.35R_{{\text{r}}}^{0.298} R_{{\text{N}}}^{0.075} D_{{\text{d}}}^{ - 8.45} F_{{\text{s}}}^{ - 0.767} R_{{\text{f}}}^{ - 2.72} R_{{\text{e}}}^{4.70} L_{{\text{o}}}^{ - 8.77} {\text{HI}}^{ - 0.006} \\ R^{2} & = 0.89 \\ \end{aligned}$$
(7)

The linear and nonlinear MDMs were applied tohe sub-watershed dataset to test and verify their applicability for the study region. The comparison of observed and expected values using the evolved model with the remaining data set (15 sub-watershed) is presented in graphical form in Fig. 2, along with graphical validation in Fig. 3. Table 5 also shows the values of qualitative parameters for the built model. It was discovered that the model performs well in terms of predicting the sediment yield index, which is critical for effective soil conservation programs.

Fig. 2
figure 2

Comparison of observed and predicted sediment yield Index during calibration stage a Linear model; b Nonlinear morphometric deterministic model

Full size image
Fig. 3
figure 3

Comparison of observed and predicted sediment yield Index during validation stage a Linear model; b Nonlinear morphometric deterministic model

Full size image
Table 5 Estimated values of regression parameters linear and nonlinear MDM, and coefficient of determination (R2) for the dependent and independent variables
Full size table

Morphometric deterministic model (MDM) validation

The linear and nonlinear MDM were validated for the remaining sub-watershed (Mo 1–15) dataset. The value of the (R2) coefficient of determinations for all the linear and nonlinear models observed to be 0.88 and 0.95, respectively. The values of NSE, MAE and WI of linear models were found of (88.09, 42.77, 0.96), nonlinear model were (94.73, 25.91, 0.98), respectively (Table 6). Validation statistics of all the models were found best fit to satisfy the criteria of a good model (Table 6).

Table 6 Performance evaluation of linear and nonlinear MDM
Full size table

Conclusions

The aim of this study was to develop a morphometric deterministic model using input parameters such as morphometric parameter (Rr, RN, Dd, Fs, Rf, Re, Lo, HI). The established linear and nonlinear morphometric deterministic models performed admirably. As a result, the best performance model for nonlinear MDM has been declared. The study area was found to be suitable for the deterministic models constructed using the most powerful morphometric parameter. Independent variables of morphometric parameters have a major impact on sediment yield forecasting.