Abstract
Using the outlier robust extreme learning machine (ORELM) method, the discharge coefficient of side weirs placed on rectangular and trapezoidal canals was simulated for the first time in this study. The parameters governing the discharge coefficient of side weirs including Froude number (Fr), the ratio of the weir length to the main channel length (L/b), the ratio of the flow depth at the upstream of the side weir to the main channel width (y1/b) and the ratio of the crest height of the side weir to the flow depth at the upstream of the side weir (W/y1), the ratio of the weir length to the main channel width (L/y1), and the side wall slope parameter (m) were initially detected. Using the parameters governing, eight different input combinations were defined. By randomly selection approach, 65% of the data were considered to train the ORELM models and the rest of samples were applied to test them. The correlation coefficient, Nash–Sutcliffe efficiency coefficient, and Scatter Index for this model were calculated to be 0.937, 0.869 and 0.092, respectively. The results of sensitivity analysis indicated the ORELM model was more sensitive to the W/y1 and L/b than Fr and y1/b. The results of the ORELM model were also compared with the support vector machine optimized with genetic algorithm (SVM-GA) and extreme learning machine (ELM)) and four multiple linear regression models, with a better performance of the ORELM model. The ORELM models demonstrated a higher precision and correlation with experimental values.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
As one of the main hydraulic structures, a side weir is installed to divert and regulate flow on the sidewall of the main channels. Such structures have many applications in irrigation and drainage networks, urban runoff collection systems and water and wastewater treatment plants (Bagheri et al. 2014).
The discharge coefficient is treated as the most significant parameter for design a side weir which many researchers have conducted several analytical and numerical studies on it (Akhbari et al. 2017; Mirzaei and Sheibani 2020). For channels with different slopes, they reported the changes in the discharge coefficient versus the Froude number, suggesting that the discharge coefficient decreased by increasing the Froude number. Furthermore, an experimental research on the discharge coefficient of weirs located on rectangular and trapezoidal canals was carried out by Keshavarzi and Ball (2014). They came to the conclusion that the discharge coefficient was a function of the Froude number, the ratio of the crest height of the side weir to the flow depth at the upstream of the weir, and the wall slope of the main channel. Moreover, Bagheri et al. (2014) evaluated the discharge coefficient of rectangular side weirs experimentally. The effects of hydraulic and geometric parameters on the changes in the discharge coefficient were evaluated and the variations in the free flow surface were calculated.
The limitation of the multiple linear regressions (MLRs) that applied in experimental-based studies to provide a relationship between input and output parameters is the low generalizability of this approach to estimate samples that have no role in model calibrations. Indeed, the MLR fits the model to find the target value and there is no any training phase to teach model for unseen samples. To overcome this drawbacks, an accurate and reliable tool known as artificial intelligence model have been utilized for simulating and estimating different phenomena. The discharge coefficient of side weirs has been simulated across various algorithms and models of artificial intelligence throughout recent decades (Salmasi and Sattari 2017; Niazkar and Afzali 2018; Olyaie et al. 2019).
Using Gene Expression Programming (GEP) model, the discharge coefficient of rectangular side weirs was estimated by Ebtehaj et al. (2015a). They proposed a formula using hydraulic and geometric parameters to determine the discharge coefficient. They also compared the results of the developed GEP with existing models and showed that the GEP was more accurate. Using group method of data handling (GMDH), Ebtehaj et al. (2015b) estimated the discharge coefficient of side weirs. They also compared the results with Artificial Neural Network (ANN) and showed that the GMDH was more accurate. Moreover, Khoshbin et al. (2016) presented an optimized hybrid model for estimating the discharge coefficient of side weirs through the combination of the adaptive neuro-fuzzy inference system (ANFIS), the genetic algorithm (GA) and the singular value decomposition (SVD). By conducting a sensitivity analysis, the parameters influencing the discharge coefficient of side weirs located on trapezoidal channels were investigated by Azimi et al. (2017a). They defined the superior model and the most significant input parameter using the extreme learning machine (ELM). Azimi et al. (2017b) used the GEP to simulate discharge coefficient of side weirs on trapezoidal channels through subcritical conditions. They provided an equation for the discharge coefficient calculation. Subsequently, Azimi et al. (2019a) developed six different models for estimating the discharge coefficient of weirs located on a trapezoidal channel by the means of the support vector machine approach. In determining the discharge coefficient, they implemented the superior model by performing a sensitivity analysis.
Bagherifar et al. (2020) simulated the flow field within the circular flumes along with the rectangular side weirs through a computational fluid dynamics (CFD) model. The results showed that the CFD model estimated the flow characteristics with a reasonable performance. The authors demonstrated that the specific energy at upstream and downstream of the side weir was approximately constant.
According to the unique characteristics of the Extreme leaning machine (ELM) (Huang et al. 2006) as an efficient, effective machine learning algorithm (Huang 2014) in solving complex nonlinear problems has attracted many researchers' attention (Azimi et al. 2017a; Ebtehaj et al. 2018; Zeynoddin et al. 2018; Bonakdari et al. 2019; Azimi and Shiri 2021). Some of the advantages of this method are: (1) in addition to the ability to approximate the estimator function, it can map a training inputs variables to the corresponding output one and can perform fast and accurate parallel computations during testing and training processes. (2) Various experimental studies showed that the ELM technique has better generalization and scalability performance than classical neural network methods such as the multi-layer perceptron and the support vector machine (Huang et al. 2011; Ebtehaj et al. 2016; Azimi and Shiri 2021). (3) The modeling speed in the ELM is noticeably high while other classical methods are burdened with increased communication costs for training the model. In fact, this feature is the most noticeable advantage of the method over classical machine learning algorithms so that all parameters relevant to hidden nodes (i.e., biases and input weights) are randomly produced without encountering with training samples and tuning (Huang et al. 2006).
In the current study, a novel version of ELM known as Outlier Robust ELM (ORELM) (Zhang and Luo 2015) is applied for estimating the discharge coefficient of side weir for the first time. The novelty of the present study is third-fold. (1) The ORELM is applied for the first time in the discharge coefficient of side weir, (2) by exploring the literature, it can be concluded that no previous study on the estimating of side weir has used comparative analysis on the probable input combinations for the discharge coefficient of side weir situated on rectangular and trapezoidal channels. In the current study, input combination is carried out on eight different models inputs, with six to four input variables as ORELM 1 to ORELM 8. (3) Most previous equations were proposed based on restricted database ranges. However, in this study, a wide range of datasets were used which combine four different experimental datasets. Besides, the results of the ORELM are compared with the existing artificial intelligence-based methods in estimating of the discharge coefficient. The best ORELM model is compared with three artificial intelligence (AI) and four empirical approaches. According to the performed analyses, the superior ORELM possesses better performance in comparison with these AI-based and empirical models.
Material and methods
Discharge coefficient of side weir
The parameters influencing the discharge coefficient of rectangular side weirs are written as follows (Azimi et al. 2017b):
where Fr is the Froude number of flow at the upstream of the side weir, L is the side weir length; b is the main channel width, \(P\) is the crest height of the side weir, \(y_{1}\) is the flow depth at the upstream of the side weir and \(S_{0}\) is slope of the main channel bed. To make the introduced parameters dimensionless, the ratio of the side weir length to the main channel width \(\left( {{L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b}} \right)\), the ratio of the side weir length to the flow depth at the upstream of the side weir \(\left( {{L \mathord{\left/ {\vphantom {L {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}} \right)\), and the ratio of the side weir crest height to the flow depth at the upstream of the side weir \(\left( {{W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}} \right)\) are defined (Azimi et al. 2017b):
Also, Borghei et al. (1999) reported that the effects of the main channel bed slope are marginal and can be ignored in the subcritical flow regime. In this study, the main channel is a trapezoidal channel. It is worth mentioning that the effect of side wall slope (m) is an effective factor on the discharge coefficient (Azimi et al. 2017b). Thus, Eq. (2) is expressed as follows:
In addition, to study all parameters influencing the side weir discharge coefficient located on trapezoidal channels, the influence of the ratio of the flow depth at the upstream of the side weir to the trapezoidal channel bed width \(\left( {{{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } b}} \right. \kern-\nulldelimiterspace} b}} \right)\) on the discharge coefficient is taken into account. So, Eq. (3) is written in the form of Eq. (4) (Azimi et al. 2017b):
Therefore, to develop the artificial intelligence models, the parameters of Eq. (4) are utilized. In Fig. 1, the input parameter combinations of the various ORELM models are shown.
Data sets used in this study
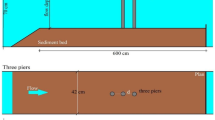
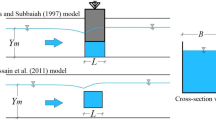
A detailed database is used in this paper to model the discharge coefficient of side weirs. To this end, four different experimental models including Cheong (1991), Emiroglu et al. (2011), Keshavarzi and Ball (2014) and Bagheri et al. (2014) are implemented. Cheong’s (1991) model involves a straight trapezoidal channel with the length of 10 m and the bed width of 0.67 m in which the side weir is placed on the sidewall at a distance of two-thirds of the main channel length from the inlet. Slope of the trapezoidal channel sidewalls in Cheong (1991)'s model is adjustable and the opening length at the location of the side weir varies by poly-wood sheets with variable lengths. Moreover, Emiroglu et al. (2011)'s model is composed a straight rectangular channel with the length of 12 m and the height and the width of it are both equal to 0.5 m. Also, Keshavarzi and Ball (2014)'s model is an open trapezoidal channel with the length of 36 m, the height of 0.5 m and the bed width of 0.4 m. In Keshavarzi and Ball (2014)'s model, a side weir with the length of 0.4 m and the height of 0.13 m is installed at the middle of the channel. In addition, Bagheri et al. (2014)'s experimental model consists of 8 m long open rectangular channel with a side weir placed on the sidewall of the main channel at a 4.5 m distance from the inlet. The width and length of the main channel are, respectively, 0.4 m and 0.6 m and the main channel bed slope is horizontal. The number of the experimental measurements used in this study is 314. Approximately 65% of the experimental samples are randomly selected to train models of artificial intelligence and the remaining 35% is used to test them. Figure 2 demonstrates the layout of the experimental models used in this analysis. The maximum, minimum, and average values of the applied experimental measurements are tabulated in Table 1.
Outlier robust extreme learning machine (ORELM)
A method for generating the single-layer feed-forward neural network (SLFFNN) is the Extreme Learning Machine (ELM) technique (Huang et al. 2006).
Assuming Z training samples as \(\{ ({\mathbf{k}}_{j} ,{\mathbf{q}}_{j} )\}_{j = 1}^{Z}\) where \({\mathbf{k}}_{j} \in R^{n}\) is the matrix of problem inputs and \(q_{j} \in R\), and if the proposed model has the ability to establish mapping between \({\mathbf{k}}_{j}\) and \(q_{j}\) with reasonable accuracy, the ELM with the activation function f(k) and N hidden layer neurons can be expressed as follows (Huang et al. 2006):
where \(\gamma_{j}\) is the output weight matrix connecting the jth hidden layer neuron to the output neuron (target variable), f(k) is known as the activation function, \({\mathbf{G}}_{j} = [g_{j1} ,g_{j2} ,g_{j3} ,...,g_{jn} ]\) is the input weight matrix so that connects the jth hidden layer neuron to input neurons and bj is the bias relevant to the jth hidden layer neurons. In addition, \({\mathbf{G}}_{j} \cdot {\mathbf{k}}_{i}\) is the internal multiplication of Gj and ki. If we express Z obtained relationships from Eq. (5) in a matrix form, the following linear system is achieved (Huang et al. 2006):
Here,
According to the above relationship, it is shown that the only parameter which requires to be calculated is the output weight matrix (γ) and the other ones (the bias and the output weight matrix) are constant. It is obvious that the matrix W is non-square in most cases and there might be no answer for γ as \({\mathbf{W}}\gamma = {\mathbf{y}}\) (Huang et al. 2006). To overcome this issue, the optimal answer is obtained using the least square solution. To this end, the main aim is to minimize the loss function:
Eventually, the optimal response of the problem for minimizing the l2-norm is as follows:
where \({\mathbf{W}}^{ + }\) is Moore–Penrose generalized inverse (MPGI) of W (Rao and Mitra 1971). As the number of training samples is greater than the number of hidden layer nodes (Z > N), it is possible to rewrite the above equation as follows:
Since outliers possess a little part of training samples, the value of this feature for training error € can be specified by sparsity. It is clear that sparsity is reflected by the l0-norm better than the l2-norm. Therefore, in the ORELM, we are trying to find the output weight matrix (γ) with the least value of the l2-norm so that the value of e to be sparse:
The above relationship is a non-convex programming problem. Since the sparse term can be obtained using the l1-norm (Chuang et al. 2002; Daszykowski et al. 2007) it is clear that by replacing the l0-norm by the l1-norm in Eq. (9) in addition to having overall minimization convex, satisfies the sparsity feature. Thus, Eq. (9) is rewritten as follows:
The above equation is a constrained convex problem that suits the related domain of the augmented Lagrange multiplier (ALM). Hence, the ALM is provided as follows:
where η is the penalty parameter and \(\alpha \in R^{n}\) is the Lagrange multiplier vector. Also, \(\eta = 2Z/\left\| {\mathbf{y}} \right\|_{1}\) (Yang and Zhang 2011). The ALM algorithm yields the optimal answers (γ, e) and the value of α through an augmented Lagrangian multipliers minimization process:
To produce next generations through the minimization process, the following relationships are solved by the ALM:
Although the developed ORELM has advantages including high ability to map nonlinearly between inputs and outputs, rapid training time that overcome the limitation of the classical time-consuming approaches, minimum user intervention and high generalization, it also has disadvantage. The main disadvantage of this method is random generation of the input weights and bias of hidden neurons that can be affected in the generalization ability of the developed model. To overcome this drawback, it is recommended to run this method for different times and check the generalizability of it at testing samples that had no role in model calibration. The flowchart of ORELM model is presented in Fig. 3.
Flowchart of the ORELM model (Zhang and Luo 2015)
Goodness of fit
The correlation coefficient (R), variance accounted for (VAF), Root Mean Square Error (RMSE), Scatter Index, Mean Absolute Relative Error (MARE) and Efficiency of Nash–Sutcliffe (NSC) are used as follows in this study (Azimi and Shiri 2020a):
where \(O_{i}\) is observed values, \(F_{i}\) represents values predicted by numerical models, \(\overline{O}\) is the average of observed values and \(n\) is the number of observed values. In the current study, five criteria were applied since the correlation of the ORELM models were assessed by using the R and NSC indices, whereas the relative errors of the models were evaluated by means of the SI and MARE criteria. Moreover, the value of absolute errors were examined through the RMSE indicator. The total number of used experimental measurements was 314 cased, which 65% of the samples were used for training the ORELM models, and the remaining 35% were used for testing of the ORELM models.
Results and discussion
The number of secret layer neurons is initially optimized in the next sections and various activation functions are investigated subsequently. After that, the superior model and the most effective input parameters are identified through a sensitivity analysis. In addition, with some artificial intelligence and regression models, the ORELM superior model is compared. In these models, an analysis of uncertainty and a reliability analysis are also performed. Finally, for the superior model, a partial derivative sensitivity analysis (PSDA) is conducted. It should be noted that only the testing mode results are presented in this research.
Number of hidden layer neurons
The number of ORELM hidden layer neurons is investigated in this section. The selection of optimal neurons increases the artificial intelligence model's efficiency in terms of modeling accuracy and computational time (Azimi and Shiri 2021). The number of hidden layer neurons is initially selected to be equal to 5, and this number increases gradually to 24. The most optimal number of hidden layer neurons is chosen to be 22. The values of different statistical indices measured for all hidden layer neurons are presented in Fig. 4. For the model with five hidden neurons, the values of R, RMSE and NSC are computed to be 0.773, 0.091 and 0.563, respectively. However, for the model with 24 hidden layer neurons, SI, MARE and R values are obtained to be 0.116, 0.089 and 0.913, respectively. It is worth mentioning that by increasing the hidden layer neurons to a certain extent, the accuracy of the artificial intelligence model does not increase significantly. Therefore, it is believed that the optimum number of hidden layer neurons in this study is 22. A comparison of the discharge coefficients simulated by the model with 22 hidden layer neurons with the experimental data is provided in Fig. 5. For the model with 22 hidden layer neurons, the values of R, MARE and NSC are approximated to be 0.924, 0.091 and 0.852, respectively.
Activation function
In the following, the ORELM activation functions are studied. In this paper, for activation functions including sig, sin, hardlim, tribas and radbas are utilized for the ORELM model. Figure 6 displays the results of the statistical indices measured for these functions. Based on the modeling results, the values of RMSE, SI and NSC for the activation function sig are computed to be 0.056, 0.114 and 0.826, respectively. In addition, the MARE, R and SI values for the sin activation function are 0.128, 0.849 and 0.151, respectively. Also, for the activation function hardlim, RMSE and NSC are approximated to be 0.102 and 0.481, respectively. Moreover, the RMSE and MARE statistical indices for the activation function tribas are obtained to be 0.089 and 0.159, respectively. In addition, for the activation function radbas, the values of R, SI and NSC are calculated to be 0.846, 0.167 and 0.713, respectively. Thus, according to different activation functions, the function sig is introduced as the superior one and used in the following modeling process for simulating the discharge coefficient. The results of the discharge coefficients simulated by the activation function sig and the comparison with the experimental values are shown in Fig. 7.
Sensitivity analysis
The performance of different ORELM models is evaluated in this chapter by performing a sensitivity study. Figure 8 displays the results of the various statistical indices calculated for these models. For example, the ORELM 1 model simulates the discharge coefficient values by the parameters \(Fr,{L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b},{L \mathord{\left/ {\vphantom {L {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }},m,{{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } b}} \right. \kern-\nulldelimiterspace} b},{W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\). For the ORELM 1 model, the values of R, RMSE and MARE are obtained to be 0.910, 0.056 and 0.088, respectively. It should be noted that for the ORELM 2 model the influence of the input parameter \({W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\) is eliminated and this model simulates the discharge coefficient values in terms of the other input parameters including \(Fr,{L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b},{L \mathord{\left/ {\vphantom {L {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }},m,{{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } b}} \right. \kern-\nulldelimiterspace} b}\). For the ORELM 2 model, the values of SI, NSC and RMSE are estimated to be 0.130, 0.759 and 0.064, respectively. Moreover, the values of R, SI and NSC for the ORELM 3 model are equal to 0.922, 0.110 and 0.850, respectively. For this model, the effects of the dimensionless parameter \({{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } b}} \right. \kern-\nulldelimiterspace} b}\) are removed and this model simulates the target function values by other dimensionless parameters including \(Fr,{L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b},{L \mathord{\left/ {\vphantom {L {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }},m,{W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\). For estimating the discharge coefficient by the ORELM 4 model, the influence of trapezoidal wall slope \(\left( m \right)\) is neglected and this model simulates the discharge coefficient values using other dimensionless parameters such as \(Fr,{L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b},{L \mathord{\left/ {\vphantom {L {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }},{{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } b}} \right. \kern-\nulldelimiterspace} b},{W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\). The values of the MARE, NSC and SI statistical indices for the ORELM4 model are yielded 0.086, 0.845 and 0.106, respectively. It is worth mentioning that the values of R, RMS and NSC for the ORELM5 model are equal to 0.926, 0.050 and 0.854, respectively. To forecast the discharge coefficient by the ORELM 5 model, the impact of the dimensionless parameter \({L \mathord{\left/ {\vphantom {L {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\) is eliminated and this model predicts the discharge coefficient values by the parameters \(Fr,{L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b},m,{{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } b}} \right. \kern-\nulldelimiterspace} b},{W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\). Also, the ORELM6 model estimates the discharge coefficient values by the dimensionless parameters \(Fr,{L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b},{L \mathord{\left/ {\vphantom {L {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }},m,{{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } b}} \right. \kern-\nulldelimiterspace} b},{W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\) and the influence of the ratio of the side weir length to the trapezoidal channel bed width \(\left( {{L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b}} \right)\) is eliminated for this model. For ORELM 6, the values of RMSE, MARE and SI are obtained to be 0.058, 0.103 and 0.118, respectively. For the ORELM 7 model, the values of R, NSC and MARE are also approximated to be 0.901, 0.795 and 0.101, respectively. The ORELM 7 model is a function of the parameters \({L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b},{L \mathord{\left/ {\vphantom {L {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }},m,{{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } b}} \right. \kern-\nulldelimiterspace} b},{W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\) and the impact of the Froude number \(\left( {{\text{Fr}}} \right)\) at the upstream of the side weir is ignored for this model. According to the modeling results, the dimensionless parameters \(Fr,{L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b},{{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } b}} \right. \kern-\nulldelimiterspace} b},{W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\) have the greatest impact on the simulation of the side weir. Thus, the ORELM 8 model is developed by these input parameters. With the highest accuracy and the lowest error, this model simulates the discharge coefficient values. Figure 9 displays the results of the simulated discharge coefficients along with the observed values. For the ORELM 8 model, the values of R, RMSE and MARE are equal to 0.937, 0.045 and 0.081, respectively.
Based on the performed sensitivity analysis, the ORELM 8 and ORELM 2 models have the highest and the lowest accuracies, respectively. Furthermore, eliminating the dimensionless parameters \({W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\) and \({L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b}\) declines the modeling accuracy incredibly. So, these dimensionless parameters are ascertained as the most influencing input parameters on the simulation of the discharge coefficient by the ORELM model.
Therefore, the performed sensitivity analysis demonstrated that ORELM 8 was the best model in order to estimate the discharge coefficient. After ORELM 8, ORELM 5, ORELM 3, ORELM 4, ORELM 1, ORELM 7 and ORELM 6 were, respectively, identified as the second, third, fourth, fifth, sixth and seventh-best models for estimating the target function. However, ORELM 2 showed the worst performance to model the discharge coefficient of side weirs.
Furthermore, W/y1 possessed the highest level of effectiveness on the ORELM network so as to predict the discharge coefficient, while the L/b, Fr, m, and y1/b factors were, respectively, recognized as the second, third, fourth and fifth-important input parameters. It is worth noting that the slope of side wall (m) was insignificant input variables so as to approximate the target value.
Comparison of ORELM model with AI-based and regression-based models
In this section, the superior model (ORELM 8) is compared with three artificial intelligence models developed by Roushangar et al. (2016), and Azimi et al. (2017a) as well as four regression models defined by Singh et al. (1994) (Reg 1), Borghei et al. (1999) (Reg 2), Emiroglu et al. (2011) (Reg 3) and Bagheri et al. (2014) (Reg 4). It is worth mentioning that Roushangar et al. (2016) using the support vector machines-genetic algorithm (SVM-GA), and Azimi et al. (2017a) using the extreme learning machine (ELM) managed to simulate discharge coefficient values. The Reg 1, Reg 2 and Reg 4 models were, respectively, derived from the Singh et al. (1994), Borghei et al. (1999) and Bagheri et al. (2014) experimental studies. Emiroglu et al. (2011) and Roushangar et al. (2016) validated the Reg 3 and SVM-GA models by using the Emiroglu et al. (2011) experimental measurements. Borghei et al. (1999), Emiroglu et al. (2011), and Bagheri et al. (2014), whereas Azimi et al. (2017a, b) applied the measurements presented by Cheong (1991) for training and testing the ELM model. It should be stated that almost all previous studies estimated the discharge coefficients instead of discharge and also the empirical and artificial intelligence-based equations were presented to approximate the discharge coefficient not the discharge. Therefore, evaluation of the side weir discharge coefficient is quite reasonable in the current study.
Figure 10 provides a comparison of the values of the various statistical indices for artificial intelligence and regression models. Also, Fig. 11 demonstrates the comparison of the discharge coefficient simulated by different artificial intelligence and regression models. Based on the comparison, the value of R for the ELM, and SVM-GA models are computed to be 0.162, -0.484 and 0.482, respectively. Also, for the Reg1, Reg2 and Reg3 models, the NSC values are obtained equal to 0.135, -0.617 and -0.256, respectively. In addition, the values of RMSE, SI and MARE for the Reg4 model are equal to 0.142, 0.288 and 0.207, respectively.
In comparison with other studies carried out on the simulation of the discharge coefficient so far, the ORELM 8 model therefore has the highest precision and the lowest error, as shown. In other words, the ORELM 8 model is more flexible than other artificial intelligence and regression studies in simulating the discharge coefficient. For instance, the accuracy of ORELM model was roughly 87% greater than the ELM model, whereas the correlation of ORELM model was nearly 94% higher than the SVM-GA model. Moreover, the precision of the ORELM model was approximately 74%, 69% and 61% better than Reg 1, Reg 2 and Reg 3 models. The made comparison showed a good generalization ability of the applied ORELM model in comparison with the previous investigation, meaning that the ORELM algorithm was used in a wide range of experimental measurements, while other regression and AI-based equations were proposed just for some specific experimental values. Therefore, the presented ORELM model was more generalized algorithm compared with its counterparts. Additionally, the ORELM model had high level of precision and correlation with experimental values.
In addition, the 95% uncertainty is performed for the artificial intelligence and regression models and the results are given in Table 2. The mathematical details of the 95% uncertainty can be found at Saberi-Movahed et al. (2020). The 95% uncertainty is calculated by (Saberi-Movahed et al. 2020):
The 95% uncertainty for the ELM, and SVN-GA models are 0.0022, 0.0057 and 0.0019, respectively. Moreover, the 95% uncertainty for the Reg 1, Reg 2, Reg 3 and Reg 4 models are obtained to be 0.0014, 0.0013, 0.0012 and 0.0012, respectively, while this value for the ORELM8 model is estimated to be 0.0009. Based on the results of the 95% uncertainty, the ORELM8 model has the lowest uncertainty.
In the following, the reliability is conducted for the artificial intelligence and regression models. The mathematical details of the reliability can be found at Saberi-Movahed et al. (2020).
The reliability is computed as follows:
here ki is estimated by using two phases. Firstly, the relative average error (RAE) is calculated as a vector whose ith component is as below:
Secondly, if RAEi ≤ Δ, then ki = 1, otherwise, ki = 0, here Δ is the threshold value of the target function, meaning that ki is determined as the number of times the value of RAE is less than or equal to that of Δ. Regarding the Chinese Standards, the optimal value of Δ is 0.2 (Saberi-Movahed et al. 2020). The results of the analysis are listed in Table 3. For the ELM and SVM-GA models, the reliability value is estimated to be 13.245% and 2.649%, respectively. In addition, this value for the Reg 1, Reg 2, Reg 3 and Reg 4 models are computed to be 39.073, 31.788, 65.894 and 57.947, respectively. It is worth noting that for the ORELM 8 model, the reliability value is computed to be 93.378% indicating high accuracy and reliability of the ORELM 8 model.
Partial derivative sensitivity analysis (PDSA)
For the superior model (ORELM 8), a partial derivative sensitivity analysis (PDSA) is performed in this section. The PSDA is typically used to measure the effect of input parameters on the target parameter (Azimi et al. 2019b; Azimi and Shiri 2020b). In other words, the PSDA is a method for identifying the changing pattern of the objective parameter according to input parameters. The positive PSDA implies an increase in the objective function (discharge coefficient), while the negative sign implies a decrease in the target function. In other words, the relative derivative of each input parameter is computed according to the target function in this process. According to the PDSA findings, the PSDA increases by increasing the value of the Froude number. Also, by increasing the parameter L/b, the PDSA decreases. Furthermore, by increasing the input parameters y1/b and W/y1, the PDSA decreases. The PDSA results for the ORELM 8 model are illustrated in Fig. 12.
Superior ORELM model
ORELM 8 was identified as the best model to simulate the discharge coefficient in the current study. Thus, a relationship for ORELM 5 is presented as follows:
here InW, InV, BHN and OutW are, respectively, matrices of input weights, input variables, the bias of hidden neurons and output weights and defined as bellow:
The sensitivity analysis showed that the Fr, L/b, y1/b, W/y1 had significant influence to model the discharge coefficient using the ORELM algorithm. Hence, the ORELM 8 was developed as the superior model to estimate the discharge coefficient in the present work.
The performed analyses showed that ORELM 8 had the highest level of precision and correlation and this model could simulate the discharge coefficient of side weirs with a low level of uncertainty. Moreover, the side weir height to flow depth ratio (W/y1) and the side weir length to the main channel width ratio were detected as the most striking input factors for estimating the target function.
Conclusion
The discharge coefficient of side weirs located on rectangular and trapezoidal channels was first simulated using a modern model of artificial intelligence called “outlier robust extreme learning machine (ORELM)” in this study. Initially, a comprehensive database composed of four different experimental models was utilized for validating the artificial intelligence models. It is worth remembering that 65% of the observed samples were used for training models of artificial intelligence and the remaining 35% were used for testing models of ORELM. The most important obtained results are summarized as follows:
-
The optimal number of hidden layer neurons was selected to be 22 by performing a trial and error process.
-
The sigmoid was chosen as the best activation function for the ORELM model.
-
Eight distinctive ORELM models were produced using the effective dimensionless parameters and the ORELM 8 was detected as the superior model.
-
By performing a sensitivity analysis and the parameters \({W \mathord{\left/ {\vphantom {W {y_{1} }}} \right. \kern-\nulldelimiterspace} {y_{1} }}\) and \({L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b}\) were introduced as the most influencing input parameters.
-
For the ORELM 8 model, the values of R, RMSE and MARE are approximated to be 0.937, 0.045 and 0.081, respectively.
-
To compare the results of the best ORELM-based model (ORELM 8) with the existing ones, three nonlinear artificial intelligence methods (support vector machine optimized by genetic algorithm, and extreme learning machine) and four multiple linear regression equations were employed. The results indicated that the ORELM 8 model has better results.
-
Furthermore, uncertainty and reliability analysis for the ORELM 8 model were computed 0.0009 and 93%, respectively.
-
Finally, for the ORELM 8 model, a partial derivative sensitivity analysis was performed and the PSDA increased by increasing the Froude number and by increasing the parameter L/b the PDSA decreased.
This study showed that the ORELM model which is calibrated with a large number of samples has more flexibility and better efficiency. For future works, it is highly recommended to check the performance of other string artificial intelligence such as adaptive neuro-fuzzy inference systems optimized with the new developed evolutionary algorithms such as gray wolf optimization. Additionally, the provided ORELM-based equation may be used for the estimation of the discharge coefficient in the practical applications. It is suggested that the results of the ORELM model can be compared with the computations fluid dynamics (CFD) tools.
References
Akhbari A, Zaji AH, Azimi H, Vafaeifard M (2017) Predicting the discharge coefficient of triangular plan form weirs using radian basis function and M5’methods. J Appl Res Water Wastewater 4(1):281–289
Azimi H, Shiri H (2020a) Dimensionless groups of parameters governing the ice-seabed interaction process. J Offshore Mech Arctic Eng 142(5):250
Azimi H, Shiri H (2020b) Ice-seabed interaction analysis in sand using a gene expression programming-based approach. Appl Ocean Res 98:102120
Azimi H, Shiri H (2021) Sensitivity analysis of parameters influencing the ice–seabed interaction in sand by using extreme learning machine. Nat Hazards 105(3):1–29
Azimi H, Bonakdari H, Ebtehaj I (2017a) Sensitivity analysis of the factors affecting the discharge capacity of side weirs in trapezoidal channels using extreme learning machines. Flow Meas Instrum 54:216–223
Azimi H, Bonakdari H, Ebtehaj I (2017b) A highly efficient gene expression programming model for predicting the discharge coefficient in a side weir along a trapezoidal canal. Irrig Drain 66(4):655–666
Azimi H, Bonakdari H, Ebtehaj I (2019a) Design of radial basis function-based support vector regression in predicting the discharge coefficient of a side weir in a trapezoidal channel. Appl Water Sci 9(4):1–12
Azimi H, Bonakdari H, Ebtehaj I (2019b) Gene expression programming-based approach for predicting the roller length of a hydraulic jump on a rough bed. ISH J Hydraul Eng. https://doi.org/10.1080/09715010.2019.1579058
Bagheri S, Kabiri-Samani AR, Heidarpour M (2014) Discharge coefficient of rectangular sharp-crested side weirs Part II: Domínguez’s method. Flow Meas Instrum 35:116–121
Bagherifar M, Emdadi A, Azimi H, Sanahmadi B, Shabanlou S (2020) Numerical evaluation of turbulent flow in a circular conduit along a side weir. Appl Water Sci 10(1):1–9
Bonakdari H, Ebtehaj I, Samui P, Gharabaghi B (2019) Lake water-level fluctuations forecasting using minimax probability machine regression, relevance vector machine, gaussian process regression, and extreme learning machine. Water Resour Manag 33(11):3965–3984
Borghei SM, Jalili MR, Ghodsian M (1999) Discharge coefficient for sharp-crested side weir in subcritical flow. J Hydraul Eng 125(10):1051–1056
Cheong H (1991) Discharge coefficient of lateral diversion from trapezoidal channel. J Irrig Drain Eng 117(4):461–475
Chuang CC, Su SF, Jeng JT, Hsiao CC (2002) Robust support vector regression networks for function approximation with outliers. IEEE T Neural Networ 13(6):1322–1330
Daszykowski M, Kaczmarek K, Vander Heyden Y, Walczak B (2007) Robust statistics in data analysis: a review—basic concepts. Chemometr Intell Lab 85(2):203–219
Ebtehaj I, Bonakdari H, Zaji AH, Azimi H, Khoshbin F (2015a) GMDH-type neural network approach for modeling the discharge coefficient of rectangular sharp-crested side weirs. Eng Sci Technol Int J 18(4):746–757
Ebtehaj I, Bonakdari H, Zaji AH, Azimi H, Sharifi A (2015b) Gene expression programming to predict the discharge coefficient in rectangular side weirs. Appl Soft Comput 35:618–628
Ebtehaj I, Bonakdari H, Shamshirband S (2016) Extreme learning machine assessment for estimating sediment transport in open channels. Eng Comput 32(4):691–704
Ebtehaj I, Bonakdari H, Moradi F, Gharabaghi B, Khozani ZS (2018) An integrated framework of extreme learning machines for predicting scour at pile groups in clear water condition. Coast Eng 135:1–15
Emiroglu ME, Agaccioglu H, Kaya N (2011) Discharging capacity of rectangular side weirs in straight open channels. Flow Meas Instrum 22(4):319–330
Huang GB (2014) An insight into extreme learning machines: random neurons, random features and kernels. Cogn Comput 6(3):376–390
Huang GB, Zhu QY, Siew CK (2006) Extreme learning machine: theory and applications. Neurocomputing 70(1–3):489–501
Huang GB, Zhou H, Ding X, Zhang R (2011) Extreme learning machine for regression and multiclass classification. IEEE T SYST MAN CYB 42(2):513–529
Keshavarzi A, Ball J (2014) Discharge coefficient of sharp-crested side weir in trapezoidal channel with different side-wall slopes under subcritical flow conditions. Irrig Drain 63(4):512–522
Khoshbin F, Bonakdari H, Ashraf Talesh SH, Ebtehaj I, Zaji AH, Azimi H (2016) Adaptive neuro-fuzzy inference system multi-objective optimization using the genetic algorithm/singular value decomposition method for modelling the discharge coefficient in rectangular sharp-crested side weirs. Eng Optimiz 48(6):933–948
Mirzaei K, Sheibani HR (2020) Experimental investigation of arched sharp-crested weir flow and comparing it with rectangular weir. Iran J Sci Technol T Civil Eng. https://doi.org/10.1007/s40996-020-00425-6
Niazkar M, Afzali SH (2018) Application of new hybrid method in developing a new semicircular-weir discharge model. Alexandria Eng J 57(3):1741–1747
Olyaie E, Banejad H, Heydari M (2019) Estimating discharge coefficient of PK-weir under subcritical conditions based on high-accuracy machine learning approaches. Iran J Sci Technol T Civil Eng 43(1):89–101
Rao CR, Mitra SK (1971) Generalized inverse of matrices and its applications John Wiley & Sons. Inc, New York
Roushangar K, Khoshkanar R, Shiri J (2016) Predicting trapezoidal and rectangular side weirs discharge coefficient using machine learning methods. ISH J Hydraul Eng 22(3):254–261
Saberi-Movahed F, Najafzadeh M, Mehrpooya A (2020) Receiving more accurate predictions for longitudinal dispersion coefficients in water pipelines: training group method of data handling using extreme learning machine conceptions. Water Resour Manage 34(2):529–561
Salmasi F, Sattari MT (2017) Predicting discharge coefficient of rectangular broad-crested gabion weir using M5 tree model. Iran J Sci Technol T Civil Eng 41(2):205–212
Singh R, Manivannan D, Satyanarayana T (1994) Discharge coefficient of rectangular side weirs. J Irrig Drain Eng 120(4):814–819
Yang J, Zhang Y (2011) Alternating direction algorithms for ℓ1-problems in compressive sensing. SIAM J Sci Comput 33:250–278
Zeynoddin M, Bonakdari H, Azari A, Ebtehaj I, Gharabaghi B, RiahiMadavar H (2018) Novel hybrid linear stochastic with non-linear extreme learning machine methods for forecasting monthly rainfall a tropical climate. J Environ Manage 222:190–206
Zhang K, Luo M (2015) Outlier-robust extreme learning machine for regression problems. Neurocomputing 151:1519–1527
Funding
The author(s) received no specific funding for this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Razmi, M., Saneie, M. & Basirat, S. Estimating discharge coefficient of side weirs in trapezoidal and rectangular flumes using outlier robust extreme learning machine. Appl Water Sci 12, 176 (2022). https://doi.org/10.1007/s13201-022-01698-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-022-01698-0