Abstract
Submarine groundwater discharge (SGD) is described as submarine inflow of fresh and brackish groundwater from land into the sea. The release of sewages from point and non-point source pollutants from industries, agricultural and domestic activities gets discharged through groundwater to ocean creating natural disparity like decreasing flora fauna and phytoplankton blooms. Hence, to quantify fluxes of SGD in coastal regions is important. Quantification of SGD was attempted in Coleroon estuary, India, using three dissimilar methods like water budget, Darcy law and manual seepage meter. Three seepage meters were installed at two prominent litho units (alluvium and fluvio marine) at a distance of (0–14.7 km) away from Bay of Bengal. The water budget and Darcy law-quantified submarine seepage at a rate of 6.9 × 106 and 3.2 × 103 to 308.3 × 103 m3 year−1, respectively, and the seepage meter quantified seepage rate of 0.7024 m h−1 at an average. Larger seepage variations were isolated from three different techniques and the seepage rates were found to be influenced by hydrogeological characteristics of the litho units and distance from the coast.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
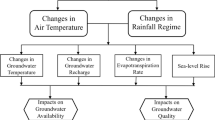
Submarine groundwater discharge (SGD) is one of the major water conduits that connect the land and ocean in global water cycle. SGD originating in freshwater aquifers to ocean or from saline water to aquifers has been recently isolated as a major factor influencing the coastal zone (Taniguchi et al. 2002). The groundwater discharging from coastal aquifers and/or the incoming saline water contains elevated concentrations of nutrients, inorganic and organic substances and radionuclides triggering the coastal areas towards environmental degradation.
In the last few decades, nutrients transporting from land to ocean have increased as a result of anthropogenic activities (Diaz and Rosenberg 1995; Soetaert and Middelburg 2006; Elsdon et al. 2009; Ouyang 2012; Wang et al. 2014; Gaume et al. 2016). In coastal environments globally, this has triggered eutrophication and hypoxia (Rabalais and Turner 1996; Seitzinger et al. 2010). Additionally, unequal changes within riverine nutrient concentrations on account of human activities include altered food-web constructions and cause dangerous algal blooms. (Soetaert and Middelburg 2006). The boundary between the fresh water discharge and saline ocean water produces the boundary of salinity gradient from land to sea. Hence, SGD integrates the recirculating sea water and fluxes of nutrients from sea to costal aquifers (Swarzenski and Baskaran 2007). In particular, SGD has been recognized as an important source of nutrients (Garcia Solsona et al. 2010), dissolved inorganic carbon (Cai et al. 2003) or trace metals (Beck 2007) to coastal waters, since they are considered to be the principal drivers of ecological change in coastal communities (Howarth et al. 2000). Through SGD the continuous loading of nutrients and trace metals alters the water quality resulting in environmental degradation of coastal regions (LaRoche et al. 1997; Black et al. 2009; Lee et al. 2011; Rodellas et al. 2015; Trezzi et al. 2016). Hence, quantification of SGD is important and also a challenging task due to slow, diffuse and heterogeneous nature of the discharge that occurs below the water surface.
There are four different methods to quantify SGD (Burnett et al. 2006; Wang et al. 2014): (1) groundwater flow models, (2) seepage meters, (3) natural tracers including nutrients, trace elements, radioisotopes, salinity and major ion chemistry and (4) water budget and Darcy law method. Groundwater modeling is applied in quantifying SGD by observation, measurements and mathematical methods (Cox et al. 1997). Numerical models have emerged as viable tools for understanding and quantifying SGD (Uchiyama et al. 2000; Langevin 2001; Kaleris et al. 2002; Destouni and Prieto 2003; Oberdorfer 2003a, b; Smith and Nield 2003; Smith and Zawadzki 2003; Haider et al. 2015; Gopinath et al. 2016a). Quantification of SGD in Western Australia by MODFLOW has been attempted by McDonald and Harbaugh (1988) and Harbaugh et al. (2000). SGD by FEFLOW code in Berling, Germany, by Diersch (1996) and Destouni and Prieto (2003) used the finite-element SUTRA code in NE gulf cost, Mexico, Voss (1984) developed a finite-difference code to simulate SGD in coastal aquifers of Mediterranean Sea, Uchiyama et al. (2000) developed a finite-difference code to simulate SGD and associated nutrient transport at Hasaki Beach, Japan. Langevin (2001) used the finite-difference SEAWAT code in Biscayne Bay, Florida, to simulate SGD, Kaleris et al. (2002) developed a constant density flow model using MODFLOW to simulate SGD in Baltic sea. Major nutrients are the most studied constituents of SGD due to their significant role in driving ecological changes in coastal communities (Howarth et al. 2000). Several SGD studies have been conducted to identify potential sources and interactions of nutrients in the Ocean (Corbett et al. 1999, 2000a; Dillon et al. 1999; Top et al. 2001). Agricultural development in near-shore areas, leading to increased inputs of nitrogen (N) and phosphorus (P) from fertilizer and wastewater has been attempted in different parts of the globe (Burnett 1999; Corbett et al. 1999; Moore 1996, 1999; Valiela et al. 1990) and role of micro nutrients like DIN, DIP and DSi in quantifying SGD (Slomp and Van Cappellen 2004; Knee and Paytan 2011; Garcia Solsona et al. 2010; Rodellas et al. 2012) has been discussed. A few studies have documented trace metal fluxes into the ocean associated with SGD (e.g., Beck 2007; Windom et al. 2006). Quantification of SGD using Rn isotopes has been attempted in many parts of the globe (Burnett et al. 2001; Cable et al. 1996; Corbett et al. 2000a, b; McCoy et al. 2007; Charette et al. 2005; Krest et al. 1999; Moore 1996). The use of 3H, 4He isotopes have also been utilized in recent SGD studies (Castro, 2004; McCoy et al. 2007; Top et al. 2001). GIS-based quantification of SGD was done using major ion chemistry, salinity, EC, SAR and mixing ratios (Somay and Gemici 2009; Srinivasamoorthy et al. 2011; Gopinath et al. 2016b; Prakash et al.2017). Basin-scale estimations of fresh SGD using water balance and Darcy law method have been performed in many places (Allen 1976; Muir 1968; Pluhowski and Kantrowitz 1964; Sekulic and Vertacnik 1996; Kroeger et al. 2007). Studies using various types of seepage meters to measure SGD flux have been attempted globally (Lee 1977; Taniguchi and Fukuo 1993; Cable et al. 1997; Taniguchi and Iwakawa 2001; Taniguchi et al. 2006). From the several methods attempted, seepage meter is one of the best methods to measure the groundwater discharge or inflow in locations where sediment interface and fluid fluxes are large (Winter 1981; Shaw and Prepas 1989). Hence, the present focus of the study is to quantify and characterize the rate, pattern and variability of submarine groundwater discharge using water budget, Darcy law and seepage meters.
Hydrology and hydrogeology
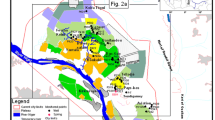
The river Coleroon is one of the tributaries of river Cauvery that originates at Mukkombu, 17 km away from Trichy and configures Bay of Bengal in Kodiyampalayam near Chidambaram, Tamil Nadu, after flowing a stretch of 160 km. The Coleroon estuary is a semi-arid estuary located on the east coast of India lying between longitude 79°42′14.56″ and 79°49′39.13″E and latitude of 11°19′37.79″ and 11°22′13.74″N with an aerial extent of 18.78 km2 (Fig. 1) with an average depth of 1 m and a tidal range of 1.0 m (Tide forecast of India May 2015). The temperatures as moderated by the sea with a mean winter temperature of 26.62 °C while summer temperature averages 31.08 °C with an approximate evapotranspiration rate of 617 mm year−1 (IMD 2014). The regional climate is dominated by monsoons, with average monthly precipitation of 124 mm month−1 during wet season (September–December), and 229.5 and 72.2 mm month−1 during dry season (January–August) (PWD 2014). The river Coleroon has a maximum elevation of 5 m and slopes down towards the coast. The estuary is covered by two predominant geological formations such as alluvium and fluvio marine sediments (Fig. 1) and geomorphological features like coastal plain, flood plain and alluvial plain are distributed in the study area. Many well-connected irrigational tanks are present around the river flow. The average freshwater discharge in the river is 263 mm year−1 (Jain 2012) and it carries an annual sediment load of 24 t km−2 year−1 (Vaithiyanathan et al. 1992). The sediment transport is mainly by rivers and sand moved by coastal currents. Coleroon estuary combines two different aquifers like unconsolidated alluvium aquifer and quaternary shallow (fluvio marine sediments) aquifer. Both the aquifers act as major water-bearing aquifers in the study area. The aquifers of this group occur at 2–3 m bgl (below ground level) within the depth of 45 m bgl and comprise sand, silt and clayey sand. Most of the dug wells are found at a depth of 8–12 m bgl, shallow tube wells are present at a depth of 20–50 m. The groundwater discharge from alluvium aquifer is 5–10 L per second with a drawdown of 0.5–2 m and transmissivity (T) range between 438 and 1900 m2 day−1 with storage (S) of 7.72 × 10−5–9.5 × 10−3. The discharge rate in quaternary shallow aquifer is < 1–63 L per second with a drawdown of 2–5 m and transmissivity (T) ranges between 11 and 1100 m2 day−1 with storage (S) of 4.8 × 10−1 to 4.4 × 10−10 with a specific capacity of 13.43–870 lpm m−1 (CGWB 2009). Due to the permeable nature of the aquifers, SGD might be a major source for freshwater and allied nutrients to the coastal regions.
The Coleroon River, a major tributary of river Cauvery, is the key supply for both commercial and recreational users for many decades. Land use within the study area is largely of residential, commercial, industrial and agricultural activities. Hence, the river has experienced chronic hypoxia due to release of effluents from point and non-point source pollutants like nutrients, pesticides, heavy metals and major ions (Ramanathan et al. 1988; Seralathan and Setharamaswamy 1982a, b). Hence, it has been proposed to isolate the spatial and temporal distribution of SGD at selected locations using seepage meters and validated using Darcy’s law and water budget calculations in transporting freshwater to Bay of Bengal. Much attention has been given to the surficial aquifer, since water flow to the aquifer immediately by precipitation, recharge and surface flows including SGD. The proposed study is first of its kind in the study area.
Materials and methods
A total of three seepage meters (Fig. 2) were constructed from the ends of 20 L drums similar to those described in Lee (1977) (Fig. 3). Each has a 1-cm vent hole, left open during placement so that pressure quickly equilibrated with the bay. First seepage meter (S1) was fixed in the alluvium formation 14.7 km distance from the Coast. Second seepage meter (S2) was fixed at fluvio marine sediments 13.5 km from the Coast and the third seepage meter (S3) was also fixed in fluvio marine sediments at a distance of 5.7 km from the river mouth. These meters were pushed into the sediments > 15 cm to assure a complete seal around the base of the meter. Each bag was pre-filled with 100 mL of distilled water to prevent under filling (Shaw and Prepas 1989) and allowed for flow measurement in the sediments. Discharged water was collected in a thin-walled plastic bag attached with a quick-connect fitting. After deployment, the bags were weighed to determine the amount of groundwater seepage along with measurement of salinity, EC, pH and TDS by Hanna potable water quality analyzer. The sampling campaign was conducted during May 2015, arrayed perpendicular to the coast (Fig. 1). Seepage waters were sampled every hour from morning 6 am to evening 6 pm by considering the Tidal cycle and subjected to physio-chemical analysis.

(modified after Lee 1977)
Mannual seepage meter established for the present study
Lee type seepage meter (Lee 1977)
Methods to estimate submarine groundwater discharge
Measuring submarine groundwater discharge and related chemical fluxes to the oceans poses unique challenges due to the involvement of subsequent equipment to measure the discharge. The dynamic nature of the groundwater–sea water interactions in the coastal zone hampers the accurate quantification of the SGD. Relatively short time series and the scarcity of hydrogeological data constitute another serious impediment to the accurate estimation of SGD. The most common methods to quantify the SGD are using the seepage meters and water budget techniques. Since, varied methods sometimes agree well or in other cases lead to large discrepancies (Knee and Paytan 2011). These discrepancies will shed more light on understanding the sophisticated system. Hence, attempt has validated using techniques like water budget, Darcy law and seepage meters.
A water budget calculates the amount of water entering in and out of a system. It calculates groundwater flow as equal to precipitation by removing the surface runoff and evapotranspiration from the system. It assumes freshwater input to the groundwater system by precipitation discharges as SGD (Oberdorfer 2003a, b). This is one of the indirect methods to estimate the annual fresh groundwater discharge for a river basin (Burnett et al. 2006; Kroeger et al. 2007). Water balance method has been attempted successfully by Garrels and MacKenzie (1971), Lvovich (1974) and Zektser et al. (1973). For the present study watershed water budget methodology suggested by Kroeger et al. (2007) has been attempted. The water budget equation for the estimation of fresh SGD (Burnett et al. 2006) is as follows:
where P is precipitation/rainfall, ET is evapotranspiration, DS is surface discharge, DG is fresh groundwater discharge, and dS is the change in water storage assumed to be insignificant (Burnett et al. 2006). The modified equation as proposed by Kroeger et al. (2007) for calculating SGD is as follows:
(all the units expressed in millimeter per year) where SGD (DG) is calculated from precipitation (P) after incorporating corrections for evapotranspiration (ET) and stream flow (DS). Since water table elevation in the surficial aquifer is close to land surface (CGWB 2009), the groundwater watershed assumption has been adopted for the proposed drainage basin as suggested by Kroeger et al. (2007).
Darcy’s law explains the flow of water (Q, L3 T−1) through an aquifer is directly proportional to both the cross-sectional area (A, L−1) and hydraulic gradient (dh/dl dimension less) and equals the hydraulic conductivity (K, LT−1). Hence, Darcy law for flow is Q = −KA dh/dl. The ability and driving force of water through aquifer is guided by hydraulic conductivity and hydraulic head. The assumption of the Darcy’s law is that the water migrating in the aquifers will reach the ocean as SGD. The horizontal discharge of groundwater (V) has been attempted using Darcy’s law (Freeze and Cherry 1979; Kroeger et al. 2007). The calculations were made by multiplying the hydraulic gradients and porosity between sea level and groundwater level and dividing by the hydraulic conductivity using the following equations:
where V is flow velocity of fresh groundwater in the aquifer (m day−1), K is aquifer hydraulic conductivity (m day−1), i is the hydraulic gradient in the aquifer (m m−1), Q is amount of fresh groundwater discharge (m3 day−1), and A is aquifer cross-sectional area. The hydraulic conductivity assumed for the alluvium and fluvio marine aquifers were 10−1 and 10−3 cm s−1, respectively, the hydraulic gradient assumed were based on the topographic and water level variations.
Measurements of groundwater seepage rates are often made using manual seepage meters. Seepage meters were first developed by Israelsen and Reeve (1944) to measure the water loss from irrigation canals. Lee (1977) designed a seepage meter consisting of steel drum fitted with a sample port and a plastic collection bag. The drum forms a chamber that is inserted open end down into the sediment. Water seeping through the sediment will displace water trapped in the chamber forcing it up through the port into the plastic bag. The change in volume of water in the bag over a measured time interval provides the flux measurement. Based on the lee type seepage meter we assembled a manual seepage meter (Fig. 2), which is 1 feet high with 1 feet diameter and 0.5 feet radius, one end of the 20-L steel drum each has a 1-cm vent hole, left open during placement so that pressure quickly equilibrated with the bay, the small hole was connected to hose and the other side of the hose is connected to 1-L plastic bag. The drum forms a compartment that is inserted open end down into the sediment. Water seeping through the sediment will displace water trapped in the compartment forcing it up through the port into the plastic bag.
Results and discussion
The area of the proposed study has been calculated and data for parameters like precipitation, evapotranspiration and stream flow were collected from (IMD 2014; PWD 2014). Based on the water budget method, the rate of SGD calculated is 19 × 103 m3 day−1 in total (Table 1) and found to be 1.4 times higher than the rate of stream flow.
For the SGD estimation by Darcy’s law, the hydraulic conductivity has been calculated for two different aquifers (alluvium and fluvio marine) at three different locations, where the seepage meters have been installed. The hydraulic conductivity calculated for the alluvium and fluvio marine sediments were 10−1 and 10−3 cm s−1, respectively. The aquifer cross-sectional area ‘A’ calculated was 26,717.1, 28,294.2 and 38,343.2 m2, respectively, for three different locations. The SGD calculated in alluvium formation at distance of 14.7 km from the coast was 844.86 m3 day−1 and the fluvio marine formations at a distance of 13.5 km from the coast accounts 8.94 m3 day−1 and 12.12 m3 day−1 and for the third location at a distance of 5.7 km away from the coast. Higher SGD was noted in alluvium formation when compared with the other two fluvio marine formations, which might be due to greater hydraulic conductivity (Table 2) noted in the alluvium formation (Oberdorfer 2003a, b; Simmons et al. 1991). Lower flow observed in fluvio marine sediments might be the lower permeability of the formations resulting in reduced groundwater discharge. The measured seepage rates are noted in the table. The highest SGD rate of 0.1119 m h−1 was observed in seepage meter 1 and minimum was noted in all the three seepage meters with average values of 0.057, 0.0276 and 0.0245 m h−1, respectively (Table 3, Fig. 4). The amount of fresh water discharge observed per day accounts 36.6 × 103 m3 day−1 for the first seepage meter and 18.74 × 103 and 22.5 × 103 m3 day−1 for seepage meter 2 and 3, respectively. Lower seepage rate was observed in seepage meter 3 fixed close to the coast and higher seepage rate was observed in seepage meter 1 fixed at distance from the coast. In general, seepage rates decrease with distance away from the coast (Taniguchi et al. 2006) but inverse relation was observed between the seepages and distance from the coast. Maximum seepage rate was observed in seepage meter 1 might be due to the high permeability or upward flow due to regional groundwater discharge (Freeze and Cherry 1979).
The seepage waters collected were analyzed for physiochemical parameters like pH, EC, TDS and salinity (Table 4) and found to be varying with locations. Attempts have been made to isolate fresh SGD, recirculated SGD and saline SGD. The maximum pH (7.8) was noted in seepage meter 2, The maximum EC (35.1 mS), TDS (18.6 ppt) and salinity (22.8 ppt) were noted at seepage meter 3 which is very near to the coast and lower EC (1.84 mS), TDS (0.98 ppt) and salinity (1.13 ppt) were observed in seepage meter 1 away from coast and intermediate values of EC (7.4 mS), TDS (3.87 ppt) and salinity (4.8 ppt) were observed in seepage meter 2 fixed in between seepage meter 1 and 3.
Seepage 1 was installed at 14.7 km away from the coast (Fig. 1) in alluvial formations encompassing sand as the dominant litho units. Since the hydraulic conductivity of sand was higher (10−1 cm s−1) so was the SGD rate (1.5 × 103 m3 h−1) but with low physio-chemical parameters (Fig. 5). The pH ranges from 7.17 to 7.57 with an average of 7.30, EC ranges between 1.6 and 1.84 mS with an average of 1.71 mS, TDS 0.85–0.98 ppt with average 0.908 ppt and salinity 1.04–1.13 ppt with average 1.09 ppt. All the parameters were within the limit indicating fresh groundwater water discharge (FSGD).
The second seepage meter S2 was installed at 13.5 km away from the coast (Fig. 1). The geology of the area is mainly of fluvio marine sediments encompassing silt, sand and clay formations with low conductivity values (10−3 cm s−1), hence with lower SGD value of 0.78 × 103 m3 h−1. The statistics for the physio-chemical parameters were pH ranges between 7.17 and 7.8 with average of 7.53, EC between 4.83 and 7.4 mS with average of 6.23 mS, TDS between 2.6 and 3.87 with average of 3.32 ppt and salinity between 3.2 and 4.8 ppt with average 4.1 ppt (Fig. 6). The concentrations were higher than fresh groundwater and lower than saline water indicating the zone as mixed between fresh and saline water [subterranean estuary (STE)].
The third seepage meter (S3) was installed at 5.7 km away from the coast (Fig. 1). This location consists of the fluviomarine sediments formation of silt, sand and clay with lower conductivity values (10−3 cm s−1), but the recorded SGD rate (0.9 × 103 m3 h−1) was lower than seepage 1 but higher than seepage 2. The physio-chemical parameters recorded were with pH ranges between 6.54 and 7.1 with average of 6.77 and EC between 11.7 and 35.1 mS with average of 31.55 mS, TDS between 5.35 and 18.6 with average of 16.59 ppt and salinity between 8.04 and 22.8 ppt with average of 20.60 ppt. Higher concentrations indicate the influence of recirculated submarine groundwater (RSGD) due to tidal influences (Fig. 7). The possible sources for SGD are explained in schematic diagram Fig. 8. A large variation in SGD might be attributed to the spatial and temporal variation of the study site as suggested by Shaw and Prepas (1989). When compared with the calculated water budget method of SGD (795 m3 h−1), the Darcy law-calculated SGD values were lower (35.20, 0.37 and 0.50 m3 h−1). This in turn indicates the difference in parameters considered for calculating the discharge using water budget and Darcy methods. In water budget method the discharge has been attempted using data like precipitation, evapotranspiration and gradient and for Darcy law parameters like porosity, permeability, aquifer flow velocity, hydraulic conductivity and hydraulic gradient were considered. The above properties contrast on the litho units except evapotranspiration and precipitation. Two different units, alluvium and fluvio marine sediments, were isolated from the study area. The hydraulic conductivity of alluvium formation ranges 10−1 cm s−1 and in fluvio marine sediments it ranges 10−3 cm s−1, hence SGD in fluvio marine sediments are lower (0.37 and 0.50 m3 h−1) when compared with alluvium aquifer (35.20 m3 h−1). Within the fluvio marine sediments two distinguished SGD were recorded. Higher discharge (0.50 m3 h−1) was noted close to the Bay of Bengal coast (5.7 km) with an aquifer cross-sectional area of 38,343.2 m2 and low discharge (0.37 m3 h−1) noted inland (13.5 km) with an aquifer cross section of 28,294.2 m2. Compared to Darcy’s and water budget method, seepage meter methods gives superior SGD rates (S1—1.5 × 103, S2—0.78 × 103 and S3—0.9 × 103 m3 h−1) and the seepage rates of the aquifers are controlled by the hydraulic conductivity of that aquifer. The average SGD rate from the installed seepage meters was 9.8 × 106 m3 year−1. Attempt has been made to compare the present SGD with global averages (Table 5). From the comparison, the rate of SGD fluxes in the present study using water budget calculations was many folds higher than Tampa bay. SGD fluxes calculated using Darcy law method in the present study were many folds higher when compared with Tampa Bay. The present study fluxes calculated using seepage meter were 0.28 times lower than the study conducted in Orelans and 87 times higher than the study conducted in Greater lakes. This in turn indicates varying climatic condition of the study area which is semi-arid in nature and also might be due to varying litho units with dissimilar hydraulic conductivity values.
Conclusion
Quantification of SGD was attempted in Coleroon estuary using three different methods like water budget, Darcy law and manual seepage meter. The water budget-calculated SGD were 19088.71 m3 day−1 and was higher than the stream flow rate. The Darcy law calculations suggest SGD in alluvium formation as 844.86 m3 day−1 and for fluvio marine formations as 8.94 and 12.12 m3 day−1. The seepage meter suggested highest SGD rate of 0.1119 m h−1 in seepage meter 1 and minimum was noted in all the three seepage meters. Lower seepage rate was observed in seepage meter 3 fixed close to the coast implying inverse relation between seepage and distance from coast due to high permeability or upward flow due to regional groundwater discharge. The analyzed physiochemical parameters suggest seepage meter 1 as freshwater discharge with lower values and the second seepage meter with intermediate values as zone mixed between fresh and saline water. Higher parameters were noted in seepage meter 3 suggesting influence of recirculated ocean water. Present SGD was compared with global averages which suggests that varying climatic condition and dissimilar hydraulic conductivity influence the seepage rate in the proposed study area.
References
Allen AD (1976) Outline of the hydrogeology of the superficial formations of the Swan Coastal Plain. Western Australia Geol Surv Ann Rep, pp 31–42
Beck AJ (2007) Submarine groundwater discharge (SGD) and dissolved trace metal cycling in the subterranean estuary and coastal ocean, PhD dissertation. Stony Brook University, p 308
Black FJ, Payian A, Knee KL, De Sieyes NR, Ganguli PM, Gray E, Flegal R (2009) Submarine groundwater discharge of total mercury and monomethylmercury to central coastal waters. Environ Sci Technol 43:5652–5659
Burnett WC (1999) Offshore springs and seeps are focus of working group. EOS Trans Am Geophys Union 80:13–15
Burnett WC, Kim G, Lane-Smith D (2001) A continuous radon monitor for assessment of radon in coastal ocean waters. J Radioanal Nucl Chem 249:167–172
Burnett WC, Aggarwal PK, Aureli A, Bokuniewicz H, Cable JE, Charette MA, Kontar E, Krupa S, Kulkarni KM, Loveless A, Moore WS, Oberdorfer JA, Oliveira J, Ozyurt N, Povinec P, Privitera AMG, Rajar R, Ramessur RT, Scholten J, Stieglitz T, Taniguchi M, Turner JV (2006) Quantifying submarine groundwater discharge in the coastal zone via multiple methods. Sci Total Environ 367:498–543
Cable J, Bugna G, Burnett W, Jb Chanton (1996) Application of 222Rn and CH4 for assessment of groundwater discharge to the coastal ocean. Limnol Oceanogr 41:1347–1353
Cable JE, Burnett WC, Chanton JP, Corbett DR, Cable PH (1997) Field evaluation of seepage meters in the coastal marine environment. Estuar Coast Shelf Sci 45:367–375
Cai Y, Sudburry A, Fernandez A, Hay BJ (2003) Organic compounds and trace metals of anthropogenic origin in sediments from Montego Bay, Jamaica: assessment of sources and distribution pathways. Environ Pollut 123(2):291–299
Castro MC (2004) Helium sources in passive margin aquifers—new evidence for a significant mantle 3He source in aquifers with unexpectedly low in situ 3He/4He production. Earth Planet Sci Lett 222:897–913
CGWB (2009) Central Groundwater Board district groundwater brochure Cuddalore and Nagapattinam district, Tamil Nadu Government of India. http://cgwb.gov.in/DistrictProfile/TamilNadu/Cuddalore.pdf
Charette MA, Sholkovitz ER, Hansel CM (2005) Trace element cycling in a subterranean estuary, part 1. Geochemistry of the permeable sediments. Geochim Cosmochim Acta 69:2095–2109
Cherkauer DS, Nader DC (1989) Distribution of groundwater seepage to large surface water bodies- the effect of hydraulic heterogeneities. J Hydrol 109(1–2):151–165
Corbett DR, Chanton JP, Burnett WC (1999) Patterns of groundwater discharge into Florida Bay. Limnol Oceanogr 44(4):1045–1055
Corbett DR, Dillon K, Burnett WC (2000a) Tracing groundwater flow on a barrier island in the north-east Gulf of Mexico. Estuar Coast Shelf Sci 51(2):227–242
Corbett DR, Dillon K, Burnett WC, Chanton J (2000b) Estimating the groundwater contribution into Florida Bay via natural tracers 222Rn and CH4. Limnol Oceanogr 45(7):1546–1557
Cox ME, Preda M, McNeil V (1997) Brisbane River Moreton Bay wastewater management study. Report at School of Natural Resources Sciences, Queensland University of Technology
Destouni G, Prieto C (2003) On the possibility for generic modeling of submarine groundwater discharge. Biogeochemistry 66(1–2):171–186
Diaz RJ, Rosenberg R (1995) Marine benthic hypoxia: a review of its ecological effects and the behavioral responses of benthic macro fauna. Oceanogr Mar Biol Annu Rev 33:245–303
Diersch HG (1996) Interactive, graphics-based finite element simulation system FEFLOW for modeling groundwater flow, contaminant mass and heat transport. WASY Institute for Water Resource Planning and System Research Ltd, Berlin
Dillon KS, Corbett DR, Chanton JP (1999) The use of sulfur hexafluoride (SF6) as a tracer of septic tank effluent in the Florida Keys. J Hydrol 220(3–4):129–140
Elsdon TS, Marthe BNAD, Noël JD, Diepen Bronwyn MG (2009) Extensive drought negates human influence on nutrients and water quality in estuaries. Sci Total Environ 407:3033–3043
Freeze RA, Cherry JA (1979) Groundwater. Prentice Hall, New Jersey, p 604
Gaines A, Giblin A, Mlodzinska-Kijowski Z (1983) Freshwater discharge and nitrate input into Town Cove. In: The coastal impact of groundwater discharge: an assessment of anthropogenic nitrogen loading in Town Cove, Orleans, Woods Hole Oceanographic Institution, pp 13–37
Garcia Solsona J, Garcia Orellana P, Masque V, Rodellas M, Mejıas B, Ballesteros JA, Dominguez (2010) Groundwater and nutrient discharge through karstic coastal springs (Castello Spain). Biogeosciences 7:2625–2638
Garrels RM, MacKenzie FT (1971) Evolution of sedimentary rocks. Norton and Co, New York, p 397
Gaume MU, Santos IR, Carlos LD (2016) Submarine groundwater discharge as a source of dissolved nutrients to an arid coastal embayment (La Paz, Mexico). Environ Earth Sci 75:154. https://doi.org/10.1007/s12665-015-4891-8
Gopinath S, Srinivasamoorthy K, Saravanan K, Suma CS, Prakash R, Senthilnathan D, Chandrasekaran N, Srinivas Y, Sarma VS (2016a) Modeling saline water intrusion in Nagapattinam coastal aquifers, Tamilnadu, India. Model Earth Syst Environ 2:2. https://doi.org/10.1007/s40808-015-0058-6
Gopinath S, Srinivasamoorthy K, Vasanthavigar M, Saravanan K, Prakash R, Suma CS, Senthilnathan D (2016b) Hydrochemical characteristics and salinity of groundwater in parts of Nagapattinam district of Tamil Nadu and the Union Territory of Puducherry. India Carbonates Evaporites. https://doi.org/10.1007/s13146-016-0300-y
Haider K, Engesgaard P, Sonnenborg TO, Kirkegaard C (2015) Numerical modeling of salinity distribution and submarine groundwater discharge to a coastal lagoon in Denmark based on airborne electromagnetic data. Hydrogeol J 23:217–233. https://doi.org/10.1007/s10040-014-1195-0
Harbaugh AW, Banta ER, Hill MC, McDonald MG (2000) MODFLOW-2000, the U.S. Geological Survey modular ground-water model—user guide to modularization concepts and the ground-water flow process. U.S. Geological Survey Open-File Report, pp 92–121
Howarth RW, Anderson D, Cloern J, Elfring C, Hopkinson C, Lapointe B, Malone T, Marcus N, McGlathery K, Sharpley A, Walker D (2000) Nutrient pollution of coastal rivers, bays, and seas. Issues Ecol 7:1–15
IMD (2014) Indian Meteorological Department, climate data in Nagapattinam and Cuddalore Districts, Government of India
Israelsen OW, Reeve RC (1944) Canal lining experiments in the delta area, Utah. Utah Agric Exp Sta Tech Bull 313:52
Jain (2012) India’s water balance and evapotranspiration. Curr Sci 102:7–10
Kaleris V, Lagas G, Marczinek S, Piotrowski JA (2002) Modelling submarine groundwater discharge: an example from the western Baltic Sea. J Hydrol 265(1–4):76–99
Knee KL, Paytan A (2011) Submarine groundwater discharge: a source of nutrients, metals, and pollutants to the coastal ocean. Estuar Coast Sci 4:205–233
Krest JM, Moore WS, Rama (1999) 226Ra and 228Ra in the mixing zones of the Mississippi and Atchafalaya Rivers: indicators of groundwater input. Mar Chem 64:129–154
Kroeger Peter W, Swarzenski WM, Greenwood Jason, Reich Christopher (2007) Submarine groundwater discharge to Tampa Bay: nutrient fluxes and biogeochemistry of the coastal aquifer. Mar Chem 104:85–97
Langevin CD (2001) Simulation of ground-water discharge to Biscayne Bay, southeastern Florida. U.S. Geological Survey Water-Resources Investigations 00-4251, p 127
LaRoche J, Nuzzi R, Waters R, Wyman K, Falkowski PG, Wallace DWR (1997) Brown tide blooms in Long Island’s coastal waters linked to inter annual variability in groundwater flow. Glob Change Biol 3:397–410
Lee DR (1977) A device for measuring seepage flux in lakes and estuaries. Limnol Oceanogr 22:140–147
Lee YW, Rahman MDM, Kim G, Han S (2011) Mass balance of total mercury and monomethylmercury in coastal embayments of a volcanic islands: significance of submarine groundwater discharge. Environ Sci Technol 45:9891–9900
Lvovich MI (1974) World water resources and their future. Nauka, Moscow, p 448
McCoy CA, Corbett DR, Cable JE, Spruill RK (2007) Hydrogeological characterization and quantification of submarine groundwater discharge in the southeast Coastal Plain of North Carolina. J Hydrol 339:159–171
McDonald MG, Harbaugh AW (1988) A modular three-dimensional finite-difference ground-water flow model. US Geological Surv Tech Water Resour Investig 6:586
Moore W (1996) Large ground-water inputs to coastal waters revealed by 226Ra enrichment. Nature 380(575):612–614
Moore W (1999) The subterranean estuary: a reaction zone of ground water and sea water. Mar Chem 65:111–125
Muir KS (1968) Groundwater reconnaissance of the Santa Barbara—Montecito Area, Santa Barbara County, California. U. S. Geol Surv Water Supply 1859:28
Oberdorfer JA (2003a) Hydrogeologic modeling of submarine groundwater discharge: comparison to other quantitative methods. Biogeochemistry 66:159–169
Oberdorfer JA (2003b) Hydrogeologic modeling of submarine groundwater discharge: comparison to other quantitative methods. Biogeochemistry 66(1–2):159–169
Ouyang Y (2012) Estimation of shallow groundwater discharge and nutrient load into a river. Ecol Eng 38:101–104
Pluhowski EJ, Kantrowitz IH (1964) Hydrology of the Babylon-Islip Area, Suffolk County, Long Island, New York. US Geol Surv Water Supply Pap 1768:128
Povinec PP, Aggarwal PK, Aureli A, Burnett WC, Kontar EA, Kulkarni KM, Moore WS, Rajar R, Taniguchi M, Comanducci JF (2006) Characterization of submarine groundwater discharge offshore south-eastern Sicily. J Environ Radio Act 89:81–101
Prakash R, Srinivasamoorthy K, Gopinath S, Saravanan K (2017) Preliminary study on the decadal changes in temperature and rainfall on the hydrochemistry of surface and groundwater in Coleroon river estuarine zone, east coast of India. J Clim Change 3(2):43–58. https://doi.org/10.3233/JCC-170013
PWD (2014) Public Works Department. Rainfall data in Nagapattinam and Cuddalore districts, Government of Tamilnadu
Rabalais NNRE, Turner D (1996) Nutrient changes in the Mississippi River and system responses on the adjacent continental shelf. Estuaries 19:386–407
Ramanathan AL, Subramanian V, Vaithiyanathan P (1988) sediment and chemical characteristics of the upper reaches of the Cauvery estuary east coast of India. Indian J Mar Sci 17:114–120
Rodellas V, Garcia-Orellana J, Garcia-Solsona E, Masque P, Domínguez JA, Ballesteros BJ, Mejías M, Zarroca M (2012) Quantifying groundwater discharge from different sources into a Mediterranean by using 222Rn and Ra isotopes. J Hydrol 2012:466–467
Rodellas V, Garcia-Orellana J, Masque P, Feldman M, Weinstein Y (2015) Submarine groundwater discharge as a major source of nutrients to the Mediterranean Sea. Proc Natl Acad Sci USA 112:3926–3930
Seitzinger SP, Mayorga E, Bouwman AF, Kroeze C, Beusen AHW, Billen G, Van Drecht G, Dumont E, Fekete BM, Garnier J, Harrison JA (2010) Global river nutrient export: a scenario analysis of past and future trends. Glob Cycles Biogeochem 24:GB0A08
Sekulic B, Vertacnik A (1996) Balance of average annual fresh water inflow into the Adriatic Sea. Water Resour Dev 12:89–97
Seralathan P, Setharamaswamy A (1982a) Geochemistry of the modern deltaic sediments of the Cauvery river east coast of India. Indian J Mar Sci 16:31–38
Seralathan P, Setharamaswamy A (1982b) Distribution of clay minerals in Cauvery delta. Indian J Mar Sci 11:167–169
Shaw RD, Prepas EE (1989) Anomalous short-term influx of water into seepage meters. Limnol Oceanogr 34:1343–1351
Simmons GMJRWG, Reay S, Smedley Williams MT (1991) Assessing submarine groundwater discharge in relation to land use. New Perspect Chesapeake Bay Syst Chesapeake Res Consort Publ 137:635–644
Slomp C, Van Cappellen P (2004) Nutrient inputs to the coastal ocean through submarine groundwater discharge: controls and potential impact. J Hydrol 295(1–4):64–86
Smith AJ, Nield SP (2003) Groundwater discharge from the superficial aquifer into Cockburn Sound Western Australia: estimation by inshore water balance. Biogeochemistry 66(1–2):125–144
Smith L, Zawadzki W (2003) A hydrogeologic model of submarine groundwater discharge: Florida inter comparison experiment. Biogeochemistry 66(1–2):95–110
Soetaert K, Middelburg JJ (2006) Long-term change in dissolved inorganic nutrients in the heterotrophic Scheldt estuary (Belgium, The Netherlands). Limnol Oceanogr 51(1–2):409–423
Somay MA, Gemici U (2009) Assessment of the salinization process at the coastal area with hydrogeochemical tools and Geographical Information Systems (GIS): Selçuk Plain, Izmir, Turkey. Water Air Soil Pollut 201:55–74
Srinivasamoorthy K, Vasanthavigar M, Vijayaraghavan K, Sarathidasan, Gopinath (2011) Hydrochemistry of groundwater in a coastal region of Cuddalore district, Tamilnadu India: implication for quality assessment. Arab J Geosci. https://doi.org/10.1007/s12517-011-0351-2
Swarzenski PW, Baskaran M (2007) Uranium distributions in the coastal waters and pore waters of Tampa Bay, Florida. Mar Chem 104:43–57
Taniguchi M, Fukuo Y (1993) Continuous measurements of ground-water seepage using an automatic seepage meter. Ground Water 31:675–679
Taniguchi M, Iwakawa H (2001) Measurements of submarine groundwater discharge rates by a continuous heat-type automated seepage meter in Osaka Bay, Japan. J Groundw Hydrol 43:271–277
Taniguchi M, Burnett WC, Cable JE, Turner JV (2002) Investigations of submarine groundwater discharge. Hydrol Process 16:2115–2129
Taniguchi M, Burnett WC, Dulaiova H, Kontar EA, Povinic PP, Moore WS (2006) Submarine groundwater discharge measured by seepage meters in Sicilian coastal waters. Cont Shelf Res 26:835–842
Tide forecast of India May (2015) Tidal data for Nagapattinam and Cuddalore districts, Government of India
Top Z, Brand L, Corbett R (2001) Helium as a tracer of ground water input into Florida Bay. J Coast Res 17:859–868
Trezzi G, Garcia-Orellana J, Rodellas V, Santos-Echeandia J, Tovar-Sánchez A, Garcia-Solsona E, Masque P (2016) Submarine groundwater discharge: a significant source of dissolved trace metals to the North Western Mediterranean Sea. Mar Chem 186:90–100
Uchiyama Y, Nadaoka K, Rolke P (2000) Submarine groundwater discharge into the sea and associated nutrient transport in a sandy beach. Water Resour Res 36(6):1467–1479
Vaithiyanathan P, Ramanathan A, Subramanian V (1992) sediment transport in the Cauvery river basin sediments characteristics and controlling factor. J Hydrol 139:197–210
Valiela I, Costa J, Foreman K (1990) Transport of groundwater-borne nutrients from watersheds and their effects on coastal waters. Biogeochemistry 10:177–197
Voss CI (1984) A finite-element simulation model for saturated-unsaturated, fluid-density-dependent ground-water flow with energy transport or chemically-reactive single-species solute transport. US Geol Surv Water Resour Investig 84:4369
Wang X, Jinzhou D, Tao J, TingyuWen Sumei L, Jing Z (2014) An estimation of nutrient fluxes via submarine groundwater discharge into the Sanggou Bay—a typical multi-species culture ecosystem in China. Mar Chem 167:113–122
Windom HL, Moore WS, Niencheski LFH, Jahnke RA (2006) Submarine groundwater discharge: a large, previously unrecognized source of dissolved iron to the South Atlantic Ocean. Mar Chem 102:252–266
Winter TC (1981) Uncertainties in estimating the water balance of lakes. Water Resour Bull 17:82–115
Zektser IS, Ivanov VA, Meskheteli AV (1973) The problem of direct groundwater discharge to the seas. J Hydrol 20:1–36
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Prakash, R., Srinivasamoorthy, K., Gopinath, S. et al. Measurement of submarine groundwater discharge using diverse methods in Coleroon Estuary, Tamil Nadu, India. Appl Water Sci 8, 13 (2018). https://doi.org/10.1007/s13201-018-0659-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-018-0659-0