Introduction

Drinking water industry has been confronted with two aspects of strict water quality standards and reduction of production cost. Coagulation is an important process, and directly related to production cost and quality in drinking water treatment plant (WTP). The coagulation is a nonlinear and complicated process, because many physical and chemical variables influence the process. Conventionally, the determination of coagulant dosage in drinking WTP is carried out by experienced operators. However, although the operators determine coagulant dosage according to current quality of the raw water and the settled water, the dosage is still not necessarily optimal, because the operators cannot handle the errors which will occur after several hours (Zhang and Stanley 1999). Therefore, it is necessary to develop decision support models that are able to predict the treated water quality and the required coagulant dosage.

The models can be considered as process and inverse process of coagulation. In general, a process model is used to predict the treated water quality by process inputs, such as raw water quality and coagulant dosage. This model can be used to determine coagulant dosage by trial and error and can be used to understand factors which affect the process for process analysis and for new operators’ training (Baxter et al. 2001b). In addition, the process model can be used to assess in real time the adequacy of coagulant dosage based on the operator’s experience. Thus, the model can contribute to ensure the stability of operation. On the contrary, an inverse process model is used to predict coagulant dosage using the treated water quality and the raw water quality. Therefore, the inverse process model can be used to predict directly the optimal coagulant dosage based on the raw water quality and the desired treated water quality.

In recent years, a variety of artificial intelligence (AI) techniques, such as neural networks and fuzzy inference systems, have been used in modeling of complex nonlinear water treatment processes. The use of artificial neural networks (ANN) has obtained popularity in modeling of coagulation process in WTP (Gagnon et al. 1997; Robenson et al. 2009; Kennedy et al. 2015). ANNs have a great potential for representing nonlinear complex processes without structural knowledge of the processes. In the previous researches, ANNs were applied to develop process and inverse process models for coagulation to assist operators to determine coagulant dosage and to optimize the process. Baxter et al. (1999) developed a full-scale ANN process model to predict clarifier effluent color at the Rossdale WTP in Edmonton, Alberta, Canada. Zhang and Stanley (1999) developed both process and inverse process ANN models to predict the settled water turbidity and the optimal alum dosage at the same WTP. Yu et al. (2000) developed an ANN inverse process model to predict the coagulant dosage at a WTP in Taipei City, Taiwan. Maier et al. (2004) developed both process and inverse process models using multilayer perceptrons (MLP) to predict several treated water quality parameters and alum dosage at a WTP in southern Australia. Robenson et al. (2009) developed an inverse process ANN model to predict the optimal coagulant dosage with consideration of treated water quality at Segama WTP in Malaysia. Griffiths and Andrews (2011a) developed both process and inverse process seasonal ANN models to predict settled water turbidity and optimal alum dosage at Elgin Area WTP, Canada. Kennedy et al. (2015) evaluated four different hybrid ANN process models for predicting turbidity and dissolve organic matter removal during coagulation process using daily full-scale data at Akron WTP, Ohio, USA.

Another powerful technique for modeling nonlinear systems is neuro-fuzzy which has an ability to handle uncertain and noisy data from fuzzy inference system and learning ability from neural networks. Adaptive neuro-fuzzy inference system (ANFIS) is one type of neuro-fuzzy systems (Jang 1993). ANFIS does not have the limitation of ANN in being trapped in local minima. It can estimate values that are outside the range of the training data. In general, the results of ANFIS model are superior than ANN that they are more accurate and have less uncertainty (Talebizadeh and Moridnejad 2011). In the literature, ANFIS has shown effective results in modeling for predicting coagulant dosage (Gagnon et al. 1997; Wu and Lo 2008; Heddam et al. 2012). However, all these researches are based on operators’ past behavior corresponding to influent quality without considering the process output, such as the settled water turbidity. In other words, none of previous researches has applied ANFIS models on the dynamics of coagulation process.

As a result of development of supervisory control and data acquisition (SCADA), the amount of data collected at WTP has increased enormously in recent years. In this situation, clustering technique is a good method for analyzing huge amount of information by classifying data into groups. Moreover, it is very useful for categorizing multi-dimensional data in clusters, allowing users to acquire effective information in decision making for complex water treatment processes. Maier et al. (2004) used Kohonen self-organizing map (SOM) to divide data into three subsets for developing ANN models. Park et al. (2008) used k-means clustering to classify data sets in making decision model for coagulant dosage. Juntunen et al. (2013) applied SOM and k-means clustering for modeling water quality in drinking WTP to assess the essential characteristics of the process. They concluded that the whole model should be able to adapt to different conditions by making separated sub-models for different states of the process, because a single uniform model always had problem in modeling complex relationships in the whole WTP process. Some studies also demonstrated that models composed of sub-models could be effective by modeling each state of the process, such as seasonal models (Gagnon et al. 1997; Griffiths and Andrews 2011a, b).

The main objective of this research is to develop enhanced models that are able to predict better the settled water turbidity and to determine optimal hourly coagulant dosage on full-scale condition in drinking WTP. To develop well-adjusted prediction models to different process states, k-means clustering method is integrated with ANFIS technique. Models by ANFIS and ANN are also developed for performance comparison. The proposed hybrid of k-means-ANFIS approach is the first attempt in modeling dynamic coagulation process.

Materials and methods

Treatment process and data set

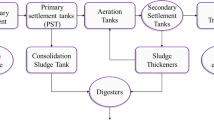
Bansong WTP is located in Changwon city, South Korea and operated by Korea water resources corporation (k water) which is a government-owned company. Raw water is supplied through 15.5 km buried pipeline from intake pump station at Nakdong River. It has treatment capacity of 120,000 m3 per day and serves population and industrial complex in Changwon city. Bansong WTP adopts the conventional treatment process which consists of pre-chlorination, coagulation, flocculation, sedimentation, filtration, and post-chlorination. In addition, pre-ozonation facilities started operation in May, 2014. Coagulant of polyaluminium hydrogen chloride silicate (PAHCS) has been injected to the coagulation chambers since 2014. A simple flow diagram of the treatment process is given in Fig. 1.

Fig. 1
figure 1

Schematic diagram of Bansong WTP process

Full size image

At Bansong WTP, pH, turbidity, temperature, conductivity of raw water, and settled water turbidity are measured by online analyzer. These parameters describing raw water characteristics have direct influences on coagulation process. pH determines the solubility of the coagulant and effects floc characteristics. Turbidity controls the coagulation for low TOC raw water to destabilize suspended colloids or to create a good settling floc. Temperature has effect on efficiency of primary particle removal and rate of floc formation. Conductivity is a measure of electric current in the water by the ionized substance; therefore, it also influences on the dissolved solids. Two flow rates affect settling and detention time which are influent the flow rate and the effluent flow rate after sedimentation process. On the other hand, coagulant dosage is determined manually by operators’ judgment based on look-up table, variation of raw water quality, and the settled water turbidity trend. These water quality and operation data are recorded by SCADA system in real time, and transferred to the main database system. In this research, hourly data sets of the parameters during the whole period of 2014 are collected from the database server. They are used as input and output data required for models development. Total of 8760 records are gathered including water quality, flow rate, and coagulant dosage. According to the general guideline, at least one full cycle of data set should be applied to represent the data set (Baxter et al. 2002).

Data preprocessing

To obtain the relationship between input and output of coagulation model, time shifting of data is necessary, because coagulant dosage and raw water quality at the current time influence on the future settled water quality rather than the current settled water (Griffiths and Andrews 2011b). Therefore, data of the settled water quality are shifted forward from the time of the current raw water quality and coagulant dosage. Duration of time shifting depends on hydraulic retention time in accordance with flow rate through flocculation chamber and sedimentation basin. The hydraulic retention time is calculated using outflow rate of the settled water and the total volume of the travel processes as expressed by the following equation (Griffiths and Andrews 2011b):

$$t_{\text{r}} = k + \frac{{V_{k} }}{{Q_{k + 1} }}$$
(1)

where t r is hydraulic retention time (hour) between the current point of coagulant dosage and target point; k is hours required until V i /Q i+1 is less than one; \(V_{i} = V_{i - 1} /Q_{i}\); Q i is flow rate per hour at the ith hour; \(i\) is 1-h unit time index (\(i = 1, 2, \ldots , k\)); and V o is volume of flocculation chamber and sedimentation basin.

After time-shifting processing, the number of data sets is reduced to 8755. The statistical characteristics of the preprocessed data are summarized in Table 1.

Table 1 Statistical summary of water quality and operational parameters for models’ development
Full size table

k-means clustering

Cluster analysis is a method to identify subgroups from a large number of objects based on characteristics of the objects. There are two widely used clustering algorithms: hierarchical and k-means clustering. Hierarchical clustering provides higher quality on likelihood classification for small data sets, whereas k-means is less sensitive to outliers and more efficient for processing large sample sizes (>500) (Mooi and Sarstedt 2011; Abbas 2008). Due to these advantages, k-means clustering has been used for analyzing data in many fields, including water treatment plant (Aguado et al. 2008; Zhu et al. 2015). k-means clustering uses a centroid-based approach to minimize intra-cluster variation (MacQueen 1967). It classifies total objects into k number of clusters with their similarity based on distance matrix. The centroid, which is the center of a cluster, is defined as a point to which the sum of distances from all objects in that cluster is minimized using similarity measure, such as Euclidean distance. Unlike hierarchical clustering, k-means clustering operates on real observed data; therefore, it is often more suitable than hierarchical clustering for large amounts of data. k-means clustering algorithm proceeds as follows (MacQueen 1967):

$$J = \mathop \sum \limits_{i = 1}^{k} \mathop \sum \limits_{{x_{j} \; \in \;S_{i} }} \left\| {x_{j} - c_{i}^{2} } \right\|$$
(2)

where J is the objective function; x j is data vector given a set of observations (\(j = 1, 2, \ldots ,n )\); k is the number of clusters; S i is cluster; and c i is cluster center.

  1. 1.

    Define k clusters with certain rules, and assign k random data vectors as the initial centroid of clusters.

  2. 2.

    Assign each object to the nearest cluster by calculating the distance between each object and the corresponding centroid vector.

  3. 3.

    Update a new centroid vector for each cluster.

  4. 4.

    If the result meets termination criterion (value of minimal objective function or maximum iteration number), the algorithm stops, otherwise, go to step 2.

Adaptive neuro fuzzy inference system (ANFIS)

Neuro-fuzzy network is composed of artificial neural network and fuzzy inference system. The Takagi–Sugeno is a famous fuzzy inference model for data-based fuzzy modeling (Michael 2005). The Sugeno fuzzy model generates fuzzy rules from a given input and output data set (Takagi and Sugeno 1985). ANFIS introduced by Jang (1993) is capable of approximating any continuous functions on a compact set to any degrees of accuracy, thus it has shown good prediction performance in various areas related to water research in the literature (Shu and Ouarda 2008; Al-Abadi 2014). ANFIS combines the fuzzy inference system with multilayer feed-forward neural network as a general structure, where if–then rules with proper membership functions and the specified input–output pairs used. Jang’s ANFIS is generally represented by a five-layer feed-forward neural network. Figure 2 shows ANFIS architecture corresponding to the first-order Sugeno fuzzy model. This network has two inputs (x, y) and one output (f). Each input is represented by two membership functions, and the output is represented by a first-order polynomial. A typical rule of ANFIS can be expressed as

$${\text{If}} \;x\; {\text{is}}\; A_{1} \; {\text{and}}\; y\; {\text{is}}\; B_{1} \quad {\text{THEN}} \;f_{1} = p_{1} x + q_{1} y + r_{1}$$
(3)
$${\text{If}} \;x\; {\text{is}}\; A_{2} \; {\text{and}}\; y\; {\text{is}}\; B_{2} \quad {\text{THEN}} \;f_{2} = p_{2} x + q_{2} y + r_{2}$$
(4)
Fig. 2
figure 2

Architecture of adaptive neuro fuzzy inference system

Full size image

where A 1, A 2 and B 1, B 2 are membership functions of input variables x and y, respectively; p 1, q 1, r 1 and p 2, q 2, r 2 are parameters of the output function. The role of each layer in ANFIS is as follows (Michael 2005):

Layer 1 is a fuzzification layer. Each node in this layer calculates membership value of an input variable. When Gaussian membership function is used, the output corresponding to i node for input x can be computed as

$$\mu_{{A_{i} }} = {\text{e}}^{{\frac{{ - (x - c_{i} )^{2} }}{{2\sigma_{i}^{2} }}}} ,\quad i = 1, 2$$
(5)

where σ i are c i are parameters that control shape of the Gaussian function of node i with maximum equal to 1 and minimum equal to 0. Parameters in this layer are referred as antecedent parameters.

Layer 2 is a rule layer. Each node in this layer corresponds to a single Sugeno-type fuzzy rule. Every node receives inputs from the respective nodes in layer 1 and calculates firing strength of the rule by multiplying the incoming inputs:

$$w_{i} = \mu_{{A_{i} }} (x)\mu_{{B_{i} }} (y), \quad i = 1, 2.$$
(6)

Layer 3 is a normalization layer. Each node in this layer calculates normalized firing strength from the ratio of each node’s firing strength to the sum of all rules’ firing strengths. It represents the degree of contribution of a given rule to the final result. The ith node of this layer is computed as

$$\overline{{w_{i} }} = \frac{{w_{i} }}{{w_{1} + w_{2} }}, \quad i = 1, 2.$$
(7)

Layer 4 is a defuzzification layer. Each node in this layer is connected to the respective node in layer 3, and also the initial inputs x and \(y\). Thus, the output of each node in this layer is determined as the product of the normalized firing strength and the first-order polynomial function:

$$\overline{{w_{i} }} f_{i} = \overline{{w_{i} }} ( p_{i} x + q_{i} y + r_{i} ), \quad i = 1, 2$$
(8)

where p i , q i, and r i are consequent parameters of rule i.

Layer 5 is a summation layer. This neuron computes the sum of outputs of all defuzzification nodes and produces the overall output, f:

$$f = \mathop \sum \limits_{i} \overline{{w_{i} }} f_{i} = \frac{{\mathop \sum \nolimits_{i} w_{i} f_{i} }}{{\mathop \sum \nolimits_{i} w_{i} }}.$$
(9)

The parameters for optimization in ANFIS are the antecedent parameters {\(\sigma_{i} , c_{i}\)} which represent the shape and location of the input membership functions, and the consequent parameters {p i , q i , r i } which describe the overall output of the system. In ANFIS, the parameters associated the membership functions of input and output are trained using a hybrid learning algorithm that combines the least-square estimator and the gradient descent method (Jang 1993). Identification of parameters associated with the consequent part of fuzzy rules in the complicated system is important. There are two most commonly used models for identification of fuzzy inference system in ANFIS. They are grid partition and clustering methods. The grid partition method has a critical drawback that all combinations of membership functions for each input make excessive number of rules; therefore, it causes a huge amount of calculation and inferior performance to clustering method in predicting coagulant dosage (Heddam et al. 2012). Thus, these parameters are usually extracted from the observed data using clustering method. Among various clustering methods, subtractive clustering method is the best for the condition, where the number of clusters for a given data set is not known (Talebizadeh and Moridnejad 2011).

Artificial neural network (ANN)

Artificial neural network is a massive parallel information processing system composed of a number of simple processing elements known as neurons or nodes (Haykin 1998). MLP is the most popularly used feed-forward hierarchical ANN which is used to map any random input with the corresponding output. Therefore, MLP has been used for a variety of studies for modeling and prediction on water research (Mondal et al. 2012; Al-Abadi 2014). MLP is comprised of different layers of neurons: one input layer, one or more hidden layers, and one output layer (Fig. 3).

A neuron receives input signals, then processes them by applying weights, and finally forwards an output signal to the following interconnected neurons. The expression of the output y(x) of MLP, which has three layers composed of an input layer with n neurons receiving input x i signals, a hidden layer with H neurons, and a layer with one output neuron, is given by

$$y(x) = f\left( {\mathop \sum \limits_{j = 1}^{H} W_{j} h_{j} + b_{1} } \right) {\text{and }}h_{j} = f_{j} \left( {\mathop \sum \limits_{i = 1}^{n} w_{ji} x_{i} + b_{j0} } \right)$$
(10)

where h j is net input; W j denotes the weight between the hidden layer and the output layer; w ji is the weight between the input layer and hidden layer; b is bias value; and f is the activation function. Most prominent used activation functions for neural networks are linear and sigmoid transfer functions. The initial assigned interconnection weights are progressively adjusted during the training process. In this process, the predicted outputs by MLP are compared with target outputs, and errors are back propagated to minimize the errors. Levenberg–Marquardt (LM) algorithm is highly recommended back-propagation algorithm for optimizing the interconnection weights, because it is the fastest and gives better performance for a simple structure networks (Hagan and Menhaj 1994).

Fig. 3
figure 3

MLP architecture of three layers and one output

Full size image

Hybrid of k-means clustering and ANFIS

The architecture of k-means-ANFIS is shown in Fig. 4. It consists of six key components: input and output database, data division unit, k-means cluster unit, fuzzy system generator, fuzzy inference system, and adaptive neural network representing the fuzzy system. After data division processing, each training, validation, and test data sets are assigned to clusters formed by k-means algorithm. Each cluster is trained independently with training and validation sets by ANFIS to obtain the optimal fuzzy inference system. Then, the fuzzy inference systems are kept and merged into a single entire system. For the test phase, inputs are provided to the corresponding fuzzy inference system depending on their belongings, which are determined by Euclidean distances between cluster centers and inputs, and then outputs are obtained. The combination of two algorithms is implemented in MATLAB.

Fig. 4
figure 4

Architecture of k-means-ANFIS model

Full size image

Indices of model performance

To evaluate the performance of k-means-ANFIS and to compare with the other models, several statistical indices are used: root mean square error (RMSE), mean absolute percentage error (MAPE), correlation coefficient (R), and coefficient of determination (R 2). The lower RMSE and MAPE, the higher R and R 2 values mean better performance. In addition, R 2m which was proposed by Roy and Roy (2008) is included to evaluate the robustness and the reliability of the models. This index evaluates the similarity between R 2 and \(R_{\text{o}}^{ 2}\). It has value higher than 0.5 when the model has good performance, where \(R_{\text{o}}^{ 2}\) indicates the coefficient of determination between the observed values and the predicted values expected from a perfect fit line. These evaluation indices are defined as follows:

$${\text{RMSE}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} (P_{i} - O_{i} )^{2} }}{k}}$$
(11)
$${\text{MAPE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{P_{i} - O_{i} }}{{O_{i} }}} \right| \times 100$$
(12)
$$R = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (O_{i} - \overline{O} )(P_{i} - \overline{P} )}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} (O_{i} - \overline{O} )^{2} \mathop \sum \nolimits_{i = 1}^{n} (P_{i} - \overline{P} )^{2} } }}$$
(13)
$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} (O_{i } - P_{i} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} (O_{i} - \overline{O} )^{2} }}$$
(14)
$$R_{\text{m}}^{ 2} = R^{2} \left( {1 - \sqrt {\left| {R^{2} - R_{\text{o}}^{ 2} } \right|} } \right)$$
(15)

where \(n\) is the number of data; P i is the predicted value and O i is the observed value; and \(\overline{P}\) and \(\overline{O}\) are the average values of the predicted and observed values, respectively.

Result and discussion

Variations of water quality and coagulant dosage

The preprocessed data show a significant variation of data throughout the year of 2014, as shown in Fig. 5. The turbidity has substantially high coefficient of variation with abrupt rise up to about 440 NTU during rainy season. The variations of temperature and conductivity are considerably high throughout four seasons as well. Low temperature under about 5 °C is seen in several months and the conductivity decreases during rainy season. The pH increases over pH 8.0 during dry season with low temperature and some periods in summer. The variation of the settled water turbidity is high due to the large variation of the raw water turbidity. It exceeds over 1 NTU in some cases during summer season. The PAHCS is dosed at the rate from around 14–40 mg/L during non-rainy seasons; however, around 70 mg/L is dosed during rainy season.

Fig. 5
figure 5

Variations of water quality and PAHCS dosage

Full size image

The results of k-means clustering on raw water quality

To identify distinctive process states according to the influent water, four-dimensional raw water quality is classified by k-means clustering. In general, data normalization is useful to generate good clusters and to improve the accuracy of clustering. The raw water quality data are converted into specific ranges by Z-score method, so that different ranges of four parameters can be treated equally for fair comparison. Z-score conversion is effective for k-means algorithm (Mohamad and Usman 2013). The original data (x) are normalized using the average value (\(\overline{x}\)) and standard deviation (s) as shown in Eq. (15). As the result, all parameters have zero mean and unit variance:

$$Z{\text{ - score}} = \frac{{x - \overline{x} }}{s}.$$
(16)

In k-means clustering, the number of clusters has to be decided in advance. In this research, the optimal number of clusters is determined using Davies–Bouldin criterion (Davies and Bouldin 1979) and Silhouette criterion (Rousseeuw 1987). In Davies–Bouldin method, the number of clusters is optimal when Davies–Bouldin index has minimal value, which indicates that distances among clusters are far. Whereas, Silhoutte plot shows graphically how well all objects lie within their corresponding clusters and provides the silhouette value which is a measure of how similar each point is to points in its own cluster. Davies–Bouldin index and Silhouette plot for the observed data are shown in Fig. 6. From Silhouette plot, most points in four clusters have positive Silhouette values higher than 0.6 (average Silhouette value 0.61), which indicate that the clusters are separated well from the neighboring clusters.

Fig. 6
figure 6

Silhouette plot of four clusters and Davies–Bouldin index in k-means clustering

Full size image

These clusters represent four different states of raw water quality and can be characterized manifestly as center vectors of the clusters, as shown in Table 2. Cluster 1 which is the smallest cluster represents extremely high turbidity, the lowest pH, and conductivity during rainy summer season. Cluster 2 describes raw water quality with high turbidity, low-to-medium pH, and the highest temperature from summer to late fall season. Cluster 3 refers to the water state in which temperature is the lowest, pH is the highest, and turbidity is the lowest during cold season that spans from December to April. Cluster 4 includes the largest sample size and the most frequent condition. In cluster 4, the data of water quality spread from April to December, representing water quality that is the closest to the average but medium-to-high temperature value. The whole data sets of a year are categorized successfully according to the distinct characteristics of the parameters by k-means algorithm, as shown in Fig. 7. From the viewpoint of models development, the number of data in cluster 1 is not sufficient for good training in neural networks compared with the other clusters; therefore, the data are integrated with cluster 2.

Table 2 Cluster center of raw water quality by k-means clustering
Full size table
Fig. 7
figure 7

Cluster-specific allocation of data sets according to four-dimensional raw water quality parameters

Full size image

ANFIS and ANN models

To determine contribution of the input parameters to the models, the correlation coefficients (R) are calculated, as shown in Table 3. High turbidity impact is shown with high value of R. Conductivity has the most influence on turbidity of the settled water, while it has the least influence on coagulant dosage. Both in and out flow rates are low influential parameters. Consequently, four raw water quality parameters and coagulant dosage are selected as input of the process model, and four raw water quality parameters and settled water turbidity are chosen as input of the inverse process model. The value of R which is higher than 0.1 is set as the threshold for selecting input parameters in the models (Chen and Liu 2014).

Table 3 Correlation coefficients between model outputs and input parameters
Full size table

In good data division, statistical properties, such as mean and standard deviation of subsets of the data, should be similar to guarantee that the subsets represent the whole population of study domain (Sahoo et al. 2012). In this research, 8755 data are divided into three subsets using the method proposed by Baxter et al. (2001a) by dividing data at the ratio of 3:1:1 for training, validation, and test sets, respectively. As the result, 8755 data are divided into 5253, 1751, and 1751 data sets for the training, validation, and test, respectively (Table 4).

Table 4 Statistical parameters for training, validation, and test sets
Full size table

ANFIS model is developed using genfis2 command in Fuzzy Logic Toolbox of MATLAB, which generates fuzzy inference system structure from data using subtractive clustering algorithm. First-order Sugeno model is applied as fuzzy inference system structure. In subtractive clustering, the range of a cluster in each dimension is controlled by radius parameter, and thus, finding optimal radius is important for subtractive clustering algorithm (Chiu 1994). In this research, the values from 0.07 to 0.5 (with an increment of 0.01) are investigated to find the optimal radius value which has the best performance evaluation index on the test phase. ANN model is also developed by Neural Network Toolbox in MATLAB. The number of hidden neurons is determined using the rule that the ratio of the number of training data to the number of connection weights should be 10 to 1 (Weigend et al. 1990). The parameters for ANFIS and ANN used in model development are summarized in Table 5.

Table 5 Training parameter values for ANFIS and ANN models’ development
Full size table

Simulation results of k-means-ANFIS models

The performances of three process models by k-means-ANFIS are presented in Table 6. According to the optimal cluster radii, each inference system applies 13, 55, and 113 linguistic rules, respectively. Figure 8 shows 13 rules of cluster 1 & 2 model from fuzzy logic toolbox interface in MATLAB. With this interface tool, the settled water turbidity can be estimated from the five given input values. According to the evaluation results, all sub-models have correlation coefficients higher than 0.8, which represent strong correlation between the observed and predicted values. Cluster 1 & 2 model shows the lowest performance, and it is caused by the biggest variations of turbidity in raw and settled water (0.16–1.30 NTU) with the smallest number of data. The model of cluster 3 has the best performance considered from RMSE and MAPE, while the model of cluster 4 has the best performance considered from R and R 2. Particularly, the R 2 value of cluster 4 model is over 0.8, which indicates that the model is very good (Shu and Quarda 2008).

Table 6 Performance of k-means-ANFIS process models
Full size table
Fig. 8
figure 8

13 rules of cluster 1 & 2 model to predict settled water turbidity

Full size image

The evaluation results of three inverse process models by k-means-ANFIS are shown in Table 7. According to the optimal cluster radii, the inference systems apply 8, 55, and 113 linguistic rules in the models, respectively. All models show accurate prediction ability with R and R 2 values higher than 0.8. The clusters 1 & 2 model also shows the lowest performance among the three models. This is caused by the same reason as the process model: wide coagulant dosage range (27.39–69.59 mg/L), with the smallest number of data. The model of cluster 3 has the best performance in all evaluation indices. Figure 9 illustrates 3D response surface graphs of cluster 3 model. It can be seen that coagulant dosage has complicated nonlinear relationship with raw water quality and the settled water turbidity.

Table 7 Performance of K-means-ANFIS inverse process models
Full size table
Fig. 9
figure 9

3D response surface graphs of cluster 3 model to predict coagulant dosage

Full size image

To evaluate the performance of the proposed k-means-ANIFS method, prediction performances of the six models are compared with a single ANFIS model using the same data. As shown in Table 8, the results confirm better performance of k-means-ANFIS by yielding lower RMSE and MAPE as well as higher R and R 2 than a single ANFIS except the process model of cluster 3. Although the single ANFIS model predicts very slightly better for cluster 3, it is not significant and MAPE evaluation contradicts it. Especially, both models of cluster 1 & 2 show significantly improved performances. As illustrated in Fig. 10, it can be noticed that the MFs of k-means-ANFIS spread more widely in the entire range than MFs of single ANFIS.

Table 8 Performance comparison of K-means-ANFIS and ANFIS
Full size table
Fig. 10
figure 10

Membership functions of process model of cluster 1 & 2 by a k-means-ANFIS and b ANFIS

Full size image

Table 9 gives comparative analysis of the completed k-means-ANFIS models, combining together three sub-models of process and inverse process, respectively, with ANFIS and ANN models.

Table 9 Comparative analysis of k-means-ANFIS, ANFIS, and ANN models
Full size table

According to the results, all models satisfy the evaluation criteria as good models: R > 0.8, R 2 > 0.8, \(R_{\text{m}}^{ 2}\) > 0.5. However, as shown in Table 9, k-means-ANFIS model provides better prediction results than ANFIS and ANN models for all evaluation criteria. Therefore, k-means-ANFIS method can be effectively applied to the process and the inverse process models of coagulation. The results of three models in the test phase are graphically compared by the plots of both observed and predicted values (Figs. 11, 12, 13).

Fig. 11
figure 11

Observed and predicted settled water turbidity by a k-means-ANFIS, b ANFIS, and c ANN

Full size image
Fig. 12
figure 12

Observed and predicted coagulant dosage by a k-means-ANFIS, b ANFIS, and c ANN

Full size image
Fig. 13
figure 13

Correlation plots of process models by a k-means-ANFIS, b ANFIS, and c ANN; inverse process models by d k-means-ANFIS, e ANFIS, and f ANN

Full size image

The comparison of method proposed in this research with the existing methods from several literatures on coagulation modeling is presented in Table 10. Zhang and Stanley obtained good result with R 2 value of 0.95 for inverse process model; however, the model was built based on only good cases of effluent turbidity and not covering all seasonal variations. The good performances of the models by Maier et al. resulted from small number of bench scale data. However, the model derived from bench scale data is generally unable to account for the simultaneous change in key process parameters, and often fail when applied to real WTP (Baxter et al. 1999). Robenson et al. made an accurate model using 11 inputs, but it could not catch up with the proposed model’s performance even though they used time series of coagulant dosage as input parameters. Kennedy et al. built an acceptable model with the R value of 0.91; however, it was caused by daily sampling and relatively stable raw water quality, such as turbidity from 1.9 to 37.7 NTU. Therefore, it has a limitation of real-time predictions under abrupt large changes of raw water quality. The seasonal models by Griffiths and Andrews were built under similar simulation conditions to this work, but the overall performances of the seasonal models are lower than k-means-ANFIS models despite using more inputs. The results in this section demonstrate that k-means-ANFIS models are superior to those in the literatures under the condition when real-time predicting is required for WTP which has big fluctuation of raw water quality throughout a year.

Table 10 Summary of process and inverse process ANN models on coagulation in the literatures
Full size table

Conclusions

In this research, hybrid of k-means-ANFIS method was proposed and applied to predict the settled water turbidity and the optimal coagulant dosage with full-scale data from Bansong WTP (South Korea). The general ANFIS and ANN models were implemented for comparison as well. k-means clustering successfully characterized the wide-range influent conditions into four distinct groups. Then, four sub-models representing different process states of raw water quality were developed and merged into three sub-models. The evaluation results demonstrated high performance of the hybrid approach of k-means clustering and ANFIS. On the whole, the sub-models of k-means-ANFIS performed better than a single ANFIS model, especially it could achieve the most improved prediction results for cluster 1 & 2 models occupying rainy season. The prediction improvement of rainy season in R 2 index was 21.2% for the process model and 12.6% for the inverse process model. It indicates that k-means-ANFIS models can be used as a robust tool during rainy season which is the most challenging period of operation. In comparison with the general ANFIS and ANN, k-means-ANFIS also provided the best results in all evaluation indices: RMSE, MAPE, R, R 2, \(R_{\text{m}}^{ 2}\). Therefore, the proposed hybrid approach can be used effectively for modeling the process and the inverse process of coagulation. It can provide operators with effective decision supports on both water quality control and operational costs.