Introduction

Dyes are harmful pollutants which can cause environmental and ecosystem problems. Their removal from aqueous solution has been widely investigated by the scientists making use of different kinds of adsorbents such as agricultural byproducts, activated carbons, graphene oxide, minerals, polymers, metal oxides, and so forth. Among the variety of dyes, crystal violet (CV) represents one of the most important cationic ones. It is also known as hexamethyl pararosaniline chloride and used in many industrial fields like cosmetic, food, paper-making, printing, leather and textile processing industries (Chen et al. 2008). The latter fields correspond to the biggest users of dyes. In fact, there are more than 10,000 dyes currently used in such industries and over 280,000 tons of the textile dyes are produced annually worldwide (Mass and Chaudhari 2005). The cationic dyes are more toxic than the anionic dyes (Hao et al. 2000). In general, synthetic dyes, which are stable to light, temperature and microbial attack, may also cause allergic dermatitis, cancer and mutation (Rauf et al. 2009; Santhy and Selvapathy 2006). Several technologies have been employed to clean dye containing wastewater, including biological (Javaid et al. 2011) and physico-chemical (Qian et al. 2013) procedures, membranes filtration (Kurt et al. 2012), ozonation (Aziz et al. 2012), advanced oxidation (Yasar et al. 2013) and adsorption (Mittal et al. 2012a, b; Lotito et al. 2012). Each of these processes, however, faces certain technical and economical limitations. Adsorption on solid surfaces is an innovative and economical alternative due to the ease of operation and lower prices (Ali 2012; Ali and Gupta 2006). It has been extensively used in the treatment processes of colored waters. Activated carbon has long been used as a standard adsorbent for color removal, but it remains expensive (Gupta et al. 2011; Khani et al. 2010; Saleh and Gupta 2012). For this reason, the development of low-cost alternative, reusable, locally available adsorbents has been the focus of recent research. These adsorbents made from natural material require chemical and physical modifications to improve their performance and adsorption capacity (Mittal et al. 2009a, b, 2010; Rehman et al. 2012, 2013). As one example of such cheaper substances, clays are widely used as they are readily available and act both as adsorbents and catalysts (Roulia and Vassiliadis 2005). Owing to their interesting physico-chemical properties (lamellar structure, high surface area and large cation exchange capacity), clays have great potential to fix pollutants, such as heavy metals and organic compounds.

The present research is within the scope of the search for natural and abundant sources of adsorbents as clays and cheaper minerals. More interesting is the fact that the local clay of the present study has not been previously investigated. Indeed, the present work is to characterize it and investigate the adsorption process of crystal violet dye. The second crucial idea of this study was to determine optimum adsorption conditions using the response surface methodology (RSM) based on Box–Behnken statistical design. The RSM is based on a combination of mathematical and statistical techniques. It has been employed to analyze the influences of main factors, as well as their effect on dependent variables during the experiments. Therefore, optimum conditions for desired responses can be predicted (Chowdhury et al. 2011, 2013; Hamsaveni et al. 2001; Hasan et al. 2009; Muhamad et al. 2013). The effects of initial dye concentration, adsorbent dose and contact time on the removal efficiency were evaluated and were considered as the operational variables in the present study.

Materials and methods

Preparation and characterization of the local clay

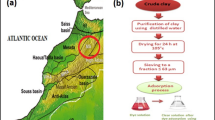
A green colored clay was obtained from the region Berkane, north eastern Morocco. The adsorbent was crushed, and sieved to a particle size less than 63 μm, and dried at 100 °C for 24 h. The specific surface area of the adsorbent was measured by the Brunauer–Emmett–Teller (BET) method with an AUTOSORB-1 (Quantachrome Corporation). The mineralogical phase characterization was carried out by quantitative X-ray diffraction (XRD). Samples were run on a Bruker D8 Advance with Cu-Kα, 2 radiation (0.15418 nm) equipped with a Lnyxeye (C) stripe detector (2θ) from 5° to 65° with a step width of 0.024° and 168 s counting time per step. The divergence slit was set to a constant footprint size of 12 mm of the beam on the sample. The particle size was determined by Fraunhofer method using a Beckman Coulter LS Particle Size Analyzer. The presence of functional groups present on the local clay was examined by Fourier transform infrared (FTIR in the range of 400–4000 cm−1) spectroscopy method using a FTIR spectrometer (VERTEX 70). The surface elemental composition of the adsorbent used in this study was determined using an EDX detector in combination with a field emission scanning electron microscope (Quanta 650 FEG, ESEM-Fa FEI). Electrophoretic mobilities of the local clay were determined by a Brookhaven-PALS apparatus at room temperature. pH-measurements involved calibration of the pH-measurement device (Orion pH-meter. and Thermo-science Fisher electrode) with four commercial buffers.

The local clay was used as received without any pretreatment in the adsorption experiments.

Dye solution

CV was purchased from Sigma-Aldrich. The structures and some characteristics of CV dye (Ahmad 2009) are illustrated in Table 1.

Table 1 Characteristics of (CV)
Full size table

The stock solution of CV dye was prepared by dissolving 1 g of dye in 1 L of distilled water. Different concentrations of CV dye used in this experiment were prepared by diluting the stock solution with distilled water. Separated analyses were done at λ max = 590 nm using a UV–Visible spectrophotometer (VR-2000).

Experimental procedure

Batch adsorption experiments were carried out at room temperature, using a jar test assembly. The latter consists in contacting and stirring at 200 rpm jars containing 200 ml suspensions of the CV solutions of different known total concentrations (50, 100 and 150 mg L−1) with known adsorbent masses (1, 5, 2 and 2.5 g). Samples were taken for analysis from each jar at 15, 30 and 45 min, respectively. UV–Vis. analysis, employing the spectrophotometer VR-2000, is used to determine residual concentrations of CV after solid–liquid separation. The chosen wavelength corresponds to the maximum absorbance of the sample and is at λ = 590 nm. The residual dye content was determined by interpolation using the previously established calibration curve. The study of the adsorption of a compound on an adsorbent allows us to examine the influence of the contact time on its retention. This study was carried out to determine the adsorbed quantities of the dye from its initial contact until dynamic equilibrium. To determine the waiting time for dynamic equilibrium, a preliminary adsorption experiment was carried out which involved introducing a precisely weighed quantity of adsorbent into a volume of 500 mL of solution containing dye at a concentration of 50 mg L−1. Subsequently samples were taken at well-defined (short) time intervals (every 2 min). The colored solution was separated from the adsorbent by centrifugation at 3400 rpm and analyzed as specified above. From the results of these preliminary tests, the time intervals were fixed at 15, 30, and 45 min.

The percent (%) CV removal was calculated using Eq. (1):

$$\% {\text{Removal}} = 100(c_{0} - c_{\text{e}} )/c_{0} ,$$
(1)

where C 0 and C e are the initial and final concentration (mg L−1), respectively.

Design of experiment and optimization

Box–Behnken design for Response surface methodology is used by experimentalists to examine the relationship between one or more dependent response variables and a set of quantitative experimental factors (independent variables). In the present study this design was utilized to determine the effect of three factors (initial dye concentration, adsorbent dosage and contact time) on the removal efficiency of CV dye using a local clay over three levels. The ranges and levels of the experimental parameters are depicted in Table 2. The total number of experiments can be calculated using Eq. (2):

$$N = 2^{F} + 2F + \chi_{0} ,$$
(2)

where N, F and χ 0 are the number of experimental runs, the factor number and the number of replicates at the central point, respectively. In the present study, the values of N, F and χ 0 were 17, 3 and 5, respectively (Soltani et al. 2013). The relationship between coded and real values of variables can be measured using to the following Eq. (3) (Myers and Montgomery 2002; Poroch-Seritan et al. 2011; Zarei et al. 2010):

$$x_{0} = (X_{i} - X_{0} )/\delta X,$$
(3)

X 0 and X i represent the coded and real values of the independent variables, respectively. However, X 0 and δX are the values of X i at the central point and step change, respectively.

Table 2 Coded and real values of the operational parameters for Box–Behnken statistical design
Full size table

A second-order polynomial response surface model for the fitting of experimental data can be described using Eq. (4):

$$\gamma = b_{\text{o}} + \sum\nolimits_{i = 1}^{n} {b_{i} x_{i} } + \sum\nolimits_{i = 1}^{n} {(b_{ii} x_{ii}^{{^{2} }} )} + \sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {b_{ij} x_{i} x_{j} } } ,$$
(4)

where γ is the predicted response (removal efficiency %), x i denotes independent variables, b o is a constant offset term and b i are linear coefficients. Furthermore, b ii and b ij are the regression coefficients for the quadratic and interaction effects, respectively (Amenaghawon et al. 2013; Khajeh 2009; Shakeel et al. 2014). The values of these coefficients (b i , b ii and b ij ) are determined by Eq. (5):

$$b = (X^{T} X)_{ - 1} X^{T} Y,$$
(5)

where b is a vector of coefficients, X is the design matrix for coded levels of variables and Y represents the vector of response (Khayet et al. 2011; Poroch-Seritan et al. 2011).

Results and discussion

Characterization of the adsorbent material

FT-IR analysis was used to evaluate the role of functional groups situated on the surface of adsorbent in the adsorption process. The FTIR spectrum of the local clay (Fig. 1) showed several absorption bands, the peak at 3606 cm−1 attributed to the vibration band of structural hydroxyl groups. Broad bands at 3397 and 1636 cm−1 show the axial deformation and angular deformation of the hydration water (Iliescu et al. 2014). The peaks centred at 797 and 1442 cm−1 correspond to Si–O in SiO2 and CO3, stretching vibration, respectively, whereas the bands at 508 cm−1 represent the Si–O–Si vibrations of quartz. The vibration bands at 692 and 909 cm−1 for the local clay are assigned to the deformations of Si–O–Al and Al–OH, respectively.

Fig. 1
figure 1

FT-IR spectra of the local clay

Full size image

Electrokinetic experiments were carried out to provide information about the charge state of the particles. Figure 2 shows that the clay bears a negative net charge within the shear plane above pH 2. This is typical of many clay particles and explained by the permanent negative charge caused by isomorphous substitution.

Fig. 2
figure 2

Electrophoretic mobility of the local clay as a function of pH in MilliQ-water. pH adjustment was done using NaOH and HCl solutions

Full size image

SEM-EDX analyses yielded the results summarized in Table 3. The values given represent the average and standard deviation of five distinct measurement points. Sodium was found in only one spot.

Table 3 Atom percent analysis results, data collected at five distinct spots, standard deviation*10
Full size table

The main components typical of the local clay are Si and Al. Minor components like K, Mg, Fe or Ti are also expected for natural clay samples. The carbon contribution could be from accessory minerals (Calcite) or adventitious carbon. The iron present gives the clay its greenish color.

The morphological structure of the adsorbent was characterized by scanning electron microscopy. The SEM images of the local clay taken at different magnifications in Fig. 3a–e show that it is a heterogeneous material consisting of particles of irregular shapes having considerable layers.

Fig. 3
figure 3

SEM images of the local clay

Full size image

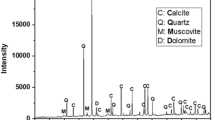
The clay is well crystallized as can be shown its X-Rays powder diffractogram depicted on Fig. 4. The mineral generally consists of SiO2 plus minor additional components, mainly represented by the band around 2T = 2θ which we could not assign. The main oxides based on elemental analysis of the local clay composition (Table 4) are silica (63%), aluminum (≈15%) and iron (≈5%). These oxides are important as possible participants in dye-adsorption. The clay also includes significant quantities of unburned carbon (≈8%) representing further adsorption sites for dyes (Ahmaruzzaman 2010). Moreover, it was found to contain oxides of exchangeable cations such as Ca, Mg, Na and K with varying percentage. The results agree well with the EDX data given in Table 3.

Fig. 4
figure 4

XRD patterns of local clay

Full size image
Table 4 Chemical composition of VT
Full size table

The specific surface area and total pore volume of the local clay were determined as 38.08 m2 g−1 and 8.75 cm3 g−1, respectively, a bit larger than that of Graphene Oxide (32 m2 g−1) (Mittal et al. 2010). We included in Table 5 features of the present clay compared to those of some other adsorbents reported in the literature.

Figure 5 shows a full gas adsorption and desorption curve (N2). The hysteresis for p/p 0 > ×0.5 supports the presence of some porosity. The phenomena might result from pore shape irregularity. In fact, if one can relate this to water–sol interactions, the hysteresis effect can be attributed to four main causes: (1) geometric nonuniformity of individual pores, which results from the “ink Bottle” effect, (2) different spacial connectivity between the pores during drying and wetting processes, (3) variation in liquid–solid contact angle, and (4) air entrapment (Marshall et al. 1996) (Table 5).

Fig. 5
figure 5

Complete N2 adsorption and desorption curve for local clay

Full size image
Table 5 Comparison of BET surface area of local clay with other adsorbents
Full size table

The particle size, shape and distribution have been reported to be a very important property in determining the industrial uses of clays (Murray 2000). For this purpose, Beckman Coulter LS Particle Size Analyzer was used to determine the granulometric parameters d 10, d 50 and d 90 of the local clay. The cumulative and differential particle size distributions of this material are presented in Fig. 6 resulting in 2.10, 25.47 and 110.10 μm, respectively, for d 10, d 50 and d 90.

Fig. 6
figure 6

Particle size distribution of the local clay

Full size image

Response surface modeling

We have adopted the Box–Behnken design for investigating the individual and mutual effects of the factors screened concerning the adsorption of CV dye by the local clay from aqueous solution. The (%) removal of CV in this study was observed in the range of 27.42–95.30% (Table 6). This result can be compared to values obtained on other absorbents: Biomass of Nostoc linckia (39, 3–72%) (Sharma et al. 2011), Biomass of Calotropis procera (57, 76–80.48%) (Hazrat and Shah 2008). Overall, local clay can be considered as an efficient adsorbent for treating colored waters.

Table 6 Box–Behnken design for three independent variables with the observed and predicted responses of CV dye removal (%)
Full size table

Regression between the dependent variable (dye removal) and the corresponding coded values of the three different independent variables yields the following quadratic model:

$$\gamma \% = 73.29 - 20.63x_{1} + 14.83x_{2} + 10.17x_{3} + 4.67x_{1}^{2} - 8.26x_{2}^{2} - 9.92x_{3}^{2} + 8.35x_{1} x_{2} + 6.86x_{1} x_{3} + 2.09x_{2} x_{3} .$$
(6)

The analysis of variance (ANOVA) and F test are considered to be essential to examine the significance and adequacy of the second-order regression models (Khataee et al. 2011). The results of such analysis are summarized in Table 7. The model was found to be highly significant, as evident from the Fisher’s F test (F model = 281.53) with a very low probability value (P model < 0.0001). Furthermore, the comparison of the critical F value (F 0.05, 9, 9 = 3.179) with the calculated F value (F model = 281.53) showed a critical F value of less than the calculated F value, suggesting that most of the variation in the response can be explained by the quadratic model equation (Liu et al. 2004; Sen and Swaminathan 2004; Yetilmezsoy et al. 2009).

Table 7 Analysis of variance (ANOVA) for the adsorption of CV onto VT
Full size table

Figure 7a shows a good agreement between the predicted and observed values with a high coefficient of determination (R 2 = 0.997). It reveals that most of the data variation (99.7%) was explained by the regression model and that the model explains 97.8% of the variations in dye removal. Besides, the adjusted R 2 corrects the value of R 2 for sample size and the number of terms in the applied model (Khataee and Dehghan 2011; Khataee et al. 2012). In our case, the value of adjusted multiple correlation coefficient (adj. R 2 = 0.993) was found to be smaller than R 2. This suggests that the observed results are in reasonable agreement with the predicted results (Khataee et al. 2011; Soltani et al. 2014).

Fig. 7
figure 7

The plot of predicted versus experimental dye removal of CV (a) and residual (b)

Full size image

Furthermore, the obtained P value implies importance of each factor for removal efficiency of CV dye. Therefore, it can be seen from Table 8 that all model terms such as linear (X 1, X 2 and X 3) quadratic (x 21 , X 22 and X 23 ) and interactive effects (X 1 X 2, X 2 X 3 and X 1 X 3) are statistically significant.

Table 8 Estimated regression coefficient and corresponding F and P values obtained during Box–Behnken design for the adsorption of CV onto VT
Full size table

The statistical results (Table 8) further suggested that the relative order of operational parameters for adsorption of CV can be dye concentration (F(X 1) = 1185.98) >adsorbent dosage (F(X 2) = 613.39) >contact time (F(X 3) = 288.04), making the initial dye concentration the parameter exhibiting the most significant effect on dye removal through the adsorption process. On the other hand, random dispersal of the residuals can be seen in the plots of residuals versus predicted dye removal (%), Fig. 7b, implying good agreement between predicted and experimental decolorization efficiency.

The three-dimensional (3D) response surface plots and corresponding contour plots provide information on the impact of interactions terms and their effects on the dependent variable (Adinarayana and Ellaiah 2002; Wu et al. 2009). Figure 8 illustrates the response surface for mutual effects relating to dye concentration and adsorbent dosage. As depicted, increasing adsorbent dosage along with decreasing dye concentration led to increasing dye removal (%) when the contact time was constant at 30 min. Dye removal increased with increase in adsorbent dosage and the two showed statistically significant an identical relationship (Eq. 6) as could be expected. Increased dye removal with increasing amount of adsorbent is related to the larger reactive surface area and more active sites for the adsorption of adsorbate molecules (Kousha et al. 2012). Similar behavior has been reported by Mark Daniel et al. (2013) in the case of the adsorption of Eriochrome Black T (EBT) onto activated carbon prepared from waste rice hulls.

Fig. 8
figure 8

The response surface plot (a) and corresponding counter plot (b) for the interactive effect of dye concentration and adsorbent dosage

Full size image

Contact time plays an important role in the treatment processes of colored waters (Kousha et al. 2012). Figure 9 depicts the surface plot of removal of CV as a function of contact´s time and adsorbent dosage. Removal of CV is enhanced as contact time and adsorbent dosage increase. The combined effect of adsorbent dosage and contact time were positive and statistically significant as also revealed by the contour lines and Table 7. Maximum dye removal (>83%) was observed at constant dye concentration 100 mg L−1.

Fig. 9
figure 9

The response surface plot (a) and corresponding counter plot (b) for the interactive effect of adsorbent dosage and contact time

Full size image

Figure 10 depicts the combination of the two parameters: contact´s time and initial dye concentration, with the adsorbent dosage at central point considered to be 2 g L−1. It can be seen that the lowest percent removal is optimized in higher concentrations of dye 150 mg L−1. Dye removal of CV was increased with decreasing dye concentration from 50 to 150 mg L−1. This can be explained by saturation of adsorptive sites on the surface of the clay (Deniz and Saygideger 2010). Similarly, Feng et al. (2011) observed that dye removal of methylene blue by their adsorbent increases when decreasing the dye concentration from 450 to 100 mg L−1. Statistically, the interactive effect of dye concentration and contact time is positive and significant, according to contour lines and multiple regression (Eq. 6).

Fig. 10
figure 10

The response surface plot (a) and corresponding counter plot (b) for the interactive effect of dye concentration and contact time

Full size image

Conclusion

The performance of local clay for removal of CV dye from aqueous solution was modeled and optimized using response surface methodology by the Box–Behnken model. Experiments were made as a function of three important operational parameters including initial dye concentration, adsorbent dose and contact time. The statistical analysis results suggested that a second-order polynomial regression model could properly interpret the experimental data with a coefficient of determination R 2 value 0.997 and Fisher F value of 281.53. The first-order main effects of the independent variables (X 1, X 2 and X 3) were relatively more significant than their respective quadratic effects (X 21 , X 22 and X 23 ). The graphical response surface plot demonstrated that the initial dye concentration is the most significant component of the quadratic model for the present adsorbent-adsorbate system. Optimization conditions for the maximum removal efficiency of CV were obtained by applying a desirability function in RSM. The level of the three variables, initial dye concentration 125 mg L−1, adsorbent dose 2.5 g L−1, contact time 43 min, were found to be optimum for maximum CV removal. The corresponding removal efficiency in optimum conditions was found to be 81.62% for the above conditions of operational parameters. Practically, the (%) removal is in the range of 27.42–95.30%. Conclusively, the Box–Behnken model is suitable to optimize the experiments for dye removal by adsorption, where the local clay would be an efficient adsorbent for treating CV solution. Particle Size Analyzer was used to determine the granulometric parameters d 10, d 50 and d 90 of the local clay. The cumulative and differential particle size distributions of this material are 2.10, 25.47 and 110.10 μm, respectively, for d 10, d 50 and d 90.