Cosmic topology, underdetermination, and spatial infinity

Abstract

It is well-known that the global structure of every space-time model for relativistic cosmology is observationally underdetermined. In order to alleviate the severity of this underdetermination, it has been proposed that we adopt the Cosmological Principle because the Principle restricts our attention to a distinguished class of space-time models (spatially homogeneous and isotropic models). I argue that, even assuming the Cosmological Principle, the topology of space remains observationally underdetermined. Nonetheless, I argue that we can muster reasons to prefer various topological properties over others. In particular, I favor the adoption of multiply connected universe models on grounds of (i) simplicity, (ii) Machian considerations, and (iii) explanatory power. We are able to appeal to such grounds because multiply connected topologies open up the possibility of finite universe models (consistent with our best data), which in turn avoid thorny issues concerning the postulation of an actually infinite universe.

1 Introduction

Relativistic cosmology faces an underdetermination problem: there are many cosmological models compatible with our best observational data.¹ At first blush, this may be quite unsurprising given that cosmology deals with physics at extremely large scales. A rather more surprising fact is that, even under strong hypotheses about the global structure of space (the Cosmological Principle), this underdetermination persists. In particular, we are still unable to ascertain the global topology of space.

Is there any way to break this topological underdetermination? I survey recent work in observational cosmology that has aimed to provide definitive answers on this front and conclude that the prospects for empirically determining spatial topology are not promising (Section 6). However, a familiar point in the philosophical literature is that underdetermination by data may not be so worrisome (Laudan, 1990; Earman, 1993). This is because one may be able to find significant epistemic reasons for preferring one theory (or model) over another.

As such, I argue that we can muster epistemic reasons to prefer various topologies over others. In particular, I argue that we should prefer cosmological models with multiply connected topologies on grounds of simplicity, Machian considerations, and explanatory power (Sections 7 and 8, respectively). We are able to ascribe such features to multiply connected models because they generate spatially finite universe models, which in turn avoid extremely thorny issues concerning the postulation of an actually infinite universe. Thus, though a purely observational underdetermination remains, we can avoid a more robust underdetermination, viz., one in which all epistemic reasons underdetermine the choice of topology.

Aside from these conceptual claims, I also have the less ambitious aim of bringing some recent cosmological research, viz., the study of cosmic topology, to a broader audience. I believe that cosmic topology is deserving of philosophical attention, and I hope my discussion makes clear why this is so.

2 Motivating our investigation

Here I would like to illustrate, in very general terms, the potential philosophical dividends of our investigation. In short, my goal in this paper is to make precise a particularly vexing form of underdetermination and to evaluate our prospects for dealing with it. I thereby pave the way for a cogent discussion of broader philosophical issues, especially the epistemic status of “global” spatial properties and the consequences of underdetermination for scientific realism.²

First, it is important to note that the kind of underdetermination we will consider is rather distinctive.³ Much of the philosophical literature on underdetermination focuses on the case of the underdetermination of a theory by data (either the data we currently have or all possible data). However, in the case of relativistic cosmology, we have already selected a particular physical theory, general relativity. Even with this theory fixed, our best observational data does not pick out a unique model of the theory, and, as we will see, this almost always appears to be the case.

Second, underdetermination is canonically construed as an issue for scientific realism.⁴ Following the excellent discussion in Earman (1993), this is because underdetermination generates a tension between two components of scientific realism: semantic realism, which says that we should literally construe the claims of our scientific theories, and epistemic realism, which says that observational evidence suffices to provide good reasons to believe what a theory literally says about the world. Consider two distinct scientific theories $T_{1}$ and $T_{2}$. These are distinct because, literally construed, they say different (and perhaps even incompatible) things about the world. However, if $T_{1}$ and $T_{2}$ are underdetermined by observational data, they say the same things about observables. But then we cannot maintain epistemic realism, since any piece of observable evidence for $T_{1}$ will also count as evidence for $T_{2}$.

Earman continues by classifying two categories of response to this predicament. Responses falling under the first category “retreat” by weakening either semantic or epistemic realism. If we weaken semantic realism, we can say that two ostensibly distinct, though empirically equivalent, theories $T_{1}$ and $T_{2}$ are really the same theory in disguise. That is, $T_{1}$ and $T_{2}$ are superficially different ways of describing the same factual states. If we weaken epistemic realism, we can say that both theories are “empirically adequate,” but that what they say about unobservables need not be true. Responses falling under the second category “defend” by denying that there are interesting examples of empirically equivalent theories and/or questioning that the existence of such theories actually undermines our ability to empirically choose between them.

This classification provides us with a helpful way of situating the following discussion. The topological underdetermination under investigation provides an interesting example of empirically equivalent (or observationally indistinguishable) models of a scientific theory. I say “interesting” because it is an instance of underdetermination that arises in scientific practice involving neither the postulation of cooked-up skeptical scenarios nor anemic Quinean examples concerning the intersubstitution of terms. Indeed, this topological underdetermination has long been recognized as such an example: Earman himself briefly discusses it following earlier work by Glymour and Malament.⁵ I think, however, there is more to say about the case than has been recognized.

First, there have been impressive developments in observational cosmology relating to the topological structure of space since the case was first discussed. This, on its own, merits further investigation. Second, the topological properties I consider are intimately connected to the infinitude (resp. finitude) of the spatial universe. This fact is very important and has not been exploited in the philosophical literature. I use it to argue that we have good epistemic grounds to prefer particular topologies (and hence particular cosmological models) over others. This connection also helps to clarify the responses to underdetermination sketched by Earman. In particular, it quite definitively eliminates the possibility of the first “retreat” because, roughly, a universe model with topology $\tau _{1}$ will be spatially infinite and, under suitable hypotheses, will thereby contain infinitely much matter. On the other hand, a universe model with topology $\tau _{2}$ will be spatially finite and will thereby contain only finitely much matter. Clearly, then, these two models will be radically different from an ontological perspective. They cannot be the same model “in disguise.”

Furthermore, there do not appear to be any good defensive responses to the topological underdetermination. It seems difficult to deny that this is an interesting case of empirical equivalence and, as we shall see, it seems very unlikely that empirical evidence will ever serve to provide reasons for believing one model is true rather than another. This indicates that the second “retreat” is perhaps the most attractive philosophical option remaining. However, this retreat need not take the form of, say, van Fraassen’s constructive empiricism, nor even Earman’s “gentle empiricism” (Earman, 1993, 35). In particular, I believe that a suitably modified Kantian view, following Michael Friedman’s work on the relativized a priori, is perhaps our best option. The exact details of this proposal must wait for another time.

In any case, I hope it is now clear that the topological underdetermination to be discussed is of wide-ranging philosophical significance. Let us then turn to making its contours more precise.

3 Fundamentals of spacetime structure

I begin by rehearsing some of the basic details of relativistic cosmology. Speaking circumspectly, we can say that cosmology is the study of the large scale structure of the universe. By “universe,” we might mean either everything that exists in the physical sense or that which comprises everything that exists physically. Both of these notions are useful and can be understood rigorously. Namely, we can think of the universe as the spacetime in which everything is contained together with the distribution of matter and energy in this spacetime. I am primarily interested in the former, though details about the latter will become relevant later.

Given that gravitation is the dominant force at large scales, we must consider our best extant theory of gravity: Einstein’s theory of general relativity. Thus, ultimately, cosmology is concerned with finding models of general relativity that are consistent with our data concerning the spacetime structure and energy distribution of the universe at large scales.⁶ In terms of the standard formalism, we say that a model of general relativity⁷ is a triple $(\mathcal {M}, g_{ab}, T_{ab})$, where $\mathcal {M}$ is a connected four-dimensional real smooth manifold without boundary of variable curvature,⁸$g_{ab}$ is a metric tensor (field) of type (0,2),⁹ and $T_{ab}$ is the energy-momentum tensor (field). The metric $g_{ab}$ characterizes the geometric properties, e.g., curvature and geodesics, of $\mathcal {M}$ at a given point, $p \in \mathcal {M}$. Finally, $T_{ab}$ characterizes the energy distribution of $\mathcal {M}$ and is described by suitable equations of state relating its components, again at a particular point, $p \in \mathcal {M}$.

We must now understand how these elements of models of general relativity interact. In particular, we seek a field equation relating the metric $g_{ab}$, characterizing geometry, and the energy-momentum tensor $T_{ab}$, characterizing energy distribution. This relationship is expressed as:

$$\begin{aligned} R_{ab}-\frac{1}{2}Rg_{ab}\, {+ \Lambda g_{ab}}=\kappa _{0}T_{ab}, \end{aligned}$$

(3.1)

which is now known as Einstein’s Equation.¹⁰ More precisely, the left-hand side characterizes the curvature of $\mathcal {M}$ at a point p given the specification of $g_{ab}$.

Technically, Equation 3.1 expresses ten non-linear partial differential equations of immense mathematical complexity. In order to obtain “exact solutions” that can be studied both mathematically and physically, one must lay down plausible simplifying assumptions that accord with observational data. I turn to these assumptions in a moment; however, before complicating matters, we can already express a general sort of cosmological underdetermination.

4 Underdetermination and the cosmological principle

In providing a model of general relativity, we provide a particular kind of ambient manifold structure and a metric and energy distribution solving Einstein’s Equation. How do we go about doing so? Certainly, we wish such a model to match our observations at a given point in spacetime. The hope is that our observational data can narrow down a unique model (or unique class of models).

It should be noted that by “unique” we really mean “unique up to isometry.” That is, we say that two models $(\mathcal {M}, g_{ab}, T_{ab})$, $(\mathcal {M}^{\prime }, g^{\prime }_{ab}, T^{\prime }_{ab})$ are isometric if there is a diffeomorphism¹¹$\varphi : \mathcal {M} \rightarrow \mathcal {M}^{\prime }$ such that $\varphi _{*}(g_{ab})=g^{\prime }_{ab}$.¹² This easily descends to the local case of open sets on the manifolds. The crucial point is that two isometric manifolds (resp. open sets of manifolds) do not constitute distinct physical possibilities because they cannot be distinguished using observations. This is so because the isometry preserves the metric structure across manifolds and thus preserves solutions to Einstein’s Equation.

We can now state the conditions required for isolating a unique model/class of models for general relativity. According to general relativity, anything we observe at a spacetime point p (for some $p \in \mathcal {M}$ in some model) must be causally related to p; however, signals cannot propagate faster than the speed of light. Thus, the events with which we can have causal contact sit either on or within a particular region of spacetime bounded by the paths of light that arrive at p. We denote this region by $J^{-}(p)$ and call it the past lightcone at p or simply the observable universe at p.¹³ For reasons of mathematical convenience, we follow Manchak (2009) and work primarily with the interior of $J^{-}(p)$, denoted by $I^{-}(p)$.¹⁴ Let us write $I^{-}(p_{0})$ for our observable universe.

Thus, if we are to pick out a unique class of models compatible with our observations at $p_{0}$,¹⁵ we require:

Condition 4.1

Up to isometries, there is a unique model $(\mathcal {M}, g_{ab}, T_{ab})$ that has a point $q \in \mathcal {M}$ such that $I^{-}(p_{0})$ and $I^{-}(q)$ are isometric.¹⁶

Unfortunately, it is well known that the uniqueness condition cannot be satisfied. There are various ways to see this, but perhaps the slickest is by appeal to recent results by Manchak.¹⁷ In particular, Manchak shows that virtually any model $(\mathcal {M}, g_{ab})$ (subject to a few reasonable constraints¹⁸) will be observationally indistinguishable¹⁹ from another model $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ that is not isometric to $(\mathcal {M}, g_{ab})$. Consequently, an ideal observer at $p\in \mathcal {M}$ who knows all metrical data about $I^{-}(p)$ can know very little about the global structure of their spacetime, since there will be many spacetimes possessing markedly different global properties that contain regions isometric to $I^{-}(p)$.

Thus, it would appear we are in very bad shape when we try to provide a unique model of general relativity that matches our observational data. And thus we are confronted with a severe underdetermination of models by data. What’s worse, by the above results of Manchak, this almost always appears to be the case. However, the severity of this underdetermination can be greatly reduced by restricting the models of general relativity considered. Appeal is usually made to the following:

Principle 4.2

(Cosmological Principle) On average, at large scales, the universe is spatially homogeneous and isotropic around every point.²⁰

Thus expressed, the Cosmological Principle is essentially an a priori prescription imposed on all possible models of general relativity. Once imposed, it has the effect of restricting our attention to a particularly well-behaved class of models, the Friedmann-Lemaître-Robertson-Walker (FLRW) models. There are many intricate arguments, drawing on a wide variety of considerations (some empirical), for the Cosmological Principle.²¹ These arguments are of great philosophical interest, for the Cosmological Principle, if acceptable, would significantly reduce the underdetermination. I will, however, simply assume the Cosmological Principle here. The reason for this is that, even under the strong hypothesis of the Cosmological Principle, the model underdetermination persists when we consider topological properties of our spacetime manifold $\mathcal {M}$. Indeed, somewhat astonishingly, for each metric solution of Einstein’s Equation internal to the class of FLRW models, there may be infinitely many compatible topologies. I will now discuss these models and the relevant topological properties in greater detail.

5 FLRW models and topology

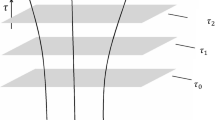
The Cosmological Principle amounts to the imposition of spatial²² symmetry constraints. In particular, spatial homogeneity means, roughly, that every point in space at a given time “looks the same,” and spatial isotropy means that there are no preferred spatial directions. We represent the spacetime manifold, $\mathcal {M}$, as the product of a three dimensional spatial manifold and a temporal continuum, i.e., $\mathcal {M}:=\mathcal {M}_{3} \times {{\,\mathrm{\mathbb R}\,}}$. The spatial manifold can then be thought of as a “stack” of surfaces, each indexed by a particular cosmic time. The metrical structure of these FLRW models is particularly tractable, and, crucially for our discussion, the spatial sections have constant curvature with values $k= \pm 1, 0$, respectively.

Once more, the essential point is that, even with all these simplifications, we have said nothing about the topology of $\mathcal {M}_{3}$. Until quite recently, it has been assumed in the cosmological literature that the topology of $\mathcal {M}_{3}$ is simply connected. Informally, in a simply connected space, any loop through a point $x_{0}$ can be continuously deformed into any other closed loop through $x_{0}$.²³ However, neither observational data nor the FLRW models themselves dictate such a choice. It is entirely possible that the spatial sections are multiply connected, i.e., there is a “hole” (or many “holes”) that renders such a continuous deformation impossible.²⁴ For instance, a hypertorus²⁵ is multiply connected, while Euclidean space is simply connected.²⁶

Let us consider the possible simply connected models (SCMs). There will then be three candidates for the spatial section $\mathcal {M}_{3}$: the 3-sphere ($\mathbb {S}^{3}$), Euclidean 3-space (${{\,\mathrm{\mathbb R}\,}}^{3}$), and the 3-hyperboloid ($\mathbb {H}^{3}$). These correspond, respectively, to the three possibilities for constant curvature, viz., $k>0$, $k=0$, and $k<0$, and will be equipped with their respective classical geometries, viz., spherical, Euclidean, and hyperbolic. The possible SCMs along with their central mathematical properties are summarized in Table 1. When we deal with SCMs, note that the determinant of the spatial extent of the universe is the curvature of $\mathcal {M}_{3}$ alone.

Table 1 Mathematical Properties of SCMs

Let us now turn to multiply connected models (MCMs). The effect of a multiply connected topology for $\mathcal {M}_{3}$ is equivalent to considering a particular simply connected space (the universal covering space, denoted by $\widetilde{\mathcal {M}}_{3}$) tiled with particular polyhedra (fundamental polyhedra).²⁷ This tiling of the covering space is achieved by the action of a group $\Gamma$ on the covering space. Since we only deal with constant curvature models, we need only consider three universal covering spaces $\mathbb {S}^{3}, {{\,\mathrm{\mathbb R}\,}}^{3}, \mathbb {H}^{3}$ under the action of such a $\Gamma$. In order to get a multiply connected topology, we form a quotient manifold $\widetilde{\mathcal {M}}_{3}/\Gamma$, which is gotten by identifying points equivalent under the action of $\Gamma$ on the covering space $\widetilde{\mathcal {M}}_{3}$, where $\widetilde{\mathcal {M}}_{3}$ which is one of the three constant curvature SCMs. For example, ${{\,\mathrm{\mathbb R}\,}}^{3}/\Gamma \cong T^{3}$, the hypertorus, where $\Gamma$ consists of discrete translations identifying faces of the fundamental polyhedra (parallelepipeds) tiling ${{\,\mathrm{\mathbb R}\,}}^{3}$.

To summarize, we can re-write Table 1 with the choice of multiply connected topology. See Table 2.

This will not affect the geometry of each case, so, e.g., geometrically ${{\,\mathrm{\mathbb R}\,}}^{3}$ and the hypertorus $T^{3}$ are the same, and so will be observationally indistinguishable, provided the topology cannot be empirically determined. However, the topology change will affect the possible size of the universe, e.g., $T^{3}$ is finite, while ${{\,\mathrm{\mathbb R}\,}}^{3}$ is infinite.

Thus, we see that the effect of considering MCMs (in addition to SCMs) produces an explosion of new FLRW models of general relativity consistent with our best data.²⁸ Once more, this is the case even under the very strong assumption of the Cosmological Principle. Is there, then, any means of breaking the underdetermination of models? In recent years, there has been active research in the field of cosmic topology whereby cosmologists have attempted to empirically ascertain the global topology of space. I will now briefly review the most promising aspects of this research.

Table 2 Mathematical Properties of MCMs

6 Recent investigations in cosmic topology

Crucially, considering MCMs provides many new options for finite universe models.²⁹ In contrast, when we consider Table 1, the only finite option is given by the spherical, positive curvature case; however, this does not accord with our best data about the “near flatness” of the universe.³⁰ Various Euclidean MCMs, on the other hand, do appear to be consistent with these observations.³¹ The hope is, then, that we live in one of a distinguished class of the MCMs called Small Universes.³² Essentially, if this were so, the observable universe at any point p, $I^{-}(p)$, exhausts the actual spatial universe at p (where p is an arbitrary point in the spacetime manifold of any Small Universe model). That is, $I^{-}(p)$ contains all of $\mathcal {M}_{3}$. Both the spatial topology and size of the universe would be, in principle, empirically determinable, and so the topological underdetermination of models would be broken.

The basic idea underlying all recent attempts at determining the spatial topology of the universe is the following. If we live in a “small” MCM, then space can be represented via a universal covering manifold tiled by a fundamental domain. That is, an MCM is topologically equivalent to an SCM subject to particular periodic boundary conditions. The immediate physical effect of this periodicity is that sources of radiation will produce multiple images (because there will be multiple shortest paths along which light travels) occurring at particular points in a lattice, which is in turn consistent with a particular multiply connected topology. Figure 1 represents the universal covering space of the two-torus, $T^{2}$, i.e., a two-dimensional MCM.³³

Fig. 1

Universal Covering Space of $T^{2}$

The shaded region is the fundamental polygon, subject to periodic boundary conditions, S is a source of radiation, O is an observer. S propagates light to O along the “intuitive” geodesic (ray SO). However, this light would also scatter in infinitely many directions, “wrap around” the universe, and generate the appearance of infinitely many “apparent” or “ghost” images $\left\{ S_{1}, \ldots , S_{8}, \ldots \right\}$. All recent work has attempted to exploit a higher-dimensional version of this representation in some way. Figure 2 represents the case of $T^{3}$ viewed from a “corner” of real space with Earth closest to us.³⁴

Thus, let us turn to the most promising technique on offer for empirically determining the topology of space, commonly called “circles in the sky.”³⁵

Fig. 2

Universal Covering Space of $T^{3}$

6.1 Circles in the sky

According to the standard Big Bang theory, the universe is generated from an extremely hot, dense energetic plasma. This plasma is entirely opaque to light because photons will scatter off of hot charged particles. As the universe expands, the plasma cools sufficiently to permit radiation to pass through it. This ancient scattered radiation has by now cooled to be observable in the microwave spectrum and is called Cosmic Microwave Background (CMB). This radiation carries coveted data about the very beginning of the universe and, as it turns out, might be useful in detecting non-trivial cosmic topologies. If we imagine the initial state of the universe as a “point,” then CMB would have scattered in every direction from this point to reach us now, forming a “sphere” of radiation processing from the center of the sphere. This sphere of radiation is called the “surface of last scattering” (SLS).

Fig. 3

Circles in the Sky for $T^{2}$

How can the SLS be used to detect cosmic topology? If the universe has a multiply connected topology, then, as we have seen, it can be represented as its covering space tiled by fundamental polyhedra. Each “copy” of the observer in each polyhedron (that is, each analogous point in each fundamental polyhedron) will come associated with its own SLS; provided that the diameter of the fundamental polyhedron does not exceed that of the diameter of the SLS, then the SLS spheres will intersect, generating a “circle” of CMB radiation. Since there will be an observer and their “copy,” these intersections will come in pairs viewed in different directions. The presence of pairs of circles in CMB radiation will then be a sign of non-trivial topology. See Fig. 3 for the circles method applied to the 2-torus with fundamental polygon a square.³⁶

One very important advantage of “circles in the sky” over other techniques on offer is that it will apply to all MCMs, and the model can be directly reconstructed from the radius, number, and distribution of the circles. However, there are still observational issues involved in the circles method. In particular, the velocity and density of the SLS can become obscured, thus affecting the accurate detection of circles (e.g., the gravitational pull of coalescing galaxies could be a potential obstruction). On the whole, however, this appears to be a very powerful method for detecting cosmic topology.

6.2 Evaluation of empirical techniques

Have traces of “small” MCMs been found by the above method? Unfortunately, the results thus far are not promising, though they have been fiercely debated. It seems that many of the favored “small” MCMs have been ruled out: no matching circles have been found for hypertori nor for other important models. However, the results employed to rule out these models do not apply to all MCMs; in particular Aurich et al. (2004) has claimed to have found some evidence for a multiply connected hyperbolic model called the Picard Horn. The Picard Horn is particularly interesting because, though one direction of its fundamental polyhedron is infinite, the space as a whole has finite volume.

Thus far, we have considered the “best case scenario” for empirically determining cosmic topology, i.e., Small Universes. It is worth asking whether we can lift this assumption and consider cases in which the universe is finite and exceeds the observational horizon, but only by a “negligible” amount. Astonishingly, there has been some recent work that has shown it would be possible to distinguish an infinite universe from a finite, though technically non-observable, universe for particular multiply connected topologies. This means that, even if we did not live in a small universe, but rather a “relatively” small universe, both the topology and size of space could be empirically detectable (Fabre et al., 2013).

Despite these developments, there has been no especially compelling evidence for a multiply connected spatial topology. As I have tried to indicate in this section, this does not, of course, rule out the possibility. It does seem, though, that the set of models both (i) consistent with our best evidence and (ii) either small or “relatively” small is shrinking.

6.3 The topological underdetermination thesis

Before turning to further complications, let us summarize our findings and make explicit our underdetermination thesis. We have taken the Cosmological Principle on board as an assumption about the global structure of space. An immediate consequence of this assumption is that we must restrict our attention to the FLRW models of general relativity. We then saw that, internal to this highly symmetric class of models, we might distinguish between simply connected models (SCMs) and multiply connected models (MCMs). The existence of a tractable (because spatially finite and particularly small) subset of MCMs, the so-called Small Universes, suggested that we might empirically investigate spatial topology. However, given the lack of empirical evidence that we live in a Small Universe, combined with the many sensitivities and difficulties of the empirical techniques used, we postulate:³⁷

Thesis 6.1

(Topological Underdetermination Thesis) For any simply connected FLRW model $(\mathcal {M}, g_{ab})$, there exists a multiply connected FLRW model $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ that is not isometric to $(\mathcal {M}, g_{ab})$ such that $(\mathcal {M}, g_{ab})$ and $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ are observationally indistinguishable.³⁸

For example, let the spatial section $\mathcal {M}_{3}$ of $\mathcal {M}$ be ${{\,\mathrm{\mathbb R}\,}}^{3}$. This is simply connected and infinite. Let the spatial section $\mathcal {M}^{\prime }_{3}$ of $\mathcal {M}^{\prime }$ be $T^{3}$, the hypertorus. This is multiply connected and finite. These two models share the exact same kinematics and dynamics and so, given the observational difficulties noted above, are observationally indistinguishable.³⁹

In sum, despite some impressive advances in the study of cosmic topology, I believe that we are still faced with a severe underdetermination of spatial topology by observational data. And this is so even under the assumption of the Cosmological Principle.

6.4 MCMs, Manchak’s theorem, and isotropy

Finally, let us consider whether our topological underdetermination would vanish if strong evidence for a particular MCM emerged, e.g., matching circles of CMB indicating a particular multiply connected topology. The first issue to examine is the nature of the “empirical evidence” that could be adduced for MCMs. Obviously, the meaning of “empirical evidence” here must be quite generous in that sense that we infer a particular topology from its “signature” in the CMB. Second, there are a number of worrisome restrictions on popular techniques for determining topology. For example, it has emerged that some techniques have complicated dependencies upon the geometry (viz., group of isometries) of a given manifold; thus, a “negative” result may not in fact be such given that some possible models cannot be detected by the technique. Finally, even the preferred circles method is susceptible to many observational difficulties.

But let’s proceed in the spirit of optimism. If it becomes clear that a particular MCM is the best explanation for a given set of observational data, have we dispensed with the topological underdetermination? Initially, it would appear that the answer is no. This is because the models we are considering are causally well-behaved, and so Manchak’s theorem on observationally indistinguishable spacetimes still applies. It is not worth rehearsing the exact details of his proof here, but the basic point is that we can form spacetimes by cutting and pasting together subsets of other spacetimes (Manchak, 2009, 55). Assume that we have been convinced that we live in a Small Universe, i.e., such that $I^{-}(p_{0})$, our observable past from point $p_{0}$, contains all of space. It can then be shown that $I^{-}(p_{0})$ can be attached to various other regions in the future of $p_{0}$, thereby generating a spacetime that is globally different from the assumed Small Universe model.

The significance of this result for Small Universes is somewhat unclear and ultimately depends upon a complicated set of considerations. For instance, one might already be concerned about the body of assumptions laid down internal to which the above observational data would be considered evidence. The fact that, even after all these assumptions have been stated, there is still the possibility that strong empirical evidence for an MCM would not break our underdetermination could incline one to a skepticism about knowledge of spatial topology. On the other hand, one might be relatively unconcerned about the assumptions in question and further contend that Manchak’s result, in the face of evidence for an MCM, lacks bite. Namely, the cutting and pasting technique generates a spacetime that has a decidedly “cooked-up” look, and this is a much less reasonable explanation for the evidence in question.

Following the discussion in Cinti and Fano (2021), we can make our concerns about Manchak’s result more precise.⁴⁰ Their primary contention is that Manchak’s construction is not physically reasonable and thus the implications of his result for physical cosmology are overstated. That is, Manchak has only shown that “[...] the mathematics of General Relativity allows for certain structures, not that these structures are physically relevant, and thus relevant to our actual attempts at modelling the universe” (Cinti & Fano, 2021, 104). In particular, they argue that the spacetime $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ produced by Manchak is “pathological” because it possesses features that lack a physical explanation in terms of some physical process. This is because $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$, in virtue of its production by the cutting and pasting construction, has singularities in the form of deleted boundaries of 3-spheres.⁴¹ However, no physical explanation is provided for the existence of these singularities, e.g., gravitational collapse of a body. In fact, by Manchak’s own lights, no such physical explanation could ever be produced because such a physical process would violate another property of $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ stated in his theorem, i.e., that $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ and $(\mathcal {M}, g_{ab})$ are locally isometric.⁴² Clearly, if there were such a physical process responsible for the singularities in $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$, there would be no corresponding process in $(\mathcal {M}, g_{ab})$, thereby violating the local isometry of $(\mathcal {M}, g_{ab})$ and $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$. The authors continue by isolating a particular formal condition, local b-boundary inextendibility, which they argue characterizes a physically reasonable spacetime, and show that Manchak’s $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ fails to satisfy this condition.⁴³

I find the discussion of Cinti and Fano (2021) quite compelling. As such, we should conclude that, if strong evidence supporting a particular MCM emerges, e.g., matching circles in the CMB, then we should accept this evidence on its face rather than appeal to Manchak’s skeptical scenario. However, as I have noted, there are many reasons to doubt that such evidence is forthcoming. Furthermore, Cinti and Fano (2021) bolsters the aims of the present paper insofar as it indicates the importance of topological underdetermination.⁴⁴ This is because I have not merely provided “possible geometric objects which might be studied in General Relativity,” but rather have shown that there are spacetimes that are both physically reasonable and observationally indistinguishable. Thus, I have produced a case of “genuine” underdetermination in physical cosmology.

I would like to close this section by making our statement of the Cosmological Principle more precise. This is because all MCMs⁴⁵ violate the global isotropy of space, i.e., there will be “principal” or “preferred” directions in space reflecting the identification of faces of the fundamental polyhedron under the action of group $\Gamma$. However, these preferred directions will only be present beyond a particular length scale, and so “local isotropy everywhere” still holds in MCMs.⁴⁶ This local isotropy, along with spatial homogeneity, ensures consistency with our best data. Thus, we have identified precisely the assumption that would rule out MCMs, viz., the imposition of global isotropy. Providing an argument for this claim would be difficult indeed, and typically something weaker is assumed (Ellis, 2007; Beisbart, 2009). In any case, given the difficulty in justifying global isotropy and the potential benefits imparted by MCMs (see below), our Cosmological Principle should take the form of “spatial homogeneity + local isotropy everywhere."

I will now argue that, though an observational underdetermination of spatial topology seems unavoidable, there are nonetheless reasons to prefer MCMs thereby avoiding a robust underdetermination. I consider reasons that exploit the relationship between multiply connected topologies and finite universe models compatible with our best data.

7 Issues concerning the infinite

It is a truism that many questions arise when we countenance an infinite universe. Can the actual infinite be instantiated in the physical world? What are some philosophical implications of an actually infinite universe? I cannot, of course, do justice to these questions here; rather, I wish to illuminate how they relate to our topological underdetermination. The logical flow of the argument is as follows: by Thesis 6.1, the topology of space is observationally underdetermined. However, in virtue of the relationship between the infinitude-finitude of the spatial universe and spatial topology, MCMs enjoy theoretical virtues that SCMs do not. In particular, here I will argue that MCMs possess a particular kind of simplicity because there are spatially finite MCMs consistent with our best data.^47,48 In virtue of this finitude (and hence simplicity), particular MCMs avoid difficulties latent in cosmological models that postulate the existence of an actually infinite universe.⁴⁹ Thus, we have good reasons for preferring MCMs, thereby providing a means for dispensing with a robust topological underdetermination, viz., an underdetermination in which all epistemic reasons underdetermine the choice of topology.

Before turning to my main discussion concerning the relationship between spatial topology and the size of the universe, I must clear some ground. In recent years, various authors have claimed that it is a direct consequence of inflationary theory that the universe is actually infinite, and this claim has been used to support substantive philosophical conclusions.⁵⁰ However, the claim that inflationary theory implies an actually infinite universe relies upon a feature of the idealized mathematical model of inflation that is difficult to support on either physical or philosophical grounds (Ellis & Stoeger, 2009). In virtue of this fact, along with the various ontological and physical scruples one might have about inflationary theory, we should resist arguments from inflationary theory for the infinitude of the universe.

Consequently, it would appear that the topology of the spatial sections will be the primary determinant of the size of the spatial universe (constrained by the value of curvature k). As such, our choice of topology is immediately related to questions of the cogency of an actually infinite universe. Thus, if there are serious philosophical and physical problems with an infinite universe, this should motivate the choice of a topology that avoids ascribing an actually infinite size to space.

7.1 Actual infinities in cosmology

I would like to begin by considering Brundit and Ellis (1979) in which a particularly strange consequence of an actually infinite universe is dramatized. Although the conclusion drawn by the paper is not my primary objection to positing actually infinite universe models, the discussion serves as a useful starting point for a few reasons. First, it is one of the few articles that emphasizes the difficulties latent in the use of infinite universe models.⁵¹ Second, the authors realize the possible theoretical dividends of positing a multiply connected topology, though they dispense with this option much too quickly.

Brundrit and Ellis argue that, provided we live in an FLRW universe that is nearly flat ($k \approx 0$), it is highly probable that⁵²

[...] there exist infinitely many worlds on which there are ‘duplicate’ populations (i.e., populations identical in number and genetic structure) to that on our own world (Brundit & Ellis, 1979, 37).

Furthermore,

It soon becomes clear that it is difficult to provide a precise argument against there existing elsewhere in the Universe an identical person reading the identical article on ‘Life in the Infinite Universe’...for, with an infinite family of histories to look at, it is difficult to provide an incontrovertible argument as to why a particular history should occur only once. [...] There is no need to postulate some hypothetical statistical ensemble—it exists in the infinite universe! (Brundit & Ellis, 1979, 38)

This is a remarkable and somewhat dizzying conclusion. Nonetheless, though the reduplication is odd and unsettling, its strangeness need not incline us to posit one model over another. However, I will show that there are a number of theoretical disadvantages that come with the postulation of an actually infinite spatial universe and the attendant possibility of infinite populations and infinitely much matter.

Before detailing these disadvantages, I would like to examine the options available to us for dispensing with them. First, further developments in quantum theory or in our understanding of how “very small” variations of parameters may affect population formation might be of use. A survey of these possibilities would, however, merit an extensive independent discussion. Brundrit and Ellis themselves propose that one could: (i) deny the application of probability theory to scientific models; (ii) deny the Cosmological Principle; (iii) assume that the spatial sections have multiply connected topologies. Option (i) seems incredibly restrictive and should be set aside. Option (ii), though a licit possibility, is a standing assumption of this paper and is employed in much cosmological research. Finally, option (iii), as we have seen, provides particular universe models in which the spatial sections are finite, thereby disrupting the reduplication argument and the postulation of infinite quantities. It is set aside in Brundit and Ellis (1979) because

[T]here appears to be no philosophical reason—based on the uniformity principle, or any other principle—why the space-sections should not have their ‘natural’ [simply connected] topologies (40).

I would like to press on this reasoning. Indeed, it seems that this is a case in which appeal to the classical theoretical virtue of simplicity may be of use. Of course, the notion of “simplicity” is extremely slippery and multi-faceted (though no more so than that of “naturality”). As such, let us try to be a little more precise.⁵³ Two distinct sorts of simplicity are commonly acknowledged: ontological and syntactic. Ontological simplicity is given by the number and complexity of entities postulated by a theory, while syntactic simplicity is given by the number and complexity of the laws of the theory.⁵⁴ Following Quine, these two aspects are often thought to be inversely related: an expansion in ontology usually results in a contraction in laws, while an expansion of hypotheses/laws usually results in a contraction of entities. However, as we shall see, this relationship is highly non-obvious and difficult to evaluate.

Another distinction is also required: when considering ontological simplicity, one can have either a qualitative species or a quantitative species. In the former, the number of kinds (however one construes a “kind”) is minimized, while in the latter the number of entities simpliciter is minimized. I am here concerned with the quantitative ontological simplicity of MCMs. Let me now elucidate the theoretical advantages afforded by this simplicity.⁵⁵

First, one might think that the postulation of actual infinities is unscientific in the sense that an actually infinite quantity is untestable.⁵⁶ So, if one thinks that science should deal with statements that are at least in principle testable, actual infinities, e.g., actually infinite spatial sections, actually infinite populations of organisms, should be avoided. Put differently: our best science should not postulate entities that are, by their nature, beyond the scope of science itself. Furthermore, it would seem that, since actual infinities are unobservable and untestable, any scientific theory that makes use of actual infinities (in an essential way) is committed to some form of mathematical platonism.⁵⁷ Platonism, as is well-known, involves a host of philosophically questionable theses, most notably that abstract entities are assumed to exist independently of any means of human definition, construction, or observation. Furthermore, on its face, platonism is at odds with scientific realism, especially its epistemic component (see Section 2). I think it preferable to avoid these issues whenever possible.

Second, if one finds this response too hard-nosed, there are a few specific consequences of an infinite universe that would require explanation: most obviously, the generation of infinitely much space at the time of the Big Bang. Furthermore, since we are working under the auspices of FLRW models, we will also have to explain the generation of infinitely much matter (due to the homogeneity of these models).⁵⁸ Of course, one might then ask why the existence of infinitely much matter and space is more in need of explanation than the existence of finitely much. I would then be inclined to fall back on the first consideration: the existence of finitely much matter and space is in principle testable, while this is not true in the infinite case.

Finally, considered in the context of extant theories of quantum gravity (and more broadly grand unification programmes in physics), the existence of actually infinite space is problematic. In particular, if one subscribes to string theory, then one deals with additional “small” compactified dimensions. Without any reason for thinking that our three “ordinary” spatial dimensions are distinguished in some way, it seems much more reasonable that our “ordinary” dimensions are also compact, as given by a finite MCM.⁵⁹

7.1.1 Objection: syntactic complexity

However, following the Quinean insight above, the use of an MCM will require the postulation of additional laws and hypotheses, thus increasing the syntactic complexity of our cosmological model. Starting from a strictly mathematical perspective, an MCM is rather more complicated than an SCM: we must pass to the universal covering space, consider which polyhedra tile the space, etc. This requires the use of various theorems linking SCMs, MCMs, and their geometries. Even from a physical perspective, an MCM could generate a further complexity: the need to reinterpret particular observations of radiation as “ghost images.” Namely, in an SCM, there is (generally) a 1-1 correspondence between an object in space and an event in spacetime, e.g., a star produces observable radiation.⁶⁰ In an MCM this correspondence fails; there are, rather, multiple spacetime events associated with a single entity in space. However, unlike the complexities generated by positing an infinite universe, e.g., why infinitely much space and matter, we have a good handle on the mathematics and physics underlying the added syntactic complexity. Thus, I am inclined to think the ontological simplicity gained outweighs the additional syntactic complexity of MCMs.

Finally, adopting an MCM would raise the question: why that particular multiply connected topology (with its particular fundamental polyhedron of particular size)? However, if we no longer expect spatial topology to be empirically determinable, I do not see why we should expect our best cosmology to answer this question. Indeed, no explanation is provided for the preference of a simply connected topology, and so this issue is a wash.⁶¹

In sum, I propose that we have good reason to prefer MCMs over SCMs in virtue of their simplicity (of the kind indicated) and the advantages this simplicity affords our physical theorizing. Thus, though we have a topological underdetermination by observational data, we can still avoid a robust underdetermination by attending to theoretical virtues. More explicitly, consider Thesis 6.1 once more. Let $(\mathcal {M}, g_{ab})$ be an FLRW model with simply connected topology and let $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ be an FLRW model with multiply connected topology such that $(\mathcal {M}, g_{ab})$ and $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ are observationally indistinguishable. I have argued that we should select $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ as our preferred model in virtue of the fact that such a model could have finite spatial sections consistent with our best data. In virtue of this spatial finitude, $(\mathcal {M}^{\prime }, g^{\prime }_{ab})$ enjoys the sort of simplicity discussed above and avoids the difficulties presented by models that employ actually infinite spatial sections. Thus, we have good theoretical reasons to prefer MCMs, and thus we need not resign ourselves to a robust topological underdetermination.

7.2 Einstein and Mach’s principle

Another consideration that might dispense with a robust topological underdetermination involves Mach’s Principle. In its original formulation, Mach’s Principle was developed as a challenge to a substantivalist conception of space.⁶² Mach’s central idea was that the inertia of a given body derives from its relation to the “fixed stars” and matter throughout the universe rather than its relation to the “absolute space” postulated by Newton. In more modern terminology, we might say that Mach’s Principle is the claim that all inertial properties of an object are entirely determined by the distribution of mass-energy throughout space.⁶³ I now turn to an argument originating from Einstein that relates Mach’s Principle to the extent of space (and thus to its topology).

In The Meaning of Relativity, Einstein provides three arguments “against the conception of a space-infinite” (Einstein, 1950, 107). The first argument is of the same sort I have offered above: namely, from the standpoint of general relativity, the postulation of a finite universe is “very much simpler” (though he does not give any indication of what this is supposed to mean) than the infinite case. He does not mention topological considerations, but, as we have seen, multiply connected topologies appear to be the only possible way that the universe could turn out finite.⁶⁴ In any case, I take this argument to be further grist for my mill.

Let us now turn to his second argument from Mach’s Principle:

But in the second place the theory of relativity makes it appear probable that Mach was on the right road in his thought that inertia depends upon the mutual interaction of matter. For we will show in the following that, according to our equations, inert masses do act upon each other in the sense of the relativity of inertia, even if only very feebly. What is to be expected along the lines of Mach’s thought? (Einstein, 1950, 100)

Einstein then proceeds to list three consequences of Mach’s Principle and demonstrates that, internal to the formalism of general relativity, these consequences are borne out.⁶⁵ Given his derivation of these consequences, he concludes that our interpretation of general relativity should validate Mach’s Principle. He continues,

The idea that Mach expressed, that inertia depends upon the mutual action of bodies, is contained, to a first approximation, in the equations of the theory of relativity; [...] But this idea of Mach’s corresponds only to a finite universe (Einstein, 1950, 107-108).

The point here is one that we have already seen. Einstein’s Equation does not specify solutions that can be studied from a physical standpoint. Further assumptions, usually expressed as “boundary conditions at infinity,” are required. However, these boundary conditions simply replace the role played by Newtonian absolute space. This is because, when boundary conditions are specified, it is no longer simply the presence of mass-energy that determines the geometry of spacetime, and hence mass-energy no longer determines the inertial properties of any given object. For instance, general relativity appears to validate the idea that, in a universe without matter, there is nonetheless an “absolute” flat (Minkowskian) spacetime structure, as dictated by the imposition of natural Minkowskian boundary conditions.

In response to these concerns, Einstein suggested a radical way to deal with the problem: simply postulate a finite universe model, thereby obviating the need for boundary conditions at infinity that contradict Mach’s Principle. Concisely, we might say, “[I]t is likely that the requirement of Mach’s Principle is identical with the requirement of a finite universe” (Wheeler, 1964, 306). Thus, since our best experimental evidence indicates that the universe is not sufficiently dense to force finiteness, the presence of a multiply connected spatial topology would be the only way to produce a finite universe model. And so, if one is convinced by (some version of) Mach’s principle, one should be compelled to select a multiply connected spatial topology.⁶⁶

The reasons for preferring a multiply connected topology that proceed from Machian considerations are not obviously of the same sort adduced above. It is, however, possible to think in these terms, since we get both an ontological and syntactic simplicity. The former is clear; the latter occurs because, instead of having to specify boundary conditions for each possible solution of Einstein’s Equation, we add a single stipulation (multiply connected topology) to the mathematics of our physical theory that eliminates the need for boundary conditions. Nonetheless, as in both Mach’s case and Einstein’s case, the reason for eliminating boundary conditions is not a desire for simplicity, but rather a preference for a highly plausible metaphysics of space and characterization of inertial properties (as well as the purely formal consequences derived by Einstein).

8 The explanatory power of MCMs

To close, I would like to consider the explanatory power of positing a finite MCM. I examine two sorts of recent cosmological data for which a finite MCM would appear to be a good (or even the best available) explanation.

Following the common practice of cosmologists, we have assumed the Cosmological Principle and thereby have considered FLRW models. However, as we have noted, the assumption of the Cosmological Principle is an a priori prescription imposed on all possible models of general relativity. To what extent is the spatial isotropy and homogeneity⁶⁷ assumed in the Principle observationally justified? It turns out that spatial isotropy about our location is strongly supported by observational evidence, consisting of both the observation of luminous sources and the CMB radiation discussed in Section 6. As George Ellis has noted,

Considered on a large enough angular scale, astronomical observations are very nearly isotropic about us, both as regards source observations and background radiation; indeed the latter is spectacularly isotropic, better than one part in $10^{4}$ after a dipole anisotropy, understood as resulting from our motion relative to the rest frame of the universe, has been removed. Because this applies to all observations (in particular, there are not major observed matter concentrations in some other universe region), this establishes that in the observable region of the universe, to high accuracy both the space-time structure and the matter distribution are isotropic about us (Ellis, 2007, 1225).

Clearly, this isotropy (and homogeneity) cannot be explained by the commonly used FLRW models, as such models assume these properties. It would be desirable, however, to have some sort of explanation for them. It is commonly postulated that spatial homogeneity results from an inflationary period in the early universe (Guth, 1981) and (Gibbons et al., 1983); however, it has been shown that inflation would only produce the observed homogeneity if the pre-inflationary universe were already sufficiently homogeneous (Luminet & Lachiéze-Rey, 1995). Thus, inflationary theory only pushes the problem back. As usual, a fully developed theory of quantum cosmology and quantum universe formation would deal with this issue, but no such theory is yet operative.

However, the postulation of a finite MCM seems a reasonable and readily available explanation of the phenomenon of homogeneity.⁶⁸ More precisely, a finite MCM with especially small volume would produce the special initial conditions necessary for a “chaotic” (in the sense of inhomogeneous) early universe to transition to a homogeneous one. The details here are extremely complex and depend upon the dynamics of the precise models considered, but the basic point is that, at a sufficiently young age, a small MCM is causally connected. In virtue of causal connectedness at an early age, the universe can homogenize before the the scattering of the CMB. Thus, the isotropy of the CMB reflects the homogeneity of the early universe, which is itself explained and made possible by a causal process occurring in a sufficiently small MCM.⁶⁹ It is worth noting that more calculations have to be done before MCMs can confidently discharge this explanatory role. Nonetheless, they serve as one of the best available explanations of the homogeneity and isotropy of space.

I would like to close with what I take to be the strongest explanatory function of finite MCMs. As we have noted, the key data for observational cosmologists are surveys of the CMB.⁷⁰ It was hoped that CMB data could decisively reveal the spatial topology of the universe via such methods as circles in the sky; however, we have adopted a position of justified pessimism towards this endeavor. Nonetheless, particular measurements of the CMB may provide reasons to posit a finite MCM. I will now show why this is so.

Of particular interest are temperature fluctuations (anisotropies) in the CMB as these can yield information about the physical conditions of the early universe. (It is worth noting that these anisotropies are, on the whole, minuscule, so they in no way impugn the large scale isotropy of the CMB; see Ellis’s quote above.) It is believed that the early universe was crossed by acoustic waves soon after the Big Bang and, in turn, these waves left imprints on the universe ($\approx$ 380,000 years after the Big Bang) as density fluctuations in the primordial plasma. The anisotropies detected in the CMB reflect these density fluctuations, which can be mathematically constructed from vibrational modes of space.⁷¹

Suppressing the mathematical details of the spherical harmonics, the crucial quantity for measuring anisotropies is the full-sky two-point correlation function of temperature fluctuation $\delta T(\hat{\textbf{n}})$, observed for our sky in the direction of unit vector $\hat{\textbf{n}}$. This function is written as

$$\begin{aligned} C^{\text {obs}}(\theta ):= \langle \delta T(\hat{\textbf{n}}), \delta T(\hat{\textbf{n}}^{\prime }) \rangle \end{aligned}$$

(8.1)

where $\hat{\textbf{n}} \cdot \hat{\textbf{n}}^{\prime } = \cos \theta$. The brackets denote averaging over directions $\hat{\textbf{n}}$ and $\hat{\textbf{n}}^{\prime }$ separated by angle $\theta$. Using CMB datasets, values of $C^{\text {obs}}(\theta )$ have been computed for $0 \le \theta \le 180$ (degrees). However, there are a number of “intriguing discrepancies” between the observational values of $C^{\text {obs}}(\theta )$ and predictions of the “standard” cosmological model, which is flat, infinite, and Euclidean with simply connected topology (this model is often written as $\Lambda$CDM). In particular, for angular scales over 60 degrees, there is very little correlation between the CMB observations and $\Lambda$CDM simulations. As has been noted in very recent studies, especially Aurich et al. (2021), this discrepancy finds “a natural explanation in cosmic topology.” That is, a finite MCM would make good sense of this discrepancy because the spatial sections are finite and so space is not large enough to support the longer wavelengths produced by larger angles. Indeed, as of yet, there appears to be no other explanation of this phenomenon of “angular power spectrum suppression.”⁷²

It is important to note, however, that this does not impugn our underdetermination thesis (Thesis 6.1). The observational constraints and extreme sensitivities of even our best methods (circles in the sky, statistical techniques for anisotropies) warrant a healthy does of skepticism. Nonetheless, especially given the discussion of anisotropies, finite MCMs remain a live possibility and, furthermore, provide the best explanation for our current data.

9 Conclusion

I have argued that, even assuming the Cosmological Principle, the topology of space is underdetermined by observational evidence. Indeed, even if we had strong evidence for a particular spatial topology, it would still be a live option that the underdetermination persists (recall, however, the concerns about Manchak’s theorem). Nonetheless, I believe that we have good reasons to prefer multiply connected topologies; in particular, I argued that we should prefer MCMs on grounds of simplicity, Machian considerations, and explanatory power. Thus, we have good reasons to think that a robust underdetermination is avoidable.

I think that, in our case, we should retain a good deal of epistemic modesty. Problems concerning global spacetime structure are famously intractable,⁷³ and so our conclusions about them should be tentative. My hope is that further scientific developments, especially in quantum gravity, will help to shed light on the topology of space and the attendant philosophical issues here discussed. Let me conclude, then, by discussing (extremely coarsely) some exciting results in quantum gravity that involve non-trivial topologies.

Over the past 50 or so years, a central area of research in quantum gravity has been that of black hole thermodynamics. In the early 1970s, it was argued that black holes described by classical general relativity, when taken in isolation, behave like ordinary thermal systems.⁷⁴ This idea was significantly strengthened by the discovery of Hawking radiation, i.e., the discovery that black holes emit thermal radiation when quantum field theory is applied to a black hole spacetime (Hawking, 1975). Since then, the standard story has been that “the laws of black hole thermodynamics [...] are the ordinary laws of thermodynamics applied to a black hole” (Wald, 1994, 174).⁷⁵ In particular, given that familiar thermodynamical systems all admit a statistical-mechanical description, so too should black holes. Crucially, then, it makes sense to study the entropy of a black hole.⁷⁶

We are now in a position to introduce “the” information loss paradox in black hole thermodynamics. Following Wallace (2020) and Cinti and Sanchioni (2021), we distinguish two main versions: (1) the Black Hole Information Paradox (BHIP) and (2) the Page Time Paradox (PTP).⁷⁷ I begin with BHIP as this is the most commonly discussed.

The discovery of Hawking radiation implies that the mass (and thus surface area) of a black hole could decrease due to the emission of thermal radiation. Furthermore, given sufficiently much time and a sufficiently small black hole, the black hole in question could “evaporate.” This leads to some troubling consequences first detailed in Hawking (1976). Here Hawking argued that the evolution of a closed system containing an evaporating black hole will fail to be unitary. However, failure of unitarity is troubling, first, because black hole evaporation is a quantum process and every quantum process is unitary. Second, as the title of Hawking (1976) suggests, failure of unitarity indicates the breakdown of (various senses of) predictability in physics, e.g., we start with “a system in a pure initial state [...] for which there is some non-degenerate observable whose value may be predicted with certainty,” but end up with a system in a mixed state for which there is no such observable (Belot et al., 1999, 190). Thus, we can conclude that “information” about the universe is lost in the course of black hole evaporation.⁷⁸

There has been a great deal of controversy over BHIP, e.g., whether it is, in fact, a paradox or simply an argument for the failure of unitarity in black hole evaporation. On the other hand, as stressed in Wallace (2020), PTP appears to be a genuine paradox and is deemed a serious concern by many high-energy physicists; it is also the relevant version of the paradox for our purposes (see below). In essence, it concerns the inconsistency between Hawking’s computation of black hole entropy in semi-classical gravity and the predictions of black hole statistical mechanics.⁷⁹ PTP is typically discussed in the context of string theory and many proposed solutions appeal to the AdS-CFT (anti de Sitter-conformal field theory) duality. I cannot touch upon the details here, but the point is that many physicists, by virtue of this duality, have been convinced that black hole evaporation is in fact unitary.⁸⁰ The question thus becomes: how is this possible?

This brings us to some recent proposed solutions and their connections to non-trivial topologies.⁸¹ A useful tool for measuring information loss is the fine-grained or von Neumann entropy (for Hawking radiation). In the process of black hole evaporation, this entropy initially increases, given the entanglement of Hawking radiation with particles in the black hole interior. However, if evaporation is unitary, as many now believe, the entropy must fall to zero, following the so-called Page curve. Unfortunately, Hawking’s calculation of entropy in Hawking (1975) predicts that the entropy will monotonically increase. The task then becomes: how can Hawking’s calculation be corrected in order to agree with unitarity? In Almheiri et al. (2020), the authors propose that “the first principles computation of the fine-grained entropy using the gravitational path integral receives large corrections from non-perturbative effects” (ibid., 2). In particular, the computation of the gravitational path integral using (n copies of) the original black hole agrees with Hawking’s initial calculation of the von Neumann entropy. However, the authors incorporate “replica wormholes,” additional gravity configurations that come to dominate the gravitational path integral and ultimately lead to an entropy that agrees with unitarity. Importantly for our purposes, these replica wormholes are gravity configurations with non-trivial topology. Thus, the results of Almheiri et al. (2020) (and related work), suggest that the presence of a non-trivial topology could be indicated by emerging empirical evidence, e.g., computations of black hole entropy, in new theoretical frameworks. In any case, it should be clear that the topological properties with which we have been concerned sit at a nexus of ongoing work in physics that promises to yield rich food for philosophical thought.