Ultradiscrete hard-spring equation and its phase plane analysis

Abstract

Ultradiscretization enables us to construct a piecewise linear equation which approximates a given subtraction-free difference equation. Recently proposed “ultradiscretization with parity variables” (pUD) can treat an equation with subtraction. However, its solution may have an infinite number of branches under some specific conditions. In this paper, solutions of pUD for the hard-spring equation is investigated. The pUD equation is reinterpreted as the mapping which maps a set on the phase plane to another one, and the behaviour of the solutions are analyzed through approximative transition diagrams.As a result, the infinite branches are translated into a few finite branches and allowed easier understanding.

1 Introduction

Ultradiscretization [1] is a limiting procedure which constructs a cellular automaton [2] from a given difference equation. Its research arose in the field of integrable systems. It has been reported in many papers that integrable structure in the original difference equation inherits to the resulting CA. Even for some non-integrable systems, it is illustrated that ultradiscretization works well in the sense that a mathematical structure survives through this procedure [3, 4]. Hence, ultradiscretization is expected to be a new and useful tool to analyze nonlinear systems.

However, ultradiscretization has a serious restriction called ‘negative difficulty’. That is, the difference equation must be subtraction-free. In addition, its solution should be positive definite. Some methods have been attempted for overcoming this difficulty [5, 6]. Ultradiscretization with parity variables (pUD) [7] is one of the such methods. We explain its detail later. This procedure can treat a difference equation with subtraction or non-definite signed solutions. Instead of this advantage, a solution may lose uniqueness under a specific condition. Actually, the solution $X_n$ for the specific n is given by the inequality such as $X_n \le A$ (referred to as an indeterminate solution). This ambiguity is translated as branches to an infinite number of values, or as an ‘infinite multi-valued mapping’. The procedure of pUD was applied to some q-Painlevé equations and its special solutions were discussed [8,9,10]. For verifying whether pUD is also useful to study other nonlinear systems, the pUD analogue of the hard-spring equation was investigated in [11]. In this previous research, the solutions for wide range of initial values, and the solutions were classified into some types. For example, the exactly four-periodic solutions, the four-periodic solutions after some time steps, the indeterminate solutions summarizable by bounded diagrams, and the indeterminate solutions with unbounded diagrams are found. These are important results but we need some kind of broad perspective for understanding global structure of these solutions.

In this paper, we again investigate the same pUD equation studied in [11]. We actively utilize the phase plane analysis [12], and reinterpret the pUD equation as the mapping which maps a set on the phase plane to another one. This “approximative” viewpoint enables us to draw the transition diagrams which have such sets as its nodes, in which we see the infinite multi-valued mapping as a finite multi-valued mapping. By these diagram, the structure of indeterminate solution is visually understood. This paper is organized as follows. We review the construction of the pUD equation in Sect. 2. In Sect. 3 following the method developed in [13], we summarize its time evolution to some tables and illustrate it by some figures of the phase plane. Then, we draw the transition diagrams and analyze the structure of the solution orbits. Finally, we give concluding remarks in Sect. 4.

2 Ultradiscrete hard-spring equation and phase plane

2.1 Ultradiscretization with parity variables

We explain the procedure of pUD. We consider an explicit difference equation which does not include subtraction. We write its dependent variable as $x_n$. The subtraction-free setting implies that $x_n$ takes positive values only. After transformation upon introduction of a parameter $\varepsilon >0$,

$$\begin{aligned} x_n=\textrm{e}^{\frac{X_n}{\varepsilon }}, \varepsilon >0, \end{aligned}$$

(1)

we apply $\varepsilon \log$ to both sides of the equation and take the limit $\varepsilon \rightarrow +0$. Then, multiplication, division and addition for the original variable $x_n$ are replaced by addition, subtraction and the max operation among new dependent variables $X_n$, respectively. Here, the formula

$$\begin{aligned} \lim _{\varepsilon \rightarrow +0}\varepsilon \log \left( \textrm{e}^{\frac{A}{\varepsilon }}+\textrm{e}^{\frac{B}{\varepsilon }}\right)&=\max (A,\ B) \end{aligned}$$

(2)

is used. This is the procedure of ultradiscretization. However, this procedure cannot handle an explicit difference equation with subtraction, whose solution may take negative values. For the sake of solving this issue, ultradiscretization with parity variables (pUD) was proposed.

In the procedure of pUD, we introduce the sign variable $\xi _n$ and the “amplitude” variable $X_n$ for the dependent variable $x_n$ by

$$\begin{aligned} \xi _n:=&\dfrac{x_n}{|x_n|},\ \textrm{e}^{\frac{X_n}{\varepsilon }}:=|x_n|. \end{aligned}$$

(3)

Moreover, using the function s,

$$\begin{aligned} s(\xi ):=&{\left\{ \begin{array}{ll} 1&{}(\xi =+1)\\ 0&{}(\xi =-1), \end{array}\right. } \end{aligned}$$

(4)

we perform the following transformation:

$$\begin{aligned} x_n=\xi _n\textrm{e}^{\frac{X_n}{\varepsilon }}=\bigl (&s(\xi _n)-s(-\xi _n)\bigr )\textrm{e}^{\frac{X_n}{\varepsilon }}. \end{aligned}$$

(5)

After transposing the negative terms to the other side of the equation, we apply $\varepsilon \log$ to both sides and take the limit $\varepsilon \rightarrow +0$. Here, we use the formula

$$\begin{aligned} S(\xi ):=&{\left\{ \begin{array}{ll} 0&{}(\xi =+1)\\ -\infty &{}(\xi =-1) \end{array}\right. } \end{aligned}$$

(6)

$$\begin{aligned} \lim _{\varepsilon \rightarrow +0}\varepsilon \log&\left( s(\xi )\textrm{e}^{\frac{A}{\varepsilon }}+\textrm{e}^{\frac{B}{\varepsilon }}\right) =\max (S(\xi )+A,\ B). \end{aligned}$$

(7)

This is the procedure of pUD. Subtraction is handled by transposed terms. As well as the original ultradiscretization, multiplication, division and addition are replaced by addition, subtraction and the max operation, respectively. The sign is included in the resulting expression as the terms $S(\pm \xi _n)$.

In general, the obtained equation by pUD takes an implicit form, $\max (\dots ) = \max (\dots )$. Therefore, its solution may lose uniqueness. This indefiniteness makes the solution space richer, but may do analysis complicated.

2.2 Ultradiscretization with parity variables of the hard-spring equation

The hard-spring equation is given by

$$\begin{aligned} \frac{{\text {d}}^2x}{{\text {d}}t^2}+kx+lx^3=0, \end{aligned}$$

(8)

where $x=x(t)$ and $k,l>0$ are constants. This equation is an integrable system since it has the conserved quantity

$$\begin{aligned} H(t)=\frac{1}{2}\left( \frac{{\text {d}}x}{{\text {d}}t}\right) ^2+\frac{1}{2}kx^2+\frac{1}{2}lx^4=0. \end{aligned}$$

(9)

We give an integrable discretization of (8) given in [14]. We write $t=n\delta$, $x(t)=x_n$. Our discrete equation is written as

$$\begin{aligned}{} & {} x_{n+1}-2x_n+x_{n-1}+2c_1\delta ^2\left( x_{n+1}+x_{n-1}\right) +4c_2\delta ^2 x_n\nonumber \\{} & {} +2c_3\delta ^2 x_n^2\left( x_{n+1}+x_{n-1}\right) =0. \end{aligned}$$

(10)

Since (10) has a conserved quantity

$$\begin{aligned} H_{n} = \frac{{x_{n}}^2 -2x_{n}x_{n-1} + {x_{n-1}}^2}{2\delta ^2} + c_{1}({x_{n}}^{2} + {x_{n-1}}^2) + 2c_{2}x_{n}x_{n-1} + c_{3}{x_{n}}^{2} {x_{n-1}}^2 ,\qquad \end{aligned}$$

(11)

this equation is an integrable equation. For the purpose of pUD, we introduce the sign variable $\xi _n$, the amplitude variable $X_n$ for $x_n$ by (3) and new parameters by

$$\begin{aligned} \textrm{e}^{\frac{\alpha _i}{\varepsilon }}:=c_i\ (i=1, 2, 3),{} & {} \textrm{e}^{\frac{\Delta }{\varepsilon }}:=\delta . \end{aligned}$$

(12)

We substitute (5) into (10), we obtain

$$\begin{aligned}&\bigl (s(\xi _{n+1})-s(-\xi _{n+1})\bigr )\textrm{e}^{\frac{X_{n+1}}{\varepsilon }} -2\bigl (s(\xi _n)-s(-\xi _n)\bigr )\textrm{e}^{\frac{X_n}{\varepsilon }} +\bigl (s(\xi _{n-1})-s(-\xi _{n-1})\bigr )\textrm{e}^{\frac{X_{n-1}}{\varepsilon }}\nonumber \\&\quad +2\textrm{e}^{\frac{\alpha _1+2\Delta }{\varepsilon }}\left\{ \bigl (s(\xi _{n+1})-s(-\xi _{n+1})\bigr )\textrm{e}^{\frac{X_{n+1}}{\varepsilon }} +\bigl (s(\xi _{n-1})-s(-\xi _{n-1})\bigr )\textrm{e}^{\frac{X_{n-1}}{\varepsilon }}\right\} \nonumber \\&\quad +4\textrm{e}^{\frac{\alpha _2+2\Delta }{\varepsilon }}2\bigl (s(\xi _n)-s(-\xi _n)\bigr )\textrm{e}^{\frac{X_n}{\varepsilon }}\nonumber \\&\quad +2\textrm{e}^{\frac{\alpha _3+2\Delta +2X_n}{\varepsilon }}\left\{ \bigl (s(\xi _{n+1})-s(-\xi _{n+1})\bigr )\textrm{e}^{\frac{X_{n+1}}{\varepsilon }} +\bigl (s(\xi _{n-1})-s(-\xi _{n-1})\bigr )\textrm{e}^{\frac{X_{n-1}}{\varepsilon }}\right\} =0.\nonumber \\ \end{aligned}$$

(13)

For simplicity of notation, we write $X_{n+1}$, $X_n$, $X_{n-1}$ as $X_+$, X, $X_-$, respectively. Moreover, we put $\alpha _i+2\Delta = \widehat{\alpha _i}$. If we transfer the negative terms and take the limit $\varepsilon \rightarrow +0$, we have

$$\begin{aligned}&\max \bigl [S(\xi _{n+1})+X_+,\ S(\xi _{n+1})+\widehat{\alpha _1}+X_+,\ S(\xi _{n+1})+\widehat{\alpha _3}+2X+X_+,\nonumber \\&S(-\xi _n)+X,\ S(\xi _n)+\widehat{\alpha _2}+X,\nonumber \\&\bigl .S(\xi _{n-1})+X_-,\ S(\xi _{n-1})+\widehat{\alpha _1}+X_-, S(\xi _{n-1})+\widehat{\alpha _3}+2X+X_-\bigr ]\nonumber \\&=\max \bigl [S(-\xi _{n+1})+X_+,\ S(-\xi _{n+1})+\widehat{\alpha _1}+X_+,\ S(-\xi _{n+1})+\widehat{\alpha _3}+2X+X_+,\nonumber \\&S(\xi _n)+X,\ S(-\xi _n)+\widehat{\alpha _2}+X,\nonumber \\&\bigl .S(-\xi _{n-1})+X_-,\ S(-\xi _{n-1})+\widehat{\alpha _1}+X_-,\ S(-\xi _{n-1})+\widehat{\alpha _3}+2X+X_-\bigr ]. \end{aligned}$$

(14)

By considering the four types of combinations of signs $\xi _{n+1}$, $\xi _n$, $\xi _{n-1}$, (14) is written into some equations without the function S. We use, for simplicity, the notations

$$\begin{aligned}&a=\max \bigl [0,\ \widehat{\alpha _1},\ \widehat{\alpha _3}+2X\bigr ] \end{aligned}$$

(15)

$$\begin{aligned}&b=\max \bigl [\widehat{\alpha _2}+X,\ X_-,\ \widehat{\alpha _1}+X_-,\ \widehat{\alpha _3}+2X+X_-\bigr ] \end{aligned}$$

(16)

$$\begin{aligned}&=\max \bigl [\widehat{\alpha _2}+X,\ X_-+a\bigr ]\nonumber \\&d=X \end{aligned}$$

(17)

$$\begin{aligned}&b'=\widehat{\alpha _2}+X \end{aligned}$$

(18)

$$\begin{aligned}&d'=\max \bigl [X,\ X_-,\ \widehat{\alpha _1}+X_-,\ \widehat{\alpha _3}+2X+X_-\bigr ]\nonumber \\&=\max \bigl [X,\ X_-+a\bigr ]. \end{aligned}$$

(19)

The rewritten equations are as follows. For $\xi _{n+1}=\xi _n=\xi _{n-1}$,

$$\begin{aligned} \max \bigl [&X_++a,\ b\bigr ]=\max \bigl [d\bigr ], \end{aligned}$$

(20)

for $-\xi _{n+1}=\xi _n=\xi _{n-1}$,

$$\begin{aligned} \max \bigl [&b\bigr ]=\max \bigl [X_++a,\ d\bigr ], \end{aligned}$$

(21)

for $\xi _{n+1}=\xi _n=-\xi _{n-1}$,

$$\begin{aligned} \max \bigl [&X_++a,\ b'\bigr ]=\max \bigl [d'\bigr ], \end{aligned}$$

(22)

and for $\xi _{n+1}=-\xi _n=\xi _{n-1}$,

$$\begin{aligned} \max \bigl [&b'\bigr ]=\max \bigl [X_++a,\ d'\bigr ]. \end{aligned}$$

(23)

Table 1 Evolution of $X_+$

If we consider magnitude relationship between b and d (or $b'$ and $d'$), (20)–(23) are further rewritten as explicit forms summarized in Table 1 with $5\times 5$ cells (“NS” means “no solution”). We explain Table 1. Assume that $(\xi _n, X_n)$ and $(\xi _{n-1}, X_{n-1})$ are given. We study how $(\xi _{n+1}, X_{n+1})$ is determined. We first notice the relationship of the signs $\xi _n$ and $\xi _{n-1}$. Here, we consider the case where $\xi _n=\xi _{n-1}$. This case is located at the second and third columns in Table 1. However, we do not know $\xi _{n+1}$. Therefore, we try both cases of (I) $\xi _{n+1}=\xi _n=\xi _{n-1}$ and (II) $-\xi _{n+1}=\xi _n=\xi _{n-1}$, which corresponds to (20) and (21), respectively. We further consider three cases for amplitude, that is, (i) $b>d$, (ii) $b=d$ and (iii) $b<d$.

Let us firstly study the case (I) and (i). The equation for the amplitude $X_{n+1}$ is (20) and it has no solution from $\max \bigl [X_++a,\ b\bigr ]=\max \bigl [d\bigr ]$. Hence, the (2, 2) cell in Table 1 is filled by “NS”. Next, we study the case (II) and (i). The equation is (21) and it is rewritten as $X_+=b-a$ from $\max \bigl [b\bigr ]=\max \bigl [X_++a,\ d\bigr ]$. Hence, the (2, 3) cell in Table 1 is filled by $X_+=b-a$. Secondly, we consider another relation between amplitudes, that is, (ii) $b=d$. In this case, both of (20) and (21) are satisfied by the inequality $X_+\leqq \max [b,d]-a$, which means $X_+$ becomes indeterminate. At this time, $\xi _{n+1}$ is also indeterminate since two cases $\xi _{n+1}=\pm 1$ give the same result. These correspond to the (3, 2) and (3, 3) cells in Table 1. Finally, we consider the case of (iii) $b<d$. For (I) and (iii), our Eq. (20) is rewritten as $X_+=d-a$ from $\max \bigl [X_++a,\ b\bigr ]=\max \bigl [d\bigr ]$. This case corresponds to the (4, 2) cell in Table 1. For (II) and (iii), our Eq. (21) has no solution from $\max \bigl [b\bigr ]=\max \bigl [X_++a,\ d\bigr ]$. This case corresponds to the (4, 3) cell in Table 1. By studying the cases $\xi _n=-\xi _{n-1}$ and magnitude relation between $b'$ and $d'$ in a similar manner, we obtain Table 1. Note that the four expressions (20)–(23) can be represented as $X_+ = \max [b^(\!'^),d^(\!'^)]-a$ or $X_+\leqq \max [b^(\!'^),d^(\!'^)]-a$ in any case.

Table 2 Evolution of $X_+$ with $\widehat{\alpha _2}\gtreqqless 0$

We go to the next step. Table 1 is written in terms of (16)–(19), which include max operations (except for d of (17)). However, for later analysis, we prefer the expressions without max operations. Hence, we further introduce the cases whether $\widehat{\alpha _2}$ is positive or 0 or negative. Noting

$$\begin{aligned} \max [b^(\!'^),d^(\!'^)]= {\left\{ \begin{array}{ll} \max \bigl [\widehat{\alpha _2}+X,\ X_-+a\bigr ], &{}(\widehat{\alpha _2}>0)\\ \max \bigl [X,\ X_-+a\bigr ], &{}(\widehat{\alpha _2}\leqq 0), \end{array}\right. } \end{aligned}$$

(24)

we find that further cases $X+\widehat{\alpha _2}\gtreqqless X_-+a$ or $X\gtreqqless X_-+a$ are necessary for our purpose. We use the following notations for shorter expression:

$$\begin{aligned} {\left\{ \begin{array}{ll} \textrm{C}_g: X+\widehat{\alpha _2}> X_-+a \\ \textrm{C}_e: X+\widehat{\alpha _2} = X_-+a \\ \textrm{C}_\ell : X+\widehat{\alpha _2}< X_-+a \\ \textrm{C}'_g: X > X_-+a \\ \textrm{C}'_e: X = X_-+a \\ \textrm{C}'_\ell : X < X_-+a. \end{array}\right. } \end{aligned}$$

(25)

By introducing these cases, we refine Table 1 to Table 2 with $11 \times 6$ cells. For example, we notice the (2, 3) cell in Table 1 filled by $X_+=b-a =\max [\widehat{\alpha _2}+X,\ X_-+a]-a$. In the case of $\widehat{\alpha _2}>0$, it becomes

$$\begin{aligned} X_+= {\left\{ \begin{array}{ll} \widehat{\alpha _2}+X-a &{} (\textrm{C}_g)\\ X_- &{} (\textrm{C}_e)\\ X_- &{} (\textrm{C}_\ell ), \end{array}\right. } \end{aligned}$$

(26)

which is located at the (2, 4) cell in Table 2. In the case of $\widehat{\alpha _2}=0$, it becomes

$$\begin{aligned} X_+= {\left\{ \begin{array}{ll} \text {NS} &{} (\textrm{C}'_g)\\ \text {NS} &{} (\textrm{C}'_e)\\ X_- &{} (\textrm{C}'_\ell ), \end{array}\right. } \end{aligned}$$

which is located at the (5, 4) cell in Table 2. In the case of $\widehat{\alpha _2}<0$, we have

$$\begin{aligned} X_+= {\left\{ \begin{array}{ll} \text {NS} &{} (\textrm{C}'_g)\\ \text {NS} &{} (\textrm{C}'_e)\\ X_- &{} (\textrm{C}'_\ell ) \end{array}\right. } \end{aligned}$$

and this result is located at the (8, 4) cell of Table 2. By continuing similar operations, Table 2 can be created.

Finally, we rewrite a of (15) according to the magnitude relation between the terms with X and other terms. Namely, we obtain

$$\begin{aligned} a= {\left\{ \begin{array}{ll} \max \bigl [0,\ \widehat{\alpha _1}\bigr ] &{}\left( X<\frac{\max \bigl [0,\widehat{\alpha _1}\bigr ]-\widehat{\alpha _3}}{2}\right) \\ \max \bigl [0,\ \widehat{\alpha _1}\bigr ]=\widehat{\alpha _3}+2X &{} \left( X=\frac{\max \bigl [0,\widehat{\alpha _1}\bigr ]-\widehat{\alpha _3}}{2}\right) \\ \widehat{\alpha _3}+2X &{} \left( X>\frac{\max \bigl [0,\widehat{\alpha _1}\bigr ]-\widehat{\alpha _3}}{2}\right) . \end{array}\right. } \end{aligned}$$

Therefore, it is found that if we see the boundary of the above classification in Table 2 on the phase plane $(X_-,X)$, it is not a straight line but a broken line at the point $X=(\max \bigl [0,\widehat{\alpha _1}\bigr ]-\widehat{\alpha _3})/2$.

If we introduce the above classification and rewrite our conditions $\textrm{C}_g$, $\textrm{C}_e$, $\textrm{C}_\ell$ and so on (see (25)), we obtain the following expressions without max operations. That is, if $\widehat{\alpha _2}>0$,

$$\begin{aligned} \textrm{C}_g \Leftrightarrow {\left\{ \begin{array}{ll} X>X_-+\max \bigl [0,\widehat{\alpha _1}\bigr ]-\widehat{\alpha _2} &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]>\widehat{\alpha _3}+2X\right) \\ X<-X_--\widehat{\alpha _3}+\widehat{\alpha _2} &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]<\widehat{\alpha _3}+2X\right) \end{array}\right. } \\ \textrm{C}_e \Leftrightarrow {\left\{ \begin{array}{ll} X=X_-+\max \bigl [0,\widehat{\alpha _1}\bigr ]-\widehat{\alpha _2} &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]>\widehat{\alpha _3}+2X\right) \\ X=-X_--\widehat{\alpha _3}+\widehat{\alpha _2} &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]<\widehat{\alpha _3}+2X\right) \end{array}\right. } \\ \textrm{C}_\ell \Leftrightarrow {\left\{ \begin{array}{ll} X<X_-+\max \bigl [0,\widehat{\alpha _1}\bigr ]-\widehat{\alpha _2} &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]>\widehat{\alpha _3}+2X\right) \\ X>-X_--\widehat{\alpha _3}+\widehat{\alpha _2} &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]<\widehat{\alpha _3}+2X\right) \end{array}\right. } \end{aligned}$$

and if $\widehat{\alpha _2}\leqq 0$,

$$\begin{aligned} \textrm{C}'_g \Leftrightarrow {\left\{ \begin{array}{ll} X>X_-+\max \bigl [0,\widehat{\alpha _1}\bigr ] &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]>\widehat{\alpha _3}+2X\right) \\ X<-X_--\widehat{\alpha _3} &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]<\widehat{\alpha _3}+2X\right) \end{array}\right. } \\ \textrm{C}'_e \Leftrightarrow {\left\{ \begin{array}{ll} X=X_-+\max \bigl [0,\widehat{\alpha _1}\bigr ] &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]>\widehat{\alpha _3}+2X\right) \\ X=-X_--\widehat{\alpha _3} &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]<\widehat{\alpha _3}+2X\right) \end{array}\right. } \\ \textrm{C}'_\ell \Leftrightarrow {\left\{ \begin{array}{ll} X<X_-+\max \bigl [0,\widehat{\alpha _1}\bigr ] &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]>\widehat{\alpha _3}+2X\right) \\ X>-X_--\widehat{\alpha _3} &{}\left( \max \bigl [0,\ \widehat{\alpha _1}\bigr ]<\widehat{\alpha _3}+2X\right) . \end{array}\right. } \end{aligned}$$

2.3 Time evolution of the amplitude on the phase plane

In the previous subsection, we have studied the time evolution of $(\xi _{n+1},X_+)$ with conditions for $(\xi _{n-1},X_-)$ and $(\xi _{n},X)$. The time evolution of a discrete dynamical system is often studied by plotting the solution $(x_n,x_{n+1})$, $n\ge 0$ on one phase plane. In this subsection, we apply the same method to our pUD system. For this purpose, we define some sets on the phase plane of $(X_-,\ X)$ (or $(X,\ X_+)$) as follows.

If $\widehat{\alpha _2}\le 0$, we define

$$\begin{aligned} {\left\{ \begin{array}{ll} P1=\{(X_-,\ X)|X_-=-\frac{\max [0,\ \widehat{\alpha _1}]+\widehat{\alpha _3}}{2},\ X=\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\} \\ L4=\{(X_-,\ X)|X=X_-+\max [0,\ \widehat{\alpha _1}],\ X<\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\} \\ L1=\{(X_-,\ X)|X=X_-\}\setminus (P1\cup L4) \\ L2=\{(X_-,\ X)|X=-X_--\widehat{\alpha _3},\ X>\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\} \\ L3=\{(X_-,\ X)|X_-<-\frac{\max [0,\ \widehat{\alpha _1}]+\widehat{\alpha _3}}{2},\ X=\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\} \\ S1= \begin{aligned} \{(X_-,\ X)|&{}(X>-X_--\widehat{\alpha _3},\ X>X_-)\\ &{}\cup (X<X_-+\max [0,\ \widehat{\alpha _1}],\ X>X_-)\} \end{aligned} \\ S2=\{(X_-,\ X)|X<-X_--\widehat{\alpha _3},\ X>\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\}\\ S3=\{(X_-,\ X)|X>X_-+\max [0,\ \widehat{\alpha _1}],\ X<\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\}. \end{array}\right. } \end{aligned}$$

(27)

These sets are shown in the left figure in Fig. 1. Note that the axes in these figure are drawn with its origin at P1 instead of (0, 0). In a similar way, we define the sets for $\widehat{\alpha _2}>0$,

$$\begin{aligned} {\left\{ \begin{array}{ll} P1=\{(X_-,X)|X_-=-\frac{\max [0,\ \widehat{\alpha _1}]+\widehat{\alpha _3}}{2}+\widehat{\alpha _2},\ X=\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\} \\ L4=\{(X_-,X)|X=X_-+\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _2},\ X<\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\} \\ L1=\{(X_-,X)|X=X_-\}\setminus (P1\cup L4) \\ L2=\{(X_-,\ X)|X=-X_--\widehat{\alpha _3}+\widehat{\alpha _2},\ X>\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\} \\ L3=\{(X_-,X)|X_-<-\frac{\max [0,\ \widehat{\alpha _1}]+\widehat{\alpha _3}}{2}+\widehat{\alpha _2},\ X=\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\}\\ S1= \begin{aligned} \{(X_-,\ X)|&{}(X>-X_--\widehat{\alpha _3}+\widehat{\alpha _2},\ X>X_-)\\ &{}\cup (X<X_-+\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _2},\ X>X_-)\} \end{aligned} \\ S2=\{(X_-,\ X)|X<-X_--\widehat{\alpha _3}+\widehat{\alpha _2},\ X>\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\}\\ S3=\{(X_-,X)|X>X_-+\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _2},\ X<\frac{\max [0,\ \widehat{\alpha _1}]-\widehat{\alpha _3}}{2}\}. \end{array}\right. } \end{aligned}$$

(28)

Fig. 1

Sets on phase plane with $\widehat{\alpha _2}\le 0$

Fig. 2

Sets on phase plane with $\widehat{\alpha _2}>0$

These sets are shown in the left figure in Fig. 2 (The origin is again P1). We refer to a set $P1 \cup L2 \cup S2 \cup L3 \cup S3 \cup L4$ as “cone” in this study.

Similarly, we define sets on the phase plane $(X,\ X_+)$. The results are shown in the right figure in Figs. 1 and  2, respectively. Note that the axes are drawn with the origin P2. We also note that the sets in the right figure are drawn by displace those in the left figure symmetrically with respect to L1. We refer to the image of the cone mentioned above as the same word “cone.”

Now, we study where a point on the phase plane of the left figure in Fig. 2 (or Fig. 1) is mapped on the right figure. As the first example, we consider the case of $\xi _n=\xi _{n-1}$ with $\widehat{\alpha _2}>0$ and summarize the result to Table 3. This case corresponds to the cells from (2, 3) to (4, 4) of Table 2. Only the (2, 4) cell has a solution and the three conditions $\textrm{C}_g$, $\textrm{C}_e$ and $\textrm{C}_\ell$ (see (25)) should be considered.

Firstly, under the condition $\textrm{C}_\ell$, which corresponds to the fourth column of Table 3, the time evolution is $X_+=X_-$ and therefore an original point $(X_-, X)$ is mapped to $(X,X_+)=(X,X_-)$ being symmetry with respect to the line L1. Secondly, under the condition $\textrm{C}_e$, which corresponds to the third column of Table 3, we have the same result as $\textrm{C}_\ell$. Finally, under the condition $\textrm{C}_g$, which corresponds to the second column of Table 3, the time evolution is $X_+=\widehat{\alpha _2}+X-a$. Hence, we find that the image of this mapping is this break line $X_+=\widehat{\alpha _2}+X-a$. The upper row in Table 3 illustrates each area corresponding to 3, respectively, and the lower row shows where the original area is mapped. This is how to create Table 3.

Table 3 Mapping of amplitude for $\widehat{\alpha _2}>0,\ \xi _n=\xi _{n-1}$

Table 4 Mapping of amplitude for $\widehat{\alpha _2}>0,\ \xi _n\ne \xi _{n-1}$

Similarly, Table 4, 5, 6, 7 and 8 are obtained. As an important example, we also explain the case of $\xi _n\ne \xi _{n-1}$ and $\textrm{C}_e$ with $\widehat{\alpha _2}>0$ corresponding to the third column of Table 4. In this case, the time evolution is the indeterminate type, $X_+ \le X_-$. We can choose an infinite number of points $(X_+,X)$ as the image of the original point $(X_-,X)$. This situation is illustrated in the lower row, the third column by the “filled” cone, $(X,X_+)=(X,Y)$ where

$$\begin{aligned} Y\le X+\widehat{\alpha _2}-a = {\left\{ \begin{array}{ll} X-\max [0,\widehat{\alpha _1}] + \widehat{\alpha _2} &{} ((X_-,X)\in L2)\\ -X -\widehat{\alpha _3} + \widehat{\alpha _2}&{} ((X_-,X)\in L4). \end{array}\right. } \end{aligned}$$

Table 5 Mapping of amplitude for $\widehat{\alpha _2}=0,\ \xi _n=\xi _{n-1}$

Table 6 Mapping of amplitude for $\widehat{\alpha _2}=0,\ \xi _n\ne \xi _{n-1}$

Table 7 Mapping of amplitude for $\widehat{\alpha _2}<0,\ \xi _n=\xi _{n-1}$

Table 8 Mapping of amplitude for $\widehat{\alpha _2}<0,\ \xi _n\ne \xi _{n-1}$

Next, in order to trace the time evolution in one phase plane, we draw our areas for $(X_-,X)$ plane and $(X,X_+)$ plane into one coordinate plane. Then, we should consider “positional relationship” between two cones, one has the edge $L2 \cup L4 \cup P1$ and the other has $L5 \cup L7 \cup P2$. We have three types of relationship: “overlapping,” “sticking,” and “separating.” Fig. 3, 4, 5, 6 and 7 show all positions of two cones. Note that the “overlapping” type appears only for $\widehat{\alpha _2}> 0$. The other types appear for any $\widehat{\alpha _2}$.

We note that these three types of “separating,” “sticking,” and “overlapping” are inevitably determined by the magnitude relationship between $\widehat{\alpha _1}$ and $\widehat{\alpha _2}$, which is summarized in Table 9. For example, “overlapping” happens under the condition of $\widehat{\alpha _2}>0\ \text{ and }\ \widehat{\alpha _2}>\widehat{\alpha _1}$ and this is given on the second column of Table 9. The other cases, “sticking” and “separating” appear on the third and fourth column of Table 9, respectively.

Fig. 3

“separating” cones with $\widehat{\alpha _2}\le 0$

Fig. 4

“sticking” cones with $\widehat{\alpha _2}\le 0$

Fig. 5

“separating” cones with $\widehat{\alpha _2}>0$

Fig. 6

“sticking” cones with $\widehat{\alpha _2}>0$

Fig. 7

“overlapping” cones with $\widehat{\alpha _2}>0$

Table 9 Relationship between parameters and cone-position

3 Transition diagrams

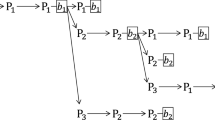
We have to remember that we should include information of the sign variables. For this purpose, we prepare four copies of the phase plane for $(X_-, X)$ corresponding to the sign $(\xi _{n-1},\xi _n) = (+,+)$, $(+,-)$, $(-,+)$ and $(-,-)$, respectively. Here, for simplicity, we write $+1$ and $-1$ as $+$ and −, respectively. We use the $(\xi _{n-1}e^{X_-})$ v.s. $(\xi _{n}e^{X})$ coordinates and four copies are placed on each quadrant as shown in Fig. 8. Our cones are also drawn in each quadrant. Note that we here draw only the case of “sticking” for simplicity.

Fig. 8

Phase plane which four copies are patched

For distinguishing the pair of the sign, we represent our sets defined by (27) or (28) with black-and-white shape. That is, in Fig. 8, a pair of signs $(+,+)$ is represented by a white circle, $(+,-)$ by a black circle, $(-,-)$ by a black-painted diamond, and $(-,+)$ by a white-painted diamond.

Fig. 9

Transition diagram appearing for all types and $\widehat{\alpha _2}$

Now, we generally put $Z=(\xi _{n-1},\ \xi _n,\ X_{n-1},\ X_n)$ and investigate the time evolution for a set of assigned initial values. For example, we start from a set of initial values $Z_0=(+,\ +,\ X_-,\ X),\ (X_-,\ X)\in S1$. We point out in advance that the result is summarized by one diagram in Fig. 9. The evolution of the amplitude and the sign can be traced by referring to Tables 3,  4, 5, 6, 7, 8 and 2, respectively. From this initial values, we find the following time evolution for any $\widehat{\alpha _2}$:

$$\begin{aligned} Z_0&=(+,\ +,\ X_-,\ X),\ (X_-,\ X)\in S1\\ \mapsto Z_1&=(+,\ -,\ X,\ X_-),\ (X,\ X_-)\in S6\\ \mapsto Z_2&=(-,\ -,\ X_-,\ X),\ (X_-,\ X)\in S1\\ \mapsto Z_3&=(-,\ +,\ X,\ X_-),\ (X,\ X_-)\in S6\\ \mapsto Z_4&=Z_0. \end{aligned}$$

The sign-inverted solution

$$\begin{aligned} Z_0^*&=(-,\ -,\ X_-,\ X),\ (X_-,\ X)\in S1\\ \mapsto Z_1^*&=(-,\ +,\ X,\ X_-),\ (X,\ X_-)\in S6\\ \mapsto Z_2^*&=(+,\ +,\ X_-,\ X),\ (X_-,\ X)\in S1\\ \mapsto Z_3^*&=(+,\ -,\ X,\ X_-),\ (X,\ X_-)\in S6\\ \mapsto Z_4^*&=Z_0^* \end{aligned}$$

is also obtained easily. These solutions are trivially four-periodic. Here, we reinterpret this situation as follows. This system maps a set S1 with the sign $(+,+)$ to another set S6 with $(+,-)$ (namely, S1 with $(+,+)$ $\mapsto$ S6 with $(+,-)$, not S1 with $(+,+)$ $\rightarrow$ S6 with $(+,-)$), and then S1 with $(-,-)$ and finally S6 with $(-,+)$. We call this reinterpretation “approximative”, which is useful for complicated indeterminate solutions as we see later. We illustrate the above solutions as the approximative transition diagram shown in Fig. 9. We see a simple cycle among four nodes. It is noted that this solution are uniquely determined in any step, in other words, we do not encounter an indeterminate solution. This situation is expressed in Fig. 9 by which two nodes are connected with a single arrow only. This transition is common to any value of $\widehat{\alpha _2}$ and positioning cases. Looking at Fig. 8, we can see that this transition rotates S1 or S6 or L1 with a pair of sign by 90 degrees clockwise at one time.

Fig. 10

Transition diagram appearing for all types with $\widehat{\alpha _2}<0$

Figure 10 shows a transition that is common to all positional cases of $\widehat{\alpha _2}<0$. For example, let us start from a point $ZZ_0=(+,\ +,\ X_-,\ X)$, $(X_-,\ X)\in L2$. In Table 2, we can choose the (9, 3) or (9, 4) cell. This means that the indeterminate solution has appeared here. If we choose the (9, 4) cell and the equal case $X_+ = X_-$, the sign is determined by the (11, 4) cell as $\xi _{n+1}=-$ and we have the next point $ZZ_1=(+,\ -,\ X,\ X_-)$, $(X,\ X_-)\in L7$. Moreover, since $ZZ_1$ corresponds to the $\textrm{C}_\ell$ case of the (10, 5) cell, we find the after the next point is uniquely determined as $ZZ_2=(-,\ -,\ X_-,\ X)$, $(X_-,\ X)\in L2$. However, since the next point $ZZ_3$ becomes indeterminate again, we need a similar case consideration. From the above (and further calculation), we, for example, obtain the development such as

$$\begin{aligned} ZZ_0&=(+,\ +,\ X_-,\ X),\ (X_-,\ X)\in L2\\ \mapsto ZZ_1&=(+,\ -,\ X,\ X_-),\ (X,\ X_-)\in L7\\ \mapsto ZZ_2&=(-,\ -,\ X_-,\ X),\ (X_-,\ X)\in L2\\ \mapsto ZZ_3&=(-,\ +,\ X,\ X_-),\ (X,\ X_-)\in L7\\ \mapsto ZZ_4&=ZZ_0.\ \end{aligned}$$

This solution orbit is understood approximatively as L2 with $(+,+)$ $\mapsto$ L7 with $(+,-)$ $\mapsto$ L2 with $(-,-)$ $\mapsto$ L7 with $(-,+)$ $\mapsto$ L2 with $(+,+)$.

If, for the same initial point $ZZ_0$, we choose another cell (9, 3) and the equal case $X_+ = X_-$, we have a different point $ZZ_1'=(+,\ +,\ X,\ X_-)$, $(X,\ X_-)\in L7$. After the next point becomes $ZZ_2'=(+,\ -,\ X_-,\ X)$, $(X_-,\ X)\in L2$ from the case $\textrm{C}_{\textrm{e}}$ of the (8, 4) cell. Further the next point uniquely becomes $ZZ_3'=(-,\ -,\ X,\ X_-)$, $(X,\ X_-)\in L7$. From these and further calculation, we find the solution such as

$$\begin{aligned} ZZ_0&=(+,\ +,\ X_-,\ X),\ (X_-,\ X)\in L2\\ \mapsto ZZ_1'&=(+,\ +,\ X,\ X_-),\ (X,\ X_-)\in L7\\ \mapsto ZZ_2'&=(+,\ -,\ X_-,\ X),\ (X_-,\ X)\in L2\\ \mapsto ZZ_3'&=(-,\ -,\ X,\ X_-),\ (X,\ X_-)\in L7\\ \mapsto ZZ_4'&=(-,\ +,\ X_-,\ X),\ (X_-,\ X)\in L2\\ \mapsto ZZ_5'&=ZZ_1'.\ \end{aligned}$$

This solution orbit is understood approximatively as L2 with $(+,+)$ $\mapsto$ L7 with $(+,+)$ $\mapsto$ L2 with $(+,-)$ $\mapsto$ L7 with $(-,-)$ $\mapsto$ L2 with $(-,+)$ $\mapsto$ L7 with $(+,+)$.

Furthermore, for the same initial point $ZZ_0$, we can choose the next point $ZZ_1''=(+,\ +,\ X,\ _< X_-),\ (X,\ _< X_-)\in S5$. Then, after the next point uniquely becomes $ZZ_2''=(+,\ -,\ _< X_-,\ X),\ (_< X_-,\ X)\in S2$ from the cell (8, 4) with $\textrm{C}_\ell$, where $_< X_-$ means any value Y satisfying $Y<X_-$. Further the next point is uniquely determined as $ZZ_3'=(-,\ -,\ X,\ X_-),\ (X,\ X_-)\in L7$ from the cell (10, 5) with $\textrm{C}_g$, which has already appeared above. This solution behaves as

$$\begin{aligned} ZZ_0&=(+,\ +,\ X_-,\ X),\ (X_-,\ X)\in L2\\ \mapsto ZZ_1''&=(+,\ +,\ X,\ _< X_-),\ (X,\ _< X_-)\in S5\\ \mapsto ZZ_2''&=(+,\ -,\ _< X_-,\ X),\ (_< X_-,\ X)\in S2\\ \mapsto ZZ_3''&=ZZ_3'=(-,\ -,\ X,\ X_-),\ (X,\ X_-)\in L7\\ \mapsto ZZ_4''&=ZZ_4'=(-,\ +,\ X_-,\ X),\ (X_-,\ X)\in L2\\ \mapsto ZZ_5''&=ZZ_1'=(+,\ +,\ X,\ X_-),\ (X,\ X_-)\in L7\\ \mapsto ZZ_6''&=ZZ_2'=(+,\ -,\ X_-,\ X),\ (X_-,\ X)\in L2\\ \mapsto ZZ_7''&=ZZ_3', \end{aligned}$$

which is unique except for $ZZ_1''$. This solution orbit is understood approximatively as L2 with $(+,+)$ $\mapsto$ S5 with $(+,+)$ $\mapsto$ S2 with $(+,-)$ $\mapsto$ L7 with $(-,-)$ $\mapsto$ L2 with $(-,+)$ $\mapsto$ L7 with $(+,+)$ $\mapsto$ L2 with $(+,-)$ $\mapsto$ L7 with $(-,-)$. Although we omit details, we also can choose $ZZ_1'''=(+,\ -,\ X,\ _< X_-),\ (X,\ _< X_-)\in S5$.

Investigating all (but finite number of) cases, we obtain the “approximative” transition diagram shown in Fig. 10. In usual meaning, we have encountered infinitely multi-valued mapping when we determine the next point from the initial point. However, by our approximative point of view, we understand it as only four-valued mapping. This situation is expressed in Fig. 10 by which four arrows are left from L2 of white circle and of black diamond, respectively.

Let us study features of the orbits in the diagram of Fig. 10. We see two cyclic transition in this diagram. One is L2 with $(+,+)$ $\mapsto$ L7 with $(+,-)$ $\mapsto$ L2 with $(-,-)$ $\mapsto$ L7 with $(-,+)$ $\mapsto$ L2 with $(+,+)$, which have already mentioned. The other is L7 with $(+,+)$ $\mapsto$ L2 with $(+,-)$ $\mapsto$ L7 with $(-,-)$ $\mapsto$ L2 with $(-,+)$ $\mapsto$ L7 with $(+,+)$. If we once leave the former cycle at a branching point, we cannot go back to it and the orbit eventually stays the later cycle. Hence, the former one looks “unstable” and the later does “stable”. Because of this, it is claimed that the effect of the indeteminate solution is not serious in this case.

Fig. 11

Transition diagrams for “sticking” type with $\widehat{\alpha _2}<0$

Figure 11 shows the diagram for “sticking” positional type with $\widehat{\alpha _2}<0$. We find the self-loop at P1 and L4. We again can be summarized infinitely multi-valued mapping as four-valued one. However, we must encounter the indeterminate solutions with an infinite number of times. Hence, this diagram is rather complex than Fig. 10.

Figure 12 shows the diagram for the “separating” positional type with $\widehat{\alpha _2}<0$. In a similar way to Fig. 10, we see a “stable” cycle and an “unstable” one. We have obtained all diagrams for $\widehat{\alpha _2}<0$ by Figs. 9, 10, 11 and 12. Note that we see all sets (P1, L1, S1, and so on, with four signs respectively) only once. Hence, we find that we have traced all orbits on the phase plane for $\widehat{\alpha _2}<0$.

We give some results for $\widehat{\alpha _2}>0$.

Fig. 12

Transition diagrams for “separating” type with $\widehat{\alpha _2}<0$

Fig. 13

Transition diagram appearing for all types and $\widehat{\alpha _2}>0$

Figure 13 shows the approximative transition diagram which is common to all of the positional types with $\widehat{\alpha _2}>0$. We see a “stable” cycle and an “unstable” one.

Fig. 14

Transition diagrams for “sticking” type with $\widehat{\alpha _2}>0$

Figure 14 shows the diagram which corresponds to the “sticking” positional type with $\widehat{\alpha _2}>0$.

Fig. 15

Transition diagrams for “separating” type with $\widehat{\alpha _2}>0$

Figure 15 shows the diagram which corresponds to the “separating” positional type with $\widehat{\alpha _2}>0$. We see a “stable” cycle and an “unstable” one. We remain the “overlapping” positional type. Although we have studied it, its explanation is rather complicated (We shall report it in forthcoming paper). If we consider Figure 9, 13, 14 and 15 and the “overlapping” type, we see all sets only once and therefore we find that we have traced all orbits on the phase plane for $\widehat{\alpha _2}>0$.

In closing this section, we give Table 10 which summarizes the relationship among the sign of $\widehat{\alpha _2}$, type of the positional relationship, and the transition diagrams.

Table 10 Summary of $\widehat{\alpha _2}$, positional relationship, transition diagrams

4 Concluding remarks

In [11], the ultradiscrete analogue of the hard-spring equation with parity variables was presented, and its solutions for various (but, not all) initial values were classified into some types. It was quite helpful to regard an infinite number of values as one point on the solution orbit for studying the indeterminate solution.

In this study, we focused on the same equation as [11] and we have applied further approximative method depeloped in [13], that is, reinterpreting the pUD system as the mapping which maps a set on the phase plane to the other. Moreover, the positional relationship of “cones” on the phase plane closely effects the solution behaviour. This relation is determined only by the magnitude relationship of the system parameters $\widehat{\alpha _1}$ and $\widehat{\alpha _2}$, which was not pointed out in [11]. From these viewpoints, certain new perceptions have been obtained for the solutions of the pUD system as follows. Because all domains on the phase plane appeared, all initial values have been examined, which completely cover those of [11]. As a result, the condition under which an indeteminate solution does not appear has been clarified, that is, to start from a point on the phase plane included in Fig. 9. When the positional relationship of cones is “separating” or “sticking”, we have captured an infinite number of branches in usual sense as a finite number of ones. This result implies that the pUD equation is still a kind of cellular automaton, because it has a finite number of “states”, but its dynamics is not always “auto” because of non-uniqueness.

Furthermore, the approximative way enables us to understand the earlier work from a broader point of view. For example, in [11], the existence of exactly four-periodic solution was pointed out. However, by our analysis, such solutions appear in several transition diagrams. Namely, all orbits of Fig. 9 and the “stable” orbit of Figs. 10, 12, 13, and 15 . Note that they were not distinguished in [11]. This study has clarified that they belong to different transition diagrams each other. We have also found that almost solution orbits (as sets) show cyclic behaviour on the phase plane with help of the transition diagrams.

Our method reported in this paper enables us to easily compare some pUD equations each other. For example, it is possible to compare the pUD analogues of several difference equations for the same differential equation, which may give a new contribution to studying nonlinear systems. It is also an interesting problem to investigate differences between integrable and non-integrable pUD systems by this approximative method.

We comment one issue in [11], that is, how to analyze the solution with “diagram of unbounded type,” which seems to need an infinite number of cases for tracing the orbit. We have found that we encounter this type of solution if and only if the the positional relationship is “overlapping” and understood why such many cases appear. We shall report its details in the forthcoming paper.