Inertial projected gradient method for large-scale topology optimization

Abstract

We present an inertial projected gradient method for solving large-scale topology optimization problems. We consider the compliance minimization problem, the heat conduction problem and the compliant mechanism problem of continua. We use the projected gradient method to efficiently treat the linear constraints of these problems. Also, inertial techniques are used to accelerate the convergence of the method. We consider an adaptive step size policy to further reduce the computational cost. The proposed method has a global convergence property. By numerical experiments, we show that the proposed method converges fast to a point satisfying the first-order optimality condition with high accuracy compared with the existing methods. The proposed method has a low computational cost per iteration, and is thus effective in a large-scale problem.

1 Introduction

Topology optimization is a method to obtain an optimal structural design depending on the objective by mathematical programming. The extensive study of topology optimization dates back to the seminal work by Bendsøe and Kikuchi [6] in 1988. Since then, a wide range of applications have been suggested in fluid, heat, electromagnetic, acoustic, and aerospace engineering [7, 13]. A topology optimization problem of continua is formulated as an infinite-dimensional optimization problem. We can discretize the problem by the finite element method and obtain a conventional finite-dimensional optimization problem [7, 9]. The discretized problem is a large-scale nonconvex optimization problem with some constraints. Moreover, it requires the finite element analysis (FEA), which is a solution of a linear equation, for calculating the objective function value and the gradient of the objective function at each iteration. This property makes the computational cost of topology optimization even larger.

There are various types of approaches to reduce the computational cost of topology optimization. In topology optimization, most of the computational cost is spent on FEA. Accordingly, there are many studies on reducing the computational cost of FEA [11, 34,35,36, 38, 39].

In this paper, we attempt to reduce the computational cost by reducing the number of iterations using an efficient and faster optimization algorithm. In a large-scale topology optimization problem, common nonlinear optimization algorithms such as the interior-point method and the sequential quadratic programming are often impractical because of the huge iteration cost (computational cost per iteration). Therefore, algorithms designed specifically for structural (topology) optimization such as the optimality criteria method [6] and the method of moving asymptotes [31, 32] are commonly used. See [27] for a comparative study on the optimization algorithms for topology optimization. Some studies on faster optimization algorithms for topology optimization are found in [20, 28].

Recently, first-order optimization methods which only require the first-order derivatives of the objective (and constraint) functions have been attracting much attention in the machine learning community. First-order methods are suited for large-scale problems because of their low iteration cost in time and memory storage. Second-order methods such as the Newton method and the interior-point method require the (approximated) second-order derivative and solution of linear equations. The iteration cost grows drastically as the problem size increases, and thus second-order methods are impractical for a large-scale problem. Although the convergence of first-order methods is basically slower than that of second-order methods, there are studies on accelerating the convergence of first-order methods. For an unconstrained convex optimization problem where the objective function f has Lipschitz continuous gradient (also called that the objective function is L-smooth), Nesterov’s accelerated gradient method [23] achieves the convergence rate at $f({\varvec{x}}^k)-f({\varvec{x}}^*)\le O(1/k^2)$, while the steepest descent method converges with rate O(1/k) where k is the iteration counter and ${\varvec{x}}^*$ is the optimal solution. The above convergence rate is often equivalently described by the iteration complexity: $O(1/\epsilon ^{1/2})$ iterations to acheive $f({\varvec{x}}^k)-f({\varvec{x}}^*)\le \epsilon$. Beck and Teboulle [4] combined Nesterov’s acceleration technique with the proximal gradient method for convex optimization problems, which is a generalization of the projected gradient method, to treat simple nondifferentiable functions and constraints.

The accelerated gradient method has also been extended to an optimization problem with a nonconvex objective function with Lipschitz continuous gradient. In unconstrained nonconvex optimization, the optimality measure $f({\varvec{x}}^k)-f({\varvec{x}}^*)$ used in convex optimization is not appropriate since there may exist multiple local minima. Therefore, the number of iterations k required to acheive $\Vert \nabla f({\varvec{x}}^k)\Vert \le \epsilon$ (the iteration complexity) is considered. The steepest descent method has $O(1/\epsilon ^2)$ iteration complexity. The accelerated gradient methods by [15, 18] have the same order of iteration complexity as the steepest descent method in nonconvex case, but have the accelerated convergence rate in convex case same as Nesterov’s accelerated gradient method. Although they do not have theoretically improved convergence rates in nonconvex optimization, their empirical performance is expected to be better than that of first-order methods without acceleration since the iteration complexity is worst-case under all L-smooth functions f. With the additional assumption of Lipschitz continuity of the Hessian of the objective function, Carmon et al. [10] acheived an improved iteration complexity of $O(\epsilon ^{-7/4}\log (1/\epsilon ))$ and Li and Lin [19] acheived $O(\epsilon ^{-7/4})$. The former method requires more complicated update scheme. The methods by [10, 19] only treat unconstrained problems. The accelerated gradient methods for nonconvex optimization are still developing. See [3, 12, 22] for more details in first-order methods and their acceleration.

Although the accelerated proximal gradient method has been applied to optimization problems in computational plasticity [17, 29, 30], there are very few applications to topology optimization. Li and Zhang [21] applied the accelerated mirror descent method to a robust topology optimization problem under stochastic load uncertainty. They used stochastic optimization techniques to efficiently obtain a robust design. However, as they applied a convex optimization algorithm to nonconvex optimization problems, the convergence of the method is not guaranteed.

In [24], the authors applied the accelerated projected gradient method based on [15] to the compliance minimization problem in topology optimization. Although we call the proposed method the “accelerated” projected gradient method, the convergence rate is not improved theoretically from the classical projected gradient method for a nonconvex objective function. Moreover, to guarantee the convergence, the method requires additional FEAs at each iteration.¹ Therefore, in this paper, we adopt an inertial projected gradient method based on iPiano [25] instead. The main advantage of this algorithm is that it contains no auxiliary variables and requires a smaller number of FEAs than [15] to guarantee global convergence. It has an inertial term in its update formula to accelerate the convergence. Although the theoretical convergence rate is the same as that of the projected gradient method (and that of the method in [15]), practical performance is expected to be better than the projected gradient method. We consider an adaptive step size policy to further reduce the computational cost. The proposed method is easy to implement and guaranteed to converge to a stationary point which satisfies the first-order optimality condition. This convergence guarantee is important to properly stop the algorithm and obtain a high-quality solution. We also extend the results to the heat conduction problem and the compliant mechanism problem. We show that the projection onto the feasible set can be easily calculated for each of the equality and inequality constraints on the structural volume, and thus the inertial projected gradient method can be efficiently applied to the topology optimization problems considered in this paper.

In numerical experiments, we consider the compliance minimization problem, the heat conduction problem and the compliant mechanism problem, and compare the proposed method with the optimality criteria method [6], the method of moving asymptotes (MMA) [31,32,33], and the MATLAB fmincon (interior-point method and sequential quadratic programming). We show that the proposed method has a low iteration cost and converges fast. Moreover, the solution obtained by the proposed method satisfies the first-order optimality condition with higher accuracy than those obtained by the existing method.

This paper is organized as follows: In Sect. 2, we provide the fundamentals of topology optimization and the problem formulation. In Sect. 3, we briefly discuss the projected gradient method and the projection onto the feasible set of topology optimization problems. Then, we explain the proposed method, the inertial projected gradient method and its step size policy. In Sect. 4, we show the results of numerical experiments. Finally, some concluding remarks are provided in Sect. 5.

All of the norms $\Vert \cdot \Vert$ in this paper are the Euclidean norm of a vector. The inner product is denoted by $\langle \cdot ,\cdot \rangle$. We use ${\varvec{0}}$ and ${\varvec{1}}$ to denote the vectors with all components equal to 0 and 1, respectively. Moreover, $\max \{0,\cdot \}$ and $\min \{1,\cdot \}$ are the componentwise operations acting on a vector.

2 Problem formulation

Fig. 1

A finite element discretization of the design domain of a topology optimization problem. The eth component $x_e\ (e=1,\ldots ,n)$ of the the density vector ${\varvec{x}}$ corresponds to the density of the eth finite element

We consider three topology optimization problems with simple linear constraints: the compliance minimization problem, the heat conduction problem and the compliant mechanism problem. The problem setting in this paper is based on [1, 7].

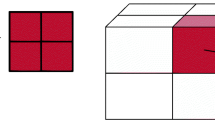
Consider a topology optimization problem the design domain of which is discretized by the conventional finite element method. An example of discretization of the design domain is shown in Fig. 1. For simplicity, we divide the design domain into n identical square finite elements with unit volume. The design variable of the optimization problem is the density vector ${\varvec{x}}\in {\mathbb {R}}^n$, the eth component $x_e$ of which denotes the density of the eth finite element. Each density $x_e$ takes the value in [0, 1]. When $x_e=0$, the element e is regarded as void and when $x_e=1$, the element e is regarded as material. Thus ${\varvec{x}}$ corresponds to a design of the structure. We use the SIMP (solid isotropic material with penalization) method [5] to penalize the intermediate values in (0, 1).

2.1 Compliance minimization problem

Fig. 2

Problem setting of the compliance minimization problem (top) and its optimal design (bottom)

Consider the compliance minimization problem shown in Fig. 2. The top figure in Fig. 2 describes an example of problem setting and the bottom figure describes the optimal solution of the discretized problem with uniform square finite elements in the way shown in Fig. 1. The aim is to maximize the stiffness of structure when the external force is applied. In the SIMP method, the global stiffness matrix can be defined as

$$\begin{aligned} {K({\varvec{x}})=\sum _{e=1}^n {(E_\textrm{min}+(E_0-E_\textrm{min}) x_e^p )} K_e,} \end{aligned}$$

(1)

where $p>1$ is the penalty parameter, $E_0\gg E_\textrm{min}>0$ are constants and $K_e$ is the local stiffness matrix which is a constant symmetric matrix. In addition, we use the density filter [9] to prevent mesh dependency; refining the mesh leads to a different optimal structural design, not a refined structural design. The density filter is a linear operator acting on the density vector ${\varvec{x}}$. Therefore, by using a constant matrix $H\in {\mathbb {R}}^{n\times n}$, the filtered density vector can be written as $\tilde{{\varvec{x}}}=H{\varvec{x}}$.

The compliance minimization problem is defined as follows:

$$\begin{aligned} \begin{aligned}&\underset{{\varvec{x}}\in {\mathbb {R}}^n,\tilde{{\varvec{x}}}\in {\mathbb {R}}^n,{\varvec{u}}\in {\mathbb {R}}^m}{\text {Minimize}}{} & {} {\varvec{p}}^\text {T}{\varvec{u}}\\ {}&\ \ \ \ \mathrm {subject\ to}{} & {} K(\tilde{{\varvec{x}}}){\varvec{u}}={\varvec{p}},\\ {}{} & {} {}&{\varvec{1}}^\text {T}\tilde{{\varvec{x}}}=V_0,\\ {}{} & {} {}&\tilde{{\varvec{x}}}=H{\varvec{x}},\\ {}{} & {} {}&{\varvec{0}}\le {\varvec{x}}\le {\varvec{1}}. \end{aligned} \end{aligned}$$

(2)

Here, ${\varvec{p}}\in {\mathbb {R}}^m$ is the constant load vector, ${\varvec{u}}\in {\mathbb {R}}^m$ is the global nodal displacement vector, m is the number of degrees of freedom of the nodal displacements, and $V_0\in (0,n)$ is the upper limit of the structural volume. Problem (2) can be rewritten as the following optimization problem with a nonconvex objective function and linear constraints:

$$\begin{aligned} \begin{aligned}&\underset{{\varvec{x}}\in {\mathbb {R}}^n}{\text {Minimize}}{} & {} f({\varvec{x}})\mathrel {\mathop :}={\varvec{p}}^\text {T}K(H{\varvec{x}})^{-1}{\varvec{p}}\\ {}&\mathrm {subject\ to}{} & {} {\varvec{1}}^\text {T}H{\varvec{x}}=V_0,\\ {}{} & {} {}&{\varvec{0}}\le {\varvec{x}}\le {\varvec{1}}. \end{aligned} \end{aligned}$$

(3)

Note that, in practice, we do not calculate the inverse matrix of the global stiffness matrix, rather we solve the equilibrium equation $K(\tilde{{\varvec{x}}}){\varvec{u}}={\varvec{p}}$ (corresponding to FEA) at each iteration. Subsequently we use the solution ${\varvec{u}}$ of FEA to calculate the objective function ${\varvec{p}}^\textrm{T}{\varvec{u}}$. Also, the gradient of the objective function is calculated by substituting ${\varvec{u}}$ into the following formula:

$$\begin{aligned} {\frac{\partial f}{\partial x_e}=-\sum _{i=1}^n h_{ie}p{\tilde{x}}_i^{p-1}(E_0-E_\textrm{min}){\varvec{u}}^\textrm{T}K_i{\varvec{u}}\quad (e=1,\ldots ,n),} \end{aligned}$$

(4)

where $h_{ij}$ is the (i, j)th entry of H. Each component of the gradient $\nabla f({\varvec{x}})$ is non-positive, because $K_e\ (e=1,\ldots ,n)$ is positive semidefinite. This is why we consider equality volume constraint in (2).

2.2 Heat conduction problem

Fig. 3

Problem setting of the heat conduction problem (left) and its optimal design (right)

The heat conduction problem aims to maximize the heat conduction from the entire design domain under uniformly distributed heating to the designated region where the temperature is constant T (lower than that of the entire design domain) as shown in Fig. 3. It can be formulated in the same way as the compliance minimization problem (2). The vector ${\varvec{u}}$, the stationary solution of the discretized heat equation, consists of the temperature of each node. Note that the steady state heat equation and the equilibrium equation of linear elasticity are both described by the Poisson equation. We put ${\varvec{p}}=c_\textrm{T}{\varvec{1}}$ using a scaling parameter $c_\textrm{T}$. Then the problem (2) corresponds to the minimization problem of the average temperature of the design domain (the problem to find the optimal shape of the heat conductor to minimize the average temperature of the design domain). See [7] for details.

2.3 Compliant mechanism problem

Fig. 4

Problem setting of the compliant mechanism problem (left) and its optimal design (right)

A compliant mechanism transmits the force and motion through elastic body deformation. In Fig. 4, we aim to design a compliant mechanism which maximizes the displacement in the direction of vector ${\varvec{u}}_\textrm{out}$ when the force is applied in the direction of vector ${\varvec{p}}$. The spring with stiffness $k_\textrm{in}$ and $k_\textrm{out}$ are added to the points at which ${\varvec{p}}$ is applied and ${\varvec{u}}_\textrm{out}$ is measured, respectively. The compliant mechanism problem is defined as follows [7]:

$$\begin{aligned} \begin{aligned}&\underset{{\varvec{x}}\in {\mathbb {R}}^n,\tilde{{\varvec{x}}}\in {\mathbb {R}}^n,{\varvec{u}}\in {\mathbb {R}}^m}{\text {Minimize}}{} & {} {\varvec{q}}^\text {T}{\varvec{u}}\\ {}&\ \ \ \ \mathrm {subject\ to}{} & {} K(\tilde{{\varvec{x}}}){\varvec{u}}={\varvec{p}},\\ {}{} & {} {}&{\varvec{1}}^\text {T}\tilde{{\varvec{x}}}\le V_0,\\ {}{} & {} {}&\tilde{{\varvec{x}}}=H{\varvec{x}},\\ {}{} & {} {}&{\varvec{0}}\le {\varvec{x}}\le {\varvec{1}}. \end{aligned} \end{aligned}$$

(5)

The main difference from the compliance minimization problem is the objective function. The coefficient in the objective function ${\varvec{q}}$ is different from the right hand side of the equilibrium equation ${\varvec{p}}$. The gradient of the objective function is calculated by

$$\begin{aligned} {\frac{\partial f}{\partial x_e}=-\sum _{i=1}^n h_{ie}p{\tilde{x}}_i^{p-1}(E_0-E_\textrm{min}){\varvec{u}}^\textrm{T}K_i\bar{{\varvec{u}}}\quad (e=1,\ldots ,n),} \end{aligned}$$

(6)

where $\bar{{\varvec{u}}}$ is the solution of so-called adjoint equation $K(\tilde{{\varvec{x}}})\bar{{\varvec{u}}}={\varvec{q}}$. This equation can be efficiently solved using the Cholesky decomposition, because the coefficient matrix is the same as the equilibrium equation. Note that a component of the gradient is not necessarily non-positive in this case, and thus the volume constraint is imposed as an inequality constraint.

Problems (2) and (5) can be written as follows:

$$\begin{aligned} {\underset{{\varvec{x}}\in S}{\text {Minimize }}f({\varvec{x}}),} \end{aligned}$$

(7)

where S is the feasible set defined by

$$\begin{aligned} {S=\{{\varvec{x}}\in {\mathbb {R}}^n\mid {\varvec{v}}^\textrm{T}{\varvec{x}}=V_0,\ {\varvec{0}}\le {\varvec{x}}\le {\varvec{1}}\}} \end{aligned}$$

(8)

or

$$\begin{aligned} {S=\{{\varvec{x}}\in {\mathbb {R}}^n\mid {\varvec{v}}^\textrm{T}{\varvec{x}}\le V_0,\ {\varvec{0}}\le {\varvec{x}}\le {\varvec{1}}\}.} \end{aligned}$$

(9)

Although we have ${\varvec{v}}=H^\textrm{T}{\varvec{1}}$ in this paper, the coefficient of the volume constraint is in general not necessarily equal to ${\varvec{1}}$ (as the volume of each element can differ from each other). In the next section, we present algorithms to solve problem (7).

3 Inertial projected gradient method for topology optimization

3.1 Projected gradient method

The projected gradient method [16] is a classical optimization algorithm for an optimization problem in the form of (7) with a smooth objective function $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ and a closed convex feasible set $S\subset {\mathbb {R}}^n$. It is a special case of the proximal gradient method which has been attracting much attention in recent years [3, 4, 22]. The projected gradient method finds a solution by repeating the following formula starting from the initial point ${\varvec{x}}^0\in S$:

$$\begin{aligned} {{\varvec{x}}^{k+1}={\Pi }_S({\varvec{x}}^k-\alpha _k \nabla f({\varvec{x}}^k)).} \end{aligned}$$

(10)

Here, $\alpha _k>0$ is the step sizes, and ${\Pi }_S({\varvec{w}})\in S$ is the projection of a given vector ${\varvec{w}}\in {\mathbb {R}}^n$ onto S defined as follows:

$$\begin{aligned} {{\Pi }_S({\varvec{w}})\mathrel {\mathop :}=\underset{{\varvec{x}}\in S}{\mathrm {arg\,min}} \Vert {\varvec{x}}-{\varvec{w}}\Vert .} \end{aligned}$$

(11)

That is, ${\Pi }_S({\varvec{w}})$ is the closest point in S from ${\varvec{w}}$. The projected gradient method coincides with the steepest descent method when $S={\mathbb {R}}^n$.

3.2 Projection onto the feasible set

To use the projected gradient method effectively, the projection onto the feasible set must be easily calculated. We present an easy way to calculate the projection in our problems, for each of the equality volume constraint cases in (8) and the inequality volume constraint case in (9). The algorithm of the projection in our problems is similar to that of the projection onto the probability simplex (see e.g. [26]).

3.2.1 Case of equality volume constraint

Consider S in (8). The projection ${\Pi }_S({\varvec{w}})$ is equal to the unique optimal solution of the following problem:

$$\begin{aligned} \begin{aligned}&\underset{{\varvec{x}}\in S}{\textrm{Minimize}}\ \frac{1}{2}\Vert {\varvec{x}}-{\varvec{w}}\Vert ^2. \end{aligned} \end{aligned}$$

(12)

This is a convex optimization problem, and the following KKT ($\text {Karush--Kuhn--Tucker}$) condition is the necessary and sufficient condition for optimality:

$$\begin{aligned} \begin{aligned}&{\varvec{x}}-{\varvec{w}}-{\varvec{\lambda }}+{\varvec{\nu }}+\mu {\varvec{v}}={\varvec{0}},\\&{\varvec{v}}^\textrm{T}{\varvec{x}}=V_0,\ \ {\varvec{0}}\le {\varvec{x}}\le {\varvec{1}},\\&{\varvec{\lambda }}\ge {\varvec{0}},\ \ {\varvec{\nu }}\ge {\varvec{0}},\\ {}&{\varvec{\lambda }}^\textrm{T}{\varvec{x}}=0,\ \ {\varvec{\nu }}^\textrm{T}({\varvec{x}}-{\varvec{1}})=0, \end{aligned} \end{aligned}$$

(13)

where ${\varvec{\lambda }}$, ${\varvec{\nu }}\in {\mathbb {R}}^n$ and $\mu \in {\mathbb {R}}$ are the Lagrange multipliers.

We find the unique point ${\varvec{x}}$ which satisfies (13) for given ${\varvec{w}}$, and it is the projection ${\Pi }_S({\varvec{w}})$. By the first equality in (13), we obtain ${\varvec{x}}={\varvec{w}}+{\varvec{\lambda }}-{\varvec{\nu }}-\mu {\varvec{v}}$. To satisfy ${\varvec{0}}\le {\varvec{x}}\le {\varvec{1}}$, ${\varvec{\lambda }}\ge {\varvec{0}}$, ${\varvec{\nu }}\ge {\varvec{0}}$, ${\varvec{\lambda }}^\textrm{T}{\varvec{x}}=0$ and ${\varvec{\nu }}^\textrm{T}({\varvec{x}}-{\varvec{1}})=0$, we set ${\varvec{\lambda }}=\max \{0,-({\varvec{w}}-\mu {\varvec{v}})\}$ and ${\varvec{\nu }}=\max \{0,{\varvec{w}}-\mu {\varvec{v}}-{\varvec{1}}\}$. Then, for given ${\varvec{w}}$, ${\varvec{x}}$ is a function depending only on $\mu$:

$$\begin{aligned} {{\varvec{x}}(\mu ;{\varvec{w}})\mathrel {\mathop :}=\max \{0,\textrm{min}\{1,{\varvec{w}}-\mu {\varvec{v}}\}\}.} \end{aligned}$$

(14)

Therefore, we need to find $\mu ^*$ such that ${\varvec{x}}(\mu ^*;{\varvec{w}})$ satisfies the rest of the condition (13): the volume constraint ${\varvec{v}}^\textrm{T}{\varvec{x}}(\mu ^*;{\varvec{w}})=V_0$. As ${\varvec{v}}^\textrm{T}{\varvec{x}}(\mu ;{\varvec{w}})$ is a monotonically decreasing piecewise linear function of $\mu$ and $0<V_0<n$, $\mu ^*$ exists in $[\min \{w_1/v_1,\ldots ,w_n/v_n\}-1,\max \{w_1/v_1,\ldots ,w_n/v_n\}]$.

In practice, all we need to do is to find the solution $\mu ^*$ of

$$\begin{aligned} {{\varvec{v}}^\textrm{T}{\varvec{x}}(\mu ;{\varvec{w}})=V_0} \end{aligned}$$

(15)

by e.g. the bisection method (in the numerical experiments, we use MATLAB fzero function). The projection is then calculated by

$$\begin{aligned} {{\Pi }_{S}({\varvec{w}})={\varvec{x}}(\mu ^*;{\varvec{w}}).} \end{aligned}$$

(16)

3.2.2 Case of inequality volume constraint

In the case that the volume constraint is an inequality constraint, the projection can be calculated in a manner similar to Sect. 3.2.1. The KKT condition is as follows:

$$\begin{aligned} \begin{aligned}&{\varvec{x}}-{\varvec{w}}-{\varvec{\lambda }}+{\varvec{\nu }}+\mu {\varvec{v}}={\varvec{0}},\\&{\varvec{v}}^\textrm{T}{\varvec{x}}\le V_0,\ \ {\varvec{0}}\le {\varvec{x}}\le {\varvec{1}},\\&{\varvec{\lambda }}\ge {\varvec{0}},\ \ {\varvec{\nu }}\ge {\varvec{0}},\ \ \mu \ge 0,\\&{\varvec{\lambda }}^\textrm{T}{\varvec{x}}=0,\ \ {\varvec{\nu }}^\textrm{T}({\varvec{x}}-{\varvec{1}})=0,\ \ \mu ({\varvec{v}}^\textrm{T}{\varvec{x}}-V_0)=0. \end{aligned} \end{aligned}$$

(17)

If ${\varvec{x}}(0;{\varvec{w}})$ satisfies the volume constraint ${\varvec{v}}^\textrm{T}{\varvec{x}}(0;{\varvec{w}})\le V_0$, then ${\varvec{x}}(0;{\varvec{w}})$ satisfies the KKT condition (17), and hence

$$\begin{aligned} {{\Pi }_{S}({\varvec{w}})={\varvec{x}}(0;{\varvec{w}}).} \end{aligned}$$

(18)

If ${\varvec{v}}^\textrm{T}{\varvec{x}}(0;{\varvec{w}})>V_0$, then there exists $\mu ^*\in [0,\max \{w_1/v_1,\ldots ,w_n/v_n\}]$ such that ${\varvec{v}}^\textrm{T}{\varvec{x}}(\mu ^*;{\varvec{w}})=V_0$. Then the projection is written as

$$\begin{aligned} {{\Pi }_{S}({\varvec{w}})={\varvec{x}}(\mu ^*;{\varvec{w}}).} \end{aligned}$$

(19)

The constraints of the topology optimization problems in this paper are expressed as the intersection of box constraints (${\varvec{a}}\le {\varvec{x}}\le {\varvec{b}}$) and a single linear constraint. Therefore, we only need to find the scalar Lagrange multiplier $\mu$ which can be efficiently calculated by e.g. the bisection method. Note that, in a problem with general linear constraints, the calculation of projection becomes convex quadratic programming and computationally expensive in a large-scale problem.

3.3 Inertial projected gradient method

The projected gradient method has a low iteration cost and is suited for a large-scale optimization problem such as a topology optimization problem. However, the convergence of the projected gradient method is not very fast. Recently, the acceleration techniques of the projected gradient method and, more generally, the proximal gradient method have been attracting much attention.

There are several different kinds of acceleration techniques for the projected gradient method for nonconvex optimization. We adopt iPiano (inertial proximal algorithm for nonconvex optimization) [25] to solve topology optimization problems. Its simple update scheme is suited for topology optimization. It does not require additional evaluations of the objective value. Most accelerated projected gradient methods [15, 18] require evaluations of the objective value more than once at each iteration to update the design variable or to guarantee the convergence. Moreover, some methods [37] require FEA at an infeasible point where the global stiffness matrix may become singular. Although iPiano does not have a faster convergence rate than the projected gradient method, in the numerical examples we show that it is practically faster than the projected gradient method for topology optimization problems.

In iPiano, the design variable is updated as follows:

$$\begin{aligned} {{\varvec{x}}^{k+1}={\Pi }_S ({\varvec{x}}^k-\alpha _k\nabla f({\varvec{x}}^k)+\beta _k({\varvec{x}}^k-{\varvec{x}}^{k-1})),} \end{aligned}$$

(20)

where $\alpha _k>0$ and $\beta _k\ge 0$ are step size parameters discussed in Sect. 3.4. The term $\beta _k({\varvec{x}}^k-{\varvec{x}}^{k-1})$ in (20) is a so-called inertial (or momentum) term which accelerates the convergence. When $\beta _k\equiv 0$, (20) coincides with the classical projected gradient method (10).

3.4 Step size policy

To achieve faster and guaranteed convergence to a stationary point, the choice of the step size parameters is crucial. One choice is to use constant step size parameters. To choose constant step size parameters of a first-order method, the Lipschitz constant of the gradient of the objective function is often used as a guideline. For a differentiable function $\Psi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}$, we call $L\ge 0$ the Lipschitz constant of $\nabla \Psi$ over $D\subset {\mathbb {R}}^n$ if it satisfies

$$\begin{aligned} {\Vert \nabla \Psi ({\varvec{x}})-\nabla \Psi ({\varvec{y}})\Vert \le L\Vert {\varvec{x}}-{\varvec{y}}\Vert \quad (\forall {\varvec{x}},{\varvec{y}}\in D).} \end{aligned}$$

(21)

If such an L exists, we say that $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ is L-smooth over D. Many first-order methods including the proposed method assume the L-smoothness of the objective function. In the topology optimization problems in Sect. 2, the objective functions are L-smooth over S, since they are rational functions and twice continuously differentiable on $[0,1]^n$. See [3] for more details on the L-smoothness. In [25], the condition for constant step size parameters of iPiano (20) to guarantee the convergence is introduced as follows:

$$\begin{aligned} {\alpha _k\equiv \alpha <\frac{2(1-\beta )}{L},\quad \beta _k\equiv \beta \in [0,1).} \end{aligned}$$

(22)

Although this constant step size policy is simple, there are two drawbacks. One is that it requires a good estimation of L, the Lipschitz constant of the gradient of the objective function. This estimation is difficult in topology optimization. The other is that a constant step size cannot benefit from a smaller local value of L. The Lipschitz constant over $D'\subset D$ can possibly be much less than the Lipschitz constant over D, and the points generated by an algorithm can be restricted to a smaller subset of D as iterations progress. In this case, the acceptable step size for the convergence guarantee becomes greater than (22) as iterations progress. For faster convergence, it is better to adjust the step size parameters at each iteration.

In case that the step size parameters change at each iteration, they must satisfy the following conditions to guarantee the convergence [25]:

$$\begin{aligned} {\alpha _k=2(1-\beta _k)/(2{a_2}+L_k),\quad \beta _k=\left. (b-1)\Big / \left( b-\frac{1}{2}\right) \right. ,} \end{aligned}$$

(23)

where $b=\left( a_1+\frac{L_k}{2}\right) /\left( a_2+\frac{L_k}{2}\right)$ and $a_1\ge a_2>0$ are constant parameters, and $L_k$ is a parameter satisfying the following descent condition:

$$\begin{aligned} {f({\varvec{x}}^{k+1})\le f({\varvec{x}}^{k})+\langle \nabla f({\varvec{x}}^{k}),{\varvec{x}}^{k+1}-{\varvec{x}}^{k}\rangle +\frac{L_k}{2}\Vert {\varvec{x}}^{k+1}-{\varvec{x}}^k\Vert ^2.} \end{aligned}$$

(24)

Note that if $L_k\ge L$, (24) is always satisfied (see e.g. [3] for the proof). However, too large $L_k$ leads to a small step size and hence slow convergence. Also, too small $L_k$ leads to a large step size and numerical instability or even divergence. Thus, we need to choose $L_k$ appropriately for fast and stable convergence.

Backtracking is a popular way to choose the step size parameter $L_k$ in a first-order method (see e.g. [3]). In the backtracking procedure, we start with a sufficiently small initial value s for $L_k$ and repeat multiplying $\eta >1$ until the descent condition (24) is satisfied, i.e. we set $L_k =s\eta ^l$ where l is the smallest nonnegative integer such that $L_k =s\eta ^l$ satisfies (24). However, the backtracking procedure requires evaluations of the objective value many times to check if the descent condition (24) is satisfied (Note that if we change the value of $L_k$, the objective value $f({\varvec{x}}^{k+1})$ of the left-hand side of (24) changes). This means we need to perform FEA many times to decide the step size parameters, which is computationally expensive.

Therefore, we estimate the initial value for the backtracking procedure by

$$\begin{aligned} {L_k=\max \left\{ L_\textrm{min},\frac{\Vert \nabla f({\varvec{x}}^k)-\nabla f({\varvec{x}}^{k-1})\Vert }{\Vert {\varvec{x}}^k-{\varvec{x}}^{k-1}\Vert }\right\} ,} \end{aligned}$$

(25)

where $L_\textrm{min}$ is a small positive constant to avoid the numerical instability, and we choose sufficiently large $L_0$ for the first iteration of the inertial projected gradient method. If $L_k$ in (25) does not satisfy (24), then we update $L_k\leftarrow \eta L_k$ in the same way as the conventional backtracking procedure. The estimate (25) is motivated by the definition of L in (21). By definition, we see that $L_k$ in (25) is no smaller than $L_\textrm{min}$ and no greater than L. Although $L_k\ge L$ is a sufficient condition to satisfy (24), in numerical examples, $L_k$ in (25) satisfies the descent condition (24) in most cases, and no additional FEAs are needed. By this step size policy, we can automatically adjust the step size regardless of the problem setting (e.g. the design domain, the boundary conditions and the number of finite elements).

Remark

The step size (25) has a relationship with the Barzilai–Borwein step sizes [2]. For the simplicity of notation, we set ${\varvec{s}}^{k-1}={\varvec{x}}^k-{\varvec{x}}^{k-1}$ and ${\varvec{y}}^{k-1}=\nabla f({\varvec{x}}^k)-\nabla f({\varvec{x}}^{k-1})$. The relationship

$$\begin{aligned} {\frac{|\langle {\varvec{s}}^{k-1},{\varvec{y}}^{k-1}\rangle |}{\Vert {\varvec{s}}^{k-1}\Vert ^2} \le \frac{\Vert {\varvec{y}}^{k-1}\Vert }{\Vert {\varvec{s}}^{k-1}\Vert } \le \frac{\Vert {\varvec{y}}^{k-1}\Vert ^2}{|\langle {\varvec{s}}^{k-1},{\varvec{y}}^{k-1}\rangle |}} \end{aligned}$$

(26)

immediately follows from the Cauchy–Schwarz inequality. The right-hand side and the left-hand side of (26) are inverses of the Barzilai–Borwein step sizes. The Barzilai–Borwein step sizes are derived from an approximation to the secant equation underlying the quasi-Newton method, and converge fast for convex quadratic programming. We can use the inverse of the Barzilai–Borwein step sizes instead of $\Vert {\varvec{y}}^{k-1}\Vert /\Vert {\varvec{s}}^{k-1}\Vert$ in (25). However, a large step size leads to many FEAs, and a small step size leads to slow convergence, thus we use (25).

Based on all of the above discussions, the algorithm of the inertial projected gradient method for topology optimization is described in Algorithm 1. The stopping criteria are discussed in the next section. Each iteration of Algorithm 1 consists of vector additions, scalar multiplications and projections other than FEA, thus computationally cheap even if the problem size is very large.

4 Numerical examples

We conduct the numerical experiments in three examples: the compliance minimization problem, the heat conduction problem and the compliant mechanism problem. We compare the proposed method with popular optimization algorithms for topology optimization: the optimality criteria method (OC) [1, 6] and the globally convergent version of the method of moving asymptotes (GCMMA) [32, 33]. As GCMMA is designed for an inequality-constrained optimization problem, for the numerical experiments on GCMMA we change the volume constraints in the compliance minimization problems and the heat conduction problems to the inequality-volume constraint ${\varvec{v}}^\textrm{T}{\varvec{x}}\le V_0$.² We also make comparisons with the general nonlinear optimization algorithms: the interior-point method (IPM) and the sequential quadratic programming (SQP) of MATLAB fmincon. We use the limited-memory-BFGS (L-BFGS) formula for the Hessian approximation in IPM and SQP. The L-BFGS formula has a low iteration cost and is more suited for a large-scale problem than the BFGS formula or the exact Hessian.

The experiments have been run on iMac (Intel(R) Core i9, 3.6 GHz CPU, 128 GB RAM) and MATLAB R2020b. The MATLAB code of topology optimization is based on [1, 7, 14]. The following values are common in all the experiments: $E_0=1$, $E_\textrm{min}=10^{-3}$ and $p=3$. The Poisson ratio in the local stiffness matrix $K_e\ (e=1,\ldots ,n)$ is 0.3. The filter radius used for the density filter is 0.05 times the number of elements in the horizontal direction. The initial point of each algorithm is ${\varvec{x}}^0=(V_0/n){\varvec{1}}$. The parameters of the proposed method are follows: $L_0=10$, $L_\textrm{min}=10^{-3}$, $\eta =1.5$, $a_1=0.1$ and $a_2=10^{-6}$.

4.1 Optimality measure and stopping criterion

The proposed method aims to find a stationary point of problem (7), i.e. the point satisfying the first-order optimality condition (see e.g. [8]):

$$\begin{aligned} {\langle \nabla f({\varvec{x}}^*),{\varvec{x}}-{\varvec{x}}^*\rangle \ge 0\ \ (\forall {\varvec{x}}\in S).} \end{aligned}$$

(27)

For a given differentiable function $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$, a convex set $S\subset {\mathbb {R}}^n$ and $\alpha >0$, define the gradient mapping $G_\alpha :{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ by

$$\begin{aligned} {G_\alpha ({\varvec{x}})\mathrel {\mathop :}=\frac{1}{\alpha }({\varvec{x}}-{\Pi }_S({\varvec{x}}-\alpha \nabla f({\varvec{x}}))).} \end{aligned}$$

(28)

As a first-order optimality measure, we use the Euclidean norm of the gradient mapping $\Vert G_\alpha ({\varvec{x}})\Vert$. We can easily see $G_\alpha ({\varvec{x}})$ coincides with the gradient $\nabla f({\varvec{x}})$ when $S={\mathbb {R}}^n$. Thus, the gradient mapping is a generalization of the gradient. Moreover, $\Vert G_\alpha ({\varvec{x}})\Vert$ is a continuous function of ${\varvec{x}}$, and $\Vert G_\alpha ({\varvec{x}})\Vert =0$ if and only if ${\varvec{x}}$ is a stationary point of the problem in the form of (7) (see [3] for the proof). Thus, we can use the gradient mapping $\Vert G_\alpha ({\varvec{x}})\Vert$ as a first-order optimality measure of ${\varvec{x}}$. We set $\alpha =1$ for simplicity. Note that $G_1({\varvec{x}}^k)$ corresponds to the proximal residual defined in [25]. This optimality measure can be used for any algorithms. We calculate $\Vert G_1({\varvec{x}}^k)\Vert$ at each iteration of each algorithm independent of the update of the design variables ${\varvec{x}}^k$ so that we can equally measure the first-order optimality of each point generated by each algorithm. We use $\Vert G_1({\varvec{x}}^k)\Vert <\epsilon$ as a stopping criterion for sufficiently small $\epsilon >0$.

The reason why we adopt the gradient mapping for comparison is that other choices are inaccurate or unable to equally compare the optimality of points generated by different algorithms. As the projected gradient method and OC do not calculate the Lagrange multipliers at each iteration, it is difficult to adopt the KKT residual norm, which is used in GCMMA and MATLAB fmincon. Also, the change of the objective function value $f({\varvec{x}}^{k+1})-f({\varvec{x}}^k)$ or the design variable $\Vert {\varvec{x}}^{k+1}-{\varvec{x}}^k\Vert$ can be strongly influenced by a step size, i.e. if we choose an arbitrary small step size, these values become arbitrarily small, and the algorithm terminates with a very small number of iterations even though the current point is not optimal.

4.2 Compliance minimization problem

We consider the compliance minimization problem of the MBB beam shown in Fig. 2. Note that, by utilizing the symmetry, we consider only the right half of the entire design domain. The upper limit of the volume is $V_0=0.5n$. The magnitude of the external force is 1.

4.2.1 Effectiveness of acceleration and step size policy

We compare the proposed method with the original (non-inertial) projected gradient method (PG) to show the effectiveness of the acceleration by the inertial term. Also, to show the effectiveness of the proposed step size policy, we compare it with the constant step size policy (22).

The objective function value and the norm of the gradient mapping at each iteration of 500 iterations for $n=2700$ are shown in Figs. 5 and 6, respectively. Note that we omit after 100 iterations in Fig. 5 because of small changes. Also, we omit the figures of the obtained solutions, as not much difference is seen.

Fig. 5

Objective function value

Fig. 6

Optimality measure

Although the proposed method does not have an improved convergence rate theoretically, both the objective function value and the norm of the gradient mapping decrease faster than PG as shown in Figs. 5 and 6. Moreover, when we use a constant step size parameter $L_k=10\ (\forall k)$ or $L_k=0.5\ (\forall k)$, the convergence gets slow. In particular, the result of $L_k=0.5$ shows that too large step size leads to numerical instability (large objective values at the first few iterations). In contrast, the step size parameter $L_k$ of the proposed method changes drastically at the first few iterations as shown in Fig. 7. This shows that the proposed step size policy effectively adjusts the step size for faster convergence.

Fig. 7

$L_k$ by the proposed step size policy

4.2.2 Comparison with existing methods

We compare the proposed method with OC, GCMMA, IPM and SQP. We use the same stopping criterion $\Vert G_1({\varvec{x}}^k)\Vert <10^{-3}$ for all the algorithms. The maximum number of iterations is 2000. The total computational time and the computational time per iteration in seconds versus the number of finite elements n are shown in Figs. 8 and 9, respectively. Note that the graphs of Proposed and OC are overlapped in Fig. 9. The computational time of SQP is shown only for small values of n because it increases rapidly as n becomes large. To see how the objective value and the optimality measure decrease, we show these values of the proposed method, OC, MMA and IPM with 2000 iterations when $n=$ 10,800 in Figs. 10 and 11. Note that the proposed method satisfies the stopping criterion before 2000 iterations. The obtained designs are shown in Fig. 12. Table 1 lists the detailed results: the number of iterations “$\mathrm {iter.}$”, the number of FEA, the total computational time t, the computational time per iteration $t_\textrm{it}$, and the objective value $f({\varvec{x}})$ and the Euclidean norm of the gradient mapping $\Vert G_1({\varvec{x}})\Vert$ at the last iteration. Note that IPM automatically stops before 2000 iterations for $n=$ 10,800, 19,200 and 30,000, although the obtained solution does not satisfy the stopping criterion. This is because the MATLAB fmincon stops automatically if the step size becomes too small.

Fig. 8

Total computational time (compliance minimization problem)

Fig. 9

Computational time per iteration (compliance minimization problem)

Fig. 10

Objective function value (compliance minimization problem, $n=$ 10,800)

Fig. 11

Optimality measure (compliance minimization problem, $n=$ 10,800)

Fig. 12

Solutions by each algorithm (compliance minimization problem, $n=$ 10,800)

Table 1 Numerical results of the compliance minimization problem

From Figs. 8 and 9, we see that the computational cost per iteration of IPM and SQP increases drastically as the number of finite elements n increases. SQP has a particularly high iteration cost as it solves a quadratic programming problem at each iteration. Therefore, these nonlinear programming solvers are impractical in a large-scale optimization problem. We omit IPM and SQP in numerical experiments hereafter, as they are particularly slow. GCMMA also has a high iteration cost compared to the proposed method and OC as it solves a convex subproblem at each iteration. The proposed method and OC consist of the vector addition, the scalar multiplication and the bisection method (solution of a single variable equation), and hence have low iteration costs. The number of FEA of the proposed method in Table 1 shows that the proposed step size policy effectively estimates an appropriate step size for stable convergence because almost no additional FEA is needed. As shown in Table 1, OC and GCMMA do not stop until the 2000 iteration. In fact, Fig. 11 shows that the optimality measures of OC and GCMMA do not decrease sufficiently. Note that OC is a heuristic algorithm and the convergence to a stationary point is not guaranteed. In contrast, the proposed method stops at fewer iterations than the other algorithms, and hence the proposed method has a shorter computational time as observed in Fig. 8. Figure 10 shows that the objective function value of the proposed method also decreases faster than those of the other algorithms. Moreover, the solution of the proposed method satisfies the optimality condition with higher accuracy as shown in Fig. 11, which means that the solution is a more reliable optimal solution. In Fig. 12, the obtained solutions are slightly different (compare the angles of the right inclined bars). There is no guarantee that the solution obtained by OC is a local optimum since OC is heuristic (the objective function value is larger as shown in Table 1). In contrast, the solution obtained by the proposed method can be considered at least a stationary point.

4.2.3 Large-scale problems

To show the effectiveness of the proposed method in large-scale problems, we make a comparison with OC and GCMMA. To see the practical performance, we use different stopping criteria, which are commonly used for the three algorithms. The stopping criterion of the proposed method and OC is $\Vert G_1({\varvec{x}}^{k})\Vert <10^{-3}$ [14, 27] and $\Vert {\varvec{x}}^{k+1}-{\varvec{x}}^{k}\Vert <10^{-3}$ [25], respectively. GCMMA stops when the Euclidean norm of the KKT residual [32, 33] is less than $10^{-3}$. The maximum number of iterations is 3000.

We show the number of iterations until the stopping criteria are satisfied for small-scale problems in Fig. 13. OC satisfies the stopping criteria for only small values of n as shown in Fig. 13. As OC does not satisfy the stopping criteria until the maximum number of iterations, the computational time of OC becomes huge when n gets large. Therefore, we omit OC for large-scale problems. A convergence guarantee is important to properly stop the algorithm and obtain a high-quality solution.

The total computational time and the optimality measure $\Vert G_1({\varvec{x}}^{k})\Vert$ of the solutions in large-scale problems are shown in Figs. 14 and 15, respectively. We also add the results of the proposed method with the stopping criterion $\Vert G_1({\varvec{x}}^{k})\Vert <10^{-2}$.

Fig. 13

Number of iterations (small-scale problem)

Fig. 14

Total computational time (large-scale problem)

Fig. 15

Optimality measure when each algorithm stops (large-scale problem)

Figure 14 shows that the proposed method and GCMMA converge at a moderate amount of time for large-scale problems. However, the solutions of GCMMA satisfy the optimality condition only with low accuracy compared with the proposed method with $\Vert G_1({\varvec{x}}^{k})\Vert <10^{-3}$, as shown in Fig. 15. The proposed method with the stopping criterion $\Vert G_1({\varvec{x}}^{k})\Vert <10^{-2}$ can obtain the solutions satisfying the optimality condition with similar or higher accuracy than those of GCMMA for much shorter computational time. This shows the effectiveness of the proposed method for obtaining an optimal solution with moderate accuracy in a large-scale problem.

4.3 Heat conduction problem

In this section, we consider the heat conduction problem shown in Fig. 3. We use the following parameters: $V_0=0.4n$ and ${\varvec{p}}=(10/n){\varvec{1}}$.

We compare the proposed method with OC and GCMMA. The stopping criterion of the algorithms is $\Vert G_1({\varvec{x}}^k)\Vert <10^{-3}$ and the maximum number of iterations is 2000. The total computational time versus the number of finite elements n is shown in Fig. 16. Note that OC and GCMMA reach the maximum number of iterations. The objective value and the optimality measure until 2000 iterations for $n=$ 10,000 are shown in Figs. 17 and 18, respectively. Note that the proposed method satisfies the stopping criterion before 2000 iterations. The designs obtained by the three algorithms are shown in Fig. 19. Table 2 lists the detailed results in the same manner as Table 1 for the compliance minimization problem.

Fig. 16

Total computational time (heat conduction problem)

Fig. 17

Objective function value (heat conduction problem, $n=$ 10,000)

Fig. 18

Optimality measure (heat conduction problem, $n=$ 10,000)

Fig. 19

Solutions obtained by the three algorithms (heat conduction problem, $n=$ 10,000)

Table 2 Numerical results of the heat conduction problem

Figure 16 and Table 2 show a trend similar to the compliance minimization problem; the proposed method has a low iteration cost, achieves faster convergence and satisfies the optimality condition with higher accuracy than the other methods. Figure 19 shows that the designs obtained by the three algorithms are different from each other. This suggests that the heat conduction problem has more local optimal solutions than the compliance minimization problem.

4.4 Compliant mechanism problem

In this section, we consider the compliant mechanism problem shown in Fig. 4. Note that, by utilizing the symmetry, we consider only the lower half of the entire design domain. We use the following parameters: $V_0=0.3n$ and $k_\textrm{in}=k_\textrm{out}=0.01$. The magnitude of the external force is 1.

We compare the proposed method with OC and GCMMA. The stopping criteria of the algorithms are $\Vert G_1({\varvec{x}}^k)\Vert <10^{-3}$ and $f({\varvec{x}}^k)<-0.1$. The latter criterion is added to obtain a meaningful solution. The direction of the vector ${\varvec{u}}_\textrm{out}$ in Fig. 4 is the negative direction of the nodal displacement in the global coordinate system. Therefore, we seek to find a solution with a negative objective value. The maximum number of iterations is 2000. The total computational time versus the number of finite elements n is shown in Fig. 20. The objective value and the optimality measure until 2000 iterations for $n=9800$ are shown in Figs. 21 and 22, respectively. The designs obtained by the three algorithms are shown in Fig. 23. Table 3 lists the detailed results in the same manner as Table 1 for the compliance minimization problem.

Fig. 20

Total computational time (compliant mechanism problem)

Fig. 21

Objective function value (compliant mechanism problem, $n=9800$)

Fig. 22

Optimality measure (compliant mechanism problem, $n=9800$)

Fig. 23

Solutions by each algorithm (compliant mechanism problem, $n=9800$)

Table 3 Numerical results of the compliant mechanism problem

Figure 20 and Table 3 show a trend similar to the compliance minimization problem; the proposed method has a low iteration cost, achieves faster convergence and satisfies the optimality condition with higher accuracy than the other methods. However, as shown in Fig. 21, the decrease of the objective value of the proposed method slows down in the region where the sign of the objective value changes (the direction of the displacement of the output node changes). A typical design of that region is shown in Fig. 24. In that region, the norm of the gradient of the objective function is small. GCMMA is also slowed down in that region because it required 25 evaluations of the objective values at the first 5 iterations. Figure 23 shows that the design obtained by the three algorithms are similar to each other.

Fig. 24

Design at the 20th iteration of the proposed method ($\Vert \nabla f({\varvec{x}}^k)\Vert =3.10\times 10^{-3}$)

5 Conclusion

In this paper, we have presented an inertial projected gradient method for solving large-scale topology optimization problems. For a topology optimization problem under a single linear equality or inequality constraint with a box constraint, we have shown that the projection onto the feasible set can be efficiently computed, and hence the projected gradient method can be applied effectively. We have proposed to use an inertial version of the projected gradient method by Ochs et al. [25] to accelerate the convergence. We have also considered an adaptive step size policy to further reduce the computational cost. The proposed method is easy to implement. Moreover, the proposed method has the global convergence property.

In numerical examples, we have shown that the iteration cost of the proposed method is as low as that of the optimality criteria method. It has been demonstrated that the conventional algorithms used for topology optimization (the optimality criteria method and the method of moving asymptotes) achieve the first-order optimality condition with low accuracy. In contrast, the proposed method converges fast to a point satisfying the first-order optimality condition with higher accuracy. The proposed method is also effective for large-scale problems. We have shown that, for a topology optimization problem with simple linear constraints such as the compliance minimization problem, it is more efficient to use the proposed method than to use a general-purpose nonlinear programming solver such as the interior-point method and the method of moving asymptotes, because the proposed method takes advantage of a simple problem structure.

We have dealt with topology optimization problems with only linear constraints. To deal with large-scale optimization problems with nonlinear constraints, other first-order algorithms are to be considered. Large-scale optimization is rapidly growing especially in machine learning and data science communities. There may be some efficient large-scale optimization techniques that can be useful for developing new topology optimization algorithms.