Topology optimization with local stress constraints: a stress aggregation-free approach

Abstract

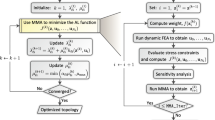
This paper presents a consistent topology optimization formulation for mass minimization with local stress constraints by means of the augmented Lagrangian method. To solve problems with a large number of constraints in an effective way, we modify both the penalty and objective function terms of the augmented Lagrangian function. The modification of the penalty term leads to consistent solutions under mesh refinement and that of the objective function term drives the mass minimization towards black and white solutions. In addition, we introduce a piecewise vanishing constraint, which leads to results that outperform those obtained using relaxed stress constraints. Although maintaining the local nature of stress requires a large number of stress constraints, the formulation presented here requires only one adjoint vector, which results in an efficient sensitivity evaluation. Several 2D and 3D topology optimization problems, each with a large number of local stress constraints, are provided.

Appendices

Appendix A: Augmented Lagrangian method for inequality constraints

The procedure described in Section 4 is designed to solve optimization problems with equality constraints. For the sake of completeness, and to provide the reader interested in applying the AL method to problems with inequality constraints, we present an extension of the AL method for inequality constraints. As usual, we handle inequality constraints by introducing slack variables s_j,j = 1,…,N_c to the optimization problem (Nocedal and Wright 2006). Consider the following optimization problem with inequality constraints:

$$ \begin{array}{ll} \underset{\textbf{z}\in\mathbb{R}^{n}}{\min} ~~&f(\textbf{z})\\ ~~~\text{s.t.} ~~&g_{j}(\textbf{z}) \leq 0~~\forall j=1,\ldots,N_{c}\\ &\textbf{L}\leq\textbf{z}\leq \textbf{U}, \end{array} $$

(37)

where L and U define the lower and upper bounds of the design variables, respectively. Introducing slack variables, constraints g_j(z) ≤ 0 are rewritten as follows:

$$ h_{j}(\textbf{z})=g_{j}(\textbf{z})+s_{j}=0,~s_{j}\ge0,~j=1,\ldots,N_{c}. $$

(38)

Consequently, the approximate sub-problem that needs to be solved at the k th step of the AL method is as follows:

$$ \begin{array}{ll} \underset{\textbf{z},~\textbf{s}}{\min} ~~&J^{(k)}(\textbf{z},\textbf{s})=f(\textbf{z})+\sum\limits_{j=1}^{N_{c}}\left[\lambda_{j}^{(k)}\!\left( g_{j}(\textbf{z})+s_{j}\right)+\frac{\mu^{(k)}}{2}\left( g_{j}(\textbf{z})+s_{j}\right)^{2}\right]\\ ~~~\text{s.t.} ~~&\textbf{L}\leq\textbf{z}\leq \textbf{U}\\ &s_{j}\ge 0~~\forall j=1,\ldots,N_{c}. \end{array} $$

(39)

The minimization of J^(k)(z,s) with respect to the slack variables is obtained explicitly for any fixed z by solving the optimization problem as follows:

$$ \begin{array}{ll} \underset{s_{j}}{\min} ~~&\left[\lambda_{j}^{(k)}\left( g_{j}(\textbf{z})+s_{j}\right)+\frac{\mu^{(k)}}{2}\left( g_{j}(\textbf{z})+s_{j}\right)^{2}\right]\\ ~~~\text{s.t.} ~~&s_{j}\ge 0. \end{array} $$

(40)

The optimization statement (40) is defined in terms of the slack variable, s_j, associated with constraint g_j. As a result, its solution can be found in closed form using the stationary conditions of the Lagrangian of Eq. (40), which leads to the following:

$$ s_{j}=\max\left[0,-\left( \frac{\lambda_{j}^{(k)}}{\mu^{(k)}}+g_{j}(\textbf{z})\right)\right]~~\forall j=1,\ldots,N_{c}. $$

(41)

Substituting (41) into (38) leads to the following:

$$ h_{j}(\textbf{z})=\max\left[g_{j}(\textbf{z}),-\frac{\lambda_{j}^{(k)}}{\mu^{(k)}}\right]~~\forall j=1,\ldots,N_{c}. $$

(42)

Using (42), the inequality constraints g_j(z) ≤ 0 of (37) can be replaced by equality constraints, allowing the problem to be solved using the procedure described for solving the equality-constrained problem (6). As inferred from (42), the slack variables do not need to be computed explicitly, facilitating the implementation of the AL method with inequality constraints. One must recall that the Lagrange multiplier estimators, $\lambda _{j}^{(k)}$, and the penalty factor, μ^(k), remain constant for each AL sub-problem, and thus the AL function is continuously differentiable (with respect to the design variables) at each AL step. Despite the presence of the maximum function, the AL function used with (42) is differentiable even at the points in which $g_{j}(\textbf {z})=-\lambda _{j}^{(k)}/\mu ^{(k)}$.¹⁶ If (17) is substituted into (42), it follows that g_j(z) = h_j(z), which is the case in our implementation of the AL-based method. However, if one were to use a different stress constraint definition that can take negative values, then (42) (in its explicit form) would be necessary in the implementation.

Appendix B: Apparent “local” von Mises stress vs. stress measure

Here, we clarify the difference between the apparent “local” von Mises stress, σ^v, and the stress measure, $\widetilde {\sigma }^{\text {v}}$, described in Section 5.2. Using a stress measure of the form $\widetilde {\sigma }^{\text {v}}=\rho ^{\alpha }\sigma ^{\text {v}}$ is a typical procedure in the context of stress-based topology optimization (e.g., Bruggi and Duysinx 2012; Lee et al. 2012), because the apparent “local” von Mises stress is large in regions of low density. The high stresses in regions of low density can be seen in Fig. 14a (only regions with density above 0.05 are shown), which displays the normalized apparent “local” von Mises stress for the 16,380 mesh solution with linear filter of the L-bracket example in Table 3. We observe that the largest apparent local stress occurs at the boundaries between solid and void, in which the density is small due to the filter operator. In contrast, Fig. 14b shows the normalized stress measure of the same solution, in which the stress measure strictly satisfies the stress limit of 1. By adopting $\widetilde {\sigma }^{\text {v}}=\rho ^{0.5}\sigma ^{\text {v}}$, we reduce the effect of the vaguely defined stress in the regions of low density.

Fig. 14

Normalized apparent “local” von Mises stress a and normalized stress measure b for the 16,380 mesh solution with linear filter of the L-bracket example in Table 3. The stress is only displayed for the regions with density above 0.05. Because both stresses are normalized, the value of 1 represents the stress limit

Appendix C: Comparison of the piecewise vanishing constraint with ε-relaxation

We compare the optimization results obtained using our piecewise vanishing constraint with those obtained using the ε-relaxed constraint (Cheng and Guo 1997). The ε-relaxation approach used here is the one proposed by Cheng and Guo (1997) and Petersson (2001) in which we start with a value of ε = 0.01, and we set the lower bound of the design variable to ε². The value of ε is divided by two every time that we restart the AL parameters to gradually decrease the value of ε reaching a final value of ε = 0.000625. We also update the lower bound of the design variable so that it is always equal to ε².

Figure 15 displays the results that we obtain using each of these constraints. As compared to the designs obtained using the piecewise vanishing constraint, those obtained using the ε-relaxed constraint have a significantly larger volume and contain regions of pure solid material (which appear sub-optimal) near the bottom left corner of the bracket. Based on the information displayed on Fig. 15, the results obtained using the piecewise vanishing constraint outperform those obtained using ε-relaxation constraint in terms of both optimized volume and quality of results.

Fig. 15

Optimized topologies for an L-bracket obtained using the piecewise vanishing constraint (top) and using the ε-relaxed constraint (bottom)

Appendix D: Effect of weight factors γ_e

The introduction of weight factors γ_e is one of the main characteristics of the present formulation. Here, we investigate the effects of using the weight factors in the optimization results obtained for the L-bracket. Figure 16 presents the results that we obtain using γ_e, as well as, those not using γ_e. We observe that, as compared to the results obtained with γ_e, those obtained without γ_e have a higher final volume and have fewer beam-like elements. The factor γ_e helps the optimizer to overcome unfavorable local optima by increasing the relevance of the objective function in elements which have low stress value. If γ_e is not considered, the optimizer is likely to get trapped in a bad local optima with high volume, preventing it to achieve structures with more slender elements, as we expect for this benchmark problem.

Fig. 16

Optimized topologies for an L-bracket obtained when weight factors γ_e are considered (top) and when they are not considered (bottom)

Appendix E: Effect of scale factor η

The scale factor, η, is introduced to normalize the values of the AL penalization parameters, μ^(k) and $\lambda _{j}^{(k)}$, such that we eliminate the need for adjusting the numerical values of μ⁽¹⁾ and $\lambda _{j}^{(1)}$ for problems with different number of constraints. We demonstrate the effectiveness of the parameter η through the numerical results shown in Fig. 17. These results correspond to the optimized topologies obtained for the L-bracket when the parameter η is either used or not. For the case when the parameter η is not used, we re-calibrate the values of μ⁽¹⁾ and $\lambda _{j}^{(1)}$ for a mesh size of 16,380 elements, and these values are used to obtain the optimized topologies for the other mesh sizes. As the mesh is refined (i.e., as the number of constraints increases), the results obtained when η is not used are clearly worse than those obtained when η is used. That is because when η is not considered, the magnitude of the penalty parameter of the AL function (19) increases as the number of constraints increases. Without the η parameter to normalize this effect, the optimizer becomes trapped in local optima with higher volume.

Fig. 17

Optimized topologies for an L-bracket obtained when scale factor η is considered (top) and when it is not considered (bottom)

Appendix F: Effect of the number of AL parameter restarts

We investigate the effect of restarting the AL parameters, $\lambda _{j}^{(k)}$ and μ^(k), as well as the weight factors, $\gamma _{e}^{(k)}$, on the final solution (cf. Section 7.1). As illustrated by Fig. 18, restarting these parameters helps us achieve a solution with overall lower volume. The results presented in the figure correspond to the final solutions of the L-bracket problem with 16,380 elements that we obtained using the filter reduction approach for various numbers of restarts.

Fig. 18

Effect of the number of AL parameter restarts on the optimized topologies obtained for an L-bracket meshed with 16,380 elements: a no restart; b one restart; c two restarts; d three restarts; and e four restarts. As the number of restarts increases, the small-scale artifacts are removed and the optimized volume fraction becomes smaller

As shown by the results in Fig. 18, the topology obtained with no restart contains several small-scale artifacts, which cannot be removed without increasing the stress in the structure. As a result, the solution gets trapped in an unfavorable local optimum with higher volume. After the first restart, the small-scale features disappear and the final volume becomes smaller. If we keep restarting the AL parameters and weight factors when the optimization stagnates, the total volume that we are able to reach keeps decreasing because the optimizer is able to find local optima with lower volume.

Appendix G: Effect of stress limit $\sigma _{\lim }$

We analyze the effect of the stress limit, $\sigma _{\lim }$, in the optimization results obtained for the L-bracket with 16,380 elements. The optimization results obtained using our AL-based framework with the filter reduction scheme are depicted in Fig. 19. The results demonstrate that increasing the stress limit leads to designs with lower volume fraction and more slender members, yet all these designs are topologically similar. A more significant change of topology is observed when $\sigma _{\lim }\ge 80$ Pa, in which the vertical member of the left edge of the L-bracket begins to tilt. The results also demonstrate that the optimized volume decreases monotonically as we increase the stress limit. Although not shown in the figure, our numerical results also indicate that the minimum stress limit possible for this optimization problem is around 37 Pa. That is because the final volume obtained from the optimization results increase significantly as the stress limit approaches this value.

Fig. 19

Optimized volume of the L-bracket meshed with 16,380 elements as a function of the stress limit

Appendix H: Nomenclature

α :

Parameter used to update penalty parameter μ^(k)

λ ^(k) :

Vector of approximated Lagrange multipliers at the k th iteration of the AL method

ξ :

Adjoint vector used for sensitivity evaluation

η :

Scale factor used in the AL function (19)

γ_L, γ_U:

Lower and upper bounds of weight factors γ_e, respectively

γ _e :

Weight factor for element e used in the modified AL function (19)

μ ^(k) :

Penalty parameter at the k th iteration of the AL method

ν :

Poisson’s ratio of solid material

$\sigma _{e}^{\text {v}}$ :

von Mises stress at the centroid of element e

$\sigma _{\lim }$ :

Stress limit for a given material

𝜖 :

Ersatz stiffness

ε :

Relaxation parameter in ε-relaxed approach

ρ :

Vector of filtered densities

$\tilde {\rho }_{e}$ :

Volume fraction of element e, defined using a smooth Heaviside projection function

Δ:

Infinitesimal quantity

E ₀ :

Young’s modulus of solid material

J^(k)(z):

Augmented Lagrangian function at iteration k

N _c :

Number of stress constraints

N _e :

Number of elements in a finite element mesh

β:

Mass penalization parameter used in the smooth Heaviside projection function

K :

Global stiffness matrix

P :

Filter matrix

f :

Global force vector

k _e :

Element stiffness matrix

s :

Vector of slack variables

u :

Global displacement vector

z :

Vector of design variables

a_i, b_i:

Parameters used to define the evolution of weight factors γ_e (i = 1, 2)

f :

Objective function

g_j(z):

j th stress constraint

h :

Equality constraint

h_j(z):

j th modified stress constraint used in the AL method with inequality constraints

m(z):

Mass of the structure

p :

Stiffness penalization parameter

q :

Relaxation parameter in qp-relaxed approach

r :

Filter radius

s :

Exponent of the polynomial filter

v _e :

Volume of element e for density equal one