Abstract
Discrete Fenchel duality is one of the central issues in discrete convex analysis. The Fenchel-type min–max theorem for a pair of integer-valued M\(^{\natural }\)-convex functions generalizes the min–max formulas for polymatroid intersection and valuated matroid intersection. In this paper we establish a Fenchel-type min–max formula for a pair of integer-valued integrally convex and separable convex functions. Integrally convex functions constitute a fundamental function class in discrete convex analysis, including both M\(^{\natural }\)-convex functions and L\(^{\natural }\)-convex functions, whereas separable convex functions are characterized as those functions which are both M\(^{\natural }\)-convex and L\(^{\natural }\)-convex. The theorem is proved by revealing a kind of box integrality of subgradients of an integer-valued integrally convex function. The proof is based on the Fourier–Motzkin elimination.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Discrete Fenchel duality is one of the central issues in discrete convex analysis [7, 16, 17, 19, 20]. In this paper we establish a Fenchel-type min–max formula for a pair of integer-valued integrally convex and separable convex functions.
Integrally convex functions, due to Favati–Tardella [3], constitute a fundamental function class in discrete convex analysis, and almost all kinds of discrete convex functions are known to be integrally convex. Indeed, separable convex, L-convex, L\(^{\natural }\)-convex, M-convex, M\(^{\natural }\)-convex, L\(^{\natural }_{2}\)-convex, and M\(^{\natural }_{2}\)-convex functions are known to be integrally convex [17]. Multimodular functions [10] are also integrally convex, as pointed out in [18]. Moreover, BS-convex and UJ-convex functions [8] are integrally convex. Discrete midpoint convex functions [15] and directed discrete midpoint convex functions [29] are also integrally convex.
The concept of integral convexity is used in formulating discrete fixed point theorems and found applications in economics and game theory [12, 20, 30]. A proximity theorem for integrally convex functions is established in [14] together with a proximity-scaling algorithm for minimization. Fundamental operations for integrally convex functions such as projection and convolution are investigated in [13, 21, 22]. Integer-valued integrally convex functions enjoy integral biconjugacy [24]. Section 2 of this paper describes the definition and technical properties of integrally convex functions that we need in this paper.
The discrete Fenchel-type min–max theorem is formulated in terms of conjugate functions. For an integer-valued function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) with \(\mathrm{dom\,}f \ne \emptyset\), we define \(f^{\bullet }: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) by
called the integral conjugate of f. Here, \(\langle p, x \rangle = \sum _{i=1}^{n} p_{i} x_{i}\) is the inner product of \(p=(p_{1}, p_{2}, \ldots , p_{n})\) and \(x=(x_{1}, x_{2}, \ldots , x_{n})\), and for a function \(h: {\mathbb {Z}}^{n} \rightarrow {\mathbb {R}}\cup \{ -\infty , +\infty \}\) in general, \(\mathrm{dom\,}h = \{ x \in {\mathbb {Z}}^{n} \mid -\infty< h(x) < +\infty \}\) is called the effective domain of h. Note that \(f^{\bullet }(p)\) may be \(+\infty\) and hence using “\(\sup\)” (supremum) in (1.1) would be formally more precise but we choose to use “\(\max\)” (maximum). The concave version of the conjugate function can also be defined for an integer-valued function \(g: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\). Namely, we define \(g^{\circ }: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\) by
and call this function \(g^{\circ }\) the integral concave conjugate of g, while \(f^{\bullet }\) is called the integral convex conjugate of f to distinguish between convex and concave versions. We have \(g^{\circ }(p) = -f^{\bullet }(-p)\) if \(g(x) = -f(x)\).
The discrete Fenchel-type duality theorem asserts the min–max formula
for a pair of functions \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) and \(g: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\). It is supposed that f and g are equipped with certain discrete convexity and concavity and some additional regularity conditions are assumed. Such a theorem can be traced back to the Fenchel-type duality theorem for submodular set functions by Fujishige [6] (see [7, Theorem 6.3]). The Fenchel-type min–max theorem for a pair of M\(^{\natural }\)-convex functions by Murota [16] (see [17, Theorem 8.21]) generalizes the min–max formulas for polymatroid intersection, valuated matroid intersection, and the Fenchel-type duality theorem for submodular set functions (see [17, Section 8.23]). As is well known, the existence of such min–max formula guarantees the existence of a certificate of optimality for the problem of minimizing \(f(x) - g(x)\) over \(x \in {\mathbb {Z}}^{n}\).
The main result of this paper (Theorem 1.1 below) is the Fenchel-type min–max formula (1.3) where f is an integer-valued integrally convex function and g is an integer-valued separable concave function. A function \(\varPsi : {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\) in \(x=(x_{1}, x_{2}, \ldots ,x_{n}) \in {\mathbb {Z}}^{n}\) is called separable concave if it can be represented as
with univariate discrete concave functions \(\psi _{i}: {\mathbb {Z}}\rightarrow {\mathbb {Z}}\cup \{ -\infty \}\), which means, by definition, that \(\mathrm{dom\,}\psi _{i}\) is an interval of integers and
The integral concave conjugate of \(\varPsi\) is given by
where
Theorem 1.1
(Main result) For an integer-valued integrally convex function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) with \(\mathrm{dom\,}f \ne \emptyset\) and an integer-valued separable concave function \(\varPsi : {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\) with \(\mathrm{dom\,}\varPsi \ne \emptyset\), we have
where the minimum or the maximum is assumed to be finite.
For example, suppose that f(x) represents a certain loss function in an integer vector x and we want to minimize the loss f(x) with an additional term for regularization such as the \(\ell _{1}\)-norm \(\Vert x \Vert _{1}\) and the squared \(\ell _{2}\)-norm \(\Vert x \Vert _{2}^{2}\). Then our problem is to minimize \(f(x) + C \Vert x \Vert _{1}\) or \(f(x) + C \Vert x \Vert _{2}^{2}\) with \(C > 0\), which is in the form of minimizing \(f(x) - \varPsi (x)\) over \(x \in {\mathbb {Z}}^{n}\) with a separable concave function \(\varPsi (x)\). If the loss function f(x) can be chosen to be an integer-valued integrally convex function, which does not seem to be so restrictive, we may apply Theorem 1.1. Note that Theorem 1.1 implies the existence of a certificate of optimality for the problem of minimizing \(f(x) - \varPsi (x)\) over \(x \in {\mathbb {Z}}^{n}\); see Sect. 3.1 for detail.
We prove Theorem 1.1 by revealing a kind of box integrality of subgradients of an integer-valued integrally convex function. Let \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) be an integer-valued function. The subdifferential of f at \(x \in \mathrm{dom\,}f\) is defined as
and an element p of \(\partial f(x)\) is called a subgradient of f at x. An integer vector p belonging to \(\partial f(x)\) is called an integral subgradient, and the condition
is sometimes referred to as the integral subdifferentiability of f at x. It has been shown by Murota–Tamura [24] that (1.10) holds for any integer-valued integrally convex function f and \(x \in \mathrm{dom\,}f\).
Our proof of Theorem 1.1 is based on a strengthening of integral subdifferentiability (1.10) with an additional box condition. For two integer vectors \(\alpha \in ({\mathbb {Z}}\cup \{ -\infty \})^{n}\) and \(\beta \in ({\mathbb {Z}}\cup \{ +\infty \})^{n}\) with \(\alpha \le \beta\), we define notation
which represents the set of real vectors between \(\alpha\) and \(\beta\). An integral box will mean a set B of real vectors represented as
for some \(\alpha \in ({\mathbb {Z}}\cup \{ -\infty \})^{n}\) and \(\beta \in ({\mathbb {Z}}\cup \{ +\infty \})^{n}\) with \(\alpha \le \beta\).
Our main technical result is the following, with which our main result (Theorem 1.1) is proved in Sect. 3.3.3.
Theorem 1.2
(Main technical result) Let \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) be an integer-valued integrally convex function, \(x \in \mathrm{dom\,}f\), and B be an integral box. If \(\partial f(x) \cap B\) is nonempty, then \(\partial f(x) \cap B\) is a polyhedron containing an integer vector. If, in addition, \(\partial f(x) \cap B\) is bounded, then \(\partial f(x) \cap B\) has an integral vertex.
The content of the above theorem may be expressed succinctly as:
This paper is organized as follows. Section 2 is a review of relevant results on integrally convex functions. Section 3 presents the Fenchel-type min–max formula for a pair of integer-valued integrally convex and separable convex functions (Theorem 1.1) with its implications and significances in discrete convex analysis as well as the derivation of the theorem from Theorem 1.2. Section 4 establishes the main technical result (Theorem 1.2) by means of the Fourier–Motzkin elimination.
2 Integrally convex functions
In this section we summarize fundamental facts about integrally convex functions.
For \(x \in {\mathbb {R}}^{n}\) the integral neighborhood of x is defined as
It is noted that strict inequality “ < ” is used in this definition and hence N(x) admits an alternative expression
where, for \(t \in {\mathbb {R}}\) in general, \(\left\lfloor t \right\rfloor\) denotes the largest integer not larger than t (rounding-down to the nearest integer) and \(\left\lceil t \right\rceil\) is the smallest integer not smaller than t (rounding-up to the nearest integer). For a set \(S \subseteq {\mathbb {Z}}^{n}\) and \(x \in {\mathbb {R}}^{n}\) we call the convex hull of \(S \cap N(x)\) the local convex hull of S at x. A nonempty set \(S \subseteq {\mathbb {Z}}^{n}\) is said to be integrally convex if the union of the local convex hulls \(\overline{S \cap N(x)}\) over \(x \in {\mathbb {R}}^{n}\) is convex [17]. This is equivalent to saying that, for any \(x \in {\mathbb {R}}^{n}\), \(x \in \overline{S}\) implies \(x \in \overline{S \cap N(x)}\). An integrally convex set S is “hole-free” in the sense that \(S = \overline{S} \cap \mathbb {Z}^{n}\).
It is recognized only recently [22] that the concept of integrally convex sets is closely related (or essentially equivalent) to the concept of box-integer polyhedra. Recall from [28, Section 5.15] that a polyhedron \(P \subseteq {\mathbb {R}}^{n}\) is called box-integer if \(P \cap \{ x \in {\mathbb {R}}^{n} \mid a \le x \le b \}\) is an integer polyhedron for each choice of integer vectors a and b. It is easy to see that if a set \(S \subseteq {\mathbb {Z}}^{n}\) is integrally convex, then its convex hull \(\overline{S}\) is a box-integer polyhedron, and conversely, if P is a box-integer polyhedron, then \(S = P \cap {\mathbb {Z}}^{n}\) is an integrally convex set.
For a function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {R}}\cup \{ +\infty \}\) with \(\mathrm{dom\,}f \ne \emptyset\), the convex envelope of f means the (point-wise) largest convex function \(g: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}\cup \{ +\infty \}\) that satisfies \(g(x) \le f(x)\) for all \(x \in {\mathbb {Z}}^{n}\). The convex envelope of f is denoted by \(\overline{f}\). If \(\overline{f}(x) = f(x)\) for all \(x \in {\mathbb {Z}}^{n}\), we call f convex extensible and refer to \(\overline{f}\) also as the convex extension of f.
Let \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {R}}\cup \{ +\infty \}\) be a function with \(\mathrm{dom\,}f \ne \emptyset\). The local convex extension \(\tilde{f}: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}\cup \{ +\infty \}\) of f is defined as the union of all convex envelopes of f on N(x). That is,
where \(\varLambda (x)\) denotes the set of coefficients for convex combinations indexed by N(x):
If \({\tilde{f}}\) is convex on \({\mathbb {R}}^{n}\), then f is said to be integrally convex [3]. In this case we have \({\tilde{f}} (x) = \overline{f}(x)\) for all \(x \in {\mathbb {R}}^{n}\). The effective domain of an integrally convex function is an integrally convex set. A set \(S \subseteq {\mathbb {Z}}^{n}\) is integrally convex if and only if its indicator function \(\delta _{S}: {\mathbb {Z}}^{n} \rightarrow \{ 0, +\infty \}\) defined by
is integrally convex.
Integral convexity of a function can be characterized as follows. The condition (c) below is a local condition under the assumption that the effective domain is an integrally convex set.
Theorem 2.1
([3, 14, 15]) Let \(f: \mathbb {Z}^{n} \rightarrow \mathbb {R} \cup \{ +\infty \}\) be a function with \(\mathrm{dom\,}f \ne \emptyset\). Then the following properties are equivalent, where \(\tilde{f}\) is the local convex extension of f defined by (2.3).
(a) f is integrally convex.
(b) For every \(x, y \in {\mathbb {Z}}^{n}\) with \(\Vert x - y \Vert _{\infty } \ge 2\) we have
(c) The effective domain \(\mathrm{dom\,}f\) is an integrally convex set, and (2.5) holds for every \(x, y \in {\mathbb {Z}}^{n}\) with \(\Vert x - y \Vert _{\infty } =2\).
Remark 2.1
The concept of integrally convex functions is introduced in [3] for functions defined on integer intervals (discrete rectangles). The extension to functions with general integrally convex effective domains is straightforward, which is found in [17]. Theorem 2.1 originates in [3, Proposition 3.3], which shows the equivalence of (a) and (c) when the effective domain is an integer interval (box), while the equivalence of (a) and (c) for a general integral convex effective domain is proved in [14, Appendix A]. The equivalence of (a) and (b) in Theorem 2.1 is shown in [15, Theorem A.1]. \(\square\)
Example 2.1
A function \(\varPhi : {\mathbb {Z}}^{n} \rightarrow {\mathbb {R}}\cup \{ +\infty \}\) in \(x=(x_{1}, x_{2}, \ldots ,x_{n}) \in {\mathbb {Z}}^{n}\) is called separable convex if it can be represented as
with univariate discrete convex functions \(\varphi _{i}: {\mathbb {Z}}\rightarrow {\mathbb {R}}\cup \{ +\infty \}\), which means, by definition, that \(\mathrm{dom\,}\varphi _{i}\) is an interval of integers and
A separable convex function is integrally convex. \(\square\)
Example 2.2
A symmetric matrix \(Q =(q_{ij})\) that satisfies the condition
is called a diagonally dominant matrix (with nonnegative diagonals). If Q is diagonally dominant in the sense of (2.8), then \(f(x) = x^{\top } Q x\) is integrally convex [3, Proposition 4.5]. The converse is also true if \(n \le 2\) [3, Remark 4.3]. \(\square\)
Example 2.3
A function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {R}}\cup \{ +\infty \}\) is called 2-separable convex if it can be expressed as the sum of univariate convex, diff-convex, and sum-convex functions, i.e., if
where \(\varphi _{i}, \varphi _{ij}, \psi _{ij}: \mathbb {Z} \rightarrow \mathbb {R} \cup \{ +\infty \}\) \((i, j =1,\ldots ,n; \ i \not = j)\) are univariate convex functions. A 2-separable convex function is known [29] to be integrally convex. A quadratic function \(f(x) = x^{\top } Q x\) with Q satisfying (2.8) is an example of a 2-separable convex function. \(\square\)
A minimizer of an integrally convex function can be characterized by a local minimality condition as follows.
Theorem 2.2
([3, Proposition 3.1]; see also [17, Theorem 3.21]) Let \(f: \mathbb {Z}^{n} \rightarrow \mathbb {R} \cup \{ +\infty \}\) be an integrally convex function and \(x^{*} \in \mathrm{dom\,}f\). Then \(x^{*}\) is a minimizer of f if and only if \(f(x^{*}) \le f(x^{*} + d)\) for all \(d \in \{ -1, 0, +1 \}^{n}\).
We need the following fact for the proof of Theorem 1.1. Recall that the convex envelope of a function f is denoted by \(\overline{f}\), which coincides with \({\tilde{f}}\) in (2.3) if f is integrally convex. It is noted that the statement cannot be extended to a pair of general integrally convex functions.
Proposition 2.1
(1) Let \(f: \mathbb {Z}^{n} \rightarrow \mathbb {R} \cup \{ +\infty \}\) be an integrally convex function, and \(\varPhi : \mathbb {Z}^{n} \rightarrow \mathbb {R} \cup \{ +\infty \}\) a separable convex function. Then \(\overline{f + \varPhi } = \overline{f} + \overline{\varPhi }\).
(2) Let \(S \subseteq {\mathbb {Z}}^{n}\) be an integrally convex set and \(D = \{ x \in {\mathbb {Z}}^{n} \mid \alpha \le x \le \beta \}\) for some \(\alpha \in ({\mathbb {Z}}\cup \{ -\infty \})^{n}\) and \(\beta \in ({\mathbb {Z}}\cup \{ +\infty \})^{n}\) with \(\alpha \le \beta\). Then \(\overline{S \cap D} = \overline{S} \cap \overline{D}\).
Proof
(1) Fix \(x \in {\mathbb {R}}^{n}\). Since f is integrally convex, we have \(\overline{f}(x) = \sum \{ \lambda _{y} f(y) \mid y \in N(x) \}\) for some \(\lambda \in \varLambda (x)\) (cf., (2.4) for notation). By separable convexity, we have \(\overline{\varPhi }(x) = \sum _{y \in N(x)} \lambda _{y} \varPhi (y)\) with the same coefficient \(\lambda\). This implies
while the reverse inequality \(\overline{f}(x) +\overline{\varPhi }(x) \le (\overline{f + \varPhi })(x)\) is obvious from the definition of convex envelopes.
(2) This follows from (1) with \(f = \delta _{S}\) and \(\varPhi = \delta _{D}\). Note that \(f + \varPhi = \delta _{S \cap D}\), \(\overline{f} = \delta _{\overline{S}}\), \(\overline{\varPhi } = \delta _{\overline{D}}\), etc. \(\square\)
The integral conjugate \(f^{\bullet }\) of a function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) is also an integer-valued function defined on \({\mathbb {Z}}^{n}\). So we can apply the transformation (1.1) to \(f^{\bullet }\) to obtain \(f^{\bullet \bullet } = (f^{\bullet })^{\bullet }\), which is called the integral biconjugate of f. Although the integral conjugate \(f^{\bullet }\) of an integer-valued integrally convex function f is not necessarily integrally convex ([23, Example 4.15], [24, Remark 2.3]), it is known [24] that the integral biconjugate \(f^{\bullet \bullet }\) coincides with f itself.
Theorem 2.3
([24]) For every integer-valued integrally convex function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) with \(\mathrm{dom\,}f \ne \emptyset\), we have \(f^{\bullet \bullet }(x) =f(x)\) for all \(x \in {\mathbb {Z}}^{n}\).
The reader is referred to [13, 14, 24] for recent developments in the theory of integral convexity, and to [17, Section 3.4] for basic facts about integral convexity.
3 Discrete Fenchel duality theorem
3.1 Main theorem and its implications
In this section we address the main result of this paper, which has already been presented in Introduction as Theorem 1.1, where the proof will be given in Sect. 3.3. Recall the notations
as well as the expressions of \(\varPsi\) in (1.4) and \(\varPsi ^{\circ }\) in (1.6).
Theorem 1.1
(Main result, again) For an integer-valued integrally convex function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) with \(\mathrm{dom\,}f \ne \emptyset\) and an integer-valued separable concave function \(\varPsi : {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\) with \(\mathrm{dom\,}\varPsi \ne \emptyset\), we have
where the minimum or the maximum is assumed to be finite.
Remark 3.1
The assumption on the left-hand side of (3.3) being finite means that \(\mathrm{dom\,}f \cap \mathrm{dom\,}\varPsi \ne \emptyset\) and the set \(\{ f(x) - \varPsi (x) \mid x \in {\mathbb {Z}}^{n} \}\) of function values is bounded from below. Since the function \(f(x) - \varPsi (x)\) is integer-valued, this assumption immediately implies that there exists x that attains the minimum. It will be shown in Lemma 3.2 in Sect. 3.3.4 that, if the maximum on the right-hand side of (3.3) is finite, then the minimum on the left-hand side is also finite. \(\square\)
Remark 3.2
When \(\varPsi\) is a linear function, say, \(\varPsi (x) = \langle c, x \rangle\) with \(c \in {\mathbb {Z}}^{n}\), the formula (3.3) reduces to a triviality. Indeed, in this case we have \(\varPsi ^{\circ }(p) = 0\) for \(p = c\) and \(\varPsi ^{\circ }(p) =-\infty\) for \(p \ne c\), and hence
The formula (3.3) is also a triviality when \(\mathrm{dom\,}f \subseteq \{ 0,1 \}^{n}\). In this case, we may assume \(\varPsi (x) = \langle c, x \rangle\) with \(\mathrm{dom\,}\varPsi = {\mathbb {Z}}^{n}\), and the above argument applies. In this connection it is recalled that every function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) with \(\mathrm{dom\,}f \subseteq \{ 0,1 \}^{n}\) is integrally convex. \(\square\)
Theorem 1.1 implies a min–max theorem for separable convex minimization on a box-integer polyhedron (see Sect. 2 for the definition of a box-integer polyhedron).
Theorem 3.1
For a nonempty box-integer polyhedron \(P \ (\subseteq {\mathbb {R}}^{n})\) and an integer-valued separable convex function \(\varPhi : {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) with \(\mathrm{dom\,}\varPhi \ne \emptyset\), we have
where \(\mu (p)= \min \{ \langle p, x \rangle \mid x\in P \}\) and the minimum or the maximum in (3.4) is assumed to be finite.
Proof
Denote the indicator function of \(P \cap {\mathbb {Z}}^{n}\) by \(\delta\), which is an integer-valued integrally convex function because P is a box-integer polyhedron. With the use of \(\varPsi (x) = -\varPhi (x)\) we have
On the other hand, on noting
we obtain
Therefore, (3.4) is equivalent to
which is a special case of (3.3) in Theorem 1.1. \(\square\)
Remark 3.3
Theorem 3.1 generalizes a recent result of Frank–Murota [5, Theorem 3.4], which asserts the min–max formula (3.4) when P is a box-TDI polyhedron and the minimum is finite. Note that a box-TDI polyhedron is a special case of a box-integer polyhedron. See, e.g., [28] for the definition of a box-TDI polyhedron. \(\square\)
Theorem 1.1 also implies a min–max theorem of Cunningham–Green-Krótki [2] obtained in a study of b-matching degree-sequence polyhedra and the box convolution theorem of bisubmodular functions by Fujishige–Patkar [9]. See [25, Section 3.4] for the detail.
Another Fenchel-type min–max formula can be obtained by combining our main result (Theorem 1.1) with the biconjugacy theorem (Theorem 2.3). Let \(\mathcal {G}\) denote the set of integral conjugates of integer-valued integrally convex functions. By the biconjugacy theorem, we can alternatively say that \(\mathcal {G}\) is the set of integer-valued functions g whose integral conjugate is an integer-valued integrally convex function. That is,
Theorem 3.2
For a function \(g: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) in \(\mathcal {G}\) with \(\mathrm{dom\,}g \ne \emptyset\) and an integer-valued separable concave function \(\varPsi : {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\) with \(\mathrm{dom\,}\varPsi \ne \emptyset\), we have
where the minimum or the maximum is assumed to be finite.
Proof
First note that the integral concave conjugate \(\varPsi ^{\circ }\) of \(\varPsi\) is also an integer-valued separable concave function. By replacing \((f, \varPsi )\) in (3.3) with \((g^{\bullet }, \varPsi ^{\circ })\) we obtain
With the biconjugacy \(\varPsi ^{\circ \circ }= \varPsi\) and \(g^{\bullet \bullet }=g\), where the former is well known and the latter is due to Theorem 2.3, we can rewrite this formula to
which is equivalent to (3.6). \(\square\)
It is often possible [4, 5] to obtain an explicit form of the integral conjugate function of an integer-valued separable convex (or concave) function. For example, we have:
3.2 Fenchel duality for other function classes
The discrete Fenchel-type duality theorem, in its general form, asserts the min–max formula
under the assumption that f and g are equipped with certain specified discrete convexity and concavity. In this section we summarize our present knowledge by compiling the results of this paper and the known facts in discrete convex analysis [17].
To this end we introduce notations for classes of functions \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\):
We also use notation \(\mathcal {F}^{\bullet }\) for the set of integral conjugates of functions in \(\mathcal {F}\); similarly for \(\mathcal {G}^{\bullet }\), \(\mathcal {L}^{\bullet }\), etc. Then we have
where the relations \(\mathcal {L}^{\bullet } = \mathcal {M}\) and \(\mathcal {M}^{\bullet } = \mathcal {L}\) are known as the discrete conjugacy theorem [17, Theorem 8.12]. We have the following inclusion relations:
where \(\mathcal {L} \cap \mathcal {M} = \mathcal {S}\) is stated in [17, Theorem 8.49].
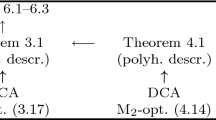
By combining Theorems 1.1 and 3.2 and the known facts [17, Theorem 8.21] we obtain the following table to summarize our present knowledge about the min–max formula (3.9). For example, “Th.1.1” in the upper-right corner of the table indicates that (3.9) for (f, g) with \(f \in \mathcal {F}\) and \(-g \in \mathcal {S}\) is established in Theorem 1.1 of this paper. An entry “Cor.” at (f, g) means that (3.9) holds for this (f, g), which is a corollary of a result indicated in the same row or column (because of the inclusion relations (3.10)). An entry “CntEx” at (f, g) means that there is a counterexample that denies (3.9) for this (f, g).
The following two examples show that the min–max formula (3.9) is not necessarily true for M\(^{\natural }\)-convex f and L\(^{\natural }\)-concave g. By the inclusion relations in (3.10), they also serve as counterexamples for all entries “CntEx” in (3.11). In the following, \(\overline{f}\) denotes the convex envelope of f and \(\overline{g}\) the concave envelope of g; we have \(\overline{f}, \overline{g}: {\mathbb {R}}^{2} \rightarrow {\mathbb {R}}\) (finite-valued).
Example 3.1
([19, Example 5.6]) Let \(f, g: {\mathbb {Z}}^{2} \rightarrow {\mathbb {Z}}\) be defined as
We have
(cf., (3.18), (3.19)). The min–max identity fails because of the integrality gap in the minimization problem. Finally we add that the function
is an integrally convex function. \(\square\)
Example 3.2
([19, Example 5.7]) Let \(f, g: {\mathbb {Z}}^{2} \rightarrow {\mathbb {Z}}\) be defined as
We have
(cf., (3.18), (3.19)). The min–max identity fails because of the integrality gap in the maximization problem. Finally we add that the function \(h(x_1,x_2) = \max (0,x_{1}+x_{2}) - \min (x_{1},x_{2}) = \max (|x_1|, |x_2|)\) is integrally convex. \(\square\)
3.3 Proof of Theorem 1.1
The main theorem (Theorem 1.1) is proved in this section. The proof consists of four steps. In Steps 1 to 3, we prove the min–max formula (3.3) under the assumption that the minimum in (3.3) is finite, while Step 4 deals with the other case where the maximum in (3.3) is assumed to be finite.
3.3.1 Step 1: weak duality
We start with the generic form of the Fenchel duality:
For any functions \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) and \(g: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\) and for any integer vectors x and p, we have the following obvious relations:
This implies “ \(\min \ge \max\) ” in (3.14), that is,
This is called the weak duality, whereas (3.14) is the strong duality.
Since the functions f and g are integer-valued, the minimum on the left-hand side of (3.14) is either a (finite) integer or \(-\infty\) when \(\mathrm{dom\,}f \cap \mathrm{dom\,}g \ne \emptyset\). Therefore, if the minimum is finite, then there exists a vector \(x^{*} \in {\mathbb {Z}}^{n}\) that attains the minimum.
To prove strong duality (3.14) from weak duality (3.16), it suffices to show the existence of an integer vector \(p^{*}\) for which the inequality in (3.15) is an equality for \(x = x^{*}\). Thus the proof of (3.14) is reduced to showing the existence of \(p^{*} \in {\mathbb {Z}}^{n}\) satisfying
3.3.2 Step 2: convex extension
We continue to work with the generic form (3.14) and consider the continuous relaxation of the dual (maximization) problem, in which the variable p may be a real vector.
To this end, we assume that f is extensible to a convex function \(\overline{f}: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}\cup \{ +\infty \}\) and g is extensible to a concave function \(\overline{g}: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}\cup \{ -\infty \}\). For technical reasons, it is further assumed that \(\overline{f}\) and \(-\overline{g}\) are locally polyhedral convex functions in the sense that they are polyhedral convex functions when restricted to any finite integral box. (This technical condition is met when f is an integrally convex function and g is a separable concave function.)
The definitions of conjugate functions are adapted for real vectors p as
which are compatible with (3.1) and (3.2) for integer vectors p. Then we have:
where the vertical equality “ || ” connecting the right-hand sides of (3.18) and (3.19) is the Fenchel duality in convex analysis [1, 11, 26], which holds if \(\overline{f}\) and \(-\overline{g}\) are locally polyhedral convex functions and the minimum is finite.
In general, we may have strict inequalities in (3.18) and (3.19), as is demonstrated by (3.12) in Example 3.1 and (3.13) in Example 3.2, respectively. The following lemma states that an equality does hold in (3.18) in the setting of Theorem 1.1.
Lemma 3.1
For an integer-valued integrally convex function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) with \(\mathrm{dom\,}f \ne \emptyset\) and an integer-valued separable concave function \(\varPsi : {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\) with \(\mathrm{dom\,}\varPsi \ne \emptyset\), we have
and hence
where the minimum on the left-hand side is assumed to be finite.
Proof
Since f is integrally convex and \(\varPsi\) is separable concave, the difference \(f - \varPsi\) is convex extensible and its convex extension is equal to \(\overline{f} - \overline{\varPsi }\) by Proposition 2.1, that is, \(\overline{f - \varPsi } = \overline{f} - \overline{\varPsi }\). Therefore,
which shows (3.20). Then (3.21) follows from the equality “ || ” between the right-hand sides of (3.18) and (3.19). \(\square\)
Let \(x^{*} \in {\mathbb {Z}}^{n}\) be an optimal solution to the primal problem (i.e., a minimizer on the left-hand side of (3.21)). Let \({\hat{p}} \in {\mathbb {R}}^{n}\) be an optimal solution to the dual problem (i.e., a maximizer on the right-hand side of (3.21)), which is guaranteed to exist by the Fenchel duality in convex analysis (for continuous variables). Then we have
As is well known, this condition can be expressed in terms of subdifferentials as follows. First we have
where the definition of \(\partial f(x)\) is given in (1.9). On setting \(\varPhi (x):= -\varPsi (x)\) we similarly have
Accordingly, (3.22) can be rewritten as
Since such \({\hat{p}}\) exists, we have, in particular, that
3.3.3 Step 3: dual integrality
By adding integrality requirement to (3.23), we obtain the condition
for an integral dual optimal solution \(p^{*}\). Note that this is equivalent to (or rewriting of) the optimality condition given in (3.17) (with \(g=\varPsi = -\varPhi\)). Thus, our task of proving Theorem 1.1 is reduced to showing
Since \(\varPhi\) (\(=-\varPsi\)) is an integer-valued separable convex function defined on \({\mathbb {Z}}^{n}\), the subdifferential \(\partial \varPhi (x^{*})\) is an integral box. Hence we have
for some \(\alpha \in ({\mathbb {Z}}\cup \{ -\infty \})^{n}\) and \(\beta \in ({\mathbb {Z}}\cup \{ +\infty \})^{n}\).
Let \(B=- \partial \varPhi (x^{*})\). Then (i) B is an integral box by (3.27) and (ii) \(\partial f(x^{*}) \cap B \ne \emptyset\) by (3.24). We want to show that these conditions imply \(\partial f(x^{*}) \cap B \cap {\mathbb {Z}}^{n} \ne \emptyset\) in (3.26). The main technical result (Theorem 1.2) states that this is indeed the case, completing the proof of Theorem 1.1. The proof of Theorem 1.2 is given in the next section.
3.3.4 Step 4: finiteness assumption
It remains to show that the finiteness of the maximum in (3.3) implies the finiteness of the minimum in (3.3).
Lemma 3.2
For an integer-valued integrally convex function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) and an integer-valued separable concave function \(\varPsi : {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ -\infty \}\), if \(\max \{ \varPsi ^{\circ }(p) - f^{\bullet }(p) \mid p \in {\mathbb {Z}}^{n} \}\) is finite, then \(\min \{ f(x) - \varPsi (x) \mid x \in {\mathbb {Z}}^{n} \}\) is also finite.
Proof
Suppose that the maximum, \(\max \{ \varPsi ^{\circ } - f^{\bullet } \}\), is finite. Since \(\varPsi ^{\circ }(p) - f^{\bullet }(p)\) is integer-valued, there exists an integer vector \(p^{*}\) that attains the maximum. By the weak duality (3.16), this implies that the minimum, \(\min \{ f - \varPsi \}\), is finite or else \(+\infty\). To prove by contradiction, suppose that the minimum is \(+\infty\), which means \(\mathrm{dom\,}f \cap \mathrm{dom\,}\varPsi = \emptyset\). By Proposition 2.1 (2), we then have \(\overline{\mathrm{dom\,}f} \cap \overline{\mathrm{dom\,}\varPsi } = \emptyset\). By the separation theorem (in convex analysis), there exists a hyperplane separating \(\overline{\mathrm{dom\,}f}\) and \(\overline{\mathrm{dom\,}\varPsi }\). Since \(\mathrm{dom\,}f\) and \(\mathrm{dom\,}\varPsi\) are integrally convex sets, we can take an integer vector as the normal vector to define the separating hyperplane. That is, there exist \(q \in {\mathbb {Z}}^{n}\) and \(C \in {\mathbb {Z}}\) such that
Then we have
from which we obtain a contradiction
Therefore, \(\min \{ f - \varPsi \}\) must be finite. \(\square\)
4 Integral subgradients
4.1 Results
In this section we are interested in integral subgradients of an integer-valued integrally convex function \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\). Recall the definition of the subdifferential
at \(x \in \mathrm{dom\,}f\). An integer vector p belonging to \(\partial f(x)\), if any, is called an integral subgradient of f at x.
Integral subdifferentiability of integer-valued integrally convex functions is recently established by Murota–Tamura [24].
Theorem 4.1
([24]) Let \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) be an integer-valued integrally convex function. For every \(x \in \mathrm{dom\,}f\), we have \(\partial f(x) \cap {\mathbb {Z}}^{n} \ne \emptyset\).
The main technical result of the present paper (Theorem 1.2) is a strengthening of this theorem with an additional box condition. Recall that an integral box means a set B of real vectors represented as
with two integer vectors \(\alpha \in ({\mathbb {Z}}\cup \{ -\infty \})^{n}\) and \(\beta \in ({\mathbb {Z}}\cup \{ +\infty \})^{n}\) satisfying \(\alpha \le \beta\). For convenience, we present the theorem again. The proof is given in Sects. 4.2–4.4.
Theorem 1.2
(Main technical result, again) Let \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) be an integer-valued integrally convex function, \(x \in \mathrm{dom\,}f\), and B be an integral box. If \(\partial f(x) \cap B\) is nonempty, then \(\partial f(x) \cap B\) is a polyhedron containing an integer vector. If, in addition, \(\partial f(x) \cap B\) is bounded, then \(\partial f(x) \cap B\) has an integral vertex.
As an immediate corollary, we can obtain the following statement.
Corollary 4.1
Let \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) be an integer-valued integrally convex function, \(x \in \mathrm{dom\,}f\), and \(p \in \partial f(x)\). Then there exists an integer vector \(q \in \partial f(x)\) satisfying \(\lfloor p_{i} \rfloor \le q_{i} \le \lceil p_{i} \rceil\) \((i=1,2,\ldots , n)\).
Proof
Let \(B=[\alpha ,\beta ]_{{\mathbb {R}}}\) be the integral box defined by \(\alpha _{i}=\lfloor p_{i} \rfloor\) and \(\beta _{i} = \lceil p_{i} \rceil\) for \(i=1,2,\ldots , n\). Then \(p \in \partial f(x) \cap B\), which shows \(\partial f(x) \cap B \ne \emptyset\). By Theorem 1.2, there exists \(q \in \partial f(x) \cap B \cap {\mathbb {Z}}^{n}\), which is an integer vector q in \(\partial f(x)\) satisfying \(\lfloor p_{i} \rfloor \le q_{i} \le \lceil p_{i} \rceil\) \((i=1,2,\ldots , n)\). \(\square\)
In the following we make supplementary remarks concerning the contents of Theorems 1.2 and 4.1.
Remark 4.1
Integral subdifferentiability is not guaranteed without the assumption of integral convexity. See [16, Example 1.1].
\(\square\)
Remark 4.2
Theorem 4.1 states that \(\partial f(x) \cap {\mathbb {Z}}^{n} \ne \emptyset\), but it does not claim a stronger statement that \(\partial f(x)\) is an integer polyhedron. See [24, Remark 3.1]. \(\square\)
Remark 4.3
It is pointed out in [24, Remark 4.1] that, if \(\partial f(x)\) is a bounded polyhedron for an integer-valued integrally convex function f, then \(\partial f(x)\) has an integral vertex, although not every vertex of \(\partial f(x)\) is integral. A concrete example is given here.
Let \(D = \{ x \in \{ -1,0,+1 \}^{3} \mid |x_{1}| + |x_{2}| + |x_{3}| \le 2 \}\), which is an integrally convex set. Define f on D by \(f(\mathbf{0}) = 0\) and \(f(x) = 1\) \((x \in D {\setminus }\{ \mathbf{0}\})\). This f is an integer-valued integrally convex function and \(\partial f(\mathbf{0})\) is a bounded polyhedron described by the following inequalities:
The polyhedron \(\partial f(\mathbf{0})\) has eight non-integral vertices \((\pm 1/2, \pm 1/2, \pm 1/2)\) (with arbitrary combinations of double signs) and six integral vertices \((\pm 1, 0, 0)\), \((0, \pm 1, 0)\), and \((0,0, \pm 1)\). \(\square\)
It is in order here to briefly mention how Theorem 1.2 is proved in the remainder of this section. Let \(P:= \partial f(x)\) for notational simplicity, and for each \(\ell = 1,2,\ldots ,n\), let \([P]_{\ell }\) denote the projection of P to the space of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\). Since P is a polyhedron, each \([P]_{\ell }\) is also a polyhedron. In [24], a hierarchical system of inequalities to describe \([P]_{\ell }\) for \(\ell = 1,2,\ldots ,n\) (Theorem 4.2 in Sect. 4.2) was derived by means of the Fourier–Motzkin elimination and then Theorem 4.1 was proved as a fairly easy consequence of this description. We extend this approach to prove Theorem 1.2. Namely, in Theorem 4.3 in Sect. 4.3, we derive a hierarchical system of inequalities to describe the projection \([P \cap B]_{\ell }\) of \(P \cap B\) to the space of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\) for \(\ell = 1,2,\ldots ,n\). Here again we rely on the Fourier–Motzkin elimination.
4.2 Fourier–Motzkin elimination for the subdifferential \(\partial f(x)\)
In this section we briefly describe the approach of [24] to prove Theorem 4.1 (integral subdifferentiability) with the aid of the Fourier–Motzkin elimination. In so doing we intend to clarify the geometrical essence of the argument in [24] in a form convenient for the proof of Theorem 1.2 (integral subdifferentiability with a box). Recall our notation P for the subdifferential \(\partial f(x)\) (for a fixed \(x \in \mathrm{dom\,}f\)) and \([P]_{\ell }\) for the projection of P to the space of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\), where \(\ell = 1,2,\ldots ,n\).
To obtain an expression of \(\partial f(x)\), we can make use of Theorem 2.2 for the minimality of an integrally convex function. Namely, in the definition of \(\partial f(x)\) in (4.1), it suffices to consider \(y=x + d\) with \(d \in \{-1,0,+1\}^n\), and then
We represent the system of inequalities
for d with \(f(x+d) < +\infty\) in a matrix form as
Let I denote the row set of A and
We denote the ith row vector of A by \(a_{i}\) for \(i \in I\). The row set I is indexed by \(d \in \{ -1,0,+1 \}^{n}\) with \(f(x+d) < +\infty\), and \(a_{i}\) is equal to the corresponding d for \(i \in I\); we have \(a_{ij} = d_{j}\) for \(j=1,2,\ldots , n\) and
Note that \(a_{ij} \in \{ -1,0,+1 \}\) and \(a_{i} \in \{ -1,0,+1 \}^{n}\) for all i and j.
An inequality system to describe the projections \([P]_{\ell }\) for \(\ell = 1,2,\ldots ,n\) can be obtained by applying the Fourier–Motzkin elimination procedure [27] to the system of inequalities (4.3), where the variable \(p_{1}\) is eliminated first, and then \(p_{2}, p_{3}, \ldots\), to finally obtain an inequality in \(p_{n}\) only.
By virtue of the integral convexity of f, a drastic simplification occurs in this elimination process. The inequalities that are generated are actually redundant and need not be added to the current system of inequalities, which is a crucial observation made in [24]. It is shown in [24] that the Fourier–Motzkin elimination procedure applied to (4.3) results in a system of inequalities that is equivalent to (4.4) below:
Here the index sets are defined as follows: Let \({\hat{I}}_{0}^{0} = I\) and for \(j=1, 2,\ldots ,n\), define
where \({\hat{I}}_{j}^{+}\) and/or \({\hat{I}}_{j}^{-}\) may possibly be empty. This result can be rephrased in terms of projections as follows.
Theorem 4.2
([24]) Let \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) be an integer-valued integrally convex function and \(x \in \mathrm{dom\,}f\). For each \(\ell = 1,2,\ldots ,n\), the projection of \(\partial f(x)\) to the space of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\) is described by the last \(n-\ell +1\) inequalities in (4.4) for \(p_{\ell },p_{\ell +1},\ldots ,p_n\).
4.2.1 Proof of Theorem 4.1 by Theorem 4.2
Since \(\partial f(x)\) is nonempty, there exists a real vector p satisfying all the inequalities in (4.4). It is even true that, for any choice of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\) satisfying the last \(n-\ell +1\) inequalities of (4.4), the (\(\ell -1\))-st inequality of (4.4) prescribes a nonempty interval for a possible choice of \(p_{\ell -1}\). As for integrality, the last inequality in (4.4) shows that we can choose an integral \(p_{n} \in {\mathbb {Z}}\), since \(b_{i} \in {\mathbb {Z}}\) for \(i \in {\hat{I}}_{n}^{-} \cup {\hat{I}}_{n}^{+}\). Then the next-to-last inequality shows that we can choose an integral \(p_{n-1} \in {\mathbb {Z}}\), since \(a_{kn}p_{n} - b_{k} \in {\mathbb {Z}}\) for \(k \in {\hat{I}}_{n-1}^{-}\) and \(b_{i} - a_{in}p_{n} \in {\mathbb {Z}}\) for \(i \in {\hat{I}}_{n-1}^{+}\). Continuing in this way we can see the existence of an integer vector \(p \in {\mathbb {Z}}^{n}\) satisfying (4.4). This shows \(\partial f(x) \cap {\mathbb {Z}}^{n} \ne \emptyset\), which completes the proof of Theorem 4.1.
Remark 4.4
It follows immediately from Theorem 4.2 that \(P \cap B\) (\(= \partial f(x) \cap [\alpha ,\beta ]_{{\mathbb {R}}}\)) is described by the following inequalities:
where the index sets \({\hat{I}}_{j}^{+}\) and \({\hat{I}}_{j}^{-}\) are defined in (4.5). It is certainly true that p belongs to \(P \cap B\) if and only if p satisfies all inequalities in (4.6). But it is not true that the projection \([P \cap B]_{\ell }\) of \(P \cap B\) to the space of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\) is described by the last \(n-\ell +1\) inequalities. (This is because \([P \cap B]_{\ell }\) may differ from \([P]_{\ell } \cap [B]_{\ell }\), with \([B]_{\ell }\) denoting the projection of B.) In particular, it may not be true that the last inequality
describes the projection of \(P \cap B\) to the \(p_{n}\)-axis, which is demonstrated by a simple example in Example 4.1 below. An important consequence of this phenomenon is that we are not allowed to prove Theorem 1.2 on the basis of (4.6) by extending the proof of Theorem 4.1 based on Theorem 4.2 (described above). This is the reason for our (rather long) proof of Theorem 1.2 given in Sects. 4.3 and 4.4. \(\square\)
Example 4.1
Let \(f: {\mathbb {Z}}^{2} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) be a function defined on \(\{ -1,0, +1 \}^{2}\) by
which is integer-valued and integrally convex. The subdifferential \(P = \partial f(0,0)\) is described by the following inequalities:
for which the Fourier–Motzkin elimination results in
Let B be an integral box described by
A system of inequalities describing \(P \cap B\) is obtained by combining (4.8) and (4.9) as
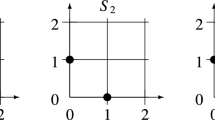
which corresponds to (4.6). However, the last inequality \(-3 \le p_{2} \le 3\) here does not describe the projection of \(P \cap B\) to the \(p_{2}\)-axis, which, actually, is the interval \(-2 \le p_{2} \le 2\) as Fig. 1 shows. \(\square\)
\(P \cap B\) in Example 4.1
4.3 Fourier–Motzkin elimination for \(\partial f(x) \cap B\)
Recall notations \(P=\partial f(x)\) and
where the possibility of \(\alpha _{j} = -\infty\) and/or \(\beta _{j}= +\infty\) is allowed. In this section we are concerned with a system of inequalities that describe the projections \([P \cap B]_{\ell }\) for \(\ell = 1,2,\ldots ,n\). The result is stated in Theorem 4.3, with which Theorem 1.2 (the main technical result of this paper) is proved.
Recall that P is described by the system of inequalities \(A p \le b\) in (4.3). For each \(\ell =1,2, \ldots ,n\), we look at those inequalities which contain the variable \(p_{\ell }\). Using the sets of indices defined as
the inequalities of \(A p \le b\) are classified as
With the use of \(\alpha _{j} \le p_{j} \le \beta _{j}\) for \(j =1,2, \ldots ,\ell -1\), we can eliminate \(p_{1},\ldots ,p_{\ell -1}\) from (4.12), (4.13), and (4.14), to obtain
while we have
from (4.10). It follows from (4.15), (4.16), (4.18), and (4.19) that the interval for \(p_{\ell }\) is given by
Note that the inequality (4.20) is solved for \(p_{\ell }\) with the upper and lower bounds depending on \(p_{\ell +1}, \ldots , p_{n}\) and independent of \(p_{1}, \ldots , p_{\ell -1}\). It is emphasized that, for each \(\ell\), the single inequality (4.20) is equivalent to the set of inequalities consisting of (4.15), (4.16), (4.18), and (4.19).
We denote by \(\mathrm {IQ}(\ell )\) the system of inequalities consisting of (4.15), (4.16), (4.17) for \(\ell\), and (4.18) and (4.19) for \(\ell ,\ell +1,\ldots ,n\), that is,
Note that \(\mathrm {IQ}(\ell )\) is a system of inequalities in variables \(p_{\ell },p_{\ell +1},\ldots , p_{n}\), and is free from \(p_{1},\ldots , p_{\ell -1}\). The number of inequalities in \(\mathrm {IQ}(\ell )\) is equal to \(|I|+ 2(n-\ell +1)\), and \(\mathrm {IQ}(1)\) is nothing but the combined system \(A p \le b, \ \alpha \le x \le \beta\).
It follows from the derivation above that, for \(\ell = 1,2,\ldots ,n\), each inequality in \(\mathrm {IQ}(\ell )\) is valid for \([P \cap B]_{\ell }\), that is, every point in \([P \cap B]_{\ell }\) satisfies \(\mathrm {IQ}(\ell )\). The following theorem states that the converse is also true, that is, \(\mathrm {IQ}(\ell )\) gives a precise description of \([P \cap B]_{\ell }\). The proof of this theorem is given in Sect. 4.4.
Theorem 4.3
Let \(f: {\mathbb {Z}}^{n} \rightarrow {\mathbb {Z}}\cup \{ +\infty \}\) be an integer-valued integrally convex function, \(x \in \mathrm{dom\,}f\), and B be an integral box. For each \(\ell = 1,2,\ldots ,n\), the projection of \(\partial f(x) \cap B\) to the space of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\) is described by the system \(\mathrm {IQ}(\ell )\).
Proof of Theorem 1.2by Theorem 4.3
Since \(\partial f(x) \cap B\) is nonempty by assumption, there exists a real vector p satisfying the inequalities in (4.20) for \(\ell =1,2, \ldots ,n\). It is even true that, for any choice of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\) satisfying (4.20) for \(\ell , \ell +1, \ldots ,n\), the inequality of (4.20) for \(\ell -1\) prescribes a nonempty interval for a possible choice of \(p_{\ell -1}\). Note that (4.17) for \(\ell\) is an inequality to be counted as (4.15) or (4.16) for some \(\ell ' \ge \ell +1\) or else a trivial inequality between two constants.
As for integrality, the inequality of (4.20) for \(\ell =n\), i.e.,
shows that we can choose an integral \(p_{n} \in {\mathbb {Z}}\), since \(b_{i} \in {\mathbb {Z}}\) for all i, and \(\alpha _{j} \in {\mathbb {Z}}\cup \{ -\infty \}\) and \(\beta _{j} \in {\mathbb {Z}}\cup \{ +\infty \}\) for all j. Then the inequality of (4.20) for \(\ell =n-1\) shows that we can choose an integral \(p_{n-1} \in {\mathbb {Z}}\), since its upper and lower bounds are both integers. Continuing in this way we can see the existence of an integer vector \(p \in {\mathbb {Z}}^{n}\) satisfying (4.20) for all \(\ell\). This shows \(\partial f(x) \cap B \cap {\mathbb {Z}}^{n} \ne \emptyset\), which completes the proof of Theorem 1.2.
Example 4.2
We illustrate \(\mathrm {IQ}(\ell )\) for the simple example in Example 4.1. By (4.9) we have \((\alpha _{1}, \beta _{1}) = (2,+\infty )\) and \((\alpha _{2}, \beta _{2}) = (-4,4)\). The inequalities in (4.7) for \(P = \partial f(0,0)\) can be expressed as \(A p \le b\) with
where we assume that the row set of A is indexed by \(I=\{ r_{1}, r_{2},\ldots , r_{8} \}\) and the column set by \(\{ 1,2 \}\). First, for \(\ell = 1\), we have \(I_{1}^{+} = \{ r_{1}, r_{2}, r_{5} \}\), \(I_{1}^{-} = \{ r_{3}, r_{4}, r_{6} \}\), and \(I_{1}^{0} = \{ r_{7}, r_{8} \}\). Accordingly, (4.15) and (4.16) for \(\ell = 1\) are given by
Then (4.20) for \(\ell = 1\) is given by
The system \(\mathrm {IQ}(1)\) consists of all the inequalities in (4.7) and (4.9).
Next, for \(\ell = 2\), we have \(I_{2}^{+} = \{ r_{1}, r_{3}, r_{7} \}\), \(I_{2}^{-} = \{ r_{2}, r_{4}, r_{8} \}\), and \(I_{2}^{0} = \{ r_{5}, r_{6} \}\). Accordingly, (4.15) and (4.16) for \(\ell = 2\) are given by
and (4.20) for \(\ell = 2\) is given by
The system (4.17) for \(\ell = 2\) consists of two trivial inequalities:
Then the system \(\mathrm {IQ}(2)\) consists of (4.15)\(_{\ell = 2}\), (4.16)\(_{\ell = 2}\), (4.17)\(_{\ell = 2}\), and \(-4 \le p_{2} \le 4\) in (4.9); note that the other inequality \(2 \le p_{1}\) in (4.9) is not a member of \(\mathrm {IQ}(2)\).
Using \((\alpha _{1}, \beta _{1}) = (2,+\infty )\) and \((\alpha _{2}, \beta _{2}) = (-4,4)\), we obtain
in agreement with Fig. 1. It is noted, however, that \(\mathrm {IQ}(2)\) contains redundant inequalities. \(\square\)
4.4 Proof of Theorem 4.3
In this section we give a proof of Theorem 4.3, which states that the projection \([P \cap B]_{\ell }\) is described by \(\mathrm {IQ}(\ell )\) for \(\ell =1,2,\ldots ,n\), where \(P=\partial f(x)\), \(B=[\alpha ,\beta ]_{{\mathbb {R}}}\), and
defined in (4.21) with
See (4.11) for the definitions of \(I_{\ell }^{+}\), \(I_{\ell }^{-}\), \(I_{\ell }^{0}\), \(J_{\ell i}^{+}\), and \(J_{\ell i}^{-}\). We already know that each member of \(\mathrm {IQ}(\ell )\) is a valid inequality for \([P \cap B]_{\ell }\), and we need to prove that those inequalities are, in fact, sufficient for the description of \([P \cap B]_{\ell }\).
The subdifferential \(P=\partial f(x)\) is described by \(A p \le b\) in (4.3) and the integral box B by \(\alpha \le x \le \beta\). Hence \(P \cap B\) is described by the combined system \(A p \le b, \ \alpha \le x \le \beta\). By applying the Fourier–Motzkin elimination procedure [27] to this combined system \(A p \le b, \ \alpha \le x \le \beta\), we can obtain an inequality system to describe the projections \([P \cap B]_{\ell }\) for \(\ell = 1,2,\ldots ,n\). In the Fourier–Motzkin elimination, the variable \(p_{1}\) is eliminated first, and then \(p_{2}, p_{3}, \ldots\), to finally obtain an inequality in \(p_{n}\) only.
It is worth while to reiterate here the technical subtlety explained in Remark 4.4 concerning the relation between \([P \cap B]_{\ell }\) and \([P]_{\ell } \cap [B]_{\ell }\), where \([P]_{\ell }\) and \([B]_{\ell }\) denote the projections of P and B, respectively, to the space of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\). By Theorem 4.2, the projection \([P]_{\ell }\) is described by (4.4) for \(p_{\ell },p_{\ell +1},\ldots ,p_n\), while \([B]_{\ell }\) is described obviously by \(\alpha _{j} \le p_{j} \le \beta _{j}\) \((j=\ell , \ell +1,\ldots ,n)\). If we had \([P \cap B]_{\ell } = [P]_{\ell } \cap [B]_{\ell }\), we could describe \([P \cap B]_{\ell }\) by (4.6). But this is not the case, as demonstrated by Example 4.1.
In the following we prove, by induction on \(\ell =1,2,\ldots ,n\), that the projection \([P \cap B]_{\ell }\) to the space of \((p_{\ell },p_{\ell +1},\ldots ,p_n)\) is described by the system \(\mathrm {IQ}(\ell )\). This statement is obviously true for \(\ell = 1\), since \(\mathrm {IQ}(1)\) coincides with combined system \(A p \le b, \ \alpha \le x \le \beta\). Fix \(\ell\) with \(1 \le \ell \le n-1\), and assume that \([P \cap B]_{\ell }\) is described by \(\mathrm {IQ}(\ell )\).
In the following we shall prove that \([P \cap B]_{\ell +1}\) is described by \(\mathrm {IQ}(\ell +1)\) by applying the Fourier–Motzkin elimination procedure to \(\mathrm {IQ}(\ell )\) to eliminate the variable \(p_{\ell }\). The procedure consists of the following four types of elimination operations.
-
The addition of (4.18) and (4.19) results in an obvious inequality \(\alpha _{\ell } \le \beta _{\ell }\).
-
The addition of (4.16) for \(k \in I_{\ell }^{-}\) and (4.18) results in
$$\begin{aligned} \sum _{j \in J_{\ell k}^{+} } \alpha _{j} - \sum _{j \in J_{\ell k}^{-} } \beta _{j} - \beta _{\ell } + \sum _{j=\ell +1}^{n} a_{kj}p_{j} \le b_{k}. \end{aligned}$$According to the value of \(a_{k, \ell + 1} \in \{ +1, -1, 0 \}\), this inequality is contained in (4.15), (4.16), or (4.17) for \(\ell +1\), and hence is contained in \(\mathrm {IQ}(\ell +1)\).
-
The addition of (4.15) for \(i \in I_{\ell }^{+}\) and (4.19) results in
$$\begin{aligned} \sum _{j \in J_{\ell i}^{+} } \alpha _{j} + \alpha _{\ell } - \sum _{j \in J_{\ell i}^{-} } \beta _{j} + \sum _{j=\ell +1}^{n} a_{ij}p_{j} \le b_{i}, \end{aligned}$$which is, similarly, a member of \(\mathrm {IQ}(\ell +1)\).
-
The addition of (4.15) for \(i \in I_{\ell }^{+}\) and (4.16) for \(k \in I_{\ell }^{-}\) results in
$$\begin{aligned} \sum _{j \in J_{\ell i}^{+} } \alpha _{j} + \sum _{j \in J_{\ell k}^{+} } \alpha _{j} - \sum _{j \in J_{\ell i}^{-} } \beta _{j} - \sum _{j \in J_{\ell k}^{-} } \beta _{j} + \sum _{j=\ell +1}^{n} (a_{ij}+a_{kj})p_{j} \le b_{i} + b_{k}. \end{aligned}$$(4.22)We prove later that this is a redundant inequality, implied by \(\mathrm {IQ}(\ell +1)\).
Thus, all the inequalities generated by the Fourier–Motzkin elimination procedure applied to eliminate the variable \(p_{\ell }\) from \(\mathrm {IQ}(\ell )\) are, in fact, implied by \(\mathrm {IQ}(\ell +1)\). On the other hand, \([P \cap B]_{\ell }\) is described by \(\mathrm {IQ}(\ell )\) by the induction hypothesis, and each inequality of \(\mathrm {IQ}(\ell +1)\) is valid for \([P \cap B]_{\ell +1}\). It then follows that \([P \cap B]_{\ell +1}\) is described by \(\mathrm {IQ}(\ell +1)\), as desired.
The rest of this section is devoted to the proof that the inequality (4.22) is implied by \(\mathrm {IQ}(\ell +1)\). We may assume that \(\alpha _{j}\) and \(\beta _{j}\) appearing in (4.22) are all finite-valued, since otherwise this inequality is trivially true. It turns out to be convenient to introduce a factor of 1/2 to (4.22), to obtain
In the following we aim at proving (4.23) in place of (4.22).
Consider an inequality
which is obtained from (4.23) by replacing \(\alpha _{j}\) and \(\beta _{j}\) to \(p_{j}\). In this expression cancellations of the form of \(+p_{j} - p_{j}\) occur for \(j \in (J_{\ell i}^{+} \cap J_{\ell k}^{-}) \cup (J_{\ell k}^{+} \cap J_{\ell i}^{-})\). On omitting these cancelling terms we obtain
With the use of coefficients \(c= (c_{1},c_{2},\ldots ,c_{n})\) defined by
we can express (4.25) more compactly as
where \(c p = \sum _{j=1}^{n} c_{j} p_{j}\). By the definition (4.26) we have
We observe that the inequality (4.24) is, in fact, derived from \(A p \le b\) by adding (4.12) for \(i \in I_{\ell }^{+}\) and (4.13) for \(k \in I_{\ell }^{-}\) (and dividing by two). By the definition of \(A p \le b\) in (4.3), we have
as well as \(c = (a_{i} + a_{k})/2\), where \(a_{i}, a_{k} \in \{ -1, 0, +1\}^{n}\). Recall that I denotes the row set of the matrix A and \(a_{h}=(a_{h1},a_{h2},\ldots ,a_{hn})\) is the hth row vector of A for \(h \in I\).
The following lemma depends heavily on the integral convexity of f.
Lemma 4.1
There exist a subset \(I' \ (\subseteq I)\) and positive weights \(\lambda _{h}\) indexed by \(h \in I'\) (for convex combination) such that
Proof
We have \(b_{i}=f(x + a_{i}) - f(x)\), \(b_{k}=f(x + a_{k}) - f(x)\), and \(c = (a_{i} + a_{k})/2\). By the integral convexity of f, there exist \(y^{(1)}, y^{(2)}, \ldots , y^{(m)} \in N(x+(a_{i}+a_{k})/2)\) such that
where \(\lambda _h > 0\) for \(h =1,2,\ldots ,m\) and \(\sum _{h=1}^{m} \lambda _h = 1\). Let \(a_{h}\) be the row vector of A that is equal to \(y^{(h)} - x \in \{ -1, 0, +1\}^{n}\), and \(I'\) be the subset of I corresponding to \(y^{(h)} - x\) for \(h =1,2,\ldots ,m\). Then (4.36) shows (4.31) and (4.32). The last three conditions (4.33), (4.34), and (4.35) hold, since \(a_{h}\) belongs to N(c) for all \(h \in I'\). \(\square\)
Lemma 4.1 enables us to show that the inequality (4.25) (or (4.27)) can be derived from the inequalities corresponding to \(I'\):
Indeed, by (4.30), (4.31), and (4.32), we obtain
In the following, we use a variant of this argument to show that another (related) inequality
can be derived from \(\mathrm {IQ}(\ell +1)\). Note that (4.38) resembles (4.25). Indeed, (4.38) is obtained from (4.25) by replacing \(+p_{j}\) to \(+\alpha _{j}\) and \(-p_{j}\) to \(-\beta _{j}\).
Lemma 4.2
The inequality (4.38) is implied by \(\mathrm {IQ}(\ell +1)\).
Proof
Consider inequalities
These inequalities are contained in \(\mathrm {IQ}(\ell +1)\), because each inequality in (4.39) is of the form of (4.15), (4.16) or (4.17) for \(\ell +1\), depending on \(a_{h,\ell +1} \in \{ +1, -1, 0 \}\).
Since \(a_{h \ell } = 0\) by (4.29) and (4.33), we have
for all \(h \in I'\). Therefore, (4.39) may be rewritten as
It should be clear that these inequalities are contained in \(\mathrm {IQ}(\ell +1)\).
To show that the inequality (4.38) is derived from (4.40), we form a convex combination of (4.40) using the weight \((\lambda _{h} \mid h \in I')\) in Lemma 4.1. By the definition of \(c_{j}\) in (4.26), we see that
On substituting
given in (4.31), we further obtain
where (4.33), (4.34), and (4.35) are used for the last equality. On the other hand, the convex combination of (4.40) shows
where the second inequality is due to (4.32). By combining (4.41) and (4.42) we obtain (4.38). \(\square\)
Finally, we observe that, while (4.38) is implied by \(\mathrm {IQ}(\ell +1)\) by Lemma 4.2, the inequality (4.23) in question is obtained as the sum of (4.38) and a trivial inequality
Therefore, (4.23) is implied by, or redundant to, \(\mathrm {IQ}(\ell +1)\). This completes the proof of Theorem 4.3.
References
Borwein, J.M., Lewis, A.S.: Convex Analysis and Nonlinear Optimization: Theory and Examples, 2nd edn. Springer, New York (2006)
Cunningham, W.H., Green-Krótki, J.: \(b\)-Matching degree-sequence polyhedra. Combinatorica 11, 219–230 (1991)
Favati, P., Tardella, F.: Convexity in nonlinear integer programming. Ricerca Oper. 53, 3–44 (1990)
Frank, F., Murota, K.: Discrete decreasing minimization, Part II: Views from discrete convex analysis, arXiv:1808.08477 (2018). Ver 4: June 30, (2020)
Frank, F., Murota, K.: A discrete convex min–max formula for box-TDI polyhedra. Math. Oper. Res. published on-line (2021). https://doi.org/10.1287/moor.2021.1160
Fujishige, S.: Theory of submodular programs: a Fenchel-type min–max theorem and subgradients of submodular functions. Math. Program. 29, 142–155 (1984)
Fujishige, S.: Submodular Functions and Optimization, 2nd edn. Annals of Discrete Mathematics 58, Elsevier, Amsterdam (2005)
Fujishige, S.: Bisubmodular polyhedra, simplicial divisions, and discrete convexity. Discrete. Optim. 12, 115–120 (2014)
Fujishige, S., Patkar, S.B.: The box convolution and the Dilworth truncation of bisubmodular functions. Report No. 94823-OR, Forschungsinstitut für Diskrete Mathematik, Universität Bonn (1994)
Hajek, B.: Extremal splittings of point processes. Math. Oper. Res. 10, 543–556 (1985)
Hiriart-Urruty, J.-B., Lemaréchal, C.: Fundamentals of Convex Analysis. Springer, Berlin (2001)
Iimura, T., Murota, K., Tamura, A.: Discrete fixed point theorem reconsidered. J. Math. Econ. 41, 1030–1036 (2005)
Moriguchi, S., Murota, K.: Projection and convolution operations for integrally convex functions. Discret. Appl. Math. 255, 283–298 (2019)
Moriguchi, S., Murota, K., Tamura, A., Tardella, F.: Scaling, proximity, and optimization of integrally convex functions. Math. Program. 175, 119–154 (2019)
Moriguchi, S., Murota, K., Tamura, A., Tardella, F.: Discrete midpoint convexity. Math. Oper. Res. 45, 99–128 (2020)
Murota, K.: Discrete convex analysis. Math. Program. 83, 313–371 (1998)
Murota, K.: Discrete Convex Analysis. Society for Industrial and Applied Mathematics, Philadelphia (2003)
Murota, K.: Primer of Discrete Convex Analysis-Discrete versus Continuous Optimization (in Japanese). Kyoritsu Publishing Co., Tokyo (2007)
Murota, K.: Recent developments in discrete convex analysis. In: Cook, W., Lovász, L., Vygen, J. (eds.) Research Trends in Combinatorial Optimization, Chapter 11, pp. 219–260. Springer, Berlin (2009)
Murota, K.: Discrete convex analysis: a tool for economics and game theory. J. Mech. Inst. Des. 1, 151–273 (2016)
Murota, K.: A survey of fundamental operations on discrete convex functions of various kinds. Optim. Methods Softw. 36, 472–518 (2021)
Murota, K.: On basic operations related to network induction of discrete convex functions. Optim. Methods Softw. 36, 519–559 (2021)
Murota, K., Shioura, A.: Relationship of M-/L-convex functions with discrete convex functions by Miller and by Favati-Tardella. Discret. Appl. Math. 115, 151–176 (2001)
Murota, K., Tamura, A.: Integrality of subgradients and biconjugates of integrally convex functions. Optim. Lett. 14, 195–208 (2020)
Murota, K., Tamura, A.: Discrete Fenchel duality for a pair of integrally convex and separable convex functions. arXiv:2108.10502v2 (2021)
Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)
Schrijver, A.: Theory of Linear and Integer Programming. Wiley, New York (1986)
Schrijver, A.: Combinatorial Optimization-Polyhedra and Efficiency. Springer, Heidelberg (2003)
Tamura, A., Tsurumi, K.: Directed discrete midpoint convexity. Jpn. J. Ind. Appl. Math. 38, 1–37 (2021)
Yang, Z.: Discrete fixed point analysis and its applications. J. Fixed Point Theory Appl. 6, 351–371 (2009)
Acknowledgements
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Murota, K., Tamura, A. Discrete Fenchel duality for a pair of integrally convex and separable convex functions. Japan J. Indust. Appl. Math. 39, 599–630 (2022). https://doi.org/10.1007/s13160-022-00499-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13160-022-00499-x
Keywords
- Discrete convex analysis
- Fenchel duality
- Integrally convex function
- Integral subgradient
- Fourier–Motzkin elimination