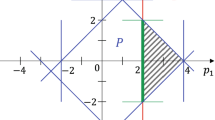
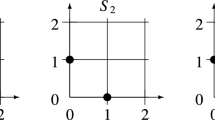
Abstract
Integrally convex functions constitute a fundamental function class in discrete convex analysis. This paper shows that an integer-valued integrally convex function admits an integral subgradient and that the integral biconjugate of an integer-valued integrally convex function coincides with itself. The proof is based on the Fourier–Motzkin elimination. The latter result provides a unified proof of integral biconjugacy for various classes of integer-valued discrete convex functions, including L-convex, M-convex, L\(_{2}\)-convex, M\(_{2}\)-convex, BS-convex, and UJ-convex functions as well as multimodular functions. Our results of integral subdifferentiability and integral biconjugacy make it possible to extend the theory of discrete DC (difference of convex) functions developed for L- and M-convex functions to that for integrally convex functions, including an analogue of the Toland–Singer duality for integrally convex functions.
Similar content being viewed by others
Notes
\(\mathrm{cl}(\overline{\mathrm{dom_{{\mathbb {Z}}}}f})\) coincides with the closed convex hull of \(\mathrm{dom_{{\mathbb {Z}}}}f\) [5, Section 1.4].
In Lemma 4.2 of [10] an additional condition “\(\partial _\mathbb {R} f(x) = \mathrm{cl}(\overline{\mathrm{dom_{{\mathbb {Z}}}}f})\)” is involved in the definition of \(\mathcal {F}_G\) in (4.18). However, we can verify that this condition is not needed.
As the proof shows, the integral convexity of g is not needed. That is, (3.6) holds for any \(g: \mathbb {Z}^{n} \rightarrow \mathbb {Z} \cup \{+\infty \}\), as long as \(h: \mathbb {Z}^{n} \rightarrow \mathbb {Z} \cup \{+\infty \}\) is integrally convex.
References
Favati, P., Tardella, F.: Convexity in nonlinear integer programming. Ric. Oper. 53, 3–44 (1990)
Fujishige, S.: Submodular Functions and Optimization. Annals of Discrete Mathematics, vol. 58, 2nd edn. Elsevier, Amsterdam (2005)
Fujishige, S.: Bisubmodular polyhedra, simplicial divisions, and discrete convexity. Discrete Optim. 12, 115–120 (2014)
Hajek, B.: Extremal splittings of point processes. Math. Oper. Res. 10, 543–556 (1985)
Hiriart-Urruty, J.-B., Lemaréchal, C.: Fundamentals of Convex Analysis. Springer, Berlin (2001)
Iimura, T., Murota, K., Tamura, A.: Discrete fixed point theorem reconsidered. J. Math. Econ. 41, 1030–1036 (2005)
Maehara, T., Murota, K.: A framework of discrete DC programming by discrete convex analysis. Math. Program. Ser. A 152, 435–466 (2015)
Moriguchi, S., Murota, K.: Projection and convolution operations for integrally convex functions. Discrete Appl. Math. 255, 283–298 (2019)
Moriguchi, S., Murota, K., Tamura, A., Tardella, F.: Scaling, proximity, and optimization of integrally convex functions. Math. Program. 175, 119–154 (2019)
Murota, K.: Discrete convex analysis. Math. Program. 83, 313–371 (1998)
Murota, K.: Discrete Convex Analysis. Society for Industrial and Applied Mathematics, Philadelphia (2003)
Murota, K.: Note on multimodularity and L-convexity. Math. Oper. Res. 30, 658–661 (2005)
Murota, K.: Primer of Discrete Convex Analysis—Discrete Versus Continuous Optimization. Kyoritsu Publishing Co., Tokyo (2007). (in Japanese)
Murota, K.: Discrete convex analysis: a tool for economics and game theory. J. Mech. Inst. Des. 1, 151–273 (2016)
Murota, K., Shioura, A.: Relationship of M-/L-convex functions with discrete convex functions by Miller and by Favati-Tardella. Discrete Appl. Math. 115, 151–176 (2001)
Schrijver, A.: Theory of Linear and Integer Programming. Wiley, New York (1986)
Singer, I.: A Fenchel-Rockafellar type duality theorem for maximization. Bull. Aust. Math. Soc. 20, 193–198 (1979)
Toland, J.F.: A duality principle for non-convex optimisation and the calculus of variations. Arch. Ration. Mech. Anal. 71, 41–61 (1979)
Yang, Z.: Discrete fixed point analysis and its applications. J. Fixed Point Theory Appl. 6, 351–371 (2009)
Acknowledgements
The authors thank Satoru Fujishige and Hiroshi Hirai for helpful comments. This work was supported by CREST, JST, Grant Number JPMJCR14D2, Japan; JSPS KAKENHI Grant Numbers 26280004, 16K00023; and JSPS Core-to-core program “Foundation of a Global Research Cooperative Center in Mathematics Focused on Number Theory and Geometry.”
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Murota, K., Tamura, A. Integrality of subgradients and biconjugates of integrally convex functions. Optim Lett 14, 195–208 (2020). https://doi.org/10.1007/s11590-019-01501-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-019-01501-1