1 Introduction

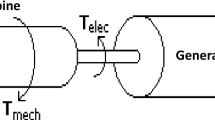
The shift from an electricity system that is dominated by traditional synchronous power plants to one that is potentially dominated by variable renewable energy (VRE) will pose a range of technical challenges. One aspect of these challenges, which have been reviewed previously by Hodge et al. [7], is the alternating current (AC) frequency stability of the power system. In systems with high shares of synchronous generators, the physical rotational inertia of the generators inherently slows down fluctuations in the voltage frequency in the grid. Solar PV and many wind power setups are inverter-based and do not have this inherent property. Therefore, new measures are required to control the frequency. An inverter converts direct current (DC) electricity, which is obtained from solar PV and some wind-power setups, to AC electricity, which is required by the grid.

While inertia is important for slowing down the frequency changes caused by load imbalances, a change in frequency can also be mitigated by rapid power reserves that eliminate the imbalance. Thus, while frequency reserves (FR) are always needed, a low availability of inertia can be compensated by a high availability of fast frequency reserves (FFR; [3]). Technologies that are able to provide FFR include wind power, batteries, electric boilers, heat pumps and electrolyzers. Batteries and wind power can also simulate the inertial power responses of synchronous machines using grid-forming inverters. However, there is limited access to these technologies and a lack of experience as to how to utilize them to balance the load and control the frequency in a large-scale, real-world system.

While cost-minimizing modeling has been used extensively to investigate various aspects of future high-VRE-share systems [see, for example, the review of Ringkjøb et al. [9]], frequency control (FC) was not considered in such modeling until recently. Welsch et al. [14] have found that long-term investment models that do not consider short-term variability significantly underestimate generation capacity investments, using an investment model that considers reserves. Wang et al. [12] have explored the impact of the primary frequency response on the generation capacity investments for a detailed grid, albeit with limited geographic scope and without considering battery storage. González-Inostroza et al. [5] have studied the roles of batteries, hydropower and VRE in providing FFR, at varying levels of system inertia, and have found that the exclusion of batteries from the FFR supply is more costly than the exclusion of VRE. Ullmark et al. [11] have examined the impacts of frequency reserves and inertia on investments and dispatch in four different geographic contexts with high VRE shares, also finding that batteries are one of the key technologies for providing FC.

In summary, previous studies indicate that compared to today’s electricity system, VRE-dominated electricity systems will meet the need for FC in a very different manner, with greater emphasis on FFR and synthetic inertia. Batteries are identified as playing a key role in the provision of these services. The aim of this work is to investigate when and how the electricity system will transit from traditional FC, which relies heavily on synchronous generators, to inverter-based FC, which may rely heavily on batteries. The interplay between flexibility provision on intra-hourly and inter-hourly time-scales is also examined, to identify potential synergies or double-usage between technologies used for electricity supply, inter-hourly variation management, and FC.

2 Grid stability and frequency control

Maintaining stability within the electrical grid requires stringent control of its voltage and frequency under both normal conditions and following some fault event. Voltage is controlled through the supply of reactive power, which can be achieved using static devices that do not require the supply of additional energy. In contrast, FC requires the production and consumption of active power (and, thus, investments in energy storage and/or additional fuel costs). Technologies that are used in the production and consumption of active power for FC typically also offer reactive power control. At the same time, the fact that reactive power is energy-neutral means that the interaction between the reactive power supply and dispatch is limited, especially in systems that have a high share of VRE, where a lower percentage of the reactive power supply comes from synchronous generators. As such, this work only looks at the FC aspect of grid stability, dividing it into Inertia and Frequency reserves (FR), as explained below.

2.1 Inertia

When a power imbalance occurs in conventional electricity grids, the deficiency or surplus is taken from, or stored in, the rotational inertia of all the connected synchronous machines. More inertia means a larger pool of rotational mass to store or take energy from, and thereby a slower change in the rotational speed and grid frequency. This rate of change of frequency (RoCoF) is an important metric to control, as a larger RoCoF means that there is less time for the reserves to activate, and a too-large RoCoF can damage the connected synchronous machines. As such, the minimum amount of available inertia depends on the highest acceptable RoCoF and the largest plausible sudden imbalance. The latter, the dimensioning fault, is referred to as N − 1 and is often determined by the largest single generator unit or associated infrastructure, such as transmission lines.

2.2 Frequency reserves (FR)

Given a grid with sufficient inertia to limit the RoCoF to acceptable levels when there is a dimensioning fault, there is still a need to eliminate quickly the power imbalance, so as to arrest the frequency change. Therefore, the available power reserves must, at all times, at least match the size of the dimensioning fault and must react in a sufficiently rapid fashion to prevent the frequency from deviating beyond the acceptable limits, as specified in each system’s grid code. Furthermore, additional reserves may be needed to accommodate stochastic load variations, generation ramping limitations, and VRE forecast errors. Since VRE is not dispatched and there may be a delay between its expected and actual generation, some reserves may be needed to counteract the load imbalance until the VRE output matches its expected value.

3 Methodology

3.1 Scope

To investigate the ways in which the supply of inertia and FR develop during the transition of the electricity system, we apply a cost-minimizing energy system investment model, which has been developed to include requirements regarding inertia and FR. Since these requirements are expected to depend on the electricity system composition, the modeling is applied to conditions that reflect three different geographic cases: the Iberian Peninsula, the British Isles and Northern Europe. These are referred to as Iberia, Brit, and Nordic+, respectively, and consist of 3–5 subregions (listed in Table 3) based on clustered NUTS-2 regions. The clustering is made to find a balance between preserving transmission bottlenecks and lowering geographical resolution and thus model complexity. These are illustrated in Fig. 1 and they differ in terms of existing generation and transmission capacities, VRE potentials and their profiles, as well as their electricity load profiles. Nordic+ is characterized by large hydro power resources and good wind conditions. Brit also has good wind conditions but very low hydro power capacity, while Iberia has good solar resources and some hydro power. These differences give the investigation a set of generation mixes to apply to, with different shares of wind and solar power, and different needs for flexibility investments. Especially for Nordic+, the choice of which regions to include is not obvious, as there is strong interconnectivity in northern and central continental Europe. The possible implications of the choice made in this work is commented in Sect. 5.

Fig. 1
figure 1

Partial map of Europe illustrating the three regional cases applied in this work with respect to existing generation and transmission capacities, VRE potentials and profiles, and electricity loads and profiles

Full size image

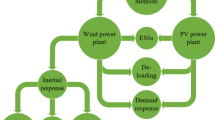
The modeling in this work includes a range of thermal, variable renewable, and flexibility technologies, as listed in Appendix 2. This includes on- and offshore wind power, roof and large-scale solar PV, and thermal power of different efficiencies and fuel types. Real-world generating capacity included as input to the model is implemented with the real fuel type and approximated efficiency (based on year of commission), also for technologies not available for new investments in the model. The technologies that make up the FR supply in the implementation used in this work are illustrated in Fig. 2. These include batteries, hydrogen storage units, dispatchable power generation, flexible power-to-heat, and battery electric vehicles, as well as curtailed energy from wind and solar PV. While Fig. 2 uses the terms “excess” and “unused”, the contributions from each technology to the electricity and reserve supply are optimized simultaneously. For a more detailed description of the implementation, see Eqs. (18)–(23) in Sect. 3.2.

Fig. 2
figure 2

Schematic of the various FR supply sources, with ‘Min()’ boxes indicating that the smallest of the inputs is passed on. The storage units considered in this work are batteries and hydrogen caverns. BEV battery electric vehicles

Full size image

3.2 Energy system model

The model used in this study builds on the linear dispatch and investment optimization model used by Ullmark et al. [11], which in turn is based on the studies of Göransson et al. [6] and Johansson and Göransson [8]. The model includes a linearized unit commitment implementation with minimum load, start-up cost and time, as well as a part-load cost, as described by Weber [13]. In the present work, the model has been extended to allow for brownfield scenarios, accounting for existing electricity generation capacity and its age structure, as well as electricity export to neighboring regions. Thus, the modeling starts out from an existing system which gradually, year by year, receives new investments to replace units that either have reached the end of their technical lifetime or become non-competitive. The model version developed in this work is able to optimize (linearized) dispatch, electricity export and investments for up to five neighboring regions with an hourly resolution. Consecutive time-steps, with hourly resolution, are applied to represent short- and long-term storage technologies that may play important roles in the provision of FC. While there is perfect foresight within a year, years are modeled sequentially, such that investments made in the previous years are input data for the following modeling year.

In the following equations, common sets are R for region, T for time and P for technology, and common variables are i for added capacity, g for generation and e for electricity export between regions. A recurring parameter in the equations is E, which is the pre-existing capacity of technology P entered as an input, including both the real-life capacity and investments from previous model years. For more details on the sets, variables and parameters used in the mathematical description, see Table 1.

Table 1 Sets, variables and parameters used in the mathematical description of the model
Full size table

Objective function


Equation (1) shows the objective function to be minimized (separately) for each year for the three regional cases of Iberia, Brit and Nordic+. Each region consists of a number of sub-regions (r). The investments in transmission capacity between regions r and r’, \({i}_{r,{r}^{^{\prime}},p}^{tran}\), are symmetrical such that \({i}_{r,{r}^{^{\prime}},p}^{tran}={i}_{{r}^{^{\prime}},r,p}^{tran}\) for all r and r’. \({C}_{p}^{OPEX}\) is a combination of both the variable O&M and fuel costs, as well as a CO2-tax (see Appendix 2). The generation variable is split into generation in new units,\({g}_{r,t,p}\), and generation in old units,\({g}_{r,t,p}^{existing}\), to account for differences in their techno-economic properties.

$$\mathrm{min}\sum_{r\in R}\left(\sum_{p \in P}{i}_{r,p}\times {C}_{p}^{inv}+ \sum_{{r}^{^{\prime}},b \in \mathrm{ R},B}{i}_{r,{r}^{^{\prime}},b}^{tran}\times {C}_{r,{r}^{^{\prime}},b}^{trans}+\sum_{t,p \in T,{P}^{gen}}\left({g}_{r,t,p}{\times C}_{p}^{OPEX}+{g}_{r,t,p}^{existing}{\times C}_{p}^{existing,OPEX}\right)+\sum_{p \in P}{i}_{r,p}{\times C}_{p}^{fixOM}+\sum_{t,p \in T,{P}^{gen}}\left(\left({g}_{r,t,p}^{active}-{g}_{r,t,p}\right)\times {C}_{p}^{part} +\left({g}_{r,t,p}^{existing,active}-{g}_{r,t,p}^{existing}\right)\times {C}_{p}^{existing,part}\right)+\sum_{t,p \in T,{P}^{gen}}\left({g}_{r,t,p}^{start}\times {C}_{p}^{start}+{g}_{r,t,p}^{existing, start}\times {C}_{p}^{existing,start}\right)\right)$$
(1)

Demand balance


While minimizing the total system cost per year, the system must conform to a range of constraints. Equation (2) ensures that sufficient electricity is produced in each hour, taking into account new loads from industry and an increasingly electrified transport sector [for a full description, see the aggregated representation in Taljegard et al. [10]]. A part of the BEV load, i.e., 20–50% of the total depending on the scenario, is assumed to be flexible and is accounted for through the BEV storage balance, while the remainder is assumed to be inflexible and is accounted for through \({D}_{r,t}^{BEV}\). The flexible load share and vehicle-to-grid share are described further in Sect. 3.4.

$$\sum_{p \in {\mathrm{P}}^{gen}}\left({g}_{r, t,p}+{g}_{r, t,p}^{existing}\right)+\sum_{p \in {P}^{ESS}}\left({s}_{r,t,p}^{discharge}-{s}_{r,t,p}^{charge}\right)-\sum_{{r}^{\mathrm{^{\prime}}}, p \in \mathrm{ R}, {P}^{tran}}{e}_{r,{r}^{\mathrm{^{\prime}}},t}^{netexport}- \sum_{p \in {P}^{PtH}}\left({g}_{r,t,p}+{g}_{r,t,p}^{existing}\right)+{(s}_{r,t}^{EV,discharge}-{s}_{r,t}^{EV,charge})={D}_{r,t}^{elec}+{D}_{r}^{ammonia}+{D}_{r}^{steel}+{D}_{r}^{cement}+{D}_{r,t}^{BEV}, \forall r,t\in R,T$$
(2)

Equation (3) ensures that sufficient heat is produced for the district heating systems during each district heating time-period u. Each value of u covers 2 weeks, and this implementation is used to approximate the flexibility of district heating networks with some heat storage, as described further in Sect. 3.4. In Eq. (3), an inequality sign is used instead of an equality sign so that the modeled CHP plants can disregard the heat production and run for only electricity production, if optimal. In reality, the power-to-heat ratio is often somewhat flexible to avoid overproduction of hot water [1].

$$\sum_{t,p \in \mathrm{ u},{\mathrm{P}}^{PtH}}\left({g}_{r, t,p}+{g}_{r, t,p}^{existing}\right)\times CO{P}_{p}+\sum_{t,p \in \mathrm{ u},{\mathrm{P}}^{CHP}}\left(\frac{{g}_{r, t,p}}{{\alpha }_{p}}+\frac{{g}_{r, t,p}^{existing}}{{\alpha }_{p}^{existing}}\right)\ge \sum_{t \in \mathrm{ u}}{D}_{r,t}^{heat}, \quad \forall r,u\in R,U$$
(3)

Limitations on generation

Equation (4) limits the generation to the level of investment in the respective technology. For wind and solar power and run-of-river hydropower, the variable generation profiles are applied in this equation through \({W}_{t,p}\) in the right-hand side (RHS). For thermal power plants, \({g}_{r,t,p}^{active}\) is used to apply additional restrictions related to the minimum load, start-up cost, and part-load cost. For the start-up cost, capacity being started up is measured through increases in \({g}_{r,t,p}^{active}\), and differences between \({g}_{r,t,p}^{active}\) and \({g}_{r,t,p}\) cause a part-load cost. A full description of this implementation can be found in Göransson et al. [6]. Since any capacity that already exists prior to the modeled year can have properties that are different, such as lower efficiency, the new and old capacities are distinguished by duplicate variables and equations using their respective parameters. This distinction is of particular relevance for thermal generation. Equation (5) exemplifies this mirroring of Eq. (4). However, for storage technologies, the old and new capacities are lumped together, as shown in Eq. (6).

$${g}_{r,t,p}\le {g}_{r,t,p}^{active}\le {i}_{r,p}\times {W}_{t,p},\quad \forall t,p\in T,P\backslash {P}^{ESS}$$
(4)
$${g}_{r,t,p}^{existing}\le {g}_{r,t,p}^{active,existing}\le {E}_{r,p}\times {W}_{t,p},\quad \forall t,p\in T,P\backslash {P}^{ESS}$$
(5)
$${g}_{r,t,p}\le {i}_{r,p}+{E}_{r,p},\quad \forall t,p\in T,{P}^{ESS}$$
(6)

Storage balance

The storage balance between batteries and hydrogen storage units is expressed by Eq. (7), where the (dis)charge rate of storage technology p is limited in Eq. (8) by investments in the accompanying charging or discharging technology. In addition, the (dis)charge rate is limited by \({S}_{p}^{rate}\) to avoid rates that might damage the storage.

$${g}_{r,t+1,p}= {g}_{r,t,p}+{s}_{r,t,p}^{charge}\times {\eta }_{p}^{ESS}-\frac{{s}_{r,t,p}^{discharge}}{{\eta }_{p}^{ESS}}, \quad \forall r,t,p\in R,T,{P}^{ESS}$$
(7)
$$-\left({i}_{r,p}+{E}_{r,p}\right)\times {S}_{p}^{rate}\le -{i}_{r,{q}^{in}}-{E}_{r,{q}^{in}}\le {s}_{r,t,p}^{discharge}-{s}_{r,t,p}^{charge}\le {i}_{r,{q}^{out}}+{E}_{r,{q}^{out}}\le \left({i}_{r,p}+{E}_{r,p}\right)*{S}_{p}^{rate},\quad \forall r,t,\left(p,{q}^{in},{q}^{out}\right)\in R,T,Q$$
(8)

Inter-regional connections


The addition of electricity export between neighboring regions is performed by adding the variables \({e}_{r,{r}^{^{\prime}},t }^{netexport}\) and \({i}_{r,{r}^{^{\prime}},p}^{tran}\) as well as the constraints in Eqs. (9)–(11). Equations (9) and (10) ensure that there is symmetrical transmission capacity and trading between each pair of regions, respectively. Equation (11) limits the levels of import and export to the transmission capacity, which for AC transmission is determined by estimated distances between grid connection points in each regions and number of transmission lines. For the investigated regions, the resulting transmission capacities is validated with real transmission capacities to ensure that reasonable distances are used.

$${i}_{r,{r}^{^{\prime}},p}^{tran} = {-i}_{{r}^{^{\prime}},r,p}^{tran} , \quad \forall r,{r}^{^{\prime}},p\in R,R,{P}^{trans}$$
(9)
$${e}_{r,{r}^{^{\prime}},t }^{netexport} = -{e}_{{r}^{^{\prime}},r,t }^{netexport},\quad \forall r,{r}^{^{\prime}},t\in R,R,T$$
(10)
$$-\left({i}_{r,{r}^{^{\prime}},p}^{tran}+{E}_{r,{r}^{^{\prime}},p}^{trans}\right)\le {e}_{r,{r}^{^{\prime}},t }^{netexport}\le {i}_{r,{r}^{^{\prime}},p}^{tran}+{E}_{r,{r}^{^{\prime}},p}^{trans},\quad \forall r,{r}^{^{\prime}},t,p\in R,R,T,{P}^{trans}$$
(11)

Inertia


The FC additions made in this work include the three variables of available inertia (\(a{s}_{r,t}^{inertia}\)), available reserves (\(a{s}_{r,t,o}^{FR}\)), and exported reserves (\(a{s}_{r,{r}^{^{\prime}},t,o}^{FR,netexport}\)), and equations relating to the supply and demand of inertia and reserves, as well as the export of excess reserves to neighboring regions. Equation (12) sums the individual sources for the inertial power response, which must meet or exceed the regional N-1 for each hour. It is assumed that power-to-heat technologies can stop, and/or adjust, their electricity consumption with very little delay, making it so they can contribute their full electricity consumption level to the inertial power response.

$${I}_{r}^{N-1}\le {\sum }_{p\in {P}^{inertia}}\left({(g}_{r,t,p}^{active}+{g}_{r,t,p}^{existing,active})\times {I}_{p}^{power}\right)+{\sum }_{p\in {P}^{ESS}}\left(a{s}_{r,t,p}^{inertia,ESS}\right)+a{s}_{r,t}^{inertia,BEV}+{\sum }_{p\in {P}^{PtH}}\left({g}_{r,t,p}+{g}_{r,t,p}^{existing}\right),\quad \forall r,t\in R,T$$
(12)

The inertia supply variable \(a{s}_{r,t}^{inertia,ESS}\) is, in turn, limited by Eqs. (13) and (14). In Eq. (13), \(a{s}_{r,t}^{inertia,ESS}\) is limited by the energy level in the storage at the beginning of each timestep (\({g}_{r,t,p})\), considering also the planned (dis)charge (\({s}_{r,t,p}^{charge}-{s}_{r,t,p}^{discharge}\)) and the duration of the inertial power response (\({I}^{dur})\). In Eq. (14), \(a{s}_{r,t}^{inertia,ESS}\) is limited by the net discharge capacity not in use.

$$a{s}_{r,t,p}^{inertia,ESS}\le \left({g}_{r,t,p}\times {\eta }_{t}^{ESS}+{s}_{r,t,p}^{charge}-{s}_{r,t,p}^{discharge}\right)\times \frac{3600}{{I}^{dur}}, \forall r,t,p\in R,T,{P}^{ESS}$$
(13)
$$a{s}_{r,t,p}^{inertia,ESS}-{s}_{r,t,p}^{charge}+{s}_{r,t,p}^{discharge}\le {i}_{r,{q}^{out}}+{E}_{r,{q}^{out}}, \forall r,t,(p,{q}^{out},{q}^{in})\in R,T,Q$$
(14)

The constraints on \(a{s}_{r,t}^{inertia,BEV}\) are similar to those imposed on \(a{s}_{r,t,p}^{inertia,ESS}\), except for an additional term, \({D}_{r,t}^{BEV},\) in Eq. (15), which accounts for the EV driving demand during each hour t. In Eq. (16), \({V}_{r,t}^{discharge}\) represents the hourly discharge capacity of the parked BEV fleet, given by the driving input profiles [for more information on the driving profiles, see Taljegard et al. [10]].

$$a{s}_{r,t}^{inertia,BEV}\le \left({g}_{r,t}^{BEV}+{s}_{r,t}^{BEV,charge}-{s}_{r,t}^{BEV,discharge}-{D}_{r,t}^{BEV}\right)\times \frac{3600}{{I}^{dur}}, \forall r,t\in R,T$$
(15)
$$a{s}_{r,t}^{inertia,BEV}-{s}_{r,t}^{BEV,charge}+{s}_{r,t}^{BEV,discharge}\le {V}_{r,t}^{discharge}, \forall r,t\in R,T$$
(16)

Frequency reserve


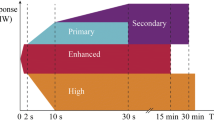
The reserve supply and demand include a new set, O, for the intra-hourly periods in all of which the reserve demand must be met. The reserve demand, shown in Eq. (17), depends on three factors: stochastic load variations (\({I}_{r,t,o}^{SLV}\)); the largest dimensioning fault (\({I}_{r}^{N-1}\)); and the inter-hourly wind and solar variations. Of these factors, it is assumed that imbalances due to the dimensioning fault happen suddenly and require both fast and slow reserves, while stochastic load variations accumulate over time, and the increase or decrease of VRE is known at least 5 min before it occurs and, thus, does not need a reserve response faster than 5 min. This 5 min is also shown in Table 5, and represented in Eq. (17) through \({O}_{o}^{VRE}\).

$$a{s}_{r,t,o}^{FR}\ge {I}_{r,t,o}^{SLV}+{I}_{r}^{N-1}+{\sum }_{p\in {P}^{VRE}}{i}_{r,p}\times max\left({W}_{r,t,p}-{W}_{r,t-1,p}, {W}_{r,t+1,p}-{W}_{r,t,p}\right)\times {O}_{o}^{VRE}, \quad\forall r,t,o\in R,T,O$$
(17)

While Eq. (17) imposes the reserve demand as a lower limit on \(a{s}_{r,t,o}^{FR}\), Eq. (18) sets the upper limit as the sum of the reserve supplies from thermal power plants, hydro power plants, power-to-heat (PtH), energy storage systems and the BEV fleet. The ability of each technology to provide FR is shown in Table 2, and represented by \({O}_{p,o}^{off}\), \({O}_{p,o}^{on}\), and \({O}_{o}^{hydro}\).

Table 2 The factor of rated capacity to which production can be increased, from part-load or offline mode, for each technology and FR interval
Full size table

Equations (19)–(23) govern the supplies from thermal plants, energy storage systems and BEV. In Eq. (19), capacity running at part-load contributes with reserves according to \({O}_{p,o}^{on}\), while offline capacity can start up and contribute according to \({O}_{p,o}^{off}\).

$$a{s}_{r,t,o}^{FR}\le a{s}_{r,t,o}^{FR,thermal}+a{s}_{r,t,o}^{FR,thermal,existing}+{\sum }_{p\in {P}^{PtH}}{g}_{r,t,p}+{\sum }_{p\in {P}^{ESS}}a{s}_{r,t,p,o}^{FR,ESS}+{\sum }_{p\in {P}^{VRE}}\left({i}_{r,p}\times {W}_{t}-{g}_{r,t,p}+{E}_{r,p}\times {W}_{t}-{g}_{r,t,p}^{existing}\right)+a{s}_{r,t,o}^{FR,BEV}+{(i}_{r,hydro}-{g}_{r,t,hydro} ){\times O}_{o}^{hydro},\quad \forall r,t,o\in R,T,O$$
(18)
$$a{s}_{r,t,o}^{FR,thermal}\le {\sum }_{p\in {P}^{thermal}}\left(({g}_{r,t,p}^{active}-{g}_{r,t,p})\times {O}_{p,o}^{on}+{({i}_{r,p}-g}_{r,t,p}^{active})\times {O}_{p,o}^{off}\right), \quad\forall r,t,o\in R,T,O$$
(19)

Equation (19) is mirrored for \(a{s}_{r,t,o}^{FR,thermal,existing}\) in the model. One implication of the way in which the same technology can contribute to both the inertia and reserves supplies is that there is no redundancy for multiple imagined dimensioning faults and reserve demands during the same hour. On the other hand, this is consistent with dimensioning for N − 1, as opposed to N − 2 or any other number of sequential faults.

$$a{s}_{r,t,p,o}^{FR,ESS}-{s}_{r,t,p}^{charge}+{s}_{r,t,p}^{discharge}\le {i}_{r,{q}^{out}}+{E}_{r,{q}^{out}},\quad \forall r,t,(p,{q}^{out},{q}^{in}),o\in R,T,Q,O$$
(20)
$${\sum }_{o\in O}\left(a{s}_{r,t,p,o}^{FR,ESS}\times \frac{{O}_{o}^{dur}}{3600}\right)\le {g}_{r,t,p}\times {\eta }_{t}^{ESS}+{s}_{r,t,p}^{charge}-{s}_{r,t,p}^{discharge},\quad \forall r,t,p\in R,T,{P}^{ESS}$$
(21)
$$a{s}_{r,t,o}^{FR,BEV}-{s}_{r,t}^{BEV,charge}+{s}_{r,t}^{BEV,discharge}\le {V}_{r,t}^{discharge},\quad \forall r,t,o\in R,T,O$$
(22)
$${\sum }_{o\in O}\left(a{s}_{r,t,o}^{FR,BEV}\times \frac{{O}_{o}^{dur}}{3600}\right)\le {g}_{r,t}^{BEV}\times {\eta }_{t}^{ESS}+{s}_{r,t}^{charge,BEV}-{s}_{r,t}^{discharge,BEV}-{D}_{r,t}^{BEV},\quad \forall r,t\in R,T$$
(23)

It should be noted that while this implementation of inertia and the reserve supply from energy storage systems depends on the storage level and available discharge capacity, utilizing a storage unit for reserve supply does not directly affect the storage level. On the one hand, this could lead to an overestimation of the ability of the energy storage units to provide reserves. On the other hand, the average intra-hourly load variations and VRE-ramping should drop to zero as time passes. Furthermore, the VRE-dominated systems (where energy storage may have higher relevance), are also characterized by large amounts of curtailed wind and solar PV generation, which may be used to alleviate energy shortfalls following a reserve demand. Still, an additional scenario is presented at the end of Sect. 4 in which energy corresponding to the largest single reserve contribution in the last 6 h is “locked” in the storage, to allow time for hypothetical replenishment of the used energy.

3.3 Frequency control assumptions

This section describes the assumed values for the largest dimensioning fault (N − 1), other reserve demands, inertial power responses and reserve response times required as inputs to the model.

Since the model used in this work does not use discrete plant investments, the N − 1 values cannot be discretely dependent upon the investments made by the model. Instead, constant values are used based on the current dimensioning fault in each synchronous grid, divided up according to each modeled region’s yearly load. The resulting values are listed in Table 3. Ireland is assumed to be synchronous with Great Britain for the sake of the N-1, to avoid one region with an anomalously large inertia demand. In a previous study, the current authors investigated inertia and reserve in isolated regions for future scenarios with high shares of VRE, including Ireland [11].

Table 3 N − 1 values used for each modeled copper-plate region
Full size table

The values listed in Table 3 are used, in the modeling, as the minimum inertial power responses required so as not to exceed a RoCoF of 1.5 Hz/s, which has been proposed by ENTSO-E [2] as the limit for windows of 1 s. For inverter-based power sources, such as batteries, the available inertial power response is given by the unused discharge capacity [see Eqs. (13) and (14) in Sect. 3.2]. Table 4 lists the inertia constants for the different synchronous machines included in the modeling. The per-unit inertial power response, \(\Delta P\), is calculated using Eq. (24), where H is the inertia constant (listed in Table 4), f is the grid frequency, and \(\frac{dF}{dt}\) is the maximum RoCoF.

Table 4 Inertia constants and inertial power responses for the different synchronous generator types included in this work
Full size table
$$\frac{2H}{f}*\frac{dF}{dt}=-\Delta P$$
(24)

In addition to N − 1, reserve demands are implemented to account for stochastic load variations and to accommodate VRE ramping. The reserve demand for VRE ramping is implemented to increase with increasing investments in VRE technologies and is equal to the hour-to-hour variations in VRE output, as a proxy for the reserves that may be needed while the VRE is ramping. The reserve demand for stochastic load variations is estimated using the following heuristic formula from the UCTE Operation Handbook:

$${R}_{i}=\sqrt{a*{L}_{i, max}+{b}^{2}}-b$$
(25)

where \({R}_{i}\) is the load variation level for day i with daily max load \({L}_{i, max}\). The parameters a and b are empirically established and given in the handbook, and their values are 10 MW and 150 MW, respectively.

However, not all imbalances happen suddenly and require fast reserves. In this work, it is assumed that only faults happen suddenly, whereas VRE ramping and stochastic load variations give rise to reserve demand according to Table 5. While the amplitude of the stochastic load variations is calculated using Eq. (25), the time to reach that amplitude is assumed to follow the equation for a first-order response, \(1-{e}^{-1/\tau}\), with a time constant of 60, which is the same as FCR-N in the Nordic grid [4]. It should be noted that the first intra-hourly interval, 1–5 s, is only implemented for post-2020 scenarios due to the large amount of inertia in the existing systems, as well as the inability of the current system to provide reserves within 1 s.

Table 5 Shares of each reserve demand source active in each intra-hourly interval
Full size table

3.4 Scenarios and input data

With the aim of investigating how the supply of inertia and FR vary with the transition, as well as which supplying technologies will be important throughout the transition from today’s systems to the future high-VRE share systems, a wide range of scenarios is investigated. These scenarios are listed in Table 6 and cover system flexibility and technological availability, as well as whether or not FC is implemented. Each scenario is run in a dispatch-only mode (only PtH and peaking technology investments are allowed as backstop) for Year 2020, and thereafter at three future time-points with increasing load and CO2 cost and decreasing existing capacity (due to expired technical lifetimes). The future time-points are denoted as the near-, mid-, and long-term futures, respectively. From an energy systems transition perspective, these may be seen as approximately representing the time-points of Years 2025, 2030 and 2040 in terms of investment costs, loads, as well as existing transmission and generating capacities. The CO2 costs are 25, 70, 100 and 140 €/tonne, for Years 2020, 2025, 2030 and 2040, respectively.

Table 6 List and descriptions of the scenario groups and geographic cases included in this work
Full size table

In varying the system flexibility, the HighFlex and LowFlex scenarios provide insights into how different system flexibility pathways influence the FC supply. By varying the technologies available for reserve supply, the technology scenarios in Table 6 show which technologies are the most difficult to replace and identify the cost-optimal replacements. Each scenario is considered for the three separate geographic cases: the British Isles, the Iberian Peninsula, and Northern Europe.

The energy demands in this work consist of the traditional electricity demand and the heat demands in regions with district heating. An additional electricity load is provided in the forms of electrified transport and industry sectors. This additional load in the modeled years is listed in Table 7.

Table 7 District heating and non-traditional loads (in TWh) from transportation and industry
Full size table

District heating is included because of its interactions with the electricity system through existing and new combined heat and power (CHP) and power-to-heat (PtH) plants. In this work, some built-in flexibility is assumed in the district heating networks due to thermal inertia and the adoption of hot-water storage units. This flexibility is implemented as a bi-weekly demand instead of an hourly demand, as shown in Eq. (3) in Sect. 3.2. The demand from EV is based on driving patterns [10] and varies from hour to hour. In the LowFlex scenario, it is assumed that 30% of the BEV fleet can be charged strategically, but with no V2G. In the HighFlex scenario, it is assumed that 50% of the BEV fleet can be charged strategically, and that 30% of the BEV fleet can be used for V2G. For steel, cement and ammonia production processes, the load is distributed evenly across the year, although the production of hydrogen can be flexible if there is investment in hydrogen storage.

4 Results

Figure 3 shows an overview of the electricity supply in each geographic case and year in the absence of FC constraints. As can be seen, there are significant differences between the cases in terms of the rate at which fossil fuels are phased out and the contributions of hydropower, wind power and solar PV to the electricity supply. In all the geographic cases, both wind and solar power increase to eventually provide most of the energy in the long-term future, while the total load increases and the share of fossil-fueled thermal power plants and nuclear power decreases. However, only in Iberia does solar power overtake wind power as the dominant electricity supply technology.

Fig. 3
figure 3

Yearly electricity supply development from Year 2020 to the long-term future for each generation technology type in each geographic case and system flexibility scenario, without any frequency control constraints

Full size image

For the scenarios investigated, it was found that the need to provide FC had no impact on the electricity system composition or cost in the HighFlex scenarios (< 0.01% change in total system cost). In the HighFlex scenarios, it was found that the demands for FR and inertia could be fulfilled by strategic charging and discharging of electric vehicles. In addition, it was found that including an inertia requirement without the FR demand had no impact on cost in any year or region, since synchronous generators, unused battery capacity, and curtailed wind power production always suffice to fulfill the required inertia in the absence of an FR demand. Thus, the results presented will focus on the LowFlex scenarios and only consider full, or no, FC implementation.

The shares of the total FR supplied by different technologies for each geographic case are shown in Fig. 4 (left-hand y-axes). The open diamond symbols show the differences in total system cost when FC constraints are included, as compared to when these constraints are omitted (right-hand y-axes). Figure 4 reveals how the FC constraints increase the system cost mainly in Year 2020, in the LowFlex scenario. In Year 2020, thermal power supplies a significant share of the electricity, and the reserve demand requires increased part-load operation of this thermal generation. When new investments are allowed, in the near-term future, the impact of FC on the total system cost is greatly reduced because the reserve demand is met through increased investment in batteries. In the subsequent years, the difference in cost falls further (and is partly recovered in the Brit case), as both the new and previously installed extra batteries help to supply the reserves. Thus, while the battery share of the total reserve supply is relatively low, during the hours that it does supply the reserves it replaces costly options and drastically reduces the cost of FC. It is found that the reserve share from batteries is amplified during hours when the cost of FC is high (see Figure 8 in Appendix 1, which gives the reserve share weighted for the hourly reserve prices). The system cost of FC provision is, thus, highly dependent upon the investment cost for batteries.

Fig. 4
figure 4

The bars indicate the reserve shares per technology on the left-hand y-axis, for each year and region. The diamond symbols indicate the increases in system cost with frequency control constraints, expressed as the system cost increase divided by the electricity production, on the right-hand y-axis

Full size image

In Fig. 5, the bars instead show the share of the hourly reserve price [approximated by the marginal cost of FR supply, Eq. (18)] associated with each intra-hourly reserve interval. It is clear that the shift to using batteries for reserve supply, as indicated in Fig. 4, also changes the interval during which it is most expensive for the electricity system to meet the need for FR. When analyzing the individual intervals, it is important to remember the two factors that differentiate them: (1) the technologies that can supply FR in the given interval; and (2) the level of the demand for FR in that interval. While later intervals have a higher reserve demand (as shown in Table 5) to deal with VRE ramping and stochastic load variations, they also have a higher potential for thermal plant participation. When the reserves are mainly supplied by thermal or hydro power, as in the Year 2020 scenarios (Fig. 4), the first intervals (< 5 min) drive the cost for supplying the reserves, as these are the most difficult intervals for the thermal and hydro plants to manage. In the near-, mid-, and long-term futures, when batteries can be used to supply reserves, the main interval that drives the cost is instead 5–15 min, which has a full reserve demand but not as-high participation from thermal plants as the later intervals. The 15–30 min and 30–60 min intervals also carry marginal reserve costs in the mid- and long-term futures, given that their longer durations make them harder for batteries to satisfy during hours of low storage levels.

Fig. 5
figure 5

On the left-hand y-axis, the bars show the reserve shares per interval, weighted for the hourly reserve cost for each year, interval and region. The right-hand y-axis shows the increased system cost with frequency control constraints, expressed as the system cost increase divided by the electricity production

Full size image

For Iberia, with good conditions for solar PV, the FFR interval (1–5 s) plays a significant role in the near-term future when the system has a lower battery capacity. In Iberia, the battery power capacity is dimensioned after the daily surplus and shortfall caused by the high penetration of solar PV, as opposed to the slower and longer variations caused by wind power, which predominates in the Nordics and the British Isles. The occasions on which the reserve demand is a binding constraint in Iberia (1335 out of 8760 h) are generally when the batteries are fully discharging. The earlier intervals are then the most expensive, as these are the most difficult for other technologies to supply. However, in the long-term future when thermal power plants are used less, the later intervals with a higher FR demand are the hardest to supply also in Iberia.

Table 8 gives a number of indicators of the impact of FC for each geographic case and year. The reserves from VRE in Brit for Year 2020 (Fig. 4) are reflected in Table 8, where it can be seen that the curtailment is doubled to 8.4% to provide additional reserves at the expense of part of the VRE share. When applying the FC constraints in the model, the changes in investments and electricity supply are small, as indicated by the VRE and thermal share columns, and they are mainly related to investments in batteries. In the Iberia case, the impacts on the indicators in Table 8 are particularly low. This is partly due to the higher battery power capacity that is invested in to absorb the solar PV peaks, but is also due to an excess of installed generation capacity. In the Iberia case in Year 2020, the highest hourly net load is 53.1 GW, while the installed capacity of dispatchable generation is 60.3 GW. In an additional scenario for the Iberia case (not included in Table 8), without excess generating capacity, the addition of FC constraints increases the battery storage investments by up to 1 GWh and the system cost by about 0.1 G€/year, although the thermal cycling costs remain unchanged.

Table 8 Indicator values for the base scenarios, with changes from adding FC constraints in parentheses. Hours with marginal FR cost refer specifically to the number of hours when the cost is > 10 €/MWh
Full size table

In an additional scenario in which battery participation in the FR supply locks the corresponding energy level for 12 h (the Locked bat reserves scenario), investments in battery storage are further increased and, consequently, the total system cost increases by an additional 1% in the Iberia and Brit cases, and up to 3.5% in the Nordic+ case. The number of hours during which the supply of FR causes an increase in the system cost also increases.

Figure 6 shows the generation for 1 week with and without FC constraints in the Brit case in the near-term future. The studied week in February has a high load and is dominated by thermal generation. As can be seen, during some hours, peak generation in the form of gas-turbines (GT) is used. The FR cost line shows several occasions with an hourly marginal cost that is associated with the supply of reserves, where the cost arises from a change in the dispatch to make more reserves available. In Fig. 6, the additional reserves during these hours are obtained by increasing thermal generation and, thereby, freeing up battery discharge capacity for reserves.

Fig. 6
figure 6

Generation, storage level and reserve costs for the Brit case and near-term future, for the first week in February

Full size image

The dispatch changes shown in Fig. 6 also occur in the mid- and long-term futures, albeit to lesser extents. The number of occasions on which the FC constraints influence the dispatch, beyond small increases in part-load operation, is indicated by the number of hours with a reserve price above 10 €/MW in Table 8, which decreases from 570 h in the near-term future to 78 h in the long-term future for the Brit case. In the long-term future, the FC constraints lead to higher battery power capacities in the Brit and Nordic+ regions, to be used in situations when batteries are used for both energy arbitrage and reserve supply. In Iberia, the battery power capacity is already higher than in the other regions due to the high penetration of solar PV. This higher battery power capacity is primarily used during the middle of the day to absorb otherwise-curtailed solar PV production, and thus it does not conflict with the energy reserves, as in the Brit and Nordic+ situations. In terms of exchanged electricity, the addition of FC constraints has a negligible effect (< 1%) for all regional cases in the long-term future, and the largest effects are seen in the Ref. Year 2020. The largest change is seen for the Ref. Year 2020 in Brit, where electricity exchange is reduced by 12%. To the limited extent that electricity export is reduced, this leaves transmission lines less used so that more reserves can be traded when needed.

Figure 7 compares investments in electricity generation and storage technologies to provide flexibility for the No FC (left-hand panels) and Full FC scenarios (right-hand panels), for the four time periods. First, this shows that there is little difference in the total generation technology investments when FC constraints are added, although biogas GT investments are made earlier (already in Year 2020) when adding FC constraints in the Nordic+ and Brit regions. Some biogas GT investments are seen also in the No FC case to compensate for missing or incorrect data in the real-life capacity database, as well as capacity deficiencies caused by the geographical scope. Solar PV investments are also slightly increased in the mid- and long-term futures. Second, the results show that while requirements for FC increase the investments battery power capacity in all the geographic cases, the battery storage capacity increases in Iberia, decreases in Nordic+, and initially decreases and then increases in Brit. This is due to the differences in solar PV investments during these years.

Fig. 7
figure 7

Installed capacities of power generation (GW) and storage (in GWh) for each year and scenario. Note the different y-axis for the subplots on the right-hand side

Full size image

Excluding technologies from the FR supply, one at a time, reveals that the availability of batteries for FC is highly important for keeping the cost of FC low, although in the Nordic+ case, excluding FR from power-to-heat technologies also increases battery investments and the system cost. In the absence of batteries, the reserve share from all other sources increases, with PtH and curtailed VRE as the only remaining suppliers of fast reserves. In this case, the system cost, curtailment and thermal cycling costs all increase for all the investigated time-points and regions.

5 Discussion

The results of this work indicate that the provision of FC has a weak impact on the cost and composition of electricity systems that have a high VRE share. In the systems investigated, FC is met by a combination of thermal generation, power-to-heat technologies, curtailed VRE, hydropower and batteries. Many of the resources deployed for FC have other major functions in the electricity systems investigated and are, therefore, available for FC at low or no cost. The main impact of FC on the electricity systems investigated is a small additional investment in battery capacity.

The way in which the model supplies inertia and reserves for FC corresponds to operation planning with perfect forecasting of loads and VRE generation levels. However, since the thermal generation deployed is dominated by gas turbines with short start-up times, combined with batteries that have a high cycling frequency, this implies that scheduling can be performed close to the hour of operation with reliance on good forecasts. Modeling with perfect foresight for battery usage is mainly a problem if the battery cycles are long and during periods without access to curtailed VRE energy. In the near-term, the investigated systems are limited to about 50% VRE and the batteries are used for shorter (1–3 day) cycles. In the long-term future, the battery cycles are longer and thus, the modeling deviates more from a real-life case. On the other hand, longer cycles generally mean fewer cycles without access to curtailed VRE, as well as more time to increase thermal generation if needed. Yet, with the less-than-perfect forecasts of the real world, batteries will be less efficiently operated and more battery capacity will be required to perform the same inter-hourly variation management. While this increases the cost for inter-hourly variation management, it also means more batteries may be available for intra-hourly cycling for reserves and inertia during most hours. At the same time, imperfect forecasting could compound with other reserve demands to increase the total reserve capacity required. Whether this translates to a smaller or larger system cost impact of reserve and inertia demands is unclear and may require further research.

The geographical scope, and specifically the choice of which regions to include in the modeling, has an impact on the system through the imposed electricity export and import limits. For example, the capacity investments in Fig. 7 reveal a lack of generating capacity in Nordic+ and Brit for the Ref. Year 2020, caused either by errors in the power plant database or by the missing transmission capacity to regions not included in the model. However, while this initially causes a lack of generating capacity and a lower available flexibility through trading, this applies to both the No FC and Full FC cases and thus has a limited impact on the effects of adding FC requirements. Another relevant limitation is the coarse geographical resolution, which ignores potential transmission bottlenecks within each subregion. For the model results, this means that some of the running cost is underestimated, as transmission bottlenecks would cause more costly units to run at times. It could also complicate the placement of reserve power. On the other hand, local transmission bottlenecks could mean that more VRE is curtailed, and thus available for frequency control depending on where the issue is caused.

Another consequence of the method used in this work is that the energy in batteries can be deployed both to manage variations and to supply reserves. This is a consequence of only demanding the potential to provide reserves, but not demanding that the power output actually increases. To investigate the impact of this simplification, the results were compared to scenarios in which all the reserves from batteries make the corresponding battery level unusable for 12 h (Appendix Sect. 1). This prevents double-counting of the energy for reserves and for normal operations. The overall impact of reserving energy in batteries for the reserve supply is weak in the Brit and Iberia cases. However, in the Nordic+ case, this leads to a significant increase in battery investments and, thereby, a higher cost for FC. The Nordic+ case has, for all the modeled scenarios, significantly lower battery storage capacity investments than the other regions, which would make it more sensitive to additional limitations on battery energy levels.

The results for Iberia show that, even in the LowFlex scenario, the inclusion of FC constraints has almost no impact on the system cost. As mentioned in Sect. 4, this is largely due to the excess CCGT capacity in Spain. The results for Iberia without overcapacity show that the impacts on part-load costs and battery investments are higher, albeit not as high as in the Nordic+ and Brit cases. This indicates that the higher relative battery power capacity in solar PV-dominated systems can alleviate the changes required to supply cost-efficiently the frequency reserves in the future.

As mentioned in Sect. 4, the addition of FC constraints in the HighFlex scenarios has no impact on the system cost or investments. Of the additional flexibility measures available in these scenarios (increased transmission capacity, hydrogen storage and increased BEV flexibility), the use of electric vehicle batteries has a particularly strong impact and the 30% V2G participation displaces much of the battery investments if applied in the LowFlex scenario. Even at 10% of the fleet participating in V2G, instead of 30%, the system cost impact of adding FC constraints is nullified.

6 Conclusions

This study investigates how frequency control (FC), through the supply of inertia and frequency reserves, develops as the electricity system is transformed, and the interplay between flexibility on inter- and intra-hourly time-scales. The results show that the addition of FC constraints has a limited impact on the system composition and cost, provided that there are markets that correspond to the needs for inertia and frequency reserves in each grid. These markets are important to ensure that sufficient incentive exists to take investments in the technologies that can provide the services to the lowest cost. The study considers three geographic regions with different conditions for wind and solar power generation. In all three investigated regions, the response to FC is similar. Only in the dispatch-only Year 2020 is thermal part-load operation significantly increased to supply FC. When investments in generation and storage technologies are allowed, FC stimulates investments in batteries. The impact of including FC on the total system cost decreases as the VRE share (and accompanying battery capacity to manage intra-hourly VRE variations) is increased.

When limiting the ability of batteries to act as dual providers for reserves and for energy supply, battery storage capacity is increased further to compensate for the sometimes lower available storage capacity. This indicates that while double use of installed battery capacity helps to reduce costs, it does not significantly change the cost-optimal technology mix to supply FC.