1 Introduction

The control of the generating units was the primary downside sweet-faced within the operation of power systems. Therefore, the ways developed to regulate individual and interconnected generators are essential nowadays.

As is well known, active power and frequency control are closely related [1]. Therefore, the correct performance of this binomial is crucial to offer excellent service to the users. In this context, the synchronous generator plays the central role together with the turbine, considered in this case as large rotating masses. Thus, it is usual to use the electrical torque (Telec) and mechanical torque (Tmech) as the crucial elements in the balance of input and output power, Fig. 1. If one is greater than the other, an imbalance has occurred. The speed of the turbine-generator set varies around its rated value [1, 2]. Such imbalances are everyday occurrences and frequently happen during the day. The controls on the turbines are responsible for regulating the rotational speed and, thus, the frequency. Hence, their role is fundamental to the service quality provided by the utility. Full details of electromechanical transients may be found in references [1, 2].

Fig. 1
figure 1

Balancing torques in the turbine-generator set

Full size image

According to Newton’s second law of rotational motion, the increase (decrease) in demand creates a torque (power) imbalance that brakes (accelerates) the synchronous machines’ rotor. These, working in synchronism, will try to balance the excess or deficit of electrical power and thus contribute to regulating the frequency in the system. Thus, the objective of automatic generation control (AGC) is threefold [1,2,3]:

  • The frequency value must be maintained at its nominal value of 50 (60) Hz, minimising its deviation during transient periods and duration

  • The agreed or contracted values of power exchanges with other parts of the system through interconnection lines between areas must be maintained

  • The active power generated is determined through economic dispatch.

The turbine-generator model consists of two main parts: the turbine and generator models. The turbine model describes the relationship between the speed of the turbine and the mechanical power it generates. The generator model describes the relationship between the mechanical power and the electrical power it produces.

Combining these two models makes it possible to calculate the electrical power generated by the turbine, which is injected into the electrical system. This power, together with the load power, determines the system’s frequency.

The turbine-generator model can be used to analyse different types of generation: hydro, nuclear, thermal, and wind. However, it is essential to note that the model can be more or less accurate depending on the type of generation considered.

Automatic generation control is sound under normal operating conditions, i.e. when the changes in demanded power are not very fast because the regulation speed is not fast enough to respond in emergencies where large power imbalances arise [1,2,3].

It is possible to imagine a system of two areas linked by a transmission link where a load modification produces a frequency change with a magnitude that depends on the governor’s characteristics and, therefore, the frequency characteristics of the system’s load. Accordingly, once a load change takes place, supplementary management should restore the frequency to its value [1, 2]. This may be accomplished by adding a reset (integral) command to the governor [4,5,6].

The additional management reference control action can force the rate error to zero by adjusting the reference point. However, this control process is much slower than the first speed because it takes effect after the central speed control (acting on all controlled units) has stabilised the system frequency. The AGC then adjusts the selected units’ load setpoints and output power to cancel out the effect of the installation’s system frequency.

Many renewable and wind energy sources are integrated into the electrical installation [7, 8]. Thanks to advanced management functions, variable speed rotary generators (VSWTG) interlocked with power electronics are widely used [9]. Since wind turbines have a slow response and limited ability to control their power, they are less suitable than conventional generators for frequency control. However, new technologies are being developed, allowing wind turbines to play a more active role in this context [10, 11]. As a result of renewable energy penetration, frequency regulation seems to get more complicated. Thus, the system rate of change of frequency (RoCoF) and frequency change rates are becoming severe [12, 13]. Therefore, the system must implement additional generators with fast ramp capability to maintain frequency stability [14]. Table 1 illustrates typical values of the nominal capacity of power plants and the value of the associated inertias.

Table 1 Summary of inertia values of different power generators (adapted from [21])
Full size table

The insertion of non-synchronous generation technologies, such as wind and solar PV, reduces inertia in power systems. Thus, power systems with a high insertion of renewable energy have a lower inertia, which may increase the risk of instability. Hence, the importance of assessing it.

The Mexican grid was built many years ago. This can cause operational problems, such as failures and blackouts, and a more significant environmental impact due to the generation of energy that pollutes. For this reason, it needs to be updated with some modern technologies.

Therefore, this work presents a proposal that provides knowledge about the system’s behaviour, aiming to improve its operation. This proposal considers the following aspects:

  • Analysis of the system’s current state concerning inertia [15,16,17]. Such an analysis is necessary to identify vulnerable regions. This makes it possible to determine the areas that need to be monitored

  • Proposal for solutions. The proposal must present solutions to improve the system’s operation and reduce polluting energy generation. These solutions must be technically feasible

  • Evaluation of the results. It is essential to evaluate the results of implementing the proposed solutions to verify that the desired objectives were achieved.

The novelty of the work consists of addressing the problem of frequency behaviour, assessing its current state for the inertial response, and proposing some means to help remedy the situation. Also, to foresee a short-term action to solve the situation of auxiliary services, considering the reduction in pollutant generation.

The paper is structured as follows: (1) A brief overview of possible energy storage elements that may be useful for regulating the frequency of the network; (2) a description of the system under study; (3) the required tasks; (4) assessment of the capacity requirements for frequency dropping support; (5) the daily number of ancillary services needed; (6) conclusions.

2 Energy storage considerations

Some authors have estimated that the global demand for energy storage systems could grow to more than 15,128 TWh by 2050 [18]. In turn, they assume that selecting one storage technology over another requires consideration of the potential trade-offs between the advantages and disadvantages of each storage system. Thus, installing a storage unit involves multiple stakeholders with different viewpoints. Hence, they determined the environmental factors to consider when selecting a particular electrical energy storage technology.

Notably, storage systems will be enforced at five stages of electricity production: within the generation, in transmission, in substations, throughout distribution, and with final consumers. Moreover, electricity is transformed into other forms of energy, depending on the type of energy. Today, these are efficient and environmentally relevant processes. Also, storage capacities have increased and now represent notorious capacities [19].

Currently, scientific studies have assessed the potential environmental impacts of some storage technologies. It was found that storage systems are environmentally beneficial, with batteries presenting ecological results during the manufacturing phase [19]. Likewise, hydrogen is a clean fuel. When consumed in a fuel cell, it produces only water. It can be used to store, transport and provide energy. These qualities make hydrogen an attractive fuel for transport and power generation applications. It can be used in industry, housing, energy storage or sustainable mobility. Some ways are more efficient than others. One of the most important alternatives for generating gaseous hydrogen is from water by electrolysis. However, other equally effective methods are currently used in industry [20]. However, high-density hydrogen storage remains a significant challenge for transportation and stationary/portable applications [21]. A comparative study between battery and hydrogen storage for a residential building showed that hydrogen storage had a higher self-sufficiency ratio but was more expensive than battery storage [22]. The round-trip efficiency of getting hydrogen by electrolysis and then into electricity is currently around 40–50% [23, 24].

While hydrogen has advantages over other energy storage options, such as its high energy density and potential for long-term storage, it also faces challenges, such as high costs and low round-trip efficiency. Therefore, choosing an appropriate energy storage option depends on the application’s requirements [22,23,24].

The criteria for selecting an optimal storage system for each network are mainly based on technical requirements such as:

  • required storage capacity,

  • available energy production capacity,

  • type of discharge needed or power transmission rate,

  • discharge time,

  • efficiency,

  • durability (cycling capability),

  • level of autonomy

Investment and operating costs, feasibility and adaptation to the generating source and environmental impacts must also be addressed. It is worth noting that the ecological impact of the technology throughout its life cycle is a growth factor as it often entails economic and social costs [25].

Lithium batteries are the most mature and widely used energy storage technology. They are relatively cheap, easy to install, and have a high energy density, which means they can store much energy in a small space. However, they have a relatively short lifetime and can be expensive to recycle.

Hydrogen is a clean and abundant form of energy that can be produced from renewable sources. Hydrogen fuel cells are efficient and have a long lifetime, but are relatively expensive and complex to install.

Overall, lithium batteries and hydrogen are promising technologies that have the potential to revolutionise the energy sector. They are more efficient and sustainable than other technologies and are being rapidly developed to improve their performance and reduce costs.

Thus, lithium batteries and hydrogen are promising technologies that have the potential to revolutionise the energy sector. However, challenges must still be overcome for these technologies to be fully competitive.

Because an almost instantaneous response is required to help with inertia response (in the order of milliseconds), batteries and flow systems are identified as the most suitable. Between the batteries, some technologies can provide high power peaks. Also, the flywheels can easily reach tens of MW and have a faster response time than that of electrochemical storage (and longer life in terms of cyclability). In the following, we assume using batteries [26,27,28].

This paper focuses on using storage schemes to provide ancillary services to the Mexican electricity grid. The goal is twofold:

  • to have the required reserve capacity,

  • to reduce the amount of CO2 emitted into the atmosphere by conventional plants.

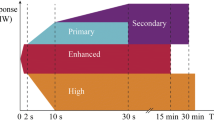
Despite their potential drawbacks, batteries are elected to assist the Mexican grid’s ancillary services, primarily because of the speed they may attend shortly. This is an essential factor in the context of frequency regulation. It is known that it consists of several stages: primary, secondary and tertiary. This document focuses on the primary response under the following assumptions [2]:

  • The primary regulation action should start immediately when a frequency deviation is detected. For frequency deviations greater than 200 mHz, 50% of the total primary regulation reserve (spinning reserve) must be used within 20 s, and 100% of the trip must be reached within 30 s;

  • all power plant units must operate without blocking their speed governors, i.e. in free mode;

  • the primary regulation reserve must be physically distributed among the different power plant units.

Likewise, one of the fundamental actions taken into account to offer a quality electric service is summarised: frequency regulation. It presents results and an assessment of such activities in the Mexican interconnected system (MIS), comprising 158 generators, 2022 buses1, and 3025 lines. Assess the degree of RoCoF and predict the capacity required by fast-acting energy storage technologies to bring them back to nominal in a short time (minutes). In addition, studies are being carried out to determine frequency deviation in the Mexican network environment with a sudden increase in load. Also, studies were carried out to evaluate its behaviour and propose built-in elements to improve it. Based on the reserve values required by the National Energy Control Center (ECC), it is suggested to provide them through energy storage technologies. Finally, reducing pollutant emissions is estimated, assuming the displaced generation of conventional technology.

3 System on test

In this section, we assume linearised models for representing the dynamics of the Mexican Interconnected System (MIS), whose primary purpose is to quantify the frequency deviations in the different regions that make up the system and thus determine its robustness to events typical of its regulation.

In the present analysis, studies are carried out on the MIS linearised model, which represents the transmission voltage levels, Fig. 2. A typical operating point for the system is used. One hundred fifty-eight generators and 2022 high-voltage nodes comprise the network and are spread over the MIS’s seven regions. The working condition hinges on the 2018 base case [29,30,31]. Due to a lack of technical information, some plants were not considered in the study because they are privately owned.

Fig. 2
figure 2

The Mexican Electrical System general structure [31]

Full size image

The MIS encompasses seven control areas working synchronously from the Central American to the United States border. These are here identified as Northwest (NW), North (N), and Northeast (NE) systems selected were West (W), Central (C), Southeast (SE), and Peninsular (P). The system is of the longitudinal topology, with their respective operational imply. Consequently, dynamic safety is usually an issue [29,30,31]. This single-line diagram evaluates the frequency and voltage deviations in the event of abrupt load changes. Table 2 shows the capacities (MW) in each MIS management area [31].

Table 2 The average load and peak generation per area (2018) (adapted from [31])
Full size table

It is noteworthy to emphasise some aspects of the frequency regulation problem. Some of them are summarised below for the MIS [2]:

  • The R-regulation value is the characteristic of a turbine that defines the automatic variation of the active power in response to frequency variations observed by the speed governor of a generating unit concerning its nominal values. Its unit is in per cent. The regulation value (R) is typically within 3 ≤ R ≤ 7.5. All characteristics R = 5% for the studies executed in this paper; such value is employed for every control area

  • The first response starts when a frequency deviation is sensed. If the frequency deviation reaches 200 mHz, 50% of the primary reserve is released within 20 s (spinning reserve);

  • All power units shall cooperate in restoring the frequency.

It is assumed that each region can provide frequency regulation, contributing to the system’s benefit.

In the MIS, a simultaneous disturbance equal to 1% of the demand in every area is applied to examine the system’s frequency behaviour. For the frequency evaluation of the seven regions, the interconnection approach is followed, Fig. 3. Table 2 shows the nominal demands.

Fig. 3
figure 3

The MIS seven control areas. The power base for per unit paraameters is 2 GW

Full size image

Mexico has several connections to the North, using HVDC technology. They have not been considered here to quantify inertia.

4 Impact of inertia per area

As depicted in Fig. 3, transmission links contain seven interconnected control areas. Simplified models have been used as presented in [5, 6]. Note that ΔPkj refers to the link performance deviations through link k − j; Δfj represents the frequency deviations in region j; the area control error (ACE) represents the control error, and T0 is the synchronisation coefficient. A permanent static error in the current flow of the connecting cable (unintentional swapping) would mean that one area would have to rely on the other constantly. Generally, each region must supply its charge [5, 6].

In Cohn’s original work [6], this strategy is used to regulate the power flow in the two-area link and is also used here, as suggested in the classical references. Such a strategy is based on sharing responsibilities for frequency regulation. Each member of the system must collaborate on this task [5]. Table 3 summarises the set of parameters used in the following formulation. In the following, the model is briefly described using a simplified (first order) representation of the elements, Fig. 4 [1, 4, 5], where \({G(s)}_{\mathrm{HTk}}= \frac{1}{(1+s{T}_{\mathrm{H}})(1+s{T}_{\mathrm{T}})}\) represents hydraulic (TH) and the turbine (TT) transfer function; \({G(s)}_{\mathrm{Pk}}= \frac{{K}_{\mathrm{P}}}{1+s{T}_{\mathrm{P}}}\) represents the power system transfer function; PDk stands for power demand; P12 is the power flow through the link between control areas 1 and 2; the speed governor has two inputs: (a) the reference power setting, ΔPref, and (b) the rotor speed change, Δf.

Table 3 Parameters used for studies (Figs. 3, 4)
Full size table
Fig. 4
figure 4

Scheme for the two-areas system regulating the tie-line [4,5,6]

Full size image

The constant R is known as the speed regulation of the governor. The hydraulic actuator has output ΔPv, and TH is the hydraulic time constant. The turbine has as its power increment the signal ΔPT, which depends entirely on the power increment of the valve ΔPv and the turbine’s operation. Kp and Tp represent the power system for closing the loop, where \({K}_{\mathrm{p}}= \frac{1}{D}\) and \({T}_{\mathrm{p}}= \frac{2H}{{f}^{0}D}\). H stands for the inertia constant, D for the load damping factor, \(D= \frac{\partial {P}_{\mathrm{D}}}{\partial f}\). Thus, in this linearised version of the problem, the load is typically represented as a sensitivity D, which implies its frequency dependence. It is assumed that the load–frequency dependency is linear, and the load would increase one per cent for a one per cent frequency increase. The term ΔPD is used to consider an increase/decrease in load, ordinaariamente.

The automatic generation control allows the rotor speed, and thus the generator frequency, to be modified. As demonstrated in [5], integral control is included to bring the steady state error to zero. Gain KI is utilised in this part of the loop and determines the response speed.

Power flow through areas i − j becomes ΔPij. Therefore, each region’s ACE is calculated as a linear combination of the frequency and the power flow error between them.

4.1 Assumptions and goals [1, 4, 5]

Kinetic energy is vital for the frequency control of an electrical power system because it compensates for load variations. When the demand for electricity increases, the frequency of the system decreases. This is because the mechanical power supplied by the turbines must equal the electrical power consumed by the loads. If the demand increases, the mechanical power must also increase. However, this is not always possible, so the kinetic energy stored in the generators is used to make up the difference. Thus, kinetic energy is a critical factor for frequency control and stability. Then, some general assumptions are made about the behaviour of the lumped region, Fig. 3.

  • The system operates in a steady state balance of power. Production balances exceed demand plus losses, PG0 = PD0 + losses. As a result, at steady state frequency becomes f0. All rotating devices contribute to the W0kin (MW s) kinetic energy

  • ΔPD implies load’s connection/disconnection, Fig. 4. According to Newton’s second law of rotational motion (implicit within the Kp − Tp transfer function for a conventional power plant), the increase (decrease) in demand creates a torque (power) imbalance that brakes (accelerates) the synchronous machines’ rotor

  • Conventionally, there is a slight delay in the actuation of the speed control valve to increase the turbine’s power output. Consequently, the speed and frequency are modified. This imbalance is compensated by two elements: (1) the overall kinetic energy; (2) the load change due to its damping factor \(D= \frac{\partial {P}_{\mathrm{D}}}{\partial f}\). For plants based on renewable resources, it is assumed that battery energy storage systems (BESS) are available and capable of providing (receiving) electrical energy to compensate for the imbalance.

Thus, for an increase in load, three mechanisms are activated.

  • the drop in kinetic energy stored in the rotating masses;

  • an increase in turbine output;

  • the release of a percentage of the load due to the drop in frequency.

Once having added integral control to the control loop, the aim is to achieve zero frequency deviation (its error decays to zero).

The BESS must also be able to withstand frequency variations. The DC/AC converter must manage the energy relocation between the source and the system in these devices.

Thus, for frequency regulation purposes, each control zone of the interconnected system is represented by an equivalent model that contributes to the overall performance. In addition, each control zone must be equipped with an automatic generation control scheme.

4.2 Formulation

To illustrate the frequency analysis formulation, the following written expressions for area 1 are used (illustratively, it is assumed to be interconnected with areas 2 and 3). The Δ symbol means deviation from an equilibrium point.

$$ \frac{{{\text{d}}\Delta f_{1} }}{{{\text{dt}}}} = \frac{1}{{T_{p1} }}\left[ { - \Delta f_{1} + K_{{{\text{p}}1}} \left( {\Delta P_{{{\text{T}},1}} - \Delta P_{{{\text{D}},1}} + \Delta P_{12} + \Delta P_{13} } \right)} \right] $$
(1)
$$ \frac{{{\text{d}}\Delta P_{{{\text{T}},1}} }}{{{\text{d}}t}} = \frac{1}{{T_{T,1} }}\left[ { - \Delta P_{{{\text{T}},1}} + \Delta H_{{{\text{T}},1}} } \right] $$
(2)
$$ \frac{{{\text{d}}\Delta P_{{{\text{H}},1}} }}{{{\text{d}}t}} = \frac{1}{{T_{{{\text{H}},1}} }}\left[ { - \Delta P_{{{\text{H}},1}} + \left( {\Delta P_{{{\text{ref}}1}} - \frac{1}{{R_{1} }}\Delta f_{1} } \right)} \right] $$
(3)
$$ \frac{{{\text{d}}\Delta P_{{{\text{ref}},1}} }}{{{\text{d}}t}} = K_{I,1} \left[ {B_{1} \Delta f_{1} - \Delta P_{12} - \Delta P_{13} } \right] $$
(4)
$$ \frac{{{\text{d}}\Delta P_{12} }}{{{\text{d}}t}} = 2\pi T^{01} \left[ {\Delta f_{2} - \Delta f_{1} } \right] $$
(5)
$$ \frac{{{\text{d}}\Delta P_{13} }}{{{\text{d}}t}} = 2\pi T^{02} \left[ {\Delta f_{3} - \Delta f_{1} } \right] $$
(6)

In terms of linear systems, the eigenvalues represent the growth or decay rate of the solutions of the differential equations describing the system. A linear system is stable if its solutions converge to a fixed point in time. Eigenvalues with negative real parts indicate that the solutions of the system converge to a fixed point. In contrast, eigenvalues with positive real parts indicate that the solutions diverge from the fixed point. In summary, the eigenvalues of a linear system determine its stability as follows:

  • Eigenvalues with negative real part: the system is stable

  • Eigenvalues with positive real part: the system is unstable

  • Eigenvalues with zero real part: the system can be stable or unstable, depending on the eigenvectors.

The interpretation of eigenvalues in the stability of a linear system is an essential tool for analysing dynamic systems. It is used in various applications, such as system control and electrical engineering.

The concept of the characteristic polynomial can be used to calculate the eigenvalues. This method consists of solving the characteristic polynomial of the state matrix A (|λI-A|), a polynomial of degree n in the variable λ, where n is the number of rows of the matrix; I becomes the identity matrix of dimension n × n. The roots of this polynomial are the eigenvalues of the matrix.

Thus, for the system in Fig. 3, a state matrix of dimension 37 is formed. The inertia reduction study for each area (when decommissioning conventional plants) is performed by observing the inter-area electromechanical modes associated with frequency stability. Figure 5a, b indicates such behaviour for two areas. These were chosen because these locations are more prone to loss of stability for decommissioning plants: the peninsular and the northwest. Figure 5c refers to the western control area. It is different because the decrease in inertia does not imply noticeable variations in the damping of the electromechanical modes.

Fig. 5
figure 5

Inter-area electromechanical modes with decreasing inertia in a peninsular, b northwest, and c western control areas

Full size image

Thus, the two mentioned areas exhibit weak synchronisation with the rest of the system and are usually energy importers; they represent regions that need to be closely monitored for security reasons. Adding clean generation, such as combined cycle or fast-start natural gas plants, could be an alternative to strengthen this part of the grid.

5 Assessing the energy storage capacity per control area

In this proposal, each control area is associated with the equivalent inertia representing the generators’ total inertia. Suppose all generators in an area are coherent after a disturbance. Then, it is assumed that a single equivalent machine can represent all generators’ behaviour, Fig. 3.

The centre of inertia (COI) concept is used in the following. For a given site with NA number of generators, the equivalent rotor speed (frequency) per area is the angular velocity’s average rotor velocity (frequency). Thus, a large centre of inertia representing the average of all frequencies per area can be defined by,

$$ f_{{{\text{COI}}}} = \frac{{\mathop \sum \nolimits_{k = 1}^{{{\text{NA}}}} H_{k} f_{k} }}{{\mathop \sum \nolimits_{k = 1}^{NA} H_{k} }} $$
(7)

where Hk is the inertia of the k-th generator and fk its corresponding frequency.

In this case, the objective is to quantify a stored capacity that could be released in all areas following a significant disturbance so that the frequency deviation is not such that the system collapses. What is desired is that after such an event, frequency returns to a stable equilibrium state. The storage capacities are chosen in the following formulation. The problem is based on optimisation:

$$ \min f\left( {\varvec{x}} \right) = w_{1} \Delta f_{{{\text{COI}}}} + w_{2} \mathop \sum \limits_{j = 1}^{{{\text{NA}}}} \left( {\Delta P_{Dj} - x_{j} } \right) $$
(8)
$$ \begin{aligned} & {\text{Subject to}} \\ &\quad :\;{\text{all}}\;\;{\text{differential}}\;\;{\text{equations}}\;\;{\text{in}}\;\;{\text{their}}\;\;{\text{linearised}}\\ &\quad\times {\text{version}}\;\;{\text{representing}}\;\;{\text{each}}\;\;{\text{control}}\;\;{\text{area}}\;\;\left( {{\text{Fig}}.{ 3}} \right) \end{aligned}$$
(9)

where ΔfCOI = fCOI − frated is the COI frequency deviation (frated is 60 Hz); NA stands for the number of control areas taken into account (in this study, seven areas); ΔPDj is the demand variation in each area; xj is the value of the available storage capacity (in this study, assuming batteries). Thus, the decision variable is the vector x (includes all xj). w1 and w2 serve to weigh the first and second terms in (8). In this application, they are set to 0.5 each.

Note that expression (8) lends itself to adding some additional aspects to consider, for example, pollution reduction, including an additional term associated with greenhouse gases [32]. It has been used in this application as it appears in (8).

The search for the optimum can be carried out in many different ways, from heuristic techniques to formal mathematical methods, such as the [33,34,35] interior point methods. All have their advantages and disadvantages, and some have essential applications. Due to its robustness in this research, the search for the optimum of (8), (9)(8)–(9) is carried out through the Levenberg–Marquardt method. It is convenient to express the optimisation problem as a sum of squares [36],

$$ {\text{J}}\left( x \right) = \left[ {f({\mathbf{x}})} \right]^{{\text{T}}} \left[ {f({\mathbf{x}})} \right] $$
(10)

where x is the vector of the unknown parameters. To minimise J(x), differentiate (10) and equate to zero. Thus, the problem can be visualised as maximising the nadir of the COI, assuming an early insertion of stored energy. The simulated disturbances are simultaneous increments of 1% of their demand in all areas, Fig. 6. The bounds over which the optimal solution of the problem (8), (9) is sought are in the search space,

$$ {1}\% {\text{ peninsular}}\;\;{\text{demand}} \le x_{j} \le {1}\% \, \;\;{\text{western}}\;\;{\text{demand}} $$
(11)
Fig. 6
figure 6

COI frequency deviation at a simultaneous 1% increase in demand for each area. Stored energy is activated. Nadir reaches a value of 0.025 Hz

Full size image

Note that a COI’s nadir of 0.025 Hz is reached for the constraints set, which is considered acceptable. Accordingly, the required storage capacity per area becomes as in Table 4 for these conditions. All this procedure has been carried out regarding the nominal inertia value per area.

Table 4 Storage capacities to limit the nadir of the COI, calculated based on the nominal inertia of each area
Full size table

For example, Fig. 7a illustrates the frequency deviation evolution of the peninsular area for a 1% increase in the total demand. Three cases are indicated: (1) with an inertia reduction of 35% without energy storage; (2) with an inertia reduction of 35% and the energy storage indicated in Table 4; (3) without inertia reduction and with energy storage. It is worth noting that such a reduction in inertia is almost on the verge of instability for the peninsular area. Therefore, it would be wise not to reach such a value.

Fig. 7
figure 7

a Frequency deviation in the peninsular area in the event of a 1% increase in the total demand. Note the improvement in frequency behaviour with energy storage, significantly when inertia is reduced by plant decommissioning; b frequency deviation in the NW area in the event of a 2% increase in the total demand. Note the slow response, even with storage inclusion

Full size image

Similarly, Fig. 7b shows the frequency deviation of the northwest area for a 2% increase in total demand when there is no reduction in inertia when there is (40%) and when storage is used or not. For all cases, the nadir is very severe (greater than 0.1 Hz), and in no condition is the steady state reached for the study time, which means the disturbance has been significant. But, in this case, no loss of frequency stability is noted.

Thus, the benefit of using energy storage elements to make them available when the system requires them is well known. It is also essential to locate them in the right place and make them available as soon as possible when needed.

It is worth noting that at this first stage of assessing an amount of stored energy, it has been assumed that such elements can respond instantaneously. They will delay their response, depending on the technology used. In this first approximation, no such delay has been taken into account.

5.1 Ancillary services requirements

Electricity grids provide ancillary services to ensure a safe and efficient electricity supply. They include frequency regulation, power reserve, disturbance response, system stability and power quality.

Frequency regulation is an essential auxiliary service to maintain the stability of the electricity system. The power grid frequency is directly related to the power generated and demand. When demand increases, the frequency decreases. When demand decreases, frequency increases. Frequency regulation ancillary services fall into two categories:

  • Primary regulation is the instantaneous response of generators to frequency variations. It is mainly provided by synchronous generators, which can vary their rotational speed to adjust the power generated. Thus, primary regulation is necessary to maintain the frequency within acceptable limits during demand variations

  • Secondary regulation is the generators’ medium and long-term response to frequency variations. It is provided by the power reserve, which is the ability of generators to increase or decrease the generated power in response to a change in demand. Thus, secondary regulation is necessary to restore the frequency to its nominal value after an event that has caused a significant frequency deviation.

Each day, for the day-ahead market, the utility publishes its capacity requirements to cope with a possible severe contingency (e.g. the trip of the largest generator in the system). Since the leading ancillary service in Mexico is frequency control, we focus on it. That is, having sufficient energy storage resources to cope with eventual severe frequency disturbances, sustaining the energy contribution for a few tens of minutes, and repeating such a cycle a few tens of times a year. All this is for each control area of the MIS.

It is necessary to emphasise now that the quantities presented in Table 4 are the minimum to overcome the inertial response problem in the network under study. However, if we now focus on the requirements for the ancillary services, the quantities grow accordingly, and we will assume that investment can be made in such requirements. Thus, Table 5 summarises such average daily requirements for ancillary services (frequency support included). The total value of 1700 MW is used as an average of the system requirements and is prepared daily by the National Energy Control Centre. The requirements per area have been calculated proportionally to the size of the area, taking Table 1 as a reference.

Table 5 Capacity per control area (ancillary services and frequency regulation) [31]
Full size table

Notice that the values of the required ancillary services per area exceed the capacities estimated in Table 4. The difference is that, for this research, only the frequency support has been considered, leaving aside the other aspects mentioned. Hence, installing the latter capabilities could be used to provide part of the daily ancillary services.

It is essential to be aware that installing energy storage devices is an investment that requires prior studies of all kinds; economic studies are vital. The economic evaluation is based primarily on data related to.

  • the capital, installation and operating costs, as well as the lifetime and efficiency of each technology;

  • the efficiency of the generation likely to be used to charge the storage devices, as well as the efficiency of the generation potentially replaced by storage and the associated fuels;

  • the social discount rate. The purpose of such studies is to examine from a social perspective whether the benefits of storage outweigh its costs.

Consequently, a cost–benefit analysis (CBA) may consider various benefits that would not be considered in a business case, benefits not included in the price of storage services, such as reduced greenhouse gas emissions.

6 Emissions reduction

Table 5 quantifies the capacity to meet the average daily ancillary service requirements. If such services are met using storage technologies (e.g. batteries), and if additionally it is assumed that these are recharged using renewable energy sources (for instance, wind generation), which have been installed to displace conventional generation, then the ancillary services are met. The pollutant emissions from such displacement are reduced. This section exhibits the quantification of such reductions.

For the reduction estimation of harmful gas emissions when conventional generators are decommissioned, use is made of historical data and in-depth research on similar actions in a significant ISO in the United States [37,38,39].

In such investigations, especially those published in [39], the author studies five cases with different percentages of wind resource penetration and formulates respective functions of the degree of decrease in pollutant emissions concerning the level of wind penetration, Fig. 8. This research proposes a very particular emission function that can be applied and customised to specific generators automatically. Such a function considers the generator’s daily operations as starting, stopping and ramping and, in doing so, produces accurate predictions. Such scenarios involve 3.5, 10.0, 16.5, 23.0, and 29.500 GW of renewable resources [39]. In Fig. 8, each group of bars shows the percentage change for each emission type and generation from the 3500 MW wind penetration scenario.

Fig. 8
figure 8

Reduced emissions as a function of different levels of wind penetration. It starts at 3.5 GW and includes displacement from Coal, Gas steam turbines, Combined cycle, and Simple cycle plants (adapted from [39])

Full size image

In Mexico, the clean energy penetration level represents a capacity of 2500–3700 MW if we consider bioenergy, photovoltaics, wind, and geothermal [29,30,31]. Table 6 is short-term predictions relating to estimates of emission reductions from technological change based on research results in [37,38,39]. The calculation is based on the two cases (10.0 and 3.5 GW) [39].

Table 6 The expected reduction in MIS emissions when assuming the embedding of energy storage technologies (1.7 GW) for ancillary services
Full size table

Calculating pollutant emission reductions is a complex task that requires a detailed analysis of emission sources and emission factors. The IPCC provides some tools and resources to assist users in this calculation. The Intergovernmental Panel on Climate Change’s calculation to quantify pollutant emission reductions is based on the following steps [40]:

  • Identification of emission sources

  • Calculation of emissions

  • Calculation of emission reductions

  • Quantification of emission reductions.

This calculation is essential for the evaluation of climate policies and the development of emission reduction strategies.

It should be noted that the results shown in Table 6 are in close agreement with calculations performed using the technique used by the Intergovernmental Panel on Climate Change (IPCC). The institution was founded in 1988 to carry out, among other things, scientific and technical assessments of climate change, its causes, potential impacts, and actions to be taken [40].

Table 6 is constructed with the reduction percentage of the 10,000 MW scenario (the size of the lower bars in Fig. 8), with the mentioned proportion and also considering the demand ratio by control area in Table 2.

The gas steam turbine shows substantial decrements in its generation output as the penetration of renewables increases. The 29,500 MW wind capacity scenario results in gas-fired steam turbine generators producing 80% less energy than in the lower wind penetration scenario. It is important to emphasise that the estimates in the following reductions result from displacing conventional electricity generation by clean generation. Otherwise, they will result in overestimates.

Of course, these emission reductions are insufficient to reach the targets committed by the country in this context. Much more action is needed. With current climate commitments, the world is heading for an unacceptable temperature rise by the end of the century. The technologies and policies required to reduce emissions already exist and must be implemented immediately. Only a few countries have committed to a timetable for achieving emissions neutrality [41].

7 Conclusions

The decommissioning of fossil fuel generators becomes an issue for the Mexican grid due to the inertia reduction. This research focuses on the impact of inertia reduction on the different control areas of the Mexican grid and the positive influence that energy storage devices can have on it. Through a multidisciplinary approach combining eigenvalue analysis and optimisation, it has been possible to quantify the possible degree of inertia reduction without detriment to frequency stability and propose the minimum necessary capacity of stored energy to impact the inertial response positively. The results reveal that it is possible to improve the operation of the network in this respect.

A strategy is also presented to quantify the degree of reduction in pollutant emissions by displacing conventional generation with energy storage elements, which is a small contribution to the policy of achieving a cleaner planet. Of course, the actions to achieve this are extensive and require higher levels of commitment. These findings open the door to further research leading to higher network security rates, all for users’ benefit.

As results show, the Mexican system consists of some robust regions, but others are weak regarding inertia and transmission links. There is a ratio of almost seven times between such regions. Thus, the eigenvalue analysis for a reduction of about 10% in the inertia value of the weak regions indicates the danger of reaching a zone of frequency instability. This makes weak regions quite vulnerable, and special attention should be given to them.

On the other hand, using energy storage technologies with fast response is proposed to assist the inertial response process. In this sense, the high responsiveness of storage elements is critical for them to participate effectively. The results for each MIS region have been shown. In this study, limited frequency excursions are intended to allow a range of [0.02, 0.03] Hz for sudden and simultaneous load changes of up to 1.0% of the nominal load. Through frequency stability studies and formulating an optimisation problem, a capacity of 345 MW of storage technologies can be estimated to assist the inertial response and keep the frequency excursion within that range, assuming they respond fast.

Storage technologies can also be helpful to supply ancillary services in the short term, replacing conventional generators for this purpose. The average daily capacity required by the system amounts to 1700 MW, which has been weighted in each control area, depending on their size, Table 5. The results show that energy storage systems (ESS) can give auxiliary services for the various management areas within the Mexican interconnected system. Storage technologies make it possible to achieve very convenient frequency deviations to avoid too severe transients.

If storage technologies meet the requirement of an average of 1700 MW for ancillary services, there will be significant daily benefits in reducing pollutant emissions, Table 6.

Although in this paper, the use of batteries as a storage element has been proposed, it could be other emerging technologies. Regarding the placement of the storage systems, their location is also essential. It will be distributed as broadly over the system as doable to hide the most prominent geographic area. It is excellent when storage is distributed across the network, connected to distributed generation plants, or located near areas of high consumption.