Modeling and Simulation of Stochastic Inverse Problems in Viscoplasticity

Abstract

In this paper, we have proposed an approach for parameter identification of random field for rigid viscoplastic material. It is assumed that the random field is stationary and Gaussian with known autocovariance function. Karhunen–Loève decomposition has been used to quantify the effects of random inputs. A method is presented that takes into account only the first two statistical moments of the analyzed displacement field, and only two values of searched process are identified—mean value and coefficient of variation in autocovariation function. It has been shown that this approach is desirable when complicated systems are analyzed. The discretization of the governing equations has been described by the finite element method. The sparse grid stochastic collocation method has been used to solve the stochastic direct problem. It is shown that for the described nonlinear equations, the response function due to searched parameters with wide bounds and with reduced number of measurement points has many local extrema and global optimization technique is required. Genetic algorithm has been adopted to compute the functional cost. Numerical example shows the identification problem for compressed cylindrical sample. It is revealed that the key factor determining the convergence of the method is the degree of reduction in the height of the tested sample.

1 Introduction

Deterministic metal-forming problems have been considered in many publications [3, 18, 23, 34, 36]. In these problems, the parameters characterizing the material properties or boundary conditions are assumed to be known (achieved as the approximation of experimental studies). This is a good approach for a theoretical study of the problem, but it fails when the real object is analyzed. Experiments show that random fluctuations of geometrical and material parameters, or load values, significantly affect the behavior of the test object. For this reason, in metal-forming processes, a stochastic approach has been used. Due to the considerable progress in computer technology and an associated significant increase in computing power, this approach, in recent years, has been widely used [1, 2, 17, 33].

The most common method of solving the above-posed problem is the Monte Carlo method and the perturbation method [21, 22, 40]. Monte Carlo method is easy to implement and does not require changes in the existing code. Despite these advantages, it often requires a huge amount of sampling that the complex nonlinear problems can lead to many hours of calculations. Perturbation method is based on the extension of a classical deterministic finite element method or the finite difference method [16]. This method based on the Taylor series of expansion allows the calculation of second-order statistics and is suitable for a small level of uncertainty, typically less than 10% for first-order technique and less than 15% for second-order [21].

In recent years, the stochastic spectral finite element method (SSFEM) and the stochastic collocation method (SCM) [5, 46] have gained a growing popularity. First one was proposed by Ghanem and Spanos [13]; subsequently, it was developed by other researchers [25, 26, 45] and applied to the problem of finite deformations [2]. Despite its high effectiveness and the possibility of its application to a number of problems, the use of the SSFEM may cause problems if governing equations are complicated and complex. In this case, it may be difficult to derive explicit forms of coefficients in the equations (large number of integration is needed). The equations in this method are coupled, but the domain decomposition method can be used to reduce the computation time [14, 41]. The idea behind the second method resembles the Monte Carlo method. The main difference is the definition of the sampling points defined as a tensor product of a set of one-dimensional quadrature points associated with probability distribution function. This method was initially applied to the numerical integration problems with the large number of dimensions [12]. It gained its significance after the introduction of the sparse grid technique [6, 39], which contributed to the considerable reduction in the sampling points in the multidimensional random space. Due to the possibility of using the already-existing source code of the deterministic program (used as the so-called black box), it has been used in the following paper. A similar approach to the analysis of the hyperelastic–viscoplastic large deformation problem has been proposed in paper [1].

Inverse problems, as ill posed, may be the cause of huge problems connected with the identification of the specified parameter in the deterministic approach, especially in cases of large sensitivity to small changes. The above-mentioned reasons may cause significant errors in solving stochastic problems, by overlapping variety of errors: measurement errors, approach errors and a random perturbation of a searched parameter [11]. Classical methods of solving inverse problems, usually based on the sensitivity analysis, may be found in the numerous works [4, 8, 28, 30, 31, 42]. Solutions of stochastic inverse problems usually associated with heat conduction can be found in the work of Zabaras and co-workers [25, 47, 48] as well as associated with current flow [37]. In these works, to solve the inverse problem, the authors have used gradient methods. Problems of parameter identification in plastic forming of porous materials can be found in [38]. The above-mentioned works assume the existence of a global minimum of response function. In general, except the global minimum, there can exist local minima that disqualify local search methods. Therefore, a non-deterministic method of the minimization of a functional achieved by the use of recently popular genetic algorithms [15, 19, 20, 24] has been proposed. This method is used to optimize problems for the deterministic plastic forming in works [9, 32].

2 Brief Description of the Direct Deterministic Problem

This chapter will first present basic equations governing the problem. These equations can be found in a number of publications on the plastic metal-forming problem [18, 34].

2.1 Rigid Viscoplasticity

The mechanism of plastic deformation of the rigid viscoplastic material is described by the following equations [23]:

$${\text{Equilibrium}}\;{\text{equation:}}\;\frac{{\partial \sigma_{ij} }}{{\partial x_{j} }} = 0 ,$$

(1)

$${\text{Yield}}\;{\text{criterion:}}\;\bar{\sigma } = \bar{\sigma }(\dot{\varepsilon },\dot{\bar{\varepsilon }}) ,$$

(2)

$${\text{Constitutive}}\;{\text{equation:}}\;\dot{\varepsilon }_{ij} = \frac{3}{2}\frac{{\dot{\bar{\varepsilon }}}}{{\bar{\sigma }}}\sigma_{ij}^{{\prime }} \;{\text{with}}\;\dot{\bar{\varepsilon }} = \sqrt {\frac{2}{3}} (\dot{\varepsilon }_{ij} \dot{\varepsilon }_{ij} )^{{\frac{1}{2}}} ,$$

(3)

$${\text{Compatibility}}\;{\text{conditions:}}\;\dot{\varepsilon }_{ij} = \frac{1}{2}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right),$$

(4)

where $\sigma_{ij}$ is a Cauchy stress tensor, $\bar{\sigma }$—effective stress, $\dot{\varepsilon }$—strain rate, $\dot{\bar{\varepsilon }}$—effective strain rate, $u$—velocity. To the above equations, boundary conditions should be attached in the form of the initial velocity and the friction at the interface between the sample and a tool.

2.2 Finite Element Approximation¹

The starting point to formulate the rigid viscoplastic finite element method is to describe the appropriate functional. Rate form of virtual work equations (matrix notation) is as follows [7, 49]:

$$\pi = \int\limits_{V} {{\varvec{\upsigma}}{\dot{{\varvec{\upvarepsilon }}}}} {\text{d}}V - \int\limits_{{S_{F} }} {\varvec{Fu}{\text{d}}S_{F} }$$

(5)

where $\varvec{F}^{\text{T}} = [\begin{array}{*{20}c} {F_{r} } & {F_{z} } \\ \end{array} ]$ represent surface tractions associated with surface $S_{F}$.

Using decomposition of Cauchy stress tensor to hydrostatic and deviatoric part ${\varvec{\upsigma}} = {\mathbf{I}}\sigma_{m} + {\mathbf{s}}$, where $\sigma_{m} = \frac{1}{3}tr\left( {\varvec{\upsigma}} \right)$, ${\mathbf{I}}$ is a second-order unit tensor, and Levy–Mises equation

$${\mathbf{s}} = \frac{2}{3}\frac{{\bar{\sigma }}}{{\dot{\bar{\varepsilon }}}}{\dot{\varvec{\upvarepsilon }}}$$

(6)

following functional can be written as:

$$\pi = \int\limits_{V} {\frac{2}{3}\frac{{\bar{\sigma }}}{{\dot{\bar{\varepsilon }}}}{\dot{\varvec{\upvarepsilon}}} \dot{\varvec{\upvarepsilon}}} {\text{d}}V + \int\limits_{V} {{\mathbf{I}}\sigma_{m} } {\dot{\varvec{\upvarepsilon }}}{\text{d}}V- \int\limits_{{S_{F} }} {\varvec{Fu}{\text{d}}S_{F} }.$$

(7)

Obtaining the solution of Eq. (5) should be determined by the form of Eq. (2), which can be a source of random uncertainty

$$\bar{\sigma } = \bar{\sigma }(\omega ,\dot{\varepsilon },\dot{\bar{\varepsilon }})$$

(8)

where $\omega$ denotes random event. Using definition of strain rate $\dot{\varepsilon }_{v} = tr\left( {{\dot{\mathbf{\varepsilon }}}} \right)$ and assuming that $\sigma_{m} = K\dot{\varepsilon }_{v}$, Eq. (7) can be written as a variation of the functional in the form:

$$\delta \pi = \int\limits_{V} {\frac{2}{3}\frac{{\bar{\sigma }}}{{\dot{\bar{\varepsilon }}}}{{\dot{\varvec \upvarepsilon }}}} \delta {{\dot{\varvec \upvarepsilon }}}{\text{d}}V + K\int\limits_{V} {\dot{\varepsilon }_{v} } \delta \dot{\varepsilon }_{v} {\text{d}}V - \int\limits_{{S_{F} }} {\varvec{F}\delta \varvec{u}{\text{d}}S_{F} } = 0$$

(9)

where $\delta {\dot{\varvec{\upvarepsilon }}}$ is the variation in strain rate, $\delta \dot{\varepsilon }_{v}$ is variation in volumetric strain rate and $K$ is a penalty constant (very large positive constant) used to remove the incompressibility constraint on admissible velocity field.

Boundary tractions in metal-forming problems are mainly frictional forces. The modeling of these forces is traditionally made in two ways: by means of a friction coefficient and by means of a friction factor [33, 34]. A directly applied friction coefficient leads to non-symmetric matrices and is not commonly used in bulk deformation metal forming. A friction factor is defined by the equation:

$$\tau = m \cdot k_{\text{y}} ,$$

(10)

where $\tau$ is the shear friction stress, $k_{\text{y}}$ is the shear yield stress of the material and $m$ is the friction factor.

In considering the boundary conditions, a major problem is faced when a point of reverse relative velocity between workpiece and die exists, and its position is not known a priori. This happens, for instance, in ring compression with high friction. The orientation of the friction force changes at that point, so an abrupt jump in its value shows up. In such a case, we can use the equation for the friction force:

$$F_{r} = - m \cdot k_{\text{y}} \left( {\left( {\frac{2}{\pi }} \right)\tan^{ - 1} \left( {\frac{{u_{\text{R}} }}{{a \cdot \left| {u_{\text{die}} } \right|}}} \right)} \right),$$

(11)

where $u_{\text{R}}$ is the magnitude of relative velocity between die and workpiece, $a$ is a constant several orders of magnitude less than the die velocity and $\left| {u_{\text{D}} } \right|$ is the magnitude of die velocity. Above-mentioned boundary conditions have been modeled similar to the works [23, 34].

3 Stochastic Direct Problem

In the stochastic collocation method, the output stochastic process is formed on the basis of the solution of the deterministic problem. The input random process in a form of coefficients in governing equations or in boundary conditions is discretized. This method will be discussed in detail further in this article.

3.1 Method of Random Field Discretization

In this work, it is assumed that the considered random fields are Gaussian processes, or such processes, for which the random variable at each point ${\varvec{x}}$ has normal distribution, as for the material parameters is the most common. It is also assumed that the random fields are stationary in a wide sense [43] by which they satisfy the following assumptions: $E\left( {\alpha ({\varvec{x}},\omega )^{2} } \right) < \infty$, $E\left( {\alpha ({\varvec{x}},\omega )} \right) = {\text{const}}$, ${\text{Cov}}(\varvec{x}_{1} ,\varvec{x}_{2} ) = \left. {{\text{Cov}}({\varvec{\uptau}})} \right|_{{{\varvec{\uptau}} = \varvec{x}_{1} - \varvec{x}_{2} }}$.

For the description of the random field $\alpha ({\varvec{x}},\omega )$, expected value is most commonly used:

$$E\left( {\alpha (\varvec{x},\omega )} \right) = \int\limits_{\Omega } {\alpha (\varvec{x},\omega ){\text{d}}{\mathscr{P}}}$$

(12)

and covariance function:

$${\text{Cov}}(\varvec{x}_{1} ,\varvec{x}_{2} ) = \int\limits_{\Omega } {\left( {\alpha (\varvec{x}_{1} ,\omega ) - E\left( {\alpha (\varvec{x}_{1} ,\omega )} \right)} \right)\left( {\alpha (\varvec{x}_{2} ,\omega ) - E\left( {\alpha (\varvec{x}_{2} ,\omega )} \right)} \right){\text{d}}{\mathscr{P}}}$$

(13)

where

$${\text{d}}{\mathscr{P}} = \varphi \left( \xi \right){\text{d}}\xi$$

(14)

is a Gaussian measure of the probability space, $\Omega \in \left( { - \infty ,\infty } \right)$ and function $\varphi \left( \xi \right)$ has normal distribution:

$$\varphi \left( \xi \right) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left( {\frac{{ - \left( {\xi - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)$$

(15)

wherein $\mu$ is the expected value and $\sigma$ is the standard deviation.

A stochastic process $Y(\varvec{x},\omega ),$ [43] where ($\varvec{x} \in A \subset R$, $\omega \in \Omega$) we call a function, in which each number x assigns a random variable $Y(\omega )$ defined in a fixed probability space $(\Omega ,{\rm Z},P)$. Here, $\Omega$ is the set of elementary events, ${\rm Z}$ and $\sigma$-algebra and $P$ is a probability measure. To obtain a computationally useful representation of the process $Y(\varvec{x},\omega )$, it will be presented in the canonical form. Among the various forms of such a representation, a spectral representation—Karhunen–Loève expansion—will be adopted for further considerations [13, 26, 47]. This expansion may be presented in the following form:

$$Y(\varvec{x},\omega ) = E\left( {Y(\varvec{x})} \right) + \sum\limits_{n = 1}^{\infty } {\xi_{n} (\omega )} \sqrt {\lambda_{n} } f_{n} (\varvec{x}).$$

(16)

In Eq. (16), $\varvec{\xi}(\omega )$ is a set of random variables. Constants $\lambda$ and functions $f(\varvec{x})$ are the eigenvalues and eigenvectors of the covariance kernel:

$$\int\limits_{A} {C(\varvec{x}_{1} ,\varvec{x}_{2} )} f(\varvec{x}_{2} ){\text{d}}\varvec{x}_{2} = \lambda f(\varvec{x}_{1} ).$$

(17)

Let us assume that the random field is two dimensional.

Hence [13]:

$$\lambda_{n} = \lambda_{i}^{(x)} \lambda_{j}^{(y)}$$

(18)

and

$$f_{n} (x,y) = f_{i}^{(x)} (x)\;f_{j}^{(y)} (y).$$

(19)

After substituting Eqs. (18) and (19) to (16), the following equation can be obtained:

$$Y(x,y,\omega ) = E\left( {Y(x,y)} \right) + \sum\limits_{i,j = 1}^{\infty } {\xi_{ij} (\omega )\sqrt {\lambda_{i}^{(x)} \lambda_{j}^{(y)} } f_{i}^{(x)} (x)\;f_{j}^{(y)} (y)} .$$

(20)

Such Karhunen–Loève expansion is usually truncated to M terms:

$$Y(x,y,\omega ) = E\left( {Y(x,y)} \right) + \sum\limits_{i,j = 1}^{M} {\xi_{ij} (\omega )\sqrt {\lambda_{i}^{(x)} \lambda_{j}^{(y)} } f_{i}^{(x)} (x)\;f_{j}^{(y)} (y)} .$$

(21)

To solve the integral Eq. (17), it is necessary to define the kernel $C(\varvec{x}_{1} ,\varvec{x}_{2} )$. Following the work of Ghanem and Spanos [13], to expand the process $Y(\varvec{x},\omega )$ the following function is adopted:

$$C(x_{1} ,x_{2} ;y_{1} ,y_{2} ) = {\text{Var}}_{Y} \cdot \exp \left( {\frac{{ - \left| {x_{1} - x_{2} } \right|}}{{b_{x} }} - \frac{{\left| {y_{1} - y_{2} } \right|}}{{b_{y} }}} \right),$$

(22)

where $b_{x}$ is a correlation length in x direction, $b_{x}$ in y direction, and ${\text{Var}}_{Y}$ is a coefficient of variation.

3.2 Sparse Grid Stochastic Collocation method (SG-SCM)

In order to discuss in detail, the SG-SCM method in the first place will present definitions necessary for the interpolation problems.

Let ${\varvec{\upxi}}$ represent a point in random space $\Gamma \subset {\mathbb{R}}^{N}$, $\Pi_{N}$ is a N-dimensional space of polynomials and $\Pi_{N}^{p}$—subspace of polynomials of degree p. Interpolation problem, as in [46], can be formulated as follows: For a set of nodes $\Theta_{N} = \left\{ {{\varvec{\upxi}}_{i} } \right\}_{i = 1}^{N}$ in N-dimensional random space $\Gamma$ and for a smooth function $f:{\mathbb{R}}^{N} \to {\mathbb{R}}$, polynomial $\mathcal{I}f$ is to be identified such that $\mathcal{I}f\left( {{\varvec{\upxi}}_{i} } \right) = f\left( {{\varvec{\upxi}}_{i} } \right)$, $\forall i = 1, \ldots ,M$.

In the case of the use of the Lagrange interpolation, interpolation polynomial can be summarized as follows:

$${\mathcal{I}}f\left( {\varvec{\upxi}} \right) = \sum\limits_{i = 1}^{M} {f\left( {{\varvec{\upxi}}_{i} } \right)L_{i} \left( {\varvec{\upxi}} \right)}$$

(23)

wherein

$$L_{i} \left( {\varvec{\upxi}} \right) = \prod\limits_{{\begin{array}{*{20}c} {j = 0} \\ {\left( {j \ne i} \right)} \\ \end{array} }}^{M} {\frac{{\xi - \xi_{j} }}{{\xi_{i} - \xi_{j} }}}$$

(24)

and

$$L_{i} \left( {\xi_{j} } \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {dla} & {i = j} \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {dla} & {i \ne j} \\ \end{array} } \\ \end{array} } \right. .$$

(25)

To formulate the stochastic direct problem, let Eq. (5) be rewritten in the form of:

$$\pi \left( {\varvec{x},\omega } \right) = \int\limits_{V} {{\varvec{\upsigma}}\left( {\varvec{x},\omega } \right){\dot{\mathbf{\varepsilon }}}} \left( {\varvec{x},\omega } \right){\text{d}}V - \int\limits_{{S_{F} }} {\varvec{F}\left( {\varvec{x},\omega } \right)\varvec{u}\left( {\varvec{x},\omega } \right){\text{d}}S_{F} } .$$

(26)

To solve the above stochastic Eq. (26) in the first step, the infinite probabilistic space is reduced to finite-dimensional one. For this purpose, we have used the assumption of finite-dimensional noise [5, 46], which says that the stochastic process can be represented by a finite number N of independent random variables $\left[ {\xi^{1} (\omega ) ,\ldots ,\xi^{N} (\omega )} \right]$. To obtain this representation, Karhunen–Loève expansion can be used, and then, Eq. (26) with boundary conditions can be written in the following form:

$${\mathcal{L}}\left( {\varvec{x},\xi^{1} \left( \omega \right), \ldots ,\xi^{N} \left( \omega \right)} \right) = \int\limits_{V} {{\varvec{\upsigma}}\left( {\varvec{x},\xi^{1} \left( \omega \right), \ldots ,\xi^{N} \left( \omega \right)} \right){{\dot{\varvec \upvarepsilon }}}} \left( {\varvec{x},\xi^{1} \left( \omega \right), \ldots ,\xi^{N} \left( \omega \right)} \right){\text{d}}V ,$$

(27)

$${\mathcal{B}}\left( {\varvec{x},\xi^{1} \left( \omega \right), \ldots ,\xi^{N} \left( \omega \right)} \right) = \int\limits_{{S_{F} }} {\varvec{F}\left( {\varvec{x},\xi^{1} \left( \omega \right), \ldots ,\xi^{N} \left( \omega \right)} \right)\varvec{u}\left( {\varvec{x},\xi^{1} \left( \omega \right), \ldots ,\xi^{N} \left( \omega \right)} \right){\text{d}}S_{F} } ,$$

(28)

$$\pi \left( {\varvec{x},\omega } \right) = {\mathcal{L}}\left( {\varvec{x},\xi^{1} \left( \omega \right), \ldots ,\xi^{N} \left( \omega \right)} \right) - {\mathcal{B}}\left( {\varvec{x},\xi^{1} \left( \omega \right), \ldots ,\xi^{N} \left( \omega \right)} \right) .$$

(29)

Let us assume that $\left\{ {\xi^{i} } \right\}_{i}^{N}$ are random variables with probability density functions $\rho_{i} {:\Gamma }^{i} \to {\mathbb{R}}$, with limited domains and

$$\rho \left( {\varvec{\upxi}} \right) = \prod\limits_{i = 1}^{N} {\rho_{i} } \left( {\xi^{i} } \right),\quad \forall {\varvec{\upxi}} \in {\Gamma = }\prod\limits_{i = 1}^{N} {\Gamma _{i} } \subset {\mathbb{R}}^{N} .$$

(30)

Then, using Doob–Dynkin lemma [27] the solution of the boundary problem (29) can be represented by the same random variables $\left\{ {\xi^{i} } \right\}_{i}^{N}$, that is $\varvec{u} = \varvec{u}\left( {\varvec{x},\xi^{1} (\omega ), \ldots ,\xi^{N} (\omega )} \right)$. Using the formula (23), we can write for each component of the vector $\varvec{u}$:

$$\tilde{u}\left( {\varvec{\upxi}} \right) \cong {\mathcal{I}}u\left( {\varvec{\upxi}} \right) = \sum\limits_{k = 1}^{M} {u\left( {{\varvec{\upxi}}_{k} } \right)L_{k} \left( {\varvec{\upxi}} \right)} .$$

(31)

The procedure of stochastic collocation for Eq. (29) is as follows:

For each collocation point $\varvec{\xi}$, equation written in variational form:

$$\left. {\delta \pi \left( {\tilde{u}\left(\varvec{\xi}\right)} \right)} \right|_{{\varvec{\xi}_{k} }} = 0,\quad \forall k = 1,2, \ldots ,M$$

(32)

is solved.

Using the property:

$$L_{i} \left( {\xi_{j} } \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {\text{dla}} & {i = j} \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {\text{dla}} & {i \ne j} \\ \end{array} } \\ \end{array} } \right.$$

(33)

M sets of uncoupled equations are obtained relative to the k.

In order to determine the rth central statistical moment, the following formula is used:

$$\mu_{r} \left( {{\varvec{v}}_{\text{node}} } \right) = \sum\limits_{k = 1}^{M} {{\varvec{v}}_{\text{node}}^{r} \left( {{\varvec{\xi }}_{k} } \right)\int\limits_{\Gamma } {L_{k} \left( {\varvec{\xi }} \right)\rho \left( {\varvec{\xi }} \right){\text{d}}{\varvec{\xi }}} }$$

(34)

where ${\varvec{v}}_{\text{node}}$ is a vector of solution at a specified finite element grid point.

To perform the procedure of stochastic collocation, a set of collocation points must be defined. If we use the cubatures to determine numerically the integral in Eq. (34), that is:

$$\int\limits_{\Gamma } {f\left( \varvec{\xi } \right){\text{d}}\varvec{\xi }} = \sum\limits_{k = 1}^{M} {w_{k} f\left( \varvec{\xi } \right)_{k} }$$

(35)

where $w_{k}$ are weights, natural choice of points will be the same set as in the cubatures. Under this assumption, computation of rth moment will be reduced to

$$\mu_{r} \left( {\varvec{v}_{\text{node}} } \right) = \sum\limits_{k = 1}^{M} {\varvec{v}_{\text{node}}^{r} \left( {\varvec{\xi }_{k} } \right)w_{k} }.$$

(36)

In the case of a multidimensional random space, the set of collocation points is built on the basis of one-dimensional quadratures $\Theta$ by the use of the tensor product. If for each of the directions $i = 1,2, \ldots ,N$ there is:

$${\mathcal{I}}^{i} u\left( \varvec{x} \right) = \sum\limits_{k = 1}^{{m_{i} }} {u\left( {\varvec{\xi}_{k}^{i} } \right)L_{k}^{i} \left(\varvec{\xi}\right)}$$

(37)

where $m_{i}$ is the number of points in the direction i, then for the multidimensional space interpolation function takes the form [10, 46]:

$${\mathcal{I}}u\left(\varvec{\xi}\right) = \left( {{\mathcal{I}}^{{i_{1} }} \otimes \cdots \otimes {\mathcal{I}}^{{i_{N} }} } \right)u\left(\varvec{\xi}\right) = \sum\limits_{{k_{1} = 1}}^{{m_{1} }} { \cdots \sum\limits_{{k_{N} = 1}}^{{m_{N} }} {u\left( {\varvec{\xi}_{{k_{1} }}^{{i_{1} }} , \ldots ,\varvec{\xi}_{{k_{N} }}^{{i_{N} }} } \right)\left( {L_{{k_{1} }}^{{i_{1} }} \left(\varvec{\xi}\right) \otimes \cdots \otimes L_{{k_{N} }}^{{i_{N} }} \left(\varvec{\xi}\right)} \right)} }$$

(38)

in which $\otimes$ denotes tensor product.

The above formula requires $M = m_{1} \ldots m_{N}$ points. In the case of using the same number of points in each space, the total number will be $M = m^{N}$. This number rapidly increases with the number of the random spaces which leads to the need of re-running the program solving the deterministic problem. To reduce the number of points, the so-called sparse grid method can be used.

One of the selection methods for the minimum number of points, from the full tensor product set is Smolyak method [39], in which a set of points is determined on the basis of

$$\Theta_{N} \equiv {\mathcal{H}}\left( {\mu ,N} \right) = \bigcup\limits_{{\mu + 1 \le \left|{\varvec i}\right| \le N + \mu }} {\left( {\Theta_{1}^{{i_{1} }} \times \cdots \times \Theta_{1}^{{i_{N} }} } \right)}$$

(39)

where $\varvec{i} = \left( {m_{1} ,m_{2} ,\ldots ,m_{N} } \right)$ is the so-called multi-index and $\mu$ is the interpolation level.

Smolyak interpolation formula is as follows

$${\mathcal{A}}_{\mu ,N} u\left(\varvec{\xi}\right)\mathcal{ = }\sum\limits_{{\mu + 1 \le \left| \varvec{i} \right| \le N + \mu }} {\left( { - 1} \right)^{{N + \mu - \left| {\mathbf{i}} \right|}} \cdot \left( {\begin{array}{*{20}c} {N - 1} \\ {N + \mu - \left| \varvec{i} \right|} \\ \end{array} } \right) \cdot \left( {{\mathcal{I}}^{{i_{1} }} u\left(\varvec{\xi}\right) \otimes \cdots \otimes {\mathcal{I}}^{{i_{N} }} u\left(\varvec{\xi}\right)} \right)} $$

(40)

4 The Inverse Problem

The accuracy of computer simulations of processes depends on the quality of mathematical models which describe those processes. The quality of models depends, in turn, on many different parameters, that need to be determined on an experimental way. If some values are determined through an experiment, and those values are then used to make a computer simulation of the same experiment, it may turn out that the result varies from the ones obtained during an experiment. Those differences result from the heterogeneity of stress fields, as well as deformations within a sample, which is a common element of the majority of metal deformation processes. To eliminate the described divergences, one needs to solve the inverse problem.

The idea of the inverse method comes down to minimizing the differences between the results of experiments $Y\left( {t,\varvec{x}} \right)$ and the results of simulations $v\left( {t,\varvec{x},\varvec{P}} \right)$. In case of the stochastic problem, the task can be reduced to the minimization of a functional which is dependent on the statistical moments of the specified order n:

$${\fancyscript{C}}_{f} (\varvec{P}) = \int\limits_{{\fancyscript{T}}} {\int\limits_{{\fancyscript{D}}} {\left( {\sum\limits_{i = 1}^{n} {\left[ {\mu_{i} \left( {Y\left( {t,\varvec{x}} \right)} \right) - \mu_{i} \left( {v\left( {t,\varvec{x},\varvec{P}} \right)} \right)} \right]^{2} } } \right){\text{d}}\varvec{x}} {\text{d}}t} ,\varvec{x} \in {\fancyscript{D}},t \in {\fancyscript{T}}$$

(41)

where

$$\mu_{n} \left( \cdot \right) = \int\limits_{ - \infty }^{\infty } {\left( \cdot \right)^{n} { \exp }\left( { - \frac{{\left( \cdot \right)^{T} \left( \cdot \right)}}{2}} \right){\text{d}}\left( \cdot \right)}$$

(42)

is the operator of nth statistical central moment with Gaussian measure and $\varvec{P}$ is the vector of searched parameters. Obviously for $n = 1$$E\left( \cdot \right) = \mu_{1} \left( \cdot \right)$ can be written.

In practice, an approach is used that is based on the criterion of least squares:

$${\fancyscript{C}}_{d} (\varvec{P}) = \sum\limits_{t = 0}^{T} {\sum\limits_{i = 1}^{n} {\left[ {\mu_{i} \left( {\varvec{Y}^{t} } \right) - \mu_{i} \left( {\varvec{v}^{t} \left( \varvec{P} \right)} \right)} \right]^{T} \left[ {\mu_{i} \left( {\varvec{Y}^{t} } \right) - \mu_{i} \left( {\varvec{v}^{t} \left( \varvec{P} \right)} \right)} \right]} }.$$

(43)

Similar approach is considered in [48]. Some parameters need to impose an additional limiting condition (e.g., to preserve the physical meaning of the law) in the form of:

$$\varvec{P}^{L} \le \varvec{P} \le \varvec{P}^{U} ,$$

(44)

where $\varvec{P}^{L}$ are lower boundary constraints and $\varvec{P}^{U}$ are upper boundary constraints.

4.1 Optimization Algorithm

The genetic algorithms are a group of optimization methods based on random factor. They are grouped with artificial intelligence tools. The inventor of these algorithms, which are based on the rules that are also used in genetics, is John Holland [20].

The base of genetic algorithms is a well-known fact of the evolution theory, which states that the organisms that are the most adjustable have the greatest chances of survival, and that their offspring greatly influences the subsequent generations of the species. This assumption is directly used in the genetic algorithms. Consecutively, the strategy used by the algorithm is similar to the natural selection; and that is the reason why the terminology is similar to the one used in genetics.

The procedure can be described as follows:

• A. Generation of initial population ${\mathbf{P}}_{i}$ for $i = 1, \ldots ,n_{\text{pop}}$ of individuals with random values is initialized. These initial individual values are chosen within user-defined bound $\left[ {P_{j}^{L} ,P_{j}^{U} } \right]$, where $P_{j}^{L}$ are lower boundary constraints and $P_{j}^{U}$ are upper boundary constraints for $j = 1, \ldots ,n$, where $n$ is the dimension of problem space. Hence,

  $$P_{i,j} = rnd_{i,j} \left( {P_{j}^{U} - P_{j}^{L} } \right) + P_{j}^{L} ;\;i = 1, \ldots ,n_{\text{pop}} ;\;j = 1, \ldots ,n$$

• B. Evaluation of fitness function subject to boundary constrains (44) for each individual,

• C. Selection The reproduction operation is carried out by choosing individuals according to their relative fitness. There are different methods to perform this operation. A method that lays out a line in which each parent corresponding to a section of the line of length proportional to its scaled value is used. The algorithm moves along the line in steps of equal size. At each step, the algorithm allocates a parent from the section it lands on. The first step is a uniform random number less than the step size,

• D. Reproduction Genetic algorithm creating children for the next generation specifies the number of individuals that are guaranteed to survive to the next generation and specifies the fraction of the next generation that are produced by crossover,

• E. Mutation Genetic algorithm makes small random changes in the individuals in the population to create mutation children. Mutation provides genetic diversity and enables the genetic algorithm to search a broader space,

• F. Steps B to E are repeated until the specified convergence of fitness function or specified number of generations is satisfied.

5 Numerical Examples

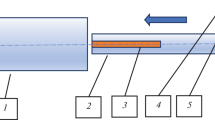
As an example, we have considered the simulation of axisymmetric compression of steel cylinder by flat dies (Fig. 1).

Fig. 1

Finite element model of ring compression test

The investigated material is assumed to follow nonlinear isotropic hardening behavior (Voce hardening law [44]) and the Perzyna flow stress model [29] is considered, which is described by the expression:

$$\bar{\sigma }(\omega ,{\mathbf{x}},\bar{\varepsilon },\dot{\bar{\varepsilon }}) = \sigma_{0} (\omega ,{\mathbf{x}},\bar{\varepsilon }({\mathbf{x}}))\left[ {1 + \left( {\frac{{\dot{\bar{\varepsilon }}({\mathbf{x}})}}{{\gamma (\omega ,{\mathbf{x}})}}} \right)^{{n(\omega ,{\mathbf{x}})}} } \right] ,$$

(45)

$$\sigma_{0} ({\mathbf{x}},\bar{\varepsilon }({\mathbf{x}})) = \left( {k({\mathbf{x}}) + R_{0} ({\mathbf{x}}) \cdot \bar{\varepsilon }({\mathbf{x}}) + R_{\inf } ({\mathbf{x}}) \cdot \left( {1 - e^{{ - b({\mathbf{x}}) \cdot \bar{\varepsilon }({\mathbf{x}})}} } \right)} \right),$$

(46)

where $k({\mathbf{x}})$ is the initial yield stress, $R_{0} ({\mathbf{x}})$, $R_{\inf } ({\mathbf{x}})$, $b({\mathbf{x}})$ are the material parameters characterizing the isotropic hardening behavior, $n(\omega ,{\mathbf{x}}) = \frac{1}{{\delta (\omega ,{\mathbf{x}})}}$ is the strain-rate hardening parameter and $\gamma (\omega ,{\mathbf{x}})$ is material viscosity parameter.

As the first example, two parameters of Eq. (45) are chosen, $\delta (\omega ,{\mathbf{x}})$ and $\gamma (\omega ,{\mathbf{x}})$. Displacement measurements in the vector ${\mathbf{Y}}$ are adopted directly from numerical simulation. It is assumed that the searched parameters are the stationary two-dimensional random fields with the characteristics $E\left( {\delta (x,y)} \right) = \delta_{0}$, $E\left( {\gamma (x,y)} \right) = \gamma_{0}$ and with the known covariance functions, namely:

$$C_{\delta } (x_{1} ,x_{2} ;y_{1} ,y_{2} ) = {\text{Var}}_{\delta } \cdot \exp \left( {\frac{{ - \left| {x_{1} - x_{2} } \right|}}{{b_{x} }} - \frac{{\left| {y_{1} - y_{2} } \right|}}{{b_{y} }}} \right) ,$$

(47)

$$C_{\gamma } (x_{1} ,x_{2} ;y_{1} ,y_{2} ) = {\text{Var}}_{\gamma } \cdot \exp \left( {\frac{{ - \left| {x_{1} - x_{2} } \right|}}{{b_{x} }} - \frac{{\left| {y_{1} - y_{2} } \right|}}{{b_{y} }}} \right),$$

(48)

where the correlation length $b_{x} = 1.0$, $b_{y} = 1.0$. The parameters $\delta_{0}$, $\gamma_{0}$ and ${\text{Var}}_{\delta }$, ${\text{Var}}_{\gamma }$ are unknown. Let us assume that other functions of the model are known, deterministic and constant (Table 1). Therefore, the searched vector is of the form ${\mathbf{P}} = \left[ {\delta_{0} ,\gamma_{0} ,{\text{Var}}_{\delta } ,{\text{Var}}_{\gamma } } \right]$. In order to perform identification of selected parameters, a set of experimental data ${\mathbf{Y}}$ should be defined. The ideal and desirable solution will be to use a displacement field at any point defined by a grid of nodes in the finite element method. In reality, measurements at the deforming sample are only possible on the outer surface [38]. In the analyzed example, it has been decided to choose to analyze the horizontal displacement of the outermost points (Fig. 2). Using the square root of the objective function (43) for the above-described set of data points and a combination of the two parameters $\delta_{0} \in \left\langle {0.3,0.6} \right\rangle$, $\gamma_{0} \in \left\langle {0.3,0.7} \right\rangle$ s⁻¹ with constant ${\text{Var}}_{\delta } = 0.01$, ${\text{Var}}_{\gamma } = 0.01$ s⁻¹, the response function is obtained. This function has local minima (Fig. 3); therefore, it decides to use the stochastic optimization method to determine the global minimum.

Table 1 Parameters used in the analysis

Fig. 2

Measurement points chosen for analysis (10 points along the vertical surface)

Fig. 3

Contour plot of response function for parameters $\delta_{0} \in \left\langle {0.3,0.6} \right\rangle$, $\gamma_{0} \in \left\langle {0.3,0.7} \right\rangle$ s⁻¹, ${\text{Var}}_{\delta } = 0.1$, ${\text{Var}}_{\gamma } = 0.1$ s⁻¹. 30% of reduction in height, first example

Using the Karhunen–Loève expansion for two-dimensional random fields, the following equations can be obtained:

$$\delta (x,y,\omega ) = E\left( {\delta (x,y)} \right) + \sum\limits_{i,j = 1}^{M} {\xi_{ij}^{\delta } (\omega )\sqrt {\lambda_{i}^{(\delta ,x)} \lambda_{j}^{(\delta ,y)} } f_{i}^{(\delta ,x)} (x)\;f_{j}^{(\delta ,y)} (y)} ,$$

(49)

$$\gamma (x,y,\omega ) = E\left( {\gamma (x,y)} \right) + \sum\limits_{i,j = 1}^{M} {\xi_{ij}^{\gamma } (\omega )\sqrt {\lambda_{i}^{(\gamma ,x)} \lambda_{j}^{(\gamma ,y)} } f_{i}^{(\gamma ,x)} (x)\;f_{j}^{(\gamma ,y)} (y)}$$

(50)

In further analysis, the proposed SG-SCM is compared to Monte Carlo method. As the relevant point, only one node (Fig. 4) is chosen. As shown (Fig. 5), there is a good correlation between the results obtained from MC method and the probability density of the normal distribution. To choose the appropriate level of interpolation $\mu$ (Smolyak sparse grid), standard deviation for order 1–3 (second moment) at chosen node is computed (Fig. 6). In order to select the appropriate values of the parameters (Karhunen–Loève expansion order, SG interpolation level), direct stochastic method (SG-SCM) analysis is performed for several configurations of these parameters (Table 2). As the basic selection criteria, minimum value of the difference between the solution of SG-SCM and the MC method and the lowest number of collocation points is chosen. Performed analysis (Figs. 6, 7) has shown that the lowest sufficient order of interpolation level can be adopted as $\mu = 1$ and order of Karhunen–Loève expansion can be adopted as $M = 3$.

Fig. 4

Equivalent plastic strain plot for 30% of reduction in height

Fig. 5

Probability density function of equivalent plastic strain for relevant node used in analysis. Dots: Monte Carlo method for 2000 samples; solid line: normal distribution mean 0.273 and standard deviation 0.0159

Fig. 6

Expected value of equivalent plastic strain for relevant node obtained with different kinds of configuration of KL expansion order versus SG interpolation level (according to Table 2.)

Table 2 Configurations of KL expansion order vs. SG interpolation level

Fig. 7

Standard deviation of equivalent plastic strain for relevant node obtained with different kinds of configuration of KL expansion order versus SG interpolation level (according to Table 2.)

Besides the choice of the appropriate measurement points, the degree of reduction in height of the sample is important. In the first step of analysis, 30% of reduction (Fig. 4) has been taken. On the graph of response function (Fig. 3), there are local extrema. Clearly visible is the global extreme ($\delta_{0} = 0.357$, $\gamma_{0} = 0.55\;{\text{s}}^{ - 1}$).

With the above assumption, the identification problem is performed. The analysis shows high efficiency and stability of the method (Figs. 8, 9, Table 3).

Fig. 8

A graph of fitness function (best value) convergence of genetic algorithm (30% of reduction in height, 3 runs, first example)

Fig. 9

A graph of fitness function (mean value) convergence of genetic algorithm (30% of reduction in height, 3 runs, first example)

Table 3 Identified parameters (30% of reduction in height, first example)

In the second step of the analysis, 50% of reduction in height is chosen (Fig. 10). Similar to the first step of analysis in the bottom of response function graph (Fig. 11), area with global extreme appears. There are also a number of local extremes, but the difference between the values of the response function is small and it is impossible to clearly define the global extreme. Occurring phenomenon can be explained by the combined effect of a small number of measurement points and a small sensitivity of the response function to changes in the parameters $\delta_{0}$ and $\gamma_{0}$ [35].

Fig. 10

Equivalent plastic strain plot for 50% of reduction

Fig. 11

Contour plot of response function for parameters $\delta_{0} \in \left\langle {0.3,0.6} \right\rangle$, $\gamma_{0} \in \left\langle {0.3,0.7} \right\rangle$ s⁻¹, ${\text{Var}}_{\delta } = 0.1$, ${\text{Var}}_{\gamma } = 0.1$ s⁻¹. 30% of reduction in height, first example

In addition, the response function for 40% reduction in height is determined. In the graph of the response function (Fig. 12), a transition state between 30 and 50% of reduction can be observed. At the bottom of the figure can be noticed clearly visible global extremes and many local extremes in the rest of the analyzed area.

Fig. 12

Contour plot of response function for parameters $\delta_{0} \in \left\langle {0.3,0.6} \right\rangle$, $\gamma_{0} \in \left\langle {0.3,0.7} \right\rangle$ s⁻¹, ${\text{Var}}_{\delta } = 0.1$, ${\text{Var}}_{\gamma } = 0.1$ s⁻¹. 40% of reduction in height, first example

As shown in the graphs (Figs. 13, 14), the identification method allows obtaining similar parameters as the simulated ones. In the third-run, the convergence is achieved but the dispersion of the values indicates the instability of the solution (Table 4).

Fig. 13

A graph of fitness function (best value) convergence of genetic algorithm (50% of reduction in height, 3 runs, first example)

Fig. 14

A graph of fitness function (mean value) convergence of genetic algorithm (50% of reduction in height, 3 runs, first example)

Table 4 Identified parameters (50% of reduction in height, first example)

As the second example, two parameters characterizing the isotropic hardening behavior of Eq. (46) (Voce hardening law) are chosen, $R_{\inf } (\omega ,{\mathbf{x}})$ and $b(\omega ,{\mathbf{x}})$. Similar to the analysis in the first example, two cases of reduction in height are chosen, 30% and 50%. In both cases, the same stochastic (interpolation level $\mu = 1$, order of Karhunen–Loève expansion $M = 3$) and parameters have been adopted as in the first example (Table 1). Using the Karhunen–Loève expansion for two-dimensional random fields, the following equations can be obtained:

$$R_{\inf } (x,y,\omega ) = E\left( {R_{\inf } (x,y)} \right) + \sum\limits_{i,j = 1}^{M} {\xi_{ij}^{{R_{\inf } }} (\omega )\sqrt {\lambda_{i}^{{(R_{\inf } ,x)}} \lambda_{j}^{{(R_{\inf } ,y)}} } f_{i}^{{(R_{\inf } ,x)}} (x)\;f_{j}^{{(R_{\inf } ,y)}} (y)}$$

(51)

$$b(x,y,\omega ) = E\left( {b(x,y)} \right) + \sum\limits_{i,j = 1}^{M} {\xi_{ij}^{b} (\omega )\sqrt {\lambda_{i}^{(b,x)} \lambda_{j}^{(b,y)} } f_{i}^{(b,x)} (x)\;f_{j}^{(b,y)} (y)} ,$$

(52)

where $E\left( {R_{\inf } (x,y)} \right) = R_{\inf ,0}$, $E\left( {b(x,y)} \right) = b_{0}$ and with the known covariance functions (similar to the first example). Therefore, the searched vector is of the form ${\mathbf{P}} = \left[ {R_{\inf ,0} ,b_{0} ,{\text{Var}}_{{R_{\inf } }} ,{\text{Var}}_{b} } \right]$. The assumed reduction in sample height is also important in identifying parameters related to Voce hardening law. For the 30% reduction in height in the response function graph, the global extreme is clearly visible (Fig. 15). The identification process is stable and converges with the solution (Figs. 16, 17). Table 5 shows the results of the analysis for three runs.

Fig. 15

Contour plot of response function for parameters $R_{\inf ,0} \in \left\langle {44.0,60.0} \right\rangle \;{\text{MPa}}$, $b_{0} \in \left\langle {14.2,20.2} \right\rangle$, ${\text{Var}}_{{R_{\inf } }} = 16.0\;{\text{MPa}}$, ${\text{Var}}_{b} = 2.0$. 30% of reduction in height, second example

Fig. 16

A graph of fitness function (best value) convergence of genetic algorithm (30% of reduction in height, 3 runs, second example)

Fig. 17

A graph of fitness function (mean value) convergence of genetic algorithm (30% of reduction in height, 3 runs, second example)

Table 5 Identified parameters (30% of reduction in height, second example)

In the second case (50% reduction in height) for assumed range of values of the parameters: $R_{\inf ,0} \in \left\langle {44.0,60.0} \right\rangle \;{\text{MPa}}$, $b_{0} \in \left\langle {14.2,20.2} \right\rangle$, ${\text{Var}}_{{R_{\inf } }} = 16.0\;{\text{MPa}}$, ${\text{Var}}_{b} = 2.0$, the response function graph has many maxima and minima (Fig. 18). In the surroundings of the global minimum (the searched solution), local maxima and minima are visible. Even the case of using a hybrid method combining the random method with the gradient optimization method will be much more difficult or even impossible. Using only gradient optimization will also be impossible in this case.

Fig. 18

Contour plot of response function for parameters $R_{\inf ,0} \in \left\langle {44.0,60.0} \right\rangle \;{\text{MPa}}$, $b_{0} \in \left\langle {14.2,20.2} \right\rangle$${\text{Var}}_{{R_{\inf } }} = 16.0\;{\text{MPa}}$, ${\text{Var}}_{b} = 2.0$. 50% of reduction in height, second example

The identification process is shown in the graphs (Figs. 19, 20). Solution has been found, and the values of the parameters are similar to the simulated ones. In the third-run, the convergence is achieved but the dispersion of the values indicate the instability of the solution (Table 6).

Fig. 19

A graph of fitness function (best value) convergence of genetic algorithm (50% of reduction in height, 3 runs, second example)

Fig. 20

A graph of fitness function (mean value) convergence of genetic algorithm (50% of reduction in height, 3 runs, second example)

Table 6 Identified parameters (50% of reduction in height, second example)

Computations are performed on computer made of 32 physical cores, 2.53 GHz clock speed each. In the case of parameter’s identification in Perzyna model (example 1), computational time is 439.217 min for 30% reduction in height and 603.078 min for 50% reduction in height. In the second example, computational time in both cases is close to the first example.

6 Concluding Remarks

The paper proposes a method of parameter’s identification of two-dimensional random field in rigid viscoplasticity. The investigated material is assumed to follow nonlinear isotropic hardening behavior (Voce hardening law), and the Perzyna flow stress model is adopted.

The analysis allows for the following conclusions:

• The degree of reduction in height significantly affects instability of solution, which is the cause of local extremes compaction in the surrounding of global extreme. This behavior can be explained by the significant plasticizing of the sample.

• SG-SCM method works well with viscoplastic forming problems, even with a small number of collocation points for multidimensional random space.

• GA works well with stochastic inverse problems assuming the use of multithreading to which the method is well adapted.

• The system response to the random disturbances modeled as a stationary Gaussian random field is also Gaussian random field.

The comparison shows that the proposed method works well with nonlinear problems and it is convergent to Monte Carlo method due to first and second statistical moments. The analysis of inverse problem has revealed that the proposed identification method is appropriate when the stochastic process with use of the first two statistical moments only and the knowledge of measurement only at external surfaces are considered.