Introduction

Water resources management (WRM) is one of the most important challenges at the global level (Abu El-Magd et al. 2023). Water is considered the most important human need for social, economical, and agricultural development (Siebert et al. 2010; Singh et al. 2012; Kubicz et al. 2021). On the other hand, the quantity and quality of water and drinking water consumption sustain lakes and wetlands and directly affect biodiversity (Khan et al. 2023). Groundwater resources generally provide about 50% of drinking water and 40% of industrial needs globally (Udmale et al. 2014). Today, groundwater resources face many problems threatening their quantity and quality (Burri et al. 2019; El Asri et al. 2019; Houéménou et al. 2020). Therefore, the different characteristics of groundwater resources are affected and lead to the destruction of these valuable reserves, which have become a major crisis in different regions (Eissa et al. 2016; Eid et al. 2023).

In Iran, as in other developing countries, groundwater quality (GWQ) is seriously threatened by excessive exploitation of groundwater resources, extensive use of chemicals, and pesticide intrusion (Panaskar et al. 2016; Akhtar et al. 2021). On the other hand, industrialization and population growth have accelerated groundwater pollution (Kumar et al. 2019a; Sarker et al. 2021). Thus, industrial and domestic wastewater has entered the water table and caused water pollution (Ojekunle et al. 2020). Determining parameters for the optimal use of groundwater resources are groundwater's chemical composition and biology (Davraz and Oezdemir 2014; Mallick et al. 2018). Groundwater resources change due to climatic and lithological conditions and processes caused by human activities (Abbasnia et al. 2019; Jehan et al. 2019). The presence of fluoride sulfate, nitrate, and the presence of metals such as calcium, magnesium, sodium, manganese, cadmium, nickel, chromium, and arsenic in water above the permissible limit causes problems for various uses, including drinking water supply and agriculture (Rashid et al. 2020; Tyagi and Sarma 2020).

Traditional methods of GWQ assessment are often expensive and time-consuming. Meanwhile, implementing machine learning algorithms (MLAs) can help adopt long-term strategies regarding the GWQ and how to use it by predicting and evaluating water quality indicators (Masoud et al. 2022; Noori et al. 2022). In some studies, several approaches such as machine learning algorithms (MLAs) and water quality index (WQI) have been used to evaluate water quality (Mohamed et al. 2014; Ramadan 2016; Adimalla et al. 2018; Hamlat and Guidoum 2018; Ahmed et al. 2020; Badeenezhad et al. 2020; Suvarna et al. 2020; El-Magd et al. 2021, 2022).

Among the parameters that help to evaluate the GWQ are total dissolved solids (TDS), Mg2+, Na+, HCO3−, and sodium absorption ratio (SAR) (Abu El-Magd et al. 2023). Some studies have evaluated the effect of human manipulation on groundwater pollution (Safa et al. 2020; Ravish et al. 2021). New and more popular models and techniques have been proposed for GWQ assessment. These methods are data-oriented and have higher accuracy. These methods have been used in several studies, such as support vector machines (SVM) and artificial neural networks (ANN) (Pei-Yue et al. 2011; El-Magd et al. 2020). Some studies based on MLAs, such as adaptive neuro-fuzzy inference system (ANFIS) and SVM, have evaluated the GWQ (Elsayed et al. 2021; Tao et al. 2022; Eid et al. 2023; Sahour et al. 2023).

The investigation of the research background showed that the GWQ had been investigated using different tools and models. In addition, WQI and sometimes MLAs have been widely used to investigate groundwater resources and GWQ. Although in many studies, only the modeling of GWQ has been addressed, and the validation of the methods and models used has not been widely investigated. Therefore, the study sought to complete the current research deficiency and validated MLAs using the GT algorithm. Game theory is one of the most important optimal methods of multi-criteria decision-making, which has low uncertainty in choosing the best criteria and alternatives compared to other multi-criteria decision-making methods. In addition, this study investigated and comprehensively analyzed the chemical status and important ions related to critical points in terms of GWQ that MLA and GT identified.

One of the main reasons for choosing the province of Chaharmahal and Bakhtiari was the heavy use of groundwater in the form of wells and springs in this region. Meanwhile, it was necessary to study the groundwater resources in this region, which account for a significant proportion of water resources and require optimal and integrated management. Therefore, this study aimed to map GWQ in the central plateau of Iran by validating MLAs, including random forest (RF), SVM, Naive Bayes, and K-nearest neighbors (KNN) algorithms using Borda scoring algorithm based on GT.

Materials and methods

Description of the study area

Chaharmahal and Bakhtiari province, with an area of 18,122 km2, is a highland covering the central plateau of Iran. Chaharmahal and Bakhtiari province is a region where almost 80% of the city is covered by mountains and hills (Rahimi 2012; Zamani-Ahmadmahmoodi et al. 2019). These mountains have 16 peaks with an altitude of more than 3500 m. The morphology of the province includes a regular alternation of northwestern and southeastern elevations separated by plains with the same trend. The average slope of the province is 42%, and more than 58% of the area has a slope of 30% or more. Precipitation in the region is often influenced by Mediterranean atmospheric currents and low Sudanese atmospheric pressure (Lashkari et al. 2021).

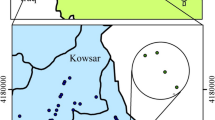
The average annual rainfall of the province is 560 mm (Arab Amiri and Mesgari 2019). Chaharmahal and Bakhtiari provinces have about 10% of the country's water resources. The country’s two major and strategic rivers, the Karon and the Zainderud, originate here. One of the main problems of this province is that a high percentage of groundwater is used for agriculture. In addition, a large percentage of drinking water is obtained from aquifers (Heshmati and Beigi 2012). The geographical location and sampling points are shown in Fig. 1.

Fig. 1
figure 1

A view of the studied area in the central plateau of Iran (Sentinel-2; 2022)

Full size image

Data sources and analyses

GWQ data are for 39 sampling sites in Chaharmahal and Bakhtiari, Iran. Water quality parameters included K+, Na+, Mg2+, Ca2+, SO42−, Cl−, HCO3−, pH, TDS, and EC (Asghari et al. 2018; Iqbal et al. 2018). These data were provided by Iran Water Resources Management Company (IWRMC). Some characteristics of the sampling sites are shown in Table 1. Table 2 also contains the values of quality factors at each point. Sentinel 2 satellite imagery, digital elevation models (DEM), and shapefiles for the sampling points were used to monitor the studied area.

Table 1 Some characteristics of sampling points are Chaharmahal and Bakhtiari Province, Iran
Full size table
Table 2 Quantitative values of groundwater quality conditioning factors, Chaharmahal and Bakhtiari Province, Iran
Full size table

Research methodology

Based on the flow chart (Fig. 2), groundwater quality parameters were quantified at each sampling point to conduct this study. Then, in ArcGIS 10.8 software, the values of each parameter were interpolated using the Kriging method, and all ten parameters were converted into grids (Ali and Ahmad 2020). These maps related to GWQ conditioning factors were shown in Fig. 3. Then, MLAs including RF, SVM, Naive Bayes, and KNN were used to construct the GWQ map (Leong et al. 2021; Ramadhani et al. 2021; Wang et al. 2021; Ilić et al. 2022). These models were coded and implemented based on Python (Lee et al. 2020). In this way, 70% of the data set was used for training and 30% for validation. Finally, the most optimal model was selected based on the error statistics, including mean absolute error (MAE), MSE (mean square error), root mean square error (RMSE), and receiver operating characteristics (ROC) (Koranga et al. 2022; Rasool et al. 2022).

Fig. 2
figure 2

Flowchart of research methodology

Full size image
Fig. 3
figure 3figure 3

Groundwater quality conditioning factors, Chaharmahal and Bakhtiari Province, Iran

Full size image

To compare MLA results, the GT algorithm was used (Padarian et al. 2020). According to the Borda scoring algorithm (Khiavi et al. 2022), ten studied parameters (K+, Na+, Mg2+, Ca2+, SO42−, Cl−, HCO3−, pH, TDS, and EC) were prioritized at 39 sampling sites. The most critical points were selected in terms of GWQ. Finally, after selecting the high, medium, and low-quality points based on GWQ, AqQA software (Wu et al. 2017) was used, and the status of the points with the highest and lowest critical conditions in terms of water type, density, CO2 content, carbonate balance, and irrigation water was examined. Explanations of the application of MLA, GT, and the software used are provided below:

Machine learning algorithms

MLA algorithms have been used to predict continuous numerical outputs (Fernández-Delgado et al. 2019). MLA is divided into three categories: supervised MLA, unsupervised MLA, and reinforcing MLA (Vafakhah et al. 2022). This study used RF, SVM, Naive Bayes, and KNN.

RF algorithm

This method is a non-parametric algorithm (Noi et al. 2017; Zhou et al. 2019). It is one of the most optimal ML methods for decision-making and in a supervised manner (Breiman 2001; Vorpahl et al. 2012). This method consists of three parts: the number of parameters used in each tree, the number of trees, and the number of nodes (Peters et al. 2008).

In this model, the random vector \({\theta }_{k}\), which is independent of the random vectors \({\theta }_{1}\dots .{\theta }_{k-1}\), is generated for the K tree. Also, all vectors have the same distribution. The regression tree grows using training data and \({\theta }_{k}\). The set of k trees is equal to \(\left\{{h}_{1}\left(x\right),{h}_{2}\left(x\right)\dots {h}_{k}(x)\right\}\), which is \(\left\{{h}_{k}\left(x\right)=h\left(x,{\theta }_{k}\right),x=\left\{{x}_{1},{x}_{2},\dots {x}_{p}\right\}\right\}\) here. These vectors are the next P input vector that makes up a forest. Generated K outputs correspond to each tree equal to \({\widehat{y}}_{1}={h}_{1}\left(x\right),{\widehat{y}}_{2}={h}_{2}\left(x\right),\dots {\widehat{y}}_{k=}{h}_{k}(x)\), where \({\widehat{y}}_{k}\) is the output of the K tree. The average of all tree predictions is calculated to obtain the final output.

SVM algorithm

This algorithm was developed 1995 as a decision model (Cortes and Vapnik 1995). It belongs to the supervised learning methods used for classification and regression. The basis of SVM is a linear classification of data. In this algorithm, we try to choose the line with the most reliable margin (BOTSIS et al. 2011). In machine learning, support vector machines with associated learning methods have been supervised to analyze the data for optimal decisions (Sharifi Garmdareh et al. 2018; Vafakhah and Khosrobeigi Bozchaloei 2020).

Suppose N samples of the population are given by \(X\in {R}^{m},{\left\{{X}_{K},{Y}_{K}\right\}}_{K=1}^{N},Y\in R\), then Eq. (1) can be a regression function as below:

$$f\left(x\right)=W\varnothing \left(X\right)+b,$$
(1)

where \(\varnothing\) represents the kernel functions, X is an input factor with m elements, Y is the output parameter, W is a weight vector, and b represents an error (Shabani et al. 2016). Cortes and Vapnik (1995) showed optimization of the following Eq. (2) where \({\varepsilon }_{k}\) and \({\varepsilon }_{k}^{*}\) are parameters to reduce training bias based on Eq. (3) (Xie et al. 2012; Shabani et al. 2016):

$$\frac{1}{2}{\Vert W\Vert }^{2}+C\sum_{k=1}^{k=N}({\varepsilon }_{k}-{\varepsilon }_{k}^{*})$$
(2)
$$\mathrm{subject to }\left\{\begin{array}{c}{Y}_{k}-{W}^{T}\varnothing \left({X}_{k}\right)-b\le \epsilon +{\varepsilon }_{k}\\ {W}^{T}\varnothing ({X}_{k}+b-{Y}_{k}\le \epsilon +{\varepsilon }_{k}^{*})\\ {\varepsilon }_{k}{\varepsilon }_{k}^{*}\ge 0\end{array}\right\}k=\mathrm{1,2},\dots ,N$$
(3)
Naive Bayes

This algorithm is a supervised method that uses Bayes’ theorem. This means that the method only assumes that each input variable is independent. This model works well despite insufficient or inappropriate data (Osisanwo et al. 2017). Depending on the data type of each characteristic, a different method is required. More specifically, the data estimate parameters from one of three standard probability distributions (Frank et al. 2000; Ren et al. 2009). A polynomial distribution can be used for categorical variables such as numbers or labels. If the variables are binary, the binomial distribution can be used. The Gaussian distribution is often used for a numeric variable, such as a measurement. This classification algorithm requires less data volume and is more efficient than others (Tsangaratos and Ilia 2016).

KNN algorithm

This algorithm is used for the classification of unknown problems assuming the presence of certain features (X) and a certain value (Y) (Avand et al. 2019). The KNN is a non-parametric model. To calculate the actual value to the nearest points, the maximum number of K in each neighbor and each selected point is used (Betrie et al. 2013). This algorithm assumes that the neighboring cells are classified into the same class based on the density function and the target matrix.

The basis of this model is to calculate the proximity of the real-time prediction value X_r = {x_1n, x_2n, x_3n, …, x_mr} to the forecast value in each observation X_t = {x_1b, x_2b, x_3b, …, x_mr} and based on the Euclidean distance function (Drt) (Naghibi et al. 2020):

$${D}_{rt}=\sqrt{\sum_{i=1}^{m}{w}_{i}{({x}_{ir}-{x}_{it})}^{2},t=\mathrm{1,2},\dots ,n},$$
(4)

where wi (i = 1, 2,..., m) is the weight of predictors whose sum is equal to one.

Borda scoring algorithm

After quantifying the GWQ parameters, this algorithm was applied to weigh the parameters and identify areas at risk. For this purpose, the quantitative values of each parameter at each sampling site were calculated. Then, the output matrix of the GT algorithm was created (Fig. 4). Finally, the sampling sites were classified into three categories high, medium, and low quality based on the game theoretic algorithm. The Borda scoring algorithm was a prioritization method for group decisions to evaluate parameters. The Borda score was determined for each candidate. It was the sum of the individual scores for each parameter (Avand et al. 2021). For every n representative, there are n ranks. Accordingly, n − 1 points were assigned to the representative with the first rank and n − 2 with the second rank, and so on (Khiavi et al. 2022). The weight of each candidate was denoted by BS (A) and noted as (Eqs. 5–8):

$$BS \left(A\right)=\left(n-1\right)*\#\left\{i|i \mathrm{ranks} A \mathrm{first}\right\}+\left(n-2\right)$$
(5)
$$*\#\left\{i|i \mathrm{ranks} A \mathrm{second}\right\}+\dots +1$$
(6)
$$*\#\left\{i|i \mathrm{ranks} A \mathrm{second to last}\right\}+0$$
(7)
$$*\#\left\{i|i \mathrm{ranks} A \mathrm{last}\right\},$$
(8)

where #{…} is the number of parameters (Balinski and Laraki 2007; Adhami and Sadeghi 2016).

Fig. 4
figure 4

(Source: Avand et al. 2021)

Simple schematic of the GT algorithm

Full size image

Application of AqQA software

Water chemists have written AqQA for water chemists. The AqQA software can perform six data homogeneity tests based on AWWA-1030-E standard methods. The AqQa tools can easily create 11 diagrams, including time series, Schoeller diagrams, ion balance, Durov, Piper, and Stiff. The main advantages of this software were mixing the sample during the simulation process, determining the equilibrium of anions and cations using the ion balance diagram, determining the chemical properties of water, determining the type of water, and calculating the main properties of liquids (dissolved solids measurement, density measurement, and others) (Ebrahime Moghadam and Abbasnejad 2020). In addition, carbon balance calculations, TDS, EC, and organic, inorganic, biological, isotopic, and radioactive analyzes make the AqQA platform a suitable tool for water quality data analysis (Salehi et al. 2016; Gholamrazai 2020).

To summarize the research methodology, a GWQ map was first created based on chemical parameters and using MLA in Python. Then, using different error statistics, the best model was selected. Then, Borda scoring was applied to identify critical points related to GWQ. Finally, AqQA software analyzed water quality conditions at critical and non-critical points. GWQ conditions were analyzed chemically and qualitatively.

Results

Results of machine learning algorithms (MLAs)

The results related to the error statistics for determining the best MLA are shown in Table 3. In addiiton, the receiver operating characteristics for evaluating the GWQ maps at each sampling point based on machine learning are shown in Fig. 5.

Table 3 Predictive capability of groundwater quality modeling using MLA
Full size table
Fig. 5
figure 5

ROC curve for groundwater quality mapping: a RF, b SVM, c Naive Bayes, d KNN

Full size image

The significant percentage of GWQ conditioning factors (K+, Na+, Mg2+, Ca2+, SO42−, Cl−, HCO3−, pH, TDS, and EC) based on the fit of the best model (RF algorithm) is shown in Fig. 6. Figure 7 also shows the GWQ map based on the RF algorithm (with the lowest error and highest AUC).

Fig. 6
figure 6

Importance of groundwater quality conditioning factors using the RF model

Full size image
Fig. 7
figure 7

Groundwater quality mapping based on the RF model, Chaharmahal and Bakhtiari Province, Iran

Full size image

Results of the GT algorithm

After creating the decision matrix for an optimal MCDM, the Borda scoring algorithm based on GT was used, and the GWQ conditioning factors were prioritized based on sample points. In this algorithm, the criteria, GWQ conditioning factors, and alternatives were sample points, and the prioritization results are included in Table 4. To compare the prioritization and identification of critical sampling points based on GWQ in three classes, Table 5 was used. The prioritization results were presented using the Borda scoring algorithm based on GT and the most optimal MLA (RF algorithm) (Table 5).

Table 4 Weighted scores of sampling points based on groundwater quality conditioning factors, Borda algorithm
Full size table
Table 5 Comparative results of prioritizing sampling points based on GTA and RF
Full size table

Results of the chemical properties of the fluid

The results of the analysis of chemical parameters (K+, Na+, Mg2+, Ca2+, SO42−, Cl−, HCO3−, pH, TDS, and EC) affecting GWQ were determined using AqQA software at critical and non-critical sampling points (the highest and lowest scores based on the RF algorithm and the Game theoric Borda scoring algorithm) and presented in Table 6. The results of the ratio of important ions, including Na+/Cl−, Ca2+ + Mg2+/HCO3− + SO4−, Ca2+/HCO3−, Mg2+/HCO3−, Ca2+/SO4− and SO4−/HCO3−, were shown in Fig. 8. The ion balance diagram for critical and non-critical points (the highest and lowest scores based on RF algorithm and Game theoric Borda scoring algorithm) in the study area, Iran, is shown in Fig. 9.

Table 6 Analysis of different parameters of GWQ in critical and non-critical points based on Borda scoring algorithm based on GT
Full size table
Fig. 8
figure 8

Ionic ratio plots of the major ions: a Na/Cl, b Ca + Mg/HCO3 + SO4, c Ca/HCO3, d Mg/HCO3, e Ca/SO4, f SO4/HCO3

Full size image
Fig. 9
figure 9

Ion balance diagram related to critical (left) and non-critical (right) points

Full size image

Discussion

The change in GWQ, usually caused by mismanagement of water harvesting, chemical fertilizers, and similar factors, has become a prelude to destroying other resources, directly or indirectly (Li et al. 2018; Kumar et al. 2019b). In many countries, including Iran, groundwater is one of the most important water sources for drinking, industry, and agriculture. Utilizing these sources and surface water containment has always been considered an option. In many parts of Iran, groundwater is essential for drinking, agricultural, and industrial water supply due to a lack of access to surface water (Mirzaei et al. 2019; Maghrebi et al. 2020). Applying appropriate management methods in using existing water resources and reducing the high cost of their development and use can also optimize the scale of use of these resources. In this study, MLA and GT were combined to investigate GWQ in the central plateau of Iran.

According to Table 3 and Fig. 5, among the MLA, including RF, SVM, Naive Bayes, and KNN, the RF algorithm with error values of MAE = 0.261, MSE = 0.111, RMSE = 0.333, and AUC = 0.930 was selected as the most optimal algorithm in GWQ mapping (Tesoriero et al. 2017; Norouzi and Moghaddam 2020; Nafouanti et al. 2021; He et al. 2022). In addition, the RF algorithm confirmed several fields (Lianjun 2016; Pham et al. 2021; Vafakhah et al. 2022). In addition, many studies highlighted the use of MLA for WRM (Starzyk 2010), landslides (Hong et al. 2015), erosion (Tien Bui et al. 2019), and urban water management (Rozos 2019). The main advantage of this algorithm over other MLAs is that this algorithm uses the best variables randomly selected from the input variables to build a tree (Demir and Sahin 2022; Vafakhah et al. 2022). This procedure reduces the overall error of the model. Another advantage of this algorithm is that it avoids model fitting. This algorithm’s insensitivity to the data's normality is another important advantage. On the other hand, it provides suitable results for classified data types and generally has a reasonable application speed compared to other MLAs (Kotsiantis and Pintelas 2004; Rahman et al. 2020).

Among the factors affecting GWQ and based on the importance of these factors, chlorine ions (Rao et al. 2012; Krishna Kumar et al. 2015) with 25% and sulfate ions (Subramani et al. 2005; Sharma and Kumar 2020) with 2.5% had the greatest and least influence on GWQ in the central plateau of Iran, respectively (Fig. 6). Based on the GWQ map using the algorithm RF (Fig. 7), 42.71% (558.12 ha) of the studied area in the central plateau of Iran was in poor condition. The percentage of classes with moderate and high GWQ in this region was 18.93% (247.35 ha) and 38.36% (501.33 ha), respectively (Ahankoub et al. 2022). In general, the results of the RF algorithm showed that parts of the central plateau of Iran were in a critical condition in terms of GWQ (Bhunia et al. 2018; Jamshidzadeh and Barzi 2018; Esfandiari et al. 2019; Talebiniya et al. 2019). In this context, (Mousavi et al. 2020) investigated the spatial and temporal changes of GWQ parameters based on drinking water and agriculture in the Lordegan Plain of Chaharmahal and Bakhtiari provinces, Iran. The results showed that TH and the TDS parameters were more beneficial for drinking water consumption. In addition, for agriculture, SAR and EC parameters were very good in the whole plain during the statistical period.

After mapping GWQ based on chemical parameters using MLAs, the GT algorithm was used to validate the RF algorithm to measure the accuracy of ML in identifying critical areas (Table 4). Based on the results of GT, sampling point 30, with a score of 356, was selected as the most critical point in terms of GWQ. In addition, point number 38, with a score of 20, was selected as the most non-critical area in the central plateau of Iran. Based on the ML results, these two sampling points gave similar results to the algorithm GT (Table 5). The results of GT showed that using different parameters was very important for checking GWQ and proved the necessity of MCDM methods (Srdjevic et al. 2012). According to Madani (2010), game-theoretic algorithms are one of the best methods to evaluate the decision-making of stakeholders and policymakers in a region. The Borda scoring algorithm considers majority opinion to determine the degree of importance (Elkind et al. 2011; Mahjouri and Bizhani-Manzar 2013). This algorithm was easy to use, which increased its popularity. Adhami and Sadeghi (2016) and Mahjouri and Bizhani-Manzar, (2013) found this method suitable for studies in which the priorities of the majority of voters are considered. Of course, GT had many advantages, but one of the main problems of this method was its semi-distribution, which was not pixel-oriented, unlike MLA (Avand et al. 2021).

After determining the most critical and non-critical points using various methods, the chemical conditions of these areas were examined using GWQ. The results presented in Table 6 confirm the results of RF and Borda scoring based on GT. Thus, the water quality condition at sampling site 30, the most critical area, was unfavorable. Thus, at this site, Mg-Cl (Zakaria et al. 2021) and the TH and TDS (Sarath Prasanth et al. 2012; Tiwari and Singh 2014; Aryafar et al. 2019; Karthik et al. 2019) were about 53% higher than at point number 38 (the most uncritical site, based on the results of RF and Borda scoring algorithm). On the other hand, carbonate balance also exhibited high variability (Morgenstern and Daughney 2012; Singh et al. 2013). In addition, the evaluation of GWQ about irrigation showed that the salinity risk at point number 30 was much higher than in other areas, and the sodium absorption ratio (SAR) was also in an inappropriate condition (Rawat et al. 2018) (Table 6). In this context, (Gharechaee et al. 2022) evaluated the vulnerability of groundwater to salinity in the southern plains of the Bakhtegan watershed in central Iran and concluded that a large part of the studied area was vulnerable to high salinity. The ion ratio between sampling sites also showed a high correlation between the values of sodium and chlorine ions, about 0.83. In China, (Zhang et al. 2021) also concluded that there was a high correlation between Na and Cl ions to study GWQ and ion ratios. This was although no significant trend was observed for the other ratios (Fig. 8). the ion balance diagram also showed that the number of ions affecting water quality was very high at the critical sampling point compared to other areas.

Conclusion

Increasing pollution due to population growth, urban wastewater discharge, industrial and agricultural wastewater disposal, and landfills have contributed to the spread of pollution and the degradation of water resources. Therefore, this study aimed to map the GWQ in the central plateau of Iran by validating the MLAs using GT algorithms. On this basis, chemical parameters related to water quality, including K+, Na+, Mg2+, Ca2+, SO42−, Cl−, HCO3−, pH, TDS, and EC, were interpolated at 39 sampling sites. Then the algorithms RF, SVM, Naive Bayes, and KNN in Python were used. The map in terms of GWQ was presented in three classes (high, moderate, and low quality). The Borda scoring algorithm was used to validate the MLA, and 39 sample points were prioritized. Finally, AqQA software was used, and the critical and non-critical points were analyzed based on the results of MLA and GT according to chemical aspects, carbonate balance, ionic ratios, and salinity. Based on the results, the RF algorithm was selected as the most optimal algorithm for GWQ mapping among the MLA algorithms. The results of the RF algorithm showed that parts of the central plateau of Iran are in a critical condition concerning GWQ. The results of GT showed that using different parameters was very important for checking GWQ and proved the necessity of MCDM methods.

The results related to the prioritization of sampling sites using the GT algorithm showed a high similarity between the results of this algorithm and the RF model in GWQ mapping. In addition, the analysis of the chemical status of the critical and non-critical points in terms of water quality based on the results of RF and GT showed that the chemical aspects, carbonate balance, SAR, HCO3- content, and salinity hazard at the critical points (based on two methods of MLA and GT) were in poor condition. In addition, the ion ratio between sampling points showed a high correlation between the values of sodium and chlorine ions. In general, it can be said that the combined application of MLA and GT based on the results of this study provides a good basis for the construction of the GWQ map in the central plateau of Iran. Due to human intervention, the development of unauthorized wells, and change in climatic components, groundwater quantity, and quality have decreased in Chaharmahal and Bakhtiari provinces of Iran. The results of this study can also help policymakers in managing groundwater resources. For future studies, it is suggested to use new deep learning algorithms and optimal MCDM methods, such as the best–worst method (BWM). With more complete and comprehensive data, GWQ should be studied in other parts of the central plateau of Iran.