A GIS-based framework using fuzzy relation equation system solutions in urban planning

Abstract

Several fuzzy decision models are proposed in literature to solve urban planning problems. In this research we present a novel GIS-based framework to solve decision problems in urban planning based on a System of Fuzzy Relation Equations in which the unknowns represent characteristics affecting observable facts constituting the input variables. Aim of this research is to partition the urban study area into subzones, each of which identifies a sub-area of the study area within which the set of analyzed characteristics are homogeneous. The study area is initially decomposed in atomic urban areas called microzones; for each microzone are calculated the greatest and lowest solutions of a System of Fuzzy Relation Equations by using the Universal solution Algorithm and are calculated and fuzzified the values of the output variables. Spatially adjoining microzones with same output variables are dissolved forming homogeneous urban areas with reference to the problem analyzed, called Urban Contexts. For each output variable a thematic map is constructed; in addition, a thematic map of its reliability is created. This framework is tested on a study area given by the district of Ponticelli in the municipality of Naples (Italy); comparison tests performed with respect to a previous GIS-based framework based on a System of Fuzzy Relation Equations show that our method provides a more detailed knowledge of the characteristics of the urban study area with reference to the problem dealt with.

1 Introduction

A System of Fuzzy Relation Equation (for short, SFRE) is given by the following system:

$$ \left\{ {\begin{array}{*{20}c} {\left( {a_{11} \wedge x_{1} } \right) \vee \cdots \vee \left( {a_{1n} \wedge x_{n} } \right) = b_{1} } \\ {\left( {a_{21} \wedge x_{1} } \right) \vee \cdots \vee \left( {a_{2n} \wedge x_{n} } \right) = b_{2} } \\ \cdots \\ {\left( {a_{m1} \wedge x_{1} } \right) \vee \cdots \vee \left( {a_{mn} \wedge x_{n} } \right) = b_{m} } \\ \end{array} } \right., $$

(1)

where the known terms b_i i = 1,…,m, with 0 ≤ b_i ≤ 1, are called the symptoms and the unknowns x_j j = 1,…,n, with 0 ≤ x_j ≤ 1, are called the causes affecting the symptoms.

The coefficient a_ij, with 0 ≤ a_ij ≤ 1, can be seen as the weight with which the jth cause affects the ith symptom.

The symbols $\wedge$ and $\vee$ denote the triangular norm and conorm operators.

In Peeva and Kyosev (2004, 2007) and Peeva (2006) a Universal solution algorithm (for short, Universal Algorithm) is proposed to find solutions to (1) applying the Gödel operators for the triangular norm and co-norm. In Kyosev (2003) the Universal Algorithm is applied to solve industrial application problems.

Di Martino and Sessa (2011a) implement the Universal Algorithm in a GIS-based framework to solve urban planning problems. They apply the Universal Algorithm on a study area; the SFRE (1) is constructed deriving the symptoms from a set of known r measurable facts (the input variables i₁,…, i_r). A set of s unknown characteristics of the study area (the output variables o₁,…, o_s) determine the causes that affects the observable facts. For example, an input variable can be given by the percentage of employed residents calculated with respect to the set of residents making up the workforce and an output variable can be given by the economic prosperity of residents which contributes to an high percent of employed residents.

Fuzzy partitions of the domains of each input variable are constructed. As an example, let i₁ be the percentage of employed residents; we create a fuzzy partition in three fuzzy sets.

• $fs_{{i_{1} 1}}$ labelled low percentage of employed residents

• $fs_{{i_{1} 2}}$ labelled medium percentage of employed residents

• $fs_{{i_{1} 3}}$ labelled high percentage of employed residents

Each symptom b_i, i = 1,…,m, is related to a fuzzy set of an input variable, where m is the sum of the number of the fuzzy sets of the domain of each input variable; its value is given by the membership degree of the measured value of the input variable to this fuzzy set.

In our example, if the value of i₁ is 20%, and the membership degree of i₁ to $fs_{{i_{1} 1}}$ is 0.9, supposing to relate the symptom b₁ to $fs_{{i_{1} 1}}$, we obtain b₁ = 0.9.

A partition in fuzzy sets of each output variable is constructed. Continuing our example, let o₁ be the economic prosperity of residents. We partition o₁ in four fuzzy sets:

• $fs_{{o_{1} 1}}$ labelled very bad economic prosperity

• $fs_{{o_{1} 2}}$ labelled bad economic prosperity

• $fs_{{o_{1} 3}}$ labelled good economic prosperity

• $fs_{{o_{1} 4}}$ labelled excellent economic prosperity

Each unknown x_j j = 1,…,n, is related to a fuzzy set of an output variable where n is the sum of the number of the fuzzy sets of each output variable.

In our example we suppose to relate x₁ to the fuzzy set $fs_{{o_{1} 1}}$, x₂ is related to the fuzzy set $fs_{{o_{1} 2}}$, x₃ is related to the fuzzy set $fs_{{o_{1} 3}}$ and x₄ is related to the fuzzy set $fs_{{o_{1} 4}}$.

The coefficients a_ij, i = 1,…,m, j = 1,…,n, representing the weight with which the jth cause affects the ith symptom, are assigned by the pool of experts.

In our example, starting from one input variable and one output variable, we construct a SFRE with n = 4 columns given by the number of unknowns.

After constructing the SFRE (1), in Di Martino and Sessa (2011a, b) is executed the Universal Algorithm in order to determine a set of solutions for the unknowns; then, to an output variable is assigned the linguistic label of the fuzzy set to corresponding to the unknown with maximal value.

For example, if, after executing the Universal Algorithm on the SFRE, we obtain x₁ = 0.15, x₂ = 0.35, x₃ = 0.42 and x₄ = 0.08, the value of the output variable o₁ will be good economic prosperity, corresponding to the linguistic label of the fuzzy set $fs_{{o_{1} 3}}$.

In Di Martino and Sessa (2011a) the authors apply this method to evaluate a set of urban features in each the district of the eastern area of the municipality of Naples (Italy). In addition, a reliability of the results obtained in each district is calculated.

The main drawback of this method is constituted by the fact that the identification of the areas for which the urban characteristics are to be evaluated is performed statically by the user. Instead, it would be extremely useful for an urban planner to use this approach to dynamically determine the zones of the urban study area that are homogeneous with respect to the characteristics analyzed.

To overcome this drawback, in this work we propose a GIS-based framework in which we apply a method proposed in Cardone and Di Martino (2018) to partition an urban study area in homogeneous areas with respect to the characteristics analyzed; in Cardone and Di Martino (2018) the study area is initially partitioned in atomic homogeneous subzones, called microzones, made up of the census areas for which characteristics relating to the resident population and the urban fabric are measured; then, based on a fuzzy rule set prepared by the pool of experts, a Mamdani fuzzy system is applied to classify each microzone; adjoint microzones belonging to the same class are dissolved to form urban homogeneous areas called Urban Contexts (for short, UCs).

In this work, for each of the microzones that make up the study area, we execute the Universal Algorithm and apply a fuzzification process to determine the values of the output variables. Then, adjoint microzones having the same values of all the output variables are dissolved forming an UC. Finally, the thematic map of the UCs is produced.

We assign to each UC a reliability given by the average of the reliabilities calculated for all its microzones, using the approach proposed in Di Martino and Sessa (2011a) to calculate the reliability of the solution.

Our method has the advantage of avoiding the user deciding how to partition the study area to evaluate the distribution of urban features; in fact, by initially partitioning the study area into microzones and running the Universal Algorithm on each microzone, the thematic map is dynamically extracted with the distribution of the characteristics to be analyzed, in which the study area is partitioned into UC's, which represent zones of the study area homogeneous with respect to the analyzed features.

In a nutshell, the main contributions of the proposed framework are:

• the application of a dynamic model that allows to obtain the best partitioning of the urban study area into UCs, homogeneous subzones with respect to all the characteristics of the study area taken into consideration; initially the SFRE method is applied to each of the microzones making up the study of area; subsequently adjacent microzones with the same values assigned to the output variables are dissolved, forming an UC;

• the construction, for each output variable, of a reliability map of each UC, which allows to evaluate the spatial distribution of the reliability of the value assigned to the output variable

1.1 Related work

In recent years, several GIS-based frameworks have been developed in which fuzzy models and fuzzy systems are integrated in problems related to urban planning and environmental and climatic risks in urban environments.

In Sicat et al. (2005) a fuzzy rule-based system is implemented in a GIS to construct agricultural land suitability maps; the fuzzy rule set is built on the knowledge and experience of farmers. Sadrykia et al. (2017) propose a fuzzy decision-making model implemented in a GIS platform to assess the seismic vulnerability of urban areas with incomplete data. Araya-Munoz et al. (2017) propose a GIS-based hybrid model in which fuzzy aggregation functions are used to assess environmental and climatic multi-hazard impacts in metropolitan areas. In Jha et al. (2020) a fuzzy hybrid model is encapsuled in a GIS-based framework to assess the groundwater quality index in urban and rural areas.

A fuzzy hybrid model in a GIS framework is proposed in Schaefer et al. (2020) to evaluate the climate resilience in metropolitan cities. In Cardone and Di Martino (2021) the authors implement a hierarchical fuzzy multicriteria decision model in a GIS platform to find the optimal localization of school buildings in urban areas. A fuzzy classification model is encapsuled in a GIS-based platform in Wang et al. (2020) for flood risk assessment in metropolitan areas.

Fuzzy relation calculus was proposed by some authors in literature in order to solve spatial analysis problems. In Groeneman et al. (1997) a fuzzy model based on fuzzy relations between land qualities and land units is applied for land evaluation; these fuzzy relations are used to describe the suitability for a particular crop. Hemetsberger et al. (2002) propose a fuzzy classification model implemented in a GIS platform for avalanche risk assessment. A fuzzy relation model applied to assess the vulnerability of aquifers is proposed in Di Martino et al. (2005a, b). Xu et al. (2011) apply a fuzzy relation model to analyze the amount of coal gas in mines; this model was applied to predict the spatial distribution of coal gas content in the air. In Moghadam et al. (2015) a framework based on fuzzy relations and a fuzzy inference system is implemented to construct mineral potential maps.

In particular, in Di Martino and Sessa (2011a, b) is presented a new GIS-based framework in which is implemented the Universal Algorithm to find the best solutions of a SFRE applied in urban planning problems. The study area is divided in homogeneous subzones; for each subzone is constructed a SFRE whose solutions determine the symptoms caused from a set of known measurable facts. The framework is applied on a study area given by the east zone of the city of Naples (Italy), divided in her four districts.

This method can be applied in various urban planning problems in which we intend to analyze the impact of parameters that characterize an urban area on measured observables. Its main drawback is the fact that the user is left to partition the study area into homogeneous subzones with respect to the parameters analyzed; the subjective view of the user can increase the uncertainty in the spatial distribution of the results.

To solve this problem we apply in a GIS framework the model proposed in Cardone and Di Martino (2018) to find the best spatial partitioning of an urban study area into homogeneous subzones with respect to the characteristics analyzed.

In our framework the urban study area is initially partitioned into microzones. The expert set the values of the coefficients a_ij, i = 1,…,m, j = 1,…,n, and constructs the fuzzy partitions of the input and the output variables. The SFRE method is applied to each microzone; adjacent microzones for which the same value has been calculated of the output variables are aggregated to form UCs; the framework will produce a thematic map of UCs for each output variable, showing the spatial distribution of the assessment of the characteristic expressed by the output variable. Furthermore, for each output variable we construct a thematic map showing the distribution by UCs of the reliability of the results.

In Sect. 2 the Universal Algorithm and the GIS-based framework proposed in Di Martino and Sessa (2011a) are introduced.

The proposed GIS-based framework is presented in Sect. 3. In Sect. 4 are shown the results of our experimental tests in which we apply our framework to a specific problem on the study area of the municipality of Naples (Italy). Final considerations are inserted in Sect. 5.

2 Preliminaries

2.1 Fuzzy relation equations system

In compact matrix representation the SFRE (1) can be written as

$$ A \cdot X = B $$

(2)

where A is the m × n matrix of the coefficients a_ij i = 1,…,m j = 1,…,n; X is the n-dimensional vector of the unknowns causes x_j j = 1,…,n; B is the m-dimensional vectors of the symptoms b_i i = 1,…,m.

The operator $\cdot$ is the max min operator in the Gödel algebra.

A vector X⁰ = (x⁰_j)_n solution of the (1) is called a point solution for the SFRE. The set S of all the point solutions of is called a complete solution set of (1). If S ≠ Ø = then the SFRE is called consistent, otherwise it is called inconsistent.

A solution $\widehat{X}\in$ S is a lower (or minimal) solution of the SFRE if for any $X\in$ S the relation X ≤ $\widehat{X}$ implies X = $\widehat{X}$, where the ≤ is the usual partial order relation between n-dimensional vectors.

The complete solution set S can contain more lower solutions, when the lower solution is unique it is called least (or minimum) solution of the SFRE. Likewise, a solution $\widehat{X}\in$ S is called upper (or maximal) solution of the SFRE if for any $X\in$ S the relation $\widehat{X}$ ≤ X implies X = $\widehat{X}$. When the upper solution is unique it is called greatest (or maximum) solution of the SFRE.

The set of close intervals {I₁,...,I_n} with I_j $\subseteq$ [0, 1] for each j in {1,…,n}is called interval solution of the SFRE if for any solution $X\in$ S, where X = (x_j)_n, results x_j $\in$ I_j for each j, with 1 ≤ j ≤ n. The components of an interval solution are called interval bounds. Any interval solution whose interval bounds are given by a lower solution from the left and the greatest solution from the right is called a maximal interval solution of the SFRE (1).

The SFRE A • X = B is said in a normal form if results in (1) b₁ ≥ b₂ ≥ … ≥ b_m. The time computational complexity to reduce a SFRE in a normal form is polynomial (Peeva and Kyosev 2004; Peeva 2006). Without loss of generality, in what follows the system (1) is supposed to be in normal form.

2.2 The Universal solution algorithm

In Peeva (1985, 1992, 2006) and Peeva and Kyosev (2004) a set of methods for finding the complete solution set of (1) are proposed and a solvability criterion is proved; This criterion is briefly described below, omitting their proofs.

The first step of this solvability criterion is to determine if the SFRE (1) is consistent. This step is composed of the following three phases:

• 1. From the matrix A is constructed the matrix A* = (a*_ij)_m×n so defined:

  $$ a_{ij}^{*} = \left\{ {\begin{array}{*{20}c} {0{\text{ if a}}_{{{\text{ij}}}} < b_{i} } \\ {b_{i} {\text{ if a}}_{{{\text{ij}}}} = b_{i} } \\ {1{\text{ if a}}_{{{\text{ij}}}} > b_{i} } \\ \end{array} } \right. $$

  (3)

  If a^*_ij = 0, it is called an S-type coefficient; otherwise, if a^*_ij = b, it is called an E-type coefficient. Finally, if a^*_ij = 1, it is called a G-type coefficient.

• 2. Let A^*(j) be the subset {a^*_1j …a^*_mj}. If A^*(j) contains at least a G-type coefficient and k (1 ≤ k ≤ m) is the greatest row number such that a^*_kj = 1 in A*(j), then the following coefficients in A^*(j) are called selected:

• a) a^*_ij for each 1 ≤ i ≤ k if a^*_ij > b_i = b_k.

• b) a^*_ij for each k < i ≤ m if a^*_ij = b_i.

  If A^*(j) does not contain any G-type coefficient but it contain at least an E-type coefficient and r (1 ≤ r ≤ m) is the smallest row number such that a^*_rj = b_i in A^*(j), then the following coefficients in A^*(j) are called selected:

• c) a^*_ij for each r < i ≤ m if a^*_ij = b_i.

• 3. The SFRE (1) is consistent if and only if for each i = 1,…,m there exist at least one selected coefficient a^*_ij and the computational complexity of the function used to determining the consistency of the SFRE is O(m∙n) (Peeva and Kyosev 2004; Peeva 2006). To verify if a SFRE is consistent or inconsistent, following (Peeva 2006), is defined a m-dimensional vector IND whose i^th component IND(i), with i = 1,…,m, is equal to the number of selected coefficients in the i^th equation. The system is consistent if and only if IND(i) ≠ 0 for each i = l,…,m.

  The phases below described to verify if the SFRE (1) is consistent are structured in pseudocode in Algorithm 1; it return TRUE if the SFRE is consistent, FALSE otherwise.

As an example, we consider the following SFRE given by 3 equations and 4 unknown:

$$ \left\{ {\begin{array}{*{20}c} {\left( {0.2 \wedge x_{1} } \right) \vee \left( {0.7 \wedge x_{2} } \right) \vee \left( {0.5 \wedge x_{3} } \right) \vee \left( {0.6 \wedge x_{4} } \right) = 0.6} \\ {\left( {0.4 \wedge x_{1} } \right) \vee \left( {0.5 \wedge x_{2} } \right) \vee \left( {0.9 \wedge x_{3} } \right) \vee \left( {0.3 \wedge x_{4} } \right) = 0.5} \\ {\left( {0.4 \wedge x_{1} } \right) \vee \left( {0.6 \wedge x_{2} } \right) \vee \left( {0.6 \wedge x_{3} } \right) \vee \left( {0.8 \wedge x_{4} } \right) = 0.7} \\ \end{array} } \right. $$

where

$$ {\text{ A }} = \left| {\begin{array}{*{20}c} {{0}{\text{.2}}} & {{0}{\text{.7}}} & {{0}{\text{.5}}} & {{0}{\text{.6}}} \\ {0.4} & {0.5} & {0.9} & {0.3} \\ {0.4} & {0.6} & {0.6} & {0.8} \\ \end{array} } \right|{\text{ B }} = \left| {\begin{array}{*{20}c} {0.6} \\ {0.5} \\ {0.7} \\ \end{array} } \right| $$

Normalizing the SFRE we obtain:

$$ {\text{ A }} = \left| {\begin{array}{*{20}c} {{0}{\text{.4}}} & {{0}{\text{.6}}} & {{0}{\text{.6}}} & {{0}{\text{.8}}} \\ {0.2} & {0.7} & {0.5} & {0.6} \\ {0.4} & {0.5} & {0.9} & {0.3} \\ \end{array} } \right|{\text{ B }} = \left| {\begin{array}{*{20}c} {0.7} \\ {0.6} \\ {0.5} \\ \end{array} } \right| $$

Using (3) is computed the matrix A^*; then, is computed the three-dimensional vector IND where IND(i) is the number of selected coefficients in the i^th equation.

$$ {\text{ A* }} = \left| {\begin{array}{*{20}c} {0} & {0} & {0} & {1} \\ 0 & 1 & 0 & {0.6} \\ 0 & {0.5} & 1 & 0 \\ \end{array} } \right|{\text{ IND }} = \left| {\begin{array}{*{20}c} 1 \\ 2 \\ 2 \\ \end{array} } \right| $$

The SFRE is consistent because each component of the vector IND is not null. The system has an unique greatest solution and a set of lowest solutions.

In Peeva and Kyosev (2004) and Peeva (2006) is proved that if the SFRE is consistent it has an unique greatest solution X^gr = ($x_{1}^{gr} , \ldots ,x_{n}^{gr} )$; the computational complexity of the algorithm executed to compute X^gr is O(m∙n). The Universal Algorithm, given in Peeva and Kyosev (2004) and Peeva (2006), allows to find the maximal interval solutions of a consistent SFRE. Below are shown the steps of the Universal Algorithm.

• 4. Calculate X^gr where its j^th component ${x}_{j}^{gr}={b}_{k}$ if A*(j) contains at least a selected G-type coefficient, ${x}_{j}^{gr}=1$ otherwise.

• 5. In order to explore the number of minimal solutions we consider the m⨯n matrix H, called help matrix, with elements:

  $$ h_{ij} = \left\{ {\begin{array}{*{20}c} {b_{i} {\text{ if a}}_{{{\text{ij}}}}^{*} {\text{ is a selected coefficient in A*(j) }}} \\ {0{\text{ otherwise}}} \\ \end{array} } \right. $$

  (4)

Let h_i = (h_ij) and h_k = {h_kj) j=1,…n, be the ith and the kth rows of the help matrix H. If for each j=1,…n, h_ij ≠ 0 implies both h_kj ≠ 0 and h_kj ≤ h_ij then the row i is called dominant row to the row k in H and the ith equation of the SFRE is called equation dominant to the kth equation (and the kth equation is called dominated by the ith).

• 6. From H is created a matrix H* of dimension m⨯n, called dominance matrix, with components:

  $$ h_{ij}^{*} = \left\{ {\begin{array}{*{20}c} {{\text{0 if the }}i^{th} {\text{ equation is dominated by at least another equation}}} \\ {h_{ij} {\text{ otherwise}}} \\ \end{array} } \right. $$

  (5)

Let |H*_i| | for each i= 1, ...,m be the number of coefficients h*_ij = b_i ≠ 0 in the i^th row of the dominance matrix H*. When this value is 0, we set |H*_i| = 1. The number of potential minimal solutions of the SFRE cannot exceed the value (Peeva and Kyosev 2004; Peeva 2006):

$$ PN3 = \mathop \prod \limits_{i = 1}^{m} \left| {H_{i}^{*} } \right| $$

(6)

• 7. Following (Peeva 1985, 2006; Peeva and Kyosev 2004), is used the symbol $\frac{{b_{i} }}{j}$ to indicate the coefficients h^*_ij = b_i ≠ 0. A solution of the ith equation can be written as

  $$ H_{i} = \mathop \sum \limits_{j = 1}^{n} \frac{{b_{i} }}{j} $$

  (7)

• 8. To determine lower solutions for the SFRE, in (Peeva and Kyosev 2004; Peeva 2006) is introduced the concept of concatenation. A concatenation of equation solutions (7) is given by:

  $$ W = \mathop \prod \limits_{i = 1}^{m} H_{i} = \mathop \prod \limits_{i = 1}^{m} \left( {\mathop \sum \limits_{j = 1}^{n} \frac{{b_{i} }}{j}} \right) $$

  (8)

The concatenation operator is:

$$ {\text{commutative}}:\frac{{b_{{i_{1} }} }}{{j_{1} }}\frac{{b_{{i_{2} }} }}{{j_{2} }} = \frac{{b_{{i_{2} }} }}{{j_{2} }}\frac{{b_{{i_{1} }} }}{{j_{1} }} $$

(9)

$$ {\text{associative}}: \frac{{b_{{i_{1} }} }}{{j_{1} }}\left( {\frac{{b_{{i_{2} }} }}{{j_{2} }}\frac{{b_{{i_{3} }} }}{{j_{3} }}} \right) = \left( {\frac{{b_{{i_{1} }} }}{{j_{1} }}\frac{{b_{{i_{2} }} }}{{j_{2} }}} \right)\frac{{b_{{i_{3} }} }}{{j_{3} }} $$

(10)

distributive with respect to the addition:

$$ \frac{{b_{{i_{1} }} }}{{j_{1} }}\left( {\frac{{b_{{i_{2} }} }}{{j_{2} }} + \frac{{b_{{i_{3} }} }}{{j_{3} }}} \right) = \frac{{b_{{i_{1} }} }}{{j_{1} }}\frac{{b_{{i_{2} }} }}{{j_{2} }} + \frac{{b_{{i_{1} }} }}{{j_{1} }}\frac{{b_{{i_{3} }} }}{{j_{3} }} $$

(11)

Two other properties of the concatenation are the adsorption for multiplication:

$$ \frac{{b_{{i_{1} }} }}{{j_{1} }}\frac{{b_{{i_{2} }} }}{{j_{2} }} = \left\{ {\begin{array}{*{20}c} {\frac{{b_{{i_{1} }} \wedge b_{{i_{2} }} }}{j}{ }if{\text{ j}}_{1} = {\text{ j}}_{2} = {\text{ j }}} \\ {is unchanged{\text{ otherwise}}} \\ \end{array} } \right. $$

(12)

and the assorption for addition:

$$ \frac{{b_{{i_{1} }} }}{{j_{1} }}\frac{{b_{{i_{2} }} }}{{j_{2} }} \cdots \frac{{b_{{i_{m} }} }}{{j_{n} }} + \frac{{b_{{k_{1} }} }}{{j_{1} }}\frac{{b_{{k_{2} }} }}{{j_{2} }} \cdots \frac{{b_{{k_{m} }} }}{{j_{n} }} = \left\{ {\begin{array}{*{20}c} {\frac{{b_{{i_{1} }} }}{{j_{1} }}\frac{{b_{{i_{2} }} }}{{j_{2} }}..\frac{{b_{{i_{m} }} }}{{j_{n} }}{ }if{\text{ b}}_{{i_{h} }} \le {\text{ b}}_{{k_{h} }} { }\forall { }h{ : 1} \le h \le {\text{m }}} \\ {is unchanged{\text{ otherwise}}} \\ \end{array} } \right. $$

(13)

Using the properties of the concatenation operator we can obtain lower solutions of the SFRE (cfr. Peeva and Kyosev 2004; Peeva 2006). In fact, given two point solutions of the complete solutions set S of the SFRE, since S is a poset in which is defined an order relation ≤, we can use the absorption for addition property of the concatenation operator to determine the smaller solutions of them.

• 9. After applying the properties (9)..(13) the concatenation (8) well be transformed in the form:

  $$ W = \frac{{b_{{1_{1} }} }}{1} \cdots \frac{{b_{{1_{2} }} }}{j} \cdots \frac{{b_{{1_{m} }} }}{n} + \cdots + \frac{{b_{{L_{1} }} }}{1}\frac{{b_{{L_{2} }} }}{j} \cdots \frac{{b_{{L_{m} }} }}{n} $$

  (14)

  where L ≤ PN3.

• 10. Are determined the L lower point solutions X^low1_{, …,}X^lowL with components:

  $$ x_{1j}^{lowt} = \left\{ {\begin{array}{*{20}c} {b_{{i_{t} }} {\text{ if b}}_{{i_{t} }} \ne 0{\text{ in (14)}}} \\ {0{\text{ otherwise}}} \\ \end{array} } \right. $$

  (15)

• 11. From each lower solution are constructed the L maximal interval solutions of the SFRE. If ${\left({x}_{1}^{lowk},\dots ,{x}_{n}^{lowk}\right)}^{-1}$ is a lower solution, the correspondent maximal interval solution is given by

  $$ {\text{X}}_{{max_{k} }} { } = \left( {\begin{array}{*{20}c} {\left[ {x_{1}^{lowk} ,x_{1}^{gr} } \right]} \\ {\left[ {x_{2}^{lowk} ,x_{2}^{gr} } \right]} \\ \ldots \\ {\left[ {x_{n}^{lowk} ,x_{n}^{gr} } \right]} \\ \end{array} } \right) $$

  (16)

Now find the maximal interval solutions of the SFRE in the previous example. In the step 4) we calculate the greatest solution:

$$ X_{gr} = \left( {\begin{array}{*{20}c} 1 \\ {0.6} \\ {0.5} \\ {0.7} \\ \end{array} } \right) $$

Now we calculate the help matrix H using (4), obtaining:

$$ {\text{H }} = \left| {\begin{array}{*{20}c} {0} & {0} & {0} & {{0}{\text{.7}}} \\ 0 & {0.6} & 0 & {0.6} \\ 0 & {0.5} & {0.5} & 0 \\ \end{array} } \right| $$

and the dominant matrix H* using (5), obtaining:

$$ {\text{H* }} = \left| {\begin{array}{*{20}c} {0} & {0} & {0} & {{0}{\text{.7}}} \\ 0 & 0 & 0 & 0 \\ 0 & {0.5} & {0.5} & 0 \\ \end{array} } \right| $$

Now we set |H*_i| | for each i = 1,…,m as the number of coefficients h*_ij = b_i ≠ 0 in the i-th row of the dominance matrix H*. When this value is 0, we set |H*_i|= 1.

We obtain: |H*₁|= 1, |H*₂|= 1, |H*₃|= 2. Then, PN3 = 2 and our SFRE has at most two lower solutions.

The two point solutions given by the first and the third row in H* are:

$$ H_{1} = \left( {\begin{array}{*{20}c} {0} \\ {0} \\ {0} \\ {{0}{\text{.7}}} \\ \end{array} } \right){ }H_{3} = \left( {\begin{array}{*{20}c} {0} \\ {{0}{\text{.5}}} \\ {{0}{\text{.5}}} \\ {0} \\ \end{array} } \right){ } $$

Their concatenation is given by:

$$ W = H_{1} H_{3} = \frac{0.7}{4}\left( {\frac{0.5}{2} + \frac{0.5}{3}} \right) $$

Using the (9)..(13) we obtain:

$$ W = \frac{0.5}{2}\frac{0.7}{4} + \frac{0.5}{3}\frac{0.7}{4}. $$

Then, L = PN3 = 2 and the two lower solutions of the SFRE are:

$$ X_{{low_{1} }} = \left( {\begin{array}{*{20}c} 0 \\ {0.5} \\ 0 \\ {0.7} \\ \end{array} } \right){ }X_{{low_{2} }} = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ {0.5} \\ {0.7} \\ \end{array} } \right){ } $$

And the two maximal interval solutions are given by:

$$ {\text{X}}_{{max_{1} }} { } = \left( {\begin{array}{*{20}c} {\left[ {0,1} \right]} \\ {\left[ {0.5,0.5} \right]} \\ {\left[ {0.0,0.6} \right]} \\ {\left[ {0.7,0.7} \right]} \\ \end{array} } \right){\text{ X}}_{{max_{2} }} { } = \left( {\begin{array}{*{20}c} {\left[ {0,1} \right]} \\ {\left[ {0,0.5} \right]} \\ {\left[ {0.5,0.6} \right]} \\ {\left[ {0.7,0.7} \right]} \\ \end{array} } \right) $$

The Universal Algorithm is shown below in pseudocode (Algorithm 2).

3 The proposed framework

We apply the SFRE resolution universal algorithm in spatial analysis to partition an urban area in homogeneous zones based on a set of characteristics.

The study area is initially partitioned in microzones, corresponding to census areas in which are aggregated information about residents, families, houses and buildings.

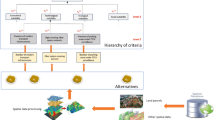
Our framework is schematized in Fig. 1.

Fig. 1

Schema of the proposed GIS-based framework

The pool of urban planner experts defines the input and the output variables; for each variable it creates a fuzzy partition and constructs the FSRE (1), assigning the value of the coefficients a_ij, where 0 ≤ a_ij ≤ 1, given by the impact of the jth cause (whose unknown value is the membership degree to a fuzzy set of the fuzzy partition of an output variable) to affect the ith symptom (whose value is membership degree to a fuzzy set of an input variable). For each microzone is applied the Universal Algorithm to solve the correspondent SFRE where the fact b_i i = 1,…,m is given by the membership degree to the correspondent fuzzy set of the ith.

To show the process of construction of the SFRE, in the following example let’s consider two input variables, given by:

• i₁ = percentage of graduate residents = number of graduate residents/number of residents over the age of 24.

• i₂ = percentage of unemployed workers = number of residents over the age of 15 unemployed looking for a new job/number of residents over the age of 15 belonging to the workforce.

and two output variables:

• o₁ = cultural level

• o₂ = standard of living

During the create input fuzzy partition process is created a fuzzy partition of i₁ given by the following three fuzzy sets, labelled:

• b₁ = low

• b₂ = medium

• b₃ = high

where each fuzzy set is related to a symptom.

Likewise, is created a fuzzy partition of i₂ given by the following three fuzzy sets, labelled:

• b₄ = low

• b₅ = medium

• b₆ = high

related to other three symptoms b₄, b₅ and b₆.

Figure 2 show an example of fuzzy partitions of the two input variables using triangular and semi-trapezoidal fuzzy sets.

Fig. 2

Fuzzy partition of the domains of the two input variables

During the create output fuzzy partition process are created the following fuzzy partition of the output variable o₁:

• x₁ = poor

• x₂ = medium

• x₃ = high

and the following fuzzy partition of the output variable o₂:

• x₄ = modest

• x₅ = medium

• x₆ = high

obtaining six unknown given by the sum of fuzzy sets of each fuzzy partition, where each fuzzy set is related to an unknown x₁.,…, x_6.

Figure 3 show an example of fuzzy partitions of the two output variables using triangular and semi-trapezoidal fuzzy sets.

Fig. 3

Fuzzy partition of the domains of the two output variables

In the construct SFRE process the pool of experts construct the following 6 × 6 size SFRE:

$$ \begin{gathered} 0.9^{x} 1v0.3^{x} 2v0.0^{x} 3v0.9^{x} 4v0.4^{x} 5v0.1^{x} 6 = b_{1} \hfill \\ 0.5^{x} 1v0.7^{x} 2v0.3^{x} 3v0.3^{x} 4v0.6^{x} 5v0.4^{x} 6 = b_{2} \hfill \\ 0.0^{x} 1v0.3^{x} 2v0.9^{x} 3v0.2^{x} 4v0.4^{x} 5v0.6^{x} 6 = b_{3} \hfill \\ 0.7^{x} 1v0.5^{x} 2v0.3^{x} 3v0.1^{x} 4v0.4^{x} 5v0.8^{x} 6 = b_{4} \hfill \\ 0.3^{x} 1v0.6^{x} 2v0.3^{x} 3v0.3^{x} 4v0.6^{x} 5v0.4^{x} 6 = b_{5} \hfill \\ 0.0^{x} 1v0.3^{x} 2v0.9^{x} 3v0.9^{x} 4v0.2^{x} 5v0.0^{x} 6 = b_{6} \hfill \\ \end{gathered} $$

The study area is partitioned in atomic microzones, For each microzone are calculated the input data (Calculate input data process); they are the crisp values measured for the input variables. Then, during the Execute Universal Algorithm process, the values of the coefficients b_i i = 1,…,m are assigned and the Universal Algorithm is execute for the selected microzone.

Continuing the previous example, we suppose to calculate the values 22% and 14% for the two input variable i₁ and i₂. In Table 1 are shown the membership degree to each fuzzy set; they are the value to assign to the correspondent symptoms.

Table 1 Example of values of the observable facts calculated for a microzone

Running the Universal Algorithm the SFRE results inconsistent. After deleting the rows where IND(i) = 0, we obtain the following consistent SFRE of two rows.

$$ \begin{gathered} 0.5^{x} 1v0.7^{x} 2v0.3^{x} 3v0.3^{x} 4v0.6^{x} 5v0.4^{x} 6 = b_{2} \hfill \\ 0.0^{x} 1v0.3^{x} 2v0.9^{x} 3v0.9^{x} 4v0.2^{x} 5v0.0^{x} 6 = b_{6} \hfill \\ \end{gathered} $$

The greatest solution is given by:

$$ X_{gr} = \left( {\begin{array}{*{20}c} {0.47} \\ {0.47} \\ {0.40} \\ {0.40} \\ {0.47} \\ {1.00} \\ \end{array} } \right) $$

We obtain the following six lower solutions:

$$ X_{{low_{1} }} = \left( {\begin{array}{*{20}c} {0.47} \\ {0.00} \\ {0.40} \\ {0.00} \\ {0.00} \\ {0.00} \\ \end{array} } \right){ }X_{{low_{2} }} = \left( {\begin{array}{*{20}c} {0.00} \\ {0.47} \\ {0.40} \\ {0.00} \\ {0.00} \\ {0.00} \\ \end{array} } \right){ }X_{{low_{3} }} = \left( {\begin{array}{*{20}c} {0.00} \\ {0.00} \\ {0.40} \\ {0.00} \\ {0.47} \\ {0.00} \\ \end{array} } \right){ } $$

$$ X_{{low_{4} }} = \left( {\begin{array}{*{20}c} {0.47} \\ {0.00} \\ {0.00} \\ {0.40} \\ {0.00} \\ {0.00} \\ \end{array} } \right){ }X_{{low_{5} }} = \left( {\begin{array}{*{20}c} {0.00} \\ {0.47} \\ {0.00} \\ {0.40} \\ {0.00} \\ {0.00} \\ \end{array} } \right){ }X_{{low_{6} }} = \left( {\begin{array}{*{20}c} {0.00} \\ {0.00} \\ {0.00} \\ {0.40} \\ {0.47} \\ {0.00} \\ \end{array} } \right){ } $$

and the corresponding max interval solutions:

$$ X_{{Max_{1} }} = \left( {\begin{array}{*{20}c} {\left[ {0.47, 0.47} \right]} \\ {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.40, 0.40} \right]} \\ {\left[ {0.00, 0.40} \right]} \\ {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.00, 1.00} \right]} \\ \end{array} } \right){ }X_{{Max_{2} }} = \left( {\begin{array}{*{20}c} {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.47, 0.47} \right]} \\ {\left[ {0.40, 0.40} \right]} \\ {\left[ {0.00, 0.40} \right]} \\ {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.00, 1.00} \right]} \\ \end{array} } \right){ }X_{{Max_{3} }} = \left( {\begin{array}{*{20}c} {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.40, 0.40} \right]} \\ {\left[ {0.00, 0.40} \right]} \\ {\left[ {0.47, 0.47} \right]} \\ {\left[ {0.00, 1.00} \right]} \\ \end{array} } \right){ } $$

$$ X_{{Max_{4} }} = \left( {\begin{array}{*{20}c} {\left[ {0.47, 0.47} \right]} \\ {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.00, 0.40} \right]} \\ {\left[ {0.40, 0.40} \right]} \\ {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.00, 1.00} \right]} \\ \end{array} } \right){ }X_{{Max_{5} }} = \left( {\begin{array}{*{20}c} {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.47, 0.47} \right]} \\ {\left[ {0.00, 0.40} \right]} \\ {\left[ {0.40, 0.40} \right]} \\ {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.00, 1.00} \right]} \\ \end{array} } \right){ }X_{{Max_{6} }} = \left( {\begin{array}{*{20}c} {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.00, 0.47} \right]} \\ {\left[ {0.00, 0.40} \right]} \\ {\left[ {0.40, 0.40} \right]} \\ {\left[ {0.47, 0.47} \right]} \\ {\left[ {0.00, 1.00} \right]} \\ \end{array} } \right){ } $$

Following (Di Martino and Sessa 2011a, b) se calculate the mean solution vectors given by the central value of each interval of the max interval solution vectors (Calculate mean solutions process).

The six mean solution vectors are:

$$ X_{{MaxM_{1} }} = \left( {\begin{array}{*{20}c} {0.47} \\ {0.235} \\ {0.40} \\ {0.20} \\ {0.235} \\ {0.50} \\ \end{array} } \right){ }X_{{MaxM_{2} }} = \left( {\begin{array}{*{20}c} {0.235} \\ {0.47} \\ {0.40} \\ {0.20} \\ {0.235} \\ {0.50} \\ \end{array} } \right){ }X_{{MaxM_{3} }} = \left( {\begin{array}{*{20}c} {0.235} \\ {0.235} \\ {0.40} \\ {0.20} \\ {0.47} \\ {0.50} \\ \end{array} } \right){ } $$

$$ X_{{MaxM_{4} }} = \left( {\begin{array}{*{20}c} {0.47} \\ {0.235} \\ {0.20} \\ {0.40} \\ {0.235} \\ {0.50} \\ \end{array} } \right){ }X_{{MaxM_{5} }} = \left( {\begin{array}{*{20}c} {0.235} \\ {0.47} \\ {0.20} \\ {0.40} \\ {0.235} \\ {0.50} \\ \end{array} } \right){ }X_{{MaxM_{6} }} = \left( {\begin{array}{*{20}c} {0.235} \\ {0.235} \\ {0.20} \\ {0.40} \\ {0.47} \\ {0.50} \\ \end{array} } \right){ } $$

To assign the linguistic labels to the output variables, in the Calculate values of the output variables process for each mean solution we assign the potential values of the output variables given to the linguistic label of the fuzzy set to which each output variable belongs with the greatest membership degree.

For example, considering the first three components of the mean solution vector ${X}_{{Ma\mathrm{xM}}_{1}}$, corresponding to the fuzzy sets labelled, respectively, as: poor, medium and high, referred the output variable o₁ = cultural level, the highest value is 0.47, corresponding to the membership degree to the fuzzy set labelled poor. Then, we assign to o₁ the linguistic label poor.

The greatest membership degrees to the fuzzy sets related to each output variable are marked in bold in each mean solution.

In Table 2 are shown the linguistic labels assigned to the two output variables for each solution.

Table 2 Potential values of the output variables assigned from each mean solution

In Di Martino and Sessa (2011a) is assigned a mean reliability to each solution given by the mean values of the membership degrees of the output variable to the correspondent fuzzy sets. For example, to the solution ${X}_{{MaxM}_{1}}$ is assigned a mean reliability (0.47 + 0.50)/2 = 0.485. To set the linguistic labels to be assigned to each output variable is selected the solution having greatest reliability. When two or more solutions have an identical reliability we select the solution with highest cardinality, where the cardinality of a solution is given by the number of solutions generating the same values assigned to the output variables.

Table 3 show the mean reliability and the cardinality calculated for each solution.

Table 3 Mean reliability and cardinality calculated for each solution

In this example are selected the potential values correspondent to the solutions ${X}_{{MaxM}_{1}}$ and ${X}_{{MaxM}_{4}}$; these solutions generate the same potential values assigned to the two output variables and have the same mean reliability; they are the same mean reliability of ${X}_{{MaxM}_{5}}$, however, they have a higher cardinality than ${X}_{{MaxM}_{5}}$.

Output of this process are the final value and the reliability assigned to each output variable for the microzone, where the reliability assigned to an output variable is given by the membership degree to the correspondent fuzzy set.

Table 4 show the value of the output variables and the reliability assigned to the microzone in our example.

Table 4 Final values of the output variable and reliability assigned to the microzone

These steps are iterated until the values of the output variables and the reliability are calculated for each microzone.

Subsequently, is executed the Construction Urban Context process in which all adjoint microzones with same values of the output variables are dissolved to form an UC. To the UC is assigned, for each output variable, a reliability given by the average of the reliability assigned to the values of this output variable in each of the microzones that make up the UC.

Finally, is executed the Create thematic maps process in which the thematic map of the UCs showing the values of each output variable are constructed. In addition, the reliability maps of each output variable for the UCs is constructed; it shows how reliable is the assignment of the calculated final value of this output variable to each UC.

Figure 4 show as an example the thematic maps produced. The study area is partitioned in UCs. For each output variable is produced the correspondent thematic map where the labels of each thematic classes are the linguistic labels of the fuzzy set of the fuzzy partition of the output variable. Next to it is shown the thematic map of the reliability of the output variable.

Fig. 4

Example of urban context output variable maps and reliability maps

We’ve implemented our method in the GIS-based suit ESRI ArcGIS 10.8. The Universal Algorithm was implemented in c++ language and encapsulated in the GIS platform.

In next section we show the results obtained applying our method on a study area for a urban planning problem. In our text we compare our results with the ones obtained using the method in Di Martino and Sessa (2011a).

4 Simulation results

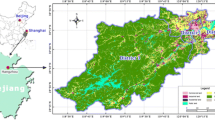
To compare our approach with the one in Di Martino and Sessa (2011a) we apply our method to the census dataset of the microzones in the districts of Ponticelli, in the municipality of Naples (Italy). The dataset is extracted from the census database provided by the ISTAT (Istituto nazionale di STATistica) for the city of Naples, containing information on population, buildings, housing, family, employment work, grouped by 219 microzones of which only 204 are inhabited zones. For each of the 204 microzones, the process described in the previous section is carried out in order to estimate the values of the output variables to be assigned to the microzone.

The study area of Ponticelli is shown in Fig. 5; in orange are visible the microzones.

Fig. 5

The study area: the district of Ponticelli and its microzones (in orange) (color figure online)

In Di Martino and Sessa (2011a) are considered 4 output variables.

• o₁ = Economic prosperity: i.e. wealth and prosperity of citizens

• o₂ = Transition into the job, i.e. ease of finding work

• o₃ = Social Environment: i.e. cultural levels of citizens

• o₄ = Housing development: i.e. presence of building and residential dwellings of new construction

Each output variable is partitioned in three fuzzy sets, labelled low, mean, and high, obtaining 12 unknowns:

• x₁ = correspondent to o₁ = low

• x₂ = correspondent to o₁ = mean

• x₃ = correspondent to o₁ = high

• x₄ = correspondent to o₂ = low

• x₅ = correspondent to o₂ = mean

• x₆ = correspondent to o₂ = high

• x₇ = correspondent to o₃ = low

• x₈ = correspondent to o₃ = mean

• x₉ = correspondent to o₃ = high

• x₁₀ = correspondent to o₄ = low

• x₁₁ = correspondent to o₄ = mean

• x₁₂ = correspondent to o₄ = high

The facts are given by the following input variables:

• i₁ = percentage of people employed = number of people employed/total work force

• i₂ = percentage of women employed = number of women employed/number of people employed

• i₃ = percentage of entrepreneurs and professionals = number of entrepreneurs and professionals/number of people employed

• i₄ = percentage of residents graduated = numbers of residents graduated/number of residents whit age > 6 years

• i₅ = percentage of new residential buildings = number of residential buildings built since 1982/total number of residential buildings

• i₆ = percentage of residential dwellings owned = number of residential dwellings owned/total number of residential dwellings

• i₇ = percentage of residential dwellings with central heating system = number of residential dwellings with central heating system/total number of residential dwellings.

The value of the input variables are obtained aggregating the ones computed for each microzone in the district of Ponticelli. In Table 5 are shown the values of the 7 input variables:

Table 5 Values of the input variables obtained in (Di Martino and Sessa 2011a, b)

The domain of each input variables is partitioned in three fuzzy sets labeled Low, Medium and High. Figure 6 show the fuzzy partitions of the seven input variables.

Fig. 6

Fuzzy partitions of the seven input variables

The SFRE constructed by the domain expert is given by 10 equations in the 12 unknown x_j. The matrix A of dimension 10 × 12 and the vector B of dimension 10 × 1 are given by:

$$\text{A }=\left|\begin{array}{cccccccccccc}\text{0.5}& \text{1.0}& \text{0.0}& \text{0.4}& 1.0& 0.2& 0.2& 0.7& 0.3& 0.1& 0.3& 0.2\\ 0.2& 0.1& 0.0& 0.2& 0.1& 0.0& 0.2& 0.1& 0.0& 0.0& 0.0& 0.0\\ 0.2& 0.8& 0.2& 0.2& 0.8& 0.2& 0.2& 0.8& 0.2& 0.0& 0.0& 0.0\\ 1.0& 0.2& 0.0& 1.0& 0.1& 0.0& 0.8& 0.2& 0.2& 0.3& 0.1& 0.0\\ 0.4& 0.8& 0.1& 0.3& 0.9& 0.1& 0.2& 0.8& 0.1& 0.1& 0.3& 0.0\\ 0.0& 0.1& 1.0& 0.1& 0.3& 0.7& 0.1& 0.3& 0.7& 0.0& 0.1& 1.0\\ 0.3& 0.7& 0.3& 0.2& 0.8& 0.2& 0.2& 0.8& 0.2& 0.3& 0.7& 0.3\\ 0.0& 0.1& 0.2& 0.0& 0.1& 0.2& 0.0& 0.1& 0.2& 0.0& 0.1& 0.2\\ 0.2& 0.1& 0.0& 0.4& 0.2& 0.1& 0.4& 0.2& 0.1& 0.7& 0.2& 0.0\\ 0.1& 0.2& 0.0& 0.1& 0.2& 0.0& 0.1& 0.2& 0.0& 0.3& 0.5& 0.1\end{array}\right|\text{ B }=\left| \begin{array}{c}{b}_{2}\\ {b}_{4}\\ {b}_{5}\\ {b}_{7}\\ {b}_{11}\\ {b}_{15}\\ {b}_{17}\\ {b}_{18}\\ {b}_{19}\\ {b}_{20}\end{array}\right|$$

where, the correspondent input variable and the linguistic label of the fuzzy set for each symptom are shown in Table 6, 7.

Table 6 Input variable and linguistic label of each symptom in the SFRE

Table 7 Values of the symptom measured for the study area of Ponticelli in Di Martino and Sessa (2011a)

The values assigned to the bi in Di Martino and Sessa (2011a) are obtained aggregating the measures of the input variables for all the 219 microzones in the district of Ponticelli.

The linguistic labels solutions obtained for the four output variables are given in Table 8. The reliability of the solutions is 0.69.

Table 8 Final linguistic labels obtained for the output variables in the district of Ponticelli in Di Martino and Sessa (2011a)

The results in Table 8 highlight that the population of the Ponticelli district is on average well-off and with a sufficient degree of employment, albeit with a low cultural level. Furthermore, in recent decades there has not been an increase in the residential urban fabric in the district.

In order to explore in greater spatial detail how the social fabric varies in the district, now we apply the proposed method executing the Universal Algorithm for each microzone.

To analyze the spatial distribution of each input variable we create a thematic map of the input variable in which each microzone is classified with the linguistic labels of the fuzzy set to which it belongs with the highest membership degree.

These thematic maps are shown in in Figs. 7, 8, 9, 10, 11, 12, 13.

Fig. 7

Thematic map of i₁

Fig. 8

Thematic map of i₂

Fig. 9

Thematic map of i₃

Fig. 10

Thematic map of i₄

Fig. 11

Thematic map of i₅

Fig. 12

Thematic map of i₆

Fig. 13

Thematic map of i₇

Of particular evidence in the seven maps, we note:

• the prevalence of a high percentage of employed workers (input variable i₁) and of properties owned (i₆) mainly in the western area of the neighborhood;

• a low percentage of employed women (i₂) and graduates (i₄) mainly in areas of the eastern area of the neighborhood;

• a low percentage of new buildings (i₅) especially in the western areas of the district in correspondence with historical centers.

After running the Universal Algorithm on all microzones, and assigning linguistic labels to the output variables, the Construction Urban Context process is started in which all the adjacent microzones having the same values of the output variables are dissolved together to form an UC.

Output of this process is the construction of 84 UCs, into which the study area is divided. The thematic map in Fig. 14 shows the UCs, highlighted with red outline. The microzones are shown with a dashed gray outline.

Fig. 14

Partitioning of the district of Ponticelli in UCs

For each output variable is constructed a thematic map showing the spatial distribution of the characteristic represented by the output variable for UC.

In Figs. 15, 16, 17, 18 are shown the thematic maps of the four output variables.

Fig. 15

UCs thematic map of o₁

Fig. 16

UCs thematic map of o₂

Fig. 17

UCs thematic map of o₃

Fig. 18

UCs thematic map of o₄

The four thematic maps highlight a similar distribution of the output variables o₁, o₂ and o₃, respectively, economic prosperity, transaction in job and social environment. In UCs corresponding to more consolidated urban centers and closer to the historic center of the municipality of Naples they have a high linguistic label, while in more peripheral areas, mainly in the eastern area of the district, they have a "low" linguistic label. On the contrary, in the first UCs the linguistic label assigned to the output variable o₄, housing development, is low, while in the more peripheral UCs mainly in the eastern area of the neighborhood it has the value high. These results show that the district of Ponticelli is mainly divided into two macro-zones: the first, further west, near the historic center of the city, corresponding to a consolidated historic center, richer and with a higher cultural level; the second, in the eastern area of the district, corresponding to peripheral areas, with a greater presence of buildings and industrial warehouses, poorer, but which, unlike the other macro-zone, is undergoing greater urban development, with a greater presence of newly built residential buildings.

Table 9 show, for each output variable the distribution of the number of inhabitants in the UCs classified, respectively, as low, medium and high.

Table 9 Distribution of the number of inhabitants in UCs classified as low, medium and high for each output variable

The three histograms in Fig. 19 show the percentage trend of the number of inhabitants in the three types of UC’s.

Fig. 19

Distribution of the percent of inhabitants in UCs classified as low, medium and high for each output variable

These results show, in general, for the output variables o₁ and o₂, an almost similar distribution of the number of inhabitants in UCs classified as low, medium and high: over 40% of the inhabitants reside in UCs classified as low, approximately 15% in UCs classified as medium and approximately 45% in UCs classified as high. Regarding the output variables o₃, almost 40% of the inhabitants reside in UCs classified as low, about 6% in UC's classified as medium and about 55% in UCs classified as high. Finally, regarding the output variables o₄, about 55% of the inhabitants reside in UCs classified as low, about 7% in UC's classified as medium and almost 40% in UCs classified as high.

The results of the analyses carried out on the resident population and shown in Table 9 and Fig. 19 confirm the contrast of two main types of urban fabric, the first characterized by a population with a high cultural level and economically well-off that has the facility to find work he lives in a consolidated urban fabric with few newly built houses, the second one, on the other hand, is characterized by a population of modest cultural level and middle-lower class, living in an urban fabric of new economic-popular construction.

This breakdown of the district of Ponticelli into two opposing types of urban fabric did not arise in the results obtained by applying the model proposed in Di Martino and Sessa (2011a, b) and shown in Table 8, in which the district is represented by an atomic entity.

In Figs. 20, 21, 22, 23 are shown the reliability maps of the four output variables.

Fig. 20

UCs reliability map of o₁

Fig. 21

UCs reliability map of o₂

Fig. 22

UCs reliability map of o₃

Fig. 23

UCs reliability map of o₄

In all the four reliability thematic maps, for about 60% of the UCs the reliability is over 0.6; for about 25% of the UCs the reliability is in the interval [0.4, 0.6]. Only to about 15% of the UCs is assigned a reliability less than 0.4. It follows that, approximately, for each output variable, the reliability of the results can be considered acceptable.

These results, compared with the synthetic ones in Table 8, highlight that our method provides the urban planner with a deeper knowledge of the area of ​​study than that obtained by applying the method proposed in Di Martino and Sessa (2011a).

In fact, on the one hand it allows to detect sub-areas of the study area with homogeneous urban characteristics, in accordance with the analyzed problem: the UCs, on the other hand it allows to analyze the spatial variation of the output variables considered. By applying the proposed method it was possible to determine that the district of Ponticelli is, approximately, composed of two areas, one characterized by greater per capita wealth, greater ease in finding work and a greater cultural level of the residents, the other, located approximately in the eastern area of the district, with a low economic prosperity, a moderately modest cultural level and a low employment level, but where there are new residential buildings and, therefore, can constitute a development area of future urban settlements. The partitioning into these two macro-areas is consistent with the current urban structure of the district in which a rich eastern macro-area made up of consolidated buildings and a poorer western peripheral area, with a more recent urban development coexist.

Finally, our method constructs, for each output variable, a thematic map with the spatial distribution of its reliability, allowing us to evaluate in which areas the uncertainty related to its evaluation is greater or less.

5 Final considerations and future perspectives

We propose a GIS-based framework encapsulating the Universal Algorithm applied to find solutions to the SFRE inverse problem in urban planning. With the support of a pool of expert are set the input and output variables and is constructed the SFRE. The study area is partitioned in atomic microzones, then, in each microzone is applied a method proposed in Di Martino and Sessa (2011a).

To assess the values of the output variables after solving the SFRE. Then, all the adjoint microzones with identical values of the output variables are dissolved to constitute homogeneous sub-areas of the study areas called Urban Contexts. For each UC the thematic maps of the output variables and the thematic maps of the correspondent reliabilities.

This approach is applied to a urban planning problem on the study area given by the district of Ponticelli in the municipality of Naples (Italy). The results show the study area is approximately formed by two types of zones: a historic urbanized area with an average high economic prosperity and occupancy rate of inhabitants, but with low presence of new homes, and an area with lower population density, but with a high development of new residential buildings.

The proposed GIS-based framework can provide valid cognitive support of the study area useful for urban planning decision making activities.

In the future we intend to test the proposed framework for other case studies and urban planning issues. Furthermore, we intend to integrate this framework with other functionalities that include multicriteria decision analysis methods in an evolved GIS-based environment to offer the decision maker complete support for decision analysis in urban planning.