1 Introduction

Graph convolutional networks (GCNs) (Zhang et al. 2018b; Kipf and Welling 2017; Li et al. 2018; Yao et al. 2019) show natural advantages for dealing with many real-world problems which can be modeled as graph networks (Bruna et al. 2014; Hamilton et al. 2017; Monti et al. 2017; Defferrard et al. 2016). Each convolution in these GCNs is based on one-step neighborhood aggregation scheme. GCNs directly apply multiple graph convolution layers to obtain multi-step neighborhoods information and learn graph representations. Limited to the over-smoothing (Li et al. 2018) of GCNs with more layers, GCNs are difficult to leverage the hierarchical property of convolutional neural networks (CNNs) such as AlexNet (Krizhevsky et al. 2012) and MACNN (Lai et al. 2020). Therefore, GCNs are usually shallow and generally do not exceed four layers (Zhou et al. 2018). For instance, there are only two layers in GCN (Kipf and Welling 2017). This shallow mechanism limits the expressive power of learning graph representations and label propagation (Sun et al. 2020). To address the limitations, researchers propose some approaches which are summarized in the following two-fold.

  1. 1.

    To improve the expressive power, Li et al. (2019b) propose DeepGCNs with very deep networks using deep CNNs concepts such as residual connections (He et al. 2016) and dense connections (Huang et al. 2017). Nevertheless, deep networks with many parameters are extremely hard to train on large graphs.

  2. 2.

    High-order graph convolution models (Abu-El-Haija et al. 2019a, b; Luan et al. 2019) such as MixHop (Abu-El-Haija et al. 2019b) directly capture the interaction of neighboring nodes at different distances to achieve performance improvement. As the number of order increases, the parameters of these models will increase and these models become more complex. This is hard to train and may suffer from overfitting.

Fig. 1
figure 1

Our MulStepNET background

Full size image
Fig. 2
figure 2

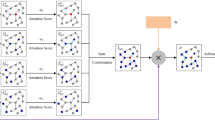
Our MulStepNET architecture. This figure describes the architecture when k is 5. Our MulStepNET consists of an input layer, a multi-step graph convolution layer, and an output layer. The multi-step graph convolution includes three stages: multi-power adjacency matrix, multi-step feature propagation, and multi-step linear transformation

Full size image

In order to reduce excess complexity and parameters, a recent surge of interest has focused on Simple Graph Convolution (SGC) (Wu et al. 2019). Wu et al. (2019) have shown that by repeatedly removing the nonlinearities between graph convolution layers of GCN and collapsing normalized adjacency matrices between consecutive layers, the complexity of GCN is reduced. In addition, they significantly reduce parameters through reparameterizing weight matrices into a single weight matrix. Nevertheless, SGC has difficulty in distinguishing the feature information of neighboring nodes at various distances, which limits the expressive power.

To address the limits, we propose a novel architecture of stronger multi-step graph convolutional network (MulStepNET). Figure 1 shows the background and need for designing our MulStepNET. As illustrated in Fig. 2, our MulStepNET leverages multi-step neighborhoods information by constructing multi-power adjacency matrix with simple grouping and attention mechanism and applies the attention mechanism to flexibly adjust the contributions of neighboring nodes at various distances. Based on the multi-power adjacency matrix, we design a stronger multi-step graph convolution to aggregate more nodes features and learn global graph structure. Further, we build an one-layer network model with the fewest parameters to avoid overfitting and reduce complexity. Meanwhile, the model with large k-steps (zero-step to k-step) graph convolution widens the receptive field and improves the learning ability. Our contributions are as follows:

  • To enlarge the receptive field, we construct a multi-power adjacency matrix with simple grouping and attention mechanism by combining the adjacency matrices of different powers. Based on the multi-power adjacency matrix, we develop a new multi-step graph convolution that can flexibly adjust the weights of neighboring nodes at different distances. This may improve the learning ability.

  • To the best of our knowledge, it is the first work to propose an one-layer architecture with larger steps graph convolution. Compared with prior methods, in terms of complexity and parameters, our architecture performs as well as SGC and outperforms other methods while capturing more nodes and global information.

  • We conduct extensive experiments on node classification tasks. Experimental results show that the proposed method compares favorably against state-of-the-art approaches in terms of classification performance and stability.

2 Preliminaries and related works

Graph convolutional networks are successfully applied to non-Euclidean and Euclidean applications and are quickly evolving (Wang and Ye 2018; Yao et al. 2019; Kampffmeyer et al. 2019; Chen et al. 2018; Guo et al. 2019; Yu and Qin 2020). We mainly review the work most relevant to our approach.

An undirected graph \({\mathcal {G}}\) with n vertices and e edges is denoted as \({\mathcal {G}}=(\varepsilon ,\nu , A)\), where \(\varepsilon\) and \(\nu\) are respectively the set of edges and vertices. The edge relationships of \({\mathcal {G}}\) can be described by adjacency matrix \(A\in {\mathbb {R}}^{n\times n}\). We introduce \(X\in {\mathbb {R}}^{n\times c_{0}}\) to denote node feature matrix with \(c_{0}\) features per node.

Similar to CNNs, the convolution of GCN (Kipf and Welling 2017) is to learn the feature representation of nodes over multiple graph convolution layers. At layer j, we denote the adjacency matrix \(A_{j}\) and the node hidden representation \(H_{j}\) as input, the output node representation \(H_{j+1}\) can be written as:

$$\begin{aligned} H_{j+1} = \text{ReLU}\left( {\tilde{D}}_{j}^{-\frac{1}{2}}{\tilde{A}}_{j}{\tilde{D}}_{j}^{-\frac{1}{2}}H_{j}W_{j}\right) , \end{aligned}$$
(1)

where \({\tilde{A}}_{j}\) denotes a new adjacency matrix with self-loops, with \({\tilde{A}}_{j}=A_{j}+I_{j}\). \(I_{j}\) and \({\tilde{D}}_{j}\) are identity matrix and degree matrix respectively. We describe \(H_{1}\) (j=1) as original input feature matrix X and use gradient descent to train weight matrix \(W_{j}\). Stacking the layer twice, the two-layer GCNs can be described as:

$$\begin{aligned} Y_{\text{GCN}} = \text{softmax}\left( {\tilde{D}}_{j}^{-\frac{1}{2}}\!{\tilde{A}}_{j}\!{\tilde{D}}_{j}^{-\frac{1}{2}}\!\text{ReLU}\!\left({\tilde{D}}_{j}^{-\frac{1}{2}}\!{\tilde{A}}_{j}\!{\tilde{D}}_{j}^{-\frac{1}{2}}\!X\!W_{1}\right) \!W_{2}\right) , \end{aligned}$$
(2)

where \(W_{1}\) and \(W_{2}\) are different weight matrices, softmax is a normalization classifier.

Abu-El-Haija et al. (2019b) propose high-order graph convolution (HGC) model to improve expressive power by mixing multi-hop neighborhoods information. We normalize the adjacency matrix \({\tilde{A}}_{j}\) into normalized adjacency matrix \({\hat{A}}_{j}\), with \({\hat{A}}_{j}={\tilde{D}}_{j}^{-\frac{1}{2}}{\tilde{A}}_{j}{\tilde{D}}_{j}^{-\frac{1}{2}}\). Then the model is as follow:

$$\begin{aligned} H_{j+1} = \text{ReLU}({\hat{A}}_{j}^{1}H_{j}W_{1}|{\hat{A}}_{j}^{2}H_{j}W_{2}|\cdots |{\hat{A}}_{j}^{k}H_{j}W_{j}), \end{aligned}$$
(3)

where \({\hat{A}}_{j}^{k}\) is the k power of \({\hat{A}}_{j}\), and | denotes column concatenation. Lei et al. (2020) develop HGC model and reduce the parameters of Abu-El-Haija et al. (2019b) via weight sharing mechanism.

We write a K-layer GCN in general form as:

$$\begin{aligned} {\hat{Y}} = \text{softmax}({\hat{A}}_{j}\text{ReLU}(\!\cdots \! {\hat{A}}_{j}\text{ReLU}({\hat{A}}_{j}XW_{1})W_{2}\cdots )W_{K}) . \end{aligned}$$
(4)

According to the hypothesis of Wu et al. (2019), for the K-layer GCN , we remove all ReLU functions and reparameterize all weight matrices \((W_{1},W_{2},\ldots W_{K})\) into a single weight matrix W via \(W=W_{1}W_{2}\cdots W_{K}\). The K-layer GCN becomes:

$$\begin{aligned} {\hat{Y}} = \text{softmax}({\hat{A}}_{j}^{K}XW), \end{aligned}$$
(5)

where \({\hat{A}}_{j}^{K}\) denotes K power of \({\hat{A}}_{j}\). The model is called as Simple Graph Convolution (SGC) (Wu et al. 2019). Although the model has fewer computations and parameters, the model can not distinguish the features information of neighboring nodes at different distances. This restricts the ability of learning graph representations. There are many other simple or linear models (Thekumparampil et al. 2018; Cai and Wang 2018; Eliav and Edith 2018). By applying these models to the tasks of Li et al. (2019a) and Al-Sharif et al. (2020), these models are more powerful.

Recently, many graph attention models (Veličković et al. 2018; Thekumparampil et al. 2018; Zhang et al. 2018a) try to assign suitable weights based on node features in the graph and achieve better performance on graph learning tasks. Nevertheless, these models with attention mechanism bring the concerns of high complexity and nuisance parameters. There are many other researches (Zhou et al. 2018; Wu et al. 2020) for comprehensive review.

3 The proposed method

We are committed to developing a method that can simultaneously capture neighboring nodes information at different distances and global graph structure while fitting few parameters and being computationally efficient. In this section, we propose a novel one-layer MulStepNET architecture. Further, we introduce our multi-step graph convolution that can simultaneously capture neighboring nodes information at more distant distances and analyze the computational complexity and parameters.

3.1 The overall architecture

In CNNs, we increase the expressivity of extracting features via many and deeper convolutional layers, which enlarges the scale of receptive field. However, GCN with multiple layers (exceed 2 layers) can suffer from over-smoothing (Li et al. 2018), which hurts classification performance on graph learning tasks. To improve the performance, an effective way is to use high-order graph convolutions with different weight matrices to gather more neighborhoods information at various distances (Abu-El-Haija et al. 2019b). As the number of order increases, the parameters will significantly increase and the model will lead to redundant computation. This is hard to train and brings potential concerns of overfitting. For SGC (Wu et al. 2019), although the simplified mechanism speeds up model training and avoids the excess complexity, SGC fails to adjust and distinguish the contributions of neighboring nodes at different distances. This limits the learning ability. Motivated by the above analyses, we propose our MulStepNET architecture (Fig. 2). A key innovation of MulStepNET is a novel multi-step graph convolution layer. Instead of aggregating the information of one-step neighboring nodes, our multi-step graph convolution combines these neighborhoods information at different distances and captures the high-order interaction between nodes.

We summarize the main differences of our MulStepNET and the models most relevant to our approach as follows. In SGC, the model applies the K power of the normalized adjacency matrix \({\hat{A}}\) to obtain the neighboring nodes that are K-hops away. In our MulStepNET, we design a multi-power adjacency matrix (the k powers of the \({\hat{A}}\), namely 0 power to k power of the \({\hat{A}}\), \(k>K\), see Sect. 3.2) to obtain the neighboring nodes that are k-hops away. In addition, we use a new attention mechanism to distinguish the contributions that may be important for classification. In MixHop, (1) the model constructs high-order graph convolution using different weight matrices to capture the feature information of neighboring nodes at different distances; (2) the model uses column concatenation to combine these information; (3) the model has a two-layer structure. In our MulStepNET, (1) we propose the multi-step graph convolution based on single weight matrix to capture the feature information of neighboring nodes at more distant distances; (2) we consider these information by the multi-power adjacency matrix, rather than the column concatenation; (3) we construct an one-layer structure with fewer computations and parameters; (4) we can adjust the contributions via the attention mechanism.

3.2 Multi-step graph convolution layer

Multi-step graph convolution has three stages: multi-power adjacency matrix, multi-step feature propagation, and multi-step linear transformation. We introduce each stage in detail as follows.

Multi-power adjacency matrix We use adjacency matrix A to describe the edge weights between nodes that are one-step away in the graph. The adjacency matrix A fails to denote the edge weights of k-step (\(k>1\)) neighboring nodes. The information propagation of graph is propagated among edges in the graph. We introduce \(A^{k}\) (the k power of A) to describe the k-step edge weights which indicate the relationship of k-step neighboring nodes in the graph. In order to better capture more nodes and global graph information, we combine different powers of A into a single multi-power adjacency matrix \({\hat{A}}_{ok}\).

$$\begin{aligned} {\hat{A}}_{ok}&=\beta _{0} {\hat{A}}^{0}+\beta _{13}({\hat{A}}^{1}+{\hat{A}}^{2}+{\hat{A}}^{3})+\beta _{24}({\hat{A}}^{2}+{\hat{A}}^{3}+{\hat{A}}^{4}) \\ &\quad + \cdots +\beta _{(k-2)k}({\hat{A}}^{k-2}+{\hat{A}}^{k-1}+{\hat{A}}^{k}), \end{aligned}$$
(6)

where \({\hat{A}}_{ok}\) denotes the multi-power adjacency matrix. \({\hat{A}}^{1}\) is normalized adjacency matrix, with \({\hat{A}}^{1}\!=\!{\tilde{D}}^{-\frac{1}{2}}\!{\tilde{A}}{\tilde{D}}^{-\frac{1}{2}}={\tilde{D}}^{-\frac{1}{2}}(A+I){\tilde{D}}^{-\frac{1}{2}}\). Here I and \({\tilde{D}}\) denote identity matrix and the degree matrix of \({\tilde{A}}\), with \({\tilde{D}}_{ii}=\sum _{j}{\tilde{A}}_{ij}\). We provide a higher weight to nodes’s own features via \({\hat{A}}^{0}\) because the own features may be more important, with \({\hat{A}}^{0}=I\). Furthermore, we utilize \({\hat{A}}^{2},{\hat{A}}^{3},\ldots ,{\hat{A}}^{k}\) to obtain two-step and larger step neighbors information in the graph. In order to consider more similarity of adjacent powers of \({\hat{A}}\) and distinguish the difference between other powers of \({\hat{A}}\), we divide different powers of \({\hat{A}}\) as multiple simple groups including \(\{{\hat{A}}^{0}\}, \{{\hat{A}}^{1},{\hat{A}}^{2},{\hat{A}}^{3}\},\{{\hat{A}}^{2},{\hat{A}}^{3},{\hat{A}}^{4}\},\ldots ,\{{\hat{A}}^{k-2},{\hat{A}}^{k-1},{\hat{A}}^{k}\}\) and flexibly adjust the weights of these groups via a series of attention multipliers \(\beta _{0},\beta _{13},\beta _{24},\ldots ,\beta _{(k-2)k}\in R\). By adjusting the weights, we can adjust the contributions of neighboring nodes at different distances. Each group except \({\hat{A}}^{0}\) leverages and shares the information of same groups. This can be regarded as an attention mechanism with simple grouping. We combine all groups with these attention multipliers to obtain much information and learn global graph topology.

Theorem 1

Multi-power adjacency matrix is an operator of preserving graph topology.

Proof

Let \({\hat{A}}^{0}\in R^{n\times n}\) (n nodes), then \({\hat{A}}^{0}=I\in R^{n\times n}, {\hat{A}}^{1},{\hat{A}}^{2},\ldots ,{\hat{A}}^{k}\in R^{n\times n}\), and \({\hat{A}}_{ok} =\beta _{0}{\hat{A}}^{0}+\beta _{13}({\hat{A}}^{1}+{\hat{A}}^{2}+{\hat{A}}^{3})+\beta _{24}({\hat{A}}^{2}+{\hat{A}}^{3}+{\hat{A}}^{4})+\cdots +\beta _{(k-2)k}({\hat{A}}^{k-2}+{\hat{A}}^{k-1}+{\hat{A}}^{k})\in R^{n\times n}\). Equation (6) shows that multi-power adjacency matrix is element-wise operation. Obviously, the spatial location of \({\hat{A}}_{ok}\) is the same as \({\hat{A}}\), thus preserving the topology of the graph.

Equation (6) and Theorem 1 show that our multi-power adjacency matrix can capture more nodes and global graph information while preserving the graph topology.

Multi-step feature propagation Given the node feature matrix X, the feature propagation of graph convolution in GCN is defined as follows:

$$\begin{aligned} H_{1} = {\hat{A}}X. \end{aligned}$$
(7)

Equation (7) shows that the feature propagation propagates node information to one-step neighboring nodes as well as the node itself via \({\hat{A}}\). However, the feature propagation fails to obtain two-step and larger step neighboring nodes information. To circumvent the limits, we design a novel multi-step feature propagation scheme in Eq. (8).

$$\begin{aligned} H_{ok} = {\hat{A}}_{ok}X. \end{aligned}$$
(8)

Instead of propagating one-step neighboring nodes information, our multi-step feature propagation can capture the information of k-steps nodes while keeping larger receptive field.

Multi-step linear transformation After the multi-step feature propagation, a multi-step linear transformation is applied to the \(H_{ok}\) by \(H_{ok}W\).

$$\begin{aligned} Y_{ok} = {H}_{ok}W, \end{aligned}$$
(9)

where W denotes weight matrix which is shared among all nodes.

Based on Eqs. (8) and (9), we conclude that our multi-step graph convolution takes the following form:

$$\begin{aligned} Y_{ok} = {\hat{A}}_{ok}XW. \end{aligned}$$
(10)

Our algorithm is summarized in Algorithm 1. Existing convolutions generally only aggregate neighborhoods information at up to four-steps distances, however our convolution with large k-steps can simultaneously capture neighborhoods information at more distant distances. Specifically, compared with GCN’s convolution that can only capture one-step neighboring nodes information, our multi-step graph convolution can capture the high-order interaction information between neighboring nodes. Compared with SGC’s convolution that can not distinguish the features information of neighboring nodes at various distances, our multi-step graph convolution can adjust the contributions of these features information and obtain more nodes information and better learn global graph topology.

figure a

3.3 Output layer

Similar to GCN, we predict the label of nodes using a softmax classifier. The output prediction \(Y_{\text{MulStepNET}}\) can be expressed as:

$$\begin{aligned} Y_{\text{MulStepNET}} = \text{softmax}(\text{ReLU}(Y_{ok})). \end{aligned}$$
(11)

We follow the loss function from Kipf and Welling (2017).

3.4 Analysis of complexity and parameters

Since the calculation of \(H_{ok}\) requires no weight, we calculate \(H_{ok}={\hat{A}}_{ok}X\) in a feature preprocessing step. That is, we can regard \(H_{ok}\) as a fixed feature extractor, then our calculation is very efficient. As described in Sect. 3.2, if \({\hat{A}}\in {\mathbb {R}}^{n\times n}\), \(X\in {\mathbb {R}}^{n\times c_{0}}\), \(W\in {\mathbb {R}}^{c_{0}\times c_{1}}\) (\(c_{1}\) filters). Then \({\hat{A}}_{ok}\in {\mathbb {R}}^{n\times n}\), \(H_{ok}\in {\mathbb {R}}^{n\times c_{0}}\), \(Y_{ok}=H_{ok}W\in {\mathbb {R}}^{n\times c_{1}}\). In our model, \(c_{1}\) is the number of classes. The proposed MulStepNET architecture takes \(O (n\times c_{0}\times c_{1})\) computational time and \(O (c_{0}\times c_{1})\) parameters. The complexity and parameters are the same as SGC. Obviously, our MulStepNET takes fewer computations and parameters due to without hidden layer, when compared to GCN. To the best of our knowledge, our MulStepNET and SGC achieve the best performance in terms of computational time and parameters.

4 Experiments

In this section, we perform experiments on citation network datasets to evaluate the performance of our MulStepNET in terms of prediction accuracy and stability. We compare our MulStepNET against recent state-of-the-art approaches including graph networks and high-order graph convolutions in terms of classification accuracy, complexity, and parameters on benchmark datasets. Further, we conduct experiments using different k to investigate the relationship between model width and prediction accuracy. In addition, we prove that own node features are more important for prediction. Lastly, we investigate the influence of attention multipliers and show the significant trends of the proposed method.

Table 1 Dataset statistics
Full size table

4.1 Datasets

To prove the expressive power of the proposed MulStepNET to learn global graph topology, we evaluate on citation network datasets chosen from benchmarks commonly used on semi-supervised node classification tasks. The datasets are: Pubmed, Cora, and Citeseer (Kipf and Welling 2017). Following Kipf and Welling (2017) and Yang et al. (2016), we summarize the statistics of the datasets as shown in Table 1.

4.2 Baselines and experimental setting

In the performance comparison on semi-supervised node classification tasks, we consider baselines based on graph networks as well as recent high-order graph convolution methods. These graph networks are: Diffusion Convolutional Neural Networks (DCNN) (Atwood and Towsley 2016), Gated Graph Neural Networks (GGNN) (Li et al. 2015), Graph Convolutional Networks with Chebyshev (ChebNet) (Defferrard et al. 2016), Message Passing Neural Networks (MPNN) (Gilmer et al. 2017), Graph Convolutional Network (GCN) (Kipf and Welling 2017), and Graph Attention Networks (GAT) (Veličković et al. 2018). These high-order graph convolution methods include Adaptive Lanczos Network (AdaLNet) (Liao et al. 2019), Learned MixHop (MixHop-learn) (Abu-El-Haija et al. 2019b), Lanczos Network (LNet) (Liao et al. 2019), and Simple Graph Convolution (SGC) (Wu et al. 2019).

We run all experiments using Adam optimizer with the learning rate. We now report the hyperparameters that are optimized repeatedly. Instead of using dropout in GCN, we remove dropout and set learning rate to 0.01 for Pubmed and Citeseer. To improve stability and prediction accuracy, the learning rate and dropout are set to 0.0003 and 0.95 on Cora. Besides, we apply 0.005, 0.0005, 0.0008 L2 regularization factors to avoid over-fitting on Pubmed, Cora, and Citeseer. We train 290, 43,000, 2000 epochs on Pubmed, Cora, Citeseer, respectively. We fine-tune the highest power (k power) of the adjacency matrix \({\hat{A}}\) to achieve better prediction performance on all datasets. We set k to 21, k to 8, k to 4 on Pubmed, Cora, and Citeseer, respectively. In our MulStepNET, we set these attention multipliers \(\beta _{0},\beta _{13},\beta _{24},\ldots ,\beta _{(k-2)k}\) to suitable values, with \(\beta _{0}=1.5\), \(\beta _{13}=0.8\), \(\beta _{24}=0.09\), \(\beta _{35}=0.2\), \(\beta _{46}=0.2\), \(\beta _{79}=0.4\), \(\beta _{11\cdot 13}=0.25\), \(\beta _{12\cdot 14}=0.25\), \(\beta _{13\cdot 15}=0.2\), \(\beta _{14\cdot 16}=0.2\), \(\beta _{15\cdot 17}=0.5\), other \(\beta =0.3\) on Pubmed, with \(\beta _{0}=1.5\), \(\beta _{13}=1.7\), \(\beta _{57}=0.6\), \(\beta _{68}=0.4\), other \(\beta =0.3\) on Cora, with \(\beta _{0}=0.8\), \(\beta _{13}=0.925\), \(\beta _{24}=0.5\) on Citeseer. With the above parameter settings, early stop is not adopted in all experiments due to very stable experimental results.

4.3 Results analysis

Based on Eqs. (12) and (13), we obtain the average test accuracy \({\overline{acc}}\) and standard deviation S of the proposed models.

$$\begin{aligned} {\overline{acc}} = \frac{\sum \nolimits _{i=1}^macc_i}{m} \,, \end{aligned}$$
(12)

where \({\overline{acc}}\) is the test accuracy of the ith run, and m is the number of runs.

$$\begin{aligned} S = \sqrt{\frac{\sum \nolimits _{i=1}^m(acc_i-{\overline{acc}})^{2}}{m-1}} \,. \end{aligned}$$
(13)
Table 2 Comparison with graph networks and high-order graph convolution methods on citation networks (in percent)
Full size table
Table 3 Comparison of computational complexity and the number of parameters
Full size table
Fig. 3
figure 3

Influence of model width (the highest power of \({\hat{A}}\), namely k) and own features (\({\hat{A}}^{0}\)) on node classification accuracy. MulStepNET-a denotes MulStepNET without simple grouping, attention mechanism, and \({\hat{A}}^{0}\), then \({\hat{A}}_{0k}={\hat{A}}^{1}+{\hat{A}}^{2}+\cdots ,+{\hat{A}}^{k}\). MulStepNET-b denotes MulStepNET without simple grouping and attention mechanism, then \({\hat{A}}_{0k}={\hat{A}}^{0}+{\hat{A}}^{1}+{\hat{A}}^{2}+\cdots ,+{\hat{A}}^{k}\)

Full size image
Table 4 Comparison of MulStepNET with and without \({\hat{A}}^{0}\)
Full size table
Table 5 Comparison of MulStepNET with and without attention multipliers
Full size table
Fig. 4
figure 4

Results of MulStepNET, MulStepNET without \({\hat{A}}^{0}\), and MulStepNET without attention on citation network datasets

Full size image

We compare our MulStepNET against graph networks and high-order graph convolution methods on citation networks, and the results are summarized in Table 2. Based on the results, we observe that our MulStepNET achieves the best performance including classification accuracy and stability among the state-of-the-art approaches (except SGC) on all datasets. Our MulStepNET obtains the highest prediction accuracy of 81.1, 83.7, 73.4% and very low standard deviation of 0.0, 0.1, 0.0% on Pubmed, Cora, and Citeseer respectively. In terms of accuracy comparison on all datasets, our MulStepNET improves over GCN by 2.7, 2.7, and 4.4%, improves over GAT by 2.7, 0.8, and 1.2%, and improves over SGC by 2.8, 3.3, and 2.1% respectively. Compared with SGC, our MulStepNET achieves competitive performance in terms of stability while significantly improving accuracy. Due to the smaller standard deviation in the proposed model, our MulStepNET outperforms other baselines by a large margin in terms of stability. These results demonstrate the effectiveness of MulStepNET for capturing nodes information and global graph topology.

Similar to He and Sun (2015), we use theoretical time complexity to describe the complexity, rather than the actual running time, since the actual running time is sensitive to hardware and implementations. Table 3 shows the results of the proposed MulStepNET and competing methods in terms of complexity and parameters (see Sect. 3.4 for analysis). In terms of complexity and parameters, our MulStepNET achieves as good performance as SGC, and consistently outperforms other methods. These results show the superiority for designing one-layer model.

To investigate the influence of model width and \({\hat{A}}^{0}\), we conduct these experiments using different k for our MulStepNET-a and MulStepNET-b on Pubmed, Cora, and Citeseer datasets respectively. The results are summarized in Fig. 3. We observe that our MulStepNET-a can improve accuracy as model goes wider (increase k) until the width (k) of 21, 5, and 4 on Pubmed, Cora, and Citeseer respectively. Similarly, the width becomes 21, 8, and 4 for MulStepNET-b on respective datasets. Since MulStepNET-a and MulStepNET-b with wider model may mix the features from different clusters, they hurt the performance. Compared to MulStepNET-a, MulStepNET-b with \({\hat{A}}^{0}\) significantly improves performance in most cases. This proves that the own features are more important for classification. Based on the comparison results, we determine the best model width and demonstrate the importance of own node features for designing model.

We conduct experiments based on whether MulStepNET has \({\hat{A}}^{0}\). Table 4 lists the comparison results. We can observe from the results that MulStepNET outperforms MulStepNET without \({\hat{A}}^{0}\) by margins of 1.1, 1.1 and 1.4% on Pubmed, Cora, and Citeseer respectively, which further demonstrates the contribution of own node features to performance improvement.

To investigate the influence of attention multipliers, we remove all attention multipliers from MulStepNET while keeping other settings. Table 5 lists the comparison results between MulStepNET with and without attention multipliers. The results show that MulStepNET performs better. This demonstrates the benefits of the attention multipliers.

Figure 4 shows the classification accuracy of MulStepNET, MulStepNET without \({\hat{A}}^{0}\), and MulStepNET without attention (\(\beta\)) on all three datasets, respectively. It is obviously to see that MulStepNET outperforms MulStepNET without \({\hat{A}}^{0}\) and MulStepNET without attention in terms of average accuracy and the overall trend of MulStepNET is better than MulStepNET without \({\hat{A}}^{0}\) and MulStepNET without attention. On Citeseer, the accuracy of MulStepNET is 1.9% (average value) and 1.0% (average value) higher than the classification result of MulStepNET without \({\hat{A}}^{0}\) and MulStepNET without attention, respectively. This further verifies the contribution of own node features and the attention multipliers to performance improvement.

5 Conclusion

In this paper, we propose a stronger multi-step graph convolutional network architecture, MulStepNET, on graph-structured data. Notably, our MulStepNET can obtain more nodes features information and enable adequate information propagation via multi-power adjacency matrix. Further, by precomputing the fixed feature extractor \(H_{ok}\), our computations are more efficient than GCN. Experiments on several graph classification benchmarks show natural advantages for capturing node features and entire graph structure information. We observe that our MulStepNET with the fewest parameters achieves better performance as compared to baselines. In the future, we would apply the proposed model to more application areas such as social networks.