Introduction

The geodetic vertical control at the Hong Kong territories is currently realized by heights of levelling benchmarks defined in the Hong Kong Principal Datum (HKPD). Since heights of HKPD benchmarks were determined from levelling data without involving the gravity information, these heights are neither normal nor orthometric. It was assumed that the realization of a geodetic vertical control over a relatively small area could be carried out by a least-squares adjustment of only measured levelling height differences. However, Nsiah Ababio and Tenzer (2022a) demonstrated that errors due to disregarding the gravity information in Hong Kong are quite large, varying roughly within ± 2 cm. To address this issue, they used ground and marine gravity measurements to interpolate gravity values along levelling lines and then applied the orthometric correction to measured (geometric) height differences in order to determine the Helmert orthometric heights at levelling benchmarks. The newly readjusted levelling network was presented as the Vertical Control Network 2022 (VCN2022). Following this practical development, Nsiah Ababio and Tenzer (2022b) used marine and ground gravity data to determine a detailed gravimetric geoid model at the Hong Kong territories. Consequently, they used the newly determined Helmert orthometric heights at GNSS-levelling (Global Navigation Satellite System-levelling) benchmarks to fit the gravimetric geoid model with the geometric geoidal heights (defined as the differences between the geodetic heights and the Helmert orthometric heights). In this way, the new geoid model is fully compatible with the Helmert orthometric heights. The final result was presented as the geoid model HKGEOID-2022.

The Molodensky (1945, 1948) normal heights and the Helmert (1884, 1890) orthometric heights are the most commonly used types of heights for a practical realization of geodetic vertical controls in countries where gravity along levelling lines are measured. In countries, where surface gravity values along levelling lines are not available, normal gravity values could be used to approximate measured (actual) surface gravity values along levelling lines. Heights of levelling benchmarks are—in this case—defined by normal-orthometric heights (e.g., Heiskanen and Moritz 1967). In recent decades, the international geodetic community, particualry the International Height Reference Frame working group of the International Association of Geodesy (IAG), has been focusing on unification of vertical datums established in different countries and territories around the world. Vertical datum unification often requires a conversion between different types of heights. The conversion of normal-orthometric heights to normal heights is done by applying the cumulative normal to normal-orthometric height correction. This correction is computed as a sum of the product of levelled height differences and surface gravity disturbances (Filmer et al. 2010), or more accurately as a function of the surface gravity anomalies (Tenzer et al. 2011a, b). Both gravity data types can be either computed from a global geopotential model or interpolated from terrestrial gravity measurements covering a region (or country) where a levelling network is established. In the last few decades, significant effort has been dedicated to cover large areas of the world with new gravity data by ground, shipborne, and airborne gravimetry campaigns. The gravity information along levelling lines could then be interpolated and consequently used to convert levelled height differences to either normal or orthometric height differences by applying the normal or orthometric corrections, respectively.

The conversion between normal-orthometric and normal heights is relatively rare. The conversion between normal and orthometric heights is, on the other hand, done not only in scientific studies but also for practical purposes. This height conversion is realized by applying the geoid-to-quasigeoid separation either to normal or orthometric heights. A particular example could be given for the realization of large infrastructure or hydrological projects between countries with different types of heights adopted for the official realization of their vertical geodetic controls. In this case, levelling networks are often physically connected, readjusted, and redefined in a particular system of heights. The application of the geoid-to-quasigeoid separation is even more often used for the conversion between geoid and quasigeoid models, mainly for vertical datum unification on a global or continental scale as well as between neighboring countries.

In Helmert’s definition of orthometric heights the Poincaré-Prey gravity gradient (i.e., reduction) is used to compute the mean gravity along the plumbline between the geoid and the topographic surface (i.e., within the topography). According to Helmert’s definition, the actual gravity gradient inside the topography (applied to reduce the observed surface gravity approximately to a mid-point along the plumbline between the topographic surface and the geoid) is approximated by the normal gravity gradient and the Poisson equation (to account for the effect of topographic mass density). Gravity gradient changes attributed to terrain geometry, topographic density variations, and density heterogeneities below the geoid surface (i.e., the non-topographic effect) are, however, disregarded. Since the Helmert orthometric heights are until now solely used for the practical realization of vertical geodetic controls in countries where orthometric heights are officially adopted, the conversion between orthometric and normal heights as well as between geoid and quasigeoid models is done by applying the geoid-to-quasigeoid separation that is defined approximately as a function of the Poincaré-Prey gravity gradient. This approximation yields the expression for computing the geoid-to-quasigeoid separation from the simple (incomplete) planar Bouguer gravity anomalies (cf. Heiskanen and Moritz 1967, Eq. 8–103).

Several authors proposed and tested more numerically accurate methods of computing the geoid-to-quasigeoid separation and orthometric heights. Niethammer (1932, 1939), Mader (1954), Wirth (1990), Rapp (1997), Marti (2005), Hofmann-Wellonhof and Moritz (2005), and Flury and Rummel (2009) applied the correction for a (planar) terrain geometry to the mean gravity. Tenzer and Vaníček (2003) inspected the corresponding correction for an anomalous (lateral) topographic density numerically. Sjöberg (1999, 2006, 2010), Tenzer (2004), Tenzer et al. (2005, 2006, 2015, 2020), and Foroughi and Tenzer (2017) developed and tested accurate methods of computing the geoid-to-quasigeoid separation and orthometric heights by taking into consideration also the non-topographic effect.

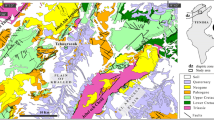
The average upper continental crustal density of 2670 kg⋅m−3 (Hinze 2003) is typically adopted to represent the constant topographic density in gravimetric geoid modelling and orthometric height determination. Nsiah Ababio and Tenzer (2023) inspected how realistically this density value represents the actual geological setting in Hong Kong, which is formed mostly by light volcanic rocks and sedimentary deposits. They used the geological map of Hong Kong and rock density samples to compile the digital rock density model. According to their estimates, the rock densities in Hong Kong vary from 2101 to 2681 kg⋅m−3, with an average value of 2303 kg⋅m−3. This relatively low density reflects the geological setting with roughly 50% of the Hong Kong territories covered by volcanic rocks that are mainly composed of bulk sequences of tuff (a highly porous rock of a relatively low density). Sedimentary rocks are also characterized by low density. The estimated average density of 2303 kg⋅m−3 differs significantly from the value of 2670 kg⋅m−3. It is thus useful to compute the geoid-to-quasigeoid separation for the average density of 2303 kg⋅m−3 instead of using a commonly adopted value. Even more appropriate is to use the digital rock density model to compute the correction for lateral topographic density and apply it to the geoid-to-quasigeoid separation. This approach was used before by Tenzer and Vaníček (2003) to improve the accuracy of Helmert orthometric heights. The rock density model is obviously also needed for an accurate determination of orthometric heights. It is worth noting that, if the accurate method were to be used to adjust levelled heights, the geoid model would need to be determined using the spatially varying topographic density model in gravity reductions for it to be appropriate for combination with corresponding levelled heights.

In this study, we computed the geoid-to-quasigeoid separation at the Hong Kong territories by applying approximate and accurate methods. The accurate computation was carried out according to expressions derived by Sjöberg (2010). Both methods are briefly recapitulated in Section 2. Input datasets are reviewed in Section 3. Results are presented and discussed in Section 4. The study is concluded in Section 5.

Geoid-to-quasigeoid separation

This section summarizes expressions used to compute the geoid-to-quasigeoid separation approximately and accurately.

Approximate method

According to the “classical” method, the geoid-to-quasigeoid separation \(\chi^{\prime}\) is computed approximately from the Bouguer gravity data using the following formula (cf. Heiskanen and Moritz 1967; Eq. 8–103)

$$\chi^{\prime} \approx \frac{{\Delta g^{{\text{B}}} }}{{\gamma_{0} }}H,$$
(1)

where \(H\) is the topographic height of a point, \(\Delta g^{{\text{B}}}\) is the simple planar Bouguer gravity anomaly, and \(\gamma_{0}\) is the normal gravity value at the ellipsoid surface.

The simple Bouguer gravity anomaly \(\Delta g^{{\text{B}}}\) is computed from the free-air gravity anomaly \(\Delta g^{{{\text{FA}}}}\) by applying the Bouguer gravity reduction \(2\pi G\rho H\), so that

$$\Delta g^{{\text{B}}} = \Delta g^{{{\text{FA}}}} - 2\pi G\rho_{0} H,$$
(2)

where \({\text{G}}\) is the universal gravitational constant, and \(\rho_{0}\) is the average topographic density.

By substituting from Eq. (2) back to Eq. (1), we arrive at

$$\chi^{\prime} = \frac{{\Delta g^{{{\text{FA}}}} }}{{\gamma_{0} }}H - \frac{{2\pi G\rho_{0} }}{{\gamma_{0} }}H^{2} .$$
(3)

Since the Bouguer gravity reduction in Eq. (3) is computed for the average topographic density \(\rho_{0}\) of 2670 kg⋅m−3, we applied the correction \(\delta \chi^{\prime}\) for anomalous (lateral) density variations. It reads

$$\delta \chi^{\prime} = - \frac{2\pi G\Delta \rho }{{\gamma_{0} }}H^{2} ,$$
(4)

where \(\Delta \rho\) denotes the anomalous topographic density that is defined as the actual density \(\rho\) minus the average topographic density \(\rho_{0}\); i.e., \(\Delta \rho = \rho - \rho_{0}\).

The application of the correction \(\delta \chi^{\prime}\) from Eq. (4) to Eq. (3) yields the following expression

$$\chi^{\prime} = \frac{{\Delta g^{{{\text{FA}}}} }}{{\gamma_{0} }}H - \frac{2\pi G}{{\gamma_{0} }}H^{2} (\rho_{0} + \Delta \rho ).$$
(5)

The expression in Eq. (5) defines the geoid-to-quasigeoid separation corrected for the effect of anomalous topographic density variations. In this approximate definition the terrain geometry and the non-topographic effect are still disregarded.

Accurate method

Sjöberg (2010) derived the expression for an accurate computation of the geoid-to-quasigeoid separation \(\chi\) in the following form

$$\chi \approx \frac{{\Delta g^{{\text{B}}} }}{{\gamma_{0} }}H + TC + GC,$$
(6)

where \(TC\) denotes the topographic correction term, and \(GC\) is the gravimetric correction term.

As seen in Eq. (6), the first term on the right-hand side is identical with the approximate definition of the geoid-to-quasigeoid separation in Eq. (1) that is described as a function of the simple planar Bouguer gravity anomaly \(\Delta g^{{\text{B}}}\) and the height \(H\) of the computation point. To obtain an accurate result, two correction terms are added, specifically the topographic correction \(TC\) and the gravimetric correction \(GC\) in Eq. (6).

The topographic correction \(TC\) is computed from (Sjöberg 2010; Eq. 16)

$$TC \approx \frac{{V_{g}^{T} - V_{t}^{T} }}{{\overline{\gamma }}}\left( {1 - \frac{H}{R}} \right),$$
(7)

where \(V_{g}^{T} {\text{ and }}V_{t}^{T}\) are the topographic potentials computed on the geoid and at the topographic surface respectively, and R is the Earth’s mean radius. It should be noted that the factor \(H/R\) in Eq. (7) is disregarded as it does not exceed 10–3 (cf. Sjöberg 2010).

The topographic potential \(V_{t}^{T}\) for a constant topographic density \({\uprho }\) is evaluated at the topographic surface point by solving the Newton volume integral in the following form (e.g., Kellogg 1967)

$$V_{t}^{T} \cong {\text{G}}\;{\uprho }\iint\limits_{\Phi } {\int_{{\;r^{\prime} = {\text{R}}}}^{{\;{\text{R}} + H^{\prime}}} {\ell^{ - 1} (r_{t} ,\psi ,R)\;} r^{{\prime}{2}} \;dr^{\prime}d}\Omega^{\prime},$$
(8)

where \(\ell {\kern 1pt}\) is the Euclidean spatial distance between computation and integration points defined for the spherical distance \(\psi\); \(r_{t}\) is the geocentric radius of computation point at the topographic surface, i.e., \(r_{t} = R + H\); \(d\Omega^{\prime} = \cos \varphi^{\prime}\,d\varphi^{\prime}\,d\lambda^{\prime}\) is an infinitesimal surface element described in the coordinate frame of spherical coordinates \(\varphi\) and \(\lambda\); and \(\Phi = \left\{ {\Omega^{\prime} = \left( {\varphi^{\prime},\lambda^{\prime}} \right):} \right.\) \(\left. {\varphi^{\prime} \in \left[ { - {\uppi }/2,\,{\uppi }/2} \right] \wedge \lambda^{\prime} \in \left[ {\left. {0,\,2{\uppi }} \right)} \right.} \right\}\) is a full spatial angle. The Earth’s spherical approximation is adopted to define the Newton integral in Eq. (8). Novák and Grafarend (2005) formulated the ellipsoidal representation of the topographic potential and attraction. Vajda et al. (2008) proposed the concept of ellipsoid-referenced topographic gravity corrections. The computation of topographic potential \(V_{g}^{T}\) on the geoid is again realized by solving the Newton volume integral in Eq. (8), but in this case the geocentric radius \(r_{t}\) (in \(\ell {\kern 1pt}\)) is replaced by the geocentric radius of the geoid \(r_{g} = R\) (in the Earth’s spherical approximation).

The gravimetric correction \(GC\) in Eq. (6) is computed as follows

$$GC = \frac{{\delta \overline{g}^{{\text{B}}} - \delta g_{t}^{{\text{B}}} }}{{\overline{\gamma }}}H$$
(9)

where \(\delta \overline{g}^{{\text{B}}}\) is the mean value of the Bouguer gravity disturbance (within the topography between sea level and the height of the computation point), and \(\delta g_{t}^{{\text{B}}}\) is the Bouguer gravity disturbance computed at the topographic surface.

Values of \(\delta g_{t}^{{\text{B}}}\) and \(\delta \overline{g}^{{\text{B}}}\) are defined by

$$\delta g_{t}^{{\text{B}}} = g_{t} - \gamma_{t} - g_{t}^{T} ,$$
(10)
$$\delta \overline{g}_{{}}^{{\text{B}}} = \frac{1}{H}\int\limits_{0}^{{H_{P} }} {\delta g_{{}}^{B} } dH \cong \Delta g_{t}^{{\text{B}}} - \frac{{V_{g}^{T} - V_{t}^{T} }}{H},$$
(11)

where \(\Delta g_{t}^{{\text{B}}}\) is the simple Bouguer gravity anomaly (see Eq. 2), and \(g_{t}^{T} \cong - \partial V_{t}^{T} /\partial r\) is the topographic attraction computed at the topographic surface. The gravity value \(g_{t}\) is measured at the topographic surface, and the corresponding normal gravity \(\gamma_{t}\) is computed from

$$\gamma_{t} = \gamma_{0} \left[ {1 - 2\left( {1 + f{ + }m \, - \, f{\text{ sin}}^{2} \varphi } \right)\frac{h}{a} + 3\left( \frac{h}{a} \right)^{2} } \right],$$
(12)

where \(f = \left( {a - b} \right)/a\) is the linear flattening of the reference ellipsoid (\(a\) and \(b\) denote the semi-major and semi-minor axes of the reference ellipsoid respectively), \(m = \omega^{2} \,a^{2} b/GM\) is the Clairaut constant, and the geodetic (ellipsoidal) height h is defined by

$$h = H + N,$$
(13)

where \(N\) is the geoid height.

Sjöberg (2006) derived the expression to compute the effect \(\delta \chi\) of anomalous topographic density in the following form

$$\delta \chi = - \frac{2\pi G\Delta \rho }{{\gamma_{0} }}\left( {H^{2} + \frac{{2H^{3} }}{3R}} \right).$$
(14)

The expression (for \(\delta \chi\)) in Eq. (14) is the same as the expression (for \(\delta \chi^{\prime}\)) in Eq. (4), except for the additional term \(2H^{3} /3R\) in the brackets that can be disregarded.

Data acquisition

This section summarizes gravity, levelling, terrain, and rock density datasets used to compute the geoid-to-quasigeoid separation.

Gravity data

The Hong Kong territories, covering a total area of about 1100 km2, are characterized by a moderately rough topography with maximum elevations reaching 957 m (Tai Mo Shan). A regional gravity survey was conducted across the territory in 1991 by the Electronic and Geophysical Services Ltd (EGS). A total of 640 gravity measurements were made in Hong Kong (EGS 1991) comprising 507 ground measurements and 133 offshore shipborne measurements, spaced at approximately 2–4 km and 2 km apart, respectively. Gravity sites were accessed by either vehicles or helicopters and observations were done with the Lacoste and Romberg G relative gravimeter. Similarly, the marine model H/U seabed gravimeter was employed to record shipborne gravity readings. Topographic heights of gravity sites were referred to the Hong Kong Principal Datum (HKPD). Locations of gravity sites are shown in Fig. 1. The observed gravity values were connected with the International Gravity Standardization Net 1971 (IGSN71) with the accuracy of about ± 0.03 mGal (Evans 1990). To increase the spatial resolution of the offshore gravity dataset, Nsiah Ababio and Tenzer (2022b) used the marine gravity data prepared by Sandwell et al. (2013) based on processing the along-track data from the CryoSat-2, Envisat, and Jason-1 altimetry satellites. The comparison of shipborne gravity measurements with altimetry-derived marine gravity values revealed their relatively good agreement with no apparent systematic bias (0.07 mGal), and a root-mean-square (RMS) of differences of ± 3.2 mGal (cf. Nsiah Ababio and Tenzer 2022b).

Fig. 1
figure 1

Gravity data distribution at the Hong Kong territories consisting of ground, shipborne, and altimetry-derived marine gravity data

Full size image

Levelling data

To inspect the result, we used the VCN2022 orthometric and normal heights determined at levelling benchmarks. The VCN2022 was presented as the final result after the application of orthometric and normal corrections to measured levelled height differences and subsequent readjustments of entire levelling network individually for normal and orthometric height differences. The VCN2022 levelling network consists of 1069 benchmarks, all of them situated at elevations below 500 m. The VCN2022 levelling network is shown in Fig. 2. The accuracy of VCN2022 orthometric and normal heights was estimated to be ± 1–2 cm (Nsiah Ababio and Tenzer 2022a).

Fig. 2
figure 2

Topography and the configuration of the VCN2022 levelling network at the Hong Kong territories

Full size image

Digital elevation model

The Shuttle Radar Topography Mission digital elevation model (SRTM DEM) with a spatial resolution of 1″ × 1″ (approximately 30 m) was used to compute the geoid-to-quasigeoid separation and the Bouguer gravity anomalies. The topography is shown in Fig. 2.

Digital rock density model

We used the detailed rock density model developed by Nsiah Ababio and Tenzer (2023) to estimate the effect of (lateral) anomalous density variations on the geoid-to-quasigeoid separation. The density model compiled on a 2″ × 2″ grid is shown in Fig. 3.

Fig. 3
figure 3

Rock density variations at the Hong Kong territories (Nsiah Ababio and Tenzer 2023)

Full size image

Results

This section presents numerical results. We first show the results of gravity data interpolation and then approximate and accurate values of the geoid-to-quasigeoid separation.

Gravity anomalies

Since the Bouguer gravity anomalies are smoother than the free-air gravity anomalies, we first computed them from the observed free-air gravity anomalies and then interpolated the Bouguer gravity anomalies on a 1’ × 1’ grid. Finally, we converted the interpolated Bouguer gravity anomalies to the free-air gravity anomalies on a 1’ × 1’ grid. The conversion between the free-air and Bouguer gravity anomalies was done by applying the simple planar Bouguer gravity reduction, while disregarding the terrain relief because of a good gravity data coverage (cf. Janak and Vaníček 2005). The Bouguer gravity reduction was computed using SRTM DEM heights and adopting the constant average topographic density of 2670 kg⋅m−3. We note here that results of numerical analysis not presented here in detail revealed that the gravity data interpolation by using only the simple (incomplete) planar Bouguer gravity anomalies is sufficient for this purpose. We found that differences in interpolated free-air gravity values (with and without considering terrain relief and topographic density variations) are less than ± 5 mGal within the Hong Kong territories. Consequently, these gravity differences correspond to orthometric height differences less than ± 1 mm. The Bouguer and free-air gravity anomalies (between latitudes 25.56° and 22.15° and longitudes 113.83° and 114.50°) are plotted in Figs. 4 and 5 respectively, with their statistics in Table 1.

Fig. 4
figure 4

The Bouguer gravity anomalies at the Hong Kong territories on a 1’ × 1’ grid

Full size image
Fig. 5
figure 5

The free-air gravity anomalies at the Hong Kong territories on a 1’ × 1’ grid

Full size image
Table 1 Statistics of the Bouguer and free-air gravity anomalies
Full size table

The geoid-to-quasigeoid separation

Based on the classical definition in Eq. (1), we computed the geoid-to-quasigeoid separation approximately from the simple Bouguer gravity anomalies. We then calculated the geoid-to-quasigeoid separation accurately according to Sjöberg (2010) by applying the topographic and gravimetric correction terms to approximate values of the geoid-to-quasigeoid separation (Eq. 6). Finally, we assessed the effect of anomalous topographic density on the geoid-to-quasigeoid separation.

The approximate and accurate values of the geoid-to-quasigeoid separation computed according to Eqs. (1) and (6) are presented in Figs. 6 and 7, and their statistical summaries are given in Table 2. As seen in Fig. 6, approximate values of the geoid-to-quasigeoid separation are everywhere negative and reach maximum negative values of -2.8 cm. The accurately computed values have a similar spatial pattern, but reach larger negative values up to -5.7 cm (see Fig. 7c). To better understand large discrepancies between accurate and approximate values, we plotted also the topographic and gravimetric correction terms that are disregarded in the classical definition of Eq. (1). As seen in Fig. 7a, the topographic correction term is closely correlated spatially with the topography and varies between -2.9 cm and 0.3 cm. The gravimetric correction term is everywhere negative and reaches maximum negative values of only -0.02 cm (see Fig. 7b). Both, the approximate value and the topographic correction are thus largely negative while also highly correlated spatially with topographic elevations, while the gravimetric correction is completely negligible. Consequently, the accurate values of the geoid-to-quasigeoid separation at the Hong Kong territories reach large negative values (-5.7 cm) at high topographic elevations.

Fig. 6
figure 6

The geoid-to-quasigeoid separation computed approximately (Eq. 1)

Full size image
Fig. 7
figure 7

The geoid-to-quasigeoid separation computed using the accurate (Sjöberg) method (Eq. 6): (a) the topographic correction, (b) the gravimetric correction, and (c) the geoid-to-quasigeoid separation

Full size image
Table 2 Statistics of the geoid-to-quasigeoid separation computed approximately (Eq. 1) and accurately (Eq. 6) using the global average topographic density (2670 kg⋅m−3)
Full size table

To check the reliability of our result, we inspected values of this separation computed over the elevated topography in Himalaya and Tibet by Foroughi and Tenzer (2017). They demonstrated that the geoid-to-quasigeoid separation reach large negative values over most of the elevated topography, while positive values are mainly distributed along the Himalayan foothills.

For the average topographic density of 2670 kg⋅m−3 the anomalous lateral density at the Hong Kong territories varies between -569 and 11 kg⋅m−3 with an average value of -334.4 kg⋅m−3 and a standard deviation of ± 234.7 kg⋅m−3. The effect of these anomalous density variations on the geoid-to-quasigeoid separation is mostly positive (see Fig. 8) and reaches a maximum value of 1.6 cm (see Table 3). Prevailing positive values are explained by the fact that the density of rocks at the Hong Kong territories is almost everywhere lower than the average topographic density of 2670 kg⋅m−3. Consequently, approximately and accurately computed values of the geoid-to-quasigeoid separation (Table 2) become smaller (Table 3) after correcting them for the anomalous topographic density term. The approximate and accurate values of the geoid-to-quasigeoid separation obtained after applying the correction for anomalous topographic density are plotted in Fig. 9. It is worth noting that according to numerical estimates by Foroughi and Tenzer (2017), this effect globally varies mostly within ± 2 cm, but eventually reaches ± 20 cm in regions with an extremely elevated topography and a complex geological setting.

Fig. 8
figure 8

The effect of anomalous density on the geoid-to-quasigeoid separation

Full size image
Table 3 The effect of anomalous topographic density on the geoid-to-quasigeoid separation (GQS) at the Hong Kong territories
Full size table
Fig. 9
figure 9

The approximate (a) and accurate (b) values of the geoid-to-quasigeoid separation corrected for the effect of anomalous topographic density

Full size image

Validation of results

As stated, Helmert’s definition is solely used to compute orthometric heights for a practical realization of geodetic vertical controls. The geoid-to-quasigeoid separation is then computed and applied to the Helmert orthometric heights in order to obtain the Molodensky normal heights, and vice versa. The differences between the Molodensky normal and Helmert orthometric heights have to be consistent with the geoid-to-quasigeoid separation (computed approximately). From the VCN2022 solution, the Helmert orthometric and Molodensky normal heights were obtained by applying their respective corrections to levelled height differences (Nsiah Ababio and Tenzer 2022a). The Molodensky normal and Helmert orthometric height differences at the VCN2022 levelling benchmarks are shown in Fig. 10, with the statistical summary in Table 4.

Fig. 10
figure 10

Differences between the Molodensky normal and Helmert orthometric heights at the VCN2022 benchmarks

Full size image
Table 4 Statistics of the Molodensky normal and Helmert orthometric heights at the VCN2022 benchmarks and their differences
Full size table

The differences between the Molodensky normal and Helmert orthometric heights at the VCN2022 benchmarks were compared with values of the geoid-to-quasigeoid separation computed approximately (Eq. 1) and accurately (Eq. 6) but without taking into consideration the anomalous density variations (because this correction was not applied to determine the Helmert orthometric heights at VCN2022 levelling benchmarks). The statistical summary of the results is given in Table 5. As seen, the approximate values of the geoid-to-quasigeoid separation fully agree with the differences between the Molodensky normal and Helmert orthometric heights, while differ significantly (up to 1.6 cm) when accurate values are considered. Note that maximum differences at levelling benchmarks (Table 4) are smaller than maximum differences between the accurate and approximate values of the geoid-to-quasigeoid separation (Table 2) computed on a regular grid. The reason is that heights of all levelling benchmarks are below 500 m, while many grid points reach large heights and consequently larger differences between approximately and accurately computed values.

Table 5 Statistics of differences between the Molodensky normal and Helmert orthometric height differences and the geoid-to-quasigeoid separation computed according to Eqs. (1) and (6) at the VCN2022 levelling benchmarks
Full size table

The agreement between differences between the Molodensky normal and Helmert orthometric heights and values of the geoid-to-quasigeoid separation computed according to Eq. (1) is not surprising because the Poincaré-Prey gravity reduction was used to compute approximately the geoid-to-quasigeoid separation as well as the mean gravity values in Helmert orthometric heights. In contrast, the topographic and gravimetric correction terms applied in the Sjöberg’s method (Eq. 6) considerably modified accurate values of the geoid-to-quasigeoid separation.

Summary and conclusions

We have compared values of the geoid-to-quasigeoid separation computed approximately and accurately (according to the method developed by Sjöberg). The accurate method takes into consideration a terrain geometry, topographic density variations, and the non-topographic effect (due to mass density heterogeneities below the geoid surface) that are disregarded in the approximate definition.

According to our results, the approximate values of the geoid-to-quasigeoid separation at the Hong Kong territories are everywhere negative and reach maximum negative values of -2.8 cm. The corresponding more accurate values (computed for the the average topographic density 2670 kg⋅m−3) are typically negative and reach the largest negative values of -5.7 cm.

Approximate values of the geoid-to-quasigeoid separation are equal to the differences between the Molodensky normal and Helmert orthometric heights at levelling benchmarks. This was explained by the fact that the Helmert orthometric heights were computed by applying the Poincaré-Prey gravity reduction. Equivalently, this reduction is adopted in the classical definition of the geoid-to-quasigeoid separation. The approximate definition, however, yields relatively large errors (due to disregarding a terrain geometry, topographic density variations, and non-topographic effect) already in a region characterized by a moderate topography with heights reaching only several hundreds of meters. It is, therefore, recommended to compute the geoid-to-quasigeoid separation and orthometric heights by applying accurate numerical schemes already in regions with moderately elevated topography.

Since geological setting at the Hong Kong territories is characterized by light volcanic rocks and sediment deposits, the computation of the geoid-to-quasigeoid separation for the commonly adopted average topographic density of 2670 kg⋅m−3 is not appropriate. To address this practical issue, we used the digital rock density model to estimate the effect of anomalous density variations on the geoid-to-quasigeoid separation. According to our result, this effect is mostly positive and reach maximum values of 1.6 cm. The application of this correction modified accurately computed values of the geoid-to-quasigeoid separation. According to our final result, the differences between the geoid and the quasigeoid (i.e., the accurately computed geoid-to-quasigeoid separation) within the Hong Kong territories vary between -4.1 and 0.2 cm.