Measurements and linearized models for golf ball bounce on a green

Abstract

A detailed set of experiments are described that capture over a 1000 different instances of the bounce of a golf ball on a green. Video analysis was used to capture ball’s velocity and spin just before and after each bounce for a wide variety of landing conditions. Data are presented from two different turfs; one artificial and one from a typical tee. Measurement errors and repeatability are analysed. The data are compared to predictions from models of rigid bounce with friction, including Penner’s modification to account for elasto-plasticity. Coefficients of restitution and friction, and Penner’s effective contact angle are fit from the data. A better fit to the data is found using a non-physical piecewise-affine landing to lift-off relationship, which distinguishes between cases that bounce in pure slip from those that undergo rolling. Nevertheless, even balls that undergo rolling are typically found to lift-off slipping, having undergone spin reversal. The findings suggest that further effort needs to be spent on finding simple physics-based models of golf ball bounce on a green.

1 Introduction

Recently, McPhee [1] undertook a comprehensive review of dynamic modelling of the flight of a golf ball. After the impact between club face and ball, the golf shot can be divided into free-flight, bounce and roll phases. Whilst the flight phase is relatively well understood, see e.g. [2], there remains much uncertainty and a paucity of open source data against which to fit a model for the bounce of a golf ball.

Elementary models of ball bounce are based on Newtonian restitution theory, which assumes an instantaneous, rigid bounce during which kinetic energy in normal direction only is dissipated by a constant factor $r^2$, where $0<r<1$ is known as Newton’s (or Poisson’s) coefficient of restitution, see e.g [3, 4]. In many ball sports, such as tennis, football or cricket, such approaches can be improved by modelling the deformation of an elastic ball with a rigid surface, see e.g. [5,6,7,8].

For golf ball–turf interaction, however, the ball is significantly stiffer than the turf, which exhibits viscoelastic behaviour. It is, therefore, common to consider the ball as being a rigid body, and only the turf as having compliance. A simple modification to the rigid bounce theory to account for the viscoelasticity of the turf is that due to Penner [9] who argues that contact forces are equivalent to the bounce against a rigid surface rotated through an angle $\beta$. Based on limited data, Penner proposed an empirical formula for calculating such an angle, depending linearly on inbound angle and speed.

Haake [10] presented the largest data set on golf ball bounce that we are aware of, which is freely available in the public domain. More than 700 measurements were taken, including different inbound conditions and at different golf courses. These data, collected in summer 1987, were used to examine the effectiveness of different viscoelastic models of golf ball bounce. The ball was launched from a modified baseball launcher into a darkened enclosure, where the bounce was recorded using a still camera and a stroboscope. The range of landing angles examined was $34.5^\circ$ to $56.1^\circ$, with the landing speed varying between $16.40$ and $27.9\, \mathrm {m\,s}^{-1}$. The landing spin was varied between $-5,640$ and $6,100$ rotations per minute, with the negative spin indicating a topspin. A two-layer system of springs and dampers was found to show best agreement with the experimental data, yet was unable to predict all features of lift-off accurately.

Subsequent models have typically been evaluated against rather less data, and are thus limited in their predictive power.

A recent study by Cross [11] reconsidered Haake’s experimental data using a variation of rigid body contact law [3], but assuming that the contact force is equivalent to a normal force offset from the centre of mass by a distance D. The numerical investigation presents evidence for linear dependence of coefficients of friction and restitution (in both normal and tangential direction), as well as the coefficient D on the angle of incidence (called $\phi$ below), with a separate fit for low-velocity bounces. Similarly to the findings of Roh and Lee [12], it is shown that the overall bounce and roll distance decreases with increasing $\phi$. A numerical model, where the distance travelled is a linear function of the incidence angle over realistic landing velocities from tee-shots, was also recently adopted for the purposes of testing compliance of balls with the rules of golf [13].

Existing data already suggest significant nonlinearity during golf ball bounce. For example Cross [14, Fig. 9] shows that fitting a ‘horizontal coefficient of restitution’ (that is the ratio of post- to pre-bounce tangential velocities) leads to a highly nonlinear function that can take either sign. More sophisticated models that feature nonlinearity allow for micro-slip [15], Hertzian contact [16], nonlinear material behaviour [17] and normal-tangential coupling [18].

To advance understanding of modern golf ball bounce and to motivate a new generation of more accurate models, it has become clear more data are required. As a consequence, we have collected new data on the motion of a golf ball, just before and after impact, over a wide range of inbound velocity and spin conditions, using state-of-the art image analysis. These data build on the earlier work of Haake by having a more comprehensive set of inbound conditions, and more repeats per condition. We also make a systematic treatment of measurement error and variability. The results are presented for two different ground types; an artificial and a natural turf. We also examine whether these data are consistent with rigid bounce models, either with or without Penner’s effective slope angle.

The rest of the paper is outlined as follows. Section 2 explains the methods of our study, including experimental set up, data analysis and how we fit the models used for comparison purposes. Section 3 contains the results, which are discussed in Sect. 4. Section 5 contains a brief conclusion.

2 Methods

2.1 Experimental set up

Two experimental campaigns were performed, see Fig. 1. In both cases, a modern, multi-piece golf ball with polyurethane cover, as used on the professional tours, was fired from a modified baseball launcher aimed downwards towards the designated surface. The ball was positioned in the launcher between two spinning wheels—one at the top and one at the bottom. The spin speed of each wheel is controlled independently. Variations of these speeds (including possible reverse spin of the upper wheel) allowed a full range of realistic speeds and spins of the golf ball to be attained, and adjustment of the incline of the launcher allowed variation of the landing angle. The wheels of the launcher were aligned so that the axis of the spin imparted on the ball was perpendicular to its plane of motion; thus minimising side spin.

In Campaign A, the ball was bounced off premium artificial golf teeing turf, 30 mm thick, adhered to a rigid wooden surface (thickness 38 mm). Campaign B used a well-maintained teeing area. In both campaigns, the launcher was moved between each repeat, so that the ball hit a different undamaged piece of surface for each recorded impact. The artificial turf was chosen to represent a typical surface that is free from natural heterogeneity, whereas Campaign B was designed to check whether similar conclusions apply to real turf.

Fig. 1

Experimental set up. The ball was launched from a modified baseball launcher (1). On leaving the launcher, the ball triggered a laser sensor (2) which in turn activated a high-speed camera (4). The recording is taken against a contrasting, black background (3). (a) Schematic drawing of the setup. (b) Photograph from the experimental session

On leaving the launcher, a high-speed camera was triggered manually or by a laser sensor to capture a video of the bounce. The recording was made using a Phantom VR603 high-speed camera, recording at between 5,000 and 10,000 frames-per-second. The lens used was a Nikon 35 mm f1.8 G AF-S DX. The default aperture setting was f4.0 with exposure time of 20 µs; however, aperture and/or exposure index were adjusted to obtain well-exposed images depending on the lighting conditions. The camera was set to align its image plane with the plane of motion of the ball. Each video clip consists of several frames just before and after the bounce. A superposition of frames from one such clip is shown in Fig. 2a.

For the purposes of automated tracking, the bounce was recorded against a plain black background. Furthermore, each ball was marked using a black permanent marker pen with a line along its seam and dots placed in a regular array around this seam. Videos were taken outdoors, in summer, for which natural lighting proved sufficient.

Fig. 2

(a) A combination of frames recorded for one bounce. The ball travels from left to right. Time intervals between frames vary and are chosen only for ease of illustration. (b) Definition sketch of the variables used throughout the analysis of the data

The settings on the launcher (wheel speeds and launch angle) were chosen to span a wide range of conditions typical to golf. Johnson et al. [19] estimate these typical landing speed, angle and spin to be, respectively, $29.5 \, \hbox {m s}^{-1}$, $36^\circ$ and $1950$ rotations per minute for a ball launched with a driver, $25 \, \hbox {m s}^{-1}$, $44^\circ$ and $4440$ rotations per minute for a launch with a 5-iron and $22 \, \hbox {m s}^{-1}$, $51^\circ$ and $9060$ rotations per minute for a ball launched with a sand wedge. The quantities were obtained using the USGA Indoor Test Range simulation using a typical elite golfer launch conditions.

Ball bounces for each setting of the launcher were repeated six times in Campaign A and either six or twelve times in Campaign B. A total of 330 bounces were recorded in Campaign A and 693 in Campaign B.

Table 1 Range of initial conditions for Campaigns A and B

2.2 Landing conditions

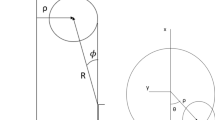
The variables used to define the ball’s landing conditions are given in Fig. 2b. It is assumed that the ball is a rigid sphere travelling in a vertical plane, with axis of rotation in the perpendicular direction. The ball’s centre of mass is assumed to be at a position (x(t), y(t)), with y measured vertically upwards; and its spin (measured anti-clockwise positive) is denoted $\omega$. Thus, upon landing $\dot{y}<0$; furthermore, $\omega >0$ represents backspin and $\omega <0$ topspin. To provide consistent and comparable measures of error, we use scaled units that give approximately comparable values for linear and rotational velocity; thus, $x$ and $y$ are measured in units of ball radii and $\omega$ in radians per second.

Table 1 presents the span of the landing conditions, both in unscaled and scaled co-ordinates. The full range of the initial conditions can be seen in Fig. 3 for each campaign. The data appears clustered as a result of the discrete launcher settings.

Fig. 3

An overview of the landing conditions for (a) Campaign A and (b) Campaign B. (c), Zoom on the initial condition space showing the corresponding categorisation of the data based on the tangential velocity at lift-off their initial conditions for (c) Campaign A; (d) Campaign B. Circled are the boundary data points used for identifying the separating hyperplane. The black asterisk marks typical landing conditions from a tee shot with a driver; speed $93.6$ feet per second ($28.5$ metres per second), landing angle of $37.3^{\circ }$ and a backspin of $34.9$ revolutions per second

2.3 Data extraction

A bespoke procedure was developed in Matlab [20] for the extraction of data from the videos. First, the ball was located in each frame (and frames where the ball was not found were removed from consideration), using the circle detection function imfindcircle which is based on the Hough transform [21]. From the change in co-ordinates of the centre between frames, the x and y velocities were established. Second, for each frame, a reduced image was taken, centred around the ball, with a small margin around it. We then used Matlab’s extractFeatures and matchFeatures functions to, respectively, identify significant features to match between frames. This, in turn, allowed us to construct a 2D matrix to represent the rotation between frames. Although automated, it was typically found that the black dots on the ball were the most commonly extracted and matched features.

In all cases, contact of the ball with the surface occurred over several frames. The initiation and end time of a bounce were estimated from the identification of abrupt changes in velocity of the lowest visible point of the ball. Also, during bounce, the view of the ball was obstructed by the turf, and locating the ball in the frame and estimating its spin became unreliable (see e.g. Fig. 4). For that reason, we decided to restrict the ball bounce analysis to inbound and outbound conditions, just before and after the bounce.

Fig. 4

Unprocessed tracing data of a ball before, during and after bounce for two different launch conditions

2.4 Data analysis

Each bounce was categorised using six quantities; horizontal velocity, vertical velocity and spin for touch down (denoted as $\dot{x}_0, \dot{y}_0$ and $\omega _0$, respectively) and lift-off ($\dot{x}_F, \dot{y}_F$ and $\omega _F$, respectively).

2.4.1 Measurement error

As indicated in Fig. 4, the data extracted was not a single point measurement of each velocity and spin, but a noisy time series of measurements, evaluated at times $t_1, t_2, \dots , t_N$, where the time interval $\Delta t = t_{i+1}-t_i$ is the frame rate, and is constant for all $i = 1, \dots N-1$. For the ball velocities, we used the straight line of best fit to the derivatives of the position measurements. That is, for the horizontal velocity, we found

$$\begin{aligned} v_x(t) = m\,t +c \end{aligned}$$

(1)

such that

$$\begin{aligned} \varepsilon _x = \sum _{i=1}^{N-1} \left| \frac{x_{i+1} - x_{i}}{\Delta t } - v_x(t_{i+1}) \right| ^2 \end{aligned}$$

(2)

is minimised. The vertical velocity estimate, $v_y(t)$, was calculated similarly. The linear fit was obtained using Matlab’s polyfit function [20]. Incorporating a linear fit accounted for possible effects of the acceleration, such as gravity in the case of the vertical velocity or drag in the case of the horizontal velocity. Parameters m and c were estimated together with their 95% confidence intervals (CI), which then yielded the 95% prediction intervals (PI) for the values of $v_x$ and $v_y$ evaluated at the time of impact or lift-off. The size of the PI gives a parsimonious estimate of measurement error for each velocity in each trial.

It was found useful to treat spin differently, as no evidence of linear changes in spin was found during the recorded short time intervals before and after bounce. We, thus, assumed that recorded spin in each interval follows a normal distribution, with the noise attributed to measurement error. A normal distribution was, thus, fit to time series for each spin measurement and the mean of this distribution was taken as the measured spin. The 95% CI of the mean was taken as the PI.

2.4.2 Repeatability

Using six or twelve repetitions for each launch setting enabled a check on whether the tests recorded with similar initial conditions led to similar outbound measurements. For each test condition, the mean and 95% CI on the mean were calculated for each quantity (horizontal velocity $\dot{x}$, vertical velocity $\dot{y}$ and spin $\omega$), on both their inbound and outbound measurements. A larger width of each CI shows a larger spread of data around the mean and less repeatability in that quantity.

2.4.3 Distinguishing between slipping and rolling

The tangential velocity of the lowest point of the golf ball should carry information about the frictional dynamics of the ball. If the velocity of this point is zero, the frictional interface will be in a state of stick which suggests that the ball is rolling. In contrast, a non-zero tangential velocity suggests that the ball is slipping against the surface. Denoting such a point as P, in the scaled variables, the tangential velocity of P is given by

$$\begin{aligned} v_P = \dot{x} + \omega . \end{aligned}$$

(3)

We separated the initial condition space into two groups, based on the measurement of the tangential velocity of P at touch down and at lift-off. If the tangential velocity was of the same sign at touch down and lift-off, then it was deemed that the ball was slipping throughout the bounce. In all other cases, we deduced that the ball must have entered rolling at some point during the bounce.

To identify a possible separation manifold between these groups, a support vector machine (SVM) classifier was trained in Matlab using the sequential minimal optimisation (SMO) algorithm [22]. The trained SVM identified data points at the boundary between the two classes, and these were used to identify the separating surface in landing condition space between rolling and slipping trajectories. After experimentation, we found that the boundary was well approximated by a plane within landing condition space, for the range considered.

2.5 Comparison with existing models

The main aim of this paper is the presentation of new, rigorously collected open source data. An additional aim is to compare these data with predictions from elementary bounce models. The outline of these models is presented in Online Resource 3.

For a quantitative comparison of the models, we define here the error function of a fit. Suppose a measurement of sample i measures the landing velocities to be $\varvec{p}_0^i = [\dot{x}_0^i, \dot{y}_0^i, \omega _0^i]^{\intercal }$, and the corresponding lift-off velocities to be $\varvec{p}_F^i = [\dot{x}_F, \dot{y}_F, \omega _F]^{\intercal }$. Let

$$\begin{aligned} \varvec{P}_F^i = [\dot{X}^i, \dot{Y}^i, \Omega ^i]^{\intercal }, \end{aligned}$$

(4)

denote the predicted lift of velocity according to a model (i.e. the model’s approximation of $\varvec{p}_F^i.$). Then the error of the model for all N samples in a campaign is defined as:

$$\begin{aligned} \delta = \frac{1}{N}\sum _{i=1}^{N} \frac{\Vert \varvec{p}_F^i - \varvec{P}_F^i \Vert }{\Vert \varvec{p}_0^i\Vert }, \end{aligned}$$

(5)

where $\Vert \cdot \Vert$ represents the usual Euclidean norm of a vector. Note that to be a meaningful error measurement, each component of $\varvec{p}_0, \varvec{p}_F, \varvec{P}_F$ must be of the same order of magnitude, highlighting the importance of working with our scaled velocity quantities. The error measure computed in (5) can be thought of as the root-mean-square error with respect to the initial kinetic energy of the system.

Similarly, we computed the mean error for each individual quantity $\dot{x}, \dot{y}, \omega$, (generically denoted as q with a predicted computed value Q) via:

$$\begin{aligned} \Delta q = \frac{1}{N}\sum _{i=1}^{N} \frac{|q_F^i - Q_F^i |}{\Vert \varvec{p}_0^i\Vert }. \end{aligned}$$

(6)

Note that the mean quantities computed by (6) neither sum nor mean to the error computed by (5)—they are simply an indicator of where the largest error is generated.

2.5.1 Rigid-bounce model

Details of the model can be found in Online Resource 3, Section 1, with the governing equation being (S3.2).

The parameters $\mu$ and r were fit from the available data using a sequential least-squares approach. First, the coefficient of restitution r was found by performing a linear fit (without offset) for each measured inbound and outbound vertical velocity, using Matlab’s linear model fitting tools. Subsequently, coefficient of friction $\mu$ was found by minimising the value of the error function (5) as $\mu$ varies.

2.5.2 Inclined surface model

Details of the model can be found in Online Resource 3, Section 2, with the governing equation being (S3.3).

The model requires fitting parameter $k_p$, representing the constant of proportionality between the effective angle and the initial conditions, in addition to $\mu$ and r. We ran Matlab’s genetic algorithm toolbox ga to fit all three parameters, minimising the error function (5). The chosen tolerance in minimising the function was $10^{-15}$. In each setting, the coefficient of restitution was specified within the frame of reference that is rotated through $\beta$.

We explored the idea of the rotated frame of reference in two ways—either the angle of rotation was determined by the initial condition, as specified by Equation (S3.3) in Online Resource 3, or supposing that the angle $\beta$ is fixed for all initial conditions.

2.5.3 A piecewise linear data fit

In addition, within each half-space, either side of the boundary between slipping and rolling identified in Sect. 2.4.3, we attempted to fit an affine transformation. That is, for the measured initial condition $\varvec{p}_0$ and outbound $\varvec{p}_F$, we approximate the latter with

$$\begin{aligned} \varvec{P}_F = A \varvec{p}_0 + \varvec{b}, \end{aligned}$$

(7)

where A is a $3\times 3$ matrix, and $\varvec{b}$ is a three-dimensional vector.

To allow for validation of the fit, we separated our data into two categories for each campaign. One data point from each launcher setting (chosen at random) was removed from the general set of data and placed into a testing set, with the remaining data points used for training of the model (7). The testing data set was used to evaluate the accuracy of the model (7), using the error measure (5) and (6).

3 Results

The full data set is presented in Figure S1.2 in Online Resource 1, with the data set available in Online Resource 2 and the videos published by Biber et al. in [23]. The data set covers a wide range of inbound velocity and spins, and includes examples of backwards bounce, that is where the sign of the horizontal velocity $\dot{x}$ reverses between impact and lift-off.

3.1 Measurement error and repeatability

Figure 5 shows histograms of the widths of the prediction intervals (PIs). These are re-scaled with respect to the mean measurement across the samples. That is, a value 1 on the horizontal axis of each histogram would correspond to the mean horizontal, vertical or angular velocity on either inbound or outbound across all samples. These PI’s provide a parsimonious estimate of the error in measuring speeds via the video analysis.

Fig. 5

Histogram of widths of PIs in (a) Campaign A; (b) Campaign B. Values are re-scaled by the mean measurement across all samples. From left to right, these are for the horizontal velocity $\dot{x}$, vertical velocity $\dot{y}$ and spin $\omega$. Green bins represent measurements taken on the inbound, red bins represent those taken on the outbound

In contrast, the repeatability of tests with identical launcher settings is illustrated in Figure S1.1 in Supplementary Information 1. Each circle denotes the mean of the respective quantity for a particular test condition, where error bars represent the 95% confidence interval about the mean.

3.2 Piecewise linear model slipping and rolling

Figure 6 presents the tangential velocity $v_P$ of point P at the time of impact and lift-off for both campaigns. In particular, observe an offset of lift-off velocities away from zero. That is, balls seem rarely, if ever, to lift-off in a state of rolling. There is always some slip at lift-off. Furthermore, notice a clear separation between those samples that lift-off with positive tangential velocity $v_P$ from those with negative $v_P$.

Fig. 6

Tangential velocities at landing and lift-off. Values for (a) Campaign A and (b) Campaign B. Noted with the dashed line is the zero lift-off tangential velocity

The cases with $v_P>0$ correspond to cases with high initial backspin. In such cases, the ball slips throughout the impact and lift-off with backspin again. Conversely, the cases with $v_P<0$ at lift-off tend to occur when either the ball landed with high topspin ($v_P<0$ both at impact and lift-off) or where at some point during the bounce phase, the ball entered rolling ($v_P<0$ initially, but $v_P>0$ at lift-off). It is only the final of these cases that we refer to as a ‘rolling’ trajectory.

The distinction between rolling and slipping bounces is visualised in three-dimensional space in Fig. 3. For each campaign, the data are separated into different regions of the landing condition space, with only a few data points being mis-labelled by the approximate dividing plane. The boundary cases are identified using the SVM algorithm, and a plane is fitted through the identified boundary points using least-squares approximation. Following separation of landing conditions conditions with such a plane, an affine transformation between incoming and outgoing speeds can be identified for each of the subsets.

The resulting fits for Campaign A were:

$$\begin{aligned} \begin{bmatrix} \dot{x}_F \\ \dot{y}_F \\ \omega _F \end{bmatrix} = {\left\{ \begin{array}{ll} \begin{bmatrix} 0.536 &{} -0.004 &{} -0.205 \\ 0.144 &{} -0.407 &{} -0.027 \\ -0.524 &{} 0.091 &{} 0.318 \end{bmatrix} \begin{bmatrix} \dot{x}_0 \\ \dot{y}_0 \\ \omega _0 \end{bmatrix}+ \begin{bmatrix} -111 \\ 23.7 \\ 39.4 \end{bmatrix} &{} \hbox {if } 0.891 \dot{x}_0 +0.763 \dot{y}_0 +\omega _0 < 600\\ &{} \\ \begin{bmatrix} 0.674 &{} 0.107 &{} -0.005 \\ 0.103 &{} -0.390 &{} 0.017 \\ -0.153 &{} 0.277 &{} 1.01 \end{bmatrix} \begin{bmatrix} \dot{x}_0 \\ \dot{y}_0 \\ \omega _0 \end{bmatrix}+ \begin{bmatrix} -154 \\ 25.0 \\ -267 \end{bmatrix}&\hbox {if } 0.891 \dot{x}_0 +0.763 \dot{y}_0 +\omega _0 > 600; \end{array}\right. } \end{aligned}$$

(8)

and similarly, for Campaign B the fits were:

$$\begin{aligned} \begin{bmatrix} \dot{x}_F \\ \dot{y}_F \\ \omega _F \end{bmatrix} = {\left\{ \begin{array}{ll} \begin{bmatrix} 0.326 &{} 0.222 &{} -0.213 \\ 0.185 &{} -0.008 &{} -0.076 \\ -0.333 &{} -0.147 &{} 0.224 \end{bmatrix} \begin{bmatrix} \dot{x}_0 \\ \dot{y}_0 \\ \omega _0 \end{bmatrix}+ \begin{bmatrix} 175 \\ 90.4 \\ -171 \end{bmatrix} &{} \hbox {if } 0.377 \dot{x}_0 +2.25 \dot{y}_0 +\omega _0 < -485\\ {} &{} \\ \begin{bmatrix} 0.606 &{} 0.649 &{} -0.007 \\ 0.146 &{} -0.089 &{} -0.006 \\ -0.192 &{} 1.01 &{} 0.887 \end{bmatrix} \begin{bmatrix} \dot{x}_0 \\ \dot{y}_0 \\ \omega _0 \end{bmatrix}+ \begin{bmatrix} 117 \\ 49.3 \\ 35.0 \end{bmatrix}&\hbox {if } 0.377 \dot{x}_0 +2.25 \dot{y}_0 +\omega _0 > -485. \end{array}\right. } \end{aligned}$$

(9)

The support vectors, which identify the boundary data, are highlighted in Fig. 3. The error values for the presented fits are given in Table 2. We also present the percentage of testing data that was mismatched following the linear approximation—that is, the percentage of data samples that a posteriori are observed to be either rolling or slipping, but the SVM classifier of the space placed them in the wrong category. Furthermore, we present a comparison of the predicted and observed data in Fig. 7.

Table 2 Error (in percent) in the fitting of disjoint linear approximations, as described by Equations (8) and (9)

Fig. 7

Comparison of the predicted lift-off values against the observed results. Solid line indicates the exact fit between prediction and observation. Triangle markers indicate samples classified as rolling, and the circular markers indicate slipping bounces. Marked with black circles are the data samples randomly selected for the testing set to examine the goodness of fits. Data are obtained from (a) Campaign A and (b) Campaign B

3.3 Rigid-bounce models

The parameters of best fit for the rigid bounce model are presented in the first column of Table 3, for each of the two campaigns. Also given are the fitting errors measured using $\delta$, and $\Delta \dot{x}$, $\Delta \dot{y}$ and $\Delta \omega$ as described in the previous section.

For Penner’s extension to the model, the results of the fit are presented in the second two columns of Table 3 for each campaign. Observe that the error is slightly smaller than for the simple rigid body fit, yet still much larger than the SVM fit. Furthermore, the approximation with a constant angle of rotation of the frame $\beta$ has slightly smaller error than Penner’s proposed approximation linear relationship discussed in section 2 of the Online Resource 3.

Table 3 Best fit of parameters from each campaign to rigid-bounce models, together with the error. See Methods for details

4 Discussion

To the best of our knowledge, the data presented in this investigation represent the most comprehensive for the bounce of a golf ball on a green in the open scientific literature. We have taken care to present all steps involved in data collection, curation and error analysis. Using video analysis and modern image processing techniques, we have been able to capture the relationships between the velocity and spin on lift-off to those on landing, for two different turfs. We have also made both this summary data and the raw videos freely available; our purpose being to enable future development and evaluation of physically realistic models of golf ball bounce. As a first step in that process, we have evaluated here three simple models; a plain rigid bounce model with restitution and Coulomb friction, Penner’s empirical extension to this model, and a simple piecewise-affine fit to the data.

We have also been careful to distinguish the prediction interval of the extraction of each quantity from the video, from the natural variability and repeatability of each measurement. Note that whilst some of the prediction intervals may appear unrealistically large for a few data points, most prediction intervals are around $5\%$ of the mean value of each quantity. Also, in all cases, we took the mean value from these intervals for performing our data analysis, for which the true error is likely to be significantly smaller.

When looking at the repeatability of the measurements, it is worth noting that in the majority of cases, the confidence intervals on the outbound measurements (horizontal bars in Figure S1.1) are wider than those on inbound. Similarly, Fig. 5 shows larger error propagation in the measurement of the outbound quantities. This indicates that behaviour of the turf was not fully deterministic, which reflects the natural variability of turf response. Although present for artificial turf (Campaign A), this effect was more noticeable for real turf (Campaign B) as could be expected.

Consideration of tangential velocities at landing and lift-off enabled us to distinguish between slip and rolling (stick) which appears to be key to understanding the dynamics of golf ball bounce. Furthermore, we found little evidence of any ball that lifts off in pure rolling (see Fig. 6). Rather, balls that enter rolling during the bounce enter slip in the opposite sense, prior to take-off.

It is striking from our model fitting results that the the piecewise-affine fit outperformed both the rigid bounce and Penner’s models, with overall prediction errors around a factor of five times smaller, for each campaign. As a note of caution, the piecewise-affine model required pre-identification using an SVM of the hyperplane that separates rolling from slipping bounces.

Note though that this fit is not physical, as it is discontinuous and offset from the origin by a positive value of $\dot{y}_F$ (which would imply a ball with zero would lift-off). This anomaly provides further evidence that a nonlinear model would be more accurate. The nonlinearity could arise due to a dynamic transition from elastic behaviour for low normal velocity and elasto-plastic behaviour for higher speed bounces. An alternative approach would be to study the bounce on a green using a finite element formulation. This allows for a numerical study of the bounce, but requires a higher computational involvement and limits the analytic insight into the behaviour of the turf and the ball during the impact.

For the rigid bounce model, Table 3 shows that prediction error for horizontal velocity and spin were beyond reasonable approximation (19.3% and 18.6%, respectively, for Campaign A; and 19.8% and 24.6%, respectively, for Campaign B).

Most likely, a better fit could be obtained with an additional tangential compliance of the ground. Such effects are explored by Biber et al. in [24].

Whilst providing a slightly better fit than the rigid bounce model, Table 3 shows that Penner’s model is still unreasonably inaccurate (14.6% and 16.1%, respectively, for Campaign A; and 9.4% and 16.4%, respectively, for Campaign B) for lift-off horizontal velocity and spin. Note that using a fixed constant angle $\beta$ gives a better fit for both campaigns than Penner’s model. At the same time, a model based on constant angle $\beta$ for all initial conditions contradicts its physical justification.

5 Conclusion

We conclude that a reliable physics-based model of golf ball bounce is still lacking. Such a model would require a complex nonlinear model of the compliant surface. Most of the discrepancy between the rigid bounce models and the data are in the tangential and spin degrees of freedom, with error in the normal direction being a factor of five smaller. This observation, along with some of the theoretical conclusions in aforementioned literature, suggests the need for a combined frictional and tangential compliance model for the ground to comprehensively study the interaction between golf ball and the green. Such models would also need to explain the evidence of nonlinearity we have found in the data.