Experimental Investigations of Carbon Fiber Reinforced Polymer Composites and Their Constituents to Determine Their Elastic Material Properties and Complementary Inhomogeneous Experiments with Local Strain Considerations

Abstract

Composite materials, such as fiber reinforced polymers, become increasingly important due to their excellent mechanical and lightweight properties. In this respect, this paper reports the characterization of a unidirectional carbon fiber reinforced polymer composite material. Particularly, the mechanical behavior of the overall composite and of the individual constituents of the composite is investigated. To this end, tensile and shear tests are performed for the composite. As a result, statistics for five transversely isotropic material parameters can be established for the composite. For the description of the mechanical properties of the constituents, tensile tests for the carbon fiber as well as for the polymer matrix are carried out. In addition, the volume fraction of fibers in the matrix is determined experimentally using an ashing technique and Archimedes’ principle. For the Young’s modulus of the fiber, the Young’s modulus and transverse contraction of the matrix, as well as the volume fraction of the constituents, statistics can be concluded. The resulting mechanical properties on both scales are useful for the application and validation of different material models and homogenization methods. Finally, in order to validate the obtained properties in the future, inhomogeneous tests were performed, once a flat plate with a hole and a flat plate with semicircular notches.

1 Introduction

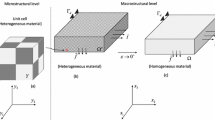
In recent years, lightweight structures became increasingly important due to their excellent mechanical and lightweight properties. With regard to the environmental and climate protection policy in future there will be considerable use of composites in the field of aircraft and automotive as well as wind energy. As a special composite material, unidirectional carbon fiber reinforced polymers (CFRP) has become prominent in the above-mentioned fields due to their good strength-to-weight ratio and high stiffness. The composite consists of the two constituents carbon fiber and polymer matrix. The description of the mechanical behavior can be done on the macro-scale for the entire composite or on the meso-scale for the individual constituents. As illustrated schematically in Fig. 1A, on the macro-scale every material point is considered as homogenized. On the meso-scale illustrated in Fig. 1B the behavior of carbon fiber and polymer matrix takes into account separately. If the proportion of fibers is also known, conclusions can be drawn about the mechanical behavior of the entire composite.

To the author’s knowledge, only a few publications are concerned with experimental investigations of the mechanical behavior of CFRP materials on both scales. In the area of tensile testing of composites and partial consideration of constituent properties, the following literature references should be mentioned: [1] and the literature referenced within is concerned with the evaluation and prediction of the macro tensile properties of CFRP laminates, where [1] primarily considers the strain rate effect at intermediate strain rates. In [2] experiments were conducted to determine orthotrophic properties of CFRP. However, it should be noted that in [2] a combination of macro and meso scale was used to determine the properties. Based on the results of the orthotropic properties, a symmetry can be seen that indicates transverse isotropy. The physical, thermal and mechanical behavior are discussed in [3] for different laminate composites in terms of moisture absorption, thermal stability, tensile strength, elastic modulus, flexural strength, flexural modulus and abrasive wear resistance. The paper [4] examines four different laminate families for their tensile behavior. [5] outlines the source of data and the methods used in deriving the material properties for unidirectional laminate and constituents. In [2] tensile tests of a composite, and there matrix are carried out. Tensile tests are not sufficient for a complete description of the mechanical behavior of a transversely isotropic composite with respect to the macroscale. In this context, no statements can be made about out-of-plane shear. The review paper [6] gives an overview of test methods for multiaxial and out-of-plane strength of composite laminates. In [7], investigation methods for shear properties of fiber composites are described in detail. The publication [8] examines both the in-plane and out-of-plane shear modulus of composites, with torsional tests presented for the out-of-plane shear modulus. The Isopesco shear test for laminate composites, applicable for both shear directions, is described in the works [9, 10].

Experimental studies on fibers are cited in the following references: In [11] the axial elastic modulus, ultimate strength and failure strain of single fibers are determined for carbon and glass fibers. Stress–strain behavior obtained from experiments on a single Kevlar KM2 fiber are presented and discussed in [12]. A feasible method in order to study the structure–mechanical heterogeneity of polyacrylonitrile-based carbon fibers is presented in [13]. The literature for the experimental polymer study, which should correspond to the surrounding matrix, is not discussed further in our paper due to the large number of variations.

The study of a composite at both scales is advantageous to characterize the mechanical behavior and to verify the associated material and homogenization models. Therefore, the experimental investigations of this work provide a basis for further research in the field of CFRP material modeling. Due to the anisotropic nature and the large number of influencing factors, such as geometry variations and fiber content, it can be assumed that uncertainties will occur when determining the mechanical properties. These uncertainties in properties, some of which are determined here, have already been addressed in [14] for the macro-scale and in [15] for the meso-scale. This is a further motivation of this work in order to determine the uncertainty on both scales and to be able to address it more closely.

The main aspects of this work, which aims to characterize the mechanical behavior of composites, in this particular case of a carbon fiber-epoxy matrix composite, are the following:

• In order to determine macro-scale properties, tensile and shear tests are performed for the overall composite. These are restricted to transversely isotropic elastic behavior.

• In order to determine the meso-scale properties, tensile tests are carried out for the carbon fiber and the epoxy matrix, as well as investigations of the volume fraction. The investigations are limited to the elastic range of the constituents.

• In order to be able to validate the properties of the respective scales, additional inhomogeneous experiments are studied.

Consequently, this paper is structured as follows: Sect. 2 deals with the characterization of mechanical properties on the macro-scale. In this context, tensile and shear tests for a CFRP and different fiber orientations are carried out and evaluated. On the meso-scale, tests are performed in Sect. 3 for the individual constituents of the composite. In addition, the volume fraction of the fiber or the surrounding matrix, respectively, is determined. Finally, plates with a hole and semicircular notches are tested in order to characterize the CFRP under inhomogeneous strain and stress states.

Fig. 1

The composite is in (A) considered as one homogeneous material on macro-scale and in (B) described by their both constituents, i.e., fiber and matrix on meso-scale. In (C) is a transversely isotropic volume element, where fibers are aligned with the 1-axis

2 Experimental Investigations of the Overall Composite

On the macro-scale, schematically illustrated in Fig. 1A, the composite is considered as macroscopically homogeneous material. In order to describe unidirectional carbon fiber reinforced polymers (CFRP), a transversely isotropic elasticity is assumed, where the plane normal to the fiber direction can be considered as an isotropic plane. In Fig. 1C, fibers are aligned with the 1-axis, which is normal to the 2–3-plane of isotropy.

In this case, the elastic material behavior can be characterized with five independent material parameters. A possible set of $n_m=5$ transversely isotropic material parameters is assembled in the macro-scale material parameter vector

$$\begin{aligned} \underline{\kappa }=[\kappa _1,\kappa _2,\kappa _3,\kappa _4,\kappa _5]^T=[E_{1}, E_{2}, G_{12}, G_{23}, \nu _{12}]^T. \end{aligned}$$

(1)

In Eq. (1) $E_{1}$ and $E_{2}$ are Young’s moduli in fiber and transverse direction, respectively. In addition, $G_{12}$ and $G_{23}$ are the in-plane and the out-of-plane shear moduli of a unidirectional material, respectively, and $\nu _{12}$ is the dimensionless Poisson’s ratio. In order, to determine the material parameters in Eq. (1) experimental tensile and shear tests can be performed.

The data used for this section are taken partly from the student works of Liu [16], Wehmeier [17] as well as Wehmeier [18].

2.1 Tensile Tests of the Overall Composite

For the purpose of the tensile tests, laminate plates of unidirectional CFRP with different fiber orientations ($0^{\circ }$, $\pm 45^{\circ }$, $90^{\circ }$) were produced. The CFRP plates were all manufactured by the SGL Group and are made of C U230-0/NF-E322/39% by means of a prepreg pressing process. The thickness per prepreg ply is approximately 0.22 mm. In terms of the manufacturing process, an orthotropic material is achieved. When a homogeneous matrix is established, the orthotropHy reduces to the transverse isotropy assumed above. This fact is taken up in the further course of the work, which assumes that, among other things, the shear modulus $G_{12}$ corresponds to the shear modulus $G_{13}$.

The plate specifications, the corresponding determinable material parameters, which are incomplete with respect to Eq. (1), and the associated standards for the respective tensile tests are listed in Table 1. The $\pm 45^{\circ }$ fiber-oriented plates, which consist of five $45^{\circ }$ and five $-45^{\circ }$ fiber-oriented plies, according to [19], are used to determine the shear modulus $G_{12}$ due to the known state of stress within the material.

Table 1 Plate specifications, determinable material parameters and test standards

At the end of the specimens tabs of glass fiber reinforced polymers (GFRP) are fixed in order to avoid failure due to clamping. Prior to cutting the tensile specimens, the end tabs are glued to the plates. A plate with fixed end tabs is shown in Fig. 2A. From each prepared plate, tensile specimens were cut out using a water jet cutter. Additionally, the black clear specimens are sprinkled with a white varnish to get a pattern, which is necessary for optical measurement system. Sprinkled specimens for each fiber orientation ($0^\circ$, $90^\circ$, $\pm 45^\circ$) are exemplified in Fig. 2B. The geometry of the tensile specimens according to the [20] standard [20] and the [19] standard [19] are depicted in Fig. 3. The nominal specimen dimensions for fiber orientations $\varphi =0^\circ$, $\varphi =90^\circ$ and $\varphi =\pm 45^\circ$ are summarized in Table 2. The tests, including the ordering of materials, were carried out twice. In this context, a distinction is made between batch 1 and batch 2. The number of samples $n_{\text {b}1}$ for batch 1 and $n_{\text {b}2}$ for batch 2 is summarized for the respective fiber orientations in Table 2 at the bottom. Furthermore, Figs. 4C, D ans Fig. 4E show schematically the different fiber orientations $\varphi =0^{\circ }$, $\varphi =90^{\circ }$ and $\varphi =\pm 45^{\circ }$, respectively, of the specimens.

Fig. 2

(A) CFRP plate with fixed GFRP end tabs and (B) sprinkled specimens to get a pattern for fiber orientations $0^{\circ }$, $90^{\circ }$ and $45^{\circ }$

Fig. 3

Geometry of specimens in mm, adopted from [20]

Table 2 Nominal sample dimensions and number of samples depending on fiber orientation according to Fig. 3

The entire experimental setup including the optical measurement system and their cameras is shown in Fig. 4A. The prepared specimens are clamped into a tensile testing machine with hydraulic clamping jaws, as illustrated in Fig. 4B for a $90^{\circ }$ fiber-oriented case. The tensile tests were performed on a servo-hydraulic MTS testing machine with a 100 kN quasi-static load capacity. Furthermore, the optical measurement system GOM Aramis, which is suited for precise material characterization is used. It enables to analyze non-homogeneous three dimensional (3D) deformations of the test samples. The used 3D Camera has a resolution of 4 megapixels and a maximum image recording rate of 24  Hz at full resolution. In a configuration with reduced resolution of 1.3 megapixels the image recording rate can be extended up to 8000  Hz and thus also the range of applications. The experiments, which are displacement controlled according to [20], are loaded in the longitudinal direction x with an angle $\varphi$ related to the fiber 1-direction. In particular, $\varphi =0^{\circ }$ and $\varphi =90^{\circ }$ correspond to longitudinal and transverse uniaxial stress loading, respectively. A load cell measures forces $\bar{F}$ at different observation states, whereby corresponding stresses in longitudinal direction $\bar{\sigma }_{x}=\bar{F}/A_0$ can be calculated using the cross-sectional area $A_0=b_1 \, h$, see Table 2.

Fig. 4

Experimental investigations: (A) Experimental setup with optical measurement system, (B) specimen fixed into clamping jaws and schematic specimens for fiber orientations (C) $\varphi =0^{\circ }$, (D) $\varphi =90^{\circ }$, (E) $\varphi =\pm 45^{\circ }$ and a machine-fixed coordinate system

By applying an optical measurement system in combination with an ARAMIS software, the strains in longitudinal x and transverse y directions $\bar{\varepsilon }_{x}$ and $\bar{\varepsilon }_{y}$, respectively, are determined. Synchronized stereo images of the pattern are recorded at different load stages using two CCD (Charge-coupled Device) cameras. The first image processing steps define the macro- image facets. These facets are tracked in each successive image with subpixel accuracy. Three dimensional coordinates, 3D displacements and the plane strains are calculated automatically using photogrammetric evaluation procedures [21]. To determine material parameters, a longitudinal or transverse strain in the plane under consideration is required. For this purpose, virtual extensometers are defined with the aid of the ARAMIS software, which can be seen in Fig. 5 as an example for the fiber orientation $\varphi =0^{\circ }$. In Fig. 5A and Fig. 5B, three extensometers are entered for the longitudinal x and transverse y directions, respectively. Average strains $\bar{\varepsilon }_{x}$ and $\bar{\varepsilon }_{y}$ in both directions are determined from the respective three extensometers.

Fig. 5

Three virtual extensometers in ARAMIS: (A) In the x-direction and (B) in the y-direction

The failure modes obtained from the tensile tests are shown in Fig. 6A and in Fig. 6B for $0^{\circ }$ and $90^{\circ }$ fiber-oriented specimens, respectively. For the $0^{\circ }$ fiber-oriented specimens, an explosive failure parallel to the fiber orientation in gauge area is evident. The $90^{\circ }$ fiber-oriented specimens fail laterally close to the clamping jaws. Due to low displacement amplitudes no failure modes are available for the $45^{\circ }$ fiber-oriented specimens. Since the main focus of the paper is on the determination of elastic properties, failure behavior is not discussed more specifically.

Fig. 6

Failure results for: (A) $0^\circ$ fiber-oriented specimen and (B) $90^\circ$ fiber-oriented specimen

Determination of $E_{1}$ and $\nu _{12}$: In order to determine the Young’s modulus $E_{1}$ in fiber direction as well as the Poisson’s ratio $\nu _{12}$, tensile tests are applied to $0^\circ$ fiber-oriented specimens illustrated in Fig. 4C. [22] provides further information regarding the test procedure and the data evaluation. The resulting curves for stress $\sigma _{1}=\bar{\sigma }_{x}$ versus strain $\varepsilon _{1}=\bar{\varepsilon }_x$ for batch 1 and batch 2 are shown in Fig. 7A, B, respectively, where a regression for the slope of each curve describes the corresponding Young’s modulus $E_{1}=\Delta \sigma _{1}/\Delta \varepsilon _{1}$ in fiber direction. Furthermore, in Fig. 7E, F experimental longitudinal strain $\varepsilon _{1}$ versus transversal strain $\varepsilon _{2}=\bar{\varepsilon }_{y}$ curves are illustrated for batch 1 and batch 2, respectively, where the slope of each regression line for each curve renders the corresponding Poisson’s ratio $\nu _{12}=-\Delta \varepsilon _{2}/\Delta \varepsilon _{1}$. The frequency distributions of $E_{1}$ and $\nu _{12}$ are illustrated in Fig. 7C, D, G, H for both batches. Note that e.g. Figure 7A, B were displayed with different settings for smoothing the curves to emphasize that there is a variety of display options. In addition, outliers in the figures may be excluded. For the parameter determination the representation has of course no influence. For the determination, the same regression method was used based on the corresponding standards.

Fig. 7

Experimental results for fiber orientation $\varphi =0^{\circ }$: Longitudinal stress $\sigma _{1}$ versus longitudinal strain $\varepsilon _{1}$ curves (A) for batch 1 and (B) for batch 2. Frequency distributions of Young’s modulus in fiber direction $E_{1}$ (C) for batch 1 and (D) for batch 2. Longitudinal strain $\varepsilon _{1}$ versus transversal strain $-\varepsilon _{2}$ curves (E) for batch 1 and (F) for batch 2. Frequency distributions of Poisson’s ratio $\nu _{12}$ (G) for batch 1 and (H) for batch 2

Determination of $E_{2}$: to determine the Young’s modulus $E_{2}$ transverse to the fiber direction, tensile tests are applied to $90^{\circ }$ fiber-oriented specimens illustrated in Fig. 4D. [22] provides further information regarding the test procedure and the data evaluation. The resulting curves for stress $\sigma _{2}=\bar{\sigma }_{x}$ versus strain $\varepsilon _{2}=\bar{\varepsilon }_x$ for batch 1 and batch 2 are shown in Fig. 8A, B, respectively, where a regression for the slope of each curve describes the corresponding Young’s modulus $E_{2}=\Delta \sigma _{2}/\Delta \varepsilon _{2}$. The frequency distributions of $E_{2}$ are illustrated in Fig. 8C, D for both batches.

Fig. 8

Experimental results for fiber orientation $\varphi =90^\circ$: Stress $\sigma _{2}$ transversal to fiber versus strain $\varepsilon _{2}$ transversal to fiber curves (A) for batch 1 and (B) for batch 2. Frequency distributions of Youngs’s modulus in transverse direction $E_{2}$ (C) for batch 1 and (D) for batch 2

Determination of $G_{12}$: to determine the shear modulus $G_{12}$ in fiber direction, tensile tests according to [20] are applied to $\varphi =\pm 45^\circ$ fiber-oriented specimens illustrated in Fig. 4E. The resulting curves for maximal shear stress $\uptau _{12}=\bar{\sigma }_{x}/2$ versus shear strain $\gamma _{12}\approx \bar{\varepsilon }_{x}-\bar{\varepsilon }_{y}$ for batch 1 and batch 2 are shown in Fig. 9A, B, respectively, where a regression for the slope of each curve describes the corresponding shear modulus $G_{12}=\Delta \uptau _{12}/\Delta \gamma _{12}$. The frequency distribution of $G_{12}$ are illustrated in Fig. 9C, D for both batches.

Fig. 9

Experimental results for fiber orientation $\varphi =\pm 45^{\circ }$: Maximal shear stress $\uptau _{12}$ versus maximal shear strain $\gamma _{12}$ curves (A) for batch 1 and (B) for batch 2. Frequency distributions of in-plane shear modulus $G_{12}$ (C) for batch 1 and (D) for batch 2

2.2 Shear Tests of the Overall Composite

To determine the two shear moduli $G_{13}$ and $G_{23}$ shear tests are carried out. For shear investigations of composite materials, the standard [23] in [23] is defined, based on Iosipescu’s original work [24]. As mentioned in Sect. 2.1, we assume a homogeneous epoxy matrix, so that the 2–3 plane can be assumed as isotropic in a simplified manner. Therefore, it immediately follows that the value of the shear modulus $G_ {12}$ is equivalent to the shear modulus $G_ {13}$. This fact is mentioned for the sake of completeness, since the method presented here is based on the shear modulus $G_ {13}$ with respect to the manufacturing process, as already described in Sect. 2.1, according to the standard [23] instead of the modulus $G_ {12}$ in Eq. (1). Later, when summarizing the determined parameters, $G_ {12}\approx G_ {13}$ is set.

Pure shear loading is required to determine the shear modulus. For this purpose, on both sides of the sample two counteracting moments are produced by two force couples, as illustrated in Fig. 10A. The applied forces are calculated from the equilibrium requirements due to the boundary conditions and the applied force F. The distance between the innermost force couple or respectively the fixtures of the machine is referred to as b. In the shear force diagram in Fig. 10B and bending moment diagram in Fig. 10C, constant shear loading and vanishing moment in the middle of the sample can be recognized, which ensures a pure shear loading state.

Fig. 10

Diagrams for the Iosipescu shear test: (A) Force loading, (B) shear force and (C) bending moment diagrams, adopted from [23]

A schematic illustration of the loading fixture is shown in Fig. 11. The specimen geometry to be used is shown in Fig. 12A, which is required to calculate the shear stress. Contrary to intuitive expectations, Isopescu showed in [24] that the $90^\circ$ notches, at least for isotropic materials, do not cause any stress concentrations, since the sides of the notches are parallel to the normal stress directions at this point on the specimen. Therefore, the value of the shear stress for this test and geometry shown in Fig. 10–Fig. 12A is the shear force divided by the net cross-sectional area. The shear forces F at different observation points correspond to the forces $\bar{F}$ measured on the load cell illustrated in Fig. 11. Thus, the shear stresses $\uptau _{xy} = \bar{F} / A$ occurring in the x-y plane at the corresponding observation points can then be calculated using the cross-sectional area $A=w\,h$.

Fig. 11

Schematic of the loading fixture, adopted from [23]

To calculate the in-plane shear modulus $G_{xy}=\Delta \uptau _{xy}/\Delta \gamma _{xy}$ between two observation points, the shear strains $\gamma _{xy}$ at observation points must be determined in addition to the shear stresses $\uptau _{xy}$. The shear strain can be determined based on [23] with the help of two orthogonal strains in the center of the specimen at an angle of $+45^{\circ }$ and $-45^{\circ }$. The gauge ranges for the two strains $\varepsilon _{+45^{\circ }}$ and $\varepsilon _{-45^{\circ }}$ are visualized in Fig. 12B. Due to the known state of strain, it finally follows that $\gamma _{xy}=|\varepsilon _{+45^{\circ }}|+|\varepsilon _{-45^{\circ }}|$. [23] provides further information regarding the test procedure and the data evaluation.

Fig. 12

V-notched beam specimen: (A) Geometry and (B) strain gauge ranges

Six variants of specimens as shown in Fig. 13A with different fiber orientations (referred as $G_{13}$ and $G_{23}$ shear tests) and different thicknesses $h_1$, $h_2$ and $h_3$ were designed according to [9]. Furthermore, Fig. 13B, c show schematically the different fiber orientations of the $G_{13}$ and $G_{23}$ shear tests, respectively. The associated dimensions of specimens are summarized in Table 3. In this context, a CFRP plate with a unidirectional fiber orientation $\varphi =0^\circ$ was fabricated for the shear tests. Since the prepreg plies used for production each have a thickness of 0.22 mm, 86 plies are used for the required total height of $d_1=19$ mm according to Table 3. The number of samples taken from a $600 \times 600$ mm plate is summarized in Table 4. The specimens are water jet cut like the tensile specimens in Sect. 2.1. In a further step, the V-notches are then milled. Additionally, the black clear specimens are sprinkled with a white varnish to get a pattern, which is necessary for optical measurement system. A sprinkled sample is exemplified in Fig. 14A. This is clamped in the testing machine with the shear test loading fixture as illustrated in the experimental setup in Fig. 14B. The same tensile testing machine (MTS 100 kN) including the load cell and the optical measurement system (GOM Aramis) are used as for the tensile tests in Sect. 2.1. The experiments, which are displacement controlled according to [23], are loaded in the longitudinal direction y with respect to the fiber direction or the type of specimens ($G_{13}$ or $G_{23}$). Two virtual extensometers are defined in ARAMIS, as illustrated in Fig. 14C, to obtain the required strains $\varepsilon _{+45^{\circ }}$ and $\varepsilon _{-45^{\circ }}$ as schematized in Fig. 12B.

Fig. 13

Schematic representation (A) of the six different sample types taken from a unidirectional CFRP plate, (B) of $G_{13}$ specimens and (C) of $G_{23}$ specimens

Table 3 Nominal specimen dimensions regarding to Fig. 12A

Table 4 Number of $G_{13}$ and $G_{23}$ shear test samples depending on specimen height h

Fig. 14

Experimental investigations: (A) A sprinkled $G_{13}$ shear test sample, (B) experimental setup and (C) virtual extensometers in ARAMIS

The failure modes obtained from the shear tests are shown in Fig. 15A and in Fig. 15(B) for the $G_{13}$ and $G_{23}$ specimens, respectively. The sample thickness has no visible influence on the failure pattern. In all samples, it can be seen that the failure is occurred in the vicinity of the V-notch. The $G_{13}$ samples fail in the horizontal direction, as can be seen in Fig. 15A. In contrast to the $G_{13}$ specimens, the $G_{23}$ specimens as shown in Fig. 15B fail in the direction of a notch surface, i.e., at $45^\circ$ to the vertical.

Fig. 15

Failure results: (A) Fractured G13 specimen and (B) fractured G23 specimen

Determination of $G_{13}$: to determine the shear modulus $G_{13}$, shear tests are applied to specimens illustrated in Fig. 13B. [23] provides further information regarding the test procedure and the data evaluation. The resulting curves for shear stress $\uptau _{13}=\uptau _{xy}$ versus shear strains $\gamma _{13}=\gamma _{xy}=|\varepsilon _{+45^{\circ }}|+|\varepsilon _{-45^{\circ }}|$ for the different specimen thicknesses $h_1=3$ mm, $h_2=5$ mm and $h_3=8$ mm are shown in Fig. 16A, B, C, respectively, where a regression for the initial slope of each curve describes the corresponding in-plane shear modulus $G_{13}$. In addition, the linear area at the beginning can be clearly seen, where the shear modulus can be identified. The frequency distributions of $G_{13}$ for the different specimen thicknesses $h_1=3$ mm, $h_2=5$ mm and $h_3=8$ mm are illustrated in Fig. 16D, E, F, respectively. It can be seen that the scatter of the results is larger for thicker samples.

Fig. 16

Shear stress versus shear strain results of $G_{13}$ shear tests for specimen thicknesses (A) $h_1=3$ mm, (B) $h_2=5$ mm and (C) $h_3=8$ mm. Frequency distributions of in-plane shear modulus $G_{13}$ for specimen thicknesses (D) $h_1=3$ mm, (E) $h_2=5$ mm and (F) $h_3=8$ mm

Determination of $G_{23}$: to determine the shear modulus $G_{23}$, shear tests are applied to specimens illustrated in Fig. 13c. [23] provides further information regarding the test procedure and the data evaluation. The resulting curves for shear stress $\uptau _{23}=\uptau _{xy}$ versus shear strains $\gamma _{23}=\gamma _{xy}=|\varepsilon _{+45^{\circ }}|+|\varepsilon _{-45^{\circ }}|$ for the different specimen thicknesses $h_1=3$ mm, $h_2=5$ mm and $h_3=8$ mm are shown in Fig. 17A, B, C, respectively, where a regression for the initial slope of each curve describes the corresponding out-of-plane shear modulus $G_{23}$. In addition, the linear area at the beginning can be clearly seen, where the shear modulus can be identified. The frequency distributions of $G_{23}$ for the different specimen thicknesses $h_1=3$ mm, $h_2=5$ mm and $h_3=8$ mm are illustrated in Fig. 17D, E, F, respectively. It appears that the scatter of the results is independent of the sample thickness.

Fig. 17

Shear stress versus shear strain results of $G_{23}$ shear tests for specimen thicknesses (A) $h_1=3$ mm, (B) $h_2=5$ mm and (C) $h_3=8$ mm. Frequency distributions of out-of-plane shear modulus $G_{23}$ for specimen thicknesses (D) $h_1=3$ mm, (E) $h_2=5$ mm and (F) $h_3=8$ mm

An overview of the range of values for the two shear moduli, depending on the thickness, is shown in a box-and-whisker plot Fig. 18 according to [25]. Furthermore, the shear modulus $G_{12}$ for batch 1($b_1$) and batch 2 ($b_2$) determined from the tensile tests are illustrated in Fig. 18. In addition to the median (horizontal line), the mean value is shown as a cross. It becomes clear that the in-plane $G_{12}$ shear modulus is similar to the $G_{13}$ shear modulus, and both are higher than the out-of-plane $G_{23}$ shear modulus. Since $G_{12}$ and $G_{13}$ are similar and also for both methods, tensile test for $45^{\circ }$ fiber-oriented specimens or shear test using the $G_{13}$ shear specimens, nearly equivalent values are obtained, a preferred method can be chosen for future investigations.

Fig. 18

Overview of the range of values for the shear modulus $G_{12}$ for batch 1($b_1$) and batch 2 ($b_2$) from the tensile tests and $G_{13}$ and $G_{23}$ from the shear tests for specimen thicknesses $h_1=3$ mm, $h_2=5$ mm and $h_3=8$ mm

The $n_m=5$ identified transversely isotropic material parameters according to Eq. (1) are summarized in Table 5, where the mean, the median and the standard deviation of each parameter are shown. Note that $G_{12}$ and $G_{13}$ are considered identical with respect to the parameter set and are therefore counted together as one parameter.

Table 5 $n_m=5$ identified transversely isotropic material parameters

Remarks:

• In addition to the fundamentals mentioned above with regard to the investigations on CFRP, there are several aspects that need to be analyzed in more detail.

• A main advantage of the (bias-extension) $\pm 45^{\circ }$-oriented tensile test is that the extremities of the fibers are free and consequently that there is no (or small) tension in the fibers [26]. One disadvantage is that the length of the specimen must be more than twice the width of the specimen. At the same time, it is assumed that the fibers of the alternating layers are bonded together, which of course presents a challenge in the fabrication of the specimens. In this context, slip must not occur [26].

• Compared to the $45^{\circ }$ tensile tests, which are cut out from relatively thin CFRP sheets, as described above, e.g. with waterjet cutting, the Isopecu shear specimens require a significantly higher manufacturing and fabrication effort and a more precise geometry tolerance must be maintained. To fit into the shear fixture, and to avoid edge loading on one side, the specimens must be cut from 19 mm thick plates. In addition, V-notches must be milled or cut in. Centering and symmetry must also be ensured when clamping in the testing machine.

• Since this paper is concerned with the determination of elastic material parameters, little attention has been paid to the failure of the specimens and the associated delamination or debonding. Figure 19 shows a fracture surface of a $90^{\circ }$ sample in which detached fibers are visible, i.e., the behavior of the fiber-matrix interface should be studied in the future.

Fig. 19

Visible fibers on the fracture surface of a $90^{\circ }$ specimen

3 Experimental Investigation of the Constituents

As illustrated schematically in Fig. 1B, on the meso-scale the behavior of carbon fiber and polymer matrix takes into account separately. In this work it is assumed that the constituents are isotropically linear elastic, i.e., the material behavior of fiber and matrix can be modeled by independent Young’s modulus E and Poisson’s ratio $\nu$. If the proportion of fibers is also known, statements can be made about the behavior of the overall composite. Therefore, $n_m = 5$ independent parameters will be determined by experimental investigations. These are summarized in the material parameter vector

$$\begin{aligned} \underline{\kappa }=[\kappa _1,\kappa _2,\kappa _3,\kappa _4,\kappa _5]^T=[E_{f}, \nu _{f}, E_{m}, \nu _{m}, c_{f}]^T, \end{aligned}$$

(2)

where $c_{f}$ is the volume fraction of the fiber and $E_{f}$, $\nu _{f}$ and $E_{m}$, $\nu _{m}$ are Young’s moduli and Poisson’s ratios of the fiber and the matrix, respectively. The determination of the Poisson’s ratio $\nu _f$ of the fiber can not be made on the basis of macroscopic experiments and is therefore not dealt with in this paper. To determine the elastic material parameters $E_{f}$, $E_{m}$ and $\nu _{m}$, a group of tensile tests was carried out. In addition to tensile tests of the individual constituents, investigations to determine the volume fraction $c_{f}$ are performed at the composite.

The data used for this section are taken partly from the student works of Liu [16] and Alheilo [27].

3.1 Tensile Tests of the Individual Constituents

To determine the elastic material parameters, tensile tests according to [22] in [22] for the matrix and [28] in [28] for the fiber were carried out. The matrix test provides the Young’s modulus $E_m$ as well as the Poisson’s ratio $\nu _m$, whereas the fiber test provides the Young’s modulus $E_f$.

The individual constituents consist of carbon filament and an epoxy resin system. In Table 6 material specifications, test standards and determinable material parameters are summarized.

Table 6 Materials used, test standards and material parameter results requested

Determination of $E_m$ and $\nu _m$: to determine the Young’s modulus $E_{m}$ as well as the Poisson’s ratio $\nu _M$, 30 tensile tests are applied to the matrix material specimens, where a broken one is depicted in Fig. 20A. [22] provides further information regarding the test procedure and the data evaluation. The matrix samples are cut out with a water jet from an ordered plate with the desired thickness of 4 mm. The dimensions of the specimens are given in Fig. 20B and in Table 7, which correspond to the tensile test description according to ISO 527-2/1B/1. The designation after the first slash (1B) indicates the type of specimen and the designation after the second slash (1) the test speed (1 mm per minute).

Fig. 20

A experimental specimen and B geometry of a matrix element

Table 7 Geometry explanation of the specimen from the matrix regarding to Fig. 20B

The experiments, which are displacement controlled, are loaded in the longitudinal direction. A load cell supplies forces $\bar{F}$ at different observation states, whereby corresponding stresses in longitudinal direction $\bar{\sigma }_{x}=\bar{F}/A_1$ for the matrix material are determined using the cross-sectional area of the narrow part $A_1=b_1 \, h$, see Table 7. A video extensometer is used to measure the strains in the longitudinal and transverse directions $\bar{\varepsilon }_{x}$ and $\bar{\varepsilon }_{y}$, respectively, independent of slip. In this context, reference points were drawn in the gauge range of the sample, which can be seen in Fig. 20A.

The resulting curves for stress $\sigma _{m}=\bar{\sigma }_{x}$ versus strain $\varepsilon _{x}=\bar{\varepsilon }_x$ for 30 experiments are shown in Fig. 21A, where a regression for the slope of each curve describes the corresponding Young’s modulus $E_{m}=\Delta \sigma _{m}/\Delta \varepsilon _{x}$ of a matrix material sample. Furthermore, in Fig. 21C experimental longitudinal strain $\varepsilon _{x}$ versus transversal strain $-\varepsilon _{y}=-\bar{\varepsilon }_{y}$ curves are illustrated, where a regression of the slope for each curve renders the corresponding Poisson’s ratio $\nu _{m}=-\Delta \varepsilon _{y}/\Delta \varepsilon _{x}$. The frequency distributions of $E_{m}$ and $\nu _m$ are illustrated in Fig. 21B, D, respectively.

Fig. 21

Experimental results for matrix material: A Longitudinal stress $\sigma _{m}$ versus longitudinal strain $\varepsilon _{x}$ curves and (B) frequency distributions of Young’s modulus $E_{m}$. C Longitudinal strain $\varepsilon _{x}$ versus transversal strain $-\varepsilon _{y}$ curves and D frequency distributions of Poisson’s ratio $\nu _{m}$

Determination of $E_f$: to determine the Young’s modulus $E_{f}$, 39 fiber tensile tests according to [28] are performed on single filaments of carbon, which are specified in Table 6. To avoid damaging of individual fibers, they are framed in tabs, as illustrated schematically in Fig. 22A. The tabs for mounting in the machine are made of thick paper. A slot of length equal to the gauge length is cut out in the middle of the tab as shown in Fig. 22A. The actual gauge length of the specimen is measured using a Vernier caliper.

The samples to be tested are mounted in the experimental setup, see for a representative example Fig. 22B. Then without disturbing the setup, both sides of the tabs are cut carefully at the mid-section as illustrated in Fig. 22A. The experiments, which are displacement controlled, are loaded in the longitudinal direction. A load cell supplies forces $\bar{F}$ at different observation states, whereby corresponding stresses in longitudinal direction $\bar{\sigma }_{x}=\bar{F}/A_0$ for the fiber material are determined using the cross-sectional area $A_0$. The cross-sectional area of a single filament is precalculated using the mean diameter, which is taken from the manufacturer’s data sheet. By applying a video extensometer, the strains in longitudinal directions $\bar{\varepsilon }_{x}$ are measured. In this context, reference points were drawn at the clamping jaws, which can also be seen in Fig. 22B.

Fig. 22

A Schematic illustration of a fiber mounted in a tab and B experimental setup

The resulting curves for stress $\sigma _{f}=\bar{\sigma }_{x}$ versus strain $\varepsilon _{x}=\bar{\varepsilon }_x$ are shown in Fig. 23A, where a regression for the slope of each curve describes the corresponding Young’s modulus $E_{f}=\Delta \sigma _{f}/\Delta \varepsilon _{x}$ of a fiber. The frequency distribution of $E_{f}$ is illustrated in Fig. 23B.

Fig. 23

Experimental results for fiber filaments: (A) Longitudinal stress $\sigma _{f}$ versus longitudinal strain $\varepsilon _{x}$ curves and (B) frequency distributions of Youngs’s modulus $E_{f}$

Additional investigations of fiber and matrix: In addition to the elastic parameters, other mechanical parameters can also be examined. For this purpose, the total stress–strain curves, i.e. up to failure, of the investigated fiber filaments and matrix specimens are presented in Fig. 24A, B, respectively. The diagrams shown previously in Figs. 21A and 23A are limited to the linear initial range for the sake of clarity. In the case of material models that take damage mechanisms into account, the critical strains of the matrix and the fiber can be necessary. In this context, histograms for the critical strains of the matrix and the fiber can be seen in Fig. 24C, D, respectively.

Fig. 24

Longitudinal stress versus longitudinal strain curves (A) of matrix and (B) of fiber filaments. Frequency distributions of critical strains (C) of the matrix and (D) of fiber filaments

3.2 Investigations of Volume Fraction

In addition to the elastic material parameters of the constituents the volume fraction of the fibers and the matrix $c_{f}$ and $c_{m}$, respectively, for the composite can be determined experimentally. In this work, two different methods, 1st Ashing technique and 2nd Archimedes’ principle are used to calculate the volume fractions, considering the manufacturer data. The specified densities for the fibers and the matrix are $\varrho _f=1.8$ g/cm$^3$ and $\varrho _m=1.2$ g/cm$^3$, respectively. The fiber volume and mass fractions required for both methods can be described, based on [29], by

$$\begin{aligned} c_{f} =\frac{\varrho _{f}\Psi _{f}}{\varrho _{m}(1-\Psi _{f})+ \varrho _{f}\Psi _{f}}=\frac{V_{f}}{V_{total}} \end{aligned}$$

(3)

and

$$\begin{aligned} \Psi _{f} =\frac{M_{f}}{M_{total}}=\frac{\varrho _{f}V_{f}}{\varrho _{total}V_{total}}= \frac{\varrho _{f}}{\varrho _{total}} c_{f}, \end{aligned}$$

(4)

respectively, where the additional variables V and M are the volume and the weight corresponding to the fiber (f), the matrix (m) and the composite (total). Next, the experimental sequence of the two methods is described.

1. Ashing technique:

The ashing technique described in the standard [30] is intended for glass fibers. For this work, the method was adapted so that it is suitable for carbon fibers. Firstly, between 1 and 2 g of CFRP samples are weighed into a ceramic crucible as shown in Fig. 25B. They are then placed in a muffle furnace (CEM type Phoenix) as illustrated in Fig. 25A. The matrix is decomposed at $600^\circ \hbox {C}$ for a period of 45 min. After cooling to room temperature, the crucible is weighed again, see Fig. 25C, and the fiber weight fraction is determined using Eq. (4). In addition, the remaining fibers after matrix decomposition are shown in Fig. 25D for illustration. Finally, the fiber volume fraction can be calculated with Eq. (3) and the manufacturer’s information on density.

Fig. 25

Ashing technique: (A) Ceramic crucible in muffle furnace, (B) a sample on the scales before heating, (C) remaining material on the scales after heating and (D) fibers remaining after matrix decomposition

The ashing technique was carried out for the plate specifications already mentioned in Table 1, i.e., for the different fiber orientations $\varphi =0^{\circ }$, $\varphi =\pm 45^{\circ }$ and $\varphi =90^{\circ }$. The results of the fiber volume fractions for 14 samples of $\varphi =0^{\circ }$ fiber orientation, for 8 samples of $\varphi =\pm 45^{\circ }$ fiber orientation and 8 samples of $\varphi =90^{\circ }$ fiber orientation are given as histograms in Fig. 27A, B, C, respectively.

2. Archimedes’ principle:

According to the Archimedes’ principle, the weight of a solid body in a liquid corresponds to that of the upward buoyant force. Hydrostatic scales can be used to weigh solids both in air and in water and thus determine the density of the body. Firstly, the weight $M_{totoal}$ of the composite sample is weighed in the air under ambient conditions, as shown in Fig. 26A. Then the weight of the same sample under distilled water $M_{{fl,total}}$ is determined. Theoretically, the two values could be used to determine the density of the sample with the formula

$$\begin{aligned} \varrho _{total}=\dfrac{M_{totoal}\, \varrho _{H_2O}}{G_{total}}, \end{aligned}$$

(5)

where $\varrho _{H_2O}$ is the density of distilled water and $G_{total}=M_{totoal}-M_{{fl,total}}$ is the buoyancy of the sample. Equation (5) is inaccurate because the influence of temperature, buoyancy of the air, buoyancy of the measuring instrument and other factors are not taken into account. Depending on the manufacturer’s specifications of the measuring instrument, the form of Eq. (5) can be adjusted accordingly. According to [31], the manual for the used density determination kit (Sartorius YDK 01), the adjusted formula that takes into account the buoyancy of the sample in the air and the buoyancy of the instrument parts is

$$\begin{aligned} \varrho _{{total}}=\dfrac{M_{{total}}\,\varrho _{H_2O}}{0.99983\,G_{{total}}}+0.0012\dfrac{\text{ g }}{\text{ cm}^3}. \end{aligned}$$

(6)

Assuming that the total mass of the sample consists only of the fiber and the matrix, Eqs. (3) and (4) can be used to describe the fiber volume fraction by the given densities $\varrho _{{total}}, \varrho _{f}, \varrho _{m}$ with

$$\begin{aligned} c_f=\dfrac{\varrho _{{total}}-\varrho _{m}}{\varrho _{f}-\varrho _{m}}. \end{aligned}$$

(7)

Fig. 26

Hydrostatic weighing: (A) Weighing the sample in air and (B) weighing the sample in distilled water

The Archimedes’ principle was carried out for the plate specifications already mentioned in Table 1, i.e., for the different fiber orientations $\varphi =0^{\circ }$, $\varphi =\pm 45^{\circ }$ and $\varphi =90^{\circ }$. The results of the fiber volume fractions for 28 $\varphi =0^{\circ }$ samples, for 8 $\varphi =\pm 45^{\circ }$ samples and for 8 $\varphi =90^{\circ }$ samples are given as histograms in Fig. 27D, E, F, respectively. Comparing Fig. 27A–C with Fig. 27D–F, it can be seen that the volume fractions determined by the Ashing technique are lower than those determined by the Archimedes’ principle. This can be due to various reasons, e.g. undesired fiber loss during ashing. In addition, a possible void content leading to an increased buoyancy of the composite in the Archimedes’ principle, cf. Equation (6), may lead to deviations in the results.

Fig. 27

Volume fractions for different fiber orientations (A) $\varphi =0^{\circ }$, (B) $\varphi =\pm 45^{\circ }$, (C) $\varphi =90^{\circ }$ and (D) $\varphi =0^{\circ }$, (E) $\varphi =\pm 45^{\circ }$, (F) $\varphi =90^{\circ }$ based on the ashing technique and the Archimedes’ principle, respectively

The 4 of $n_m=5$ identified parameters in this paper on the meso-scale according to Eq. (2) are summarized in Table 8, where the mean, the median and the standard deviation of each parameter are shown.

Table 8 $n_m=4$ of 5 identified material parameters

Although homogenization methods are not presented in this paper, the Voigt hypothesis, see e.g. [29] is a suitable approximation in the fiber direction. The Young’s modulus in the fiber direction can therefore be estimated with known constituents parameters with

$$\begin{aligned} E_{1V}\approx c_f\,E_f + (1-c_f)\,E_m, \end{aligned}$$

(8)

where the {V} in the index symbolizes the Voigt approximation. For the mean values of the parameters ($c_f$ of Ashing technique ($\varphi =0^{\circ }$)) according to Eq. (2) the following value results

$$\begin{aligned} E_{1V}\approx c_f\,E_f + (1-c_f)\,E_m=0.634\cdot 216.382 + (1-0.634)\cdot 3.026\approx 138.294. \end{aligned}$$

(9)

This estimated value lies between the two determined mean values of the composite tests regarding Table 5.

4 Inhomogeneous Experiments

In addition to the above mentioned experiments to determine the material parameters, inhomogeneous experiments were carried out. Due to special geometries of the specimen, localization, damage or other effects, it is not always possible to obtain homogeneous strain and stress states within the specimen. In this work, tensile specimens are considered whose geometry is modified to obtain an inhomogeneous behavior. Such samples or their inhomogeneous experimental behavior can be used to validate or modify the previously determined material properties.

4.1 Flat Plate with a Hole

A first example of inhomogeneous experiments is a flat plate with a circular hole as shown exemplary in Fig. 28B. The material under investigation for different fiber orientations $\varphi =^{\circ }$, $\varphi =\pm ^{\circ }$ and $\varphi =^{\circ }$ is the same as for the homogeneous experiments in Sect. 2. The geometry of a specimen is given in Fig. 28A, with a length of $L_3 = 250$ mm, a width of $b_1 = 25$ mm and a thickness of $h_{0^{\circ }}=1$ mm, $h_{\pm 45^{\circ }}=2$ mm and $h_{90^{\circ }}=2$ mm depending on the fiber orientations. The circular hole is in the center of the rectangle with a diameter of $d = 6$ mm. The distance between end tabs is $L_2=150$ mm.

The specimen leads to inhomogeneous stress and strain states which need to be measured. This is possible with optical measurement methods. In this case, the same system as for the homogeneous experiments in Sect. 2.1 is applied, to measure local displacements on the plate with hole. The experiments are displacement controlled with a global displacement $u=9$ mm in time $t=270$ s. For every experiment, the global displacement, the total forces $\bar{F}$ of a load cell and additionally the local displacement data from the optical system in horizontal direction and in vertical direction are measured. A $\varphi =^{\circ }$ sample clamped in the machine that has already failed can be seen in Fig. 28C. For the sake of clarity, only the evaluation of a $\varphi =^{\circ }$ sample is shown as an example in this publication.

Fig. 28

Plate with a hole: (A) Geometry, (B) exemplary sample and (C) a fractured sample

Figure 29 shows the force displacement curve of one representative experiment. A relatively linear increase in force up to 67 kN and the associated total displacement 6.15 mm can be seen. There are some force drops, as can be seen, for example, at point (B) of the curve where acoustic signals with low and high frequency occurred during the test, indicating matrix cracking, delamination and fiber failure, respectively. Additionally, the local strains resulting from the local displacements are considered using contour plots. In Fig. 30A–H the local major strains $\varepsilon$ at eight observation steps with regard to observation points (A)-(H) in Fig. 29 can be seen. A definition of the major strain can be found in [32]. As mentioned above, initial failure is evident at observation point (B), as indicated in Fig. 30B by a strain concentration parallel to the fiber near the hole. As the observation progresses, a failure parallel to the fiber over the entire specimen can be seen in Fig. 30B–G, eventually leading to explosive failure of the specimen, as depicted in Fig. 30H.

Fig. 29

Total force versus transverse displacement for one representative experiment

Fig. 30

Local major strains at eight observation steps with regard to points (A)–(H) in Fig. 29

4.2 Flat Plate with Semicircular Notches

As a second example of inhomogeneous geometries, semicircular notched flat plates are examined. The material under investigation for different fiber orientations $\varphi =^{\circ }$, $\varphi =\pm 45^{\circ }$ and $\varphi =90^{\circ }$ is the same as for the homogeneous experiments in Sect. 2 and the inhomogeneous experiments in Sect. 4.1. The geometry of a specimen is given in Fig. 31A. It is a flat plate with a length of $L_3 = 250$ mm, a width of $b_1 = 25$ mm and a thickness of $h_{0^{\circ }}=1$ mm, $h_{\pm 45^{\circ }}=2$ mm and $h_{90^{\circ }}=2$ mm depending on the fiber orientations. The length between end tabs is $L_2=150$ mm. Between the two semicircular notches, each with a radius of $r= 5$ mm, there is a distance of $b_2 = 15$ mm.

The experiments are displacement controlled with a global displacement $u=18$ mm in time $t=540$ s. For every experiment, the global displacement, the total forces $\bar{F}$ of a load cell and additionally the local displacement data from the optical system in horizontal direction and in vertical direction are measured. For the sake of clarity, only the evaluation of a $\varphi =\pm 45^{\circ }$ sample is shown as an example in this publication.

Fig. 31

Flat plate with semicircular notches: (A) Geometry of specimen and (B) total force versus transverse displacement for one representative experiment

Firstly, the force displacement data are analyzed. Figure 31B shows the force displacement curve of one representative experiment. After a degressive increase in force up to 4.5 kN and associated total displacement of 2 mm, a relatively linear course follows up to the final failure at 7.5 kN and associated total displacement of 14 mm. The local strains resulting from the local displacements are considered using contour plots. In Fig. 32A–H the local major strains $\varepsilon$ at eight observation steps with regard to points (A)-(H) in Fig. 31B can be seen. From contour Fig. 32B, X-shaped strain concentrations can be seen, i.e., near the notches in $\pm 45^\circ$ direction, corresponding to the fiber orientation. As can be seen from the contour plot in Fig. 32H for the last observation point (H), the specimen fails correspondingly in a $45^\circ$ direction at a notch root.

Fig. 32

Local major strains at eight observation steps with regard to points (A)–(H) in Fig. 31B

Remarks:

• In the inhomogeneous experiments shown, only the local strain and strain concentration at the hole and notches were considered. Correlating to this, there are stress concentrations. According to [33], an approximate stress concentration of $\sigma _{max}/\sigma _{\infty }=3.3$ can be estimated for the example flat plate with a hole in Sect. 4.1, whereby influences due to the material composition are not taken into account. Here, $\sigma _{max}$ and $\sigma _{\infty }$ are the maximum stress at the hole and the stress at the clamping jaws, respectively.

• The effect of fiber orientation on stress concentration in a unidirectional tensile laminate with finite width and central round hole was studied in [34]. The stress concentration factor was found to be maximum for $\varphi =0^{\circ }$ and minimum for $\varphi =45^{\circ }$.

5 Conclusion and Outlook

The aim of this paper is an extensive experimental study of a CFRP material. In particular, the mechanical properties are investigated at two different scales to be able to verify homogenization methods and material models. This means that experiments and parameter identifications are carried out on the overall composite material and the individual constituents, such as carbon fibers and epoxy matrix. For a complete description of an elastic transversely isotropic macro-scale behavior, five of five required material parameters are determined. This includes the Young’s modulus in fiber direction, the Young’s modulus transverse to the fiber direction, in-plane shear modulus, the out-of-plane shear modulus, and a Poisson’s ratio of the composite. Assuming isotropic constituents, five material parameters are also required for a complete meso-scale description. Since the transverse strain of the fiber cannot be readily determined experimentally, four of the five parameters are identified. This includes the Young’s modulus of the fiber, the Young’s modulus and Poisson’s ratio of the matrix and the volume fraction of the fiber.

Additionally, it is shown that other parameters can be determined from the experimental data, e.g. with respect to damage modeling, but not all of them are presented in this paper. Inhomogeneous tests on the composite material conclude the work. These are additionally necessary to validate the determined parameters and their respective models. In this context, tensile tests are carried out for flat plate specimens with a hole and with semicircular notches. For both cases, contour plots for the local strains following force-displacement diagrams were created.

Future developments will focus on validation with the presented inhomogeneous experiments and on the experimental- and simulation-based prediction of the curing during manufacturing process and damage of CFRP.