Abstract
The paper presents the results obtained in modeling the creep phenomenon of unidirectional composites reinforced with fibers. Thus, several models that have proven their validity and results obtained with their help are discussed. Analyzing a multitude of models described in the paper presented in references the authors describe the most used by the researchers. The micromechanical model, the homogenization method, the finite element method and the Mori–Tanaka formalism are described. These methods are most used in engineering applications studies in the last time. Following the analysis of each method, the advantages and disadvantages are presented and discussed. The results obtained are compared with experimental determinations. The application of the methods is done to composite materials reinforced with aligned carbon fiber. The methods are, sure, valid for every type of composite reinforced with fibers. Since the creep of materials is a frequently encountered phenomenon in practice, the knowledge of material properties and the existence of convenient calculation models become important for designers, which is why the paper presents the most used calculation methods to model this behavior.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The technology of advanced composites has developed to the stage where these materials are more and more in the attention of engineers in different and varied industrial fields. Viscoelastic materials manifest the phenomenon of creep, very important in practice through the consequences it can have on the behavior of structures or machines. This phenomenon is defined/utilized in commercial, military, aerospace and several other industries. Composite are ideal for structural applications where high strength-to-weight and stiffness-to-weight ratios, improved fatique resistance and improved dimensional stability are required. Despite the numerous advantages of fiber reinforced plastics over their metallic counterparts, there is a great concern regarding their long term durability due to their time-dependent behavior. That is, composite materials which contain one or more polymeric constituents, show a significant amount of time-dependent mechanical behavior in many service conditions. This effect known as “viscoelasticity” is reflected for instance, in composite materials with resin matrices for which moduli and strength properties are time dependent. In the recent years the subject of viscoelasticity has received considerable attention from both analytical as well as experimental points of view. Viscoelastic behavior must be accounted for in service environments if an efficiently design structure is to be achieved. Although most fiber reinforcements have been shown to be essentially time independent, i.e. they show minimal viscoelastic behavior, the currently used polymeric matrix exhibits significant viscoelastic response. It is indeed an oversimplification to visualize composites as anisotropic homogeneous materials and thereby ignore the role of the individual constituents—the matrix and the fibers. There are of course some properties which are predominantly controlled by only one constituent, but on the other hand, other properties may very well rely on the interaction between the resin and fibers.
Viscoelastic materials manifest the phenomenon of creep, very important in practice through the consequences it can have on the behavior of structures or machines. This phenomenon is defined as the time-dependent deformation of the studied material, if subjected to a force [1]. Usually the phenomenon manifests itself at high temperatures in relation to the temperature of the environment in which the structure or machine is currently located [2]. However, there are cases in which this phenomenon can occur even at room temperature for certain materials (such as, for example, stainless steel). Obviously this elongation of the material, which can occur after a long time of operation of a structure or machine, can lead to the destruction of the structural member. There are three intervals of creep manifestation, i.e., primary, secondary and tertiary creep [2], defined by the appearance of the creep curve. Engineering applications generally refer to the first two stages of creep. The third stage of creep is characterized by the rapid increase of the deformation rate and results in a geometric instability, i.e., it leads to the destruction of the material. The strain rate increases significantly in tertiary creep. Of course it is avoidable to reach this region so a study in this area becomes uninteresting. For practical applications, designers must know the deformation rate over time for the first two creep zones. This can be done theoretically, using creep models or by experimental investigations and corresponding measurements. Such models, useful for design activities, are presented in [2, 3]. The study of creep has been conducted in numerous papers (i.e. [4,5,6]) due to the practical importance of this phenomenon.
At the moment the engineering field is characterized by an unprecedented diversity of materials used, which correspond to certain special requirements determined by the application that is made. As a result, the properties of these materials are extremely diverse. The creep diagrams of these materials can differ greatly, if the same loading and temperature conditions are maintained. The most commonly used method of obtaining a creep diagram is the experimental method, making measurements for the material and obtaining the diagram. But this procedure, absolutely correct and established for a long time, is obviously expensive and time consuming. Numerous determinations are required, at different loads and at different temperatures. As a result, the researchers focused on obtaining these diagrams using less expensive methods. Thus in [7] is presented a scheme that proposes to perform accelerated tests to study the creep behavior of laminated composites. Obviously, this type of approach allows to decrease the time to obtain a creep diagram. The measurements aimed at short-term testing of a material at high temperature, to predict the long-term behavior of the material using the principle of time–temperature overlap (TTSP) [8,9,10]. Obviously, the development of models and calculation methods that allow the determination of creep properties would be much more advantageous. This has been done by many researchers. For example, paper [11] studies the nonlinear viscoelastic behavior of a unidirectional fiber composite. The method applied to obtain the results is the finite element method (FEM). In the paper is studied a composite that has symmetries at the geometric level but the method can be applied to a material with a more complex topology. To achieve this goal in [12,13,14] a set of nonlinear constitutive equations for viscoelastic materials is developed. One can thus obtain the possibility to study the stress field if one considers a diversity of conditions (i.e. thermal effects or humidity).. The paper [15] develops the results obtained for unidirectional composites reinforced with graphite and glass. In this way it obtained a good correlation with micromechanical models [11].
These models are improved in [16,17,18] for the study of the nonlinear creep behavior in a wide variety of materials. This was done with the help of an empirical model, obtaining a method that is very suitable for numerical approaches.
The previously presented works [16,17,18] allowed the development of a nonlinear viscoelastic model [19, 20] which was used in the analysis of graphite/epoxy composites. The model can be successfully applied to the study of orthotropic materials.
In [21] specific aspects of the viscoelastic behavior of composites were studied. Thus, it was found that a moisture concentration of about 1% is a critical limit for carbon epoxy laminates. If the limit is exceeded, the viscoelastic deformation of the material is much faster. Shear stresses exceeding 50% of the final tensile strength can lead to irreversible deformation during creep. The viscous behavior of epoxy resin matrix composites reinforced with unidirectional aramid fibers was studied in [22]. An adequate mathematical model usable in both linear and nonlinear fields was verified. The originality of the paper consists in the introduction of nonlinear viscoelastic coefficients, dependent on stress and temperature. The method of analysis proved its validity in the study of the nonlinear model presented in [12]. In [23,24,25,26] variational principles are used to improve the time-dependent elastic model with a relatively simple mathematical description. The analysis is made on composites with randomly distributed fibers, of different diameters, but with a constant average volume ratio of the fiber everywhere. In this description a fiber, geometrically perfectly circular, is surrounded by a circular matrix. The condition that allows to obtain the equivalent engineering coefficients of the material is that the stored deformation energy is equal to the one existing in the equivalent homogeneous material. In [27] the influence of temperature on a polymeric composite but at low temperatures is studied (the analyzed application is for a spacecraft). It is found that the geometry of the composite microstructure becomes a very important element. In [28] it is synthesized the results obtained by other researchers and determined the elastic constants for an orthotropic and a transverse isotropic composite. Another approach for a transverse isotropic material is the one developed by Hill [29,30,31,32], which gives us upper and lower limits of elastic constants, which are extremely useful for designers.
An extension of the well-known Mori–Tanaka method [33] for the study of the viscoelastic response of a biphasic composite is made in [34]. In [35] the nonlinear viscoelastic/viscoplastic response of graphite/bismaleimide IM6 /5260 is studied. Another micromechanical analysis of a fiber-reinforced composite is presented in [36, 37] which proved to be in good agreement with the results obtained in [11]. Biphasic composites represent the most used composite in engineering applications. As a consequence their mechanical properties have been addressed by many researchers due to the practical applications required by industry [38,39,40,41,42,43,44,45,46,47,48,49], considering different type of pair of materials used and different properties necessary to be studied. New aspects concerning of the new type of composite material are studied in [50,51,52].
The main objective of the work is to present of the most used methods for determining the behavior of fiber-reinforced composite materials. Due to the frequency with which these methods are used in engineering practice, they have proven to be extremely useful and easy to apply to obtain results in a short time and with minimal costs. The main models used by researchers are described. Experimental procedures prove the theoretical results obtained. The material presented in our review paper is strongly supported by the results obtained in [53,54,55,56,57]. Other useful results are presented in papers [58,59,60,61,62,63,64,65,66,67].
2 Micromechanical models
2.1 Micromechanical approach
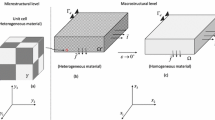
In a micromechanical analysis of the composite material it is desired to obtain the elastic constants based on models that use the values of these constants for each component of the composite. It is considered that the properties of the composite members, their placement and their dimensions are known. For example, if it is considered a unidirectional composite, the reinforcing fibers can be randomly placed in the matrix material or can be placed in a regular network with known geometric parameters. In the case of the models we use, symmetry can help us to considerably simplify the calculations.
A model of a reinforced fiber composite is presented in Fig. 1. In a micromechanical analysis the following hypothesis are made:
The fibers are continuous and circular. These fibers, oriented in the X1-direction, are distributed regularly in a rectangular array in the transversal X2–X3 plane.
The materials of fibers are considered to be linearly elastic and anisotropic. The material of the matrix is isotropic but being nonlinear viscoelastic.
No crack or holes may appear and develop and the contact between fibers and matrix is merely mechanical.
The periodicity of the structure of a one-dimensional composite material with fibers makes it possible to study a single representative unit cell (RUC) and, therefore, the size and complexity of the problem can be significantly reduced. Figure 2a shows a RUC of the previous periodic pattern (see Fig. 2). For analysis, the RUC used for the study consists of two sub-cell that together shape only a quarter of a fiber, as in Fig. 2b. The hypothesis is that the RUC is small compared to the dimensions of material.
The RUC is referred to a local frame (X1, \(x_{2}^{(\lambda )}\), \(x_{3}^{(\lambda )}\)) (Fig. 2b). We consider that the displacement in each sub-cell is obtained via the linear relations [27, 28]:
Here \(u_{i}^{o}\) are the displacement components of the origin. We note that “\(\lambda\) “ represents both, i.e., fiber (when \(\lambda = f\)) and matrix (when \(\lambda = m\)).
For a linear elastic material we have the well known relation for the engineering strain:
Equation (2) becomes, in an unified form, considering both fiber and matrix:
If \(i \ne j\) the following relation can be written:
The notation \(\gamma_{ij}^{(\lambda )} = 2\varepsilon_{ij}^{(\lambda )} ;\;i,j = 1,2,3;\;i \ne j\) , for the engineering shear strain is used.
Using Eq. (1) in Eq. (2) and considering Eqs. (3) and (4) it obtains:
The constitutive equation for a linear and transversely isotropic composite is:
or, using the engineering constants \(E_{ij}\), \(\nu_{ij}\), \(G_{ij}\):
\(E_{11}\) and \(E_{22} = E_{33}\) are the Young’s moduli, \(G_{23}\) and \(G_{12} = G_{13}\) are the shear moduli and \(\nu_{23}\) and \(\nu_{12} = \nu_{13}\) are the Poisson’s ratio. X1 is the direction of anisotropy and the X2–X3 plane is the plane of isotropy. From (12) it can be obtained:
where:
Equation (13) can be written in a compact form as:
In the case of a polymeric fiber reinforced composite the overall behavior should be considered as viscoelastic. This viscoelastic material, loaded with an applied constant stress, has a behavior described using the Boltzmann’s superposition principle described by Schapery’s equation [12], in the modified form:
where:
Using [12] the constitutive equations can be written as:
In Eq. (18), \(D_{n}\) is offered by Eq. (17), \(\nu (t)\) is the Poisson’s ratio (time-dependent), and \(\delta_{ij}\) is the Kronecker’s delta. In the present study, Poisson’s ratio is considered to be time-independent.
To determine the overall behavior of the composite, the next steps are taken. First, determine the average stress based by the stress calculated in each subcell if a constant load is applied to the RUC. Then, the average strain in the representative cell are calculated based on the strain that occur in each subcell. All these stresses and strains are mediated for the whole studied section. Thus the general behavior of the material is obtained based on the average stresses and average strains evaluated by the method described above.
2.2 Average stress
The composite material element considered is a rectangular parallelepiped having parallel edges with coordinate axes (X1, X2, X3) of volume V. The element considered is structurally representative for the whole material. We can have the problem of determining the average stress \(\overline{\sigma }_{ij}\) in the considered volume cell. The volume average of the stress is:
For a one-quarter of a fiber and matrix, it can be written:
where \(\overline{S}_{ij}^{(\lambda )}\) are the average stresses in the subcells “f” and “m”, and A and \(A_{\lambda }\) are the areas of the representative cell and of the subcells “f” and “m”, respectively. A unit depth of the representative volume has been considered, i.e., V = A × 1. Considering the notation from Fig. 2b. it results:
In a similar way, the average stress can be obtained with the relations:
It is appropriate to use polar coordinates for integration. In this case the Jacobian must be calculated:
and Eq. (23) for the fiber (sub-cell “f”) becomes:
where \(\sigma_{ij}^{(f)}\) has the components introduced in Eq. (15). Substitution of Eqs. (5)–( 11) into Eq. (25) leads to:
or:
Similarly, the average stresses in the matrix (sub-cell "m") are determined. For this one can calculate the total stress in the unit cell made up only of matrix material and then the stress in subcell "m" is obtained by subtracting that in sub-cell "f" from the total stress of the unit cell, previously determined. The following relationship is obtained:
Equation (28) together with Eq. (5)–(11) and (18) yields:
2.3 Average Strain
The average of the internal strain over volume is defines by:
and for RVE (35) is particularized by:
where \(A = A_{m} + A_{f}\) and \(\overline{\varepsilon }_{ij}^{(\lambda )}\) are the strain offered by Eqs. (5)–(11) (\(\lambda = f,m\)).
Using Eq. (1) and (3) it results (considering \(i = j = 1\))
From Eq. (37) and Eq. (36) one obtains:
or:
The procedure by which the unknowns can be determined is incremental. The unknowns are:
the six values of the stress in the two sub-cells: \(\overline{S}_{11}^{(\lambda )}\), \(\overline{S}_{22}^{(\lambda )}\), and \(\overline{S}_{33}^{(\lambda )}\);
the four micro-variables in the two sub-cells: \(\xi_{2}^{(\lambda )}\) and \(\zeta_{3}^{(\lambda )}\);
the three strains in the composite \(\overline{\varepsilon }_{11}\), \(\overline{\varepsilon }_{22}\), and \(\overline{\varepsilon }_{33}\).
The goal is to obtain a liaison between the stress in the matrix and the stress in the fiber of a RUC. The assumptions made by Aboudi in [36, 37] can be considered an oversimplification compared to the real case. If we are in the case of a biaxial state of stress in the plane (X2, X3), the relation that can be applied in the X2 direction is:
for the fiber and a similar relation for the matrix:
It results:
In the X3 direction it results the equation:
The concentration factors \(\alpha_{\lambda }\) and \(\beta_{\lambda }\) should satisfy the relations:
and
When the composite is loaded in only one of the directions, X2 or X3, the relation related to the other direction (unloaded), becomes:
and:
In the case of a uniaxial load one obtains 13 equations with 13 unknowns:
The made presentation shows that a micromechanical model for the analysis of a composite material (in our case unidirectional) is a good method of study and the result can be easily obtained. The results offer us the analytical relationships that provide the engineering constants of such a composite. Schapery's nonlinear constitutive equation in the case of a uniaxial isothermal load is the model used in the analysis. This approach allows the nonlinear viscoelastic response of the material to be taken into account. Papers with numerous experimental results [53,54,55,56,57] demonstrate the potential of applying this method.
3 Homogenization methods
3.1 Introduction
A homogenization theory is a mathematical method of mediating physical properties, a method used since about seven decades to study differential equations with periodic coefficients, which have a rapid variation. This method proves to be very suitable for studying the properties of composite materials, characterized essentially by repetitive structures. The experimental results obtained in papers indicated in the references give a good concordance with the theoretical predictions [53,54,55,56,57].
In the numerous studies of the bi- and multiphasic materials made in the last decades [33, 34, 36, 37, 39,40,41, 57] the researches lead to the subject of the homogenization method to obtain the mechanical material properties of such composites.
In the design process of a composite material, an important step is the estimation of the mechanical properties. Several calculation methods are applied to determine them. It has been found that the homogenization method has proven to be a very suitable method to be applied to the study of composite materials.
In other works, a theoretical study of the method is made, which involves the transition from a periodic structure, by homogenization, to a composite material considered homogeneous throughout its structure [44]. Various analytical and numerical methods have been proposed to obtain the properties of the homogeneous material. The obtained results were verified by experimental tests that proved a good concordance between the theoretical results obtained and the experimental ones, for a composite material reinforced with fibers [45]. The use of Euler's integration algorithm allows the development of a new method for homogenizing elasto-viscoplastic composites [68]. Three methods are used for this approach: direct, secant and tangent. A method that describes the interaction between the phases of the composite is based on the introduction of a second-order tensor. The main advantage is the unification of homogenization problems regarding heterogeneous elasto-plastic and elasto-viscoplastic materials [69, 70]. An example calculation predicts results that match values obtained by other methods. Experimental tests increase the confidence in the results obtained. Methods of improving the proposed methods and presenting practical applications are treated in [69,70,71,72,73,74,75,76,77]. Other related methods are considered in [78, 79]. The development of reliable models that can be easily applied by designers is a goal for researchers in the field. This section presents the homogenization theory to calculate the engineering constants of a composite material. The application is made for the case of a unidirectional composite reinforced with carbon fibers. Differential equations are obtained which, when solved, will provide the desired values. In order to obtain them, numerical procedures are used.
3.2 Homogenized model
After the appearance of the homogenization approach, during the development of the method, it was found to be a useful way to study the equations with partial differences with coefficients with rapid variations. The application of the homogenization theory has proved useful in the study of composite materials with periodic geometric structure allowing the determination of engineering constants useful in applications, which result from averaging operations. From a practical and design point of view, it is much more useful that such a material, with its periodic structure, can be treated as a homogeneous material, despite the fact that the material has a certain microstructure. Thus, this method replaces an equation with periodic coefficients with large variations, with an equation with constant coefficients. In this way the concept of continuum is extended to a new class of materials: microstructured materials. The basics of the method are presented in [80,81,82,83,84,85].
In this section the theory is applied to the study of the creep behavior of a carbon fiber one-directional composite.
The stress field \(\sigma^{\delta }\) for a repeating unit cells having the dimension \(\delta\) must respect the equations:
where \(\sigma_{ij}^{\delta } = \sigma_{ji}^{\delta }\), for \(i,j = 1,2,3\).
The contour conditions for the displacements are:
The boundary conditions can be written:
on the contour \(\partial_{2} \Omega\),(\(\partial_{1} \Omega \cup \partial_{2} \Omega = \partial \Omega\)). The Hook’s law reads:
or using a compact notation:
The elasticity matrix \(C\) is semi-positive definite:
for \(\alpha > 0\) and \(\forall x_{ij} ,x_{kh} \in {\text{R}}\). \(C_{ijkh} (x)\) are periodical functions of x with the period equal with the dimension \(\delta\) of the unit cell. Introduced a new function y, \(y = x/\delta\), it obtains:
The stress in the unit cell can be expressed as:
The dependence of stress on y is “quasi-periodical”. Introducing Eq. (74) in the equilibrium Eq. (67) it results:
We have used the relation:
but since \(y = x/\delta\) and thus \(dy = dx/\delta\); therefore:
The coefficients of \(\delta^{ - 1}\) in Eq. (75) must be 0, so:
Equation (58) is called the “local equation”. The first term of stress, \(\sigma_{ij}^{o}\) is theoretical, a function in two variables, y and x. But the dependence of this term on x is weak and so we can consider x being a constant in the domain \(\Gamma\). The stresses \(\sigma_{ij}^{o}\) are periodic functions on y, so (72) is defined only in the domain of a cell \(\Gamma\).
In a similar way, identifying the terms of \(\delta \;^{0}\), one obtaines:
By applying the average operator to Eq. (73), it follows:
But:
The stresses \(\sigma_{ij}^{1}\), due to the property of periodicity, take equal values on the corresponding points of the boundary of the cell \(\Gamma\). At the same points, \(n_{j}\) takes opposite values, so:
Integrating Eq. (76), it is possible to obtain the homogenized displacement field \(u^{o}\) in the domain Ω.
We denote:
The displacement field can be expressed by the series:
Here \(u^{o} (x)\) is a function only on x and the others terms \(u^{1} (x,y)\,\delta\) and \(u^{2} (x,y)\) are considered as quasi-periodical. With these new notations, using (77–79) one may write:
which can be simplified to:
where:
The infinitesimal term \(u^{1} (x,y)\,\delta\) represents a finite component of \(\varepsilon_{kh}\), that should be considered when applying the linear Hooke’s law:
From the Eq. (84), it follows:
or:
The terms \(\varepsilon_{kh,x}^{{}} (u^{o} )\) depend only on x. Equation (86) can be written in the alternative form:
Introducing:
Considering the Eqs. (87) si (88) with k(x) being an arbitrary function on x, it results:
Equation (89) becomes:
The Eq. (90) should remain valid for any strain field \(\varepsilon_{kh,x} (u^{o} )\). Thus, Eq. (90) becomes:
We have the relations (using the Green’ s theorem):
In Eq. (93), the indices i and j have been interchanged and the property \(C_{ijlm} = C_{jilm}\) has been used. From (92) and (93) it results:
Multiplying both sides of Eq. (94) by \(v\) and considering the property \(C_{ijlm} = C_{jilm}\), it follows that:
Interchanging the indices i and j one obtains:
Integration and addition Eqs. (95) and (96) while making use of the Eq. (94) leads to:
The problem is to find \(w^{kh}\) in \(V_{y}\) such that \(\forall v \in V_{y}\), Eq. (97) holds. If \(w^{kh}\) is obtained, then:
By applying the average operator, it follows:
It results:
A comparison of Eq. (100) with:
and using the notation \(\varepsilon_{kh,x} (u^{o} ) \equiv \tilde{\varepsilon }_{kh} (u^{o} )\), one obtains the homogenized coefficients:
As a consequence, it can be considered that there are two ways to determine the homogenized coefficients:
using the local equations, it is determined the strain and stress field. Then using the averages, the coefficients can be calculated;
using the variational formulation is possible to determine the function \({\text{w}}^{kh}\) which allows calculus of the coefficients.
In the case of a fiber reinforced composite, there exists a class of solution \({\text{w}}^{kh}\), with k,h = 1,2,3 which satisfies the differential equations:
with the boundary conditions:
and the supplementary conditions:
If \((x_{1} ,x_{2} ,x_{3} )\) are the principal material axis, we denote, in the case of a transversely isotropic material:
The other components of \(C_{ijkl}\) are identically zero. The stress–strain relations become:
or:
The equilibrium conditions of Eq. (61) are:
Equation (109) can be expressed in compact form:
Furthermore, Eq. (82) becomes:
and (100) becomes:
In the situation of plane strain loading conditions it results:
If the functions \({\text{w}}^{kh}\) are determined, one can write:
or, in an alternative form:
Additionally:
Equation (107) should remain valid for all \(\left\{ \varepsilon \right\}_{,x}^{{u^{o} }}\). Equation (103) becomes:
For the case of plane strain \(i = 2,3\) and \(j = 2,3\), therefore:
and:
It should be noted that the above equations do not depend on k and j. This means that if one determines for example \({\text{w}}^{22}\), the remaining functions \({\text{w}}^{33} = {\text{w}}^{23} = {\text{w}}^{32} = {\text{w}}\) are immediately obtained. The solution to these equations is:
and must satisfy the boundary conditions:
\(\left. {{\text{w}}^{kh,(f)} } \right|_{\partial \Gamma } = \quad \left. {{\text{w}}^{kh,(m)} } \right|_{\partial \Gamma }\) ,
and:
Let the repeating periodic cell be subjected to the boundary condition: \(u_{i}^{{}} = \alpha_{ij} y_{j}\). The average strain in the materials can be shown to be: \(\left\langle {\varepsilon_{ij} } \right\rangle = \overline{\varepsilon }_{ij} = \alpha_{ij}\). Furthermore, let us denote the displacement field by \({\text{w}}^{*}\) with the property \(\left. {{\text{w}}^{*} } \right|_{\partial \Gamma } = \left. {{\text{u}}\,} \right|_{\partial \Gamma }\) and \(\overline{\varepsilon }_{kh} \left( {{\text{w}}^{*} } \right) = \alpha_{ij}\). Due to the existing symmetry in the distribution of the unit cell it can be concluded that \(\left\langle {{\text{w}}^{*} } \right\rangle = 0\). Let the field \({\text{w}}\) also be introduced as:
corresponding to the boundary conditions:
and:
This function \(\left( {\text{w}} \right)\) verifies the condition of zero average and has the value zero on the contour and it is also a verification of Eq. (120). For the “quasi-periodical fields” \({\text{u}}\,_{1}\), it follows that:
The strain becomes:
and:
or:
If we consider a composite with unidirectional parallel fibers, the homogenized coefficients can be calculated via the relations:
where
One obtains:
For the plane strain loading conditions, we have:
and:
From the considerations presented above it results that in order to determine the sought coefficients \(C_{ij}^{o}\) it is necessary first to obtain the real field of deformations of the material and then to calculate the average values of the deformation in the two considered phases.
4 Mori–Tanaka method
4.1 Model
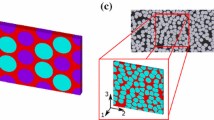
The theory developed by Mori-Tanaka can be used successfully to obtain the mechanical constants used in the calculation of a material or structures in the viscoelastic zone, particularly in the case of composites reinforced with one-dimensional fibers [34]. The analyzed material consists of an epoxy matrix with viscoelastic behavior, reinforced with parallel carbon fibers, distributed inside the matrix (Fig. 3). In this situation the resulting material is generally orthotropic. But if the fibers formed by the elliptical cylinders are distributed randomly, then the resulting composite will have a transverse isotropic behavior.
The Mori–Tanaka’s [34] mean-field theory is applied using Eshelby’s approach [8] used in [28] for a reinforced material with continuous cylindrical fiber having an elliptic section. In [86] the two phases of the composite are considered isotropic but in this presentation it is considered that the fibers have an anisotropic behavior.
We consider a comparison material (CM). Consider two identical representative volume elements (RVE), one representing the real composite and the other representing the CM. \(C_{m}\) represents the elastic coefficients matrix and \(C_{f}\) the elastic coefficients fiber. Under a traction \(\overline{\sigma }\), the average strain field in the matrix and in the fiber are different in the considered material and in the CM. Let \(\tilde{\varepsilon }\) represent the difference between the average values of the strain. The same thing happens with the stress field where the difference is \(\tilde{\sigma }\).
In the CM, we have:
a linear relation between the mean strain field \(\varepsilon\)° and the mean stress field \(\overline{\sigma }\).
The average strain field in the RVE is \(\varepsilon^{m} = \varepsilon^{0} + \overline{\varepsilon }\) and the mean stress field is \(\sigma^{m} = \overline{\sigma } + \tilde{\sigma }\). So, it results
The mean strain field in the fiber and in the matrix are different through an additional term \(\varepsilon^{pt}\) and hence \(\varepsilon^{f} = \varepsilon^{m} + \varepsilon^{pt} = \varepsilon^{0} + \tilde{\varepsilon } + \varepsilon^{pt}\). In a similar way the average stress field differs by the term \(\sigma^{pt}\) and therefore, \(\sigma^{f} = \overline{\sigma } + \tilde{\sigma } + \sigma^{pt}\). The generalized Hooke law becomes:
or:
We introduce \(\varepsilon^{pt}\) in Eq. (138).
The Eshelby’s transformation tensor P from Eq. (129) is presented in [56].
The average stress in the whole RVE, is:
reduced to:
With a similar procedure, it results:
where I is the unit tensor.
Using Eqs. (142) and (139) it results:
or:
or:
and:
The final form results:
Now it is possible to obtain:
The coefficients \(A_{ij}\) are presented in [56]. The shear strains are [30]:
To obtain the longitudinal Young’s modulus \(E_{m}\) of the considered orthotropic body, the composite specimen is subjected to a pure traction \(\overline{\sigma }_{11}\). It follows that \(\overline{\sigma }_{11} = E_{11} \overline{\varepsilon }_{11}\) for the composite and \(\overline{\sigma }_{11} = E_{m} \overline{\varepsilon }_{11}^{0}\); \(\overline{\varepsilon }_{22}^{0} = \overline{\varepsilon }_{33}^{0} = - \nu_{m} \overline{\varepsilon }_{11}^{0}\) if the comparison material is considered.
Using Eq. (148) one obtains:
where: \(a_{ij}^{{}} = A_{ij}^{{}} /A\), \(A_{ij}^{{}}\) and \(A\) are presented in [56].
One obtains:
In the same way, it results:
and
For the shear moduli, we have:
Considering:
Comparing Eq. (22) and Eq. (23) \(G_{12}\) is obtained as:
and
The Poisson’s ratio is determined with the relations:
Note that:
and:
or:
Introducing Eq. (164) in Eq. (165) one obtains:
or:
In a similar way one obtains:
and
The method presented is a convenient way for designers to quickly obtain the elastic / viscoelastic constants of a multiphase composite material. Within this method the determined values are unique, unlike most of the methods used, which are methods of boundedness, obtaining lower and upper limits of those values [87,88,89,90,91,92,93,94]. The behavior of the material over time is determined using Schapery's constitutive equation [12]. Thus, nonlinear viscoelastic materials can be studied.
5 Finite element method
The finite element method (FEM) is a useful method to study a mechanical system with elastic elements, it can also be a composite material [79]. The influence of temperature was studied using FEM in [80]. In [81], a unidirectional silicon carbide fiber composite was studied. In [82] a similar model is used. In the works [11, 83] using the FEM a transverse isotropic composite is analyzed. The symmetry of the model allows, in most cases, the analysis to be performed only on a quarter or half of the unit cell, the so-called "representative unit cell" (RUC). The finite element unit cell model is shown in Fig. 4 (model 1 and 2).
The time independent material properties for the constituents of the studied composite are:
Em = 4.14 GPa; vm = 0.22; Ef = 86.90 GPa; vf = 0.34.
The results are presented in Tables 1, 2, 3, 4, 5, 6 (\(\overline{\sigma }\) is the average stress, \(\overline{\varepsilon }\) is the average strain and RUC is the representative unit cell).
Finally, a three-dimensional model was used to determine the shear modulus and Poisson’s ratios in a plane perpendicular to \(x_{2} x_{3}\). A few of the foregoing models are listed in Table 7.
If the boundary conditions for the FE model are linear \(u_{i} = \alpha_{ij} x_{j}\) (where \(\alpha_{ij} = \alpha_{ji}\)), the average strain is \(\overline{\varepsilon }_{ij} = \alpha_{ij}\). We will show this:
Applying Green’s theorem it results:
or:
If \(i \ne j\) it results that \(\overline{\varepsilon }_{ij} = 0\). The results obtained are completely in accordance with the theoretical results. A discrepancy identified with the result of [49] can be assigned to the different type of finite elements used.
The average strains and stresses are \(\overline{\sigma }_{22} ,\overline{\sigma }_{33} ,\overline{\sigma }_{11} ,\overline{\sigma }_{23} = \overline{\tau }_{23} ,\overline{\varepsilon }_{22} ,\) \(\overline{\varepsilon }_{33} ,\overline{\varepsilon }_{11} ,\overline{\varepsilon }_{23} = 1/2\,\gamma_{23}\). Using these determined values, it is possible to obtain the mechanical constants [51]. For the longitudinal elastic modulus \(E_{11}\) it is proposed the rule of mixture [94]:
The ratios of fiber and matrix are:
and we have \(A = A_{f} + A_{m}\) , where \(A_{f}\) is the cross section of the fiber and \(A_{m}\) the cross section of the matrix.
We have:
from where it results:
and:
so:
It results to \(C_{12}\) and \(C_{66}\):
The fibers are parallel with the “1” direction and randomly distributed in the “2–3” plane which is referred to as the plane of isotropy. The bulk modulus \(K_{23}\) is:
The longitudinal Poisson’s ratio is determined with:
and the shear modulus:
or:
Using the parameter,
it results the transverse moduli and Poisson’s ratio:
and:
So it is possible to determine \(E_{11} ,\;E_{22} = E_{33} ,\;\nu_{12} = \nu_{13} ,\;\nu_{23} ,\;G_{23} ,K_{23}\).
Using the relation:
it results:
Considering the well known notations from elasticity one obtains:
and the relation:
A similar way can be used to determine the average stresses and strains in a 3D elastic solid, \(\overline{\sigma }_{11} ,\overline{\sigma }_{22} ,\overline{\sigma }_{33} ,\overline{\sigma }_{12} = \overline{\tau }_{12} ,\overline{\sigma }_{23} = \overline{\tau }_{23} ,\overline{\sigma }_{31} = \overline{\tau }_{31} ,\)\(\overline{\varepsilon }_{11} ,\overline{\varepsilon }_{22} ,\overline{\varepsilon }_{33} ,\overline{\varepsilon }_{12} = 1/2\,\gamma_{12} ,\) \(\overline{\varepsilon }_{23} = 1/2\,\gamma_{23} ,\overline{\varepsilon }_{31} = 1/2\,\gamma_{31}\).
The general Hooke’s law can be written:
The last of Eqs. (191) offers:
From Eq. (191) it is possible to write:
Using the law of mixture:
the redundant fourth relation from Eq. (191) becomes:
Summarizing the second and third equation in Eq. (191) one obtains:
Equation (191) offers:
Introducing Eq. (197) into that of \(E_{11}\) one obtains:
and it is possible to determine \(C_{12}\).
This presentation proves that FEM is a method that can be successfully applied in determining the overall mechanical properties of multiphase composites. The engineering constants required in the design process are obtained by averaging the values of stresses and strains obtained with FEM. These results were experimentally verified by different researchers resulting in a good concordance between the theoretical results obtained and the experimental verifications. Thus the method proves to be a useful and relatively simple method of identifying the constituent laws of a composite material. The obtained results were also applied to the study of the creep behavior of a composite material. In this case, relations become more complicated because in the case of creep phenomena, the influences of temperature prove to be nonlinear.
6 Discussions
In the paper experimental and analytical models are used to study the temperature dependence of the nonlinear viscoelastic response of biphasic composites. Termoset and the thermoplastic matrix system are considered. Some conclusion can be drawn:
An excellent modeling of the experiments is possible using Schapery’s approach for nonlinear viscoelastic characterization. For the materials investigated the influence of temperature on both, the nonlinear instantaneous response and the nonlinear transient response was assured. It is shown that the former is significantly less sensitive to temperature than the latter. For the temperature range investigated, it can be assumed that the instantaneous response is linear and temperature- independent over the range of stress levels relevant in practical applications. This observation is very useful because it simplifies thermoviscoelastic characterization of composite materials.
Micromecanichal model presented in the paper is capable to model a unidirectional composite subjected to longitudinal and/or transverse normal loading. Scapery’s nonlinear constitutive equation for isothermal uniaxial loading condition is incorporated into the analysis to take into account the nonlinear viscoelastic behavior.
Usually most fibers show minimal viscoelastic behavior and as a consequence one needs only to determine the time dependent properties of the matrix. This will immensely reduce the time and also the cost for the evaluation of the viscoelastic response of different types of composite materials.
An alternative analytical procedure is used in the current study to determine creep response of the composite and the neat resin specimens. The method is based on Mori–Tanaka approach but is extended into viscoelastic domain to account for the time dependent overall response of the composite body.
The analysis and methods presented in this review are effective tools for determining the time dependent overall response of any unidirectional composite under various loading conditions with reasonable accuracy. However the current analysis in the present form does not claim to characterize composite for all thermomechanical histories, such as physical and thermal aging or hygrothermal loadings.
7 Conclusions and further development
The main theoretical models used to determine the mechanical properties of composite materials with fibers were presented in the paper, with examples taken from the field of composite materials reinforced with carbon fibers.
A micromechanical model, which represents a classical approach to the problem, the homogenization method which is a mathematized method that requires knowledge of the stress and strain field for certain loading situations, the Mori-Tanaka method widely used by engineers and the finite element method were analyzed.
Each of the methods presents its advantages and disadvantages. The micromechanical models are relatively complicated and the simplifications introduced make the values obtained for the mechanical properties somewhat imprecise. The homogenization method has obvious advantages in terms of precision, but it is not easy to apply, researchers having to have special skills for manipulating equations and a deep understanding of the phenomena that occur in the material. The Mori-Tanaka method stands out for its simplicity and ease of application, and countless applications and results published by researchers are behind it. Finally, the FEM is a method that benefits from high-performance software and an extremely rich experience. The work time in this case is high, but the results can model the studied system extremely well.
The decision to apply a certain method belongs to the researchers, depending on their expertise, the complexity of the problem, the time available for the design, the costs involved and the precision with which we want to obtain the results. Since the homogenization method implies the knowledge of the stress and strain field, which implies the use of a numerical calculation method to determine this field, it seems that the application of the finite element method has some advantages in such calculations. Until now, it has been relatively little used, especially because of the complexity of modeling these materials, but we assume an accelerated development of the use of FEM in the design and development of new composite materials.
References
Cristescu N, Craciun E-M, Gaunaurd G. Mechanics of elastic composites (CRC series in modern mechanics and mathematics). Appl Mech Rev. 2004;57:B27. https://doi.org/10.1115/1.1818693.
Zaoui, A. Homogenization techniques for composite media, dans. Lecture notes in physics, vol. 272, Ch. 4. Berlin: Springer; 1987.
Garajeu, M. Contribution à L’étude du Comportement non Lineaire de Milieu Poreaux Avec ou Sans Renfort. Ph.D. Thesis, Aix-Marseille University, Marseille, France, 1995.
Brauner C, Herrmann AS, Niemeier PM, Schubert K. Analysis of the non-linear load and temperature-dependent creep behaviour of thermoplastic composite materials. J Thermoplast Compos Mater. 2016;30:302–17. https://doi.org/10.1177/0892705715598359.
Fett T. Review on creep-behavior of simple structures. Res Mech. 1988;24:359–75.
Sá MF, Gomes A, Correia J, Silvestre N. Creep behavior of pultruded GFRP elements—part 1: Literature review and experimental study. Compos Struct. 2011;93:2450–9. https://doi.org/10.1016/j.compstruct.2011.04.013.
Brinson HF, Morris DH, Yeow YI. A new method for the accelerated characterization of composite materials. In: Proceding of the Sicth international conference on experimental stress analysis, Munich, Germany, 18–22 September 1978.
Jinsheng X, Hongli W, Xiaohong Y, Long H, ChangSheng Z. Application of TTSP to non-linear deformation in composite propellant. Emerg Mater Res. 2018;7:19–24. https://doi.org/10.1680/jemmr.16.00069.
Nakano T. Applicability condition of time–temperature superposition principle (TTSP) to a multi-phase system. Mech Time-Depend Mater. 2012;17:439–47. https://doi.org/10.1007/s11043-012-9195-8.
Achereiner F, Engelsing K, Bastian M. Accelerated measurement of the long-term creep behaviour of plastics. Superconductivity. 2017;247:389–402.
Schaffer, B.G.; Adams, D.F. Nonlinear viscoelastic behavior of a composite material using a finite element micromechanical analysis; Dept. Report UWME-DR-001-101-1, Dep. Of Mech. Eng.; University of Wyoming, Laramie, WY, USA; 1980.
Schapery R. Nonlinear viscoelastic solids. Int J Solids Struct. 2000;37:359–66. https://doi.org/10.1016/s0020-7683(99)00099-2.
Violette MG, Schapery R. Time-dependent compressive strength of unidirectional viscoelastic composite materials. Mech Time-Depend Mater. 2002;6:133–45. https://doi.org/10.1023/a:1015015023911.
Hinterhoelzl R, Schapery R. FEM implementation of a three-dimensional viscoelastic constitutive model for particulate composites with damage growth. Mech Time-Depend Mater. 2004;8:65–94. https://doi.org/10.1023/b:mtdm.0000027683.06097.76.
Mohan R, Adams DF. Nonlinear creep-recovery response of a polymer matrix and its composites. Exp Mech. 1985;25:262–71. https://doi.org/10.1007/bf02325096.
Findley WN, Adams CH, Worley WJ. The effect of temperature on the creep of two laminated plastics as interpreted by the hyperbolic sine law and Activation energy theory. In: Proceedings of the proceedings-American Society for Testing and Materials, volume 48, Conshohocken, PA, USA, 1 January 1948. p. 1217–1239.
Findley WN, Khosla G. Application of the superposition principle and theories of mechanical equation of state, strain, and time hardening to creep of plastics under changing loads. J Appl Phys. 1955;26:821. https://doi.org/10.1063/1.1722102.
Findley WN, Peterson DB. Prediction of long-time creep with ten-year creep data on four plastics laminates. In: Proceedings of the American Society for Testing and Materials, volume 58. Proceedings of the sixty-first (61th) annual meeting, Boston, MA. 26–27 June, 1958.
Dillard DA, Brinson HF. A nonlinear viscoelastic characterization of graphite epoxy composites. In: Proceedings of the 1982 joint conference on experimental mechanics, Oahu, HI, USA, 23–28 May 1982.
Dillard, D.A.; Morris, D.H.; Brinson, H.F. Creep and creep rupture of laminated hraphite/epoxy composites. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 30 September 1980.
Charentenary FX, Zaidi MA. Creep behavior of carbon-epoxy (+/-45o )2s laminates. In: Hayashi K, Umekawa S, eds. Progess in sciences and composites. ICCM-IV; Tokyo, Japan, The Japan Society for Composite Materials, c/o Business Center for Academic Societies Japan 2-4-6, Yayoi, Bunkyo-ku, Tokyo 113, 1982.
Walrath DE. Viscoelastic response of a unidirectional composite containing two viscoelastic constituents. Exp Mech. 1991;31:111–7. https://doi.org/10.1007/bf02327561.
Hashin Z. On elastic behavior of fibre reinforced materials of arbitrary transverse phase geometry. J Mech Phys Solids. 1965;13:119–34.
Hashin Z, Shtrikman S. On some variational principles in anisotropic and nonhomogeneous elasticity. J Mech Phys Solids. 1962;10:335–42. https://doi.org/10.1016/0022-5096(62)90004-2.
Hashin Z, Shtrikman S. A variational approach to the theory of the elastic behavior of multiphase materials. J Mech Phyds Solids. 1963;11:127–40.
Hashin Z, Rosen BW. The elastic moduli of fiber-reinforced materials. J Appl Mech. 1964;31:223–32. https://doi.org/10.1115/1.3629590.
Bowles DE, Griffin OH Jr. Micromecjanics analysis of space simulated thermal stresses in composites. Part I: theory and unidirectional laminates. J Reinf Plast Compos. 1991;10:504–21.
Zhao YH, Weng GJ. Effective elastic moduli of ribbon-reinforced composites. J Appl Mech. 1990;57:158–67. https://doi.org/10.1115/1.2888297.
Hill R. Theory of mechanical properties of fiber-strengthened materials: I elastic behavior. J Mech Phys Solids. 1964;12:199–212.
Hill R. Theory of mechanical properties of fiber-strengthened materials: II inelastic behavior. J Mech Phys Solids. 1964;12:213–8.
Hill R. Theory of mechanical properties of fiber-strengthened materials: III self-consistent model. J Mech Phys Solids. 1965;13:189–98.
Hill R. Continuum micro-mechanics of elastoplastic polycrystals. J Mech Phys Solids. 1965;13:89–101.
Mori T, Tanaka K. Average stress in the matrix and average elastic energy of materials with Misfitting inclusions. Acta Metal. 1973;21:571–4.
Weng YM, Wang GJ. The influence of inclusion shape on the overall viscoelastic behavior of compoisites. J Appl Mech. 1992;59:510–8.
Pasricha A, Van Duster P, Tuttle ME, Emery AF. The nonlinear viscoelastic/viscoplastic behavior of IM6/5260 graphite/bismaleimide. In Proceedings of the VII international congress on experimental mechanics, Las Vegas, NV, USA, 8–11 June 1992.
Aboudi J. Micromechanical characterization of the non-linear viscoelastic behavior of resin matrix composites. Compos Sci Technol. 1990;38:371–86. https://doi.org/10.1016/0266-3538(90)90022-w.
Aboudi J. Mechanics of composite materials—a unified micromechanical approach. Amsterdam: Elsevier; 1991.
Hobiny A, et al. The effect of fractional time derivative of bioheat model in skin tissue induced to laser irradiation. Symmetry. 2020;12(4):602.
Bhatti MM, et al. Recent trends in computational fluid dynamics. Front Phys. 2020. https://doi.org/10.3389/fphy.2020.593111.
Vlase S, Teodorescu-Draghicescu H, Motoc DL, Scutaru ML, Serbina L, Calin MR. Behavior of multiphase fiber-reinforced polymers under short time cyclic loading. Optoelectron Adv Mater Rapid Commun. 2011;5:419–23.
Teodorescu-Draghicescu H, Stanciu A, Vlase S, Scutaru L, Calin MR, Serbina L. Finite element method analysis of some fibre-reinforced composite laminates. Optoelectron Adv Mater Rapid Commun. 2011;5:782–5.
Stanciu A, Teodorescu-Drǎghicescu H, Vlase S, Scutaru ML, Cǎlin MR. Mechanical behavior of CSM450 and RT800 laminates subjected to four-point bend tests. Optoelectron Adv Mater Rapid Commun. 2012;6:495–7.
Niculiţă C, Vlase S, Bencze A, Mihălcică M, Calin MR, Serbina L. Optimum stacking in a multi-ply laminate used for the skin of adaptive wings. Optoelectron Adv Mater Rapid Commun. 2011;5:1233–6.
Katouzian M, Vlase S, Calin MR. Experimental procedures to determine the viscoelastic parameters of laminated composites. J Optoelectron Adv Mater. 2011;13:1185–8.
Teodorescu-Draghicescu H, Vlase S, Stanciu MD, Curtu I, Mihalcica M. Advanced pultruded glass fibers-reinforced isophtalic polyester resin. Mater Plast. 2015;52:62–4.
Fliegener S, Hohe J. An anisotropic creep model for continuously and discontinuously fiber reinforced thermoplastics. Compos Sci Technol. 2020;194: 108168. https://doi.org/10.1016/j.compscitech.2020.108168.
Xu B, Xu W, Guo F. Creep behavior due to interface diffusion in unidirectional fiber-reinforced metal matrix composites under general loading conditions: a micromechanics analysis. Acta Mech. 2020;231:1321–35. https://doi.org/10.1007/s00707-019-02592-8.
Lal HMM, Xian G-J, Thomas S, Zhang L, Zhang Z, Wang H. Experimental study on the flexural creep behaviors of pultruded unidirectional carbon/glass fiber-reinforced hybrid bars. Materials. 2020;13:976. https://doi.org/10.3390/ma13040976.
Wang Z, Smith DE. Numerical analysis on viscoelastic creep responses of aligned short fiber reinforced composites. Compos Struct. 2019;229: 111394. https://doi.org/10.1016/j.compstruct.2019.111394.
Ramesh M, Rajeshkumar L, Bhoopathi R. Carbon substrates: a review on fabrication, properties and applications. Carbon Lett. 2021;31:557–80. https://doi.org/10.1007/s42823-021-00264-z.
Chwał M, Muc A. FEM micromechanical modeling of nanocomposites with carbon nanotubes. Rev Adv Mater Sci. 2021;60(1):342–51. https://doi.org/10.1515/rams-2021-0027.
Rumayshah KK, Dirgantara T, Judawisastra H, et al. Numerical micromechanics model of carbon fiber-reinforced composite using various periodical fiber arrangement. J Mech Sci Technol. 2021;35:1401–6. https://doi.org/10.1007/s12206-021-0306-9.
Katouzian M, Vlase S, Scutaru ML. A mixed iteration method to determine the linear material parameters in the study of creep behavior of the composites. Polymers. 2021;13(17):2907. https://doi.org/10.3390/polym13172907.
Katouzian M, Vlase S, Scutaru ML. Finite element method-based simulation creep behavior of viscoelastic carbon-fiber composite. Polymers. 2021;13(7):1017. https://doi.org/10.3390/polym13071017.
Katouzian M, Vlase S. Creep response of carbon-fiber-reinforced composite using homogenization method. Polymers. 2021;13(6):867. https://doi.org/10.3390/polym13060867
Katouzian M, Vlase S. Mori–Tanaka formalism-based method used to estimate the viscoelastic parameters of laminated composites. Polymers. 2020;12(11):2481. https://doi.org/10.3390/polym12112481.
Katouzian M, Vlase S. Creep response of neat and carbon-fiber-reinforced PEEK and epoxy determined using a micromechanical model. Symmetry. 2020;12(10):1680. https://doi.org/10.3390/sym12101680.
Kamau-Devers K, Miller SA. Using a micromechanical viscoelastic creep model to capture multi-phase deterioration in bio-based wood polymer composites exposed to moisture. Construct Build Mater. 2022;314(8):125252. https://doi.org/10.1016/j.conbuildmat.2021.125252.
Wei W, Gu CS, Guo XY, Gu ST. Micromechanical modelling of the anisotropic creep behaviour of granular medium as a fourth-order fabric tensor. Adv Mech Eng. 2021. https://doi.org/10.1177/16878140211036127.
Shokrieh Z, Shokrieh MM, Zhao Z. A modified micromechanical model to predict the creep modulus of polymeric nanocomposites. Polym Testing. 2018;65:414–9. https://doi.org/10.1016/j.polymertesting.2017.12.020.
Ma T, Wang H, Zhang DY, Zhang Y. Heterogeneity effect of mechanical property on creep behavior of asphalt mixture based on micromechanical modeling and virtual creep test. Mech Mater. 2017;104:49–59. https://doi.org/10.1016/j.mechmat.2016.10.003.
Monfared V. A micromechanical creep model for stress analysis of non-reinforced regions of short fiber composites using imaginary fiber technique. Mech Mater. 2015;86:44–54. https://doi.org/10.1016/j.mechmat.2015.03.002.
Strombro J, Gudmundson P. Mechano-sorptive creep under compressive loading—a micromechanical model. Int J Solids Struct. 2008;45(9):2420–50. https://doi.org/10.1016/j.ijsolstr.2007.12.002.
Gal E, Fish J. Anisotropic micromechanical creep damage model for composite materials: a reduced-order approach. Int J Multiscale Comput Eng. 2008;6(2):113–21. https://doi.org/10.1615/IntJMultCompEng.v6.i2.10.
Alfthan J, Gudmundson R, Ostlund S. A micromechanical model for mechanosorptive creep in paper. J Pulp Paper Sci. 2002;28(3):98–104.
Chen CH. Micromechanical modeling of creep behavior in particle-reinforced silicone-rubber composites. J Appl Mech Trans ASME. 1997;64(4):781–6. https://doi.org/10.1115/1.2788982.
Sun DZ, Sester M, Schmitt W. Development and application of micromechanical material models for ductile fracture and creep damage. Int J Fract. 1997;86(12):75–90. https://doi.org/10.1023/A:1007368722374.
Teodorescu-Draghicescu H, Vlase S, Scutaru L, Serbina L, Calin MR. Hysteresis effect in a three-phase polymer matrix composite subjected to static cyclic loadings. Optoelectron Adv Mater Rapid Commun. 2011;5:273–7.
Jain A. Micro and mesomechanics of fibre reinforced composites using mean field homogenization formulations: a review. Mater Today Commun. 2019;21: 100552. https://doi.org/10.1016/j.mtcomm.2019.100552.
Lee H, Choi CW, Jin JW. Homogenization-based multiscale analysis for equivalent mechanical properties of nonwoven carbon-fiber fabric composites. J Mech Sci Technol. 2019;33:4761–70. https://doi.org/10.1007/s12206-019-0917-6.
Koley S, Mohite PM, Upadhyay CS. Boundary layer effect at the edge of fibrous composites using homogenization theory. Compos Part B Eng. 2019;173: 106815. https://doi.org/10.1016/j.compositesb.2019.05.026.
Xin HH, Mosallam A, Liu YQ. Mechanical characterization of a unidirectional pultruded composite lamina using micromechanics and numerical homogenization. Constr Build Mater. 2019;216:101–18. https://doi.org/10.1016/j.conbuildmat.2019.04.191.
Chao Y, Zheng KG, Ning FD. Mean-field homogenization of elasto-viscoplastic composites based on a new mapping-tangent linearization approach. Sci China-Technol Sci. 2019;62:736–46. https://doi.org/10.1007/s11431-018-9393-4.
Sokołowski, D.; Kamiński, M. Computational homogenization of anisotropic carbon/rubbercomposites with stochastic interface defects. In: carbon-basednanofillers and their rubber nanocomposites, chapter 11. Elsevier: Amsterdam; 2019. p. 323–353.
Dellepiani MG, Vega CR, Pina JC. Numerical investigation on the creep response of concrete structures by means of a multi-scale strategy. Constr Build Mater. 2020;263: 119867. https://doi.org/10.1016/j.conbuildmat.2020.119867.
Choo J, Semnani SJ, White JA. An anisotropic viscoplasticity model for shale based on layered microstructure homogenization. Int J Numer Anal Methods Geomech. 2021;45:502–20. https://doi.org/10.1002/nag.3167.
Cruz-Gonzalez OL, Rodriguez-Ramos R, Otero JA. On the effective behavior of viscoelastic composites in three dimensions. Int J Eng Sci. 2020;157: 103377. https://doi.org/10.1016/j.ijengsci.2020.103377.
Chen Y, Yang PP, Zhou YX. A micromechanics-based constitutive model for linear viscoelastic particle-reinforced composites. Mech Mater. 2020;140: 103228. https://doi.org/10.1016/j.mechmat.2019.103228.
Kotha S, Ozturk D, Ghosh S. Parametrically homogenized constitutive models (PHCMs) from micromechanical crystal plasticity FE simulations, part I: sensitivity analysis and parameter identification for Titanium alloys. Int J Plast. 2019;120:296–319. https://doi.org/10.1016/j.ijplas.2019.05.008.
Sanchez-Palencia E. Homogenization method for the study of composite media. In: Verhulst F, editor. Asymptotic analysis II lecture notes in mathematics, vol. 985. Berlin/Heidelberg: Springer; 1983. https://doi.org/10.1007/BFb0062368.
Sanchez-Palencia E. Non-homogeneous media and vibration theory. In: Lecture notes in physics. Berlin/Heidelberg: Springer; 1980. Doi:https://doi.org/10.1007/3-540-10000-8.
Xu W, Nobutada O. A homogenization theory for time-dependent deformation of composites with periodic internal structures. JSME Int J Ser A Solid Mech Mater Eng. 1998;41:309–17.
Duvaut G. Homogénéisation des plaques à structure périodique en théorie non linéaire de Von Karman in Lect. Notes Math. 1977;665:56–69.
Caillerie D. Homogénisation d’un corps élastique renforcé par des fibres minces de grande rigidité et réparties périodiquement. Compt Rend Acad Sci Paris Sér. 1981;292:477–80.
Bensoussan A, Lions JL, Papanicolaou G. Asymptotic analysis for periodic structures. North-Holland, Amsterdam: American Mathematical Soc.; 1978.
Lou YC, Schapery RA. Viscoelastic characterization of a nonlinear fiber-reinforced plastic. J Compos Mater. 1971;5:208–34. https://doi.org/10.1177/002199837100500206.
Eshelby JD. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc R Soc Lond Ser A Math Phys Sci. 1957;241:376–96.
Khodadadian A, Noii N, Parvizi M, Abbaszadeh M, Wick T, Heitzinger C. A Bayesian estimation method for variational phase-field fracture problems. Comput Mech. 2020;66:1–23. https://doi.org/10.1007/s00466-020-01876-4.
Bowles D, Griffin OH. Micromechanics analysis of space simulated thermal stresses in composites. Part II: multidirectional laminates and failure predictions. J Reinf Plast Compos. 1991;10:522–39.
Adams DF, Miller AK. Hygrothermal microstresses in a unidirectional composite exhibiting inelastic material behavior. J Compos Mater. 1977;11:285–99.
Wisnom MR. Factors affecting the transverse tensile strength of unidirectional continuous silicon carbide fiber reinforced 6061 aluminum. J Compos Mater. 1990;24:707–26.
Brinson LC, Knauss WG. Finite element analysis of multiphase viscoelastic solids. J Appl Mech. 1992;59:730–7.
Hahn HG. Methode der Finiten Elemente in der Festigkeitslehre. Franfurt am Main: Akademische Verlagsgesellschaft; 1975.
Öchsner A. Micromechanics of fiber-reinforced laminae. Cham: Springer Nature; 2022.
Author information
Authors and Affiliations
Contributions
All authors participated equal to all the phases necesary to elaborate the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Katouzian, M., Vlase, S., Marin, M. et al. Creep response of fiber-reinforced composites: a review. Discov Mechanical Engineering 1, 3 (2022). https://doi.org/10.1007/s44245-022-00003-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s44245-022-00003-2