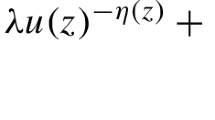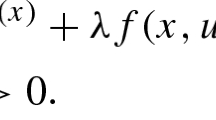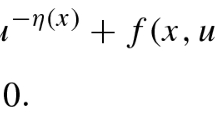Singular Anisotropic Problems with Competition Phenomena

Abstract

We consider a Dirichlet problem driven by the anisotropic (p(z), q(z))-Laplacian, with a parametric reaction exhibiting the combined effects of singular and concave-convex nonlinearities. The superlinear term may change sign. Using variational tools together with truncation and comparison techniques, we prove a global (for the parameter $\lambda >0$) existence and multiplicity theorem (a bifurcation-type theorem).

1 Introduction

Let $\Omega \subseteq {\mathbb {R}}^N$ be a bounded domain with a $C^2$-boundary $\partial \Omega$. In this paper we study the following singular anisotropic Dirichlet problem

Given $r \in C({\overline{\Omega }})$ with $1<\min \limits _{{\overline{\Omega }}} r$, by $\Delta _{r(z)}$ we denote the anisotropic r-Laplace differential operator defined by

$$\begin{aligned} \Delta _{r(z)} u= \text { div }(|\nabla u|^{r(z)-2}\nabla u) \text { for all } u \in W_0^{1,r(z)}(\Omega ). \end{aligned}$$

In contrast to the isotropic r-Laplacian (that is, $r(\cdot )$ is constant), the anisotropic operator is not homogeneous. In ($P_\lambda$) the equation is driven by the sum of two such operators with distinct variable exponents $p(\cdot )$ and $q(\cdot )$ (double phase problem). Given $\vartheta \in L^\infty (\Omega )$, we set $\vartheta _- = \text { ess}\inf \limits _{\Omega } \vartheta$ and $\vartheta _+ = \text { ess}\sup \limits _{\Omega } \vartheta$. In ($P_\lambda$) we assume that $1<\tau _-\le \tau _+< q_-\le q_+<p_-\le p_+$ and $0<\eta _-\le \eta _+<1$. The perturbation f(z, x) is a Carathéodory function (that is, for all $x \in {\mathbb {R}}$ $z \rightarrow f(z,x)$ is measurable and for a.a. $z \in \Omega$ $x \rightarrow f(z,x)$ is continuous) which exhibits $(p_+-1)$-superlinear growth as $x \rightarrow +\infty$, but need not satisfy the usual in such cases Ambrosetti–Rabinowitz condition (the AR-condition for short) and may change sign (indefinite perturbation). So, problem ($P_\lambda$) in the reaction has the combined effects of singular and concave–convex nonlinearities with two distinguishing features. First the superlinear (convex) term need not satisfy the AR-condition and second this perturbation is in general sign-changing. In the past, anisotropic singular equations were studied without the presence of the concave term $\lambda u^{\tau (z)-1}$ and with a superlinear perturbation which is positive. We refer to the works of Byun–Ko [2] and Saoudi–Ghanmi [21]. Both deal with equations driven by the anisotropic p-Laplacian only. More recently, Papageorgiou–Rădulescu–Zhang [19] considered singular anisotropic double phase problems with a superlinear positive perturbation and no concave term.

Closer to our work here is the recent paper of Papageorgiou–Winkert [14], who examined an isotropic version of problem ($P_\lambda$) (all the exponents of the problem are constant) with a superlinear positive perturbation. The definite sign of the perturbation allows the authors of [14] to produce an ordered pair of upper and lower solutions, which in turn leads to the nonemptiness of the set of admissible parameters. They prove a global existence and multiplicity result (a bifurcation-type theorem). Our aim in this paper is to extend their result to anisotropic problems with an indefinite superlinear perturbation.

Finally we mention also the recent works on some other classes of anisotropic singular problems of Papageorgiou–Winkert [13, 15] and Papageorgiou–Zhang [16, 17]; for problems in divergence form, some recent results are given in Abdalmonem–Scapellato [1], Ragusa [20] and Wei [23] for parabolic equations.

2 Mathematical Background: Hypotheses

The analysis of problem ($P_\lambda$) is based on the variable Lebesgue and Sobolev spaces. A comprehensive introduction to the subject can be found in the books of Cruz Uribe–Fiorenza [3] and of Diening–Harjulehto–Hästö–Ru̇žička [4].

We introduce the set

$$\begin{aligned} E_1= \bigg \{r \in C({\overline{\Omega }}) : \, 1<\min \limits _{{\overline{\Omega }}} r \bigg \}. \end{aligned}$$

Recall that for $r \in C({\overline{\Omega }})$, $r_-=\min \limits _{{\overline{\Omega }}}r$ and $r_+=\max \limits _{{\overline{\Omega }}}r.$ Let $L^0(\Omega )$ be the space of all measurable functions $u:\Omega \rightarrow {\mathbb {R}}$. As usual we identify two such functions which differ only on a Lebesgue null subset of $\Omega$. Given $r \in E_1$, the variable Lebesgue space $L^{r(z)}(\Omega )$ is defined by

$$\begin{aligned} L^{r(z)}(\Omega )=\left\{ u \in L^0(\Omega ): \, \rho _r(u)=\int _\Omega |u|^{r(z)} \mathrm{{d}}z <+ \infty \right\} . \end{aligned}$$

We endow this space with the so-called “Luxemburg norm” defined by

$$\begin{aligned} \Vert u \Vert _{r(z)}= \inf \left[ \lambda >0 : \, \int _\Omega \left( \frac{|u|}{\lambda }\right) ^{r(z)}\mathrm{{d}}z\le 1 \right] . \end{aligned}$$

With this norm the space $L^{r(z)}(\Omega )$ becomes a separable and uniformly convex (thus reflexive, see [12], p. 225) Banach space. Let $r^\prime \in E_1$ be the conjugate variable exponent to $r(\cdot )$, defined by

$$\begin{aligned} r^\prime (z)=\frac{r(z)}{r(z)-1} \text { or equivalently } \frac{1}{r(z)}+\frac{1}{r^\prime (z)}=1 \text { for all }z \in {\overline{\Omega }}. \end{aligned}$$

We have that

$$\begin{aligned} L^{r(z)}(\Omega )^*=L^{r^\prime (z)}(\Omega ), \end{aligned}$$

and the following Hölder-type inequality holds

$$\begin{aligned} \int _\Omega |uv|\mathrm{{d}}z \le \left[ \frac{1}{r_-}+\frac{1}{r^\prime _-}\right] \Vert u\Vert _{r(z)}\Vert v\Vert _{r^\prime (z)} \text { for all } u \in L^{r(z)}(\Omega ), \text { all } v \in L^{r^\prime (z)}(\Omega ). \end{aligned}$$

If $r_1,r_2 \in E_1$ and $r_1(z) \le r_2(z)$ for all $z \in {\overline{\Omega }}$, then

$$\begin{aligned} L^{r_2(z)}(\Omega ) \hookrightarrow L^{r_1(z)}(\Omega ) \text { continuously.} \end{aligned}$$

Using the variable Lebesgue spaces, we can define the corresponding variable Sobolev spaces. So, given $r \in E_1$, the variable Sobolev space $W^{1,r(z)}(\Omega )$ is defined by

$$\begin{aligned} W^{1,r(z)}(\Omega )=\left\{ u \in L^{r(z)}(\Omega ): \, |\nabla u| \in L^{r(z)}(\Omega ) \right\} , \end{aligned}$$

with $\nabla u$ being the weak gradient of $u(\cdot )$. This space is equipped with the following norm

$$\begin{aligned} \Vert u\Vert _{1,r(z)}=\Vert u\Vert _{r(z)}+ \Vert \nabla u\Vert _{r(z)} \text { for all } u \in W^{1,r(z)}(\Omega ), \end{aligned}$$

with $\Vert \nabla u\Vert _{r(z)} = \Vert |\nabla u | \Vert _{r(z)}$.

By $C^{0,1}({\overline{\Omega }})$ we denote the space of all Lipschitz continuous functions $u: {\overline{\Omega }} \rightarrow {\mathbb {R}}$. Given $r \in C^{0,1}({\overline{\Omega }}) \cap E_1$, we define

$$\begin{aligned} W_0^{1,r(z)}(\Omega )=\overline{C_c^\infty (\Omega )}^{\Vert \cdot \Vert _{1,r(z)}}. \end{aligned}$$

Both spaces $W^{1,r(z)}(\Omega )$ and $W_0^{1,r(z)}(\Omega )$ are separable and uniformly convex (thus reflexive) Banach spaces. Since in the definition of $W_0^{1,r(z)}(\Omega )$ we assume that the exponent $r(\cdot )$ is Lipschitz continuous, the Poincaré inequality holds, that is, there exists $c=c(\Omega )>0$ such that

$$\begin{aligned} \Vert u\Vert _{r(z)}\le c\, \Vert \nabla u\Vert _{r(z)} \text { for all } u \in W_0^{1,r(z)}(\Omega ). \end{aligned}$$

The Poincaré inequality leads to the following equivalent norm on $W_0^{1,r(z)}(\Omega )$

$$\begin{aligned} \Vert u\Vert = \Vert \nabla u\Vert _{r(z)} \text { for all } u \in W_0^{1,r(z)}(\Omega ). \end{aligned}$$

In the sequel we will use this norm on $W_0^{1,r(z)}(\Omega )$. For $r \in E_1$, we introduce the corresponding critical Sobolev exponent $r^*(\cdot )$ given by

$$\begin{aligned} r^*(z)= {\left\{ \begin{array}{ll} \dfrac{Nr(z)}{N-r(z)} &{} \text { if } r(z) <N,\\ +\infty &{} \text { if }N \le r(z). \end{array}\right. } \end{aligned}$$

There is an anisotropic version of the Sobolev embedding theorem.

Proposition 1

If $r \in C^{0,1}({\overline{\Omega }}) \cap E_1$, $r_+<N$, $q \in E_1$ and $q(z) \le r^*(z)$ (resp. $q(z) < r^*(z)$) for all $z \in {\overline{\Omega }}$, then $W_0^{1,r(z)}(\Omega ) \hookrightarrow L^{q(z)}(\Omega )$ continuously (resp. compactly).

There is a close relation between the norm $\Vert \cdot \Vert _{r(z)}$ and the modular function $\rho _r(u)=\int _\Omega |u|^{r(z)}dz$.

Proposition 2

Suppose $r \in E_1$ and $\{u_n,u \}_{n \in {\mathbb {N}}} \subseteq L^{r(z)}(\Omega )$, then we have:

• (a) $\Vert u\Vert _{r(z)}=\lambda \, \Leftrightarrow \, \rho _r\left( \frac{u}{\lambda }\right) =1$ ($\lambda >0$).

• (b) $\Vert u\Vert _{r(z)}<1 \, (\text { resp. } =1,>1) \Leftrightarrow \, \rho _r(u)<1 (\text { resp. } =1, >1)$.

• (c) $\Vert u\Vert _{r(z)}<1 \, \Rightarrow \, \Vert u\Vert _{r(z)}^{r_+}\le \rho _r(u) \le \Vert u\Vert _{r(z)}^{r_-}$.

• (d) $\Vert u\Vert _{r(z)}>1 \Rightarrow \Vert u\Vert _{r(z)}^{r_-}\le \rho _r(u) \le \Vert u\Vert _{r(z)}^{r_+}$.

• (e) $\Vert u_n\Vert _{r(z)}\rightarrow 0 \, (\text { resp. } \rightarrow +\infty ) \, \Leftrightarrow \, \rho _r(u_n)\rightarrow 0 \, (\text { resp. } \rightarrow +\infty )$.

We know that

$$\begin{aligned} W_0^{1,r(z)}(\Omega )^*=W^{-1,r^\prime (z)}(\Omega ). \end{aligned}$$

Let $A_{r}: W_0^{1,r(z)}(\Omega ) \rightarrow W^{-1,r^\prime (z)}(\Omega )$ be defined by

$$\begin{aligned} \langle A_{r}(u),h \rangle = \int _\Omega |\nabla u|^{r(z)-2}(\nabla u, \nabla h)_{{\mathbb {R}}^N}\mathrm{{d}}z \text { for all } u,h \in W_0^{1,r(z)}(\Omega ). \end{aligned}$$

This operator has the following properties (see Gasiński–Papageorgiou [6], Proposition 2.5).

Proposition 3

The operator $A_{r}(\cdot )$ is bounded (that is, maps bounded sets to bounded sets), continuous, strictly monotone (thus maximal monotone too) and of type $(S)_+$ (that is, if $u_n \xrightarrow {w} u$ in $W_0^{1,r(z)}(\Omega )$ and $\limsup \limits _{n \rightarrow +\infty } \langle A_{r}(u_n), u_n - u \rangle \le 0$, then $u_n \rightarrow u$ in $W_0^{1,r(z)}(\Omega )).$

The anisotropic regularity theory (see Fan [5] and Lieberman [11] for the corresponding isotropic theory) will lead us to the space $C_0^1({\overline{\Omega }})=\{u \in C^1({\overline{\Omega }}): u \big |_{\partial \Omega }=0\}$. This is an ordered Banach space with positive (order) cone $C_+=\left\{ u \in C_0^1({\overline{\Omega }}): u(z) \ge 0\right.$ $\left. \text { for all } z \in {\overline{\Omega }} \right\}$. This cone has a nonempty interior given by

$$\begin{aligned} \text { int }C_+=\left\{ u \in C_+ : \, u(z) > 0 \text { for all } z \in \Omega , \quad \frac{\partial u}{\partial n} \Big |_{\partial \Omega }<0\right\} , \end{aligned}$$

where $\dfrac{\partial u}{\partial n}=(\nabla u, n)_{{\mathbb {R}}^N}$ with $n(\cdot )$ being the outward unit normal on $\partial \Omega$.

Let $u_1,u_2 \in L^0( \Omega )$ such that $u_1(z) \le u_2(z)$ for a.a. $z \in \Omega$. We introduce the following sets:

$$\begin{aligned}&[u_1,u_2]=\{h \in W_0^{1,p(z)}(\Omega )\, : \, u_1(z)\le h(z)\le u_2(z) \text { for a.a. }z \in \Omega \},\\&\textrm{int}_{C_0^1({\overline{\Omega }})}[u_1,u_2]=\text { interior in } C_0^1({\overline{\Omega }}) \text { of } [u_1,u_2]\cap C_0^1({\overline{\Omega }}),\\&[u_1)=\{h \in W_0^{1,p(z)}(\Omega )\, : \, u_1(z)\le h(z) \text { for a.a. }z \in \Omega \}. \end{aligned}$$

If $h_1,h_2 \in L^0( \Omega )$, then we say that $h_1 \prec h_2$ if and only if for every $K \subseteq \Omega$ compact we have

$$\begin{aligned} 0 <c_K \le h_2(z)-h_1(z) \text { for a.a. } z \in K. \end{aligned}$$

Evidently, if $h_1,h_2 \in C(\Omega )$ and $h_1(z) <h_2(z)$ for all $z \in \Omega$, then $h_1 \prec h_2$.

Given $h \in L^0(\Omega )$, we set

$$\begin{aligned} h^+(z) =\max \{h(z),0\} \text { and } h^-(z) =\max \{-h(z),0\} \text { for all } z \in \Omega . \end{aligned}$$

We have $h^\pm \in L^0(\Omega )$, $h=h^+-h^-$, $|h|=h^++h^-$ and if $h \in W_0^{1,p(z)}(\Omega )$, then $h^\pm \in W_0^{1,p(z)}(\Omega )$.

Let X be a Banach space and $\varphi \in C^1(X,{\mathbb {R}})$. By $K_\varphi$ we denote the critical set of $\varphi (\cdot )$, that is

$$\begin{aligned} K_\varphi = \{u \in X: \varphi '(u) =0 \}. \end{aligned}$$

We say that $\varphi (\cdot )$ satisfies the “C-condition”, if it has the following property:

“Every sequence $\{u_n\}_{n \in {\mathbb {N}}} \subseteq X$ such that

$\{\varphi (u_n)\}_{n \in {\mathbb {N}}} \subseteq {\mathbb {R}}$ is bounded

and $(1 + \Vert u_n\Vert _X) \varphi '(u_n) \rightarrow 0$ in $X^*$ as $n \rightarrow +\infty$,

admits a strongly convergent subsequence”.

The hypotheses on the data of ($P_\lambda$) are the following:

$H_0$:

: $p,q \in C^{0,1}({\overline{\Omega }})$, $\tau \in C({\overline{\Omega }})$, $1<\tau _- \le \tau _+<q_-\le q_+<p_-\le p_+<N$, $\eta \in C({\overline{\Omega }})$, $0<\eta _-\le \eta _+<1$.

$H_1$:

: $f:\Omega \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ is a Carathéodory function such that $f(z,0)=0$ for a.a. $z \in \Omega$, and

(i):

$|f (z,x)| \le a(z) [1+x^{r(z)-1}]$ for a.a. $z \in \Omega$, all $x \ge 0$, with $a \in L^\infty (\Omega )_+$, $r \in C({\overline{\Omega }})$, $p_+< r_-\le r_+ < p_-^*$;

(ii):

if $F(z,x)=\int _0^x f(z,s)\mathrm{{d}}s$, then $\lim \limits _{x \rightarrow +\infty } \frac{F(z,x)}{x^{p_+}}=+\infty$ uniformly for a.a. $z \in \Omega$;

(iii):

if $e_\lambda (z,x)=\lambda \left[ x^{1-\eta (z)}+x^{\tau (z)}\right] +f(z,x)x-\lambda p_+\left[ \frac{1}{1-\eta (z)}x^{1-\eta (z)}+ \frac{1}{\tau (z)}x^{\tau (z)}\right] +p_+ F(z,x)$, then there exists $\vartheta \in L^1(\Omega )$ such that $e_\lambda (z,x)\le e_\lambda (z,y)+\vartheta (z)$ for a.a. $z\in \Omega$, all $0\le x\le y$;

(iv):

$\lim \limits _{x \rightarrow 0^+} \frac{f(z,x)}{x^{q_+-1}}=0$ uniformly for a.a. $z \in \Omega$, there exists $\delta >0$ such that $0<m_s \le f(z,x)$ for a.a. $z \in \Omega$, all $0<s\le x\le \delta$, and for every $\rho >0$ there exists ${\widehat{\xi }}_\rho >0$ such that for a.a. $z \in \Omega$, the function $x \rightarrow f(z,x) + {\widehat{\xi }}_\rho |x|^{p(z)-1}$ is nondecreasing on $[0,\rho ]$.

Remark 1

Since we are looking for positive solutions and the above hypotheses concern the positive semiaxis ${\mathbb {R}}_+=[0,+\infty )$, without any loss of generality we may assume that $f(z,x)=0$ for a.a. $z \in \Omega$, all $x\le 0$. Hypotheses $H_1$ (ii), (iii) imply that

$$\begin{aligned} \lim _{x\rightarrow +\infty } \frac{f(z,x)}{x^{p_+-1}}=+\infty \text { uniformly for a.a. }z \in \Omega . \end{aligned}$$

So, $f(z,\cdot )$ is $(p_+-1)$-superlinear, but need not satisfy the AR-condition which is common in the literature when studying superlinear problems (see Willem [24], p. 46). Instead we use the quasimonotonicity condition on $e_\lambda (z,\cdot )$ (see hypothesis $H_1$ (iii)). This is a slight generalization of a condition used by Li-Yang [10]. If there exists $M>0$ such that for a.a. $z \in \Omega$, $x\rightarrow \frac{f(z,x)}{x^{p_+-1}}$ is nondecreasing on $[M,+\infty )$, then hypothesis $H_1$ (iii) is satisfied. We stress that in contrast to [14], the perturbation here can be sign-changing.

Let $V: W_0^{1,p(z)}(\Omega ) \rightarrow W^{-1,p^\prime (z)}(\Omega )$ be defined by

$$\begin{aligned} \langle V(u),h \rangle = \int _\Omega (|\nabla u|^{p(z)-2}+ |\nabla u|^{q(z)-2})(\nabla u, \nabla h)_{{\mathbb {R}}^N}\mathrm{{d}}z \text { for all } u,h \in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

Evidently $V=A_p+A_q$ and so on account of Proposition 3, we have:

Proposition 4

The operator $V(\cdot )$ is bounded, continuous, strictly monotone (thus maximal monotone too) and of type $(S)_+$.

3 An Auxiliary Problem

In this section, we examine the following auxiliary anisotropic Dirichlet problem

The solution of this problem will help us bypass the singularity and prove the existence of admissible parameters for problem ($P_\lambda$).

Proposition 5

If hypothesis $H_0$ holds, then for every $\lambda >0$ problem ($Q_\lambda$) has a unique positive solution ${\overline{u}}_\lambda \in \mathrm{int \,}C_+$ and ${\overline{u}}_\lambda \rightarrow 0$ in $C_0^1({\overline{\Omega }})$ as $\lambda \rightarrow 0^+$.

Proof

First we show the existence of a positive solution for problem ($Q_\lambda$). To this end let $\sigma _\lambda : W_0^{1,p(z)}(\Omega ) \rightarrow {\mathbb {R}}$ be the $C^1$-functional defined by

$$\begin{aligned} \sigma _\lambda (u)= \int _\Omega \frac{1}{p(z)}|\nabla u|^{p(z)}\mathrm{{d}}z + \int _\Omega \frac{1}{q(z)}|\nabla u|^{q(z)}\mathrm{{d}}z - \int _\Omega \frac{\lambda }{\tau (z)}(u^+)^{\tau (z)}\mathrm{{d}}z \end{aligned}$$

for all $u \in W^{1,p(z)}_0(\Omega )$. If $\Vert u\Vert ,\Vert u\Vert _{\tau (z)} \ge 1$, then we have

$$\begin{aligned} \sigma _\lambda (u)\ge \frac{1}{p_+}\Vert u\Vert ^{p_-}-\frac{\lambda c_0}{\tau _-} \Vert u\Vert ^{\tau _-} \text { for some }c_0>0\text { (see Proposition }2\text {)}. \end{aligned}$$

Since $\tau _+<q_-<p_-$, it follows that

$\sigma _\lambda (\cdot )$ is coercive.

The modular functions are convex continuous, hence sequentially weakly lower semi-continuous. This fact and Proposition 1 (the anisotropic Sobolev embedding theorem) imply that

$\sigma _\lambda (\cdot )$ is sequentially weakly lower semicontinuous.

Then the Weierstrass–Tonelli theorem implies that there exists ${\overline{u}}_\lambda \in W^{1,p(z)}_0(\Omega )$ such that

$$\begin{aligned} \sigma _\lambda ({\overline{u}}_\lambda )=\inf \left[ \sigma _\lambda (u) :\, u \in W^{1,p(z)}_0(\Omega )\right] . \end{aligned}$$

(1)

Let $u \in W^{1,p(z)}_0(\Omega )$, $u \ne 0$. Then for $t\in (0,1)$ we have

$$\begin{aligned} \sigma _\lambda (tu)&\le \frac{t^{q_-}}{q_-}[\rho _p(\nabla u)+\rho _q(\nabla u)]- \frac{t^{\tau _+}}{\tau _+}\rho _\tau ( u)\\&\le c_1 t^{q_-}-c_2t^{\tau _+} \text { for some } c_1,c_2>0. \end{aligned}$$

Since $\tau _+<q_-$, choosing $t\in (0,1)$ even smaller if necessary, we have

$$\begin{aligned}&\sigma _\lambda (tu)<0,\\ \Rightarrow \quad&\sigma _\lambda ({\overline{u}}_\lambda )<0=\sigma _\lambda (0) \quad \text { (see }(1)\text {)}, \\ \Rightarrow \quad&{\overline{u}}_\lambda \ne 0. \end{aligned}$$

From (1) we have

$$\begin{aligned}&\langle \sigma _\lambda ^\prime ({\overline{u}}_\lambda ),h\rangle =0 \text { for all } h \in W_0^{1,p(z)}(\Omega ),\nonumber \\ \Rightarrow \quad&\langle V({\overline{u}}_\lambda ),h\rangle = \int _\Omega \lambda (u^+)^{\tau (z)-1}h \mathrm{{d}}z \text { for all } h \in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

(2)

In (2) we use the test function $h=-{\overline{u}}_\lambda ^- \in W_0^{1,p(z)}(\Omega )$ and obtain

$$\begin{aligned}&\rho _p(\nabla {\overline{u}}_\lambda ^-)\le 0, \nonumber \\ \Rightarrow \quad&{\overline{u}}_\lambda \ge 0, \, {\overline{u}}_\lambda \ne 0 \quad \text { (see Proposition } 2\text {)} . \end{aligned}$$

(3)

From (2) and (3) it follows that ${\overline{u}}_\lambda$ is a positive solution of ($Q_\lambda$). From [19] (Proposition A1), we have that ${\overline{u}}_\lambda \in L^\infty (\Omega )$. Then the anisotropic regularity theory (see Fan [5]) implies that ${\overline{u}}_\lambda \in C_+ \setminus \{0\}$. Finally the anisotropic maximum principle (see [19], Proposition A2) implies that

$$\begin{aligned} {\overline{u}}_\lambda \in \mathrm{int \, }C_+. \end{aligned}$$

Next we show that this positive solution of ($Q_\lambda$) is unique. For $\tau _0 \in (\tau _+,q_-)$, we consider the integral functional $j: L^1(\Omega )\rightarrow \overline{{\mathbb {R}}}={\mathbb {R}} \cup \{+\infty \}$ defined by

$$\begin{aligned} j(u)= {\left\{ \begin{array}{ll} \int _\Omega \frac{1}{p(z)}|\nabla u^{1/\tau _0}|^{p(z)}\mathrm{{d}}z+\int _\Omega \frac{1}{q(z)}|\nabla u^{1/\tau _0}|^{q(z)}\mathrm{{d}}z &{} \text { if }u \ge 0, \, u^{1/\tau _0} \in W_0^{1,p(z)}(\Omega ),\\ +\infty &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

Theorem 2.2 of Takác̆–Giacomoni [22] implies that $j(\cdot )$ is convex. Suppose ${\widetilde{u}}_\lambda$ is another positive solution of ($Q_\lambda$). Again we have ${\widetilde{u}}_\lambda \in \mathrm{int \, }C_+$. Using Proposition 4.1.22, p. 274, of Papageorgiou–Rădulescu–Repovš [18], we have

$$\begin{aligned} \frac{{\overline{u}}_\lambda }{{\widetilde{u}}_\lambda }\in L^\infty (\Omega ) \text { and } \frac{{\widetilde{u}}_\lambda }{{\overline{u}}_\lambda }\in L^\infty (\Omega ). \end{aligned}$$

(4)

Let $\mathrm{dom \,}j=\{u \in L^1(\Omega ): j(u)< +\infty \}$ (the effective domain of $j(\cdot )$) and let $h= ({\overline{u}}_\lambda ^{\tau _0}-{\widetilde{u}}_\lambda ^{\tau _0}) \in W_0^{1,p(z)}(\Omega )$. On account of (4) for $t\in (0,1)$ small we have

$$\begin{aligned} {\overline{u}}_\lambda ^{\tau _0} + th \in \mathrm{dom \,}j, \quad {\widetilde{u}}_\lambda ^{\tau _0} + th \in \mathrm{dom \,}j. \end{aligned}$$

Then since $j(\cdot )$ is convex, the directional derivatives of $j(\cdot )$ at ${\overline{u}}_\lambda ^{\tau _0}$ and at ${\widetilde{u}}_\lambda ^{\tau _0}$ in the direction h exist and using Green’s identity we have

$$\begin{aligned} j^\prime ({\overline{u}}_\lambda ^{\tau _0})(h)&= \frac{1}{\tau _0}\int _\Omega \frac{-\Delta _{p(z)} {\overline{u}}_\lambda -\Delta _{q(z)} {\overline{u}}_\lambda }{{\overline{u}}_\lambda ^{\tau _0-1}}h \mathrm{{d}}z\\&= \frac{1}{\tau _0}\int _\Omega \lambda {\overline{u}}_\lambda ^{\tau (z)-\tau _0}h \mathrm{{d}}z,\\ j^\prime ({\widetilde{u}}_\lambda ^{\tau _0})(h)&= \frac{1}{\tau _0}\int _\Omega \frac{-\Delta _{p(z)} {\widetilde{u}}_\lambda -\Delta _{q(z)} {\widetilde{u}}_\lambda }{{\widetilde{u}}_\lambda ^{\tau _0-1}}h {\textbf {d}}z\\&= \frac{1}{\tau _0}\int _\Omega \lambda {\widetilde{u}}_\lambda ^{\tau (z)-\tau _0}h \mathrm{{d}}z. \end{aligned}$$

The convexity of $j(\cdot )$ implies the monotonicity of $j^\prime (\cdot )$. Hence

$$\begin{aligned}&0 \le \int _\Omega \lambda [{\overline{u}}_\lambda ^{\tau (z)-\tau _0}- {\widetilde{u}}_\lambda ^{\tau (z)-\tau _0}]\left( {\overline{u}}_\lambda ^{\tau _0}- {\widetilde{u}}_\lambda ^{\tau _0}\right) \mathrm{{d}}z \le 0\, (\text {since} \tau _+<\tau _0),\\&\quad \Rightarrow {\widetilde{u}}_\lambda ={\overline{u}}_\lambda . \end{aligned}$$

This proves the uniqueness of the positive solution ${\overline{u}}_\lambda \in \mathrm{int \,}C_+$ of ($Q_\lambda$).

Finally we have

$$\begin{aligned} \langle V({\overline{u}}_\lambda ),h\rangle = \int _\Omega \lambda {\overline{u}}_\lambda ^{\tau (z)-1}h dz \text { for all } h \in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

Using $h={\overline{u}}_\lambda \in W_0^{1,p(z)}(\Omega )$, we obtain

$$\begin{aligned} \rho _p(\nabla {\overline{u}}_\lambda )\le \lambda \rho _\tau ( {\overline{u}}_\lambda ),&\\ \Rightarrow \quad \min \{\Vert {\overline{u}}_\lambda \Vert ^{p_+},\Vert {\overline{u}}_\lambda \Vert ^{p_-}\}&\le \lambda \max \big \{\Vert {\overline{u}}_\lambda \Vert _{\tau (z)}^{\tau _+},\Vert {\overline{u}}_\lambda \Vert ^{\tau _-}_{\tau (z)} \big \}\\&\text { (see Proposition }2\text {)}\\&\le \lambda c_3 \max \{\Vert {\overline{u}}_\lambda \Vert ^{\tau _+},\Vert {\overline{u}}_\lambda \Vert ^{\tau _-}\}\\&\text { for some } c_3>0 \text { (see Proposition } 1\text {)}. \end{aligned}$$

Recall that $\tau _+<q_-<p_-$. So, it follows that

$$\begin{aligned} {\overline{u}}_\lambda \rightarrow 0 \text { in } W_0^{1,p(z)}(\Omega ) \text { as } \lambda \rightarrow 0^+. \end{aligned}$$

(5)

The anisotropic regularity theory (see Fan [5]) implies that we can find $\alpha \in (0,1)$ and $c_4>0$ such that

$$\begin{aligned} {\overline{u}}_\lambda \in C_0^{1,\alpha }({\overline{\Omega }}), \, \Vert {\overline{u}}_\lambda \Vert _{C_0^{1,\alpha }({\overline{\Omega }})}\le c_4 \text { for all }\lambda \in (0,1]. \end{aligned}$$

(6)

We know that $C_0^{1,\alpha }({\overline{\Omega }}) \hookrightarrow C_0^{1}({\overline{\Omega }})$ compactly. So, from (6) and (5) we conclude that

$$\begin{aligned} {\overline{u}}_\lambda \rightarrow 0 \text { in } C_0^{1}({\overline{\Omega }}) \text { as } \lambda \rightarrow 0^+. \end{aligned}$$

$\square$

4 Positive Solutions

We introduce the following two sets:

$$\begin{aligned}&{\mathcal {L}}=\{\lambda >0 \, : \, \text { problem } (P_\lambda ) \text { has a positive solution}\}\\&\text { (set of admissible parameters),}\\&{\mathcal {S}}_\lambda =\{\text { set of positive solutions of } (P_\lambda )\}. \end{aligned}$$

Proposition 6

If hypotheses $H_0$, $H_1$ hold, then ${\mathcal {L}} \ne \emptyset$ and for all $\lambda >0$ $S_\lambda \subseteq \mathrm{int \,}C_+$.

Proof

Let $\delta >0$ be as postulated by hypothesis $H_1 (iv)$. On account of Proposition 5, we can find $\lambda ^*>0$ such that

$$\begin{aligned} \Vert {\overline{u}}_\lambda \Vert _\infty \le \delta \text { for all }\lambda \in (0,\lambda ^*]. \end{aligned}$$

(7)

We fix $\lambda \in (0,\lambda ^*]$ and let ${\overline{u}}_\lambda \in \mathrm{int \,}C_+$ be the unique positive solution of ($Q_\lambda$) (see Proposition 5). We introduce the Carathéodory function $g_\lambda (z,x)$ defined by

$$\begin{aligned} g_\lambda (z,x)={\left\{ \begin{array}{ll}\lambda [{\overline{u}}_\lambda (z)^{-\eta (z)}+ {\overline{u}}_\lambda (z)^{\tau (z)-1}]+f(z,x^+)&{} \text { if }x \le {\overline{u}}_\lambda (z),\\ \lambda [x^{-\eta (z)}+ x^{\tau (z)-1}]+f(z,x) &{} \text { if }{\overline{u}}_\lambda (z)<x.\end{array}\right. } \end{aligned}$$

(8)

Let $G_\lambda (z,x)=\int _0^x g_\lambda (z,s)ds$ and consider the $C^1$-functional $\varphi _\lambda :W_0^{1,p(z)}(\Omega )\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned}{} & {} \varphi _\lambda (u)=\int _\Omega \frac{1}{p(z)}|\nabla u|^{p(z)}\mathrm{{d}}z+\int _\Omega \frac{1}{q(z)}|\nabla u|^{q(z)}\mathrm{{d}}z\\{} & {} -\int _\Omega G_\lambda (z,u)dz \text { for all }u \in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

Claim: $\varphi _\lambda (\cdot )$ satisfies the C-condition.

Consider a sequence $\{u_n\}_{n \in {\mathbb {N}}}\subseteq W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned}&|\varphi _\lambda (u_n)|\le c_5 \text { for some } c_5>0, \text { all } n \in {\mathbb {N}}, \end{aligned}$$

(9)

$$\begin{aligned}&(1+\Vert u_n\Vert )\varphi ^\prime _\lambda (u_n) \rightarrow 0 \text { in } W^{-1,p'(z)}(\Omega ) \text { as } n \rightarrow +\infty . \end{aligned}$$

(10)

From (10) we have

$$\begin{aligned}&\left| \langle V(u_n),h \rangle -\int _\Omega g_\lambda (z,u_n)h \mathrm{{d}}z \right| \le \frac{\varepsilon _n \Vert h\Vert }{1+\Vert u_n\Vert }\nonumber \\&\text { for all } h \in W_0^{1,p(z)}(\Omega ), \text { with } \varepsilon _n \rightarrow 0^+. \end{aligned}$$

(11)

In (11) we choose the test function $h=-u_n^- \in W_0^{1,p(z)}(\Omega )$. Using (8) we obtain

$$\begin{aligned}&\rho _p(\nabla u_n^-)\le \varepsilon _n \text { for all } n \in {\mathbb {N}},\nonumber \\ \Rightarrow \quad&u_n^- \rightarrow 0 \text { in } W_0^{1,p(z)}(\Omega ) \text { (see Proposition }2\text {)}. \end{aligned}$$

(12)

We define

$$\begin{aligned} {\widehat{f}}_\lambda (z,x)=\lambda [x^{-\eta (z)}+x^{\tau (z)-1}]+f(z,x) \end{aligned}$$

and ${\widehat{F}}_\lambda (z,x)=\int _0^x {\widehat{f}}_\lambda (z,s)\mathrm{{d}}s$.

From (12), (9) and (8), we have

$$\begin{aligned}&\int _\Omega \frac{p_+}{p(z)}|\nabla u_n^+|^{p(z)}\mathrm{{d}}z+\int _\Omega \frac{p_+}{q(z)}|\nabla u_n^+|^{q(z)}\mathrm{{d}}z -\int _\Omega p_+{\widehat{F}}_\lambda (z,u_n^+)\mathrm{{d}}z \le c_6\nonumber \\&\text { for some } c_6>0, \text { all } n \in {\mathbb {N}},\nonumber \\ \Rightarrow \quad&\rho _p(\nabla u_n^+)+\rho _q(\nabla u_n^+) -\int _\Omega p_+{\widehat{F}}_\lambda (z,u_n^+)\mathrm{{d}}z \le c_6 \text { for all } n \in {\mathbb {N}}\nonumber \\&\text { (since } p(z)\le p_+ \text { for all } z \in {\overline{\Omega }}\text {)}. \end{aligned}$$

(13)

In (11) we choose the test function $h=u_n^+ \in W_0^{1,p(z)}(\Omega )$ and obtain

$$\begin{aligned}&-\rho _p(\nabla u_n^+)-\rho _q(\nabla u_n^+)+ \int _\Omega g_\lambda (z,u_n^+)u_n^+\mathrm{{d}}z\le \varepsilon _n \text { for all } n \in {\mathbb {N}},\nonumber \\ \Rightarrow \quad&-\rho _p(\nabla u_n^+)-\rho _q(\nabla u_n^+)+ \int _\Omega {\widehat{f}}_\lambda (z,u_n^+)u_n^+\mathrm{{d}}z\le c_7 \nonumber \\&\text { for some } c_7>0, \text { all } n \in {\mathbb {N}} \text { (see } (8)\text {)}. \end{aligned}$$

(14)

We add (13) and (14) and obtain

$$\begin{aligned} \int _\Omega e_\lambda (z,u_n^+)dz\le c_8 \text { for some } c_8>0, \text { all } n \in {\mathbb {N}}, \end{aligned}$$

(15)

(note that $e_\lambda (z,x)={\widehat{f}}_\lambda (z,x)x-p_+{\widehat{F}}_\lambda (z,x)$ for all $z \in \Omega$, all $x \ge 0$). Using (15) we will show that $\{u_n^+\}_{n \in {\mathbb {N}}}\subseteq W_0^{1,p(z)}(\Omega )$. Arguing by contradiction, suppose that at least for a subsequence we have

$$\begin{aligned} \Vert u_n^+\Vert \rightarrow +\infty \text { as } n \rightarrow +\infty , \, \Vert u_n^+\Vert \ge 1 \text { for all } n \in {\mathbb {N}}. \end{aligned}$$

(16)

We set $y_n = \dfrac{u_n^+}{\Vert u_{n}^+ \Vert }$, $n \in {\mathbb {N}}$. Then $y_n \in W_0^{1,p(z)}(\Omega )$, $y_n \ge 0$, $\Vert y_n \Vert = 1$ for all $n \in {\mathbb {N}}$. So, we may assume that

$$\begin{aligned} y_n \xrightarrow {w} y \text { in } W_0^{1, p(z)} (\Omega ), \, y_n \rightarrow y \text { in } L^{r(z)}(\Omega ), \, y \ge 0 \text { (see Proposition } 1\text {)}. \end{aligned}$$

(17)

Suppose $y \ne 0$. We set $\Omega _+=\{z\in \Omega : y(z)>0\}$. From (17) we see that $|\Omega _+|_N>0$ (by $|\cdot |_N$ we denote the Lebesgue measure on ${\mathbb {R}}^N$). We have

$$\begin{aligned} u_n^+(z) \rightarrow +\infty \text { for a.a. } z \in \Omega _+. \end{aligned}$$

(18)

Then from (18), hypothesis $H_1 (ii)$ and since $\tau _+<p_+$, we see that

$$\begin{aligned} \frac{{\widehat{F}}_\lambda (z,u_n^+(z))}{\Vert u_n^+\Vert ^{p_+}} =\frac{{\widehat{F}}_\lambda (z,u_n^+(z))}{(u_n^+(z))^{p_+}} y_n(z)^{p_+} \rightarrow +\infty \text { for a.a. } z \in \Omega _+. \end{aligned}$$

Using Fatou’s lemma, we have

$$\begin{aligned} \lim _{n\rightarrow +\infty }\int _\Omega \frac{{\widehat{F}}_\lambda (z,u_n^+)}{\Vert u_n^+\Vert ^{p_+}} \mathrm{{d}}z=+\infty . \end{aligned}$$

(19)

From (12), (9) and (8), we have

$$\begin{aligned}&-\frac{1}{q_-}\left[ \rho _p(\nabla u_n^+)+\rho _q(\nabla u_n^+)\right] +\int _\Omega {\widehat{F}}_\lambda (z,u_n^+)dz\le c_9 \nonumber \\&\text { for some } c_9>0, \text { all } n \in {\mathbb {N}},\nonumber \\ \Rightarrow \quad&\int _\Omega {\widehat{F}}_\lambda (z,u_n^+)dz\le c_9+ \frac{1}{q_-}\left[ \rho _p(\nabla u_n^+)+\rho _q(\nabla u_n^+)\right] \nonumber \\&\le c_{10}\left[ 1+\rho _p(\nabla u_n^+)\right] \text { for some } c_{10}>0,\nonumber \\&\le c_{10}\left[ 1+\Vert u_n^+\Vert ^{p_+}\right] \text { (see } (16) \text { and Proposition } 2\text {)},\nonumber \\ \Rightarrow \quad&\int _\Omega \frac{{\widehat{F}}_\lambda (z,u_n^+)}{\Vert u_n^+\Vert ^{p_+}} \mathrm{{d}}z \le c_{10}\left[ \frac{1}{\Vert u_n^+\Vert ^{p_+}}+1\right] \text { for all } n \in {\mathbb {N}}. \end{aligned}$$

(20)

Comparing (20) and (19), we have a contradiction.

Next suppose that $y=0$. Consider the function

$$\begin{aligned} \mu _n(t)=\varphi _\lambda (tu_n^+) \text { for all } t \in [0,1]. \end{aligned}$$

The function $\mu _n(\cdot )$ is continuous and we can find $t _n\in [0,1]$ such that

$$\begin{aligned} \mu _n(t_n)=\max \limits _{0\le t\le 1}\mu _n(t). \end{aligned}$$

(21)

Let $\beta >1$ and set $v_n=(2\beta )^{1/p_-}y_n$, $n \in {\mathbb {N}}$. From (17) and since we assume that $y=0$, we have

$$\begin{aligned} v_n \rightarrow&0 \text { in } L^{r(z)}(\Omega ),\nonumber \\ \Rightarrow&\int _\Omega G_\lambda (z,v_n)\mathrm{{d}}z \rightarrow 0 \text { as } n \rightarrow +\infty . \end{aligned}$$

(22)

From (16) we see that we can find $n_0\in {\mathbb {N}}$ such that

$$\begin{aligned} \frac{(2\beta )^{1/p_-}}{\Vert u_n^+\Vert } \in (0,1] \text { for all }n \ge n_0. \end{aligned}$$

(23)

Then from (21) and (23) we see that

$$\begin{aligned} \varphi _\lambda (t_nu_n^+)&\ge \varphi _\lambda ((2\beta )^{1/p_-}y_n)= \varphi _\lambda (v_n) \text { for all } n \ge n_0,\\ \Rightarrow \quad \varphi _\lambda (t_nu_n^+)&\ge \frac{1}{p_+}\int _\Omega (2\beta )^{\frac{p(z)}{p_-}}|\nabla y_n|^{p(z)} dz-\int _\Omega G_\lambda (z,v_n)\mathrm{{d}}z\\&\ge \frac{2 \beta }{p_+} \rho _p(\nabla y_n) -\int _\Omega G_\lambda (z,v_n)dz \text { (recall }\beta >1\text {)}\\&= \frac{2 \beta }{p_+} -\int _\Omega G_\lambda (z,v_n)dz \text { for all } n \ge n_0\\&\text { (since }\Vert y_n\Vert =1, \text { see Proposition } 2\text {)}. \end{aligned}$$

From (22) we see that there exists $n_1 \in {\mathbb {N}}$, $n_1\ge n_0$, such that

$$\begin{aligned} \varphi _\lambda (t_nu_n^+) \ge \frac{ \beta }{p_+} \text { for all } n \ge n_1. \end{aligned}$$

But $\beta >1$ is arbitrary. So, we infer that

$$\begin{aligned} \varphi _\lambda (t_nu_n^+) \rightarrow +\infty \text { as } n \rightarrow +\infty . \end{aligned}$$

(24)

We have

$$\begin{aligned}&0 \le t_nu_n^+\le u_n^+ \text { for all }n \in {\mathbb {N}},\nonumber \\ \Rightarrow \quad&\int _\Omega e_\lambda (z,t_nu_n^+)\mathrm{{d}}z\le \int _\Omega e_\lambda (z,u_n^+)\mathrm{{d}}z+c_{11}\nonumber \\&\text { for some } c_{11}>0, \text { all } n \in {\mathbb {N}} \text { (see hypothesis } H_1 (iii)),\nonumber \\ \Rightarrow \quad&\int _\Omega e_\lambda (z,t_nu_n^+)\mathrm{{d}}z\le c_{12} \text { for some } c_{12}>0, \text { all } n \in {\mathbb {N}} \text { (see } (15)\text {)}. \end{aligned}$$

(25)

We set

$$\begin{aligned} {\widehat{e}}_\lambda (z,x)=g_\lambda (z,x)x-p_+G_\lambda (z,x) \text { for all } z \in \Omega , \text { all } x \ge 0. \end{aligned}$$

Then from (8), (7) and hypothesis $H_1 (iv)$, we see that

$$\begin{aligned} {\widehat{e}}_\lambda (z,x)\le e_\lambda (z,x)+c_{13} \text { for some } c_{13}>0, \text { a.a. } z \in \Omega , \text { all } x \ge 0. \end{aligned}$$

(26)

Note that

$$\begin{aligned} \varphi _\lambda (0)=0, \, \varphi _\lambda (u_n^+)\le c_{14} \text { for some } c_{14}>0, \text { all } n \in {\mathbb {N}} \text { (see } (9), (12)\text {)}. \end{aligned}$$

(27)

From (24) and (27) it follows that there exists $n_2 \in {\mathbb {N}}$ such that

$$\begin{aligned} t_n \in (0,1) \text { for all } n \ge n_2. \end{aligned}$$

(28)

Then (28) and (21) imply that for all $n \ge n_2$, we have

$$\begin{aligned}&\frac{d}{dt}\mu _n(t)\Big |_{t=t_n}=0,\nonumber \\ \Rightarrow \quad&\langle \varphi _\lambda ^\prime (t_nu_n^+),u_n^+\rangle =0 \text { (by the chain rule),}\nonumber \\ \Rightarrow \quad&\langle \varphi _\lambda ^\prime (t_nu_n^+),t_nu_n^+\rangle =0 \text { for all } n \ge n_2 \text { (see } (28)\text {)}. \end{aligned}$$

(29)

For $n \ge n_2$ we have

$$\begin{aligned} \varphi _\lambda (t_nu_n^+)&= \varphi _\lambda (t_nu_n^+) - \frac{1}{p_+}\langle \varphi _\lambda ^\prime (t_nu_n^+),t_nu_n^+\rangle \quad \text { (see } (29)\text {)},\nonumber \\ \Rightarrow \quad \varphi _\lambda (t_nu_n^+)&\le \int _\Omega \left[ \frac{1}{p(z)}-\frac{1}{p_+}\right] |\nabla u_n^+|^{p(z)} \mathrm{{d}}z + \int _\Omega \left[ \frac{1}{q(z)}-\frac{1}{p_+}\right] |\nabla u_n^+|^{q(z)} \mathrm{{d}}z\nonumber \\&+\frac{1}{p_+}\ \int _\Omega {\widehat{e}}_\lambda (z,t_nu_n^+)\mathrm{{d}}z \text { (see } (28)\text {)}\nonumber \\&\le \int _\Omega \left[ \frac{1}{p(z)}-\frac{1}{p_+}\right] |\nabla u_n^+|^{p(z)} \mathrm{{d}}z + \int _\Omega \left[ \frac{1}{q(z)}-\frac{1}{p_+}\right] |\nabla u_n^+|^{q(z)} dz\nonumber \\&+\frac{1}{p_+}\ \int _\Omega e_\lambda (z,t_nu_n^+)\mathrm{{d}}z + c_{15} \text { for some } c_{15}>0 \text { (see } (26)\text {)}\nonumber \\&\le \int _\Omega \left[ \frac{1}{p(z)}-\frac{1}{p_+}\right] |\nabla u_n^+|^{p(z)} \mathrm{{d}}z + \int _\Omega \left[ \frac{1}{q(z)}-\frac{1}{p_+}\right] |\nabla u_n^+|^{q(z)} \mathrm{{d}}z\nonumber \\&+ c_{16} \text { for some } c_{16}>0 \text { (see } (25)\text {)}\nonumber \\&\le \varphi _\lambda (u_n^+) - \frac{1}{p_+}\langle \varphi _\lambda ^\prime (u_n^+),u_n^+\rangle +c_{17} \text { for some } c_{17}>0 \text { (see } (26), (15)\text {)} \nonumber \\&\le c_{18} \text { for some } c_{18}>0 \text { (see } (9), (10), (12)\text {)}. \end{aligned}$$

(30)

We compare (24) and (30) and reach a contradiction. Therefore $\{u_n^+\}_{n \in {\mathbb {N}}}\subseteq W_0^{1,p(z)}(\Omega )$ is bounded and this combined with (12) implies that $\{u_n\}_{n \in {\mathbb {N}}}\subseteq W_0^{1,p(z)}(\Omega )$ is bounded. We may assume that

$$\begin{aligned} u_n \xrightarrow {w} u \text { in } W_0^{1, p(z)} (\Omega ), \, u_n \rightarrow u \text { in } L^{r(z)}(\Omega ). \end{aligned}$$

(31)

In (11) we use the test function $h=(u_n -u) \in W_0^{1,p(z)}(\Omega )$, pass to the limit as $n \rightarrow + \infty$ and use (31). We obtain

$$\begin{aligned}&\lim _{n \rightarrow + \infty } \langle V(u_n), u_n-u \rangle =0,\\ \Rightarrow \quad&u_n \rightarrow u \text { in } W_0^{1,p(z)}(\Omega ) \text { (see Proposition } 4\text {)},\\ \Rightarrow \quad&\varphi _\lambda (\cdot ) \text { satisfies the } C\!\!-\!\text {condition} \end{aligned}$$

This proves the Claim.

On account of hypotheses $H_1 (i),(iv)$, given $\varepsilon >0$, we can find $c_{19}=c_{19}(\varepsilon )>0$ such that

$$\begin{aligned} F(z,x)\le \frac{\varepsilon }{p_+}x^{q_+}+c_{19}x^{r(z)} \text { for a.a. } z\in \Omega , \text { all } x \ge 0. \end{aligned}$$

(32)

Consider $u \in W_0^{1,p(z)}(\Omega )$ with $\Vert u\Vert \le 1$ small. We have

$$\begin{aligned} \varphi _\lambda (u)&\ge \frac{1}{p_+}\left[ \rho _p(\nabla u)+\rho _q(\nabla u)\right] -\int _{\{u \le {\overline{u}}_\lambda \}} \lambda [{\overline{u}}_\lambda ^{-\eta (z)} + {\overline{u}}_\lambda ^{\tau (z)-1} ]u^+ \mathrm{{d}}z \nonumber \\&- \frac{\lambda }{1-\eta _+}\int _{\{{\overline{u}}_\lambda<u\}} [u^{1-\eta (z)} - {\overline{u}}_\lambda ^{1-\eta (z)} ] \mathrm{{d}}z- \frac{\lambda }{\tau _-}\int _{\{ {\overline{u}}_\lambda <u\}} [u^{\tau (z)} - {\overline{u}}_\lambda ^{\tau (z)} ] dz\nonumber \\&- \int _\Omega F(z,u^+)\mathrm{{d}}z \text { (see } (8)\text {)}. \end{aligned}$$

(33)

Let ${\widehat{d}}(z)=d(z,\partial \Omega )$ for all $z \in {\overline{\Omega }}$. Then Lemma 14.16, p. 355, of Gilbarg–Trudinger [8] implies that ${\widehat{d}} \in C_+ \setminus \{0\}$. Since ${\overline{u}}_\lambda \in \textrm{int }\, C_+$ (see Proposition 5), using Proposition 4.1.22, p. 274, of [18], we can find $c_{20}>0$ such that

$$\begin{aligned} c_{20} {\widehat{d}} \le {\overline{u}}_\lambda . \end{aligned}$$

(34)

Using the anisotropic Hardy’s inequality of Harjulehto–Hästo–Koskenoja [9], we have

$$\begin{aligned} \int _\Omega \left( \frac{|u|}{{\overline{u}}_\lambda ^{\eta (z)}}\right) ^{p(z)}\mathrm{{d}}z&= \int _\Omega \left( {\overline{u}}_\lambda ^{1-\eta (z)}\right) ^{p(z)} \left( \frac{|u|}{{\overline{u}}_\lambda }\right) ^{p(z)}\mathrm{{d}}z\nonumber \\&\le c_{21} \int _\Omega \left( \frac{|u|}{{\overline{u}}_\lambda }\right) ^{p(z)}\mathrm{{d}}z \text { for some } c_{21}>0 \text { (since } {\overline{u}}_\lambda \in \mathrm{int \,}C_+\text {)}\nonumber \\&\le c_{22} \int _\Omega \left( \frac{|u|}{{\widehat{d}}}\right) ^{p(z)}\mathrm{{d}}z \text { for some } c_{22}>0 \text { (see } (34)\text {)}\nonumber \\&\le c_{22} \left\| \, \frac{u}{{\widehat{d}}} \, \right\| _{p(z)} \text { for } \Vert u\Vert \le 1 \text { small} \text { (see Proposition } 2 \text { and [9])}\nonumber \\&\le c_{23} \Vert u\Vert \text { for some } c_{23}>0. \end{aligned}$$

(35)

Also we have

$$\begin{aligned} \frac{\lambda }{1-\eta _+}\int _{\{{\overline{u}}_\lambda<u\}} u^{1-\eta (z)} \mathrm{{d}}z&\le \frac{\lambda }{1-\eta _+}\int _{\{{\overline{u}}_\lambda <u\}} \frac{u}{{\overline{u}}_\lambda ^{\eta (z)}} \mathrm{{d}}z \nonumber \\&\le \lambda c_{24} \int _\Omega \frac{|u|}{{\widehat{d}}} \mathrm{{d}}z \text { for some } c_{24}>0\nonumber \\&\le \lambda c_{25} \left\| \frac{|u|}{{\widehat{d}}} \right\| _{p(z)} \text { for some } c_{25}>0\nonumber \\&\text { (since } L^{p(z)}(\Omega ) \hookrightarrow L^1(\Omega ) \text { continuously)} \nonumber \\&\le \lambda c_{26} \Vert u\Vert \text { for some } c_{26}>0\nonumber \\&\text { (anisotropic Hardy's inequality, see [9]),} \end{aligned}$$

(36)

and

$$\begin{aligned} \frac{\lambda }{\tau _-}\int _{\{{\overline{u}}_\lambda <u\}} |u|^{\tau (z)} \mathrm{{d}}z \le \frac{\lambda }{\tau _-}\rho _\tau (u) \le \lambda c_{27}\Vert u\Vert \text { for some } c_{27}>0 \text { (}\Vert u\Vert \le 1 \text { small)}.\nonumber \\ \end{aligned}$$

(37)

We return to (33) and use (35), (36), (37) and (32). We obtain

$$\begin{aligned} \varphi _\lambda (u)&\ge \frac{1}{p_+} \Vert u\Vert ^{p_+}+ \frac{1}{p_+} \left[ \Vert u\Vert _{1,q(z)}^{q_+}- \varepsilon c_{28} \Vert u\Vert _{1,q(z)}^{q_+} \right] -c_{29} [\lambda \Vert u\Vert + \Vert u\Vert ^{r_-}]\\&\text { for some } c_{28},c_{29}>0 \text { (recall } \Vert u\Vert \le 1 \text { is small)}. \end{aligned}$$

Choosing $\varepsilon >0$ small, we have

$$\begin{aligned} \varphi _\lambda (u) \ge \left[ \frac{1}{p_+} - c_{29}( \lambda \Vert u\Vert ^{1-p_+}+\Vert u\Vert ^{r_--p_+} ) \right] \Vert u\Vert ^{p_+}. \end{aligned}$$

Consider the function

$$\begin{aligned} {\widehat{\gamma }}_\lambda (t)=\lambda t^{1-p_+}+t^{r_--p_+}, \, t \ge 0. \end{aligned}$$

Evidently ${\widehat{\gamma }}_\lambda \in C^1(0,\infty )$ and

$$\begin{aligned} {\widehat{\gamma }}_\lambda (t)\rightarrow +\infty \text { as } t \rightarrow 0^+ \text { and as } t\rightarrow +\infty \text { (since } 1<p_+<r_-). \end{aligned}$$

Therefore we can find $t_0 \in (0,1)$ such that

$$\begin{aligned}&{\widehat{\gamma }}_\lambda (t_0)= \min \limits _{t>0}{\widehat{\gamma }}_\lambda ,\\ \Rightarrow \quad&{\widehat{\gamma }}_\lambda ^\prime (t_0)=0,\\ \Rightarrow \quad&\lambda (p_+-1)t_0^{-p_+}=(r_--p_+)t_0^{r_- -p_+ -1},\\ \Rightarrow \quad&t_0=t_0(\lambda )=\left[ \frac{\lambda (p_+-1)}{r_--p_+}\right] ^{\frac{1}{r_- - 1}}. \end{aligned}$$

We have

$$\begin{aligned} {\widehat{\gamma }}_\lambda (t_0)= \lambda \left[ \frac{r_--p_+}{\lambda (p_+-1)}\right] ^{\frac{p_+ -1}{r_- - 1}}+ \left[ \frac{\lambda (p_+-1)}{r_--p_+}\right] ^{\frac{r_- - p_+}{r_- - 1}}. \end{aligned}$$

Since $p_+<r_-$, we see that

$$\begin{aligned} {\widehat{\gamma }}_\lambda (t_0) \rightarrow 0 \text { as } \lambda \rightarrow 0^+. \end{aligned}$$

Therefore we can find ${\widehat{\lambda }}_0>0$ such that

$$\begin{aligned}&\frac{1}{p_+}-c_{29}{\widehat{\gamma }}_\lambda (t_0)\ge \beta _\lambda>0 \text { for all } \lambda \in (0, {\widehat{\lambda }}_0),\nonumber \\ \Rightarrow \quad&\varphi _\lambda (u)\ge \beta _\lambda >0 \text { for all } \lambda \in (0, {\widehat{\lambda }}_0), \text { all } \Vert u\Vert =t_0(\lambda ). \end{aligned}$$

(38)

Let ${\overline{B}}_\lambda = \{u\in W_0^{1,p(z)}(\Omega ): \Vert u\Vert \le t_0(\lambda ) \}$. The reflexivity of $W_0^{1,p(z)}(\Omega )$ and the Eberlein–Šmulian theorem imply that ${\overline{B}}_\lambda$ is sequentially weakly compact. Also, the sequential weak lower semicontinuity of the modular function and Proposition 1 imply that $\varphi _\lambda (\cdot )$ is sequentially weakly lower semicontinuous. So, we can find $u_\lambda \in {\overline{B}}_\lambda$ such that

$$\begin{aligned} \varphi _\lambda (u_\lambda )=\inf \left[ \varphi _\lambda (u) :\, u \in {\overline{B}}_\lambda \right] . \end{aligned}$$

(39)

Recall that ${\overline{u}}_\lambda \in \mathrm{int \,}C_+$. So, if $u \in C_+ {\setminus } \{0\}$, we can find $t \in (0,1)$ small such that

$$\begin{aligned} 0\le tu \le {\overline{u}}_\lambda , \, 0\le tu(z)\le \delta \text { for all } z \in {\overline{\Omega }} \text { (see [12], p. 274)}. \end{aligned}$$

Using (8) and hypothesis $H_1 (iv)$, we have

$$\begin{aligned} \varphi _\lambda (tu)&\le \frac{t^{q_-}}{q_-}[\rho _p(\nabla u)+\rho _q(\nabla u)]- \lambda t \int _\Omega [{\overline{u}}_\lambda ^{-\eta (z)}+u^{\tau (z)-1}]u \mathrm{{d}}z\\&\le c_{30} t^{q_-}-\lambda c_{31}t \text { for some } c_{30},c_{31}>0 \text { (recall } \frac{u}{{\overline{u}}_\lambda ^{\eta (\cdot )}}\in L^1(\Omega )\text {)}. \end{aligned}$$

Since $1<q_-$, choosing $t\in (0,1)$ even smaller if necessary, we have

$$\begin{aligned}&\varphi _\lambda (tu)<0,\\ \Rightarrow \quad&\varphi _\lambda (u_\lambda )<0=\varphi _\lambda (0) \quad \text { (see } (39)\text {)}, \\ \Rightarrow \quad&u_\lambda \ne 0. \end{aligned}$$

Then from (38) we see that

$$\begin{aligned}&0< \Vert u_\lambda \Vert <t_0(\lambda ),\nonumber \\ \Rightarrow \quad&\langle \varphi _\lambda ^\prime (u_\lambda ),h \rangle =0 \text { for all } h \in W_0^{1,p(z)}(\Omega ),\nonumber \\ \Rightarrow \quad&\langle V(u_\lambda ),h \rangle =\int _\Omega g_\lambda (z,u_\lambda )hdz \text { for all } h \in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

(40)

We use the test function $h=({\overline{u}}_\lambda -u_\lambda )^+ \in W_0^{1,p(z)}(\Omega )$. We have

$$\begin{aligned}&\langle V(u_\lambda ),({\overline{u}}_\lambda -u_\lambda )^+ \rangle \nonumber \\&=\int _\Omega (\lambda [{\overline{u}}_\lambda ^{-\eta (z)}+{\overline{u}}_\lambda ^{\tau (z)-1}]+f(z,u_\lambda ^+))({\overline{u}}_\lambda -u_\lambda )^+\mathrm{{d}}z \text { (see } (8)\text {)}\nonumber \\&\ge \int _\Omega \lambda {\overline{u}}_\lambda ^{\tau (z)-1} ({\overline{u}}_\lambda -u_\lambda )^+dz \text { (see } (7) \text { and hypothesis } H_1 (iv)\text {)}\nonumber \\&= \langle V({\overline{u}}_\lambda ),({\overline{u}}_\lambda -u_\lambda )^+ \rangle \text { (see Proposition } 5\text {)},\nonumber \\ \Rightarrow \quad&{\overline{u}}_\lambda \le u_\lambda \text { (see Proposition } 4\text {)}. \end{aligned}$$

(41)

From (41), (8) and (40), we infer that

$u_\lambda$ is a positive solution of ($P_\lambda$).

From Proposition A1 of Papageorgiou–Rădulescu–Zhang [19], we know that $u_\lambda \in L^\infty (\Omega )$. Then the singular anisotropic regularity theory (see Saoudi–Ghanmi [21] and Giacomoni–Kumar–Sreenadh [7] for the corresponding isotropic theory) implies that $u_\lambda \in C_+{\setminus } \{0\}$. Let $\rho =\Vert u_\lambda \Vert _\infty$ and let ${\widehat{\xi }}_\rho >0$ be as postulated by hypothesis $H_1 (iv)$. We have

$$\begin{aligned}&-\Delta _{p(z)}u_\lambda -\Delta _{q(z)}u_\lambda +{\widehat{\xi }}_\rho u_\lambda ^{p(z)-1}-\lambda u_\lambda ^{-\eta (z)}\\&= \lambda u_\lambda ^{\tau (z)-1}+f(z,u_\lambda )+{\widehat{\xi }}_\rho u_\lambda ^{p(z)-1}\\&\ge 0 \text { in } \Omega ,\\ \Rightarrow \quad&u_\lambda \in \mathrm{int \, } C_+ \text { (see Proposition A2 of [13])}. \end{aligned}$$

We conclude that

${\mathcal {L}} \ne \emptyset$ and $S_\lambda \subseteq \mathrm{int \,}C_+$ for all $\lambda >0$.

$\square$

The next proposition establishes a structural property of the set ${\mathcal {L}}$, namely that it is connected.

Proposition 7

If hypotheses $H_0$, $H_1$ hold, $\lambda \in {\mathcal {L}}$ and $0<\mu <\lambda$, then $\mu \in {\mathcal {L}}$.

Proof

Let $u_\lambda \in S_\lambda \subseteq \mathrm{int \,}C_+$. From Proposition 5 we know that ${\overline{u}}_\sigma \rightarrow 0$ in $C_0^1({\overline{\Omega }})$ as $\sigma \rightarrow 0^+$. So, we can find $\sigma \in (0,\mu )$ small such that

$$\begin{aligned} {\overline{u}}_\sigma \le \min \{\delta ,u_\lambda \} \quad \text { (recall } u_\lambda \in \mathrm{int \,}C_+\text {)}. \end{aligned}$$

We introduce the Carathéodory function ${\widehat{g}}_\mu (z,x)$ defined by

$$\begin{aligned} {\widehat{g}}_\mu (z,x)={\left\{ \begin{array}{ll}\mu [{\overline{u}}_\sigma (z)^{-\eta (z)}+ {\overline{u}}_\sigma (z)^{\tau (z)-1}]+f(z,{\overline{u}}_\sigma (z))&{} \text { if }x< {\overline{u}}_\sigma (z),\\ \mu [x^{-\eta (z)}+ x^{\tau (z)-1}]+f(z,x) &{} \text { if }{\overline{u}}_\sigma (z)\le x \le u_\lambda (z),\\ \mu [u_\lambda (z)^{-\eta (z)}+ u_\lambda (z)^{\tau (z)-1}]+f(z,u_\lambda (z))&{} \text { if }u_\lambda (z)<x.\end{array}\right. }\nonumber \\ \end{aligned}$$

(42)

We set ${\widehat{G}}_\mu (z,x)=\int _0^x {\widehat{g}}_\mu (z,s)ds$ and consider the $C^1$-functional ${\widehat{\psi }}_\mu :W_0^{1,p(z)}(\Omega )\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned}{} & {} {\widehat{\psi }}_\mu (u)=\int _\Omega \frac{1}{p(z)}|\nabla u|^{p(z)}\mathrm{{d}}z+\int _\Omega \frac{1}{q(z)}|\nabla u|^{q(z)}\mathrm{{d}}z\\{} & {} -\int _\Omega {\widehat{G}}_\mu (z,u)dz \text { for all } u \in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

From (42) and Proposition 2, it is clear that ${\widehat{\psi }}_\mu (\cdot )$ is coercive. Also, it is sequentially weakly lower semicontinuous (see Proposition 1). Then by the Weierstrass-Tonelli theorem, we can find $u_\mu \in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned}&{\widehat{\psi }}_\mu (u_\mu )=\inf \left[ {\widehat{\psi }}_\mu (u) \, :\, u \in W^{1,p(z)}_0(\Omega )\right] ,\nonumber \\ \Rightarrow \quad&\langle {\widehat{\psi }}_\mu ^\prime (u_\mu ),h\rangle =0 \text { for all } h \in W^{1,p(z)}_0(\Omega ). \end{aligned}$$

(43)

In (43) first we use the test function $h=({\overline{u}}_\sigma -u_\mu )^+ \in W^{1,p(z)}_0(\Omega )$. We have

$$\begin{aligned}&\langle V(u_\mu ),({\overline{u}}_\sigma -u_\mu )^+ \rangle \\&=\int _\Omega (\mu [{\overline{u}}_\sigma ^{-\eta (z)}+{\overline{u}}_\sigma ^{\tau (z)-1} ]+f(z,{\overline{u}}_\sigma ))({\overline{u}}_\sigma -u_\mu )^+\mathrm{{d}}z \text { (see } (42)\text {)}\\&\ge \int _\Omega \mu \, {\overline{u}}_\sigma ^{\tau (z)-1} ({\overline{u}}_\sigma -u_\mu )^+\mathrm{{d}}z \text { (because } 0\le {\overline{u}}_\sigma (z)\le \delta , z \in {\overline{\Omega }}, \text {use}\, H_1(iv)\text {)}\\&\ge \int _\Omega \sigma \, {\overline{u}}_\sigma ^{\tau (z)-1} ({\overline{u}}_\sigma -u_\mu )^+\mathrm{{d}}z \text { (since } \sigma < \mu \text {)}\\&= \langle V({\overline{u}}_\sigma ),({\overline{u}}_\sigma -u_\mu )^+ \rangle \text { (see Proposition } 5\text {)},\\ \Rightarrow \quad&{\overline{u}}_\sigma \le u_\mu . \end{aligned}$$

Next in (43) we choose the test function $h=(u_\mu -u_\lambda )^+ \in W^{1,p(z)}_0(\Omega )$. We have

$$\begin{aligned}&\langle V(u_\mu ),(u_\mu -u_\lambda )^+ \rangle \\&=\int _\Omega (\mu [u_\lambda ^{-\eta (z)}+u_\lambda ^{\tau (z)-1}]+f(z,u_\lambda ))(u_\mu -u_\lambda )^+\mathrm{{d}}z \text { (see } (42)\text {)}\\&\le \int _\Omega (\lambda [u_\lambda ^{-\eta (z)}+u_\lambda ^{\tau (z)-1} ]+f(z,u_\lambda ))(u_\mu -u_\lambda )^+dz \text { (since } \mu < \lambda \text {)}\\&= \langle V(u_\lambda ),(u_\mu -u_\lambda )^+ \rangle \text { (since } u_\lambda \in S_\lambda \text {)},\\ \Rightarrow \quad&u_\mu \le u_\lambda \text { (see Proposition } 4\text {)}. \end{aligned}$$

So, we have proved that

$$\begin{aligned} u_\mu \in [{\overline{u}}_\sigma ,u_\lambda ]. \end{aligned}$$

(44)

Then from (44), (42) and (43) it follows that

$u_\mu \in S_\mu \subseteq \mathrm{int \,}C_+$ and so $\mu \in {\mathcal {L}}$.

$\square$

A quick inspection of the above proof reveals that we get, as a useful byproduct of it, the following corollary.

Corollary 1

If hypotheses $H_0$, $H_1$ hold, $\lambda \in {\mathcal {L}}$, $u_\lambda \in S_\lambda \subseteq \mathrm{int \,}C_+$ and $\mu \in (0,\lambda )$, then $\mu \in {\mathcal {L}}$ and there exists $u_\mu \in S_\mu \subseteq \mathrm{int \,}C_+$ such that $u_\mu \le u_\lambda$.

In fact with little additional effort, we can improve the above “monotonicity” property of the solution multifunction $\lambda \rightarrow S_\lambda$.

Proposition 8

If hypotheses $H_0$, $H_1$ hold, $\lambda \in {\mathcal {L}}$, $u_\lambda \in S_\lambda \subseteq \mathrm{int \,}C_+$ and $\mu \in (0,\lambda )$, then $\mu \in {\mathcal {L}}$ and there exists $u_\mu \in S_\mu \subseteq \mathrm{int \,}C_+$ such that $u_\lambda -u_\mu \in \mathrm{int \,}C_+$.

Proof

From Corollary 1 we already know that $\mu \in {\mathcal {L}}$ and there exists $u_\mu \in S_\mu \subseteq \mathrm{int \,}C_+$ such that

$$\begin{aligned} u_\mu \le u_\lambda . \end{aligned}$$

Let $\rho =\Vert u_\lambda \Vert _\infty$ and let ${\widehat{\xi }}_\rho >0$ be as postulated by hypothesis $H_1(iv)$. We have

$$\begin{aligned}&-\Delta _{p(z)}u_\mu -\Delta _{q(z)}u_\mu +{\widehat{\xi }}_\rho u_\mu ^{p(z)-1}-\lambda u_\mu ^{-\eta (z)}\nonumber \\&\le \lambda u_\lambda ^{\tau (z)-1}+f(z,u_\lambda )+{\widehat{\xi }}_\rho u_\lambda ^{p(z)-1} \text { (see hypothesis } H_1(iv)\text {)}\nonumber \\&=-\Delta _{p(z)}u_\lambda -\Delta _{q(z)}u_\lambda +{\widehat{\xi }}_\rho u_\lambda ^{p(z)-1}-\lambda u_\lambda ^{-\eta (z)}. \end{aligned}$$

(45)

Since $u_\mu \in \mathrm{int \, } C_+$, we see that $0 \prec (\lambda -\mu )u_\mu ^{\tau (z)-1}$. Hence from (45) and Proposition 2.3 of Papageorgiou-Winkert [13], we obtain

$$\begin{aligned} u_\lambda -u_\mu \in \mathrm{int \,}C_+. \end{aligned}$$

$\square$

From the proof of Proposition 7, we know that for $\sigma \in (0,\mu )$ small, we have

$$\begin{aligned} u_\mu \in [{\overline{u}}_\sigma ,u_\lambda ] \quad \text { (see } (44)\text {)}. \end{aligned}$$

In fact using Proposition 8, we can improve this.

Proposition 9

If hypotheses $H_0$, $H_1$ hold, $\lambda \in {\mathcal {L}}$, $u_\lambda \in S_\lambda \subseteq \mathrm{int \,}C_+$ and $\mu \in (0,\lambda )$, then we can find $u_\mu \in S_\mu \subseteq \mathrm{int \,}C_+$ and $\sigma \in (0,\mu )$ small such that $u_\mu \in \textrm{int}_{C_0^1({\overline{\Omega }})}[{\overline{u}}_\sigma ,u_\lambda ]$.

Proof

From Proposition 8, we already know that there exists $u_\mu \in S_\mu \subseteq \mathrm{int \,}C_+$ such that

$$\begin{aligned} u_\lambda -u_\mu \in \mathrm{int \,}C_+. \end{aligned}$$

(46)

Also if $\sigma \in (0,\mu )$ is small, we have ${\overline{u}}_\sigma \le \min \{\delta ,u_\mu \}$ (see Proposition 5). Let $\rho =\Vert u_\mu \Vert _\infty$ and let ${\widehat{\xi }}_\rho >0$ be as postulated by hypothesis $H_1(iv)$. We have

$$\begin{aligned}&-\Delta _{p(z)}{\overline{u}}_\sigma -\Delta _{q(z)}{\overline{u}}_\sigma +{\widehat{\xi }}_\rho {\overline{u}}_\sigma ^{p(z)-1}-\mu {\overline{u}}_\sigma ^{-\eta (z)}\nonumber \\&\le \sigma {\overline{u}}_\sigma ^{\tau (z)-1}+{\widehat{\xi }}_\rho {\overline{u}}_\sigma ^{p(z)-1}+f(z,{\overline{u}}_\sigma ) \quad \text { (since } {\overline{u}}_\sigma \le \delta , \text { see } H_1(iv)\text {)}\nonumber \\&\le \mu u_\mu ^{\tau (z)-1}+{\widehat{\xi }}_\rho u_\mu ^{p(z)-1}+f(z,u_\mu ) \quad \text { (see } H_1(iv)\text {)}\nonumber \\&=-\Delta _{p(z)}u_\mu -\Delta _{q(z)}u_\mu +{\widehat{\xi }}_\rho u_\mu ^{p(z)-1}-\mu u_\mu ^{-\eta (z)}. \end{aligned}$$

(47)

Since ${\overline{u}}_\sigma \in \mathrm{int \, } C_+$, on account of hypothesis $H_1(iv)$, we have

$$\begin{aligned} 0 \prec f(\cdot , {\overline{u}}_\sigma (\cdot )). \end{aligned}$$

So, from (47) and Proposition 2.3 of Papageorgiou-Winkert [13], we infer that

$$\begin{aligned} u_\mu -{\overline{u}}_\sigma \in \mathrm{int \,}C_+. \end{aligned}$$

(48)

Then (46) and (48) imply that

$$\begin{aligned} u_\mu \in \textrm{int}_{C_0^1({\overline{\Omega }})}[{\overline{u}}_\sigma ,u_\lambda ]. \end{aligned}$$

$\square$

Let ${\widehat{\lambda }}=\sup {\mathcal {L}}.$

Proposition 10

If hypotheses $H_0$, $H_1$ hold, then ${\widehat{\lambda }}<+\infty$.

Proof

Hypotheses $H_1(i),(ii),(iv)$ imply that we can find $\lambda _0>0$ such that

$$\begin{aligned} \lambda _0 x^{\tau (z)-1}+f(z,x)\ge x^{p(z)-1} \text { for a.a. } z \in \Omega , \text { all } x \ge 0. \end{aligned}$$

(49)

Let $\lambda >\lambda _0$ and suppose that $\lambda \in {\mathcal {L}}$. Then we can find $u_\lambda \in S_\lambda \subseteq \mathrm{int \,}C_+$ (see Proposition 6). Let $\Omega _0\subseteq \Omega$ be an open subset with $C^2$-boundary $\partial \Omega _0$ and such that ${\overline{\Omega }}_0 \subseteq \Omega$. We define

$$\begin{aligned} 0<m_0=\min \limits _{{\overline{\Omega }}_0}u_\lambda \quad \text { (since } u_\lambda \in \text { int }C_+). \end{aligned}$$

For $\varepsilon >0$, let $m_0^\varepsilon =m_0+\varepsilon$. Also, let $\rho = \max \{ \Vert u_\lambda \Vert _\infty ,m_0^\varepsilon \}$ and take ${\widehat{\xi }}_\rho >0$ as postulated by hypothesis $H_1(iv)$. We have

$$\begin{aligned}&-\Delta _{p(z)}m_0^\varepsilon -\Delta _{q(z)}m_0^\varepsilon +{\widehat{\xi }}_\rho (m_0^\varepsilon )^{p(z)-1}-\lambda (m_0^\varepsilon )^{-\eta (z)}\nonumber \\&\le {\widehat{\xi }}_\rho (m_0)^{p(z)-1} +\chi (\varepsilon ) \text { with } \chi (\varepsilon ) \rightarrow 0 \text { as } \varepsilon \rightarrow 0^+\nonumber \\&\le [ {\widehat{\xi }}_\rho +1] m_0^{p(z)-1}+\chi (\varepsilon )\nonumber \\&\le \lambda _0 m_0^{\tau (z)-1}+f(z,m_0)+{\widehat{\xi }}_\rho m_0^{p(z)-1}+(\lambda -\lambda _0)m_0^{\tau (z)-1}+\chi (\varepsilon ) \text { (see } (49)\text {)}\nonumber \\&\le \lambda u_\lambda ^{\tau (z)-1}+f(z,u_\lambda )+{\widehat{\xi }}_\rho u_\lambda ^{p(z)-1} \text { (see } H_1(iv)\text {)}\nonumber \\&=-\Delta _{p(z)}u_\lambda -\Delta _{q(z)}u_\lambda +{\widehat{\xi }}_\rho u_\lambda ^{p(z)-1}-\lambda u_\lambda ^{-\eta (z)} \text { in } \Omega _0. \end{aligned}$$

(50)

For $\varepsilon >0$ small, we have

$$\begin{aligned} 0<{\widehat{c}}\le (\lambda -\lambda _0)m_0^{\tau (z)-1}-\chi (\varepsilon ). \end{aligned}$$

So, from (50) and Proposition 2.3 of [13] (see also Proposition A4 of [19]), we obtain

$$\begin{aligned} m_0^\varepsilon < u_\lambda (z) \text { for all }z \in \Omega _0, \end{aligned}$$

a contradiction. Therefore ${\widehat{\lambda }}\le \lambda _0 < +\infty$. $\square$

If $\lambda \in (0,{\widehat{\lambda }})$, then we have multiplicity of positive solutions.

Proposition 11

If hypotheses $H_0$, $H_1$ hold and $\lambda \in (0,{\widehat{\lambda }})$, then problem ($P_\lambda$) has at least two positive solutions $u_0, {\widehat{u}} \in \mathrm{int \,}C_+$.

Proof

Let $\beta \in (\lambda ,{\widehat{\lambda }})$ and $\sigma \in (0,\lambda )$ small such that $\Vert {\overline{u}}_\sigma \Vert _\infty \le \delta$ (see Proposition 5). From the previous results, we know that for $u_\beta \in S_\beta \subseteq \mathrm{int \,}C_+$, we can find $u_0 \in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned} u_0 \in S_\lambda \subseteq \mathrm{int \,}C_+, \, u_0 \in \textrm{int}_{C_0^1({\overline{\Omega }})}[{\overline{u}}_\sigma ,u_\beta ]. \end{aligned}$$

(51)

As in the proof of Proposition 7, truncating the reaction at $\{{\overline{u}}_\sigma (z),u_\beta (z)\}$ (see (42)) and introducing the corresponding $C^1$-energy functional ${\widehat{\psi }}_\lambda (\cdot )$, via the direct method of the Calculus of Variations, we produce $u_0$ a global minimizer of ${\widehat{\psi }}_\lambda (\cdot )$.

Also, we introduce the following Carathéodory function

$$\begin{aligned} {\widehat{e}}_\lambda (z,x)={\left\{ \begin{array}{ll}\lambda [{\overline{u}}_\sigma (z)^{-\eta (z)}+ {\overline{u}}_\sigma (z)^{\tau (z)-1}]+f(z,{\overline{u}}_\sigma (z))&{} \text { if }x \le {\overline{u}}_\sigma (z),\\ \lambda [x^{-\eta (z)}+ x^{\tau (z)-1}]+f(z,x) &{} \text { if }{\overline{u}}_\sigma (z)<x.\end{array}\right. } \end{aligned}$$

(52)

We set ${\widehat{E}}_\lambda (z,x)=\int _0^x {\widehat{e}}_\lambda (z,s)ds$ and introduce the $C^1$-functional ${\widehat{\varphi }}_\lambda :W_0^{1,p(z)}(\Omega )\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned}{} & {} {\widehat{\varphi }}_\lambda (u)=\int _\Omega \frac{1}{p(z)}|\nabla u|^{p(z)}\mathrm{{d}}z+\int _\Omega \frac{1}{q(z)}|\nabla u|^{q(z)}\mathrm{{d}}z\\{} & {} -\int _\Omega {\widehat{E}}_\lambda (z,u)\mathrm{{d}}z \text { for all } u \in W_0^{1,p(z)}(\Omega ). \end{aligned}$$

From (42) and (52), we see that

$$\begin{aligned} {\widehat{\psi }}_\lambda \Big |_{[{\overline{u}}_\sigma ,u_\beta ]}= {\widehat{\varphi }}_\lambda \Big |_{[{\overline{u}}_\sigma ,u_\beta ]}. \end{aligned}$$

Recall that $u_0 \in \mathrm{int \,}C_+$ is a global minimizer of ${\widehat{\psi }}_\lambda (\cdot )$. Then from (51) it follows that

$$\begin{aligned}&u_0 \text { is a local } C_0^1({\overline{\Omega }})-\text { minimizer of } {\widehat{\varphi }}_\lambda (\cdot ), \nonumber \\ \Rightarrow \quad&u_0 \text { is a local } W_0^{1,p(z)}(\Omega )-\text { minimizer of } {\widehat{\varphi }}_\lambda (\cdot )\nonumber \\&\text { (see [13], Proposition A3)}. \end{aligned}$$

(53)

Using (52) we can easily check that

$$\begin{aligned} K_{{\widehat{\varphi }}_\lambda }\subseteq [{\overline{u}}_\sigma ) \cap \mathrm{int \,}C_+. \end{aligned}$$

(54)

Then (54) and (52) imply that we may assume that $K_{{\widehat{\varphi }}_\lambda }$ is finite or otherwise we already have an infinity of positive smooth solutions of ($P_\lambda$) and so we are done. So, we have that $K_{{\widehat{\varphi }}_\lambda }$ is finite and this fact together with (53) and Theorem 5.7.6, p. 449, of Papageorgiou–Rădulescu–Repovš [18] imply that we can find $\rho \in (0,1)$ small such that

$$\begin{aligned} {\widehat{\varphi }}_\lambda (u_0)<\inf \left[ {\widehat{\varphi }}_\lambda (u) :\, \Vert u -u_0\Vert =\rho \right] ={\widehat{m}}_\lambda . \end{aligned}$$

(55)

On account of hypothesis $H_1(ii)$, we see that if $u \in \mathrm{int \,}C_+$ then

$$\begin{aligned} {\widehat{\varphi }}_\lambda (tu)\rightarrow -\infty \text { as }t \rightarrow +\infty . \end{aligned}$$

(56)

Moreover, using (52) and arguing as in the proof of Proposition 7 (see the “Claim”), we show that

$$\begin{aligned} {\widehat{\varphi }}_\lambda (\cdot ) \text { satisfies the } C\!\!-\!\text {condition.} \end{aligned}$$

(57)

Then (55), (56) and (57) permit the use of the mountain pass theorem. We can find ${\widehat{u}}\in W_0^{1,p(z)}(\Omega )$ such that

$$\begin{aligned}&{\widehat{u}}\in K_{{\widehat{\varphi }}_\lambda }\subseteq [{\overline{u}}_\sigma ) \cap \mathrm{int \,}C_+ \text { (see } (54)\text {)}, \\&{\widehat{\varphi }}_\lambda (u_0)<m_\lambda \le {\widehat{\varphi }}_\lambda ({\widehat{u}}) \text { (see } (55)\text {)}. \end{aligned}$$

So, ${\widehat{u}}\ne u_0$, ${\widehat{u}}\ne 0$ and ${\widehat{u}}\in \mathrm{int \,}C_+$ is the second positive solution of problem ($P_\lambda$) with $\lambda \in (0,{\widehat{\lambda }})$. $\square$

Finally we check the admissibility of the critical parameter ${\widehat{\lambda }}>0$.

Proposition 12

If hypotheses $H_0$, $H_1$ hold, then ${\widehat{\lambda }} \in {\mathcal {L}}$.

Proof

Let $\{ \lambda _n \}_{n \in {\mathbb {N}}}\subseteq {\mathcal {L}}$ be such that $\lambda _n \uparrow {\widehat{\lambda }}$. We can find $u_n \in S_{\lambda _n}\subseteq \mathrm{int \,}C_+$ which are minimizers of ${\widehat{\psi }}_{\lambda _n}(\cdot )$ (truncation at ${\overline{u}}_\sigma$ for $\sigma \in (0,\lambda _n)$ small and at $u_\beta \in S_{\beta }\subseteq \mathrm{int \,}C_+$ with $\beta \in (\lambda _n,{\widehat{\lambda }} )$) and so

$$\begin{aligned} {\widehat{\psi }}_{\lambda _n}(u_n)&\le {\widehat{\psi }}_{\lambda _n}({\overline{u}}_\sigma )\\&=\int _\Omega \frac{1}{p(z)}|\nabla {\overline{u}}_\sigma |^{p(z)}\mathrm{{d}}z+\int _\Omega \frac{1}{q(z)}|\nabla {\overline{u}}_\sigma |^{q(z)}\mathrm{{d}}z \\&- \int _\Omega \left( \lambda _n [{\overline{u}}_\sigma ^{1-\eta (z)}+ {\overline{u}}_\sigma ^{\tau (z)}]+f(z,{\overline{u}}_\sigma ) {\overline{u}}_\sigma \right) dz \text { (see } (42)\text {)}\\&\le \rho _p(\nabla {\overline{u}}_\sigma )+\rho _q(\nabla {\overline{u}}_\sigma )-\lambda \rho _\tau ( {\overline{u}}_\sigma )-{\widehat{\eta }} \text { with } {\widehat{\eta }}\in (0,+\infty )\\&\le \rho _p(\nabla {\overline{u}}_\sigma )+\rho _q(\nabla {\overline{u}}_\sigma )-\sigma \rho _\tau ( {\overline{u}}_\sigma )-{\widehat{\eta }} \text { (since } \sigma \in (0,\lambda )\text {)}\\&= - {\widehat{\eta }}<0 \text { (see Proposition } 5\text {)},\\ \Rightarrow \quad&{\widehat{\varphi }}_{\lambda _n}(u_n)<0 \text { (since } {\widehat{\psi }}_{\lambda _n}\Big |_{[{\overline{u}}_\sigma ,u_\beta ]}= {\widehat{\varphi }}_{\lambda _n}\Big |_{[{\overline{u}}_\sigma ,u_\beta ]}). \end{aligned}$$

Also, we have ${\widehat{\varphi }}_{\lambda _n}^\prime (u_n)=0$ in $W^{-1,p^\prime (z)}(\Omega )$ for all $n \in {\mathbb {N}}$. Then as in the proof of Proposition 7 (see the “Claim”), we obtain

$$\begin{aligned} u_n \rightarrow u_*\text { in } W_0^{1,p(z)}(\Omega ) \text { as } n \rightarrow +\infty . \end{aligned}$$

We have

$$\begin{aligned}&\langle {\widehat{\varphi }}_{\lambda _n}^\prime (u_n),h\rangle =0 \text { for all } h \in W^{1,p(z)}_0(\Omega ), \text { all } n \in {\mathbb {N}}, \\ \Rightarrow \quad&\langle V(u_n),h\rangle =\int _\Omega {\widehat{e}}_{\lambda _n}(z,u_n)hdz,\\ \Rightarrow \quad&\langle V(u_*),h\rangle =\int _\Omega {\widehat{e}}_{{\widehat{\lambda }}}(z,u_*)hdz \text { for all } h \in W^{1,p(z)}_0(\Omega ). \end{aligned}$$

Also we have ${\overline{u}}_\sigma \le u_n$ for all $n \in {\mathbb {N}}$ and so ${\overline{u}}_\sigma \le u_*$ which means that $u_*\in S_{{\widehat{\lambda }}}\subseteq \mathrm{int \,}C_+$, hence ${\widehat{\lambda }}\in {\mathcal {L}}$. $\square$

We have proved that

$$\begin{aligned} {\mathcal {L}}=(0,{\widehat{\lambda }}]. \end{aligned}$$

We can state the following global existence and multiplicity theorem of problem ($P_\lambda$) (bifurcation-type theorem).

Theorem 1

If hypotheses $H_0$, $H_1$ hold, then there exists ${\widehat{\lambda }}>0$ such that:

• (a) for all $\lambda \in (0,{\widehat{\lambda }})$ problem ($P_\lambda$) has at least two positive solutions $u_0,{\widehat{u}} \in \mathrm{int \,}C_+$;

• (b) for $\lambda ={\widehat{\lambda }}$ problem ($P_\lambda$) has at least one positive solution $u_*\in \mathrm{int \,}C_+$;

• (c) for all $\lambda >{\widehat{\lambda }}$ problem ($P_\lambda$) has no positive solution.